Fracture flow using a MultiApp approach: Diffusion in mixed dimensions

Background

PorousFlow can be used to simulate flow through fractured porous media in the case when the fracture network is so complicated it cannot be incorporated into the porous-media mesh. The fundamental premise is the fractures can be considered as lower dimensional entities within the higher-dimensional porous media. This page is part of a set that describes a MOOSE MultiApp approach to simulating such models:

The diffusion equation with a mixed-dimensional problem

In this section, the diffusion equation is used to explore a mixed-dimensional problem, where the fracture is a 1D line "living inside" the 2D matrix. In reality, the fracture has a certain aperture, , but it is so small that it may be approximated by a 1D line in MOOSE and its kernels multiplied by : see mathematics and physical interpretation.

Geometry and mesh

Two cases are explored: "conforming" and "nonconforming". In the conforming case, all fracture nodes are also matrix nodes: the fracture elements are actually created from a sideset of the 2D matrix elements. The conforming case is shown in Figure 1 and Figure 2: the solution domain consists of the fracture subdomain (1D red line) and the matrix subdomain (in blue), which share nodes. In the nonconforming case, no fracture nodes coincide with matrix nodes. The nonconforming case is shown in Figure 3.

Figure 1: The geometry of the conforming case, where the red line is the fracture

Figure 2: The matrix mesh in the conforming case: the fracture lies exactly on the matrix nodes

Figure 3: The matrix mesh in the nonconforming case, where the red line is the fracture

The conforming case is explored using a non-MultiApp approach and a MultiApp approach, while the nonconforming case can only be explored using a MultiApp approach.

In all cases, the finite-element mesh dictates the spatial resolution of the numerical solution, and the analysis that follows ignores this by using the same spatial resolution in each model. However, it is important to remember that in practice, the use of finite elements means the solution is never "exact". For instance, using large matrix elements will probably lead to poor results. Further discussion may be found in the small fracture network example. Large elements also produce more noticeable overshoots and undershoots in the solution, which may be observed in the current models if the matrix ny is too small.

Physics

As described in the mathematical background, the physics is governed by

(1)

The two variables, and , are called frac_T and matrix_T in the MOOSE input files. Each obeys a diffusion equation, with heat transfer between the two variables, as written in the Eq. (1). The heat-transfer coefficient, , may be written

(2)

When using a MultiApp, the fracture appears as a set of Dirac sources in the matrix subdomain:

where

In the MultiApp approach, is generated as an AuxVariable by the fracture App, so exists only in the fracture subdomain. It is then passed to the matrix App, and applied as a DiracKernel.

The boundary conditions are "no flow", except for the very left-hand side of the fracture domain, where temperature is fixed at . The initial conditions are .

Each of the heat capacities are unity, , the conductivity in the fracture is , and is in the matrix. The fracture has aperture .

Assume that . This is the heat-transfer coefficient to use in the conforming case, since the matrix nodes align exactly with the fracture. Eq. (2) may be used for the nonconforming case. In this situation and , so .

Each simulation runs with end_time = 100.

No MultiApp: the benchmark

In the conforming case, a MultiApp approach need not be taken, and the Kernels (given by Eq. (1)) are:

[Kernels<<<{"href": "../../syntax/Kernels/index.html"}>>>]
  [dot_frac_T]
    type = CoefTimeDerivative<<<{"description": "The time derivative operator with the weak form of $(\\psi_i, \\frac{\\partial u_h}{\\partial t})$.", "href": "../../source/kernels/CoefTimeDerivative.html"}>>>
    Coefficient<<<{"description": "The coefficient for the time derivative kernel"}>>> = 1E-2
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = frac_T
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = fracture
  []
  [fracture_diffusion]
    type = AnisotropicDiffusion<<<{"description": "Anisotropic diffusion kernel $\\nabla \\cdot -\\widetilde{k} \\nabla u$ with weak form given by $(\\nabla \\psi_i, \\widetilde{k} \\nabla u)$.", "href": "../../source/kernels/AnisotropicDiffusion.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = frac_T
    tensor_coeff<<<{"description": "The Tensor to multiply the Diffusion operator by"}>>> = '1E-2 0 0 0 1E-2 0 0 0 1E-2'
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = fracture
  []
  [toMatrix]
    type = PorousFlowHeatMassTransfer<<<{"description": "Calculate heat or mass transfer from a coupled variable v to the variable u. No mass lumping is performed here.", "href": "../../source/kernels/PorousFlowHeatMassTransfer.html"}>>>
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = fracture
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = frac_T
    v<<<{"description": "The variable which is tranfsered to u using a transfer coefficient"}>>> = matrix_T
    transfer_coefficient<<<{"description": "Transfer coefficient for heat or mass transferred between variables"}>>> = 0.02
  []
  [dot_matrix_T]
    type = TimeDerivative<<<{"description": "The time derivative operator with the weak form of $(\\psi_i, \\frac{\\partial u_h}{\\partial t})$.", "href": "../../source/kernels/TimeDerivative.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = matrix_T
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = matrix
  []
  [matrix_diffusion]
    type = AnisotropicDiffusion<<<{"description": "Anisotropic diffusion kernel $\\nabla \\cdot -\\widetilde{k} \\nabla u$ with weak form given by $(\\nabla \\psi_i, \\widetilde{k} \\nabla u)$.", "href": "../../source/kernels/AnisotropicDiffusion.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = matrix_T
    tensor_coeff<<<{"description": "The Tensor to multiply the Diffusion operator by"}>>> = '1E-3 0 0 0 1E-3 0 0 0 1E-3'
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = matrix
  []
  [fromFracture]
    type = PorousFlowHeatMassTransfer<<<{"description": "Calculate heat or mass transfer from a coupled variable v to the variable u. No mass lumping is performed here.", "href": "../../source/kernels/PorousFlowHeatMassTransfer.html"}>>>
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = fracture
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = matrix_T
    v<<<{"description": "The variable which is tranfsered to u using a transfer coefficient"}>>> = frac_T
    transfer_coefficient<<<{"description": "Transfer coefficient for heat or mass transferred between variables"}>>> = 0.02
  []
[]
(modules/porous_flow/examples/multiapp_fracture_flow/fracture_diffusion/no_multiapp.i)

Evaluating the fromFracture heat transfer Kernel only on block = fracture implements the Dirac delta function in Eq. (1). The matrix temperature is shown in Figure 4

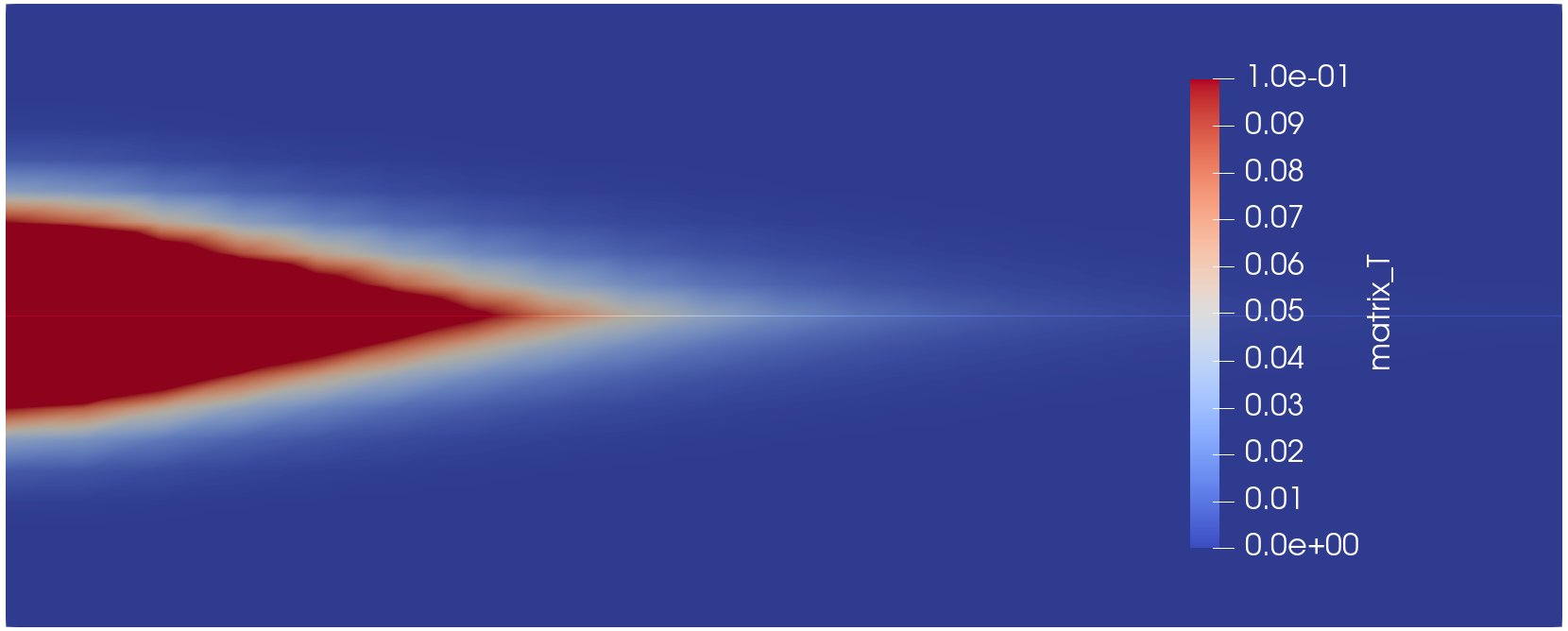
Figure 4: Benchmark matrix temperature at the end of simulation

The solution of this problem is exactly solvable in terms of error functions, and by choosing appropriate time-step and element sizes, MOOSE produces the expected result. Some examples of how MOOSE's solution depends upon time-step size are shown in Figure 5. Evidently, reducing the time-step below 10.0 does not impact the solution very much. Hence, the solution using is used as the benchmark for the remainder of this section.

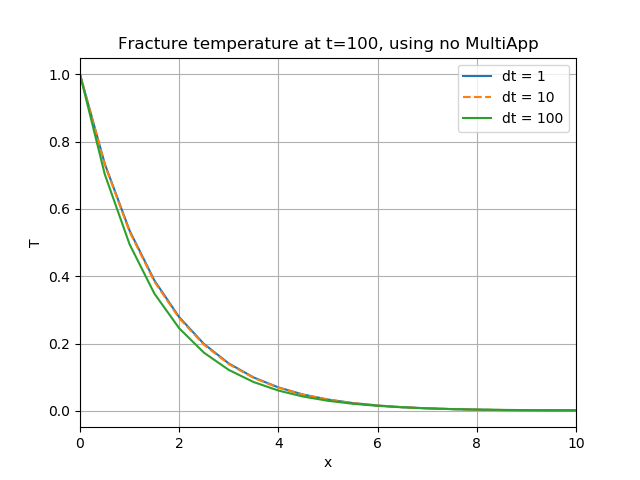
Figure 5: Impact of time-step size on the fracture temperature at the end of the simulation

A MultiApp approach for the conforming case

In this case, the matrix App is the main App, and the fracture App is the subApp. The fracture input file has the following features.

  • An AuxVariable called transferred_matrix_T that is interpolated to the fracture mesh.

  • An AuxVariable called joules_per_s that is the heat rate coming from each node. Mathematically this is , where is the "volume" modelled by the fracture node. This is populated by the save_in feature:

[Kernels<<<{"href": "../../syntax/Kernels/index.html"}>>>]
  [dot_frac_T]
    type = CoefTimeDerivative<<<{"description": "The time derivative operator with the weak form of $(\\psi_i, \\frac{\\partial u_h}{\\partial t})$.", "href": "../../source/kernels/CoefTimeDerivative.html"}>>>
    Coefficient<<<{"description": "The coefficient for the time derivative kernel"}>>> = 1E-2
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = frac_T
  []
  [fracture_diffusion]
    type = AnisotropicDiffusion<<<{"description": "Anisotropic diffusion kernel $\\nabla \\cdot -\\widetilde{k} \\nabla u$ with weak form given by $(\\nabla \\psi_i, \\widetilde{k} \\nabla u)$.", "href": "../../source/kernels/AnisotropicDiffusion.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = frac_T
    tensor_coeff<<<{"description": "The Tensor to multiply the Diffusion operator by"}>>> = '1E-2 0 0 0 1E-2 0 0 0 1E-2'
  []
  [toMatrix]
    type = PorousFlowHeatMassTransfer<<<{"description": "Calculate heat or mass transfer from a coupled variable v to the variable u. No mass lumping is performed here.", "href": "../../source/kernels/PorousFlowHeatMassTransfer.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = frac_T
    v<<<{"description": "The variable which is tranfsered to u using a transfer coefficient"}>>> = transferred_matrix_T
    transfer_coefficient<<<{"description": "Transfer coefficient for heat or mass transferred between variables"}>>> = 0.02
    save_in<<<{"description": "The name of auxiliary variables to save this Kernel's residual contributions to.  Everything about that variable must match everything about this variable (the type, what blocks it's on, etc.)"}>>> = joules_per_s
  []
[]
(modules/porous_flow/examples/multiapp_fracture_flow/fracture_diffusion/fracture_app_dirac.i)

  • A NodalValueSampler VectorPostprocessor that captures all the joules_per_s values at each fracture node

[VectorPostprocessors<<<{"href": "../../syntax/VectorPostprocessors/index.html"}>>>]
  [heat_transfer_rate]
    type = NodalValueSampler<<<{"description": "Samples values of nodal variable(s).", "href": "../../source/vectorpostprocessors/NodalValueSampler.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = none
    sort_by<<<{"description": "What to sort the samples by"}>>> = id
    variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = joules_per_s
  []
  [frac_T]
    type = NodalValueSampler<<<{"description": "Samples values of nodal variable(s).", "href": "../../source/vectorpostprocessors/NodalValueSampler.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = frac_T
    sort_by<<<{"description": "What to sort the samples by"}>>> = x
    variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = frac_T
  []
[]
(modules/porous_flow/examples/multiapp_fracture_flow/fracture_diffusion/fracture_app_dirac.i)

The matrix input file has the following features

  • Transfers that send to the fracture App, and receive the joules_per_s from the fracture App

[Transfers<<<{"href": "../../syntax/Transfers/index.html"}>>>]
  [T_to_fracture]
    type = MultiAppGeometricInterpolationTransfer<<<{"description": "Transfers the value to the target domain from a combination/interpolation of the values on the nearest nodes in the source domain, using coefficients based on the distance to each node.", "href": "../../source/transfers/MultiAppGeometricInterpolationTransfer.html"}>>>
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = fracture_app
    source_variable<<<{"description": "The variable to transfer from."}>>> = matrix_T
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = transferred_matrix_T
  []
  [heat_from_fracture]
    type = MultiAppReporterTransfer<<<{"description": "Transfers reporter data between two applications.", "href": "../../source/transfers/MultiAppReporterTransfer.html"}>>>
    from_multi_app<<<{"description": "The name of the MultiApp to receive data from"}>>> = fracture_app
    from_reporters<<<{"description": "List of the reporter names (object_name/value_name) to transfer the value from."}>>> = 'heat_transfer_rate/joules_per_s heat_transfer_rate/x heat_transfer_rate/y heat_transfer_rate/z'
    to_reporters<<<{"description": "List of the reporter names (object_name/value_name) to transfer the value to."}>>> = 'heat_transfer_rate/transferred_joules_per_s heat_transfer_rate/x heat_transfer_rate/y heat_transfer_rate/z'
  []
[]
(modules/porous_flow/examples/multiapp_fracture_flow/fracture_diffusion/matrix_app_dirac.i)

  • This latter Transfer writes its information into a VectorPostprocessor in the matrix App. That is then converted to a Dirac source by a ReporterPointSource DiracKernel:

[DiracKernels<<<{"href": "../../syntax/DiracKernels/index.html"}>>>]
  [heat_from_fracture]
    type = ReporterPointSource<<<{"description": "Apply a point load defined by Reporter.", "href": "../../source/dirackernels/ReporterPointSource.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = matrix_T
    value_name<<<{"description": "reporter value name.  This uses the reporter syntax <reporter>/<name>."}>>> = heat_transfer_rate/transferred_joules_per_s
    x_coord_name<<<{"description": "reporter x-coordinate name.  This uses the reporter syntax <reporter>/<name>."}>>> = heat_transfer_rate/x
    y_coord_name<<<{"description": "reporter y-coordinate name.  This uses the reporter syntax <reporter>/<name>."}>>> = heat_transfer_rate/y
    z_coord_name<<<{"description": "reporter z-coordinate name.  This uses the reporter syntax <reporter>/<name>."}>>> = heat_transfer_rate/z
  []
[]
(modules/porous_flow/examples/multiapp_fracture_flow/fracture_diffusion/matrix_app_dirac.i)

A MultiApp approach for the nonconforming case

This is identical to the conforming case except:

  • the matrix mesh is nonconforming, as shown above

  • the heat transfer coefficient is different, as described above

Results

The L2 error of the fracture temperature in each approach (square-root of the sum of squares of differences between the and the benchmark result) is plotted in Figure 6. As expected, the error is proportional to . The error when using the MultiApp approaches is larger than the non-MultiApp approach, because is fixed when is being solved for, and vice versa. The conforming and nonconforming cases produce similar results for larger time-steps, but as the time-step size reduces the results are slightly different, just because of the small differences in the effective finite-element discretisation.

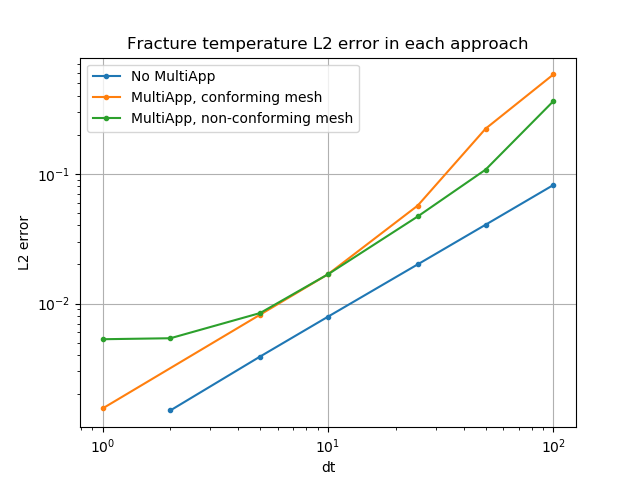
Figure 6: L2 error of each approach (with respect to the benchmark where is 0.125) to modelling the mixed-dimensional diffusion equation