Friction PendulumTM Isolator
Friction PendulumTM (FP) bearings are used to seismically isolate structures, including critical facilities such as nuclear power plants. The single concave FP bearing consists of a spherical sliding surface, a slider coated with PTFE-type composite material, and a housing plate. Figure 3 and Figure 4 shows components and part sectional view of a single concave Friction PendulumTM bearing, respectively.
](../../../media/materials/fp_isolator/fp_components.png)
Figure 3: Components of a single Friction PendulumTM bearing ((EPS), 2012)
](../../../media/materials/fp_isolator/fp_sectionalview.png)
Figure 4: Sectional view of a single concave Friction PendulumTM bearing (Kumar et al., 2015b)
Continuum modeling of FP bearings is computationally expensive and impractical for applications involving structures with tens to hundreds of bearings. Hence a two-node model developed by Kumar et al. (2015b) is adopted here. The bottom node represents the concave sliding surface, and the top node represents the articulated slider. The two-node model has six degrees of freedom (3 translations and 3 rotations), at each node and is capable of simulating nonlinear hysteric behavior in the FP bearing. The physical model and spring representation of the two-node FP isolator element is similar to that of the lead-rubber isolator as shown in fig.
Force-displacement relationship
Friction PendulumTM bearings dissipate the energy induced during an earthquake through nonlinear hysteretic behavior in shear. The lateral force-displacement relationship of a single concave FP bearing is characterized by two parameters: yield strength and post elastic stiffness, and can be represented by the bi-linear curve of Figure 1.
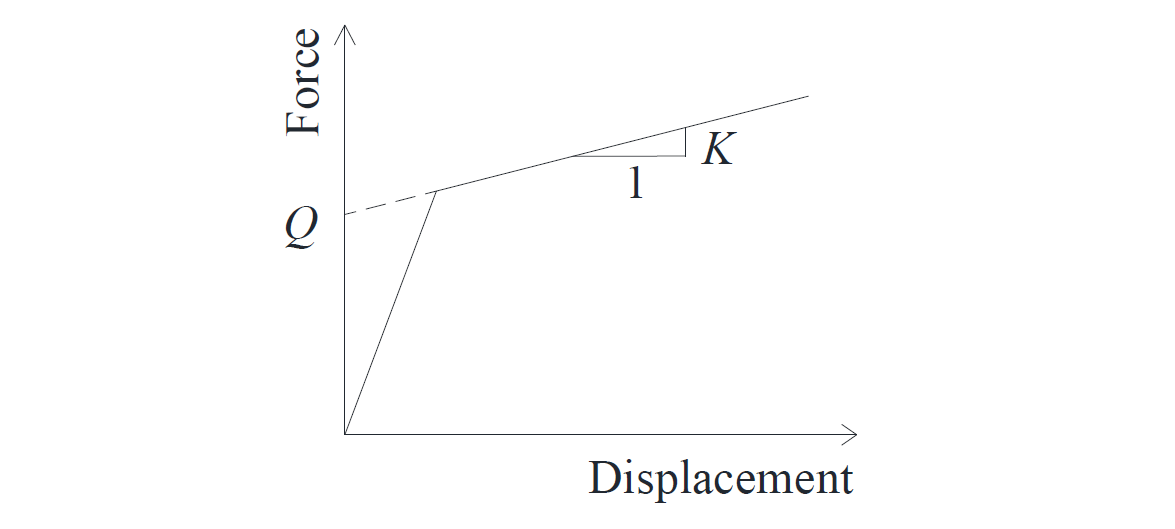
Figure 1: Lateral force-displacement relationship of a single concave FP bearing
The yield strength and the post-elastic stiffness can be calculated as,
(1)
(2)
where,
is the yield strength
is the post elastic stiffness
is the instantaneous axial load, and
is the effective radius of curvature of the sliding surface.
Parameters and depends on the coefficient of sliding friction and the axial load on the bearing. For detailed information on the numerical implementation of the nonlinear hysteretic behavior of the FP bearing in shear, refer to Kumar et al. (2015) (page:106-107). Additionally, the FP bearing exhibits very large stiffness in axial, torsional and rotational directions and is therefore modeled as a linear elastic material with large stiffness in these degrees-of-freedom.
Coefficient of sliding friction
The lateral force-displacement relationship of the FP bearing is governed by the coefficient of sliding friction. At a given instant of time the coefficient of sliding friction depends on the instantaneous sliding velocity, instantaneous axial pressure, and the temperature of the sliding interface.
(3)
where,
is the coefficient of sliding friction at given time
is the instantaneous sliding velocity
is the instantaneous axial pressure, and
is the instantaneous temperature of the sliding surface.
Kumar et al. (2015b) developed a framework to account for the variation in due to the combined effect of velocity, pressure, and temperature and it is adopted here. The sliding velocity and the axial pressure on the bearing are governed by the response of the superstructure. The temperature at the sliding surface is a function of the coefficient of friction, sliding velocity, instantaneous axial pressure and, thermal and heat flux parameters of the material (typically stainless steel):
(4)
where,
k is the thermal conductivity of the sliding interface material, and
D is the thermal diffusivity of the sliding interface material.
It is evident from Eq. (3) and Eq. (4), that and are interdependent. This complex interdependence of the coefficient of sliding friction, sliding velocity, instantaneous axial pressure, and the temperature at the sliding surface is described using the flowchart of Figure 2.
.](../../../media/materials/fp_isolator/fp_interdependence.png)
Figure 2: Interdependence of parameters governing the lateral force-displacement relationship of a FP bearing (Kumar et al., 2015b).
Dependence of the coefficient of friction on the sliding velocity
Mokha et al. (1988) proposed an expression to account for the dependence of the coefficient of friction on the instantaneous sliding velocity as
(5)
where,
is the friction coefficient at a very small sliding velocity
is the friction coefficient at a very high sliding velocity, and
is a rate parameter.
Based on the experimental data, the ratio is assumed to be a constant value of 0.5 (Kumar et al., 2015b). The modified expression for coefficient of friction as a function of instantaneous sliding velocity, at constant axial load and temperature, can be written as:
(6)
Dependence of the coefficient of friction on the axial pressure
Kumar et al. (2015b) proposed an expression for the coefficient of sliding friction as a function of axial pressure at very high sliding velocity, and is given by
(7)
where,
is the reference axial pressure
is the co-efficent of sliding friction when the axial pressure on the bearing () is equal to the reference pressure (), and
and are constants.
The assumption of for all values of axial pressure allows the coefficient of sliding friction to be expressed as the product of the coefficient of friction measured at a reference pressure and a term that depends on the instantaneous axial pressure. Based on the experiments, and can be set equal to 0.7 and 0.02 respectively (Kumar et al., 2015b). Rewriting the expression for as a function of :
(8)
Dependence of the coefficient of friction on the temperature at sliding interface
The coefficient of sliding friction decreases as the number of cycles of loading increase. Kumar et al. (2015b) proposed an expression to define the coefficient of friction as a function of the instantaneous temperature, at a reference axial pressure and very high sliding velocity as
(9)
where,
is the coefficient of friction at a temperature
is the coefficient of friction measured at the reference temperature , and
is the instantaneous temperature.
During the analysis, it is difficult to monitor the temperature over the entire sliding surface. To address the heating, Kumar et al. (2015b) proposed an alternate approach namely, to monitor the temperature at the center of sliding surface only. When the slider is above the center of sliding surface, the temperature increases, and drops as the slider moves away. This increase in temperature at the monitoring location is governed by the heat flux parameters and the path of the slider, and is given by Eq. (10)
(10)
where,
is the increase in temperature
is the depth measured from the sliding surface,
is the thermal diffusivity of the sliding interface material,
is the thermal conductivity of the sliding interface material, and
is the heat flux.
At a given instant of time, the instantaneous heat flux, at the monitoring location can be expressed as
(11)
Dependence of the coefficient of friction on the combined effects of temperature, axial pressure and sliding velocity
During an earthquake, the sliding velocity, axial pressure and the temperature at the sliding surface of a FP bearing changes continuously. The combined effect of all the three has to be considered to determine the coefficient of sliding friction. From Eq. (6), Eq. (8),and Eq. (9), the factors accounting for friction dependence on the velocity, pressure, and the temperature () can be written as
(12)
(13)
(14)
The coefficient of sliding friction as a function of the instantaneous sliding velocity, axial pressure on the bearing and the temperature at the center of the sliding surface is updated as:
(15)
where,
is the factor accounting for friction dependence on the sliding velocity
is the factor accounting for friction dependence on the axial pressure on the bearing
is the factor accounting for friction dependence on the temperature at center of the sliding surface, and
is the coefficient of sliding friction at refernce pressure , measured at high velocity of sliding with the temperature at the center of the sliding surface being .
References
- Earthquake Protection Systems (EPS).
http://www.earthquakeprotection.com/single_pendulum_bearing.html, 2012.[BibTeX]
- M Kumar, A.S Whittaker, and M.C Constantinou.
Seismic isolation of nuclear power plants using sliding bearings.
Technical Report MCEER-15-0006, Multidisciplinary Center for Earthquake Engineering Research, Buffalo, New York, 2015b.[BibTeX]
- M. Kumar, A. S. Whittaker, and M. C. Constantinou.
Seismic isolation of nuclear power plants using elastomeric bearings.
Technical Report MCEER-15-0008, Multidisciplinary Center for Earthquake Engineering Research, Buffalo, New York, 2015.[BibTeX]
- A Mokha, Constantinou. M. C, and Reinhorn. A. M.
Teflon bearings in aseismic base isolation: experimental studies and mathematical modeling.
Technical Report NCEER-88-0038, National Center for Earthquake Engineering Research, Buffalo, New York, 1988.[BibTeX]