ver-1kc-1
Sieverts’ Law Boundaries with No Volumetric Source
General Case Description
Two enclosures are separated by a membrane that allows diffusion according to Sievert's law, with no volumetric source present. Enclosure 2 has twice the volume of Enclosure 1.
Case Set Up
This verification problem is taken from Ambrosek and Longhurst (2008).
This setup describes a diffusion system in which tritium T is modeled across a one-dimensional domain split into two enclosures. The total system length is m, divided into 100 segments. The system operates at a constant temperature of 500 Kelvin. Initial tritium pressures are specified as Pa for Enclosure 1 and Pa for Enclosure 2.
The diffusion process in each of the two enclosures can be described by
and
where and represent the concentration fields in enclosures 1 and 2 respectively, is the time, and denotes the diffusivity.
This case is similar to the ver-1kb case, with the key difference being that sorption here follows Sieverts' law instead of Henry's law. The concentration in Enclosure 1 is related to the partial pressure and concentration in Enclosure 2 via the interface sorption law:
where is the ideal gas constant in J/mol/K, is the temperature in K, is the solubility, and is the exponent of the sorption law. For Sieverts' law, .
Results
We assume that , which is expected to lead to at equilibrium. As illustrated in Figure 1, the pressure jump maintains a ratio of , which is consistent with the relationship for and The concentration ratio between enclosures 1 and 2 in Figure 2 shows that the results obtained with TMAP8 are consistent with the analytical results derived from the sorption law for . As shown in Figure 3, mass is conserved between the two enclosures over time, with a variation in mass of only %. This variation in mass can be further minimized by refining the mesh, i.e., increasing the number of segments in the domain.
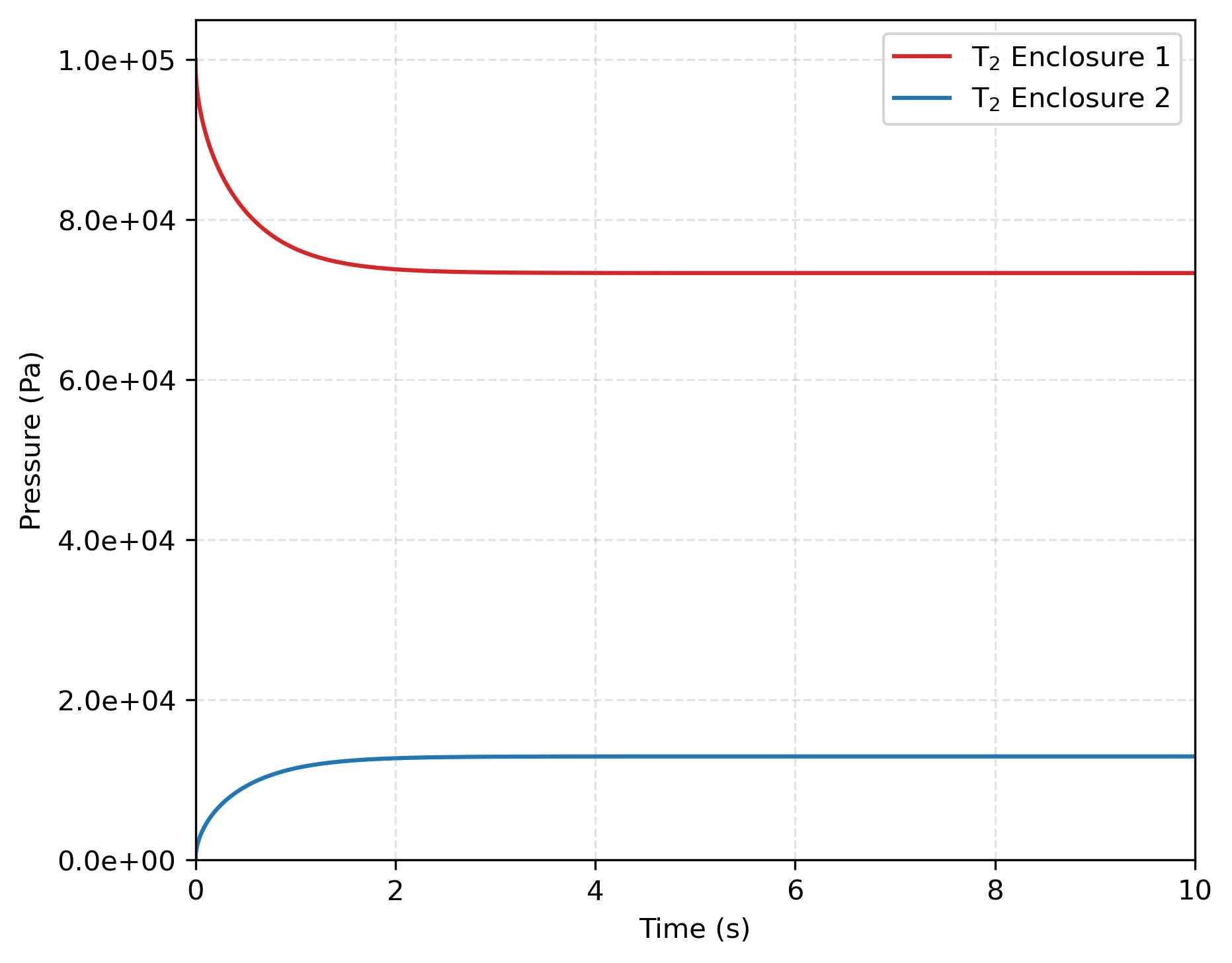
Figure 1: Evolution of species concentration over time governed by Sieverts' law with .
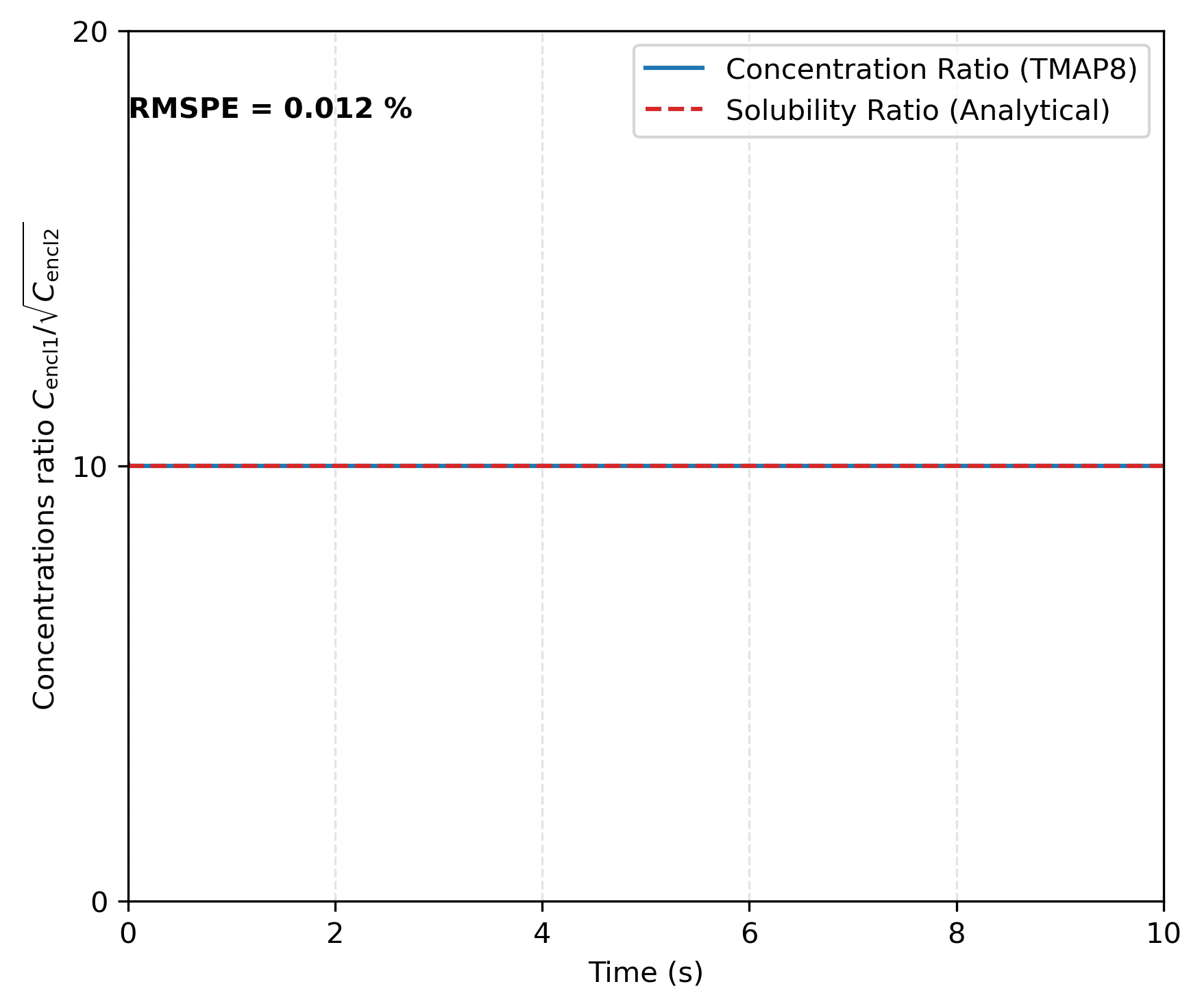
Figure 2: Concentrations ratio between enclosures 1 and 2 at the interface for . This verifies TMAP8's ability to apply Sieverts' law across the interface.
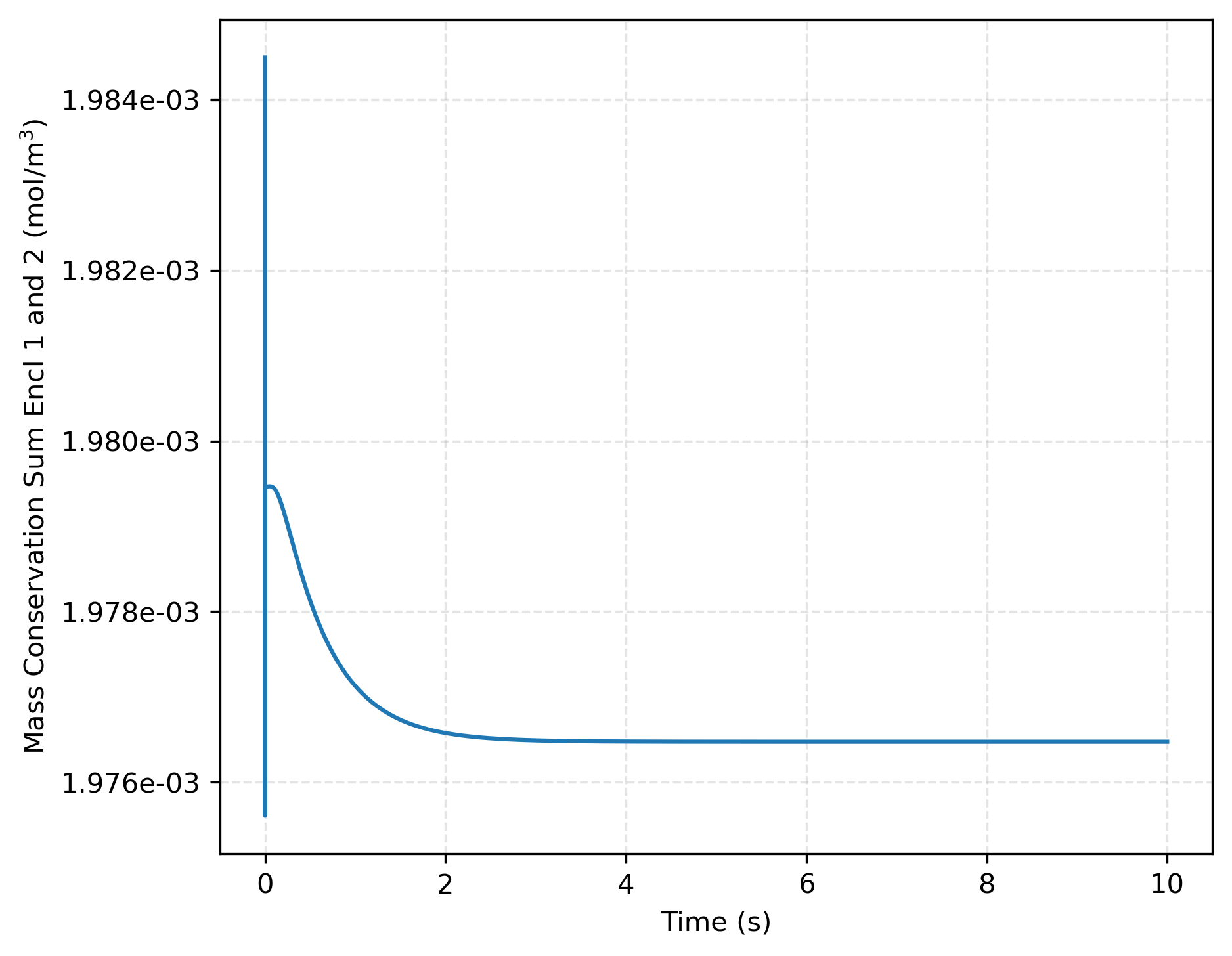
Figure 3: Total mass conservation across both enclosures over time for .
Input files
The input file for this case can be found at (test/tests/ver-1kc-1/ver-1kc-1.i). To limit the computational costs of the test cases, the tests run a version of the file with a coarser mesh and less number of time steps. More information about the changes can be found in the test specification file for this case (test/tests/ver-1kc-1/tests).
References
- James Ambrosek and GR Longhurst.
Verification and Validation of TMAP7.
Technical Report INEEL/EXT-04-01657, Idaho National Engineering and Environmental Laboratory, December 2008.[BibTeX]