General Case Description

Two enclosures are separated by a membrane that allows diffusion according to Henry’s law, with no volumetric source present. Enclosure 2 has twice the volume of Enclosure 1.

Case Set Up

This verification problem is taken from Ambrosek and Longhurst (2008).

This setup describes a diffusion system in which tritium T is modeled across a one-dimensional domain split into two enclosures. The total system length is m, divided into 100 segments. The system operates at a constant temperature of 500 Kelvin. Initial tritium pressures are specified as Pa for Enclosure 1 and Pa for Enclosure 2.

Over time, the pressures of T, which diffuses across the membrane in accordance with Henry’s law, will gradually equilibrate between the two enclosures.

The diffusion process in each of the two enclosures can be described by

and

where and represent the concentration fields in enclosures 1 and 2 respectively, is the time, and denotes the diffusivity.

The concentration in Enclosure 1 is related to the partial pressure and concentration in Enclosure 2 via the interface sorption law:

where is the ideal gas constant in J/mol/K, is the temperature in K, is the solubility, and is the exponent of the sorption law. For Henry’s law, .

Results

Two subcases are considered. In the first subcase, we assume that as is done in Ambrosek and Longhurst (2008), which is expected to lead to at equilibrium. In the second, , which is expected to lead to . This second case is added to exercise TMAP8 in a case with a concentration jump. In the first subcase, consistent with the results from TMAP7, the pressure evolution in both enclosures is shown in Figure 1 as a function of time. Both pressures find equilibrium and become equal, which is consistent with for and . The concentration ratio between enclosures 1 and 2 in Figure 2 shows that the results obtained with TMAP8 are consistent with the analytical results derived from the sorption law for . As shown in Figure 3, mass is conserved between the two enclosures over time, with a variation in mass of only %. This variation in mass can be further minimized by refining the mesh, i.e., increasing the number of segments in the domain.

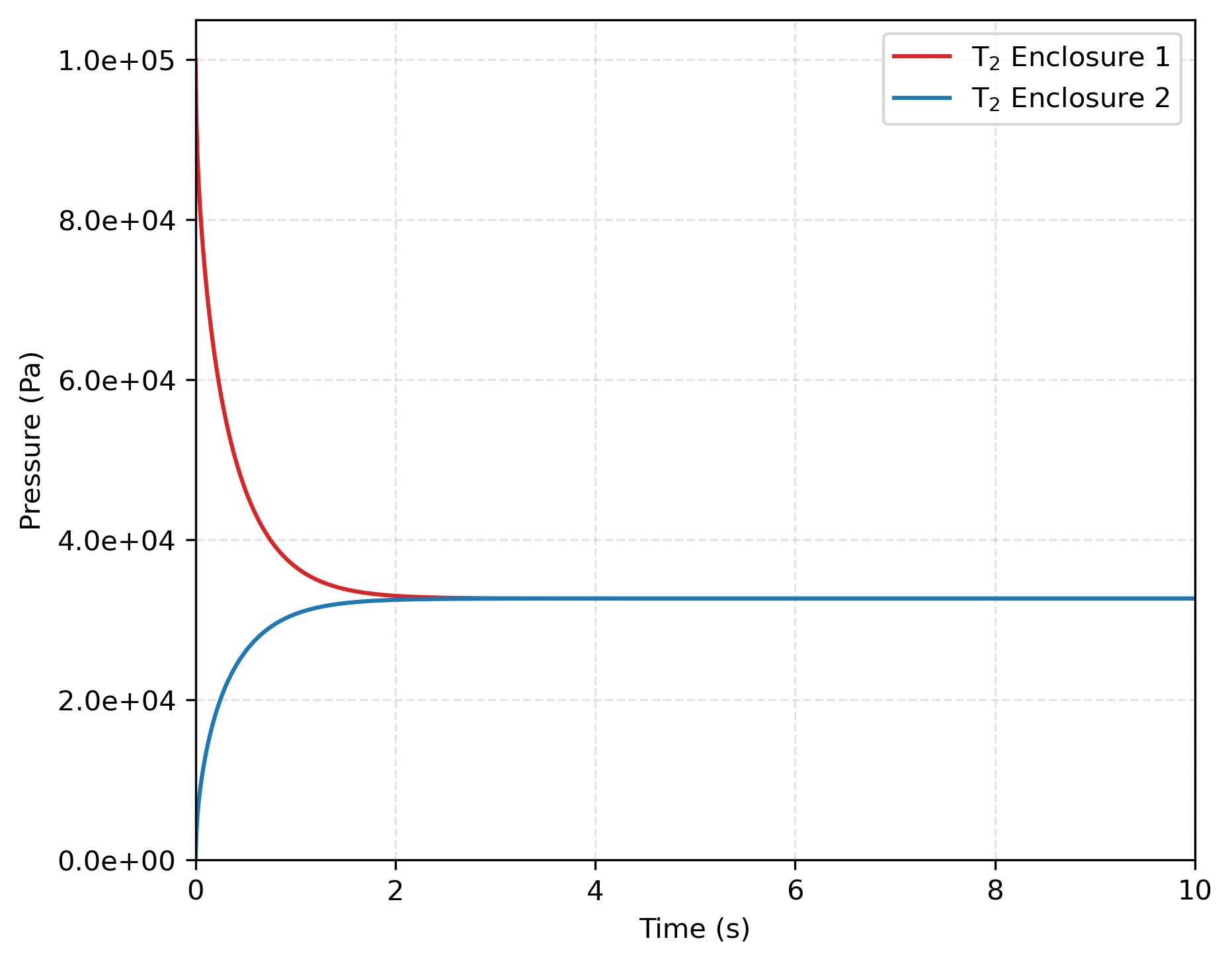
Figure 1: Equilibration of species pressures under Henry’s law for .

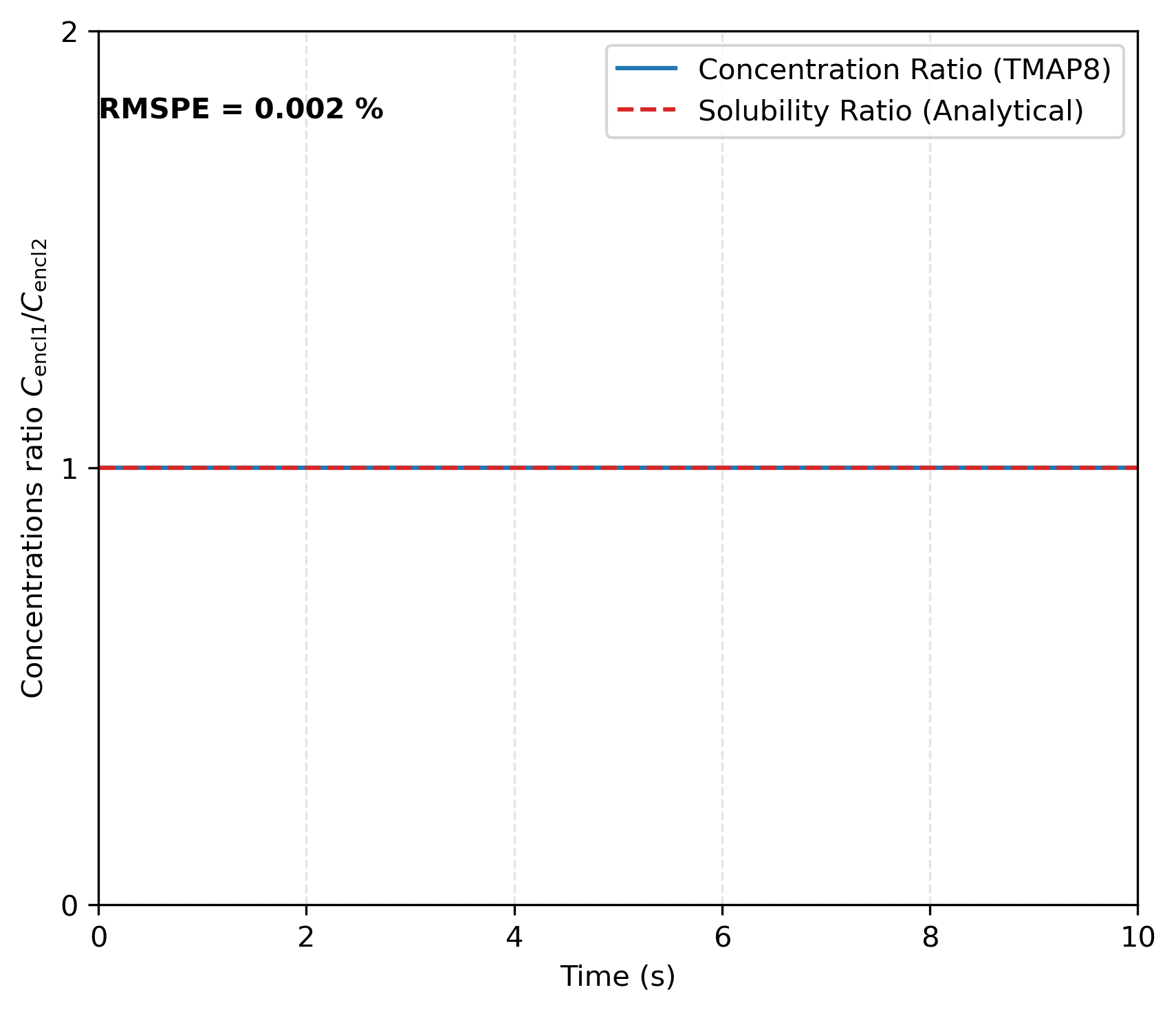
Figure 2: Concentrations ratio between enclosures 1 and 2 at the interface for . This verifies TMAP8's ability to apply the sorption law across the interface without a concentration jump.

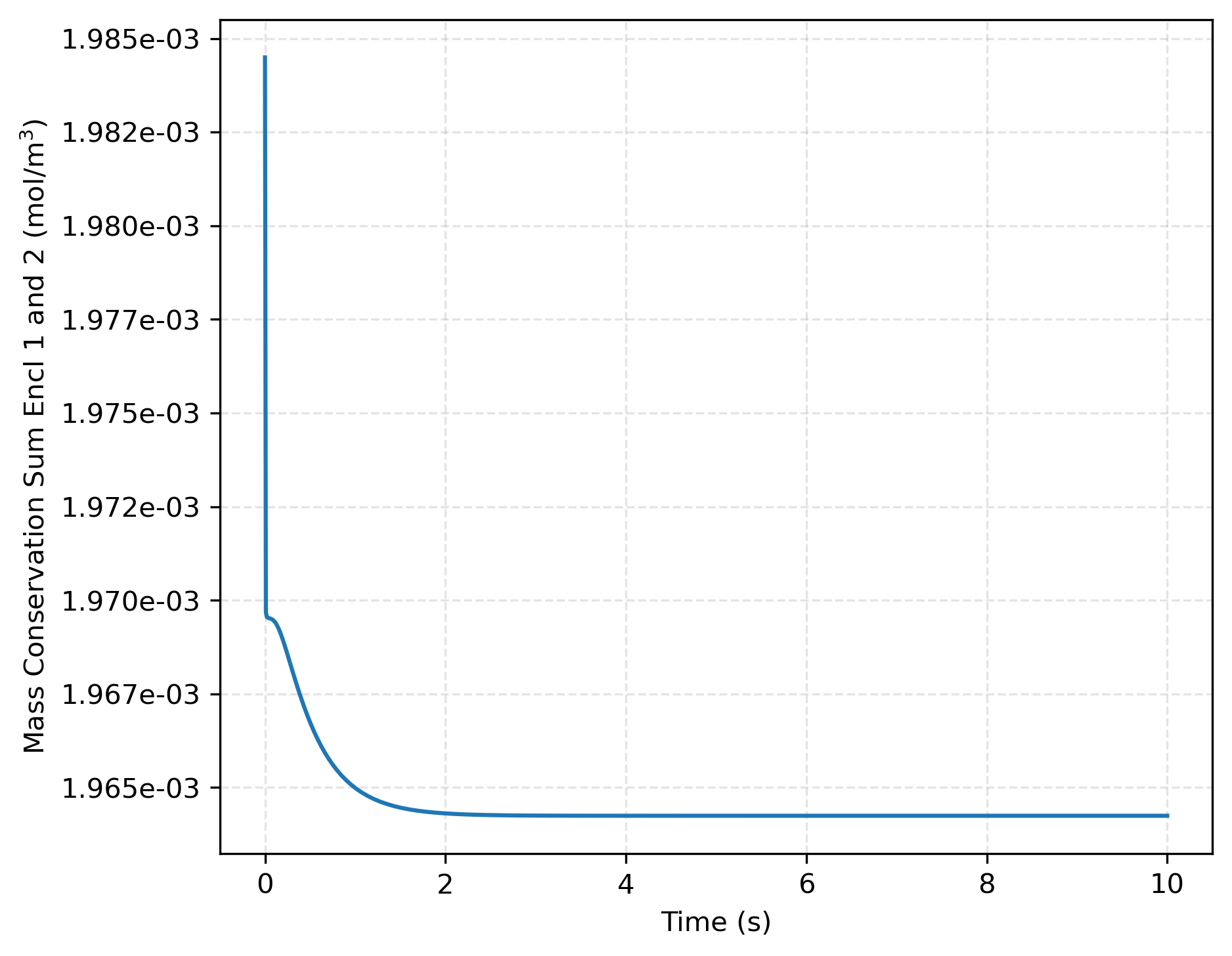
Figure 3: Total mass conservation across both enclosures over time for .

In the second subcase, the sorption law with does not lead to equal pressure in both enclosure. As illustrated in Figure 4, the pressure jump maintains a ratio of , which is consistent with the relationship for and . The concentration ratio between enclosures 1 and 2 in Figure 5 shows that the results obtained with TMAP8 are consistent with the analytical results derived from the sorption law for . Additionally, Figure 6 verifies that mass is conserved between the two enclosures over time, with a variation in mass of only %. As in the previous case, this variation in mass can be further reduced by refining the mesh.

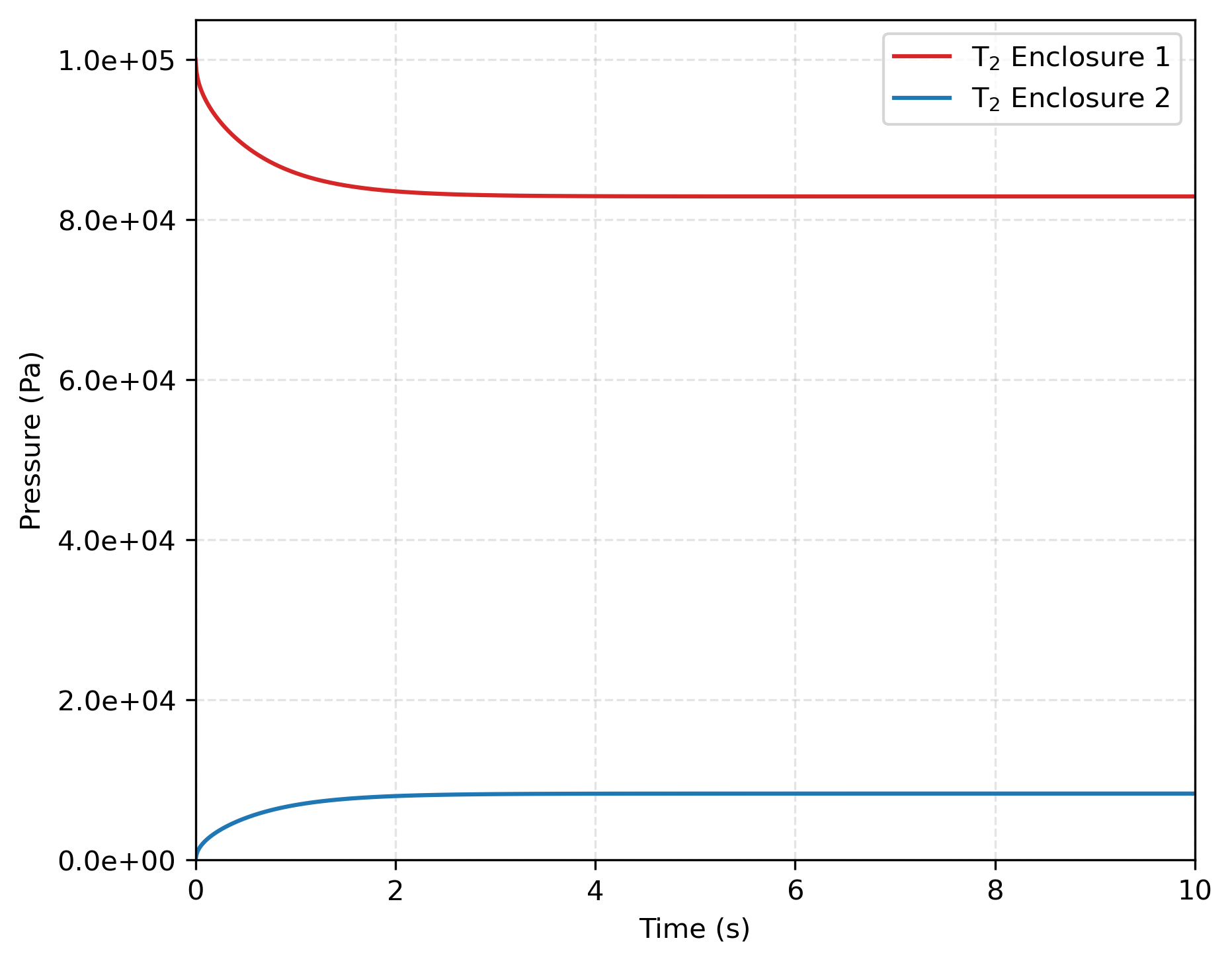
Figure 4: Pressures jump of species under Henry’s law for .

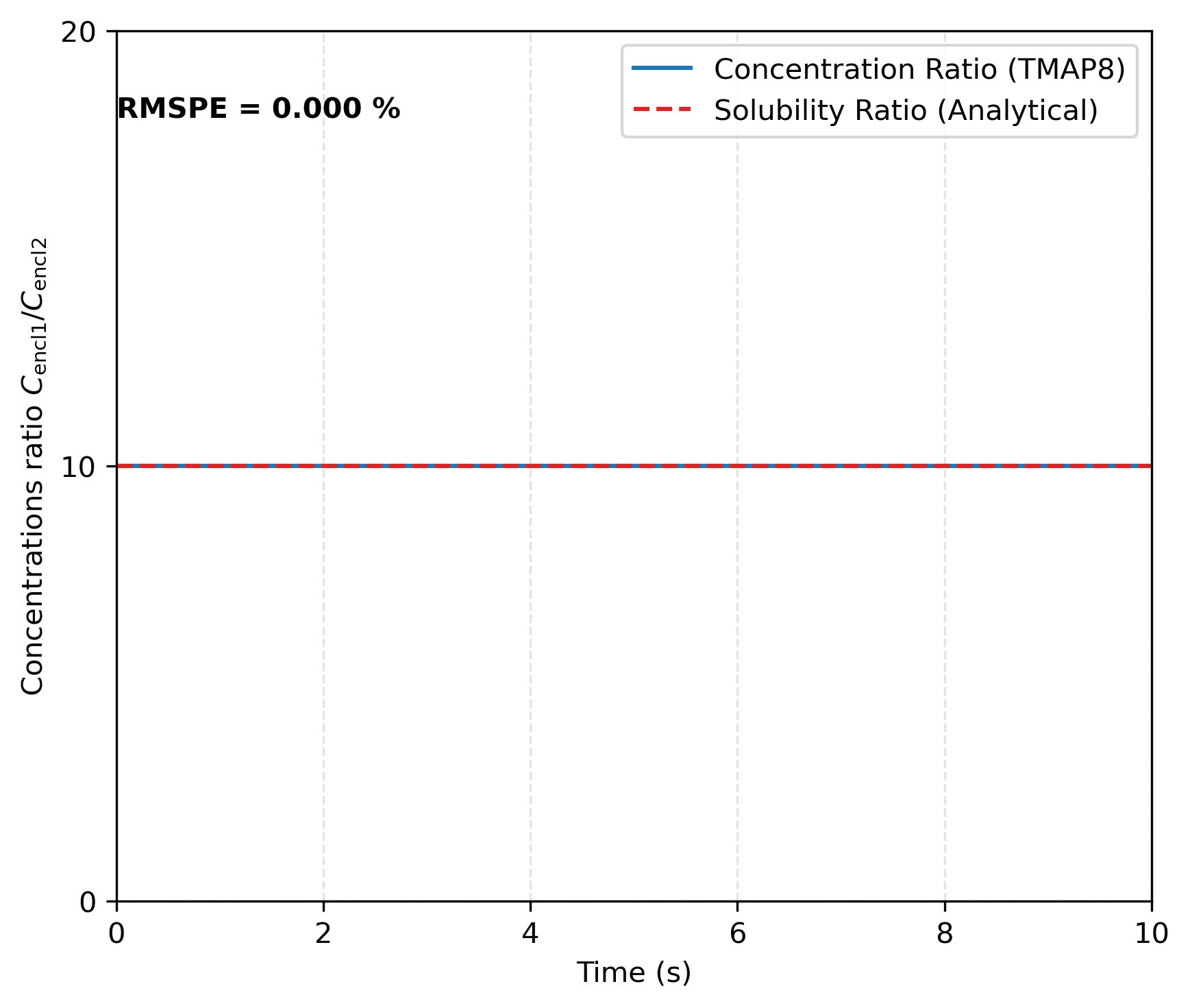
Figure 5: Concentrations ratio between enclosures 1 and 2 at the interface for . This verifies TMAP8's ability to apply the sorption law across the interface with a concentration jump.

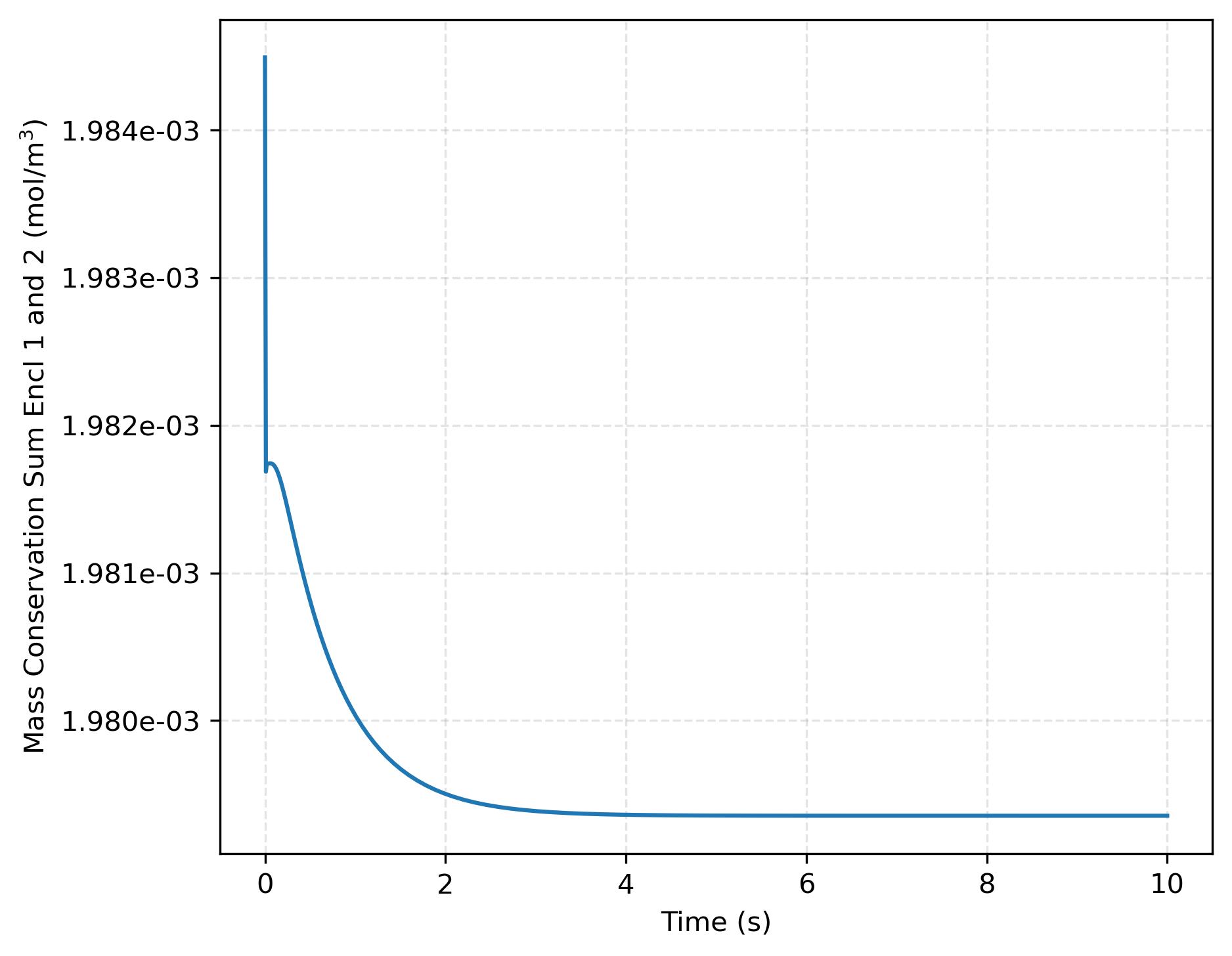
Figure 6: Total mass conservation across both enclosures over time for .

Input files

References