Introduction to MOOSE

MOOSE Framework: Overview

• Developed by Idaho National Laboratory since 2008

• Used for studying and analyzing nuclear reactor problems

• Free and open source (LGPLv2 license)

• Large user community (5000+ unique visitors/month)

• Highly parallel and HPC capable

• Developed and supported by full time INL staff - long-term support

• https://www.mooseframework.inl.gov

MOOSE Framework: Key features

• Massively parallel computation - successfully run on >100,000 processor cores

• Multiphysics solve capability - fully coupled and implicit solver

• Multiscale solve capability - multiple applications can perform computation for a problem simultaneously

• Provides high level interface to implement customized physics, geometries, boundary conditions, and material models

• Initially developed to support nuclear R&D but now widely used for non-nuclear R&D also

MOOSE Framework: Core Philosophy

• Object-oriented design : Everything is an object with clear interfaces

• Modular architecture : Mix and match components and/or physics to achieve simulation goals

• Supporting Many Physics : Framework handles numerics, you focus on physics

• Dimension-independent : Run in 1D, 2D, or 3D with minimal changes to the input file

• Automatic differentiation : No need to compute Jacobians manually

MOOSE Framework: Applications

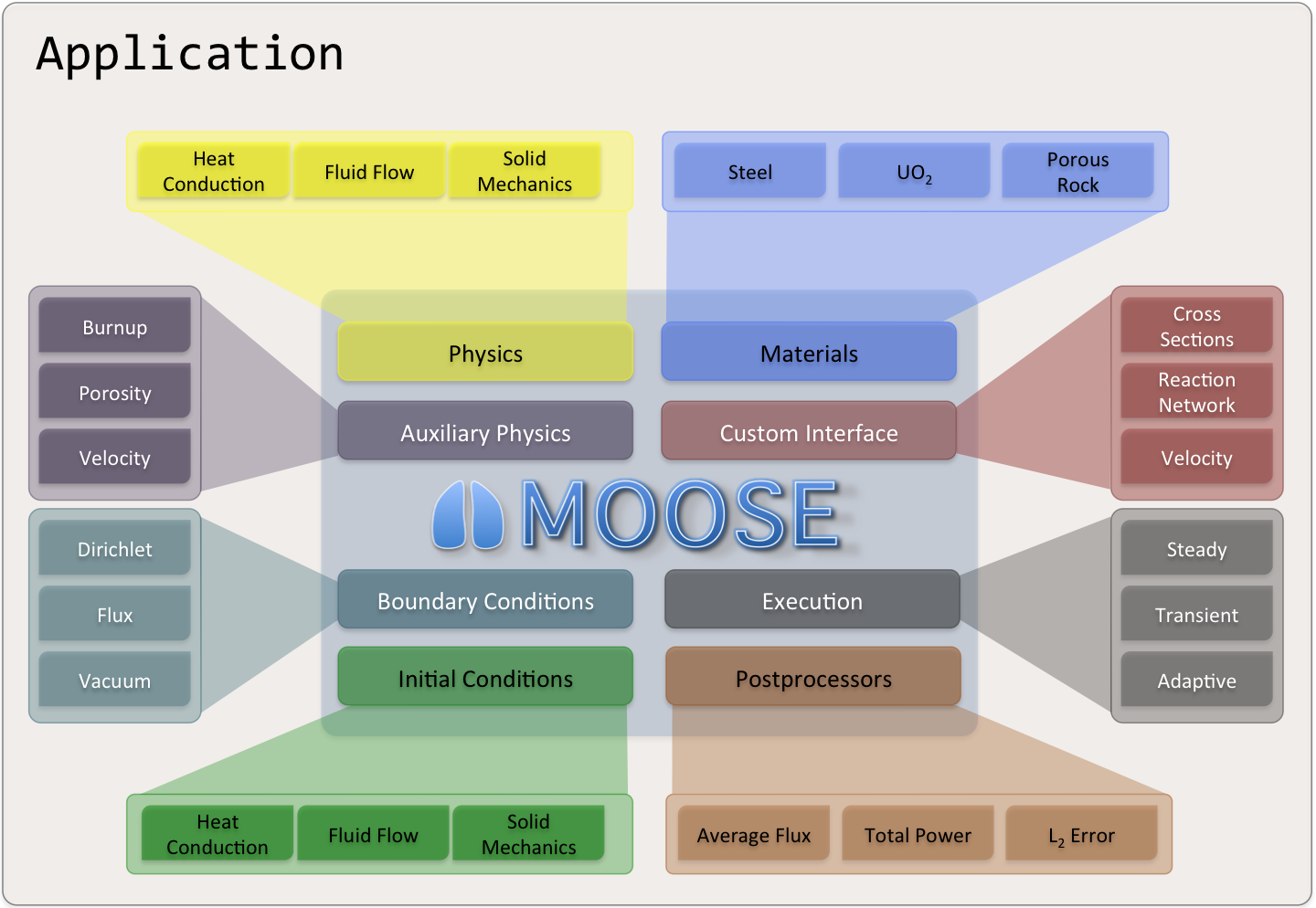
MOOSE Systems Architecture

• Each system has specific responsibilities

• Systems interact through well-defined interfaces

• Objects can be mixed and matched

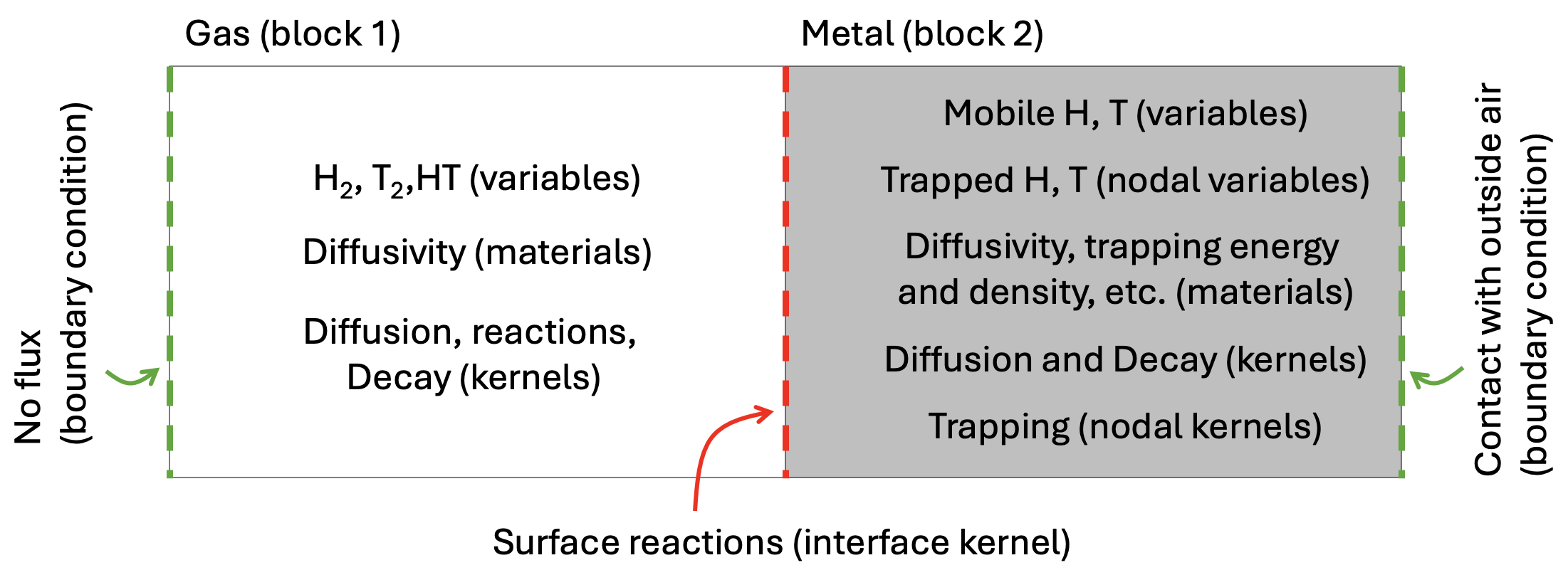
MOOSE Systems Architecture
example for a TMAP8-relevant case

The upcoming slides will describe the main components of the MOOSE systems architecture. This slide illustrates in which context different systems are used in a TMAP8-relevant case.

Let's assume one wants to model hydrogen and tritium transport through the metallic walls of a pipe. The model would include diffusion, decay, and reactions between diatomic molecules inside the pipe; surface reactions at the inner and outer walls; and diffusion, decay, and trapping for single atoms in the walls. The figure below illustrates the case and specifies how MOOSE's systems would apply when constructing the case in a MOOSE input file:

The Finite Element Method in MOOSE

MOOSE solves PDEs using the Galerkin finite element method (the finite volume method is also available for fluid flow).

Key steps:

1. Write strong form of PDE

2. Convert to weak form (multiply by test function, integrate by parts)

3. Discretize with shape functions

4. Form residual vector and Jacobian matrix

5. Solve nonlinear system with Newton's method

MOOSE handles:

• Mesh management

• Shape functions

• Quadrature rules

• Assembly process

• Parallel decomposition

Example: Strong form, weak form, and implementation

Kernels System: Building PDEs

class DiffusionKernel : public ADKernel
{
protected:
  virtual ADReal computeQpResidual() override
  {
    return _grad_test[_i][_qp] * _grad_u[_qp];
  }
};

Available variables:

• _u, _grad_u: Variable value and gradient

• _test, _grad_test: Test function value and gradient

• _qp: Quadrature point index

• _q_point: Physical coordinates

Special Note: NodalKernels System

Purpose: Compute residual contributions at nodes rather than quadrature points

  ADReal
  ReactionNodalKernel::computeQpResidual()
  {
    // Note: _qp = 0 for nodal kernels
    // (evaluated at only a single point)
    return _coef * _u[_qp];
  }
};

[NodalKernels]
  ...
  [decay]
    type = ReactionNodalKernel
    variable = C_tritium
    coef = 1.0
  []
[]

NodalKernels in TMAP8

Nodal kernels are used to model non-diffusive species. In the case of TMAP8, nodal kernels are key to modeling trapped species. For example, these are used in the Ver-1d verification case and several validation cases.

Application Examples:

• Trap filling/release (Ver-1d)

• Surface reactions at nodes

Materials System: Property Management

// Material object, in the constructor
_permeability(declareADProperty<Real>("permeability"))
// In the compute method
_permeability = 2.0;

// Consumer object (Kernel, BCs, etc.) in the constructor
_permeability(getADMaterialProperty<Real>("permeability"))

// In the "computeQp..." method
ADReal
SomeObject::computeQpResidual() {
return _permability[_qp] * _grad_u[_qp] * _grad_test[_qp];
}

Key Methods:

• declareProperty<Type>() - produce a standard material property in a material object

• getMaterialProperty<Type>() - consume a standard material property in a MOOSE object

• declareADProperty<Type>() - produce an AD material property in a material object

• getADMaterialProperty<Type>() - consume an AD material property in a MOOSE object

Boundary Condition System

Purpose: Apply constraints at domain boundaries

TMAP8 BC Example - Binary Recombination

Located in the MOOSE Scalar Transport Module. (Link)

Strong form:

Source:

#include "BinaryRecombinationBC.h"

registerMooseObject("ScalarTransportApp", BinaryRecombinationBC);

InputParameters
BinaryRecombinationBC::validParams()
{
  auto params = ADIntegratedBC::validParams();
  params.addClassDescription("Models recombination of the variable with a coupled species at "
                             "boundaries, resulting in loss");
  params.addRequiredCoupledVar("v", "The other mobile variable that takes part in recombination");
  params.addParam<MaterialPropertyName>(
      "Kr", "Kr", "The name of the material property for the recombination coefficient");
  return params;
}

BinaryRecombinationBC::BinaryRecombinationBC(const InputParameters & parameters)
  : ADIntegratedBC(parameters), _v(adCoupledValue("v")), _Kr(getADMaterialProperty<Real>("Kr"))
{
}

ADReal
BinaryRecombinationBC::computeQpResidual()
{
  return _test[_i][_qp] * _Kr[_qp] * _u[_qp] * _v[_qp];
}

More information about the surface models available in TMAP8 is available in the theory manual

InterfaceKernel System

Purpose: Couple physics across internal interfaces between subdomains

TMAP8 Usage:

• Metal/coating permeation barriers

• Multi-layer diffusion

• Interface trapping/sorption (see theory manual)

TMAP8 Example: InterfaceSorption

[InterfaceKernels]
  [interface_sorption]
    type = InterfaceSorption
    K0 = ${solubility}
    Ea = 0
    n_sorption = ${n_sorption}
    diffusivity = ${diffusivity}
    unit_scale = ${unit_scale}
    unit_scale_neighbor = ${unit_scale_neighbor}
    temperature = ${temperature}
    variable = concentration_enclosure_1
    neighbor_var = concentration_enclosure_2
    sorption_penalty = 1e1
    boundary = interface
  []
[]

Auxiliary System: Arbitrarily Calculated Variables

• Purpose: Variables that are not solved for as part of a PDE/ODE.

• Use cases: Postprocessing, visualization, coupling

Another Aux Example: Temperature

This is sampled from the val-2b validation case. First, we need to declare the temperature variable, as we would any other variable. Except, we do it here under the AuxVariables block. Then, we set up an AuxKernel to calculate it using a time-dependent function.

[AuxVariables]
  [temperature]
    initial_condition = ${temperature_initial}
  []
[]

[AuxKernels]
  [temperature_aux]
    type = FunctionAux
    variable = temperature
    function = temperature_bc_func
    execute_on = 'INITIAL LINEAR'
  []
[]

Example, cont.: Aux Temperature in a BC

Now, temperature can be used wherever a regular MooseVariable is used. For example, we use it in val-2b in an EquilibriumBC boundary condition on the left boundary.

[BCs]
  [left_flux]
    type = EquilibriumBC
    Ko = ${solubility_constant_BeO}
    activation_energy = '${fparse solubility_energy_BeO * R}'
    boundary = left
    enclosure_var = enclosure_pressure
    temperature = temperature
    variable = deuterium_concentration_BeO
    p = ${solubility_order}
  []
[]

Input File System: HIT Format

[Mesh]
  type = GeneratedMesh
  dim = 2
  nx = 10
  ny = 10
[]

[Variables]
  [u]
  []
[]

[Kernels]
  [diff]
    type = Diffusion
    variable = u
  []
[]

[BCs]
  [left]
    type = DirichletBC
    variable = u
    boundary = left
    value = 0
  []
  [right]
    type = DirichletBC
    variable = u
    boundary = right
    value = 1
  []
[]

[Executioner]
  type = Steady
  solve_type = 'PJFNK'
  petsc_options_iname = '-pc_type -pc_hypre_type'
  petsc_options_value = 'hypre boomeramg'
[]

[Outputs]
  exodus = true
[]

Inline Unit Conversions in Input Files

Built-in parser enables calculations and unit conversions directly in input files using the MOOSE fparse and units systems.

${fparse num1 * num2}  # On-the-fly calculations

${units num1 unit1 -> unit2}  # Unit conversions

param = 5.0 * ${top_level_coef1} + ${top_level_coef2}  # Replacements

Fparse / Units Conversion Usage Example

At the input file top level:

# Diffusion parameters
flux_high = '${units 1e19 at/m^2/s -> at/mum^2/s}'
flux_low = '${units 0      at/mum^2/s}'
diffusivity_coefficient = '${units 4.1e-7 m^2/s -> mum^2/s}'
E_D = '${units 0.39 eV -> J}'
initial_concentration = '${units 1e-10 at/m^3 -> at/mum^3}'
width_source = '${units 3e-9 m -> mum}'
depth_source = '${units 4.6e-9 m -> mum}'

In an object:

[Postprocessors]
  [scaled_flux_surface_right]
    type = ScalePostprocessor
    scaling_factor = '${units 1 m^2 -> mum^2}'
    value = flux_surface_right
    execute_on = 'initial nonlinear linear timestep_end'
    outputs = none
  []
[]

Solver System: PJFNK Method

Preconditioned Jacobian-Free Newton-Krylov (PJFNK)

Note that a standard Newton solve (using the exact Jacobian) with preconditioning is also available!

Automatic Differentiation in MOOSE

// Traditional approach
Real computeQpResidual() {...}
Real computeQpJacobian() {...}
Real computeQpOffDiagJacobian() {...}

// AD approach - Jacobian automatic!
ADReal computeQpResidual() {...}

MultiApp and Transfer Systems

Output System

Flexible and Extensible Output

[Outputs]
  exodus = true
  csv = true
  [custom_out]
    type = Exodus
    interval = 10
    execute_on = 'timestep_end'
  []
[]

MOOSE/TMAP8 Development Process

Nuclear Quality Assurance Level 1 (NQA-1)

Testing Framework

TMAP8 Software Quality Assurance Documentation

test/
  tests/
    kernels/
      my_kernel/
        my_kernel.i
        tests
        gold/
          my_kernel_out.e

[Tests]
  [my_test]
    type = Exodiff
    input = test.i
    cli_args = 'Kernels/my_kernel/active=true'
    exodiff = test_out.e
  []
[]

Getting Help

Resources Available (all links):

Summary: Why MOOSE for TMAP8?

• Proven framework: Used in 500+ publications, tested extensively, production-ready

• Parallel scalability: Handles problems from workstation to supercomputer

• Multiphysics capable: Natural coupling of transport phenomena

• Active development: Continuous improvements and support

• Extensible design: Easy to add new physics for tritium transport

• Quality assurance: NQA-1 process ensures reliability

• Community support: Large user base and developer team across the world

• Open source access: Free and easily available, with contributions from many different fields

Introduction to TMAP8

TMAP8 inherited features from MOOSE

TMAP8 directly inherits all of MOOSE's features, including:

• Easy to use and customize

• Takes advantage of high performance computing by default

• Developed and supported by INL staff and the community - long-term support

• Massively parallel computation

• Multiphysics solve capability

• Multiscale solve capability - multiple applications can perform computations for a problem simultaneously

• Provides high-level interface to implement customized physics, geometries, boundary conditions, and material models

• Enables 2D and 3D simulations

• Open source and available on GitHub.

TMAP8 features

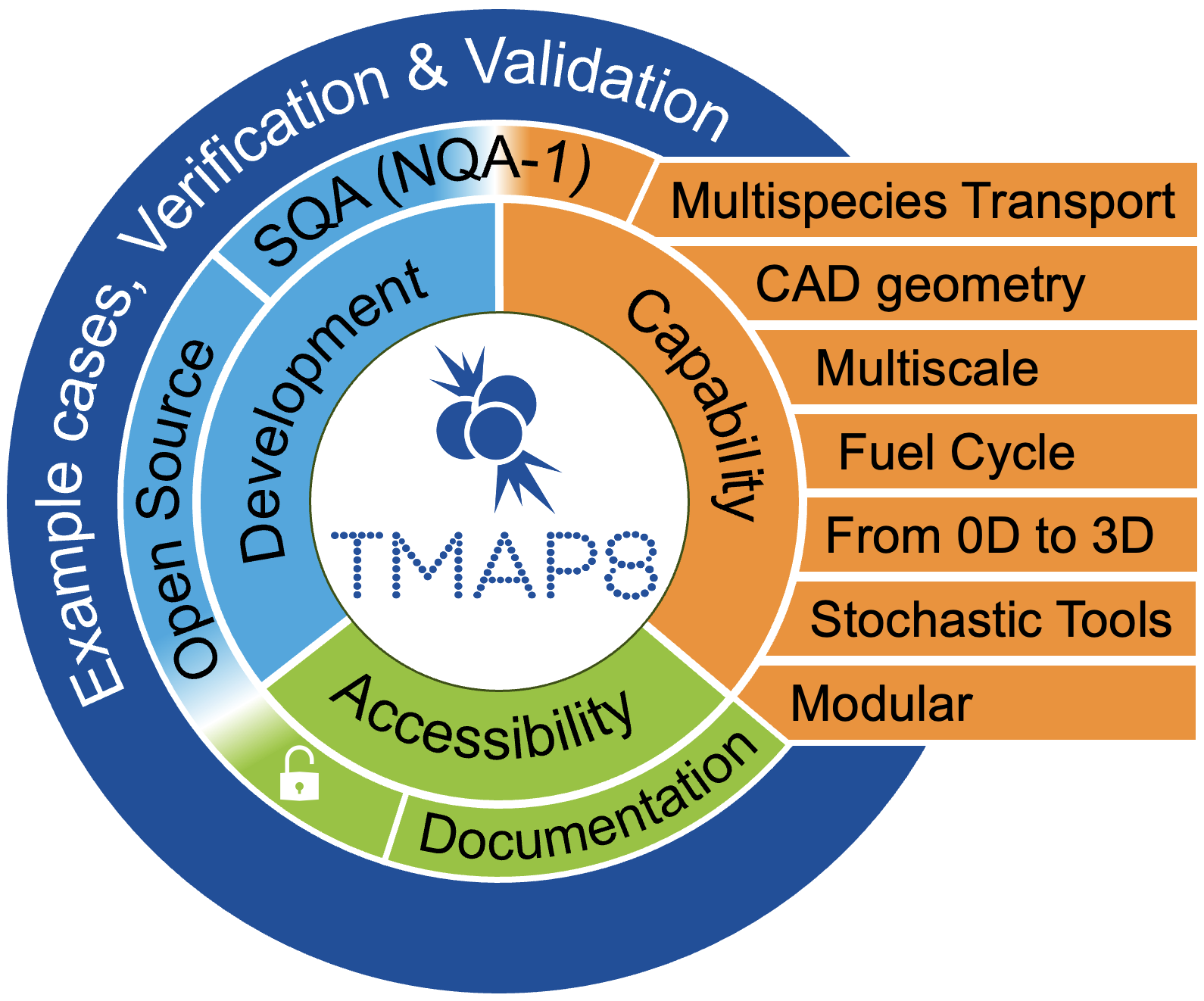
• The TMAP4/7 capabilities and physics are available in TMAP8.

• TMAP4 and TMAP7, although widely used, have limitations that TMAP8 overcomes.

• TMAP8 enables high fidelity, multi-scale, 0D to 3D, multispecies, multiphysics simulations of tritium transport, and offers massively parallel capabilities.

• TMAP8 is open source, Nuclear Quality Assurance level 1 (NQA-1) compliant, offers user support and a licensing approach (LGPL-2.1) selected for collaboration.

TMAP8 Theory

TMAP8's documentation provides a theory manual to describe the base theory used in TMAP8, focused in particular on different approaches available to model surface reactions.

However, this list is not exhaustive, and for a more comprehensive description of capabilities, theoretical concepts, and available objects, refer to:

• the publications listed in the List of Publications using TMAP8

• the List of verification cases

• the Complete TMAP8 Input File Syntax page.

For the derivation of the weak form of the tritium transport system of equations in solids, refer to the appendix of this TMAP8 publication.

TMAP8 key capabilities - fuel cycle

TMAP8 is able to perform fuel cycle calculations at the system scale.

It has been benchmarked against the fuel cycle model described by Abdou et al. (2021), and the model described in Meschini et al. (2023).

Ongoing efforts are using the MultiApp system to concurrently perform component-level calculations and use the results in fuel cycle calculations to accurately model the tritium fuel cycle.

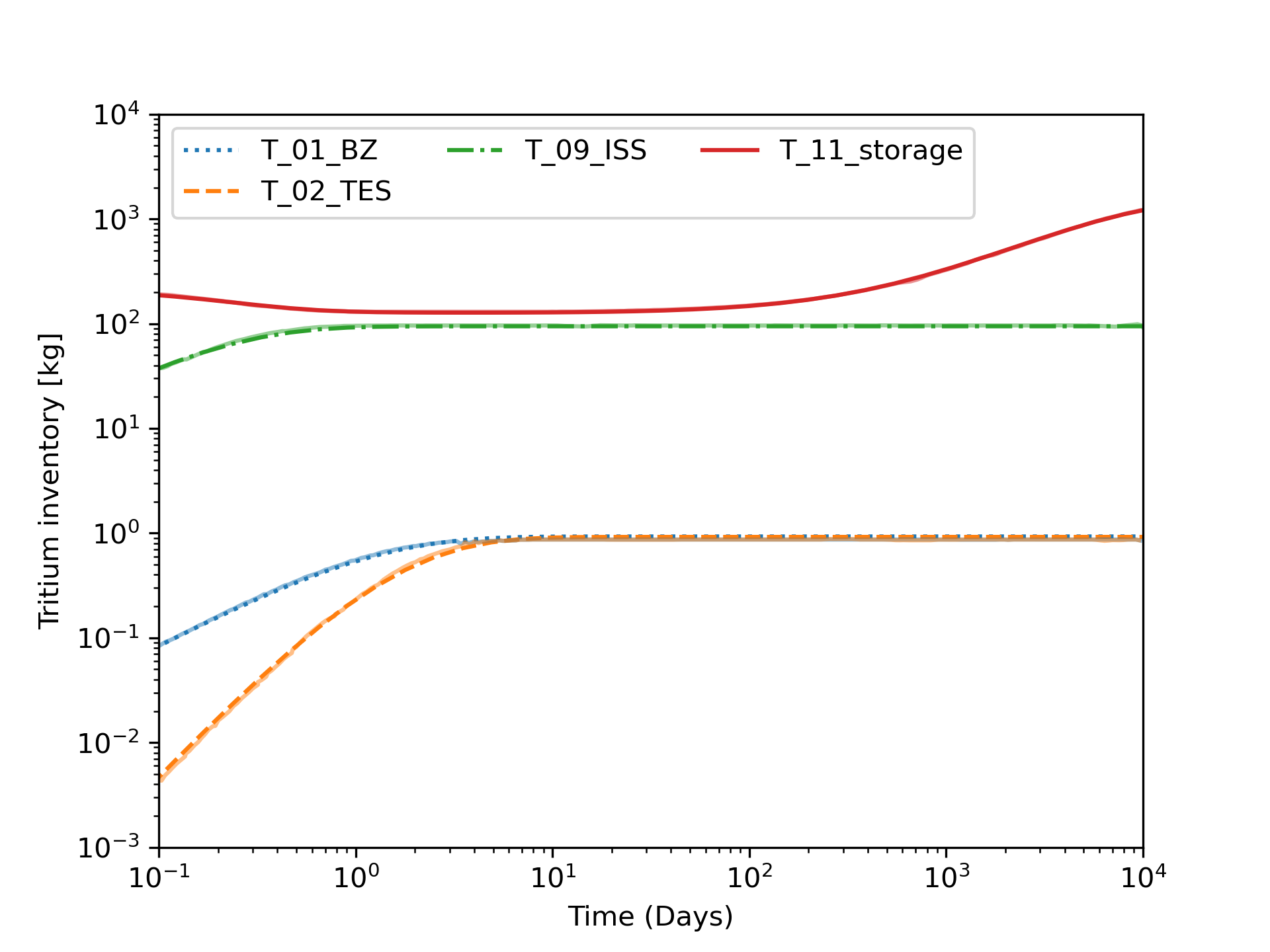
Figure from the fuel cycle example from Abdou et al.

TMAP8 key capabilities - Stochastic tools

The integration of the stochastic tools module in TMAP8 supports key capabilities:

• Model calibration

• Experimental analysis

• Uncertainty quantification

• Error identification (experimental uncertainty vs. model inadequacy vs. parameter uncertainty)

• Sensitivity analysis

• Surrogate model development

• etc.

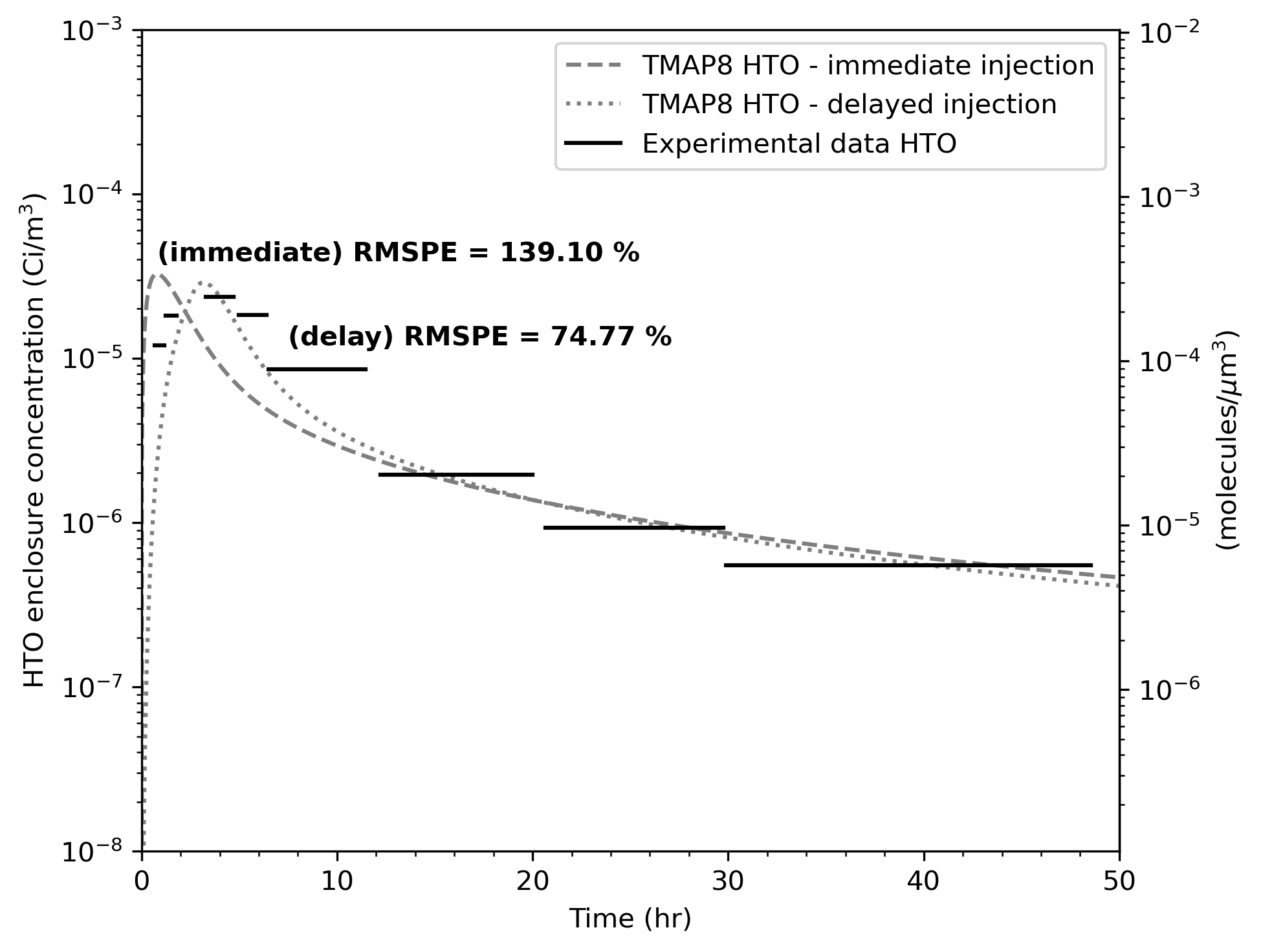
Figure from the val-2c validation case calibration.

TMAP8 key capabilities
pore-scale transport

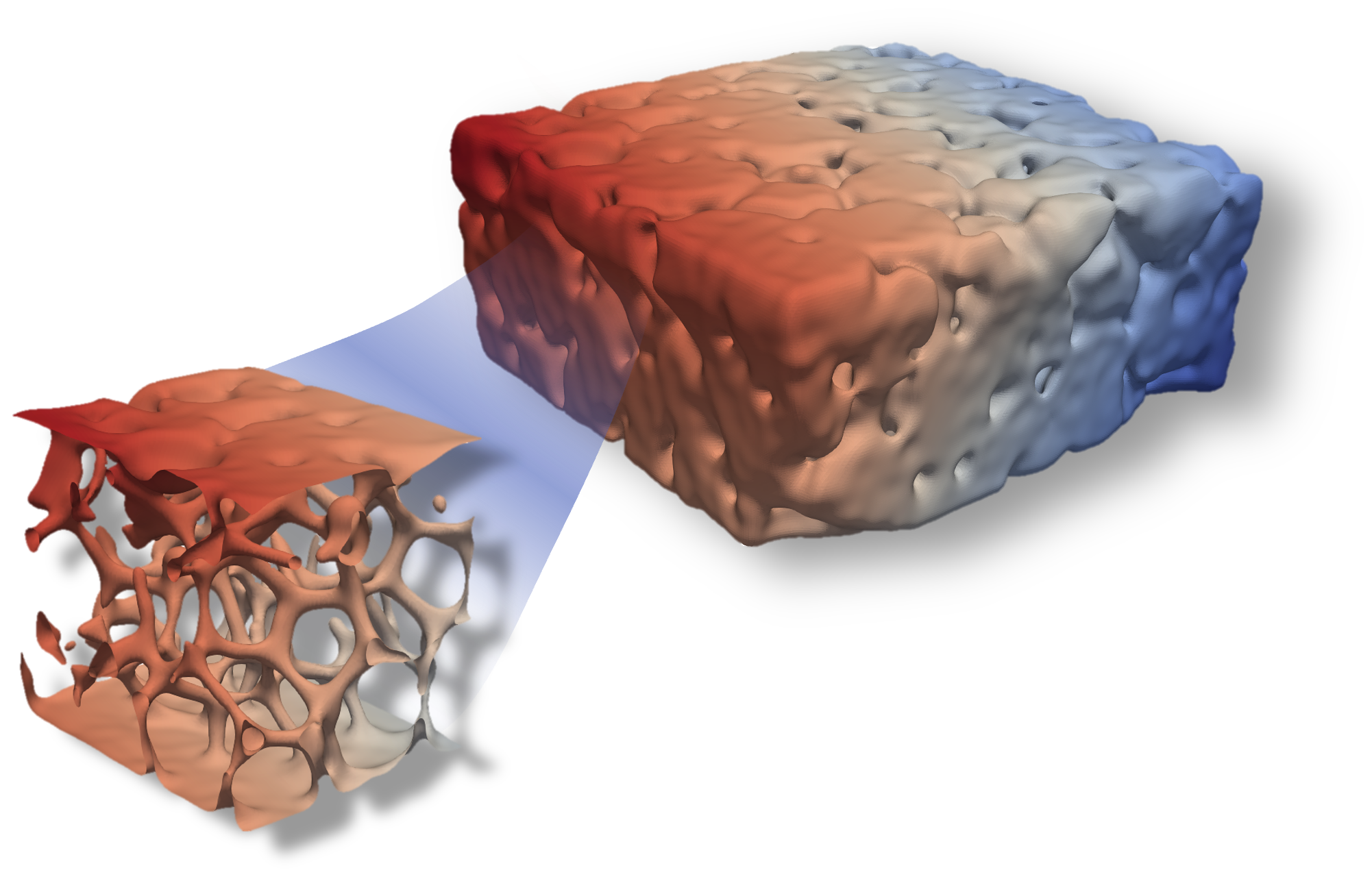
Thanks to the ImageFunction and phase-field module capabilities, TMAP8 can perform mesoscale simulations of tritium transport.

It can use sequential images of real or generated microstructures and perform tritium transport on them.

This capability is detailed in the pore-scale tritium transport example.

TMAP8 Verification & Validation (V&V)

Verification is the process of ensuring that a computational model accurately represents the underlying mathematical model and its solution. Verification can be satisfied by comparing modeling predictions against analytical solutions for simple cases, or leveraging the method of manufactured solutions (MMS), which is supported in MOOSE.

Validation, on the other hand, is the process of determining the extent to which a model accurately represents the real world for its intended uses, which requires comparison against experimental data.

TMAP8's V&V case suite now surpasses TMAP4's and TMAP7's, and continues to grow. It is a resource for users wanting to learn more about TMAP8's accuracy, and for users wanting to use them as starting point for their simulations.

Check out the TMAP8 V&V cases and all relevant input files and documentation on the:

Later in the hands on part of this workshop, we will go through some V&V cases in more detail.

TMAP8 Examples

Check out the TMAP8 example cases and all relevant input file and documentation on the:

It includes examples for fuel cycle calculations, divertor monoblock modeling, and pore microstructure modeling.

Summary

TMAP8 Verification Walkthrough:
Tritium Permeation and Trapping

Overview

• Purpose: Modeling tritium transport with progressing complexity.

  • ver-1dd: Pure diffusion without trapping (Documentation)

  • ver-1d: Diffusion with single trap type (Documentation)

  • ver-1dc: Diffusion with multiple trap types (Documentation)

• Based on established literature resources from the TMAP4 and TMAP7 eras:

  • Longhurst et al. (1992), Ambrosek and Longhurst (2005)

  • Ambrosek and Longhurst (2008)

• Expanded upon & updated in Simon et al. (2025)

• Demonstrates TMAP8's capability to handle increasingly complex tritium transport scenarios.

Physical Problem: Permeation Through a Membrane

Understanding MOOSE Input File Structure

Basic Anatomy of a TMAP8 Input File

[Block]
  [subblock]
    type = MyObject
    parameter1 = value1
    parameter2 = value2
  []
[]

Key Sections We'll Explore

• [Mesh] - Define geometry

• [Variables] - Declare unknowns to solve for

• [Kernels] - Define physics equations

• [BCs] - Define boundary conditions

• [Executioner] - Define the solution method

• [Outputs] - Setup how results should be saved

Case 1: Pure Diffusion (ver-1dd)

Governing Equation

• Simplest case: Fickian diffusion only

• No trapping mechanisms

• Baseline for comparison with trap-inclusive models

• Analytical solution available for verification

Case 1: Input File Structure - Mesh and Variables

[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = ${nx_num}
  xmax = 1
[]

[Variables]
  [mobile]
  []
[]

Case 1: Input File Structure -
Physics Implementation

[Kernels]
  [diff]
    type = Diffusion
    variable = mobile
  []
  [time]
    type = TimeDerivative
    variable = mobile
  []
[]

Case 1: Input File Structure -
Boundary Conditions

[BCs]
  [left]
    type = DirichletBC
    variable = mobile
    value = '${fparse cl / cl}'
    boundary = left
  []
  [right]
    type = DirichletBC
    variable = mobile
    value = 0
    boundary = right
  []
[]

Case 1: Input File Structure -
Postprocessors

[Postprocessors]
  [outflux]
    type = SideDiffusiveFluxAverage
    boundary = 'right'
    diffusivity = ${diffusivity}
    variable = mobile
  []
  [scaled_outflux]
    type = ScalePostprocessor
    value = outflux
    scaling_factor = ${cl}
  []
[]

Case 1: Input File Structure -
Preconditioning and Solving

[Preconditioning]
  [smp]
    type = SMP
    full = true
  []
[]

[Executioner]
  type = Transient
  end_time = ${simulation_time}
  dt = ${interval_time}
  dtmin = ${interval_time_min}
  solve_type = NEWTON
  scheme = BDF2
  nl_abs_tol = 1e-13
  petsc_options_iname = '-pc_type'
  petsc_options_value = 'lu'
  automatic_scaling = true
  verbose = true
  compute_scaling_once = false
[]

Case 1: Input File Structure - Outputs

[Outputs]
  exodus = true
  csv = true
  [dof]
    type = DOFMap
    execute_on = initial
  []
  perf_graph = true
[]

Case 1: Let's Run It!

If using a cloned and locally-built copy of TMAP8:

cd test/tests/ver-1dd/
../../../tmap8-opt -i ver-1dd.i

If using a Docker container:

cd /tmap8-workdir/tmap8/ver-1dd
tmap8-opt -i ver-1dd.i

The output can then be visualized using ParaView, or by using the comparison_ver-1dd.py script with some light modifications (change the location of the data file to the output you just generated).

What to Look For

• Convergence messages in terminal

• Exodus output files with field data (.e extension)

• CSV files with Postprocessor data

Case 1: Verification Results

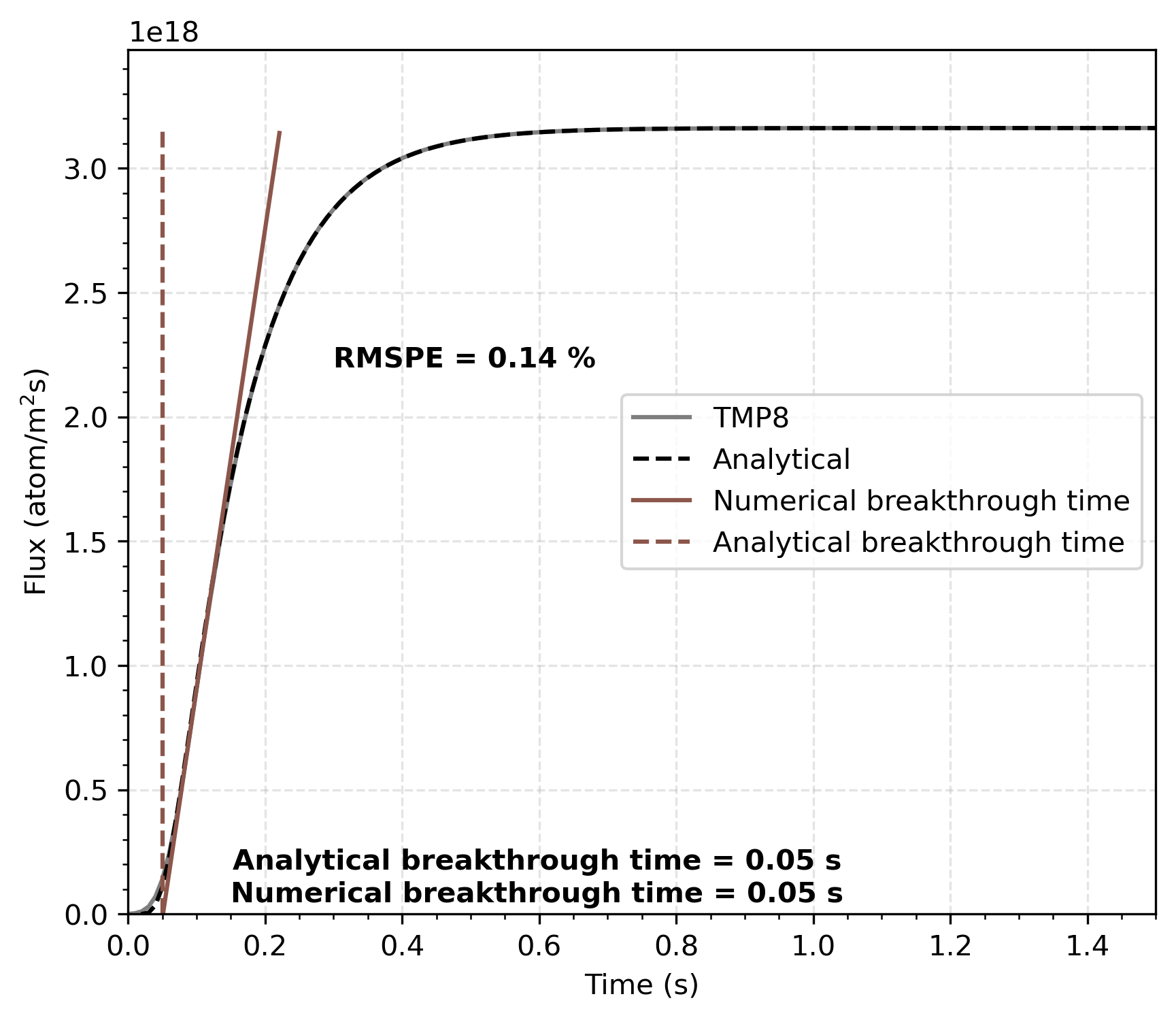
• Breakthrough time: seconds (both analytical and TMAP8)

• Excellent agreement throughout transient

Case 2: Single Trap Type (ver-1d)

In this case, we are modeling permeation through a membrane with a constant source in which traps are operative. We solve the following equations:

Trapping parameter

The breakthrough time may have one of two limiting values depending on whether the trapping is in the effective diffusivity or strong-trapping regimes. A trapping parameter is defined by:

where:

• = lattice parameter

• = Debye frequency ( )

• = trapping site fraction

• = diffusivity pre-exponential

• = diffusion activation energy

• = trap energy

• = Boltzmann's constant

• = temperature

• = dissolved gas atom fraction

Effective Diffusivity Regime

The discriminant for which regime is dominant is the ratio of to c/. If c/, then the effective diffusivity regime applies, and the permeation transient is identical to the standard diffusion transient, with the diffusivity replaced by an effective diffusivity

to account for the fact that trapping leads to slower transport.

In this limit, the breakthrough time, defined as the intersection of the steepest tangent to the diffusion transient with the time axis, will be

where is the thickness of the slab and D is the diffusivity of the gas through the material.

Strong-trapping Regime

In the deep-trapping limit, c/, and no permeation occurs until essentially all the traps have been filled. Then the system quickly reaches steady-state. The breakthrough time is given by

where is the steady dissolved gas concentration at the upstream (x = 0) side.

Case Description

In this scenario, examine reach regime using two input files:

• ver-1d-diffusion.i: where diffusion is the rate-limiting step

• ver-1d-trapping.i: where trapping is the rate-limiting step.

This is the same domain configuration as in Case 1.

Key Parameters

Case 2: Diffusion Limit Input File - Variables

In this case, we'll be highlighting the main changes from Case 1, where we only had diffusion for a single mobile species.

[Variables]
  [mobile]
  []
  [trapped]
  []
[]

• Now, we have two species, trapped and mobile. Similar to Case 1, the mobile variable is our primary variable, as we'll plot the downstream flux for comparison to analytical solutions.

• Both use the default initial concentrations of zero, as well as the default FEM families/order.

A Note on ReferenceResidualProblem

• The ReferenceResidualProblem MOOSE Problem type is designed to allow custom criteria for convergence for separate, coupled physics by using tagged vectors to designate portions of the system matrix.

• These tags are set in the [Problem] block using reference vector and extra_tag_vectors and then used in the *Kernel blocks (of all types).

[Problem]
  type = ReferenceResidualProblem
  extra_tag_vectors = 'ref'
  reference_vector = 'ref'
[]
[Kernels]
  [diff]
    type = Diffusion
    variable = mobile
    extra_vector_tags = ref
  []
[]

Case 2: Diffusion Limit Input File - Coupling Mobile and Trapped

[Kernels]
  [diff]
    type = Diffusion
    variable = mobile
    extra_vector_tags = ref
  []
  [time]
    type = TimeDerivative
    variable = mobile
    extra_vector_tags = ref
  []
  [coupled_time]
    type = CoupledTimeDerivative
    variable = mobile
    v = trapped
    extra_vector_tags = ref
  []
[]

Case 2: Diffusion Limit Input File - Trapped Physics

[NodalKernels]
  [time]
    type = TimeDerivativeNodalKernel
    variable = trapped
  []
  [trapping]
    type = TrappingNodalKernel
    variable = trapped
    alpha_t = 1e15
    N = '${fparse 3.1622e22 / cl}'
    Ct0 = 0.1
    mobile_concentration = 'mobile'
    temperature = ${temperature}
    extra_vector_tags = ref
  []
  [release]
    type = ReleasingNodalKernel
    alpha_r = 1e13
    temperature = ${temperature}
    detrapping_energy = 100
    variable = trapped
  []
[]

Case 2: Diffusion Limit Input File - Executioner

[Executioner]
  type = Transient
  end_time = 3
  dt = .01
  dtmin = .01
  solve_type = NEWTON
  petsc_options_iname = '-pc_type'
  petsc_options_value = 'lu'
  automatic_scaling = true
  verbose = true
  compute_scaling_once = false
[]

Case 2: Strong Trapping Input File -
AuxVariables and AuxKernels

For the deep trapping limit case, we'll cover the additions of objects to determine the empty trapping site concentration.

[AuxVariables]
  [empty_sites]
  []
  [scaled_empty_sites]
  []
  [trapped_sites]
  []
  [total_sites]
  []
[]

[AuxKernels]
  [empty_sites]
    variable = empty_sites
    type = EmptySitesAux
    N = '${fparse N / cl}'
    Ct0 = .1
    trap_per_free = ${trap_per_free}
    trapped_concentration_variables = trapped
  []
  [scaled_empty]
    variable = scaled_empty_sites
    type = NormalizationAux
    normal_factor = ${cl}
    source_variable = empty_sites
  []
  [trapped_sites]
    variable = trapped_sites
    type = NormalizationAux
    normal_factor = ${trap_per_free}
    source_variable = trapped
  []
  [total_sites]
    variable = total_sites
    type = ParsedAux
    expression = 'trapped_sites + empty_sites'
    coupled_variables = 'trapped_sites empty_sites'
  []
[]

Case 2: Numerical Considerations

• The trapping test input file can generate oscillations in the solution due to the feedback loop between the diffusion PDE and trap evolution ODE. Two strategies are used:

[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = 1000
  xmax = 1
[]

[Executioner]
  [TimeStepper]
    type = IterationAdaptiveDT
    dt = 1e-6
    optimal_iterations = 9
    growth_factor = 1.1
    cutback_factor = 0.909
  []
[]

[BCs]
  [left]
    type = FunctionDirichletBC
    variable = mobile
    function = 'BC_func'
    boundary = left
  []
[]

[Functions]
  [BC_func]
    type = ParsedFunction
    expression = '${fparse cl / cl}*tanh( 3 * t )'
  []
[]

Case 2: Trapping Parameter Study

As a reminder, the trapping parameter is the key discriminant to which regime is dominating.

Case 2: Diffusion-Limited Results

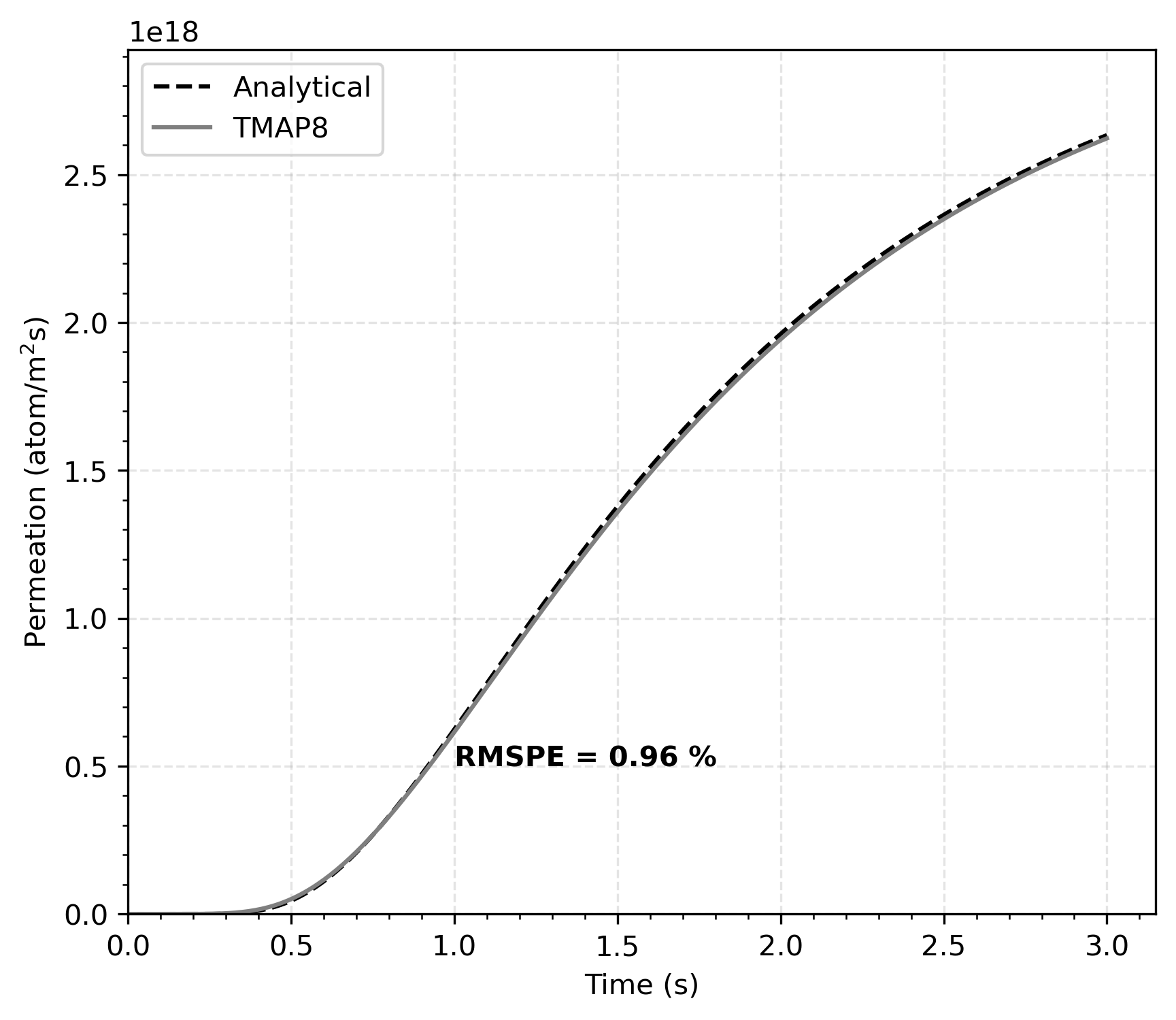
• Trapping slows but doesn't stop diffusion

• Smooth permeation curve

Case 2: Trap-Limited Results

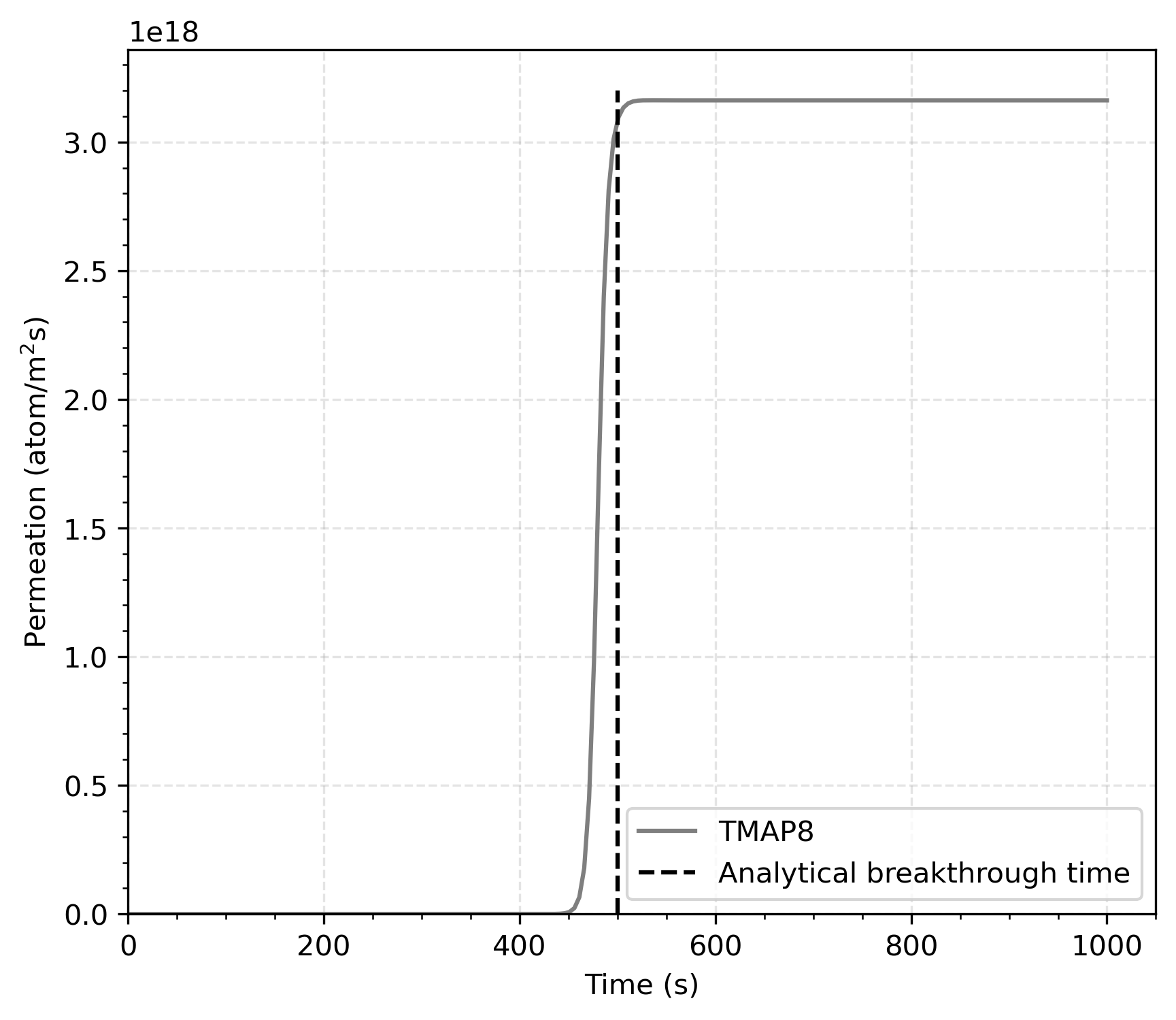
• Must fill traps before significant permeation

• Sharp transition at breakthrough

Case 3: Multiple Trap Types (ver-1dc)

Extended System of Equations

This case is very similar to Case 2, except there are now three different types of traps.

Mobile species with three trap interactions:

Each trap evolves independently (i = 1, 2, 3). Finally, for the empty trapping sites:

Case 3: Base Input File Strategy

• This case introduces the "input file include" capability in practice.

• ver-1dc_base.i contains the mesh, Problem, Variables, Kernels, NodalKernels, Preconditioning, and Executioner settings for both the standard and MMS input files.

• This is done to enable multiple input files to use the same common elements.

• This modular design:

  • Eases maintainability and repeatability

  • Reduces redundancy and errors

  • Allows for case-specific input files

  • Enables more readable highlight of unique physics

Case 3: Base Input File

# This is the base input file for the ver-1dc case.
# This input file is meant to be included within both the ver-1dc.i
# and ver-1dc_mms.i input files to be complete.
# Its purpose is to centralize the capability common to the two cases
# within one file to minimize redundancy and ease maintenance.
# It is not meant to be run on its own.

epsilon_1 = ${units 100 K}
epsilon_2 = ${units 500 K}
epsilon_3 = ${units 800 K}
temperature = ${units 1000 K}
trapping_site_fraction_1 = 0.10 # (-)
trapping_site_fraction_2 = 0.15 # (-)
trapping_site_fraction_3 = 0.20 # (-)
diffusivity = 1 # m^2/s

[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = ${nx_num}
  xmax = 1
[]

[Problem]
  type = ReferenceResidualProblem
  extra_tag_vectors = 'ref'
  reference_vector = 'ref'
[]

[Variables]
  [mobile]
  []
  [trapped_1]
  []
  [trapped_2]
  []
  [trapped_3]
  []
[]

[Kernels]
  [diff]
    type = Diffusion
    variable = mobile
    extra_vector_tags = ref
  []
  [time]
    type = TimeDerivative
    variable = mobile
    extra_vector_tags = ref
  []
  [coupled_time_1]
    type = CoupledTimeDerivative
    variable = mobile
    v = trapped_1
    extra_vector_tags = ref
  []
  [coupled_time_2]
    type = CoupledTimeDerivative
    variable = mobile
    v = trapped_2
    extra_vector_tags = ref
  []
  [coupled_time_3]
    type = CoupledTimeDerivative
    variable = mobile
    v = trapped_3
    extra_vector_tags = ref
  []
[]

[NodalKernels]
  # For first traps
  [time_1]
    type = TimeDerivativeNodalKernel
    variable = trapped_1
  []
  [trapping_1]
    type = TrappingNodalKernel
    variable = trapped_1
    alpha_t = '${trapping_rate_coefficient}'
    N = '${fparse N / cl}'
    Ct0 = '${trapping_site_fraction_1}'
    mobile_concentration = 'mobile'
    temperature = '${temperature}'
    extra_vector_tags = ref
  []
  [release_1]
    type = ReleasingNodalKernel
    alpha_r = '${release_rate_coefficient}'
    temperature = '${temperature}'
    detrapping_energy = '${epsilon_1}'
    variable = trapped_1
  []
  # For second traps
  [time_2]
    type = TimeDerivativeNodalKernel
    variable = trapped_2
  []
  [trapping_2]
    type = TrappingNodalKernel
    variable = trapped_2
    alpha_t = '${trapping_rate_coefficient}'
    N = '${fparse N / cl}'
    Ct0 = '${trapping_site_fraction_2}'
    mobile_concentration = 'mobile'
    temperature = '${temperature}'
    extra_vector_tags = ref
  []
  [release_2]
    type = ReleasingNodalKernel
    alpha_r = '${release_rate_coefficient}'
    temperature = '${temperature}'
    detrapping_energy = '${epsilon_2}'
    variable = trapped_2
  []
  # For third traps
  [time_3]
    type = TimeDerivativeNodalKernel
    variable = trapped_3
  []
  [trapping_3]
    type = TrappingNodalKernel
    variable = trapped_3
    alpha_t = '${trapping_rate_coefficient}'
    N = '${fparse N / cl}'
    Ct0 = '${trapping_site_fraction_3}'
    mobile_concentration = 'mobile'
    temperature = '${temperature}'
    extra_vector_tags = ref
  []
  [release_3]
    type = ReleasingNodalKernel
    alpha_r = '${release_rate_coefficient}'
    temperature = '${temperature}'
    detrapping_energy = '${epsilon_3}'
    variable = trapped_3
  []
[]

[Preconditioning]
  [smp]
    type = SMP
    full = true
  []
[]

[Executioner]
  type = Transient
  end_time = ${simulation_time}
  dtmax = ${time_interval_max}
  solve_type = NEWTON
  scheme = ${scheme}
  petsc_options_iname = '-pc_type'
  petsc_options_value = 'lu'
  line_search = 'none'
[]

Case 3: Defining Multiple Traps

Multiple sites can have different properties through the use of separate sets of NodalKernels to represent the unique properties of each trap.

[NodalKernels]
  [time_1]
    type = TimeDerivativeNodalKernel
    variable = trapped_1
  []

  [trapping_1]
    type = TrappingNodalKernel
    variable = trapped_1
    alpha_t = '${trapping_rate_coefficient}'
    N = '${fparse N / cl}'
    Ct0 = '${trapping_site_fraction_1}'
    mobile_concentration = 'mobile'
    temperature = '${temperature}'
    extra_vector_tags = ref
  []

  [release_1]
    type = ReleasingNodalKernel
    alpha_r = '${release_rate_coefficient}'
    temperature = '${temperature}'
    detrapping_energy = '${epsilon_1}'
    variable = trapped_1
  []
[]

Case 3: Three Trap Parameters

Three traps that are relatively weak are assumed to be active in the slab. Other parameters are the same as the trap in the effective diffusivity limit in ver-1d.

• Trap Type 1

  • Trapping site fraction: 0.1

  • = 100 K

• Trap Type 2

  • Trapping site fraction: 0.15

  • = 500 K

• Trap Type 3

  • Trapping site fraction: 0.2

  • = 800 K

Case 3: Verification Results

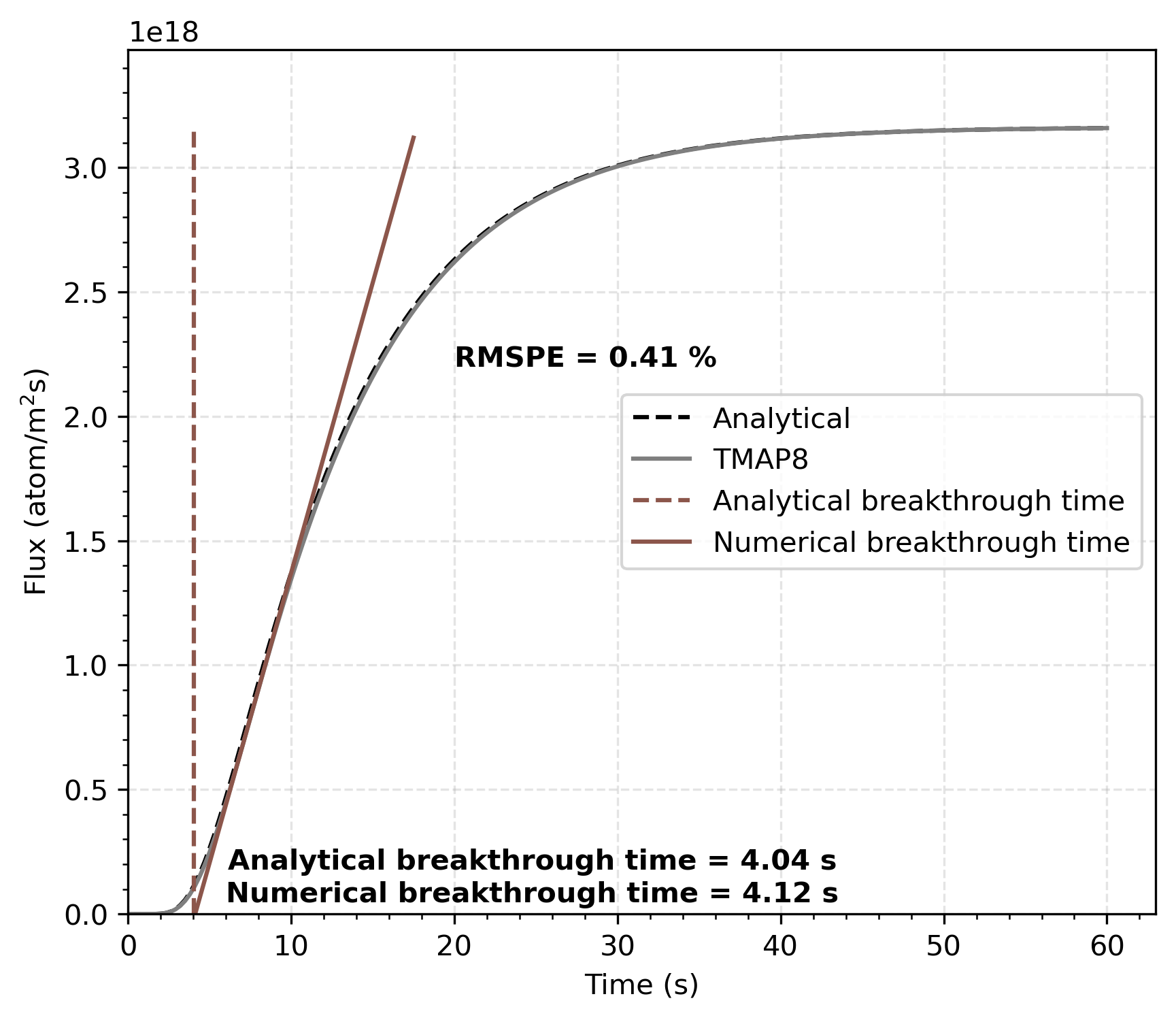
• Breakthrough time: 4.04 s (analytical) vs 4.12 s (TMAP8)

• Combined effect of all three traps

Case 3: MMS Verification Approach

Exact solutions and forcing functions:

[exact_u]
  type = ParsedFunction
  expression = 't*cos(x)'
[]
[forcing_u]
  type = ParsedFunction
  expression = '(1/2)*N*frac1*cos(x) + (1/2)*N*frac2*cos(x) + (1/2)*N*frac3*cos(x) + D*t*cos(x) + cos(x)'
  symbol_names = 'N frac1 frac2 frac3 D'
  symbol_values = '${N} ${frac1} ${frac2} ${frac3} ${diffusivity}'
[]
[exact_t1]
  type = ParsedFunction
  expression = '(1/2)*N*frac1*(t*cos(x) + 1)'
  symbol_names = 'frac1 N'
  symbol_values = '${frac1} ${N}'
[]
[forcing_t1]
  type = ParsedFunction
  expression = '(1/2)*frac1*(N*cos(x) + alphar*N*(t*cos(x) + 1)*exp(-epsilon_1/temperature) - alphat*t*(-t*cos(x) + 1)*cos(x))'
  symbol_names = 'alphar alphat N frac1 temperature epsilon_1'
  symbol_values = '${alphar} ${alphat} ${N} ${frac1} ${temperature} ${epsilon_1}'
[]
[exact_t2]
  type = ParsedFunction
  expression = '(1/2)*N*frac2*(t*cos(x) + 1)'
  symbol_names = 'frac2 N'
  symbol_values = '${frac2} ${N}'
[]
[forcing_t2]
  type = ParsedFunction
  expression = '(1/2)*frac2*(N*cos(x) + alphar*N*(t*cos(x) + 1)*exp(-epsilon_2/temperature) - alphat*t*(-t*cos(x) + 1)*cos(x))'
  symbol_names = 'alphar alphat N frac2 temperature epsilon_2'
  symbol_values = '${alphar} ${alphat} ${N} ${frac2} ${temperature} ${epsilon_2}'
[]
[exact_t3]
  type = ParsedFunction
  expression = '(1/2)*N*frac3*(t*cos(x) + 1)'
  symbol_names = 'frac3 N'
  symbol_values = '${frac3} ${N}'
[]
[forcing_t3]
  type = ParsedFunction
  expression = '(1/2)*frac3*(N*cos(x) + alphar*N*(t*cos(x) + 1)*exp(-epsilon_3/temperature) - alphat*t*(-t*cos(x) + 1)*cos(x))'
  symbol_names = 'alphar alphat N frac3 temperature epsilon_3'
  symbol_values = '${alphar} ${alphat} ${N} ${frac3} ${temperature} ${epsilon_3}'
[]

Case 3: MMS Verification Approach (continued)

Application of functions to Kernels/NodalKernels/BCs to "force" exact solution:

[Kernels]
  [diff]
    type = Diffusion
    variable = mobile
    extra_vector_tags = ref
  []
  [time]
    type = TimeDerivative
    variable = mobile
    extra_vector_tags = ref
  []
  [coupled_time_1]
    type = CoupledTimeDerivative
    variable = mobile
    v = trapped_1
    extra_vector_tags = ref
  []
  [coupled_time_2]
    type = CoupledTimeDerivative
    variable = mobile
    v = trapped_2
    extra_vector_tags = ref
  []
  [coupled_time_3]
    type = CoupledTimeDerivative
    variable = mobile
    v = trapped_3
    extra_vector_tags = ref
  []

  [forcing]
    type = BodyForce
    variable = mobile
    function = 'forcing_u'
  []
[]

[NodalKernels]
  # For first traps
  [time_1]
    type = TimeDerivativeNodalKernel
    variable = trapped_1
  []
  [trapping_1]
    type = TrappingNodalKernel
    variable = trapped_1
    alpha_t = '${trapping_rate_coefficient}'
    N = '${fparse N / cl}'
    Ct0 = '${trapping_site_fraction_1}'
    mobile_concentration = 'mobile'
    temperature = '${temperature}'
    extra_vector_tags = ref
  []
  [release_1]
    type = ReleasingNodalKernel
    alpha_r = '${release_rate_coefficient}'
    temperature = '${temperature}'
    detrapping_energy = '${epsilon_1}'
    variable = trapped_1
  []
  # For second traps
  [time_2]
    type = TimeDerivativeNodalKernel
    variable = trapped_2
  []
  [trapping_2]
    type = TrappingNodalKernel
    variable = trapped_2
    alpha_t = '${trapping_rate_coefficient}'
    N = '${fparse N / cl}'
    Ct0 = '${trapping_site_fraction_2}'
    mobile_concentration = 'mobile'
    temperature = '${temperature}'
    extra_vector_tags = ref
  []
  [release_2]
    type = ReleasingNodalKernel
    alpha_r = '${release_rate_coefficient}'
    temperature = '${temperature}'
    detrapping_energy = '${epsilon_2}'
    variable = trapped_2
  []
  # For third traps
  [time_3]
    type = TimeDerivativeNodalKernel
    variable = trapped_3
  []
  [trapping_3]
    type = TrappingNodalKernel
    variable = trapped_3
    alpha_t = '${trapping_rate_coefficient}'
    N = '${fparse N / cl}'
    Ct0 = '${trapping_site_fraction_3}'
    mobile_concentration = 'mobile'
    temperature = '${temperature}'
    extra_vector_tags = ref
  []
  [release_3]
    type = ReleasingNodalKernel
    alpha_r = '${release_rate_coefficient}'
    temperature = '${temperature}'
    detrapping_energy = '${epsilon_3}'
    variable = trapped_3
  []

  [forcing_1]
    type = UserForcingFunctionNodalKernel
    variable = trapped_1
    function = forcing_t1
  []
  [forcing_2]
    type = UserForcingFunctionNodalKernel
    variable = trapped_2
    function = forcing_t2
  []
  [forcing_3]
    type = UserForcingFunctionNodalKernel
    variable = trapped_3
    function = forcing_t3
  []
[]

[BCs]
  [dirichlet]
    type = FunctionDirichletBC
    variable = mobile
    function = 'exact_u'
    boundary = 'left right'
  []
[]

Case 3: MMS Spatial Convergence

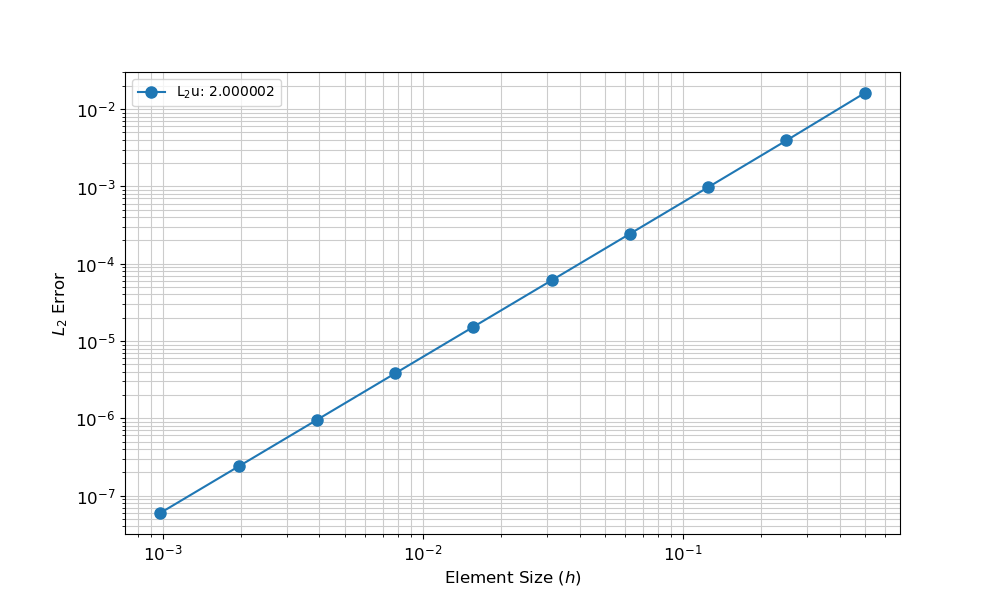
• 10 levels of mesh refinement

• Confirms proper implementation

• Quadratic convergence as expected

Modifying Input Files - Exercise

Try These Changes to ver-1dd.i:

Tips and Tricks

Debug Strategies

• Start with coarse mesh, refine gradually

• Use simple BCs first, add complexity

• Compare with analytical solutions when available

Building Complex Cases

Use a progressive development strategy:

1. Start Simple: Pure diffusion (ver-1dd)

2. Add One Trap: Test both regimes (ver-1d)

3. Multiple Traps: Build incrementally (ver-1dc)

4. Validate Each Step: Compare with theory

Performance Considerations

Computational Efficiency Tips

[Executioner]
  # For testing - coarse/fast
  nl_abs_tol = 1e-8
  nl_rel_tol = 1e-6

  # For verification - fine/accurate
  nl_abs_tol = 1e-12
  nl_rel_tol = 1e-10
[]

[Mesh]
  # Testing: nx = 100
  # Verification: nx = 1000
[]

Parallel Execution

mpirun -np 4 ~/projects/TMAP8/tmap8-opt -i input.i

Advanced Features in TMAP8

Beyond These Examples

• 2D/3D Geometries: Change dim in [Mesh]

• Multiple Materials: Use [Materials] block

• Coupled Physics: Heat transfer, mechanics

• Custom Kernels: Extend with C++

Example: Temp. Dependence Directly in Input

[Materials]
  [diffusivity]
    # (m2/s) tritium diffusivity
    type = DerivativeParsedMaterial
    property_name = 'diffusivity'
    coupled_variables = 'temperature'
    expression = '${tritium_diffusivity_prefactor}*exp(-${tritium_diffusivity_energy}/${ideal_gas_constant}/temperature)'
  []
[]

Key Takeaways

• Input File Structure: Hierarchical blocks define physics

• Progressive Complexity: Build from simple to complex

• Verification Strategy: Compare with analytical solutions

  • ver-1dd: RMSPE = 0.14%

  • ver-1d: RMSPE = 0.96%

  • ver-1dc: RMSPE = 0.41%

• Best Practices:

  • Use base input files for modularity

  • Start with coarse meshes for development

  • Validate each physics addition

  • Document parameter choices

Hands-On Exercise

Your Turn: Modify ver-1d

1. Open ver-1d-diffusion.i in your editor

2. Change detrapping energy:

3. Run the simulation

4. Compare breakthrough time with original

Questions to Consider:

• How does breakthrough time change?

• Which regime are we in now?

• What value does this correspond to?