GPBR200 Pebble Surrogate Modeling
Contact: Zachary M. Prince, [email protected]
Model link: GPBR200 Pebble Surrogate
Motivation
In the fully coupled GPBR200 model, the pebble heat conduction multi-scale simulation takes up a significant portion of the run-time and vast majority of memory. When the model is utilized for stochastic analysis, this memory usage puts a significant damper on the potential parallelism of the sampling. This is because only a small number of instances of the model would be able to run simultaneously on a single compute node. For example, the fully-coupled simulation requires approximately 75 GB and a single node on the Sawtooth HPC at INL has 160GB per node; so only two samples can be run on each node, despite having 48 available processors.
One solution to this memory constraint is to represent the pebble heat conduction with a small, fast-evaluating surrogate to the finite element model. There are four independent parameters to the pebble model: kernel radius, filling factor, power density, and pebble surface temperature. The first two are design parameters used in the sensitivity analysis demonstration; the second two are values computed by the neutronics and thermal hydraulics applications. The quantities of interest from the pebble model are the average fuel and moderator temperatures. Two surrogates for each of these quantities can thus be represented in the following form:
(1)where is a generic functional form of the surrogate.
The MOOSE stochastic tools module (STM) provides the Surrogate system, which allows training and evaluation of such surrogates (Slaughter et al., 2023). The remainder of this exposition will detail how use the STM to produce training data from the pebble heat conduction model, train a simple (but effective) surrogate model, and how to utilize the surrogate in the multiphysics simulation.
Sampling
In this input, the ParameterStudy syntax from the STM is used to randomly sample various configurations of the input parameters of the pebble model and gather the fuel and moderator temperatures. For this exposition, 10,000 samples were specified. Each sample takes approximately 150 ms to run, so executing this input with 24 processors takes about one minute.
[ParameterStudy]
input = gpbr200_ss_bsht_pebble_triso.i
parameters = 'kernel_radius
filling_factor
Postprocessors/pebble_surface_temp/default
Postprocessors/porous_media_power_density/default'
quantities_of_interest = 'fuel_average_temp/value moderator_average_temp/value'
sampling_type = lhs
num_samples = 10000
distributions = 'uniform uniform uniform uniform'
uniform_lower_bound = '1.5e-4 0.05 300 0'
uniform_upper_bound = '3.0e-4 0.2 2273 4.0e7'
compute_statistics = false
sampler_column_names = 'kernel_radius filling_factor pebble_surface_temp porous_media_power_density'
output_type = csv
[]The result is a CSV file with the parameter and temperature values for each sample. A histogram of the temperatures is shown in Figure 1.
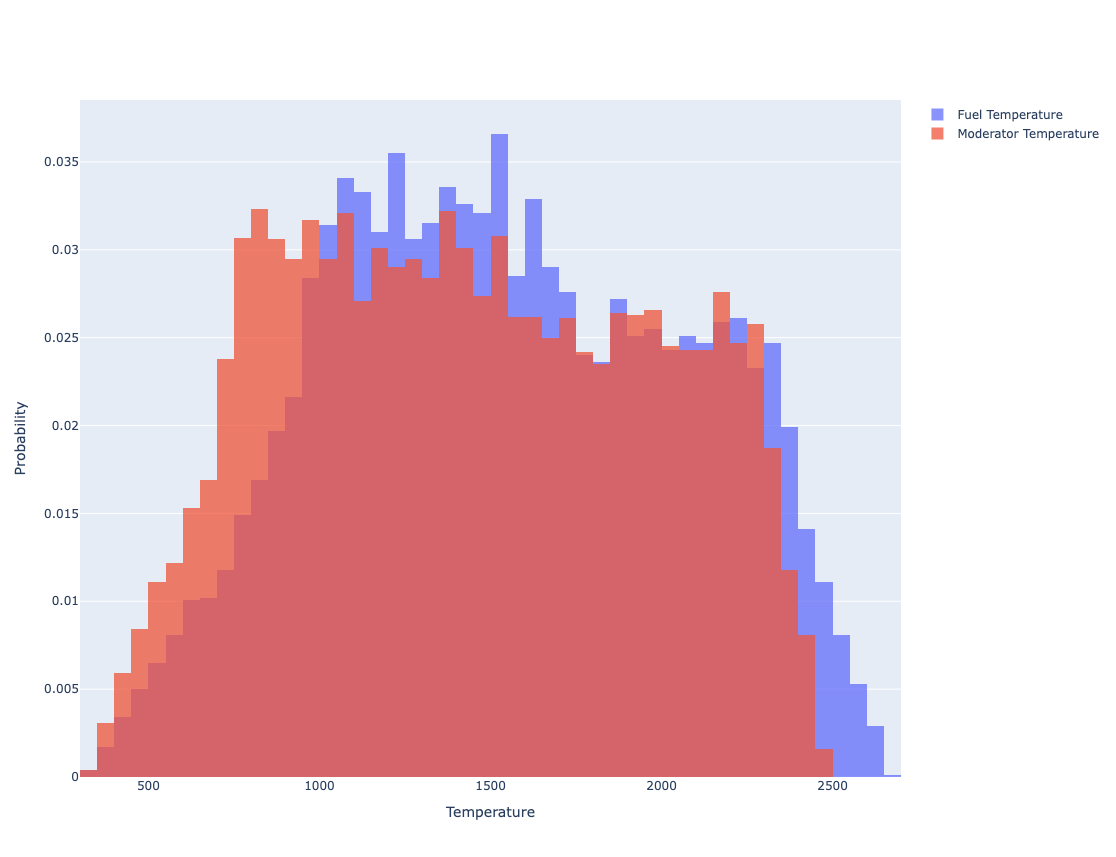
Figure 1: Probability density of fuel and moderator temperature from sampling pebble heat conduction model with 10,000 samples.
Surrogate Training
In this input, the data produced in the previous section is used to train STM surrogates. The PolynomialRegression surrogate was chosen for its simplicity and robustness.
First, the data is loaded from the CSV file into a Sampler and VectorPostprocessor.
[Samplers]
[csv]
type = CSVSampler
samples_file = stm_pebble_sampling_csv_study_results_0001.csv
column_names = 'kernel_radius filling_factor pebble_surface_temp porous_media_power_density'
[]
[]
[VectorPostprocessors]
[data]
type = CSVReaderVectorPostprocessor
csv_file = stm_pebble_sampling_csv_study_results_0001.csv
outputs = none
[]
[]Next, Trainers and Surrogates are defined, which utilize the sampling and vector-postprocessor data to produce the metadata necessary for generating the surrogate. For PolynomialRegression this involves an ordinary least-squares solve to evaluate coefficients of a multi-variate monomial. The max_degree parameter specifies the degree of the monomial produced; a 4 dimensional basis with a degree of 4 results in 70 coefficients. The cv_type parameter triggers a cross validation calculation, giving a score on how well the surrogate fits the provided training data.
[GlobalParams]
sampler = csv
cv_type = k_fold
regression_type = ols
[]
[Trainers]
[pr4_Tfuel_train]
type = PolynomialRegressionTrainer
max_degree = 4
response = data/fuel_average_temp:value
cv_surrogate = pr4_Tfuel
execute_on = TIMESTEP_BEGIN
[]
[pr4_Tmod_train]
type = PolynomialRegressionTrainer
max_degree = 4
response = data/moderator_average_temp:value
cv_surrogate = pr4_Tmod
execute_on = TIMESTEP_BEGIN
[]
[]
[Surrogates]
[pr4_Tfuel]
type = PolynomialRegressionSurrogate
trainer = pr4_Tfuel_train
[]
[pr4_Tmod]
type = PolynomialRegressionSurrogate
trainer = pr4_Tmod_train
[]
[]A CrossValidationScores reporter is defined in order to output the result of the cross validation calculation. In this example, four surrogates are trained with various degrees. Table 1 lists these scores; a smaller number means a smaller difference from the training data.
[Reporters]
[cv]
type = CrossValidationScores
models = 'pr1_Tfuel pr1_Tmod
pr2_Tfuel pr2_Tmod
pr4_Tfuel pr4_Tmod
pr6_Tfuel pr6_Tmod'
execute_on = TIMESTEP_END
[]
[]Table 1: K-fold cross validation scores for various pebble heat conduction surrogates
| Monomial Degree | Number of Coefficients | Score | Score |
|---|---|---|---|
| 1 | 5 | 47.9 | 32.9 |
| 2 | 15 | 17.7 | 11.8 |
| 4 | 70 | 6.90 | 4.68 |
| 6 | 210 | 3.43 | 2.32 |
Finally, the surrogate metadata is outputted via a SurrogateTrainerOutput object. This produces folders in the working directory which can be loaded in the future by the surrogate object for evaluation.
[Outputs]
json = true
[model]
type = SurrogateTrainerOutput
trainers = 'pr1_Tfuel_train pr1_Tmod_train
pr2_Tfuel_train pr2_Tmod_train
pr4_Tfuel_train pr4_Tmod_train
pr6_Tfuel_train pr6_Tmod_train'
[]
[]Surrogate Evaluation
This section presents the modifications to the main application input from the coupled model that replaces the pebble heat conduction multi-app with the trained surrogate models. The replacement is somewhat straight-forward: surrogates are loaded from the metadata previous produced and the SurrogateModelArrayAuxKernel evaluates the surrogates to populate the fuel and moderator temperature variables.
@@ -1,70 +1,27 @@
[MultiApps]
# Reactor TH.
[pronghorn_th]
type = FullSolveMultiApp
input_files = gpbr200_ss_phth_reactor.i
keep_solution_during_restore = true
execute_on = 'TIMESTEP_END'
- []
-
- # Pebble conduction
- [pebble_conduction]
- type = FullSolveMultiApp
- input_files = gpbr200_ss_bsht_pebble_triso.i
- no_restore = true
- positions_objects = 'element element element element element
- element element element element element
- element element element'
- cli_args = 'kernel_radius=${kernel_radius};filling_factor=${filling_factor}'
- execute_on = TIMESTEP_BEGIN
[]
[]
[Transfers]
# TO Pronghorn.
[to_pronghorn_total_power_density]
type = MultiAppCopyTransfer
to_multi_app = pronghorn_th
source_variable = total_power_density
variable = power_density
[]
# FROM Pronghorn.
[from_pronghorn_Tsolid]
type = MultiAppCopyTransfer
from_multi_app = pronghorn_th
source_variable = T_solid
variable = T_solid
[]
-
- # To pebble conduction
- [to_pebble_conduction_Tsolid]
- type = MultiAppVariableValueSamplePostprocessorTransfer
- to_multi_app = pebble_conduction
- postprocessor = pebble_surface_temp
- source_variable = T_solid
- []
- [to_pebble_conduction_power_density]
- type = MultiAppVariableValueSamplePostprocessorTransfer
- to_multi_app = pebble_conduction
- postprocessor = porous_media_power_density
- source_variable = partial_power_density
- map_array_variable_components_to_child_apps = true
- []
-
- # From pebble conduction
- [from_pebble_conduction_Tfuel]
- type = MultiAppVariableValueSamplePostprocessorTransfer
- from_multi_app = pebble_conduction
- postprocessor = fuel_average_temp
- source_variable = triso_temperature
- map_array_variable_components_to_child_apps = true
- []
- [from_pebble_conduction_Tmod]
- type = MultiAppVariableValueSamplePostprocessorTransfer
- from_multi_app = pebble_conduction
- postprocessor = moderator_average_temp
- source_variable = graphite_temperature
- map_array_variable_components_to_child_apps = true
- []
[](+ htgr/gpbr200/pebble_surrogate_modeling/gpbr200_ss_gfnk_reactor.i)
[Surrogates]
[Tfuel_model]
type = PolynomialRegressionSurrogate
filename = stm_pebble_surrogate_model_pr6_Tfuel_train.rd
[]
[Tmod_model]
type = PolynomialRegressionSurrogate
filename = stm_pebble_surrogate_model_pr6_Tmod_train.rd
[]
[]
[AuxKernels]
[Tfuel_aux]
type = SurrogateModelArrayAuxKernel
variable = triso_temperature
model = Tfuel_model
parameters = '${kernel_radius} ${filling_factor} T_solid partial_power_density'
coupled_variables = T_solid
coupled_array_variables = partial_power_density
execute_on = TIMESTEP_BEGIN
[]
[Tmod_aux]
type = SurrogateModelArrayAuxKernel
variable = graphite_temperature
model = Tmod_model
parameters = '${kernel_radius} ${filling_factor} T_solid partial_power_density'
coupled_variables = T_solid
coupled_array_variables = partial_power_density
execute_on = TIMESTEP_BEGIN
[]
[]The resulting eigenvalue from running this input is 1.00129, which is 0.4 pcm greater than the multi-app version. The approximate memory this simulation required is 4.8 GB, compared to the previous 75 GB. Furthermore, Table 2 shows the improvement in runtime compared to the multi-app simulation.
Table 2: Run times for GPBR200 multiphysics simulation using pebble surrogates with varying number of processors
| Processors | Surrogate Version (min) | Multi-App Version (min) |
|---|---|---|
| 1 | 18 | — |
| 2 | 12 | — |
| 4 | 9 | 40 |
| 8 | 6 | 26 |
| 16 | 4 | 7 |
| 32 | 3 | 4 |
References
- Andrew E Slaughter, Zachary M Prince, Peter German, Ian Halvic, Wen Jiang, Benjamin W Spencer, Somayajulu L N Dhulipala, and Derek R Gaston.
MOOSE Stochastic Tools: A module for performing parallel, memory-efficient in situ stochastic simulations.
SoftwareX, 22:101345, 2023.
doi:10.1016/j.softx.2023.101345.[BibTeX]