GPBR200 Multiphysics Coupling
Contact: Zachary M. Prince, [email protected]
Model link: GPBR200 Coupled Model
Here the input for the fully coupled GPBR200 model is presented. This combines the physics presented in the neutronics model, thermal hydraulics model, and pebble thermomechanics model.
MultiApp Structure
Figure 1 shows the MultiApp structure employed for the multiphysics, along with the transfers of coupled fields (Gaston et al., 2015). The neutronics-depletion input serves as the main application, transferring power density to the thermal hydraulics and pebble heat conduction applications. The solid temperature is received from the TH application to evaluate cross sections in the reflector regions and transferred to the pebble applications for the pebble surface boundary condition. Finally, the fuel and moderator temperatures are received from the pebble applications for cross-section evaluation in the pebble bed.
.](../../media/gpbr200/gpbr200_multiapp_diagram.jpg)
Figure 1: MultiApp structure of GPBR200 equilibrium core from Prince et al. (2024).
The order of operations for a given fixed-point iteration is:
Pebble heat conduction solves
Streamline depletion solve
Neutronics eigenvalue solve
Thermal hydraulics solve
Input Modifications
This section focuses on the key differences in the coupled inputs from the stand-alone physics inputs previously presented.
Pebble Heat Conduction Input
There are no meaningful modifications to the pebble heat conduction input, the only adjustment is in the Outputs to reduce the amount of screen output.
@@ -1,3 +1,3 @@
[Outputs]
- csv = true
+ console = false
[](+ htgr/gpbr200/coupling/gpbr200_ss_bsht_pebble_triso.i)
Thermal Hydraulics Input
The only modification to the thermal hydraulics input is the removal of the power density auxiliary kernel and the supporting volume postprocessor.
@@ -1,86 +1,76 @@
[AuxKernels]
- [power_density]
- type = ParsedAux
- variable = power_density
- expression = '${total_power} / volume'
- functor_names = 'volume'
- execute_on = 'INITIAL'
- []
[vel_x]
type = InterstitialFunctorAux
variable = vel_x
superficial_variable = superficial_vel_x
phase = fluid
porosity = porosity
[]
[vel_y]
type = InterstitialFunctorAux
variable = vel_y
superficial_variable = superficial_vel_y
phase = fluid
porosity = porosity
[]
[]
[Postprocessors]
# General checks.
[pp00_inlet_mfr]
type = VolumetricFlowRate
vel_x = 'superficial_vel_x'
vel_y = 'superficial_vel_y'
advected_quantity = rho
boundary = inlet
rhie_chow_user_object = pins_rhie_chow_interpolator
execute_on = 'INITIAL TIMESTEP_END'
[]
[pp01_outlet_mfr]
type = VolumetricFlowRate
vel_x = 'superficial_vel_x'
vel_y = 'superficial_vel_y'
advected_quantity = rho
boundary = outlet
rhie_chow_user_object = pins_rhie_chow_interpolator
execute_on = 'INITIAL TIMESTEP_END'
[]
[pp02_inlet_pressure]
type = SideAverageValue
variable = pressure
boundary = 'inlet'
execute_on = 'INITIAL TIMESTEP_END'
[]
[pp03_total_power]
type = ElementIntegralVariablePostprocessor
variable = power_density
block = '${heated_blocks}'
execute_on = 'INITIAL TIMESTEP_END'
[]
[pp04_T_oulet]
type = SideAverageValue # Fix it with weighted thing
variable = T_fluid
boundary = 'outlet'
[]
[pp05_rpv_temp]
type = ElementAverageValue
variable = T_solid
block = '${rpv_blocks}'
[]
[pp06_rpv_temp_max]
type = ElementExtremeValue
variable = T_solid
block = '${rpv_blocks}'
[]
-
- [volume]
- type = VolumePostprocessor
- block = '${heated_blocks}'
- force_preaux = true
- execute_on = 'INITIAL'
- outputs = none
- []
[]
[Outputs]
exodus = true
csv = true
execute_on = 'FINAL'
+
+ # Reduce console output
+ print_linear_residuals = false
+ print_linear_converged_reason = false
+ print_nonlinear_converged_reason = false
[](+ htgr/gpbr200/coupling/gpbr200_ss_phth_reactor.i)
Neutronics-Depletion Input
The majority of the input modifications are in the neutronics input, which serves as the main application; defining the MultiApps and Transfers.
First, the thermal hydraulics application is defined, with transfers for the power density to the sub-application and solid temperature from the application. In order to speed up steady-state convergence of the pseudo-transient simulation, keep_solution_during_restore = true is specified.
[MultiApps]
[pronghorn_th]
type = FullSolveMultiApp
input_files = gpbr200_ss_phth_reactor.i
keep_solution_during_restore = true
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
[to_pronghorn_total_power_density]
type = MultiAppCopyTransfer
to_multi_app = pronghorn_th
source_variable = total_power_density
variable = power_density
[]
[from_pronghorn_Tsolid]
type = MultiAppCopyTransfer
from_multi_app = pronghorn_th
source_variable = T_solid
variable = T_solid
[]
[]Next, the pebble heat conduction MultiApp is defined. A Positions object is defined to specify the location of the applications. For this model an application is defined for each cell in the pebble bed region. This position object is repeated for each pebble burnup group, since each group has a unique power density. The result is a total of applications. For consistency in the TRISO geometry and pebble composition, the kernel radius and filling factor are transferred at application creation via cli_args. The solid temperature is transferred to the postprocessor of the sub-applications, based on their position. The power density is similarly transferred, except the partial_power_density is an array variable where each component corresponds to a burnup group. Finally, the fuel and moderator temperature are transferred from the sub-applications, again based on their position and burnup group index.
[Positions]
[element]
type = ElementCentroidPositions
block = ${fuel_blocks}
[]
[]
[MultiApps]
[pebble_conduction]
type = FullSolveMultiApp
input_files = gpbr200_ss_bsht_pebble_triso.i
no_restore = true
positions_objects = 'element element element element element
element element element element element
element element element'
cli_args = 'kernel_radius=${kernel_radius};filling_factor=${filling_factor}'
execute_on = TIMESTEP_BEGIN
[]
[]
[Transfers]
[to_pebble_conduction_Tsolid]
type = MultiAppVariableValueSamplePostprocessorTransfer
to_multi_app = pebble_conduction
postprocessor = pebble_surface_temp
source_variable = T_solid
[]
[to_pebble_conduction_power_density]
type = MultiAppVariableValueSamplePostprocessorTransfer
to_multi_app = pebble_conduction
postprocessor = porous_media_power_density
source_variable = partial_power_density
map_array_variable_components_to_child_apps = true
[]
[from_pebble_conduction_Tfuel]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = pebble_conduction
postprocessor = fuel_average_temp
source_variable = triso_temperature
map_array_variable_components_to_child_apps = true
[]
[from_pebble_conduction_Tmod]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = pebble_conduction
postprocessor = moderator_average_temp
source_variable = graphite_temperature
map_array_variable_components_to_child_apps = true
[]
[]For easier visualization, several auxiliary variables are defined representing the max power density, fuel temperature, and moderator temperature across burnup groups.
[AuxVariables]
[Tfuel_max]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
[]
[Tmod_max]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
[]
[ppd_max]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
[]
[]
[AuxKernels]
# Max temperatures and power
[Tfuel_max_aux]
type = ArrayVarReductionAux
variable = Tfuel_max
array_variable = triso_temperature
value_type = max
execute_on = TIMESTEP_END
[]
[Tmod_max_aux]
type = ArrayVarReductionAux
variable = Tmod_max
array_variable = graphite_temperature
value_type = max
execute_on = TIMESTEP_END
[]
[ppd_max_aux]
type = ArrayVarReductionAux
variable = ppd_max
array_variable = partial_power_density
value_type = max
execute_on = TIMESTEP_END
[]
[]Results
The input must be run with an executable including Griffin, Pronghorn, and Bison, i.e. blue-crab-opt:
mpiexec -n 16 blue_crab-opt -i gpbr200_ss_gfnk_reactor.i
The resulting eigenvalue is approximately 1.00125. Figure 2 shows the resulting power density, fast scalar flux, and thermal flux. Figure 3 shows the resulting fluid velocity, pressure, temperature, and solid temperature. Figure 4 shows the resulting max power density, fuel temperature, and moderator temperature across burnup groups.
Figure 2: GPBR200 neutronics selected field variables
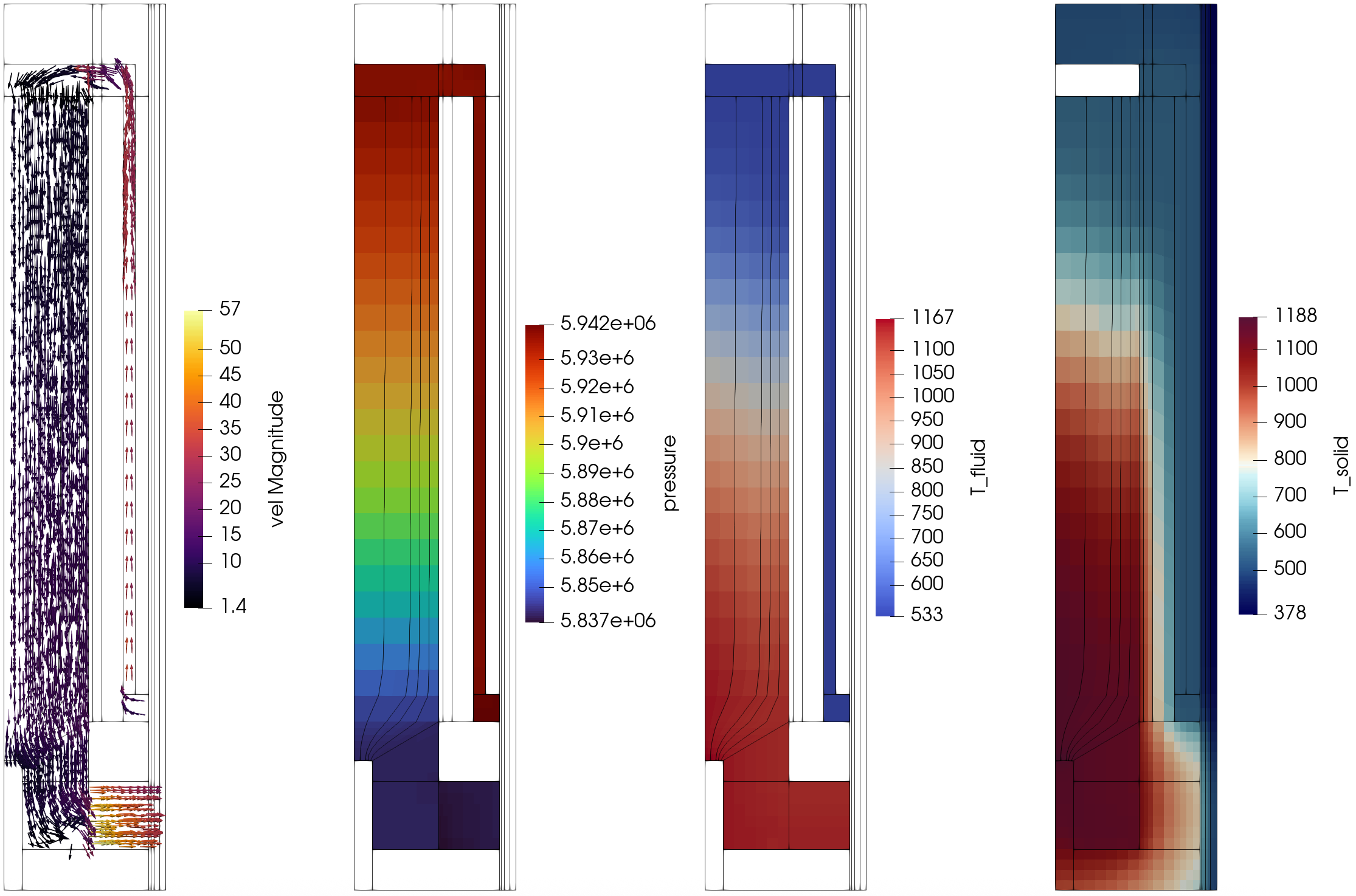
Figure 3: GPBR200 fluids selected field variables
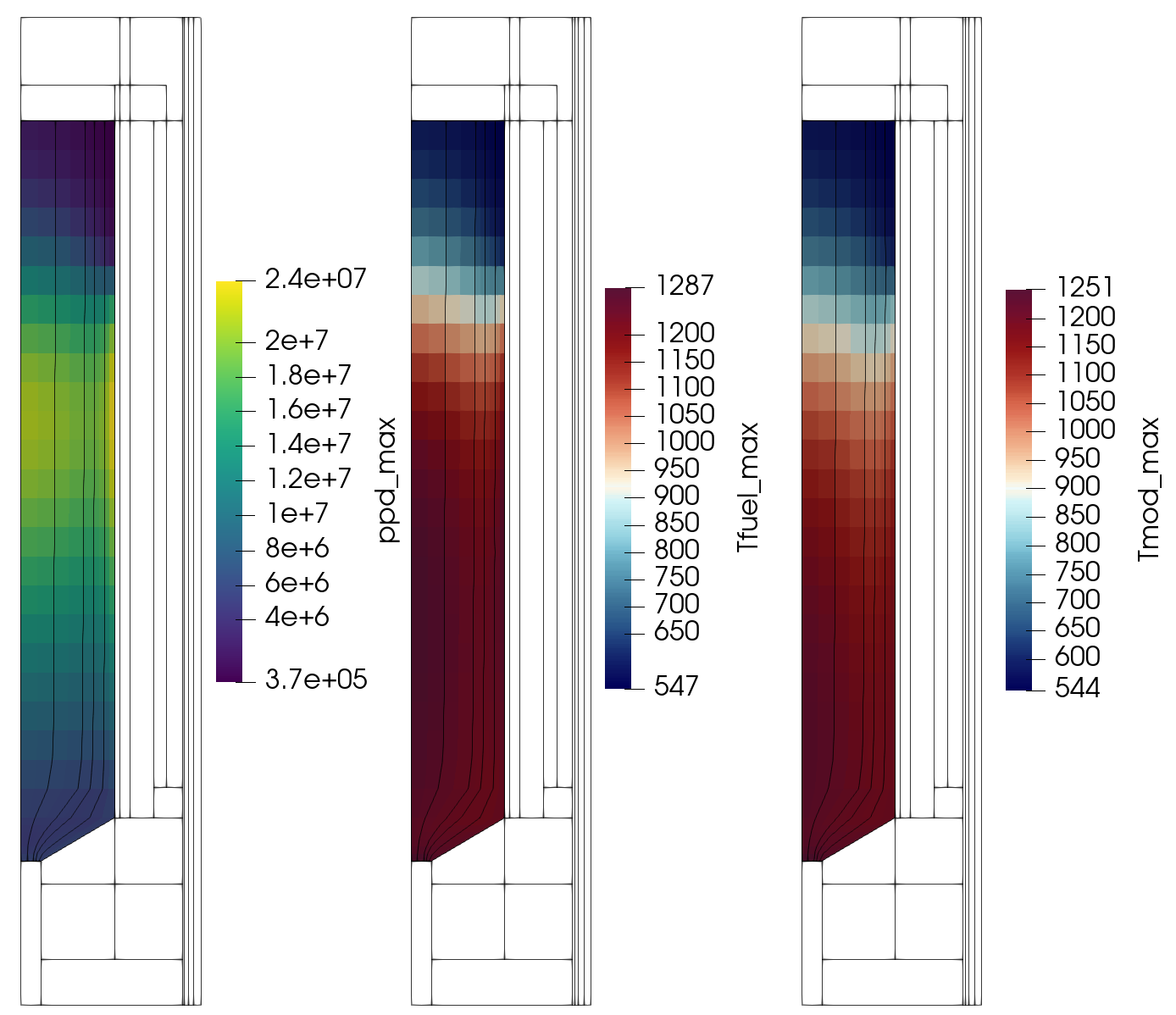
Figure 4: GPBR200 pebble heat conduction selected field variables
The use of 16 processors in the command listing is somewhat arbitrary, Table 1 shows the expected scaling performance.
Table 1: Run times for GPBR200 multiphysics simulation with varying number of processors
| Processors | Run-time (min) |
|---|---|
| 4 | 40 |
| 8 | 26 |
| 16 | 7 |
| 32 | 4 |
References
- Derek R Gaston, Cody J Permann, John W Peterson, Andrew E Slaughter, David Andrš, Yaqi Wang, Michael P Short, Danielle M Perez, Michael R Tonks, Javier Ortensi, and others.
Physics-based multiscale coupling for full core nuclear reactor simulation.
Annals of Nuclear Energy, 84:45–54, 2015.[BibTeX]
@article{Gaston2015, author = "Gaston, Derek R and Permann, Cody J and Peterson, John W and Slaughter, Andrew E and Andr{\v{s}}, David and Wang, Yaqi and Short, Michael P and Perez, Danielle M and Tonks, Michael R and Ortensi, Javier and others", title = "Physics-based multiscale coupling for full core nuclear reactor simulation", journal = "Annals of Nuclear Energy", volume = "84", pages = "45--54", year = "2015", publisher = "Elsevier" } - Zachary M. Prince, Paolo Balestra, Javier Ortensi, Sebastian Schunert, Olin Calvin, Joshua T. Hanophy, Kun Mo, and Gerhard Strydom.
Sensitivity analysis, surrogate modeling, and optimization of pebble-bed reactors considering normal and accident conditions.
Nuclear Engineering and Design, 428:113466, 2024.
doi:https://doi.org/10.1016/j.nucengdes.2024.113466.[BibTeX]
@article{prince2024Sensitivity, author = "Prince, Zachary M. and Balestra, Paolo and Ortensi, Javier and Schunert, Sebastian and Calvin, Olin and Hanophy, Joshua T. and Mo, Kun and Strydom, Gerhard", title = "Sensitivity analysis, surrogate modeling, and optimization of pebble-bed reactors considering normal and accident conditions", journal = "Nuclear Engineering and Design", volume = "428", pages = "113466", year = "2024", issn = "0029-5493", doi = "https://doi.org/10.1016/j.nucengdes.2024.113466" }
(htgr/gpbr200/pebble_thermomechanics/gpbr200_ss_bsht_pebble_triso.i)
# ==============================================================================
# Model description:
# Equilibrium core neutronics model coupled with TH and pebble temperature
# models.
# ------------------------------------------------------------------------------
# Idaho Falls, INL, April 5, 2022 14:09 PM
# Author(s)(name alph): David Reger, Dr. Javier Ortensi, Dr. Paolo Balestra,
# Dr. Ryan Stewart, Dr. Sebastian Schunert, Dr. Zachary Prince.
# ==============================================================================
# MODEL PARAMETERS
# ==============================================================================
# Geometry ---------------------------------------------------------------------
pebble_radius = 3.0e-2 # pebble radius (m)
pebble_shell_thickness = 5.0e-03 # pebble fuel free zone thickness (graphite shell) (m)
pebble_volume = '${fparse 4/3*pi*pebble_radius^3}' # volume of the pebble (m3)
pebble_core_volume = '${fparse 4/3*pi*(pebble_radius-pebble_shell_thickness)^3}' # volume of the pebble occupied by TRISO (m3)
kernel_radius = 2.1250e-04 # kernel particle radius (m)
kernel_volume = '${fparse 4/3*pi*kernel_radius^3}' # volume of the kernel (m3)
buffer_thickness = 1.00e-04 # Thickness of buffer (m)
ipyc_thickness = 4.00e-05 # Thickness of IPyC (m)
sic_thickness = 3.50e-05 # Thickness of SiC (m)
opyc_thickness = 4.00e-05 # Thickness of OPyC (m)
triso_radius = '${fparse kernel_radius + buffer_thickness + ipyc_thickness + sic_thickness + opyc_thickness}'
triso_volume = '${fparse 4/3*pi*triso_radius^3}' # volume of the particle (m3)
filling_factor = 0.0934404551647307 # Particle filling factor
# ICs --------------------------------------------------------------------------
initial_temperature = 1000.0 # (K)
initial_power = 10e6 # (W)
# ==============================================================================
# GEOMETRY AND MESH
# ==============================================================================
[Mesh]
block_id = ' 1 2 3 4 5 6 7'
block_name = 'core shell kernel buffer ipyc sic opyc'
coord_type = RSPHERICAL
[pebble_mesh]
type = CartesianMeshGenerator
dim = 1
# Uniform mesh.
dx = '2.50e-02 5.00e-03'
ix = '15 3'
subdomain_id = '1 2'
[]
[triso_mesh]
type = CartesianMeshGenerator
dim = 1
# Uniform mesh.
dx = '${kernel_radius} ${buffer_thickness} ${ipyc_thickness} ${sic_thickness} ${opyc_thickness}'
ix = '21 8 3 3 3'
subdomain_id = '3 4 5 6 7'
[]
[mesh_combine]
type = CombinerGenerator
inputs = 'pebble_mesh triso_mesh'
[]
[pebble_surface]
type = SideSetsAroundSubdomainGenerator
input = mesh_combine
block = '2'
fixed_normal = 1
normal = '1 0 0'
new_boundary = pebble_surface
[]
[triso_surface]
type = SideSetsAroundSubdomainGenerator
input = pebble_surface
block = '7'
fixed_normal = 1
normal = '1 0 0'
new_boundary = triso_surface
[]
[]
# ==============================================================================
# VARIABLES, KERNELS, AND BOUNDARY CONDITIONS
# ==============================================================================
[Variables]
[T_pebble]
block = '1 2'
initial_condition = ${initial_temperature}
[]
[T_triso]
block = '3 4 5 6 7'
initial_condition = ${initial_temperature}
[]
[]
[Kernels]
# Pebble
[pebble_diffusion]
type = ADHeatConduction
variable = T_pebble
block = '1 2'
[]
[pebble_core_heat_source]
type = BodyForce
variable = T_pebble
postprocessor = porous_media_power_density
value = '${fparse pebble_volume/pebble_core_volume}'
block = '1'
[]
# TRISO
[triso_diffusion]
type = ADHeatConduction
variable = T_triso
block = '3 4 5 6 7'
[]
[kernel_heat_source]
type = BodyForce
variable = T_triso
postprocessor = porous_media_power_density
value = '${fparse pebble_volume*triso_volume/filling_factor/pebble_core_volume/kernel_volume}'
block = '3'
[]
[]
[BCs]
[pebble_surface_temp]
type = PostprocessorDirichletBC
variable = T_pebble
postprocessor = pebble_surface_temp
boundary = 'pebble_surface'
[]
[triso_surface_temp]
type = PostprocessorDirichletBC
variable = T_triso
postprocessor = pebble_core_average_temp
boundary = 'triso_surface'
[]
[]
# ==============================================================================
# MATERIALS
# ==============================================================================
[Materials]
# Pebble.
[pebble_core]
type = ADGraphiteMatrixThermal
block = '1'
temperature = T_pebble
graphite_grade = A3_3_1800
packing_fraction = ${filling_factor}
flux_conversion_factor = 1.0 # Only used for irradiation correction
fast_neutron_fluence = 10e25
[]
[pebble_shell]
type = ADGraphiteMatrixThermal
block = '2'
temperature = T_pebble
graphite_grade = A3_3_1800
packing_fraction = 0
flux_conversion_factor = 0.8 # Only used for irradiation correction
fast_neutron_fluence = 10e25
[]
# TRISO.
[kernel]
type = ADUCOThermal
block = '3'
temperature = T_triso
# These do not matter since they are only relevant to heat capacity
initial_enrichment = 0.155
O_U = 1.5
C_U = 0.4
[]
[buffer]
type = ADBufferThermal
block = '4'
initial_density = 1050.0
[]
[ipyc]
type = ADHeatConductionMaterial
block = '5'
thermal_conductivity = 4.0
specific_heat = 1900.0
[]
[sic]
type = ADMonolithicSiCThermal
block = '6'
temperature = T_triso
thermal_conductivity_model = MILLER
[]
[opyc]
type = ADHeatConductionMaterial
block = '7'
thermal_conductivity = 4.0
specific_heat = 1900.0
[]
# Density
[density]
type = ADPiecewiseConstantByBlockMaterial
prop_name = 'density'
subdomain_to_prop_value = '1 1740.0
2 1740.0
3 10500.0
4 1050.0
5 1900.0
6 3180.0
7 1900.0'
[]
[]
# ==============================================================================
# EXECUTION PARAMETERS
# ==============================================================================
[Executioner]
type = Steady
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
line_search = 'l2'
# Linear/nonlinear iterations.
nl_rel_tol = 1e-40
nl_abs_tol = 1e-9
[]
# ==============================================================================
# POSTPROCESSORS DEBUG AND OUTPUTS
# ==============================================================================
[Debug]
show_var_residual_norms = false
[]
[Postprocessors]
# Pebble/TRISO interaction.
[pebble_core_average_temp]
type = ElementAverageValue
variable = T_pebble
block = '1'
execute_on = 'LINEAR'
[]
# FROM transfer.
[pebble_surface_temp]
type = Receiver
default = ${initial_temperature}
[]
[porous_media_power_density]
type = Receiver
default = ${initial_power}
[]
# TO transfer.
[fuel_average_temp]
type = ElementAverageValue
variable = T_triso
block = ' 3 '
[]
[moderator_average_temp]
type = ElementAverageValue
variable = T_pebble
block = ' 1 2 '
[]
[]
[Outputs]
csv = true
[]
(htgr/gpbr200/coupling/gpbr200_ss_bsht_pebble_triso.i)
# ==============================================================================
# Model description:
# Equilibrium core neutronics model coupled with TH and pebble temperature
# models.
# ------------------------------------------------------------------------------
# Idaho Falls, INL, April 5, 2022 14:09 PM
# Author(s)(name alph): David Reger, Dr. Javier Ortensi, Dr. Paolo Balestra,
# Dr. Ryan Stewart, Dr. Sebastian Schunert, Dr. Zachary Prince.
# ==============================================================================
# MODEL PARAMETERS
# ==============================================================================
# Geometry ---------------------------------------------------------------------
pebble_radius = 3.0e-2 # pebble radius (m)
pebble_shell_thickness = 5.0e-03 # pebble fuel free zone thickness (graphite shell) (m)
pebble_volume = '${fparse 4/3*pi*pebble_radius^3}' # volume of the pebble (m3)
pebble_core_volume = '${fparse 4/3*pi*(pebble_radius-pebble_shell_thickness)^3}' # volume of the pebble occupied by TRISO (m3)
kernel_radius = 2.1250e-04 # kernel particle radius (m)
kernel_volume = '${fparse 4/3*pi*kernel_radius^3}' # volume of the kernel (m3)
buffer_thickness = 1.00e-04 # Thickness of buffer (m)
ipyc_thickness = 4.00e-05 # Thickness of IPyC (m)
sic_thickness = 3.50e-05 # Thickness of SiC (m)
opyc_thickness = 4.00e-05 # Thickness of OPyC (m)
triso_radius = '${fparse kernel_radius + buffer_thickness + ipyc_thickness + sic_thickness + opyc_thickness}'
triso_volume = '${fparse 4/3*pi*triso_radius^3}' # volume of the particle (m3)
filling_factor = 0.0934404551647307 # Particle filling factor
# ICs --------------------------------------------------------------------------
initial_temperature = 1000.0 # (K)
initial_power = 10e6 # (W)
# ==============================================================================
# GEOMETRY AND MESH
# ==============================================================================
[Mesh]
block_id = ' 1 2 3 4 5 6 7'
block_name = 'core shell kernel buffer ipyc sic opyc'
coord_type = RSPHERICAL
[pebble_mesh]
type = CartesianMeshGenerator
dim = 1
# Uniform mesh.
dx = '2.50e-02 5.00e-03'
ix = '15 3'
subdomain_id = '1 2'
[]
[triso_mesh]
type = CartesianMeshGenerator
dim = 1
# Uniform mesh.
dx = '${kernel_radius} ${buffer_thickness} ${ipyc_thickness} ${sic_thickness} ${opyc_thickness}'
ix = '21 8 3 3 3'
subdomain_id = '3 4 5 6 7'
[]
[mesh_combine]
type = CombinerGenerator
inputs = 'pebble_mesh triso_mesh'
[]
[pebble_surface]
type = SideSetsAroundSubdomainGenerator
input = mesh_combine
block = '2'
fixed_normal = 1
normal = '1 0 0'
new_boundary = pebble_surface
[]
[triso_surface]
type = SideSetsAroundSubdomainGenerator
input = pebble_surface
block = '7'
fixed_normal = 1
normal = '1 0 0'
new_boundary = triso_surface
[]
[]
# ==============================================================================
# VARIABLES, KERNELS, AND BOUNDARY CONDITIONS
# ==============================================================================
[Variables]
[T_pebble]
block = '1 2'
initial_condition = ${initial_temperature}
[]
[T_triso]
block = '3 4 5 6 7'
initial_condition = ${initial_temperature}
[]
[]
[Kernels]
# Pebble
[pebble_diffusion]
type = ADHeatConduction
variable = T_pebble
block = '1 2'
[]
[pebble_core_heat_source]
type = BodyForce
variable = T_pebble
postprocessor = porous_media_power_density
value = '${fparse pebble_volume/pebble_core_volume}'
block = '1'
[]
# TRISO
[triso_diffusion]
type = ADHeatConduction
variable = T_triso
block = '3 4 5 6 7'
[]
[kernel_heat_source]
type = BodyForce
variable = T_triso
postprocessor = porous_media_power_density
value = '${fparse pebble_volume*triso_volume/filling_factor/pebble_core_volume/kernel_volume}'
block = '3'
[]
[]
[BCs]
[pebble_surface_temp]
type = PostprocessorDirichletBC
variable = T_pebble
postprocessor = pebble_surface_temp
boundary = 'pebble_surface'
[]
[triso_surface_temp]
type = PostprocessorDirichletBC
variable = T_triso
postprocessor = pebble_core_average_temp
boundary = 'triso_surface'
[]
[]
# ==============================================================================
# MATERIALS
# ==============================================================================
[Materials]
# Pebble.
[pebble_core]
type = ADGraphiteMatrixThermal
block = '1'
temperature = T_pebble
graphite_grade = A3_3_1800
packing_fraction = ${filling_factor}
flux_conversion_factor = 1.0 # Only used for irradiation correction
fast_neutron_fluence = 10e25
[]
[pebble_shell]
type = ADGraphiteMatrixThermal
block = '2'
temperature = T_pebble
graphite_grade = A3_3_1800
packing_fraction = 0
flux_conversion_factor = 0.8 # Only used for irradiation correction
fast_neutron_fluence = 10e25
[]
# TRISO.
[kernel]
type = ADUCOThermal
block = '3'
temperature = T_triso
# These do not matter since they are only relevant to heat capacity
initial_enrichment = 0.155
O_U = 1.5
C_U = 0.4
[]
[buffer]
type = ADBufferThermal
block = '4'
initial_density = 1050.0
[]
[ipyc]
type = ADHeatConductionMaterial
block = '5'
thermal_conductivity = 4.0
specific_heat = 1900.0
[]
[sic]
type = ADMonolithicSiCThermal
block = '6'
temperature = T_triso
thermal_conductivity_model = MILLER
[]
[opyc]
type = ADHeatConductionMaterial
block = '7'
thermal_conductivity = 4.0
specific_heat = 1900.0
[]
# Density
[density]
type = ADPiecewiseConstantByBlockMaterial
prop_name = 'density'
subdomain_to_prop_value = '1 1740.0
2 1740.0
3 10500.0
4 1050.0
5 1900.0
6 3180.0
7 1900.0'
[]
[]
# ==============================================================================
# EXECUTION PARAMETERS
# ==============================================================================
[Executioner]
type = Steady
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
line_search = 'l2'
# Linear/nonlinear iterations.
nl_rel_tol = 1e-40
nl_abs_tol = 1e-9
[]
# ==============================================================================
# POSTPROCESSORS DEBUG AND OUTPUTS
# ==============================================================================
[Debug]
show_var_residual_norms = false
[]
[Postprocessors]
# Pebble/TRISO interaction.
[pebble_core_average_temp]
type = ElementAverageValue
variable = T_pebble
block = '1'
execute_on = 'LINEAR'
[]
# FROM transfer.
[pebble_surface_temp]
type = Receiver
default = ${initial_temperature}
[]
[porous_media_power_density]
type = Receiver
default = ${initial_power}
[]
# TO transfer.
[fuel_average_temp]
type = ElementAverageValue
variable = T_triso
block = ' 3 '
[]
[moderator_average_temp]
type = ElementAverageValue
variable = T_pebble
block = ' 1 2 '
[]
[]
[Outputs]
console = false
[]
(htgr/gpbr200/core_thermal_hydraulics/gpbr200_ss_phth_reactor.i)
# ==============================================================================
# Model description:
# gPBR200 thermal hydraulic model
# ------------------------------------------------------------------------------
# Idaho Falls, INL, Mar. 2023
# Author(s)(name alph): David Reger, Dr. Javier Ortensi, Dr. Paolo Balestra,
# Dr. Ryan Stewart, Dr. Sebastian Schunert., Dr. Zachary M. Prince
# ==============================================================================
# MODEL PARAMETERS
# ==============================================================================
# Blocks -----------------------------------------------------------------------
risers_blocks = '1 2 3 22'
fluid_only_blocks = '4'
heated_blocks = '5 6 7 8 9'
outchans_blocks = '10'
outplen_blocks = '11'
hotleg_blocks = '12'
ref_blocks = '13 14 15 16 17'
ref2barrel_gap = '18'
barrel_blocks = '19'
barrel2rpv_gap = '20'
rpv_blocks = '21'
outlet_blocks = '${outplen_blocks} ${hotleg_blocks} ${outchans_blocks}'
porous_blocks = '${risers_blocks} ${heated_blocks} ${outlet_blocks}'
fluid_blocks = '${fluid_only_blocks} ${porous_blocks}'
solid_only_blocks = '${ref_blocks} ${barrel_blocks} ${rpv_blocks}'
pbed_blocks = '${heated_blocks}'
no_pbed_porous_blocks = '${risers_blocks} ${outlet_blocks}'
# Geometry ---------------------------------------------------------------------
pbed_r = 1.200 # Pebble Bed radius (m).
pbed_top = 11.3354 # Absolute height of the core top in the model (m).
rpv_r = 2.307 # rpv radius (m)
cavity_thickness = 1.340 # Cavity thickness from pbmr400 (m)
pebble_diameter = 0.06 # Diameter of the pebbles (m).
# Properties -------------------------------------------------------------------
global_emissivity = 0.80 # All the materials have the same emissivity (//).
reactor_total_mfr = 64.3 # Total reactor He mass flow rate (kg/s).
reactor_inlet_T_fluid = 533.25 # He temperature at the inlet of the lower inlet plenum (K).
reactor_inlet_rho = 5.364 # He density at the inlet of the lower inlet plenum (kg/m3).
reactor_outlet_pressure = 5.84e+6 # Pressure at the at the outlet of the outlet plenum (Pa).
top_bottom_cav_temperature = '${fparse 273.15 + 200.0}' # Top and Bottom cavities temperatures (K).
rccs_temperature = '${fparse 273.15 + 70.0}' # RCCS temperatures (K).
htc_cavities = 10.0 # Heat Exchange coefficient for natural circulation (W/m2K)
heat_capacity_multiplier = 1e-5
db_cnst = 0.023 # Dittus Boelter constant for area htc
pbed_porosity = 0.39 # Pebble bed porosity (//).
# Power ------------------------------------------------------------------------
total_power = 200.0e+6 # Total reactor Power (W)
# BCs --------------------------------------------------------------------------
inlet_free_area = '${fparse 2 * pi * 2.066 * 0.39}'
inlet_vel = '${fparse reactor_total_mfr/inlet_free_area/reactor_inlet_rho}'
# Initial values ---------------------------------------------------------------
pbed_free_flow_area = '${fparse pi * pbed_r * pbed_r}' # Core inlet free flow area (m2)
pbed_superficial_vel = '${fparse -reactor_total_mfr/pbed_free_flow_area/reactor_inlet_rho}' # m/s
initial_temp = 900.0 # K
[GlobalParams]
pebble_diameter = ${pebble_diameter}
acceleration = ' 0.00 -9.81 0.00 ' # Gravity acceleration (m/s2).
fp = fluid_properties_obj
[]
# ==============================================================================
# GEOMETRY AND MESH
# ==============================================================================
[Mesh]
[pebble_bed]
type = FileMeshGenerator
file = ../data/streamline_mesh_in.e
[]
coord_type = RZ
rz_coord_axis = Y
[]
[Problem]
kernel_coverage_check = false
material_coverage_check = false
[]
# ==============================================================================
# PHYSICS
# ==============================================================================
[Physics]
[NavierStokes]
[Flow]
[flow]
# Basic FVM settings
block = '${fluid_blocks}'
compressibility = 'weakly-compressible'
gravity = '0.0 -9.81 0.0'
# Porous treatment.
porous_medium_treatment = true
friction_types = 'darcy forchheimer'
friction_coeffs = 'Darcy_coefficient Forchheimer_coefficient'
porosity_interface_pressure_treatment = 'bernoulli'
# Fluid properties.
density = 'rho'
dynamic_viscosity = 'mu'
# Initial conditions.
initial_velocity = '0 pbed_superficial_vel_func 0'
velocity_variable = 'superficial_vel_x superficial_vel_y'
initial_pressure = '${reactor_outlet_pressure}'
# Fluid boundary conditions.
inlet_boundaries = 'inlet'
momentum_inlet_types = 'fixed-velocity'
momentum_inlet_functors = '-${inlet_vel} 0'
outlet_boundaries = 'outlet'
momentum_outlet_types = 'fixed-pressure'
pressure_functors = '${reactor_outlet_pressure}'
wall_boundaries = 'wall inner'
momentum_wall_types = 'slip symmetry'
[]
[]
[FluidHeatTransfer]
[energy]
block = '${fluid_blocks}'
# Fluid properties.
thermal_conductivity = 'kappa'
specific_heat = 'cp'
# Initial conditions
fluid_temperature_variable = 'T_fluid'
initial_temperature = '${initial_temp}'
# Fluid boundary conditions
energy_inlet_types = 'fixed-temperature'
energy_inlet_functors = '${reactor_inlet_T_fluid}'
energy_wall_types = 'heatflux heatflux'
energy_wall_functors = '0 0'
# Convective heat transfer.
ambient_convection_blocks = '${porous_blocks}'
ambient_convection_alpha = 'alpha'
ambient_temperature = 'T_solid'
# Interpolation schemes.
energy_advection_interpolation = average
[]
[]
[SolidHeatTransfer]
[solid]
block = '${porous_blocks} ${solid_only_blocks} ${ref2barrel_gap} ${barrel2rpv_gap}'
# Initial conditions.
solid_temperature_variable = 'T_solid'
initial_temperature = ${initial_temp}
# Solid properties
thermal_conductivity_solid = 'effective_thermal_conductivity'
cp_solid = 'cp_s_mod'
rho_solid = 'rho_s'
# Convective heat transfer.
ambient_convection_blocks = '${porous_blocks}'
ambient_convection_alpha = 'alpha'
ambient_convection_temperature = 'T_fluid'
# Heat source
external_heat_source_blocks = '${heated_blocks}'
external_heat_source = 'power_density'
[]
[]
[]
[]
[FVBCs]
[rpv_radial_radiation]
type = FVInfiniteCylinderRadiativeBC
variable = T_solid
cylinder_emissivity = '${global_emissivity}'
boundary_emissivity = '${global_emissivity}'
boundary_radius = '${rpv_r}'
cylinder_radius = '${fparse rpv_r + cavity_thickness}'
Tinfinity = '${rccs_temperature}'
boundary = 'rpv2rcav'
[]
[rpv_radial_convection]
type = FVFunctorConvectiveHeatFluxBC
variable = T_solid
T_solid = T_solid
T_bulk = '${rccs_temperature}'
boundary = 'rpv2rcav'
heat_transfer_coefficient = '${htc_cavities}'
is_solid = true
[]
[rpv_bottom_top]
type = FVFunctorConvectiveHeatFluxBC
variable = T_solid
T_solid = T_solid
T_bulk = '${top_bottom_cav_temperature}'
boundary = 'rtop rbottom'
heat_transfer_coefficient = '${htc_cavities}'
is_solid = true
[]
[]
# ==============================================================================
# AUXVARIABLES AND AUXKERNELS
# ==============================================================================
[AuxVariables]
[power_density]
family = MONOMIAL
order = CONSTANT
fv = true
block = '${heated_blocks}'
[]
[vel_x]
family = MONOMIAL
order = CONSTANT
fv = true
block = '${fluid_blocks}'
[]
[vel_y]
family = MONOMIAL
order = CONSTANT
fv = true
block = '${fluid_blocks}'
[]
[]
[AuxKernels]
[power_density]
type = ParsedAux
variable = power_density
expression = '${total_power} / volume'
functor_names = 'volume'
execute_on = 'INITIAL'
[]
[vel_x]
type = InterstitialFunctorAux
variable = vel_x
superficial_variable = superficial_vel_x
phase = fluid
porosity = porosity
[]
[vel_y]
type = InterstitialFunctorAux
variable = vel_y
superficial_variable = superficial_vel_y
phase = fluid
porosity = porosity
[]
[]
# ==============================================================================
# INITIAL CONDITIONS AND FUNCTIONS
# ==============================================================================
[Functions]
[pbed_superficial_vel_func]
type = ParsedFunction
expression = 'if(x < pbed_r & y > 1.851 & y < pbed_top, vel, 0.0)'
symbol_names = 'pbed_r pbed_top vel'
symbol_values = '${pbed_r} ${pbed_top} ${pbed_superficial_vel}'
[]
[he_conductivity_fn]
type = PiecewiseLinear
x = '300 350 400 450 500 550 600 650 700 750 800 850 900 950
1000 1050 1100 1150 1200 1250 1300 1350 1400 1450 1500'
y = '1.57e-01 1.75e-01 1.92e-01
2.08e-01 2.24e-01 2.40e-01 2.55e-01 2.69e-01 2.84e-01 2.98e-01 3.12e-01
3.25e-01 3.38e-01 3.51e-01 3.64e-01 3.77e-01 3.89e-01 4.02e-01
4.14e-01 4.26e-01 4.38e-01 4.50e-01 4.61e-01 4.73e-01 4.84e-01'
[]
[]
# ==============================================================================
# FLUID PROPERTIES, MATERIALS AND USER OBJECTS
# ==============================================================================
[FluidProperties]
[fluid_properties_obj]
type = HeliumFluidProperties
[]
[]
[FunctorMaterials]
# Fluid properties and non-dimensional numbers.
[fluid_props_to_mat_props]
type = GeneralFunctorFluidProps
pressure = 'pressure'
T_fluid = 'T_fluid'
speed = 'speed'
porosity = porosity
characteristic_length = characteristic_length
block = ${fluid_blocks}
[]
# Porosity.
[risers_blocks_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '0.22' # 18 channels and inlet structures (//).
block = '${risers_blocks}'
[]
[pbed_blocks_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '${pbed_porosity}'
block = ' ${heated_blocks}'
[]
[cavity_blocks_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '0.99' # Ideally 1.0 (//).
block = '${fluid_only_blocks}'
[]
[outchans_blocks_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '0.63' # Triangular lattice of 0.5cm radius channels and 1.7cm pitch (//).
block = '${outchans_blocks}'
[]
[outplen_blocks_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '0.40' # Triangular lattice of 4.75cm radius colums and 16.5cm pitch (//).
block = '${outplen_blocks}'
[]
[hotleg_blocks_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '0.07' # Cylindrical channel (//).
block = '${hotleg_blocks}'
[]
[all_other_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '-1' # Dummy value.
block = '${solid_only_blocks} ${ref2barrel_gap} ${barrel2rpv_gap}'
[]
# Characteristic Length.
[pbed_hydraulic_diameter]
type = GenericFunctorMaterial
prop_names = 'characteristic_length'
prop_values = '${pebble_diameter}'
block = '${pbed_blocks}'
[]
[risers_hydraulic_diameter]
type = GenericFunctorMaterial
prop_names = 'characteristic_length'
prop_values = '0.17' # Diameter of the risers channels (m).
block = '${risers_blocks} ${fluid_only_blocks}'
[]
[outlet_chans_hydraulic_diameter]
type = GenericFunctorMaterial
prop_names = 'characteristic_length'
prop_values = '0.01' # Diameter of the outlet channels (m).
block = '${outchans_blocks}'
[]
[outlet_plen_hydraulic_diameter]
type = GenericFunctorMaterial
prop_names = 'characteristic_length'
prop_values = '0.25' # Hydraulic diameter of outlet plenum (m).
block = '${outplen_blocks}'
[]
[hotleg_hydraulic_diameter]
type = GenericFunctorMaterial
prop_names = 'characteristic_length'
prop_values = '0.967' # Diameter of the hot leg (m).
block = '${hotleg_blocks}'
[]
# Solid properties.
[full_density_graphite]
type = ADGenericFunctorMaterial
prop_names = 'rho_s cp_s k_s'
prop_values = '1780 1697 26'
block = '${ref_blocks} ${risers_blocks} ${outlet_blocks} ${heated_blocks}'
[]
[core_barrel_steel]
type = ADGenericFunctorMaterial
prop_names = 'rho_s cp_s k_s'
prop_values = '7800.0 540.0 17.0'
block = '${barrel_blocks}'
[]
[rpv_steel]
type = ADGenericFunctorMaterial
prop_names = 'rho_s cp_s k_s'
prop_values = '7800.0 525.0 38.0'
block = '${rpv_blocks}'
[]
[he_rho_and_cp]
type = ADGenericFunctorMaterial
prop_names = 'rho_s cp_s'
prop_values = '6 5000'
block = '${ref2barrel_gap} ${barrel2rpv_gap}'
[]
[mod_cp_s]
type = ADParsedFunctorMaterial
expression = 'cp_s * ${heat_capacity_multiplier}'
property_name = 'cp_s_mod'
functor_symbols = 'cp_s'
functor_names = 'cp_s'
block = '${porous_blocks} ${solid_only_blocks} ${ref2barrel_gap} ${barrel2rpv_gap}'
[]
# Drag coefficients.
[pbed_drag_coefficient]
type = FunctorKTADragCoefficients
T_fluid = T_fluid
T_solid = T_solid
porosity = porosity
block = '${pbed_blocks}'
[]
[risers_drag_coefficients]
type = FunctorChurchillDragCoefficients
block = '${risers_blocks} ${fluid_only_blocks}'
[]
[outchans_drag_coefficients]
type = FunctorChurchillDragCoefficients
multipliers = '1.0e+05 1.0 1.0e+05'
block = '${outchans_blocks}'
[]
[outlet_drag_coefficients]
type = FunctorChurchillDragCoefficients
block = '${outplen_blocks}'
[]
[hotleg_drag_coefficients]
type = FunctorChurchillDragCoefficients
multipliers = '1.0 1.0e+05 1.0e+05'
block = '${hotleg_blocks}'
[]
# Heat transfer coefficients.
[pbed_alpha]
type = FunctorKTAPebbleBedHTC
T_solid = T_solid
T_fluid = T_fluid
mu = mu
porosity = porosity
pressure = pressure
block = '${pbed_blocks}'
[]
[risers_blocks_alpha]
type = FunctorDittusBoelterWallHTC
C = '${fparse db_cnst * 23.5}'
block = '${risers_blocks}'
[]
[outchans_blocks_alpha]
type = FunctorDittusBoelterWallHTC
C = '${fparse db_cnst * 400}'
block = '${outchans_blocks}'
[]
[outplen_blocks_alpha]
type = FunctorDittusBoelterWallHTC
C = '${fparse db_cnst * 63.5}'
block = '${outplen_blocks}'
[]
[rename_wall_htc_to_alpha]
type = ADGenericFunctorMaterial
prop_values = 'wall_htc'
prop_names = 'alpha'
block = '${risers_blocks} ${outchans_blocks} ${outplen_blocks}'
[]
[hotleg_blocks_alpha]
type = ADGenericFunctorMaterial
prop_names = 'alpha'
prop_values = '0.0'
block = '${hotleg_blocks}'
[]
# Effective solid thermal conductivity.
[pebble_effective_thermal_conductivity]
type = FunctorPebbleBedKappaSolid
T_solid = T_solid
porosity = porosity
solid_conduction = ZBS
emissivity = 0.8
infinite_porosity = '${pbed_porosity}'
Youngs_modulus = 9e+9
Poisson_ratio = 0.1360
lattice_parameters = interpolation
coordination_number = You
wall_distance = bed_geometry # Requested by solid_conduction = ZBS
block = '${pbed_blocks}'
[]
[porous_blocks_solid_effective_conductivity]
type = FunctorVolumeAverageKappaSolid
porosity = porosity
block = '${no_pbed_porous_blocks}'
[]
[effective_solid_thermal_conductivity]
type = ADGenericVectorFunctorMaterial
prop_names = 'effective_thermal_conductivity'
prop_values = 'kappa_s kappa_s kappa_s'
block = '${pbed_blocks} ${no_pbed_porous_blocks}'
[]
[effective_solid_thermal_conductivity_solid_only]
type = ADGenericVectorFunctorMaterial
prop_names = 'effective_thermal_conductivity'
prop_values = 'k_s k_s k_s'
block = '${solid_only_blocks}'
[]
[effective_thermal_conductivity_refl_ref2barrel_gap]
type = FunctorGapHeatTransferEffectiveThermalConductivity
gap_direction = x
temperature = T_solid
gap_conductivity_function = he_conductivity_fn
emissivity_primary = ${global_emissivity}
emissivity_secondary = ${global_emissivity}
radius_primary = 2.066
radius_secondary = 2.098
prop_name = effective_thermal_conductivity
block = '${ref2barrel_gap}'
[]
[effective_thermal_conductivity_barrel_rpv_gap]
type = FunctorGapHeatTransferEffectiveThermalConductivity
gap_direction = x
temperature = T_solid
gap_conductivity_function = he_conductivity_fn
emissivity_primary = ${global_emissivity}
emissivity_secondary = ${global_emissivity}
radius_primary = 2.143
radius_secondary = 2.215
prop_name = effective_thermal_conductivity
block = '${barrel2rpv_gap}'
[]
# Effective fluid thermal conductivity.
[pebble_bed_effective_fluid_thermal_conductivity]
type = FunctorLinearPecletKappaFluid
porosity = porosity
block = '${pbed_blocks}'
[]
[everywhere_else_effective_fluid_thermal_conductivity]
type = ADGenericVectorFunctorMaterial
prop_names = 'kappa'
prop_values = 'k k k'
block = '${no_pbed_porous_blocks} ${fluid_only_blocks}'
[]
[]
[UserObjects]
[bed_geometry]
type = WallDistanceCylindricalBed
top = '${pbed_top}'
inner_radius = 0.0
outer_radius = '${pbed_r}'
[]
[]
# ==============================================================================
# EXECUTION PARAMETERS
# ==============================================================================
[Executioner]
type = Transient
solve_type = NEWTON
petsc_options_iname = '-pc_type'
petsc_options_value = 'lu'
line_search = l2
# Scaling.
automatic_scaling = true
off_diagonals_in_auto_scaling = false
compute_scaling_once = false
# Tolerances.
nl_abs_tol = 1e-5
nl_rel_tol = 1e-6
nl_max_its = 15
# Time step control.
[TimeStepper]
type = IterationAdaptiveDT
dt = 2.5e-3
cutback_factor = 0.5
growth_factor = 2.00
optimal_iterations = 8
[]
# Steady state detection.
steady_state_detection = true
steady_state_tolerance = 1e-13
[]
# ==============================================================================
# POSTPROCESSORS DEBUG AND OUTPUTS
# ==============================================================================
[Postprocessors]
# General checks.
[pp00_inlet_mfr]
type = VolumetricFlowRate
vel_x = 'superficial_vel_x'
vel_y = 'superficial_vel_y'
advected_quantity = rho
boundary = inlet
rhie_chow_user_object = pins_rhie_chow_interpolator
execute_on = 'INITIAL TIMESTEP_END'
[]
[pp01_outlet_mfr]
type = VolumetricFlowRate
vel_x = 'superficial_vel_x'
vel_y = 'superficial_vel_y'
advected_quantity = rho
boundary = outlet
rhie_chow_user_object = pins_rhie_chow_interpolator
execute_on = 'INITIAL TIMESTEP_END'
[]
[pp02_inlet_pressure]
type = SideAverageValue
variable = pressure
boundary = 'inlet'
execute_on = 'INITIAL TIMESTEP_END'
[]
[pp03_total_power]
type = ElementIntegralVariablePostprocessor
variable = power_density
block = '${heated_blocks}'
execute_on = 'INITIAL TIMESTEP_END'
[]
[pp04_T_oulet]
type = SideAverageValue # Fix it with weighted thing
variable = T_fluid
boundary = 'outlet'
[]
[pp05_rpv_temp]
type = ElementAverageValue
variable = T_solid
block = '${rpv_blocks}'
[]
[pp06_rpv_temp_max]
type = ElementExtremeValue
variable = T_solid
block = '${rpv_blocks}'
[]
[volume]
type = VolumePostprocessor
block = '${heated_blocks}'
force_preaux = true
execute_on = 'INITIAL'
outputs = none
[]
[]
[Outputs]
exodus = true
csv = true
execute_on = 'FINAL'
[]
(htgr/gpbr200/coupling/gpbr200_ss_phth_reactor.i)
# ==============================================================================
# Model description:
# gPBR200 thermal hydraulic model
# ------------------------------------------------------------------------------
# Idaho Falls, INL, Mar. 2023
# Author(s)(name alph): David Reger, Dr. Javier Ortensi, Dr. Paolo Balestra,
# Dr. Ryan Stewart, Dr. Sebastian Schunert., Dr. Zachary M. Prince
# ==============================================================================
# MODEL PARAMETERS
# ==============================================================================
# Blocks -----------------------------------------------------------------------
risers_blocks = '1 2 3 22'
fluid_only_blocks = '4'
heated_blocks = '5 6 7 8 9'
outchans_blocks = '10'
outplen_blocks = '11'
hotleg_blocks = '12'
ref_blocks = '13 14 15 16 17'
ref2barrel_gap = '18'
barrel_blocks = '19'
barrel2rpv_gap = '20'
rpv_blocks = '21'
outlet_blocks = '${outplen_blocks} ${hotleg_blocks} ${outchans_blocks}'
porous_blocks = '${risers_blocks} ${heated_blocks} ${outlet_blocks}'
fluid_blocks = '${fluid_only_blocks} ${porous_blocks}'
solid_only_blocks = '${ref_blocks} ${barrel_blocks} ${rpv_blocks}'
pbed_blocks = '${heated_blocks}'
no_pbed_porous_blocks = '${risers_blocks} ${outlet_blocks}'
# Geometry ---------------------------------------------------------------------
pbed_r = 1.200 # Pebble Bed radius (m).
pbed_top = 11.3354 # Absolute height of the core top in the model (m).
rpv_r = 2.307 # rpv radius (m)
cavity_thickness = 1.340 # Cavity thickness from pbmr400 (m)
pebble_diameter = 0.06 # Diameter of the pebbles (m).
# Properties -------------------------------------------------------------------
global_emissivity = 0.80 # All the materials have the same emissivity (//).
reactor_total_mfr = 64.3 # Total reactor He mass flow rate (kg/s).
reactor_inlet_T_fluid = 533.25 # He temperature at the inlet of the lower inlet plenum (K).
reactor_inlet_rho = 5.364 # He density at the inlet of the lower inlet plenum (kg/m3).
reactor_outlet_pressure = 5.84e+6 # Pressure at the at the outlet of the outlet plenum (Pa).
top_bottom_cav_temperature = '${fparse 273.15 + 200.0}' # Top and Bottom cavities temperatures (K).
rccs_temperature = '${fparse 273.15 + 70.0}' # RCCS temperatures (K).
htc_cavities = 10.0 # Heat Exchange coefficient for natural circulation (W/m2K)
heat_capacity_multiplier = 1e-5
db_cnst = 0.023 # Dittus Boelter constant for area htc
pbed_porosity = 0.39 # Pebble bed porosity (//).
# BCs --------------------------------------------------------------------------
inlet_free_area = '${fparse 2 * pi * 2.066 * 0.39}'
inlet_vel = '${fparse reactor_total_mfr/inlet_free_area/reactor_inlet_rho}'
# Initial values ---------------------------------------------------------------
pbed_free_flow_area = '${fparse pi * pbed_r * pbed_r}' # Core inlet free flow area (m2)
pbed_superficial_vel = '${fparse -reactor_total_mfr/pbed_free_flow_area/reactor_inlet_rho}' # m/s
initial_temp = 900.0 # K
[GlobalParams]
pebble_diameter = ${pebble_diameter}
acceleration = ' 0.00 -9.81 0.00 ' # Gravity acceleration (m/s2).
fp = fluid_properties_obj
[]
# ==============================================================================
# GEOMETRY AND MESH
# ==============================================================================
[Mesh]
[pebble_bed]
type = FileMeshGenerator
file = ../data/streamline_mesh_in.e
[]
coord_type = RZ
rz_coord_axis = Y
[]
[Problem]
kernel_coverage_check = false
material_coverage_check = false
[]
# ==============================================================================
# PHYSICS
# ==============================================================================
[Physics]
[NavierStokes]
[Flow]
[flow]
# Basic FVM settings
block = '${fluid_blocks}'
compressibility = 'weakly-compressible'
gravity = '0.0 -9.81 0.0'
# Porous treatment.
porous_medium_treatment = true
friction_types = 'darcy forchheimer'
friction_coeffs = 'Darcy_coefficient Forchheimer_coefficient'
porosity_interface_pressure_treatment = 'bernoulli'
# Fluid properties.
density = 'rho'
dynamic_viscosity = 'mu'
# Initial conditions.
initial_velocity = '0 pbed_superficial_vel_func 0'
velocity_variable = 'superficial_vel_x superficial_vel_y'
initial_pressure = '${reactor_outlet_pressure}'
# Fluid boundary conditions.
inlet_boundaries = 'inlet'
momentum_inlet_types = 'fixed-velocity'
momentum_inlet_functors = '-${inlet_vel} 0'
outlet_boundaries = 'outlet'
momentum_outlet_types = 'fixed-pressure'
pressure_functors = '${reactor_outlet_pressure}'
wall_boundaries = 'wall inner'
momentum_wall_types = 'slip symmetry'
[]
[]
[FluidHeatTransfer]
[energy]
block = '${fluid_blocks}'
# Fluid properties.
thermal_conductivity = 'kappa'
specific_heat = 'cp'
# Initial conditions
fluid_temperature_variable = 'T_fluid'
initial_temperature = '${initial_temp}'
# Fluid boundary conditions
energy_inlet_types = 'fixed-temperature'
energy_inlet_functors = '${reactor_inlet_T_fluid}'
energy_wall_types = 'heatflux heatflux'
energy_wall_functors = '0 0'
# Convective heat transfer.
ambient_convection_blocks = '${porous_blocks}'
ambient_convection_alpha = 'alpha'
ambient_temperature = 'T_solid'
# Interpolation schemes.
energy_advection_interpolation = average
[]
[]
[SolidHeatTransfer]
[solid]
block = '${porous_blocks} ${solid_only_blocks} ${ref2barrel_gap} ${barrel2rpv_gap}'
# Initial conditions.
solid_temperature_variable = 'T_solid'
initial_temperature = ${initial_temp}
# Solid properties
thermal_conductivity_solid = 'effective_thermal_conductivity'
cp_solid = 'cp_s_mod'
rho_solid = 'rho_s'
# Convective heat transfer.
ambient_convection_blocks = '${porous_blocks}'
ambient_convection_alpha = 'alpha'
ambient_convection_temperature = 'T_fluid'
# Heat source
external_heat_source_blocks = '${heated_blocks}'
external_heat_source = 'power_density'
[]
[]
[]
[]
[FVBCs]
[rpv_radial_radiation]
type = FVInfiniteCylinderRadiativeBC
variable = T_solid
cylinder_emissivity = '${global_emissivity}'
boundary_emissivity = '${global_emissivity}'
boundary_radius = '${rpv_r}'
cylinder_radius = '${fparse rpv_r + cavity_thickness}'
Tinfinity = '${rccs_temperature}'
boundary = 'rpv2rcav'
[]
[rpv_radial_convection]
type = FVFunctorConvectiveHeatFluxBC
variable = T_solid
T_solid = T_solid
T_bulk = '${rccs_temperature}'
boundary = 'rpv2rcav'
heat_transfer_coefficient = '${htc_cavities}'
is_solid = true
[]
[rpv_bottom_top]
type = FVFunctorConvectiveHeatFluxBC
variable = T_solid
T_solid = T_solid
T_bulk = '${top_bottom_cav_temperature}'
boundary = 'rtop rbottom'
heat_transfer_coefficient = '${htc_cavities}'
is_solid = true
[]
[]
# ==============================================================================
# AUXVARIABLES AND AUXKERNELS
# ==============================================================================
[AuxVariables]
[power_density]
family = MONOMIAL
order = CONSTANT
fv = true
block = '${heated_blocks}'
[]
[vel_x]
family = MONOMIAL
order = CONSTANT
fv = true
block = '${fluid_blocks}'
[]
[vel_y]
family = MONOMIAL
order = CONSTANT
fv = true
block = '${fluid_blocks}'
[]
[]
[AuxKernels]
[vel_x]
type = InterstitialFunctorAux
variable = vel_x
superficial_variable = superficial_vel_x
phase = fluid
porosity = porosity
[]
[vel_y]
type = InterstitialFunctorAux
variable = vel_y
superficial_variable = superficial_vel_y
phase = fluid
porosity = porosity
[]
[]
# ==============================================================================
# INITIAL CONDITIONS AND FUNCTIONS
# ==============================================================================
[Functions]
[pbed_superficial_vel_func]
type = ParsedFunction
expression = 'if(x < pbed_r & y > 1.851 & y < pbed_top, vel, 0.0)'
symbol_names = 'pbed_r pbed_top vel'
symbol_values = '${pbed_r} ${pbed_top} ${pbed_superficial_vel}'
[]
[he_conductivity_fn]
type = PiecewiseLinear
x = '300 350 400 450 500 550 600 650 700 750 800 850 900 950
1000 1050 1100 1150 1200 1250 1300 1350 1400 1450 1500'
y = '1.57e-01 1.75e-01 1.92e-01
2.08e-01 2.24e-01 2.40e-01 2.55e-01 2.69e-01 2.84e-01 2.98e-01 3.12e-01
3.25e-01 3.38e-01 3.51e-01 3.64e-01 3.77e-01 3.89e-01 4.02e-01
4.14e-01 4.26e-01 4.38e-01 4.50e-01 4.61e-01 4.73e-01 4.84e-01'
[]
[]
# ==============================================================================
# FLUID PROPERTIES, MATERIALS AND USER OBJECTS
# ==============================================================================
[FluidProperties]
[fluid_properties_obj]
type = HeliumFluidProperties
[]
[]
[FunctorMaterials]
# Fluid properties and non-dimensional numbers.
[fluid_props_to_mat_props]
type = GeneralFunctorFluidProps
pressure = 'pressure'
T_fluid = 'T_fluid'
speed = 'speed'
porosity = porosity
characteristic_length = characteristic_length
block = ${fluid_blocks}
[]
# Porosity.
[risers_blocks_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '0.22' # 18 channels and inlet structures (//).
block = '${risers_blocks}'
[]
[pbed_blocks_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '${pbed_porosity}'
block = ' ${heated_blocks}'
[]
[cavity_blocks_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '0.99' # Ideally 1.0 (//).
block = '${fluid_only_blocks}'
[]
[outchans_blocks_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '0.63' # Triangular lattice of 0.5cm radius channels and 1.7cm pitch (//).
block = '${outchans_blocks}'
[]
[outplen_blocks_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '0.40' # Triangular lattice of 4.75cm radius colums and 16.5cm pitch (//).
block = '${outplen_blocks}'
[]
[hotleg_blocks_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '0.07' # Cylindrical channel (//).
block = '${hotleg_blocks}'
[]
[all_other_porosity]
type = ADGenericFunctorMaterial
prop_names = 'porosity'
prop_values = '-1' # Dummy value.
block = '${solid_only_blocks} ${ref2barrel_gap} ${barrel2rpv_gap}'
[]
# Characteristic Length.
[pbed_hydraulic_diameter]
type = GenericFunctorMaterial
prop_names = 'characteristic_length'
prop_values = '${pebble_diameter}'
block = '${pbed_blocks}'
[]
[risers_hydraulic_diameter]
type = GenericFunctorMaterial
prop_names = 'characteristic_length'
prop_values = '0.17' # Diameter of the risers channels (m).
block = '${risers_blocks} ${fluid_only_blocks}'
[]
[outlet_chans_hydraulic_diameter]
type = GenericFunctorMaterial
prop_names = 'characteristic_length'
prop_values = '0.01' # Diameter of the outlet channels (m).
block = '${outchans_blocks}'
[]
[outlet_plen_hydraulic_diameter]
type = GenericFunctorMaterial
prop_names = 'characteristic_length'
prop_values = '0.25' # Hydraulic diameter of outlet plenum (m).
block = '${outplen_blocks}'
[]
[hotleg_hydraulic_diameter]
type = GenericFunctorMaterial
prop_names = 'characteristic_length'
prop_values = '0.967' # Diameter of the hot leg (m).
block = '${hotleg_blocks}'
[]
# Solid properties.
[full_density_graphite]
type = ADGenericFunctorMaterial
prop_names = 'rho_s cp_s k_s'
prop_values = '1780 1697 26'
block = '${ref_blocks} ${risers_blocks} ${outlet_blocks} ${heated_blocks}'
[]
[core_barrel_steel]
type = ADGenericFunctorMaterial
prop_names = 'rho_s cp_s k_s'
prop_values = '7800.0 540.0 17.0'
block = '${barrel_blocks}'
[]
[rpv_steel]
type = ADGenericFunctorMaterial
prop_names = 'rho_s cp_s k_s'
prop_values = '7800.0 525.0 38.0'
block = '${rpv_blocks}'
[]
[he_rho_and_cp]
type = ADGenericFunctorMaterial
prop_names = 'rho_s cp_s'
prop_values = '6 5000'
block = '${ref2barrel_gap} ${barrel2rpv_gap}'
[]
[mod_cp_s]
type = ADParsedFunctorMaterial
expression = 'cp_s * ${heat_capacity_multiplier}'
property_name = 'cp_s_mod'
functor_symbols = 'cp_s'
functor_names = 'cp_s'
block = '${porous_blocks} ${solid_only_blocks} ${ref2barrel_gap} ${barrel2rpv_gap}'
[]
# Drag coefficients.
[pbed_drag_coefficient]
type = FunctorKTADragCoefficients
T_fluid = T_fluid
T_solid = T_solid
porosity = porosity
block = '${pbed_blocks}'
[]
[risers_drag_coefficients]
type = FunctorChurchillDragCoefficients
block = '${risers_blocks} ${fluid_only_blocks}'
[]
[outchans_drag_coefficients]
type = FunctorChurchillDragCoefficients
multipliers = '1.0e+05 1.0 1.0e+05'
block = '${outchans_blocks}'
[]
[outlet_drag_coefficients]
type = FunctorChurchillDragCoefficients
block = '${outplen_blocks}'
[]
[hotleg_drag_coefficients]
type = FunctorChurchillDragCoefficients
multipliers = '1.0 1.0e+05 1.0e+05'
block = '${hotleg_blocks}'
[]
# Heat transfer coefficients.
[pbed_alpha]
type = FunctorKTAPebbleBedHTC
T_solid = T_solid
T_fluid = T_fluid
mu = mu
porosity = porosity
pressure = pressure
block = '${pbed_blocks}'
[]
[risers_blocks_alpha]
type = FunctorDittusBoelterWallHTC
C = '${fparse db_cnst * 23.5}'
block = '${risers_blocks}'
[]
[outchans_blocks_alpha]
type = FunctorDittusBoelterWallHTC
C = '${fparse db_cnst * 400}'
block = '${outchans_blocks}'
[]
[outplen_blocks_alpha]
type = FunctorDittusBoelterWallHTC
C = '${fparse db_cnst * 63.5}'
block = '${outplen_blocks}'
[]
[rename_wall_htc_to_alpha]
type = ADGenericFunctorMaterial
prop_values = 'wall_htc'
prop_names = 'alpha'
block = '${risers_blocks} ${outchans_blocks} ${outplen_blocks}'
[]
[hotleg_blocks_alpha]
type = ADGenericFunctorMaterial
prop_names = 'alpha'
prop_values = '0.0'
block = '${hotleg_blocks}'
[]
# Effective solid thermal conductivity.
[pebble_effective_thermal_conductivity]
type = FunctorPebbleBedKappaSolid
T_solid = T_solid
porosity = porosity
solid_conduction = ZBS
emissivity = 0.8
infinite_porosity = '${pbed_porosity}'
Youngs_modulus = 9e+9
Poisson_ratio = 0.1360
lattice_parameters = interpolation
coordination_number = You
wall_distance = bed_geometry # Requested by solid_conduction = ZBS
block = '${pbed_blocks}'
[]
[porous_blocks_solid_effective_conductivity]
type = FunctorVolumeAverageKappaSolid
porosity = porosity
block = '${no_pbed_porous_blocks}'
[]
[effective_solid_thermal_conductivity]
type = ADGenericVectorFunctorMaterial
prop_names = 'effective_thermal_conductivity'
prop_values = 'kappa_s kappa_s kappa_s'
block = '${pbed_blocks} ${no_pbed_porous_blocks}'
[]
[effective_solid_thermal_conductivity_solid_only]
type = ADGenericVectorFunctorMaterial
prop_names = 'effective_thermal_conductivity'
prop_values = 'k_s k_s k_s'
block = '${solid_only_blocks}'
[]
[effective_thermal_conductivity_refl_ref2barrel_gap]
type = FunctorGapHeatTransferEffectiveThermalConductivity
gap_direction = x
temperature = T_solid
gap_conductivity_function = he_conductivity_fn
emissivity_primary = ${global_emissivity}
emissivity_secondary = ${global_emissivity}
radius_primary = 2.066
radius_secondary = 2.098
prop_name = effective_thermal_conductivity
block = '${ref2barrel_gap}'
[]
[effective_thermal_conductivity_barrel_rpv_gap]
type = FunctorGapHeatTransferEffectiveThermalConductivity
gap_direction = x
temperature = T_solid
gap_conductivity_function = he_conductivity_fn
emissivity_primary = ${global_emissivity}
emissivity_secondary = ${global_emissivity}
radius_primary = 2.143
radius_secondary = 2.215
prop_name = effective_thermal_conductivity
block = '${barrel2rpv_gap}'
[]
# Effective fluid thermal conductivity.
[pebble_bed_effective_fluid_thermal_conductivity]
type = FunctorLinearPecletKappaFluid
porosity = porosity
block = '${pbed_blocks}'
[]
[everywhere_else_effective_fluid_thermal_conductivity]
type = ADGenericVectorFunctorMaterial
prop_names = 'kappa'
prop_values = 'k k k'
block = '${no_pbed_porous_blocks} ${fluid_only_blocks}'
[]
[]
[UserObjects]
[bed_geometry]
type = WallDistanceCylindricalBed
top = '${pbed_top}'
inner_radius = 0.0
outer_radius = '${pbed_r}'
[]
[]
# ==============================================================================
# EXECUTION PARAMETERS
# ==============================================================================
[Executioner]
type = Transient
solve_type = NEWTON
petsc_options_iname = '-pc_type'
petsc_options_value = 'lu'
line_search = l2
# Scaling.
automatic_scaling = true
off_diagonals_in_auto_scaling = false
compute_scaling_once = false
# Tolerances.
nl_abs_tol = 1e-5
nl_rel_tol = 1e-6
nl_max_its = 15
# Time step control.
[TimeStepper]
type = IterationAdaptiveDT
dt = 2.5e-3
cutback_factor = 0.5
growth_factor = 2.00
optimal_iterations = 8
[]
# Steady state detection.
steady_state_detection = true
steady_state_tolerance = 1e-13
[]
# ==============================================================================
# POSTPROCESSORS DEBUG AND OUTPUTS
# ==============================================================================
[Postprocessors]
# General checks.
[pp00_inlet_mfr]
type = VolumetricFlowRate
vel_x = 'superficial_vel_x'
vel_y = 'superficial_vel_y'
advected_quantity = rho
boundary = inlet
rhie_chow_user_object = pins_rhie_chow_interpolator
execute_on = 'INITIAL TIMESTEP_END'
[]
[pp01_outlet_mfr]
type = VolumetricFlowRate
vel_x = 'superficial_vel_x'
vel_y = 'superficial_vel_y'
advected_quantity = rho
boundary = outlet
rhie_chow_user_object = pins_rhie_chow_interpolator
execute_on = 'INITIAL TIMESTEP_END'
[]
[pp02_inlet_pressure]
type = SideAverageValue
variable = pressure
boundary = 'inlet'
execute_on = 'INITIAL TIMESTEP_END'
[]
[pp03_total_power]
type = ElementIntegralVariablePostprocessor
variable = power_density
block = '${heated_blocks}'
execute_on = 'INITIAL TIMESTEP_END'
[]
[pp04_T_oulet]
type = SideAverageValue # Fix it with weighted thing
variable = T_fluid
boundary = 'outlet'
[]
[pp05_rpv_temp]
type = ElementAverageValue
variable = T_solid
block = '${rpv_blocks}'
[]
[pp06_rpv_temp_max]
type = ElementExtremeValue
variable = T_solid
block = '${rpv_blocks}'
[]
[]
[Outputs]
exodus = true
csv = true
execute_on = 'FINAL'
# Reduce console output
print_linear_residuals = false
print_linear_converged_reason = false
print_nonlinear_converged_reason = false
[]
(htgr/gpbr200/coupling/gpbr200_ss_gfnk_reactor.i)
# ==============================================================================
# Model description:
# Equilibrium core neutronics model coupled with TH and pebble temperature
# models.
# ------------------------------------------------------------------------------
# Idaho Falls, INL, April 4, 2022 11:03 AM
# Author(s)(name alph): David Reger, Dr. Javier Ortensi, Dr. Paolo Balestra,
# Dr. Ryan Stewart, Dr. Sebastian Schunert, Dr. Zachary Prince.
# ==============================================================================
# MODEL PARAMETERS
# ==============================================================================
# Power ------------------------------------------------------------------------
total_power = 200.0e+6 # Total reactor Power (W)
# Initial values ---------------------------------------------------------------
initial_temperature = 900.0 # (K)
# Geometry ---------------------------------------------------------------------
pbed_porosity = 0.39
pbed_top = 11.3354 # Absolute height of the core top in the model (m).
# Pebble Geometry --------------------------------------------------------------
pebble_radius = 3.0e-2 # pebble radius (m)
pebble_shell_thickness = 5.0e-03 # pebble fuel free zone thickness (graphite shell) (m)
pebble_volume = '${fparse 4/3*pi*pebble_radius^3}' # volume of the pebble (m3)
pebble_core_volume = '${fparse 4/3*pi*(pebble_radius-pebble_shell_thickness)^3}' # volume of the pebble occupied by TRISO (m3)
kernel_radius = 2.1250e-04 # kernel particle radius (m)
kernel_volume = '${fparse 4/3*pi*kernel_radius^3}' # volume of the kernel (m3)
buffer_thickness = 1.00e-04 # Thickness of buffer (m)
buffer_radius = '${fparse kernel_radius + buffer_thickness}' # Outer radius of buffer (m)
ipyc_thickness = 4.00e-05 # Thickness of IPyC (m)
ipyc_radius = '${fparse buffer_radius + ipyc_thickness}' # Outer radius of IPyC (m)
sic_thickness = 3.50e-05 # Thickness of SiC (m)
sic_radius = '${fparse ipyc_radius + sic_thickness}' # Outer radius of SiC (m)
opyc_thickness = 4.00e-05 # Thickness of OPyC (m)
opyc_radius = '${fparse sic_radius + opyc_thickness}' # Outer radius of OPyC (m)
triso_volume = '${fparse 4/3*pi*opyc_radius^3}' # volume of the particle (m3)
filling_factor = 0.0934404551647307 # Particle filling factor
triso_number = '${fparse pebble_core_volume * filling_factor / triso_volume}' # number of TRISO particle in a pebble (//)
# Compositions -----------------------------------------------------------------
enrichment = 0.155 # Enrichment in weight fraction
rho_kernel_UCO = 10.4 # Density of UCO (g/cm3)
ACU = 0.3920 # Carbon to Uranium atom ratio in UCO
AOU = 1.4280 # Oxygen to Uranium atom ratio in UCO
MU235 = 235.043929918 # Molar density of U235 (g/mol)
MU238 = 238.050788247 # Molar density of U238 (g/mol)
MC = 12.010735897 # Molar density of Carbon (g/mol)
MO = 15.994914620 # Molar density of Oxygen (g/mol)
enrichment_n = '${fparse enrichment/MU235 / (enrichment/MU235 + (1-enrichment)/MU238)}' # Enrichment in nuclide fration
MUCO = '${fparse MU235*enrichment_n + MU238*(1-enrichment_n) + MC*ACU + MO*AOU}' # UCO molar density (g/mol)
rhon_kernel_UCO = '${fparse rho_kernel_UCO / MUCO * 0.6022140}' # Molar density of UCO (atom/b/cm)
# Kernel number densities (n/b/cm)
rhon_kernel_U235 = '${fparse rhon_kernel_UCO * enrichment_n}'
rhon_kernel_U238 = '${fparse rhon_kernel_UCO * (1 - enrichment_n)}'
rhon_kernel_C = '${fparse rhon_kernel_UCO * ACU}'
rhon_kernel_O = '${fparse rhon_kernel_UCO * AOU}'
# Fractions of pebble volume
kernel_fraction = '${fparse kernel_volume * triso_number / pebble_volume}'
# Pebble volume densities (atoms/b/cm)
rhon_U235 = '${fparse rhon_kernel_U235 * kernel_fraction}'
rhon_U238 = '${fparse rhon_kernel_U238 * kernel_fraction}'
# Parameters describing pebble cycling -----------------------------------------
pebble_unloading_rate = '${fparse 1.5/60}' # pebbles per minute / seconds per minute.
burnup_limit_weight = 147.6 # MWd / kg
rho_U = '${fparse (rhon_U235*MU235 + rhon_U238*MU238) * 1.660539}' # Density of uranium in pebble volume (g/cm3)
burnup_conversion = '${fparse 1e9*3600*24*rho_U}' # Conversion from MWd/kg -> J/m3
# Blocks -----------------------------------------------------------------------
fuel_blocks = '5 6 7 8 9'
cns_disch_blocks = '14'
upref_blocks = '3 16'
upcav_blocks = '4'
lowref_blocks = '10 11 12 13'
crs_blocks = '17 22'
rdref_blocks = '1 2 15'
rpv_blocks = '18 19 20 21'
ref_blocks = '${cns_disch_blocks} ${upref_blocks}
${lowref_blocks}
${rdref_blocks}'
# ==============================================================================
# GLOBAL PARAMETERS
# ==============================================================================
[GlobalParams]
is_meter = true
[]
# ==============================================================================
# GEOMETRY AND MESH
# ==============================================================================
[Mesh]
[pebble_bed]
type = FileMeshGenerator
file = ../data/streamline_mesh_in.e
exodus_extra_element_integers = 'pebble_streamline_id pebble_streamline_layer_id material_id'
[]
coord_type = RZ
rz_coord_axis = Y
[]
# ==============================================================================
# AUXVARIABLES AND AUXKERNELS
# ==============================================================================
[AuxVariables]
# Temperatures.
[T_solid]
family = MONOMIAL
order = CONSTANT
initial_condition = ${initial_temperature}
block = '${fuel_blocks} ${ref_blocks} ${crs_blocks} ${rpv_blocks}' # Everything but upper cavity
[]
# Porosity
[porosity]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
initial_condition = ${pbed_porosity}
[]
[]
# ==============================================================================
# MATERIALS
# ==============================================================================
[Materials]
[reflector]
type = CoupledFeedbackNeutronicsMaterial
library_file = '../data/gpbr200_microxs.xml'
library_name = 'gpbr200_microxs'
grid_names = 'tmod'
grid_variables = 'T_solid'
isotopes = 'Graphite'
densities = '8.82418e-2'
plus = true
material_id = 2
diffusion_coefficient_scheme = local
block = '${ref_blocks}'
[]
[crs]
type = CoupledFeedbackRoddedNeutronicsMaterial
block = '${crs_blocks}'
library_file = '../data/gpbr200_microxs.xml'
library_name = 'gpbr200_microxs'
grid_names = 'tmod'
grid_variables = 'T_solid'
isotopes = ' Graphite;
Graphite B10 B11;
Graphite'
densities = '8.82418e-2
7.1628E-02 8.9463E-03 2.2229E-03
8.82418e-2'
rod_segment_length = 1e3
front_position_function = 'cr_front'
segment_material_ids = '2 2 2'
rod_withdrawn_direction = 'y'
average_segment_id = segment_id
[]
[cavity]
type = ConstantNeutronicsMaterial
block = '${upcav_blocks}'
fromFile = true
library_file = '../data/gpbr200_void.xml'
material_id = 10
[]
[]
[Functions]
# Function describing CR depth
[cr_depth]
type = ConstantFunction
value = 1.747 # Range of control rod insertion: -1.318 -> 8.93
[]
# Offset from reactor reference frame
[cr_front]
type = ParsedFunction
expression = 'top - cr_depth'
symbol_names = 'top cr_depth'
symbol_values = '${pbed_top} cr_depth'
[]
[]
[Compositions]
[uco]
type = IsotopeComposition
density_type = atomic
isotope_densities = '
U235 ${rhon_kernel_U235}
U238 ${rhon_kernel_U238}
C12 ${rhon_kernel_C}
O16 ${rhon_kernel_O}
'
[]
[buffer]
type = IsotopeComposition
density_type = atomic
isotope_densities = 'Graphite 5.26466317651E-02'
[]
[PyC]
type = IsotopeComposition
density_type = atomic
isotope_densities = 'Graphite 9.52653336702E-02'
[]
[SiC]
type = IsotopeComposition
density_type = atomic
isotope_densities = '
SI28 4.43270697709E-02
SI29 2.25082086520E-03
SI30 1.48375772443E-03
C12 4.80616002990E-02
'
[]
[matrix]
type = IsotopeComposition
density_type = atomic
isotope_densities = 'Graphite 8.67415932892E-02'
[]
[triso]
type = Triso
compositions = 'uco buffer PyC SiC PyC'
radii = '${kernel_radius} ${buffer_radius} ${ipyc_radius} ${sic_radius} ${opyc_radius}'
[]
[triso_fill]
type = StochasticComposition
background_composition = matrix
packing_fractions = ${filling_factor}
triso_particles = triso
[]
[pebble]
type = Pebble
compositions = 'triso_fill matrix'
radii = '${fparse pebble_radius - pebble_shell_thickness} ${pebble_radius}'
[]
[]
# ==============================================================================
# PEBBLE DEPLETION
# ==============================================================================
[PebbleDepletion]
block = '${fuel_blocks}'
# Power.
power = ${total_power}
integrated_power_postprocessor = total_power
power_density_variable = total_power_density
family = MONOMIAL
order = CONSTANT
# Cross section data.
library_file = '../data/gpbr200_microxs.xml'
library_name = 'gpbr200_microxs'
fuel_temperature_grid_name = 'tfuel'
moderator_temperature_grid_name = 'tmod'
burnup_grid_name = 'burnup'
constant_grid_values = 'kernrad ${fparse kernel_radius * 1000}
fillfact ${filling_factor}
enrich ${enrichment}'
# Transmutation data.
dataset = ISOXML
isoxml_data_file = '../data/gpbr200_dtl.xml'
isoxml_lib_name = 'gpbr200_dtl'
# Some of the branching ratios in the DTL are unphysical, which Griffin will
# throw a warning for unless this is specified.
dtl_physicality = 'SILENT'
# Isotopic options
n_fresh_pebble_types = 1
fresh_pebble_compositions = 'pebble'
# Pebble options
porosity_name = porosity
maximum_burnup = '${fparse 196.8 * burnup_conversion}'
num_burnup_bins = 12
# Tabulation data.
initial_moderator_temperature = '${initial_temperature}'
initial_fuel_temperature = '${initial_temperature}'
[DepletionScheme]
type = ConstantStreamlineEquilibrium
# Streamline definition
major_streamline_axis = y
# Pebble options
pebble_unloading_rate = ${pebble_unloading_rate}
pebble_flow_rate_distribution = '0.12919675255653704 0.3237409742330389 0.16364127845178317 0.1970045449547337 0.1864164498039072'
pebble_diameter = '${fparse pebble_radius * 2.0}'
burnup_limit = '${fparse burnup_limit_weight * burnup_conversion}'
# Solver parameters
sweep_tol = 1e-8
sweep_max_iterations = 20
# Output
exodus_streamline_output = false
[]
diffusion_coefficient_scheme = local
[]
# ==============================================================================
# EXECUTION PARAMETERS
# ==============================================================================
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 9
ReflectingBoundary = 'rinner'
VacuumBoundary = 'rtop rbottom router'
[diff]
scheme = CFEM-Diffusion
family = LAGRANGE
order = FIRST
n_delay_groups = 6
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
block = '${fuel_blocks} ${upcav_blocks} ${ref_blocks} ${crs_blocks}' # Excluding RPV and Barrel
[]
[]
[Executioner]
type = Eigenvalue
solve_type = 'PJFNKMO'
constant_matrices = true
petsc_options_iname = '-pc_type -pc_hypre_type -ksp_gmres_restart '
petsc_options_value = 'hypre boomeramg 100'
line_search = none
# Linear/nonlinear iterations.
l_max_its = 100
l_tol = 1e-3
nl_max_its = 50
nl_rel_tol = 1e-7
nl_abs_tol = 1e-9
# Fixed point iterations.
fixed_point_min_its = 15
fixed_point_max_its = 200
custom_pp = eigenvalue
custom_abs_tol = 5e-5
custom_rel_tol = 1e-50
disable_fixed_point_residual_norm_check = true
# Power iterations.
free_power_iterations = 4
extra_power_iterations = 20
[]
# ==============================================================================
# MULTIAPPS AND TRANSFERS
# ==============================================================================
[Positions]
[element]
type = ElementCentroidPositions
block = ${fuel_blocks}
[]
[]
[MultiApps]
# Reactor TH.
[pronghorn_th]
type = FullSolveMultiApp
input_files = gpbr200_ss_phth_reactor.i
keep_solution_during_restore = true
execute_on = 'TIMESTEP_END'
[]
# Pebble conduction
[pebble_conduction]
type = FullSolveMultiApp
input_files = gpbr200_ss_bsht_pebble_triso.i
no_restore = true
positions_objects = 'element element element element element
element element element element element
element element element'
cli_args = 'kernel_radius=${kernel_radius};filling_factor=${filling_factor}'
execute_on = TIMESTEP_BEGIN
[]
[]
[Transfers]
# TO Pronghorn.
[to_pronghorn_total_power_density]
type = MultiAppCopyTransfer
to_multi_app = pronghorn_th
source_variable = total_power_density
variable = power_density
[]
# FROM Pronghorn.
[from_pronghorn_Tsolid]
type = MultiAppCopyTransfer
from_multi_app = pronghorn_th
source_variable = T_solid
variable = T_solid
[]
# To pebble conduction
[to_pebble_conduction_Tsolid]
type = MultiAppVariableValueSamplePostprocessorTransfer
to_multi_app = pebble_conduction
postprocessor = pebble_surface_temp
source_variable = T_solid
[]
[to_pebble_conduction_power_density]
type = MultiAppVariableValueSamplePostprocessorTransfer
to_multi_app = pebble_conduction
postprocessor = porous_media_power_density
source_variable = partial_power_density
map_array_variable_components_to_child_apps = true
[]
# From pebble conduction
[from_pebble_conduction_Tfuel]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = pebble_conduction
postprocessor = fuel_average_temp
source_variable = triso_temperature
map_array_variable_components_to_child_apps = true
[]
[from_pebble_conduction_Tmod]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = pebble_conduction
postprocessor = moderator_average_temp
source_variable = graphite_temperature
map_array_variable_components_to_child_apps = true
[]
[]
# ==============================================================================
# POSTPROCESSING AND OUTPUTS
# ==============================================================================
[AuxVariables]
# Max temperatures and power
[Tfuel_max]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
[]
[Tmod_max]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
[]
[ppd_max]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
[]
[]
[AuxKernels]
# Max temperatures and power
[Tfuel_max_aux]
type = ArrayVarReductionAux
variable = Tfuel_max
array_variable = triso_temperature
value_type = max
execute_on = TIMESTEP_END
[]
[Tmod_max_aux]
type = ArrayVarReductionAux
variable = Tmod_max
array_variable = graphite_temperature
value_type = max
execute_on = TIMESTEP_END
[]
[ppd_max_aux]
type = ArrayVarReductionAux
variable = ppd_max
array_variable = partial_power_density
value_type = max
execute_on = TIMESTEP_END
[]
[]
[Outputs]
csv = true
exodus = true
[]
(htgr/gpbr200/coupling/gpbr200_ss_gfnk_reactor.i)
# ==============================================================================
# Model description:
# Equilibrium core neutronics model coupled with TH and pebble temperature
# models.
# ------------------------------------------------------------------------------
# Idaho Falls, INL, April 4, 2022 11:03 AM
# Author(s)(name alph): David Reger, Dr. Javier Ortensi, Dr. Paolo Balestra,
# Dr. Ryan Stewart, Dr. Sebastian Schunert, Dr. Zachary Prince.
# ==============================================================================
# MODEL PARAMETERS
# ==============================================================================
# Power ------------------------------------------------------------------------
total_power = 200.0e+6 # Total reactor Power (W)
# Initial values ---------------------------------------------------------------
initial_temperature = 900.0 # (K)
# Geometry ---------------------------------------------------------------------
pbed_porosity = 0.39
pbed_top = 11.3354 # Absolute height of the core top in the model (m).
# Pebble Geometry --------------------------------------------------------------
pebble_radius = 3.0e-2 # pebble radius (m)
pebble_shell_thickness = 5.0e-03 # pebble fuel free zone thickness (graphite shell) (m)
pebble_volume = '${fparse 4/3*pi*pebble_radius^3}' # volume of the pebble (m3)
pebble_core_volume = '${fparse 4/3*pi*(pebble_radius-pebble_shell_thickness)^3}' # volume of the pebble occupied by TRISO (m3)
kernel_radius = 2.1250e-04 # kernel particle radius (m)
kernel_volume = '${fparse 4/3*pi*kernel_radius^3}' # volume of the kernel (m3)
buffer_thickness = 1.00e-04 # Thickness of buffer (m)
buffer_radius = '${fparse kernel_radius + buffer_thickness}' # Outer radius of buffer (m)
ipyc_thickness = 4.00e-05 # Thickness of IPyC (m)
ipyc_radius = '${fparse buffer_radius + ipyc_thickness}' # Outer radius of IPyC (m)
sic_thickness = 3.50e-05 # Thickness of SiC (m)
sic_radius = '${fparse ipyc_radius + sic_thickness}' # Outer radius of SiC (m)
opyc_thickness = 4.00e-05 # Thickness of OPyC (m)
opyc_radius = '${fparse sic_radius + opyc_thickness}' # Outer radius of OPyC (m)
triso_volume = '${fparse 4/3*pi*opyc_radius^3}' # volume of the particle (m3)
filling_factor = 0.0934404551647307 # Particle filling factor
triso_number = '${fparse pebble_core_volume * filling_factor / triso_volume}' # number of TRISO particle in a pebble (//)
# Compositions -----------------------------------------------------------------
enrichment = 0.155 # Enrichment in weight fraction
rho_kernel_UCO = 10.4 # Density of UCO (g/cm3)
ACU = 0.3920 # Carbon to Uranium atom ratio in UCO
AOU = 1.4280 # Oxygen to Uranium atom ratio in UCO
MU235 = 235.043929918 # Molar density of U235 (g/mol)
MU238 = 238.050788247 # Molar density of U238 (g/mol)
MC = 12.010735897 # Molar density of Carbon (g/mol)
MO = 15.994914620 # Molar density of Oxygen (g/mol)
enrichment_n = '${fparse enrichment/MU235 / (enrichment/MU235 + (1-enrichment)/MU238)}' # Enrichment in nuclide fration
MUCO = '${fparse MU235*enrichment_n + MU238*(1-enrichment_n) + MC*ACU + MO*AOU}' # UCO molar density (g/mol)
rhon_kernel_UCO = '${fparse rho_kernel_UCO / MUCO * 0.6022140}' # Molar density of UCO (atom/b/cm)
# Kernel number densities (n/b/cm)
rhon_kernel_U235 = '${fparse rhon_kernel_UCO * enrichment_n}'
rhon_kernel_U238 = '${fparse rhon_kernel_UCO * (1 - enrichment_n)}'
rhon_kernel_C = '${fparse rhon_kernel_UCO * ACU}'
rhon_kernel_O = '${fparse rhon_kernel_UCO * AOU}'
# Fractions of pebble volume
kernel_fraction = '${fparse kernel_volume * triso_number / pebble_volume}'
# Pebble volume densities (atoms/b/cm)
rhon_U235 = '${fparse rhon_kernel_U235 * kernel_fraction}'
rhon_U238 = '${fparse rhon_kernel_U238 * kernel_fraction}'
# Parameters describing pebble cycling -----------------------------------------
pebble_unloading_rate = '${fparse 1.5/60}' # pebbles per minute / seconds per minute.
burnup_limit_weight = 147.6 # MWd / kg
rho_U = '${fparse (rhon_U235*MU235 + rhon_U238*MU238) * 1.660539}' # Density of uranium in pebble volume (g/cm3)
burnup_conversion = '${fparse 1e9*3600*24*rho_U}' # Conversion from MWd/kg -> J/m3
# Blocks -----------------------------------------------------------------------
fuel_blocks = '5 6 7 8 9'
cns_disch_blocks = '14'
upref_blocks = '3 16'
upcav_blocks = '4'
lowref_blocks = '10 11 12 13'
crs_blocks = '17 22'
rdref_blocks = '1 2 15'
rpv_blocks = '18 19 20 21'
ref_blocks = '${cns_disch_blocks} ${upref_blocks}
${lowref_blocks}
${rdref_blocks}'
# ==============================================================================
# GLOBAL PARAMETERS
# ==============================================================================
[GlobalParams]
is_meter = true
[]
# ==============================================================================
# GEOMETRY AND MESH
# ==============================================================================
[Mesh]
[pebble_bed]
type = FileMeshGenerator
file = ../data/streamline_mesh_in.e
exodus_extra_element_integers = 'pebble_streamline_id pebble_streamline_layer_id material_id'
[]
coord_type = RZ
rz_coord_axis = Y
[]
# ==============================================================================
# AUXVARIABLES AND AUXKERNELS
# ==============================================================================
[AuxVariables]
# Temperatures.
[T_solid]
family = MONOMIAL
order = CONSTANT
initial_condition = ${initial_temperature}
block = '${fuel_blocks} ${ref_blocks} ${crs_blocks} ${rpv_blocks}' # Everything but upper cavity
[]
# Porosity
[porosity]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
initial_condition = ${pbed_porosity}
[]
[]
# ==============================================================================
# MATERIALS
# ==============================================================================
[Materials]
[reflector]
type = CoupledFeedbackNeutronicsMaterial
library_file = '../data/gpbr200_microxs.xml'
library_name = 'gpbr200_microxs'
grid_names = 'tmod'
grid_variables = 'T_solid'
isotopes = 'Graphite'
densities = '8.82418e-2'
plus = true
material_id = 2
diffusion_coefficient_scheme = local
block = '${ref_blocks}'
[]
[crs]
type = CoupledFeedbackRoddedNeutronicsMaterial
block = '${crs_blocks}'
library_file = '../data/gpbr200_microxs.xml'
library_name = 'gpbr200_microxs'
grid_names = 'tmod'
grid_variables = 'T_solid'
isotopes = ' Graphite;
Graphite B10 B11;
Graphite'
densities = '8.82418e-2
7.1628E-02 8.9463E-03 2.2229E-03
8.82418e-2'
rod_segment_length = 1e3
front_position_function = 'cr_front'
segment_material_ids = '2 2 2'
rod_withdrawn_direction = 'y'
average_segment_id = segment_id
[]
[cavity]
type = ConstantNeutronicsMaterial
block = '${upcav_blocks}'
fromFile = true
library_file = '../data/gpbr200_void.xml'
material_id = 10
[]
[]
[Functions]
# Function describing CR depth
[cr_depth]
type = ConstantFunction
value = 1.747 # Range of control rod insertion: -1.318 -> 8.93
[]
# Offset from reactor reference frame
[cr_front]
type = ParsedFunction
expression = 'top - cr_depth'
symbol_names = 'top cr_depth'
symbol_values = '${pbed_top} cr_depth'
[]
[]
[Compositions]
[uco]
type = IsotopeComposition
density_type = atomic
isotope_densities = '
U235 ${rhon_kernel_U235}
U238 ${rhon_kernel_U238}
C12 ${rhon_kernel_C}
O16 ${rhon_kernel_O}
'
[]
[buffer]
type = IsotopeComposition
density_type = atomic
isotope_densities = 'Graphite 5.26466317651E-02'
[]
[PyC]
type = IsotopeComposition
density_type = atomic
isotope_densities = 'Graphite 9.52653336702E-02'
[]
[SiC]
type = IsotopeComposition
density_type = atomic
isotope_densities = '
SI28 4.43270697709E-02
SI29 2.25082086520E-03
SI30 1.48375772443E-03
C12 4.80616002990E-02
'
[]
[matrix]
type = IsotopeComposition
density_type = atomic
isotope_densities = 'Graphite 8.67415932892E-02'
[]
[triso]
type = Triso
compositions = 'uco buffer PyC SiC PyC'
radii = '${kernel_radius} ${buffer_radius} ${ipyc_radius} ${sic_radius} ${opyc_radius}'
[]
[triso_fill]
type = StochasticComposition
background_composition = matrix
packing_fractions = ${filling_factor}
triso_particles = triso
[]
[pebble]
type = Pebble
compositions = 'triso_fill matrix'
radii = '${fparse pebble_radius - pebble_shell_thickness} ${pebble_radius}'
[]
[]
# ==============================================================================
# PEBBLE DEPLETION
# ==============================================================================
[PebbleDepletion]
block = '${fuel_blocks}'
# Power.
power = ${total_power}
integrated_power_postprocessor = total_power
power_density_variable = total_power_density
family = MONOMIAL
order = CONSTANT
# Cross section data.
library_file = '../data/gpbr200_microxs.xml'
library_name = 'gpbr200_microxs'
fuel_temperature_grid_name = 'tfuel'
moderator_temperature_grid_name = 'tmod'
burnup_grid_name = 'burnup'
constant_grid_values = 'kernrad ${fparse kernel_radius * 1000}
fillfact ${filling_factor}
enrich ${enrichment}'
# Transmutation data.
dataset = ISOXML
isoxml_data_file = '../data/gpbr200_dtl.xml'
isoxml_lib_name = 'gpbr200_dtl'
# Some of the branching ratios in the DTL are unphysical, which Griffin will
# throw a warning for unless this is specified.
dtl_physicality = 'SILENT'
# Isotopic options
n_fresh_pebble_types = 1
fresh_pebble_compositions = 'pebble'
# Pebble options
porosity_name = porosity
maximum_burnup = '${fparse 196.8 * burnup_conversion}'
num_burnup_bins = 12
# Tabulation data.
initial_moderator_temperature = '${initial_temperature}'
initial_fuel_temperature = '${initial_temperature}'
[DepletionScheme]
type = ConstantStreamlineEquilibrium
# Streamline definition
major_streamline_axis = y
# Pebble options
pebble_unloading_rate = ${pebble_unloading_rate}
pebble_flow_rate_distribution = '0.12919675255653704 0.3237409742330389 0.16364127845178317 0.1970045449547337 0.1864164498039072'
pebble_diameter = '${fparse pebble_radius * 2.0}'
burnup_limit = '${fparse burnup_limit_weight * burnup_conversion}'
# Solver parameters
sweep_tol = 1e-8
sweep_max_iterations = 20
# Output
exodus_streamline_output = false
[]
diffusion_coefficient_scheme = local
[]
# ==============================================================================
# EXECUTION PARAMETERS
# ==============================================================================
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 9
ReflectingBoundary = 'rinner'
VacuumBoundary = 'rtop rbottom router'
[diff]
scheme = CFEM-Diffusion
family = LAGRANGE
order = FIRST
n_delay_groups = 6
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
block = '${fuel_blocks} ${upcav_blocks} ${ref_blocks} ${crs_blocks}' # Excluding RPV and Barrel
[]
[]
[Executioner]
type = Eigenvalue
solve_type = 'PJFNKMO'
constant_matrices = true
petsc_options_iname = '-pc_type -pc_hypre_type -ksp_gmres_restart '
petsc_options_value = 'hypre boomeramg 100'
line_search = none
# Linear/nonlinear iterations.
l_max_its = 100
l_tol = 1e-3
nl_max_its = 50
nl_rel_tol = 1e-7
nl_abs_tol = 1e-9
# Fixed point iterations.
fixed_point_min_its = 15
fixed_point_max_its = 200
custom_pp = eigenvalue
custom_abs_tol = 5e-5
custom_rel_tol = 1e-50
disable_fixed_point_residual_norm_check = true
# Power iterations.
free_power_iterations = 4
extra_power_iterations = 20
[]
# ==============================================================================
# MULTIAPPS AND TRANSFERS
# ==============================================================================
[Positions]
[element]
type = ElementCentroidPositions
block = ${fuel_blocks}
[]
[]
[MultiApps]
# Reactor TH.
[pronghorn_th]
type = FullSolveMultiApp
input_files = gpbr200_ss_phth_reactor.i
keep_solution_during_restore = true
execute_on = 'TIMESTEP_END'
[]
# Pebble conduction
[pebble_conduction]
type = FullSolveMultiApp
input_files = gpbr200_ss_bsht_pebble_triso.i
no_restore = true
positions_objects = 'element element element element element
element element element element element
element element element'
cli_args = 'kernel_radius=${kernel_radius};filling_factor=${filling_factor}'
execute_on = TIMESTEP_BEGIN
[]
[]
[Transfers]
# TO Pronghorn.
[to_pronghorn_total_power_density]
type = MultiAppCopyTransfer
to_multi_app = pronghorn_th
source_variable = total_power_density
variable = power_density
[]
# FROM Pronghorn.
[from_pronghorn_Tsolid]
type = MultiAppCopyTransfer
from_multi_app = pronghorn_th
source_variable = T_solid
variable = T_solid
[]
# To pebble conduction
[to_pebble_conduction_Tsolid]
type = MultiAppVariableValueSamplePostprocessorTransfer
to_multi_app = pebble_conduction
postprocessor = pebble_surface_temp
source_variable = T_solid
[]
[to_pebble_conduction_power_density]
type = MultiAppVariableValueSamplePostprocessorTransfer
to_multi_app = pebble_conduction
postprocessor = porous_media_power_density
source_variable = partial_power_density
map_array_variable_components_to_child_apps = true
[]
# From pebble conduction
[from_pebble_conduction_Tfuel]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = pebble_conduction
postprocessor = fuel_average_temp
source_variable = triso_temperature
map_array_variable_components_to_child_apps = true
[]
[from_pebble_conduction_Tmod]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = pebble_conduction
postprocessor = moderator_average_temp
source_variable = graphite_temperature
map_array_variable_components_to_child_apps = true
[]
[]
# ==============================================================================
# POSTPROCESSING AND OUTPUTS
# ==============================================================================
[AuxVariables]
# Max temperatures and power
[Tfuel_max]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
[]
[Tmod_max]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
[]
[ppd_max]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
[]
[]
[AuxKernels]
# Max temperatures and power
[Tfuel_max_aux]
type = ArrayVarReductionAux
variable = Tfuel_max
array_variable = triso_temperature
value_type = max
execute_on = TIMESTEP_END
[]
[Tmod_max_aux]
type = ArrayVarReductionAux
variable = Tmod_max
array_variable = graphite_temperature
value_type = max
execute_on = TIMESTEP_END
[]
[ppd_max_aux]
type = ArrayVarReductionAux
variable = ppd_max
array_variable = partial_power_density
value_type = max
execute_on = TIMESTEP_END
[]
[]
[Outputs]
csv = true
exodus = true
[]
(htgr/gpbr200/coupling/gpbr200_ss_gfnk_reactor.i)
# ==============================================================================
# Model description:
# Equilibrium core neutronics model coupled with TH and pebble temperature
# models.
# ------------------------------------------------------------------------------
# Idaho Falls, INL, April 4, 2022 11:03 AM
# Author(s)(name alph): David Reger, Dr. Javier Ortensi, Dr. Paolo Balestra,
# Dr. Ryan Stewart, Dr. Sebastian Schunert, Dr. Zachary Prince.
# ==============================================================================
# MODEL PARAMETERS
# ==============================================================================
# Power ------------------------------------------------------------------------
total_power = 200.0e+6 # Total reactor Power (W)
# Initial values ---------------------------------------------------------------
initial_temperature = 900.0 # (K)
# Geometry ---------------------------------------------------------------------
pbed_porosity = 0.39
pbed_top = 11.3354 # Absolute height of the core top in the model (m).
# Pebble Geometry --------------------------------------------------------------
pebble_radius = 3.0e-2 # pebble radius (m)
pebble_shell_thickness = 5.0e-03 # pebble fuel free zone thickness (graphite shell) (m)
pebble_volume = '${fparse 4/3*pi*pebble_radius^3}' # volume of the pebble (m3)
pebble_core_volume = '${fparse 4/3*pi*(pebble_radius-pebble_shell_thickness)^3}' # volume of the pebble occupied by TRISO (m3)
kernel_radius = 2.1250e-04 # kernel particle radius (m)
kernel_volume = '${fparse 4/3*pi*kernel_radius^3}' # volume of the kernel (m3)
buffer_thickness = 1.00e-04 # Thickness of buffer (m)
buffer_radius = '${fparse kernel_radius + buffer_thickness}' # Outer radius of buffer (m)
ipyc_thickness = 4.00e-05 # Thickness of IPyC (m)
ipyc_radius = '${fparse buffer_radius + ipyc_thickness}' # Outer radius of IPyC (m)
sic_thickness = 3.50e-05 # Thickness of SiC (m)
sic_radius = '${fparse ipyc_radius + sic_thickness}' # Outer radius of SiC (m)
opyc_thickness = 4.00e-05 # Thickness of OPyC (m)
opyc_radius = '${fparse sic_radius + opyc_thickness}' # Outer radius of OPyC (m)
triso_volume = '${fparse 4/3*pi*opyc_radius^3}' # volume of the particle (m3)
filling_factor = 0.0934404551647307 # Particle filling factor
triso_number = '${fparse pebble_core_volume * filling_factor / triso_volume}' # number of TRISO particle in a pebble (//)
# Compositions -----------------------------------------------------------------
enrichment = 0.155 # Enrichment in weight fraction
rho_kernel_UCO = 10.4 # Density of UCO (g/cm3)
ACU = 0.3920 # Carbon to Uranium atom ratio in UCO
AOU = 1.4280 # Oxygen to Uranium atom ratio in UCO
MU235 = 235.043929918 # Molar density of U235 (g/mol)
MU238 = 238.050788247 # Molar density of U238 (g/mol)
MC = 12.010735897 # Molar density of Carbon (g/mol)
MO = 15.994914620 # Molar density of Oxygen (g/mol)
enrichment_n = '${fparse enrichment/MU235 / (enrichment/MU235 + (1-enrichment)/MU238)}' # Enrichment in nuclide fration
MUCO = '${fparse MU235*enrichment_n + MU238*(1-enrichment_n) + MC*ACU + MO*AOU}' # UCO molar density (g/mol)
rhon_kernel_UCO = '${fparse rho_kernel_UCO / MUCO * 0.6022140}' # Molar density of UCO (atom/b/cm)
# Kernel number densities (n/b/cm)
rhon_kernel_U235 = '${fparse rhon_kernel_UCO * enrichment_n}'
rhon_kernel_U238 = '${fparse rhon_kernel_UCO * (1 - enrichment_n)}'
rhon_kernel_C = '${fparse rhon_kernel_UCO * ACU}'
rhon_kernel_O = '${fparse rhon_kernel_UCO * AOU}'
# Fractions of pebble volume
kernel_fraction = '${fparse kernel_volume * triso_number / pebble_volume}'
# Pebble volume densities (atoms/b/cm)
rhon_U235 = '${fparse rhon_kernel_U235 * kernel_fraction}'
rhon_U238 = '${fparse rhon_kernel_U238 * kernel_fraction}'
# Parameters describing pebble cycling -----------------------------------------
pebble_unloading_rate = '${fparse 1.5/60}' # pebbles per minute / seconds per minute.
burnup_limit_weight = 147.6 # MWd / kg
rho_U = '${fparse (rhon_U235*MU235 + rhon_U238*MU238) * 1.660539}' # Density of uranium in pebble volume (g/cm3)
burnup_conversion = '${fparse 1e9*3600*24*rho_U}' # Conversion from MWd/kg -> J/m3
# Blocks -----------------------------------------------------------------------
fuel_blocks = '5 6 7 8 9'
cns_disch_blocks = '14'
upref_blocks = '3 16'
upcav_blocks = '4'
lowref_blocks = '10 11 12 13'
crs_blocks = '17 22'
rdref_blocks = '1 2 15'
rpv_blocks = '18 19 20 21'
ref_blocks = '${cns_disch_blocks} ${upref_blocks}
${lowref_blocks}
${rdref_blocks}'
# ==============================================================================
# GLOBAL PARAMETERS
# ==============================================================================
[GlobalParams]
is_meter = true
[]
# ==============================================================================
# GEOMETRY AND MESH
# ==============================================================================
[Mesh]
[pebble_bed]
type = FileMeshGenerator
file = ../data/streamline_mesh_in.e
exodus_extra_element_integers = 'pebble_streamline_id pebble_streamline_layer_id material_id'
[]
coord_type = RZ
rz_coord_axis = Y
[]
# ==============================================================================
# AUXVARIABLES AND AUXKERNELS
# ==============================================================================
[AuxVariables]
# Temperatures.
[T_solid]
family = MONOMIAL
order = CONSTANT
initial_condition = ${initial_temperature}
block = '${fuel_blocks} ${ref_blocks} ${crs_blocks} ${rpv_blocks}' # Everything but upper cavity
[]
# Porosity
[porosity]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
initial_condition = ${pbed_porosity}
[]
[]
# ==============================================================================
# MATERIALS
# ==============================================================================
[Materials]
[reflector]
type = CoupledFeedbackNeutronicsMaterial
library_file = '../data/gpbr200_microxs.xml'
library_name = 'gpbr200_microxs'
grid_names = 'tmod'
grid_variables = 'T_solid'
isotopes = 'Graphite'
densities = '8.82418e-2'
plus = true
material_id = 2
diffusion_coefficient_scheme = local
block = '${ref_blocks}'
[]
[crs]
type = CoupledFeedbackRoddedNeutronicsMaterial
block = '${crs_blocks}'
library_file = '../data/gpbr200_microxs.xml'
library_name = 'gpbr200_microxs'
grid_names = 'tmod'
grid_variables = 'T_solid'
isotopes = ' Graphite;
Graphite B10 B11;
Graphite'
densities = '8.82418e-2
7.1628E-02 8.9463E-03 2.2229E-03
8.82418e-2'
rod_segment_length = 1e3
front_position_function = 'cr_front'
segment_material_ids = '2 2 2'
rod_withdrawn_direction = 'y'
average_segment_id = segment_id
[]
[cavity]
type = ConstantNeutronicsMaterial
block = '${upcav_blocks}'
fromFile = true
library_file = '../data/gpbr200_void.xml'
material_id = 10
[]
[]
[Functions]
# Function describing CR depth
[cr_depth]
type = ConstantFunction
value = 1.747 # Range of control rod insertion: -1.318 -> 8.93
[]
# Offset from reactor reference frame
[cr_front]
type = ParsedFunction
expression = 'top - cr_depth'
symbol_names = 'top cr_depth'
symbol_values = '${pbed_top} cr_depth'
[]
[]
[Compositions]
[uco]
type = IsotopeComposition
density_type = atomic
isotope_densities = '
U235 ${rhon_kernel_U235}
U238 ${rhon_kernel_U238}
C12 ${rhon_kernel_C}
O16 ${rhon_kernel_O}
'
[]
[buffer]
type = IsotopeComposition
density_type = atomic
isotope_densities = 'Graphite 5.26466317651E-02'
[]
[PyC]
type = IsotopeComposition
density_type = atomic
isotope_densities = 'Graphite 9.52653336702E-02'
[]
[SiC]
type = IsotopeComposition
density_type = atomic
isotope_densities = '
SI28 4.43270697709E-02
SI29 2.25082086520E-03
SI30 1.48375772443E-03
C12 4.80616002990E-02
'
[]
[matrix]
type = IsotopeComposition
density_type = atomic
isotope_densities = 'Graphite 8.67415932892E-02'
[]
[triso]
type = Triso
compositions = 'uco buffer PyC SiC PyC'
radii = '${kernel_radius} ${buffer_radius} ${ipyc_radius} ${sic_radius} ${opyc_radius}'
[]
[triso_fill]
type = StochasticComposition
background_composition = matrix
packing_fractions = ${filling_factor}
triso_particles = triso
[]
[pebble]
type = Pebble
compositions = 'triso_fill matrix'
radii = '${fparse pebble_radius - pebble_shell_thickness} ${pebble_radius}'
[]
[]
# ==============================================================================
# PEBBLE DEPLETION
# ==============================================================================
[PebbleDepletion]
block = '${fuel_blocks}'
# Power.
power = ${total_power}
integrated_power_postprocessor = total_power
power_density_variable = total_power_density
family = MONOMIAL
order = CONSTANT
# Cross section data.
library_file = '../data/gpbr200_microxs.xml'
library_name = 'gpbr200_microxs'
fuel_temperature_grid_name = 'tfuel'
moderator_temperature_grid_name = 'tmod'
burnup_grid_name = 'burnup'
constant_grid_values = 'kernrad ${fparse kernel_radius * 1000}
fillfact ${filling_factor}
enrich ${enrichment}'
# Transmutation data.
dataset = ISOXML
isoxml_data_file = '../data/gpbr200_dtl.xml'
isoxml_lib_name = 'gpbr200_dtl'
# Some of the branching ratios in the DTL are unphysical, which Griffin will
# throw a warning for unless this is specified.
dtl_physicality = 'SILENT'
# Isotopic options
n_fresh_pebble_types = 1
fresh_pebble_compositions = 'pebble'
# Pebble options
porosity_name = porosity
maximum_burnup = '${fparse 196.8 * burnup_conversion}'
num_burnup_bins = 12
# Tabulation data.
initial_moderator_temperature = '${initial_temperature}'
initial_fuel_temperature = '${initial_temperature}'
[DepletionScheme]
type = ConstantStreamlineEquilibrium
# Streamline definition
major_streamline_axis = y
# Pebble options
pebble_unloading_rate = ${pebble_unloading_rate}
pebble_flow_rate_distribution = '0.12919675255653704 0.3237409742330389 0.16364127845178317 0.1970045449547337 0.1864164498039072'
pebble_diameter = '${fparse pebble_radius * 2.0}'
burnup_limit = '${fparse burnup_limit_weight * burnup_conversion}'
# Solver parameters
sweep_tol = 1e-8
sweep_max_iterations = 20
# Output
exodus_streamline_output = false
[]
diffusion_coefficient_scheme = local
[]
# ==============================================================================
# EXECUTION PARAMETERS
# ==============================================================================
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 9
ReflectingBoundary = 'rinner'
VacuumBoundary = 'rtop rbottom router'
[diff]
scheme = CFEM-Diffusion
family = LAGRANGE
order = FIRST
n_delay_groups = 6
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
block = '${fuel_blocks} ${upcav_blocks} ${ref_blocks} ${crs_blocks}' # Excluding RPV and Barrel
[]
[]
[Executioner]
type = Eigenvalue
solve_type = 'PJFNKMO'
constant_matrices = true
petsc_options_iname = '-pc_type -pc_hypre_type -ksp_gmres_restart '
petsc_options_value = 'hypre boomeramg 100'
line_search = none
# Linear/nonlinear iterations.
l_max_its = 100
l_tol = 1e-3
nl_max_its = 50
nl_rel_tol = 1e-7
nl_abs_tol = 1e-9
# Fixed point iterations.
fixed_point_min_its = 15
fixed_point_max_its = 200
custom_pp = eigenvalue
custom_abs_tol = 5e-5
custom_rel_tol = 1e-50
disable_fixed_point_residual_norm_check = true
# Power iterations.
free_power_iterations = 4
extra_power_iterations = 20
[]
# ==============================================================================
# MULTIAPPS AND TRANSFERS
# ==============================================================================
[Positions]
[element]
type = ElementCentroidPositions
block = ${fuel_blocks}
[]
[]
[MultiApps]
# Reactor TH.
[pronghorn_th]
type = FullSolveMultiApp
input_files = gpbr200_ss_phth_reactor.i
keep_solution_during_restore = true
execute_on = 'TIMESTEP_END'
[]
# Pebble conduction
[pebble_conduction]
type = FullSolveMultiApp
input_files = gpbr200_ss_bsht_pebble_triso.i
no_restore = true
positions_objects = 'element element element element element
element element element element element
element element element'
cli_args = 'kernel_radius=${kernel_radius};filling_factor=${filling_factor}'
execute_on = TIMESTEP_BEGIN
[]
[]
[Transfers]
# TO Pronghorn.
[to_pronghorn_total_power_density]
type = MultiAppCopyTransfer
to_multi_app = pronghorn_th
source_variable = total_power_density
variable = power_density
[]
# FROM Pronghorn.
[from_pronghorn_Tsolid]
type = MultiAppCopyTransfer
from_multi_app = pronghorn_th
source_variable = T_solid
variable = T_solid
[]
# To pebble conduction
[to_pebble_conduction_Tsolid]
type = MultiAppVariableValueSamplePostprocessorTransfer
to_multi_app = pebble_conduction
postprocessor = pebble_surface_temp
source_variable = T_solid
[]
[to_pebble_conduction_power_density]
type = MultiAppVariableValueSamplePostprocessorTransfer
to_multi_app = pebble_conduction
postprocessor = porous_media_power_density
source_variable = partial_power_density
map_array_variable_components_to_child_apps = true
[]
# From pebble conduction
[from_pebble_conduction_Tfuel]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = pebble_conduction
postprocessor = fuel_average_temp
source_variable = triso_temperature
map_array_variable_components_to_child_apps = true
[]
[from_pebble_conduction_Tmod]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = pebble_conduction
postprocessor = moderator_average_temp
source_variable = graphite_temperature
map_array_variable_components_to_child_apps = true
[]
[]
# ==============================================================================
# POSTPROCESSING AND OUTPUTS
# ==============================================================================
[AuxVariables]
# Max temperatures and power
[Tfuel_max]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
[]
[Tmod_max]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
[]
[ppd_max]
family = MONOMIAL
order = CONSTANT
block = '${fuel_blocks}'
[]
[]
[AuxKernels]
# Max temperatures and power
[Tfuel_max_aux]
type = ArrayVarReductionAux
variable = Tfuel_max
array_variable = triso_temperature
value_type = max
execute_on = TIMESTEP_END
[]
[Tmod_max_aux]
type = ArrayVarReductionAux
variable = Tmod_max
array_variable = graphite_temperature
value_type = max
execute_on = TIMESTEP_END
[]
[ppd_max_aux]
type = ArrayVarReductionAux
variable = ppd_max
array_variable = partial_power_density
value_type = max
execute_on = TIMESTEP_END
[]
[]
[Outputs]
csv = true
exodus = true
[]