ver-1fd

Convective Heating

General Case Description

The fourth heat transfer problem taken from Ambrosek and Longhurst (2008) builds on the capabilities verified in ver-1fa, ver-1fb, and ver-1fc. The configuration is the same as in ver-1fb, except that, the current case has a convection boundary. This case is simulated in (test/tests/ver-1fd/ver-1fd.i)

The case focuses on the heating of a semi-infinite slab by convection at the boundary. The slab is initially configured with a constant temperature of 100 K throughout the slab. A convection boundary is activated at the surface from time $var element = document.getElementById("moose-equation-26a0d23d-741d-440d-bf80-5297ecf9246d");katex.render("t = 0", element, {displayMode:false,throwOnError:false});$ s. The convection temperature is in the enclosure is $var element = document.getElementById("moose-equation-3c1607a4-a601-4b9d-b543-88d0ee6720bd");katex.render("T_{\\infty} = 500", element, {displayMode:false,throwOnError:false});$ K. In the slab, the conduction coefficient is $var element = document.getElementById("moose-equation-6d0eac87-f9df-4468-9996-8dd13b8b2f11");katex.render("h = 200", element, {displayMode:false,throwOnError:false});$ W, the thermal conductivity is $var element = document.getElementById("moose-equation-f9532a4e-6d1a-4283-9ae8-771f41c14e15");katex.render("k = 801", element, {displayMode:false,throwOnError:false});$ W/m/K, and the thermal diffusivity is $var element = document.getElementById("moose-equation-c125de21-7db9-448c-9a94-133f3ae00217");katex.render("\\alpha = 1.17 \\times 10^{-4}", element, {displayMode:false,throwOnError:false});$ m $var element = document.getElementById("moose-equation-1e753c7c-1f0d-4ec4-b17f-c566800bf389");katex.render("^2", element, {displayMode:false,throwOnError:false});$ /s.

Analytical solution

The analytical solution is provided by Incropera and DeWitt (2002):

$(1)var element = document.getElementById("moose-equation-de351b1b-b31c-4359-a505-fb4c6ab894c9");katex.render(" T(x,t) = T_i + (T_{\\infty}-T_i) \\left[ \\text{erfc}\\left( \\frac{x}{2 \\sqrt{t \\alpha}} \\right)-\\exp\\left( \\frac{hx}{k} + \\frac{h^2t \\alpha} {k^2}\\right) \\text{erfc}\\left( \\frac{x}{2 \\sqrt{t \\alpha}} + \\frac{h \\sqrt{t \\alpha}}{k} \\right)\\right],", element, {displayMode:true,throwOnError:false});$ where $var element = document.getElementById("moose-equation-aa6ebf16-dfcc-4dc7-a469-7a9ea46f025b");katex.render("T_i = 100", element, {displayMode:false,throwOnError:false});$ K is the initial temperature, $var element = document.getElementById("moose-equation-f4590310-6a3e-4281-9404-83516789c445");katex.render("T_{\\infty} = 500", element, {displayMode:false,throwOnError:false});$ K is the temperature of the enclosure, $var element = document.getElementById("moose-equation-b6690aef-6d34-4006-808e-4a386b48996e");katex.render("h = 200", element, {displayMode:false,throwOnError:false});$ W/m $var element = document.getElementById("moose-equation-467a862b-4f99-41c5-b0ba-f1bd6932ab71");katex.render("^2", element, {displayMode:false,throwOnError:false});$ /K is the conduction coefficient, $var element = document.getElementById("moose-equation-02fa4322-656e-46a6-9bd1-26e9724bfd80");katex.render("k = 401", element, {displayMode:false,throwOnError:false});$ W/m/K is the thermal conductivity, $var element = document.getElementById("moose-equation-ba1d1f16-baf6-4d37-828b-be63c45905fd");katex.render("\\text{erfc}", element, {displayMode:false,throwOnError:false});$ is the complimentary error function, $var element = document.getElementById("moose-equation-87bc271a-5fae-46c5-9d48-2a74a18f82cc");katex.render("x", element, {displayMode:false,throwOnError:false});$ is the position in the slab in m, and $(2)var element = document.getElementById("moose-equation-fc6ff21c-4911-4add-acb3-3e9c8aa4afda");katex.render(" \\alpha = \\frac{k}{\\rho C_p}", element, {displayMode:true,throwOnError:false});$ is the thermal diffusivity. The volumetric specific heat is defined as $var element = document.getElementById("moose-equation-059b4972-dd90-4a46-9a0a-d0962d5a50ed");katex.render("\\rho C_p = 3.439 \\times 10^6", element, {displayMode:false,throwOnError:false});$ J/m $var element = document.getElementById("moose-equation-6bec50f5-865b-47ed-aef4-3f36b91c3de8");katex.render("^3", element, {displayMode:false,throwOnError:false});$ /K, which gives us $var element = document.getElementById("moose-equation-fc328c3f-cfcf-4e7f-aac5-01aa70c583c6");katex.render("\\alpha \\approx 1.17 \\times 10^{-4}", element, {displayMode:false,throwOnError:false});$ m $var element = document.getElementById("moose-equation-3fe7f335-fc2e-48d8-98fb-109be639014d");katex.render("^2", element, {displayMode:false,throwOnError:false});$ /s.

Note that the simulated length of the semi-infinite slab is not explicitely specified in Ambrosek and Longhurst (2008). In TMAP8, a length of $var element = document.getElementById("moose-equation-06612da3-ed89-4dea-9941-b9e5077b80c6");katex.render("l=100", element, {displayMode:false,throwOnError:false});$ cm with a zero-flux boundary condition at the end was found to be sufficient to match the analytical solution (i.e., the temperature at the desired position $var element = document.getElementById("moose-equation-2972a9b3-aaa9-4855-b11e-d879aa4dc55e");katex.render("x = 5", element, {displayMode:false,throwOnError:false});$ cm is not affected by the boundary condition at position $var element = document.getElementById("moose-equation-6a26a8ed-9dff-4301-baf3-e5f164fe52c8");katex.render("l", element, {displayMode:false,throwOnError:false});$ ), as shown in Figure 1.

warning:Typo in Ambrosek and Longhurst (2008)

In Ambrosek and Longhurst (2008), the value of $var element = document.getElementById("moose-equation-7079a8c0-d6eb-4765-a060-35dfc2365134");katex.render("k = 801", element, {displayMode:false,throwOnError:false});$ W/m/K is provided, whereas the input file lists $var element = document.getElementById("moose-equation-a8b015f3-6bd6-4bc0-a732-e634f39d8eb2");katex.render("k = 401", element, {displayMode:false,throwOnError:false});$ W/m/K. In TMAP8, we have decided to use $var element = document.getElementById("moose-equation-5c867cb3-4bfa-4e55-b660-1680ded8e957");katex.render("k = 401", element, {displayMode:false,throwOnError:false});$ W/m/K since it provides the same results as those shown in Figure 9 in Ambrosek and Longhurst (2008), and provides the appropriate value for $var element = document.getElementById("moose-equation-960dfabd-ef66-4d7f-b807-83f04f3a8ad2");katex.render("\\alpha", element, {displayMode:false,throwOnError:false});$ . Moreover, Ambrosek and Longhurst (2008) lists $var element = document.getElementById("moose-equation-6187f0fb-aecc-45ed-8e33-57bc7dc069ca");katex.render("\\alpha = 1.17 \\times 10^{-4}", element, {displayMode:false,throwOnError:false});$ m $var element = document.getElementById("moose-equation-5675df05-8a26-4766-86c0-dc0f620b014b");katex.render("^2", element, {displayMode:false,throwOnError:false});$ /s in the documentation, but the input file lists $var element = document.getElementById("moose-equation-b227be0a-c008-473d-a290-250fc590ffc9");katex.render("\\rho C_p = 3.439 \\times 10^6", element, {displayMode:false,throwOnError:false});$ instead of $var element = document.getElementById("moose-equation-f3de8a3a-bf35-46d1-b0b5-42ebfd1933f0");katex.render("\\alpha", element, {displayMode:false,throwOnError:false});$ . TMAP8 assumes a density and specific heat value to match $var element = document.getElementById("moose-equation-361d4793-3db6-4ad2-abe7-c84f5c119d4c");katex.render("\\rho C_p = 3.439 \\times 10^6", element, {displayMode:false,throwOnError:false});$ to reproduce TMAP7's input file rather than documentation.

Results

The comparison between TMAP8 predictions and the analytical solution is performed at depth $var element = document.getElementById("moose-equation-deeef2ea-2de1-4a17-8e0d-1a427a7b4c87");katex.render("x = 5", element, {displayMode:false,throwOnError:false});$ cm. These results are shown in Figure 1. They show great agreement between TMAP8 and the analytical solution with a root mean square percentage error of RMSPE = 0.29 %.

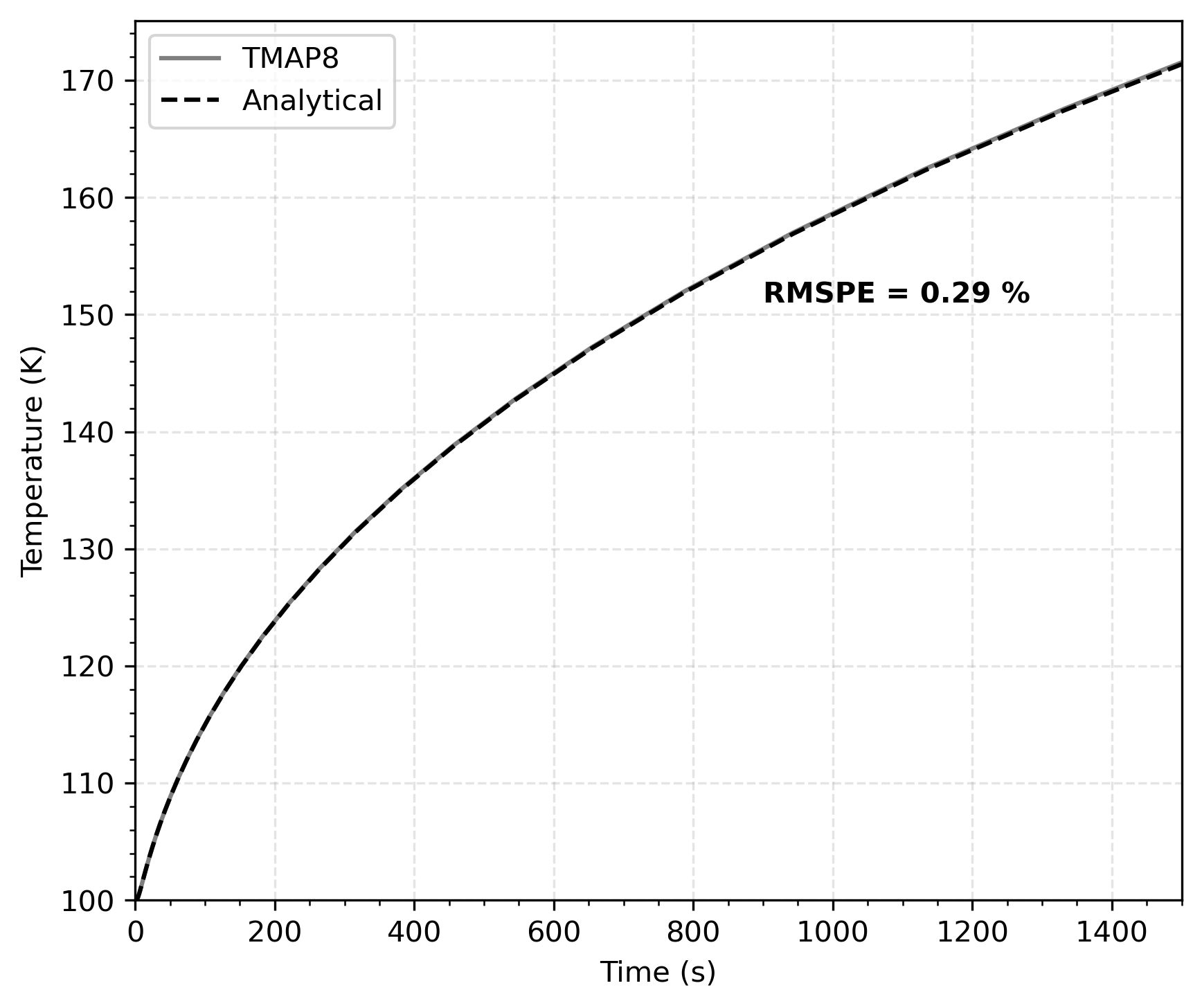
Figure 1: Comparison of temperature profiles for convective heating in a semi-infinite slab from the analytical solution and TMAP8 at depth $var element = document.getElementById("moose-equation-2d4b9054-dff7-4086-b0ca-cc052c09e672");katex.render("x = 5", element, {displayMode:false,throwOnError:false});$ cm. The RMSPE is the root mean square percentage error between the analytical solution and TMAP8 predictions.

Input files

The input file for this case can be found at (test/tests/ver-1fd/ver-1fd.i), which is also used as test in TMAP8 at (test/tests/ver-1fd/tests).

References

James Ambrosek and GR Longhurst. Verification and Validation of TMAP7. Technical Report INEEL/EXT-04-01657, Idaho National Engineering and Environmental Laboratory, December 2008.

@techreport{ambrosek2008verification,
    author = "Ambrosek, James and Longhurst, GR",
    title = "{Verification and Validation of TMAP7}",
    year = "2008",
    number = "INEEL/EXT-04-01657",
    month = "December",
    institution = "Idaho National Engineering and Environmental Laboratory"
}

F. P. Incropera and D. P. DeWitt. Fundamentals of Heat and Mass Transfer. John Wiley & Sons, 5th edition, 2002.

@book{Incropera2002,
    author = "Incropera, F. P. and DeWitt, D. P.",
    city = "New York",
    edition = "5th",
    publisher = "John Wiley \& Sons",
    title = "Fundamentals of Heat and Mass Transfer",
    year = "2002"
}

(test/tests/ver-1fd/ver-1fd.i)

# Verification Problem #1fd from TMAP7 V&V document
# Heating of a semi-infinite slab by convection at the left boundary

# Data used in TMAP7 case
position_measurement = '${units 5e-2 m}'
initial_temperature = '${units 100 K}' # T_i
enclosure_temperature = '${units 500 K}' # T_infinity
conduction_coefficient = '${units 200 W/m^2/K}' # h
thermal_conductivity = '${units 401 W/m/K}' # k
rho_Cp = '${units 3.439e6 J/m^3/K}'

# Selected for TMAP8 case
slab_length = '${units 1 m}' # semi-infinite slab
density = '${units 1000 kg/m^3}'
specific_heat = '${units ${fparse rho_Cp/density} J/kg/K}'
end_time = '${units 1500 s}'
num_nodes = 500 # (-)

[Mesh]
  type = GeneratedMesh
  dim = 1
  xmax = ${slab_length}
  nx = ${num_nodes}
[]

[Variables]
  # temperature parameter in the slab in K
  [temperature]
    initial_condition = ${initial_temperature}
  []
[]

[Kernels]
  [heat]
    type = HeatConduction
    variable = temperature
  []
  [heat_time_derivative]
    type = HeatConductionTimeDerivative
    variable = temperature
  []
[]

[BCs]
  # The right boundary of the slab is in adiabatic situation
  [rightflux]
    type = NeumannBC
    boundary = right
    variable = temperature
    value = 0
  []
  # The left boundary of the slab is a convection boundary
  [leftconvection]
    type = ConvectiveHeatFluxBC
    boundary = left
    variable = temperature
    T_infinity = ${enclosure_temperature}
    heat_transfer_coefficient = ${conduction_coefficient}
  []
[]

[Materials]
  # The diffusivity of the slab
  [diffusivity]
    type = GenericConstantMaterial
    prop_names = 'density thermal_conductivity specific_heat'
    prop_values = '${density} ${thermal_conductivity} ${specific_heat}'
  []
[]

[Preconditioning]
  [SMP]
    type = SMP
    full = true
  []
[]

[Executioner]
  type = Transient
  scheme = bdf2
  solve_type = NEWTON
  petsc_options_iname = '-pc_type'
  petsc_options_value = 'lu'
  nl_rel_tol = 1e-10
  nl_abs_tol = 1e-50
  l_tol = 1e-8
  end_time = ${end_time}
  dtmax = 2e2
  [TimeStepper]
    type = IterationAdaptiveDT
    dt = 1e-2
    optimal_iterations = 3
    iteration_window = 1
    growth_factor = 1.2
    cutback_factor = 0.8
  []
[]

[Postprocessors]
  # Used to obtain varying temperature with time at the desired position
  [temperature_at_x]
    type = PointValue
    variable = temperature
    point = '${position_measurement} 0 0'
    execute_on = 'initial timestep_end'
    outputs = 'csv'
  []
[]

[Outputs]
  exodus = true
  csv = true
[]

(test/tests/ver-1fd/ver-1fd.i)

# Verification Problem #1fd from TMAP7 V&V document
# Heating of a semi-infinite slab by convection at the left boundary

# Data used in TMAP7 case
position_measurement = '${units 5e-2 m}'
initial_temperature = '${units 100 K}' # T_i
enclosure_temperature = '${units 500 K}' # T_infinity
conduction_coefficient = '${units 200 W/m^2/K}' # h
thermal_conductivity = '${units 401 W/m/K}' # k
rho_Cp = '${units 3.439e6 J/m^3/K}'

# Selected for TMAP8 case
slab_length = '${units 1 m}' # semi-infinite slab
density = '${units 1000 kg/m^3}'
specific_heat = '${units ${fparse rho_Cp/density} J/kg/K}'
end_time = '${units 1500 s}'
num_nodes = 500 # (-)

[Mesh]
  type = GeneratedMesh
  dim = 1
  xmax = ${slab_length}
  nx = ${num_nodes}
[]

[Variables]
  # temperature parameter in the slab in K
  [temperature]
    initial_condition = ${initial_temperature}
  []
[]

[Kernels]
  [heat]
    type = HeatConduction
    variable = temperature
  []
  [heat_time_derivative]
    type = HeatConductionTimeDerivative
    variable = temperature
  []
[]

[BCs]
  # The right boundary of the slab is in adiabatic situation
  [rightflux]
    type = NeumannBC
    boundary = right
    variable = temperature
    value = 0
  []
  # The left boundary of the slab is a convection boundary
  [leftconvection]
    type = ConvectiveHeatFluxBC
    boundary = left
    variable = temperature
    T_infinity = ${enclosure_temperature}
    heat_transfer_coefficient = ${conduction_coefficient}
  []
[]

[Materials]
  # The diffusivity of the slab
  [diffusivity]
    type = GenericConstantMaterial
    prop_names = 'density thermal_conductivity specific_heat'
    prop_values = '${density} ${thermal_conductivity} ${specific_heat}'
  []
[]

[Preconditioning]
  [SMP]
    type = SMP
    full = true
  []
[]

[Executioner]
  type = Transient
  scheme = bdf2
  solve_type = NEWTON
  petsc_options_iname = '-pc_type'
  petsc_options_value = 'lu'
  nl_rel_tol = 1e-10
  nl_abs_tol = 1e-50
  l_tol = 1e-8
  end_time = ${end_time}
  dtmax = 2e2
  [TimeStepper]
    type = IterationAdaptiveDT
    dt = 1e-2
    optimal_iterations = 3
    iteration_window = 1
    growth_factor = 1.2
    cutback_factor = 0.8
  []
[]

[Postprocessors]
  # Used to obtain varying temperature with time at the desired position
  [temperature_at_x]
    type = PointValue
    variable = temperature
    point = '${position_measurement} 0 0'
    execute_on = 'initial timestep_end'
    outputs = 'csv'
  []
[]

[Outputs]
  exodus = true
  csv = true
[]

(test/tests/ver-1fd/tests)

[Tests]
  design = 'HeatConduction.md HeatConductionTimeDerivative.md'
  verification = 'ver-1fd.md'
  issues = '#12 #103'
  [ver-1fd]
    type = Exodiff
    input = ver-1fd.i
    exodiff = ver-1fd_out.e
    requirement = 'The system shall be able to model convective heating.'
  []
  [ver-1fd_csv]
    type = CSVDiff
    input = ver-1fd.i
    csvdiff = ver-1fd_out.csv
    should_execute = False  # this test relies on the output files from ver-1fd, so it shouldn't be run twice
    requirement = 'The system shall be able to model convective heating to generate CSV data for use in comparisons with the analytic solution.'
    prereq = ver-1fd
  []
  [ver-1fd_comparison]
    type = RunCommand
    command = 'python3 comparison_ver-1fd.py'
    requirement = 'The system shall be able to generate comparison plots between the analytical solution and simulated solution of verification case 1fd, modeling convective heating.'
    required_python_packages = 'matplotlib scipy numpy pandas os'
  []
[]

General Case Description
Analytical solution
Results
Input files
References