Simulating a simple GeoTES experiment
This page describes a reactive-transport simulation of a simple GeoTES scenario. The transport is handled using the PorousFlow module, while the Geochemistry module is used to simulate a heat exchanger and the geochemistry. The simulations are coupled together in an operator-splitting approach using MultiApps.
In Geological Thermal Energy Storage (GeoTES), hot fluid is pumped into an subsurface confined aquifer, stored there for some time, then pumped back again to produce electricity. Many different scenarios have been proposed, including different borehole geometries (used to pump the fluid), different pumping strategies and cyclicities (pumping down certain boreholes, up other boreholes, etc), different temperatures, different aquifer properties, etc. This page only describes the heating phase of a particularly simple set up.
Two wells (boreholes) are used.
The cold (production) well, which pumps aquifer water from the aquifer.
The hot (injection) well, which pumps hot fluid into the aquifer.
These are connected by a heat-exchanger, which heats the aquifer water produced from (1) and passes it to (2). This means the fluid pumped through the injection well is, in fact, heated aquifer water, which is important practically from a water-conservation standpoint, and to assess the geochemical aspects of circulating aquifer water through the GeoTES system.
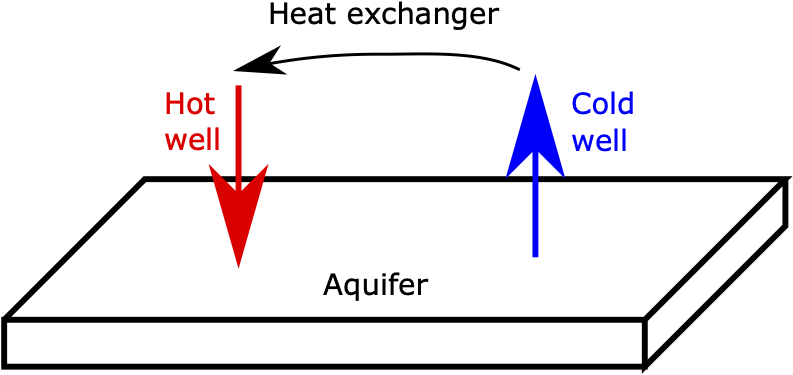
Figure 1: Schematic of the simple GeoTES simulation.
Aquifer geochemistry
It is assumed that only HO, Na, Cl and SiO(aq) are present in the system. While this is unrealistically simple for any aquifer, it allows this page to focus on the method of constructing more complicated models avoiding rather lengthy input files.
The database file
A small geochemical database involving only these species is used. Readers who are building their own database might find exploring its structure useful:
{
"Header": {
"title": "Very small MOOSE thermodynamic database",
"original": "moose/modules/geochemistry/python/original_dbs/gwb_llnl.dat",
"date": "09:14 18-08-2020",
"original format": "gwb",
"activity model": "debye-huckel",
"fugacity model": "tsonopoulos",
"logk model": "fourth-order",
"logk model (functional form)": "a0 + a1 T + a2 T^2 + a3 T^3 + a4 T^4",
"temperatures": [
0.0,
25.0,
60.0,
100.0,
150.0,
200.0,
250.0,
300.0
],
"pressures": [
1.0134,
1.0134,
1.0134,
1.0134,
4.76,
15.549,
39.776,
85.927
],
"adh": [
0.4913,
0.5092,
0.545,
0.5998,
0.6898,
0.8099,
0.9785,
1.2555
],
"bdh": [
0.3247,
0.3283,
0.3343,
0.3422,
0.3533,
0.3655,
0.3792,
0.3965
],
"bdot": [
0.0174,
0.041,
0.044,
0.046,
0.047,
0.047,
0.034,
0.0
],
"neutral species": {
"co2": {
"a": [
0.1224,
0.1127,
0.09341,
0.08018,
0.08427,
0.09892,
0.1371,
0.1967
],
"b": [
-0.004679,
-0.01049,
-0.0036,
-0.001503,
-0.01184,
-0.0104,
-0.007086,
-0.01809
],
"c": [
-0.0004114,
0.001545,
9.609e-05,
0.0005009,
0.003118,
0.001386,
-0.002887,
-0.002497
],
"d": [
0.0,
0.0,
0.0,
0.0,
0.0,
0.0,
0.0,
0.0
]
},
"h2o": {
"a": [
1.4203,
1.45397,
1.5012,
1.5551,
1.6225,
1.6899,
1.7573,
1.8247
],
"note": "Missing array values in original database have been filled using a linear fit. Original values are [500.0000, -.0005362, 500.0000, -.0007132, -.0008312, 500.0000, 500.0000, 500.0000]",
"b": [
0.0177,
0.022357,
0.0289,
0.036478,
0.045891,
0.0553,
0.0647,
0.0741
],
"c": [
0.0103,
0.0093804,
0.008,
0.0064366,
0.0045221,
0.0026,
0.0006,
-0.0013
],
"d": [
-0.0005,
-0.0005362,
-0.0006,
-0.0007132,
-0.0008312,
-0.0009,
-0.0011,
-0.0012
]
}
}
},
"elements": {
"Cl": {
"name": "Chlorine",
"molecular weight": 35.453
},
"H": {
"name": "Hydrogen",
"molecular weight": 1.0079
},
"Na": {
"name": "Sodium",
"molecular weight": 22.9898
},
"O": {
"name": "Oxygen",
"molecular weight": 15.9994
},
"Si": {
"name": "Silicon",
"molecular weight": 28.085
}
},
"basis species": {
"H2O": {
"elements": {
"H": 2.0,
"O": 1.0
},
"radius": 0.0,
"charge": 0.0,
"molecular weight": 18.0152
},
"Cl-": {
"elements": {
"Cl": 1.0
},
"radius": 3.0,
"charge": -1.0,
"molecular weight": 35.453
},
"Na+": {
"elements": {
"Na": 1.0
},
"radius": 4.0,
"charge": 1.0,
"molecular weight": 22.9898
},
"SiO2(aq)": {
"elements": {
"O": 2.0,
"Si": 1.0
},
"radius": -0.5,
"charge": 0.0,
"molecular weight": 60.0843
}
},
"secondary species": {
"NaCl": {
"species": {
"Na+": 1.0,
"Cl-": 1.0
},
"charge": 0.0,
"radius": 4.0,
"molecular weight": 58.4428,
"logk": [
1.855,
1.5994,
1.2945,
0.9856,
0.635,
0.2935,
-0.0407,
-0.3487
],
"note": "Missing array values in original database have been filled using a fourth-order fit. Original values are [1.8550, 1.5994, 1.2945, .9856, .6350, .2935, 500.0000, 500.0000]"
}
},
"free electron": {
"e-": {
"species": {
"H2O": 0.5,
"O2(g)": -0.25,
"H+": -1.0
},
"charge": -1.0,
"radius": 0.0,
"molecular weight": 0.0,
"logk": [
22.76135,
20.7757,
18.513025,
16.4658,
14.473225,
12.92125,
11.68165,
10.67105
]
}
},
"mineral species": {
"QuartzLike": {
"species": {
"SiO2(aq)": 1.0
},
"molar volume": 22.688,
"molecular weight": 60.0843,
"logk": [-5.0, -4.0, -3.0, -2.0, -1.0, 0.0, 1.0, 2.0]
},
"QuartzUnlike": {
"species": {
"SiO2(aq)": 1.0
},
"molar volume": 22.688,
"molecular weight": 60.0843,
"logk": [-1.0, -2.0, -3.0, -4.0, -5.0, -6.0, -7.0, -8.0]
}
}
}
Initial conditions
The aquifer temperature is uniformly 50C before injection and production.
The aquifer is assumed to be consist entirely of a mineral called QuartzLike and a kinetic rate is used for its dissolution. The mineral QuartzLike is similar to Quartz but it has a different equilibrium constant structure in order to emphasise the dissolution upon heating.
Each 1kg of solvent water is assumed to hold 0.1mol of Na and Cl, and a certain amount of SiO(aq). The following input file finds the free molality of SiO(aq) when in contact with QuartzLike at 50C:
# Finds the equilibrium free molality of SiO2(aq) when in contact with QuartzLike at 50degC
[UserObjects]
[definition]
type = GeochemicalModelDefinition
database_file = "small_database.json"
basis_species = "H2O SiO2(aq) Na+ Cl-"
equilibrium_minerals = "QuartzLike"
[]
[]
[TimeIndependentReactionSolver]
model_definition = definition
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
swap_out_of_basis = "SiO2(aq)"
swap_into_basis = QuartzLike
constraint_species = "H2O Na+ Cl- QuartzLike"
constraint_value = " 1.0 0.1 0.1 396.685" # amount of QuartzLike is unimportant (provided it is positive). 396.685 is used simply because the other geotes_2D input files use this amount
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_mineral"
constraint_unit = " kg moles moles moles"
temperature = 50.0
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
precision = 12
[]
[Postprocessors]
[free_moles_SiO2]
type = PointValue
point = '0 0 0'
variable = 'molal_SiO2(aq)'
[]
[]
[Outputs]
csv = true
[]
The result it molality = 0.000555052386. It is necessary to find this initial molality, only because QuartzLike is a kinetic species, so cannot appear the basis (see another similar example). If it were treated as an equilibrium species, its initial free mole number could be specified in the input file below (see an example of this).
Spatially-dependent geochemistry simulation
Because an operator-splitting approach is used, the simulation of the aquifer geochemistry may be considered separately from the porous-flow simulation and the heat exchanger simulation. This section describes how the aquifer geochemistry is simulated.
The model set-up commences with defining the basis species, minerals, and the rate description for the kinetic dissolution of QuartzLike:
[UserObjects]
[rate_quartz]
type = GeochemistryKineticRate
kinetic_species_name = QuartzLike
intrinsic_rate_constant = 1.0E-2
multiply_by_mass = true
area_quantity = 1
activation_energy = 72800.0
[]
[definition]
type = GeochemicalModelDefinition
database_file = "small_database.json"
basis_species = "H2O SiO2(aq) Na+ Cl-"
kinetic_minerals = "QuartzLike"
kinetic_rate_descriptions = "rate_quartz"
[]
[nodal_void_volume_uo]
type = NodalVoidVolume
porosity = porosity
execute_on = 'initial timestep_end' # "initial" means this is evaluated properly for the first timestep
[]
[]
The parameters in the rate description are similar to those chosen in another example.
A SpatialReactionSolver defines the initial concentrations of the species and how reactants are added to the system
[SpatialReactionSolver]
model_definition = definition
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
constraint_species = "H2O Na+ Cl- SiO2(aq)"
# ASSUME that 1 litre of solution contains:
constraint_value = " 1.0 0.1 0.1 0.000555052386"
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_concentration"
constraint_unit = " kg moles moles molal"
initial_temperature = 50.0
kinetic_species_name = QuartzLike
# Per 1 litre (1000cm^3) of aqueous solution (1kg of solvent water), there is 9000cm^3 of QuartzLike, which means the initial porosity is 0.1.
kinetic_species_initial_value = 9000
kinetic_species_unit = cm3
temperature = temperature
source_species_names = 'H2O Na+ Cl- SiO2(aq)'
source_species_rates = 'rate_H2O_per_1l rate_Na_per_1l rate_Cl_per_1l rate_SiO2_per_1l'
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
evaluate_kinetic_rates_always = true # implicit time-marching used for stability
execute_console_output_on = ''
[]
Most lines in this block need further discussion.
Since this is a
SpatialReactionSolver, the system described exists at each node in the mesh. Each node will typically have a different void volume fraction associated to it: nodes in coarsely-meshed regions will be responsible for large volumes of fluid, while nodes in finely-meshed regions, or regions with small porosity, will represent small volumes of fluid. In the above setup, just 1 liter of aqueous solution is modelled at each node. As discussed below, the rates of reactant additions will be adjusted to reflect this. It is assumed that 1 liter of aqueous solution contains 1.0kg of solvent water and the specified quantities of Na, Cl and SiO(aq).The
free_molalityconstraint on SiO(aq) is set according to the equilibrium simulation described above.It is assumed that there is 9000cm of
QuartzLikeper the 1000cm (1 liter) of aqueous solution. This corresponds to 396.685mol ofQuartzLike. The reason for choosing 9000cm ofQuartzLikeis that the aquifer porosity is assumed to be 0.1 and to be calculated using:
The initial
temperatureof the aquifer is assumed to be 50C, and during simulation it is given by theAuxVariablecalledtemperature. ThisAuxVariablewill be provided by the PorousFlow simulation described below.The
source_species_ratesare defined by therate_*_per_1lAuxVariableswhich are discussed further below.
The Mesh and Executioner are provided in the input file so that it may be run alone in a stand-alone fashion, but these are overwritten when coupled with the PorousFlow simulation (below). The remainder of the input file deals with AuxVariables that are used to transfer information to-and-from the PorousFlow simulation.
The PorousFlow simulation provides temperature, pf_rate_H2O, pf_rate_Na, pf_rate_Cl and pf_rate_SiO2 as AuxVariables. The pf_rate quantities are rates of changes of fluid-component mass (kg.s) at each node, but the Geochemistry module expects rates-of-changes of moles (mol.s) at each node. Moreover, since this input file considers just 1 liter of aqueous solution at every node, the nodal_void_volume is used to convert to mol.s/(liter of aqueous solution). For instance:
[rate_H2O_per_1l_auxk]
type = ParsedAux
coupled_variables = 'pf_rate_H2O nodal_void_volume'
variable = rate_H2O_per_1l
# pf_rate = change in kg at every node
# pf_rate * 1000 / molar_mass_in_g_per_mole = change in moles at every node
# pf_rate * 1000 / molar_mass / (nodal_void_volume_in_m^3 * 1000) = change in moles per litre of aqueous solution
expression = 'pf_rate_H2O / 18.0152 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
This input file provides the PorousFlow simulation with updated mass-fractions (after QuartzLike dissolution has occurred to increase the SiO(aq) concentration, for instance). These are based on the "transported" mole numbers at each node, which are the mole numbers of the transported species in the original basis (mole numbers of HO, Na, Cl and free moles of SiO(aq) in this case). These are recorded into AuxVariables using, for example:
[transported_H2O_auxk]
type = GeochemistryQuantityAux
variable = transported_H2O
species = H2O
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
The mass fraction is computed using, for example
[transported_mass_auxk]
type = ParsedAux
coupled_variables = 'transported_H2O transported_Na transported_Cl transported_SiO2'
variable = transported_mass
expression = 'transported_H2O * 18.0152 + transported_Na * 22.9898 + transported_Cl * 35.453 + transported_SiO2 * 60.0843'
execute_on = 'timestep_end'
[]
[massfrac_H2O]
type = ParsedAux
coupled_variables = 'transported_H2O transported_mass'
variable = massfrac_H2O
expression = 'transported_H2O * 18.0152 / transported_mass'
execute_on = 'timestep_end'
[]
The PorousFlow simulation
The PorousFlow module is used to perform the transport. It is assumed the aquifer may be adequately modelled using a 2D mesh. The injection well is at and the production well at :
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[injection_node]
input = gen
type = ExtraNodesetGenerator
new_boundary = injection_node
coord = '-30 0 0'
[]
[]
1.0 30 0 0
Recall that the PorousFlow module considers mass fractions, not mole-fractions or molalities, etc. Denoting the mass-fraction of Na by f0, the mass-fraction of Cl by f1, and the mass-fraction of SiO(aq) by f2 (the mass-fraction of HO may be worked out by summing mass-fractions to unity), the Variables are:
[Variables]
[f0]
initial_condition = 0.002285946
[]
[f1]
initial_condition = 0.0035252
[]
[f2]
initial_condition = 1.3741E-05
[]
[porepressure]
initial_condition = 2E6
[]
[temperature]
initial_condition = 50
scaling = 1E-6 # fluid enthalpy is roughly 1E6
[]
[]
The initial conditions are chosen to reflect the temperature and mole numbers of the aquifer geochemistry input file, and an initial porepressure of 2MPa is used, corresponding to an approximate depth of 200m.
Much of the remainder of this input file is typical of PorousFlow simulations. The points of particular interest here involve the transfer of information to the aquifer geochemistry simulation (above) and the heat-exchanger simulation (below).
Transfer to the aquifer geochemistry simulation
The PorousFlow input file transfers the rates of changes of each species (kg.s) at each node to the aquifer geochemistry simulation. This is achieved through saving these changes from Kernel residual evaluations into AuxKernels, using the save_component_rate_in:
[PorousFlowFullySaturated]
coupling_type = ThermoHydro
porepressure = porepressure
temperature = temperature
mass_fraction_vars = 'f0 f1 f2'
save_component_rate_in = 'rate_Na rate_Cl rate_SiO2 rate_H2O' # change in kg at every node / dt
fp = the_simple_fluid
temperature_unit = Celsius
[]
Transfer from the aquifer geochemistry simulation
At the end of each time-step, the aquifer geochemistry simulation provides updated mass-fractions to the PorousFlow simulation:
[massfrac_from_geochem]
type = MultiAppCopyTransfer
source_variable = 'massfrac_Na massfrac_Cl massfrac_SiO2'
variable = 'f0 f1 f2'
from_multi_app = react
Interfacing with the heat-exchanger simulation
This input file simulates fluid-and-heat injection through the well at and fluid-and-heat extraction from the well at .
The heat injection is modelled using a fixed value of temperature at the injection_node:
[BCs]
[injection_temperature]
type = MatchedValueBC
variable = temperature
v = injection_temperature
boundary = injection_node
[]
[]
The injection_temperature variable is set by the exchanger simulation (below) via a MultiApp Transfer. The fluid injection is modelled using a PorousFlowPolyLineSink, such as:
[inject_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Na
point_file = injection.bh
variable = f0
[]
In this block:
The
SumQuantityUOmeasures the injected mass, for purposes of checking that the correct amount of fluid has been injectedThe
${injected_rate}is a constant specified at the top of the input file as 1kg.s.m.The combination of
${injected_rate},p_or_t_vals,line_lengthandmultiplying_varmeans that thevariable(which isf0, or the mass-fraction of Na) will be subjected to a source of sizeinjection_rate_massfrac_Naat the borehole's position
The four injection_rate_massfrac_* variables are set by the exchanger simulation (below) via a MultiApp Transfer.
The fluid and heat production from the other well are also simulated by PorousFlowPolyLineSinks, such as:
[produce_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Na
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 0
point_file = production.bh
variable = f0
[]
In this block:
the
produced_mass_Narecords the amount of Na produced;the
${injected_rate}is a constant specified at the top of the input file as 1kg.s.m.the
mass_fraction_component = 0instructs PorousFlow to capture only the zeroth mass fraction (Na)
Heat energy is captured using a similar technique (notice the use_enthalpy flag):
[produce_heat]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_heat
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
use_enthalpy = true
point_file = production.bh
variable = temperature
The produced_mass_* quantities and the temperature at the production well are provided to the heat-exchanger input file (below). However, that input file works in mole units, not mass fractions, so a translation is needed:
[kg_Na_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Na
[]
[mole_rate_Na_produced]
type = FunctionValuePostprocessor
function = moles_Na
indirect_dependencies = 'kg_Na_produced_this_timestep dt'
[]
[moles_Na]
type = ParsedFunction
symbol_names = 'kg_Na dt'
symbol_values = 'kg_Na_produced_this_timestep dt'
expression = 'kg_Na * 1000 / 22.9898 / dt'
[]
The heat-exchanger simulation
This input file uses a TimeDependentReactionSolver object, but in the absence of data concerning the kinetics of QuartzLike in heat-exchangers, this mineral is treated as an equilibrium species (non-kinetic):
[TimeDependentReactionSolver]
model_definition = definition
include_moose_solve = false
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
swap_out_of_basis = "SiO2(aq)"
swap_into_basis = "QuartzLike"
constraint_species = "H2O Na+ Cl- QuartzLike"
constraint_value = " 1.0E-2 0.1E-2 0.1E-2 1E-10"
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_mineral"
constraint_unit = " kg moles moles moles"
initial_temperature = 50.0
mode = 4
temperature = 200
cold_temperature = 40.0
source_species_names = 'H2O Na+ Cl- SiO2(aq)'
source_species_rates = 'production_rate_H2O production_rate_Na production_rate_Cl production_rate_SiO2'
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
evaluate_kinetic_rates_always = true # implicit time-marching used for stability
execute_console_output_on = '' # only CSV output used in this example
[]
Notice the following points:
QuartzLikeis provided with a very small initialfree_mole_mineral_species, which means that SiO(aq) will find its initial concentration at equilibrium.mode = 4, which means "heat-exchanger" mode is used. This means, at each time-step:any fluid present in the system is removed;
fluid added by the
source_speciesis added;the system is taken to
cold_temperature;any precipitates are recorded and removed from the system (in the case of
QuartzLike, a little precipitation will occur becausecold_temperatureis less than the aquifer temperature);the system is heated to
temperature;any precipitates are recorded and removed from the system (in the case of
QuartzLike, no further precipitation will occur because it is more soluble at higher temperatures).
The
source_speciesare set by theproduction_rate_*AuxVariables. These are quantities pumped from the production well in the PorousFlow simulation, and are provided by a MultiApp Transfer from the PorousFlow simulation as described above.
This simulation provides the PorousFlow simulation with the injection temperature (200C). It also provides the mass-fractions of the injected fluid. This is achieved by recording the "transported" mole numbers:
[transported_H2O_auxk]
type = GeochemistryQuantityAux
variable = transported_H2O
species = H2O
quantity = transported_moles_in_original_basis
[]
and converting mole numbers to mass fractions:
[transported_mass_auxk]
type = ParsedAux
coupled_variables = 'transported_H2O transported_Na transported_Cl transported_SiO2'
variable = transported_mass
expression = 'transported_H2O * 18.0152 + transported_Na * 22.9898 + transported_Cl * 35.453 + transported_SiO2 * 60.0843'
[]
[massfrac_H2O]
type = ParsedAux
coupled_variables = 'transported_mass transported_H2O'
variable = massfrac_H2O
expression = '18.0152 * transported_H2O / transported_mass'
[]
Quantities of interest are recorded by Postprocessors:
[Postprocessors]
[cumulative_moles_precipitated_quartz]
type = PointValue
variable = dumped_quartz
[]
[production_temperature]
type = PointValue
variable = production_temperature
[]
[mass_heated_this_timestep]
type = PointValue
variable = transported_mass
[]
[]
Results
The figures below depict how heat has advected from the hot well to the cold well, as well as how QuartzLike dissolution has caused small changes in the porosity of the aquifer.
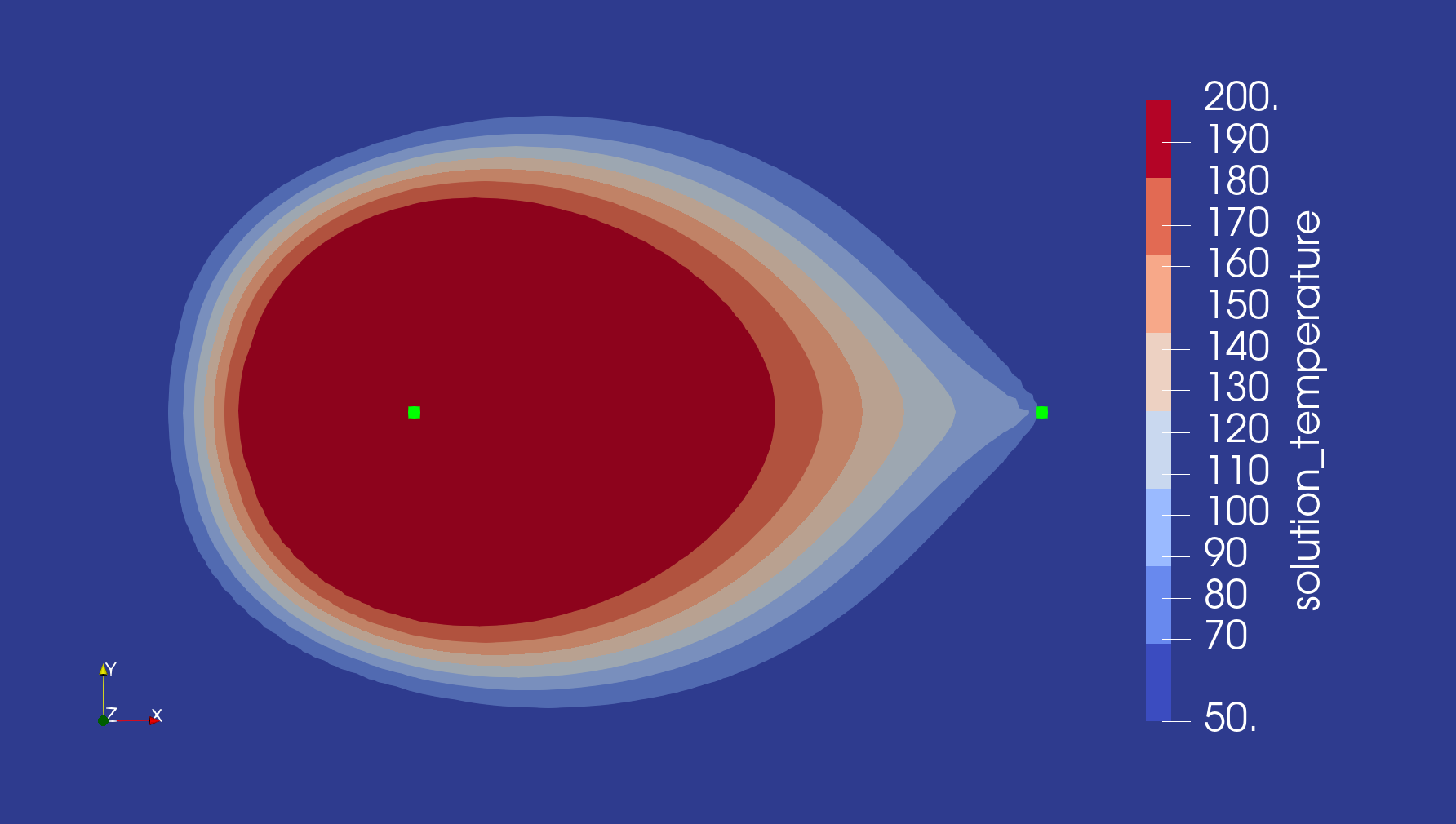
Figure 2: Aquifer temperature after injection of heated aquifer-brine into the system. The green dots show the injection and production borehole positions.
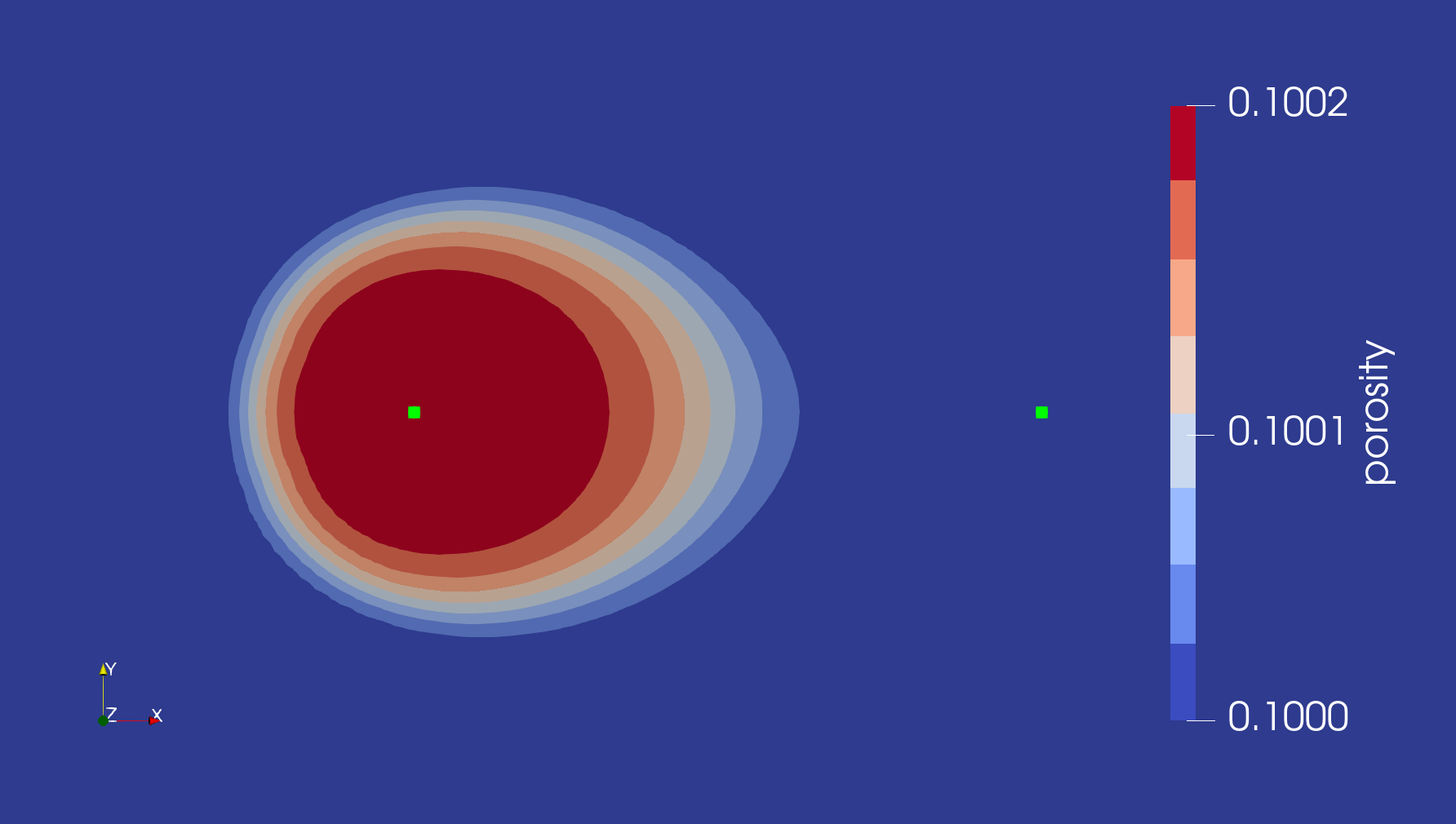
Figure 3: Aquifer porosity after injection of heated aquifer-brine into the system that causes dissolution of the aquifer quartz. The green dots show the injection and production borehole positions.
Comparison with QuartzUnlike
A very similar set of simulations, aquifer_un_quartz_geochemistry.i and exchanger_un_quartz.i may be found in the same directory. Instead of QuartzLike, these use the QuartzUnlike mineral, which precipitates upon heating rather than cooling. It is expected that the hot-fluid injection will have little impact upon the aquifer structure, but that lots of QuartzUnlike will precipitate in the heat exchanger as it heats the produced reservoir fluid. Indeed, the following figure shows this occurs:
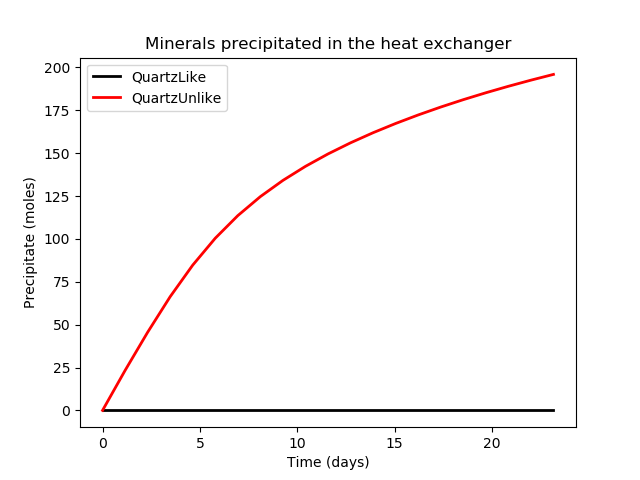
Figure 4: Minerals precipitated in the heat exchanger for the QuartzLike and QuartzUnlike cases. There are no QuartzLike precipitates because it becomes more soluble as it is heated, in contrast to the QuartzUnlike mineral.
(modules/combined/examples/geochem-porous_flow/geotes_2D/small_database.json)
{
"Header": {
"title": "Very small MOOSE thermodynamic database",
"original": "moose/modules/geochemistry/python/original_dbs/gwb_llnl.dat",
"date": "09:14 18-08-2020",
"original format": "gwb",
"activity model": "debye-huckel",
"fugacity model": "tsonopoulos",
"logk model": "fourth-order",
"logk model (functional form)": "a0 + a1 T + a2 T^2 + a3 T^3 + a4 T^4",
"temperatures": [
0.0,
25.0,
60.0,
100.0,
150.0,
200.0,
250.0,
300.0
],
"pressures": [
1.0134,
1.0134,
1.0134,
1.0134,
4.76,
15.549,
39.776,
85.927
],
"adh": [
0.4913,
0.5092,
0.545,
0.5998,
0.6898,
0.8099,
0.9785,
1.2555
],
"bdh": [
0.3247,
0.3283,
0.3343,
0.3422,
0.3533,
0.3655,
0.3792,
0.3965
],
"bdot": [
0.0174,
0.041,
0.044,
0.046,
0.047,
0.047,
0.034,
0.0
],
"neutral species": {
"co2": {
"a": [
0.1224,
0.1127,
0.09341,
0.08018,
0.08427,
0.09892,
0.1371,
0.1967
],
"b": [
-0.004679,
-0.01049,
-0.0036,
-0.001503,
-0.01184,
-0.0104,
-0.007086,
-0.01809
],
"c": [
-0.0004114,
0.001545,
9.609e-05,
0.0005009,
0.003118,
0.001386,
-0.002887,
-0.002497
],
"d": [
0.0,
0.0,
0.0,
0.0,
0.0,
0.0,
0.0,
0.0
]
},
"h2o": {
"a": [
1.4203,
1.45397,
1.5012,
1.5551,
1.6225,
1.6899,
1.7573,
1.8247
],
"note": "Missing array values in original database have been filled using a linear fit. Original values are [500.0000, -.0005362, 500.0000, -.0007132, -.0008312, 500.0000, 500.0000, 500.0000]",
"b": [
0.0177,
0.022357,
0.0289,
0.036478,
0.045891,
0.0553,
0.0647,
0.0741
],
"c": [
0.0103,
0.0093804,
0.008,
0.0064366,
0.0045221,
0.0026,
0.0006,
-0.0013
],
"d": [
-0.0005,
-0.0005362,
-0.0006,
-0.0007132,
-0.0008312,
-0.0009,
-0.0011,
-0.0012
]
}
}
},
"elements": {
"Cl": {
"name": "Chlorine",
"molecular weight": 35.453
},
"H": {
"name": "Hydrogen",
"molecular weight": 1.0079
},
"Na": {
"name": "Sodium",
"molecular weight": 22.9898
},
"O": {
"name": "Oxygen",
"molecular weight": 15.9994
},
"Si": {
"name": "Silicon",
"molecular weight": 28.085
}
},
"basis species": {
"H2O": {
"elements": {
"H": 2.0,
"O": 1.0
},
"radius": 0.0,
"charge": 0.0,
"molecular weight": 18.0152
},
"Cl-": {
"elements": {
"Cl": 1.0
},
"radius": 3.0,
"charge": -1.0,
"molecular weight": 35.453
},
"Na+": {
"elements": {
"Na": 1.0
},
"radius": 4.0,
"charge": 1.0,
"molecular weight": 22.9898
},
"SiO2(aq)": {
"elements": {
"O": 2.0,
"Si": 1.0
},
"radius": -0.5,
"charge": 0.0,
"molecular weight": 60.0843
}
},
"secondary species": {
"NaCl": {
"species": {
"Na+": 1.0,
"Cl-": 1.0
},
"charge": 0.0,
"radius": 4.0,
"molecular weight": 58.4428,
"logk": [
1.855,
1.5994,
1.2945,
0.9856,
0.635,
0.2935,
-0.0407,
-0.3487
],
"note": "Missing array values in original database have been filled using a fourth-order fit. Original values are [1.8550, 1.5994, 1.2945, .9856, .6350, .2935, 500.0000, 500.0000]"
}
},
"free electron": {
"e-": {
"species": {
"H2O": 0.5,
"O2(g)": -0.25,
"H+": -1.0
},
"charge": -1.0,
"radius": 0.0,
"molecular weight": 0.0,
"logk": [
22.76135,
20.7757,
18.513025,
16.4658,
14.473225,
12.92125,
11.68165,
10.67105
]
}
},
"mineral species": {
"QuartzLike": {
"species": {
"SiO2(aq)": 1.0
},
"molar volume": 22.688,
"molecular weight": 60.0843,
"logk": [-5.0, -4.0, -3.0, -2.0, -1.0, 0.0, 1.0, 2.0]
},
"QuartzUnlike": {
"species": {
"SiO2(aq)": 1.0
},
"molar volume": 22.688,
"molecular weight": 60.0843,
"logk": [-1.0, -2.0, -3.0, -4.0, -5.0, -6.0, -7.0, -8.0]
}
}
}
(modules/combined/examples/geochem-porous_flow/geotes_2D/aquifer_equilibrium.i)
# Finds the equilibrium free molality of SiO2(aq) when in contact with QuartzLike at 50degC
[UserObjects]
[definition]
type = GeochemicalModelDefinition
database_file = "small_database.json"
basis_species = "H2O SiO2(aq) Na+ Cl-"
equilibrium_minerals = "QuartzLike"
[]
[]
[TimeIndependentReactionSolver]
model_definition = definition
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
swap_out_of_basis = "SiO2(aq)"
swap_into_basis = QuartzLike
constraint_species = "H2O Na+ Cl- QuartzLike"
constraint_value = " 1.0 0.1 0.1 396.685" # amount of QuartzLike is unimportant (provided it is positive). 396.685 is used simply because the other geotes_2D input files use this amount
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_mineral"
constraint_unit = " kg moles moles moles"
temperature = 50.0
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
precision = 12
[]
[Postprocessors]
[free_moles_SiO2]
type = PointValue
point = '0 0 0'
variable = 'molal_SiO2(aq)'
[]
[]
[Outputs]
csv = true
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/aquifer_geochemistry.i)
# Simulates geochemistry in the aquifer. This input file may be run in standalone fashion but it does not do anything of interest. To simulate something interesting, run the porous_flow.i simulation which couples to this input file using MultiApps.
# This file receives pf_rate_H2O, pf_rate_Na, pf_rate_Cl, pf_rate_SiO2 and temperature as AuxVariables from porous_flow.i.
# The pf_rate quantities are kg/s changes of fluid-component mass at each node, but the geochemistry module expects rates-of-changes of moles at every node. Secondly, since this input file considers just 1 litre of aqueous solution at every node, the nodal_void_volume is used to convert pf_rate_* into rate_*_per_1l, which is measured in mol/s/1_litre_of_aqueous_solution.
# This file sends massfrac_Na, massfrac_Cl and massfrac_SiO2 to porous_flow.i. These are computed from the corresponding transported_* quantities.
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[]
[GlobalParams]
point = '0 0 0'
reactor = reactor
[]
[SpatialReactionSolver]
model_definition = definition
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
constraint_species = "H2O Na+ Cl- SiO2(aq)"
# ASSUME that 1 litre of solution contains:
constraint_value = " 1.0 0.1 0.1 0.000555052386"
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_concentration"
constraint_unit = " kg moles moles molal"
initial_temperature = 50.0
kinetic_species_name = QuartzLike
# Per 1 litre (1000cm^3) of aqueous solution (1kg of solvent water), there is 9000cm^3 of QuartzLike, which means the initial porosity is 0.1.
kinetic_species_initial_value = 9000
kinetic_species_unit = cm3
temperature = temperature
source_species_names = 'H2O Na+ Cl- SiO2(aq)'
source_species_rates = 'rate_H2O_per_1l rate_Na_per_1l rate_Cl_per_1l rate_SiO2_per_1l'
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
evaluate_kinetic_rates_always = true # implicit time-marching used for stability
execute_console_output_on = ''
[]
[UserObjects]
[rate_quartz]
type = GeochemistryKineticRate
kinetic_species_name = QuartzLike
intrinsic_rate_constant = 1.0E-2
multiply_by_mass = true
area_quantity = 1
activation_energy = 72800.0
[]
[definition]
type = GeochemicalModelDefinition
database_file = "small_database.json"
basis_species = "H2O SiO2(aq) Na+ Cl-"
kinetic_minerals = "QuartzLike"
kinetic_rate_descriptions = "rate_quartz"
[]
[nodal_void_volume_uo]
type = NodalVoidVolume
porosity = porosity
execute_on = 'initial timestep_end' # "initial" means this is evaluated properly for the first timestep
[]
[]
[Executioner]
type = Transient
dt = 1E5
end_time = 7.76E6 # 90 days
[]
[AuxVariables]
[temperature]
initial_condition = 50.0
[]
[porosity]
initial_condition = 0.1
[]
[nodal_void_volume]
[]
[pf_rate_H2O] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_Na] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_Cl] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_SiO2] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[rate_H2O_per_1l] # rate per 1 litre of aqueous solution that we consider at each node
[]
[rate_Na_per_1l]
[]
[rate_Cl_per_1l]
[]
[rate_SiO2_per_1l]
[]
[transported_H2O]
[]
[transported_Na]
[]
[transported_Cl]
[]
[transported_SiO2]
[]
[transported_mass]
[]
[massfrac_Na]
[]
[massfrac_Cl]
[]
[massfrac_SiO2]
[]
[massfrac_H2O]
[]
[]
[AuxKernels]
[porosity]
type = ParsedAux
coupled_variables = free_cm3_QuartzLike
expression = '1000.0 / (1000.0 + free_cm3_QuartzLike)'
variable = porosity
execute_on = 'timestep_end'
[]
[nodal_void_volume_auxk]
type = NodalVoidVolumeAux
variable = nodal_void_volume
nodal_void_volume_uo = nodal_void_volume_uo
execute_on = 'initial timestep_end' # "initial" to ensure it is properly evaluated for the first timestep
[]
[rate_H2O_per_1l_auxk]
type = ParsedAux
coupled_variables = 'pf_rate_H2O nodal_void_volume'
variable = rate_H2O_per_1l
# pf_rate = change in kg at every node
# pf_rate * 1000 / molar_mass_in_g_per_mole = change in moles at every node
# pf_rate * 1000 / molar_mass / (nodal_void_volume_in_m^3 * 1000) = change in moles per litre of aqueous solution
expression = 'pf_rate_H2O / 18.0152 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_Na_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_Na nodal_void_volume'
variable = rate_Na_per_1l
expression = 'pf_rate_Na / 22.9898 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_Cl_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_Cl nodal_void_volume'
variable = rate_Cl_per_1l
expression = 'pf_rate_Cl / 35.453 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_SiO2_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_SiO2 nodal_void_volume'
variable = rate_SiO2_per_1l
expression = 'pf_rate_SiO2 / 60.0843 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[transported_H2O_auxk]
type = GeochemistryQuantityAux
variable = transported_H2O
species = H2O
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_Na]
type = GeochemistryQuantityAux
variable = transported_Na
species = Na+
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_Cl]
type = GeochemistryQuantityAux
variable = transported_Cl
species = Cl-
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_SiO2]
type = GeochemistryQuantityAux
variable = transported_SiO2
species = 'SiO2(aq)'
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_mass_auxk]
type = ParsedAux
coupled_variables = 'transported_H2O transported_Na transported_Cl transported_SiO2'
variable = transported_mass
expression = 'transported_H2O * 18.0152 + transported_Na * 22.9898 + transported_Cl * 35.453 + transported_SiO2 * 60.0843'
execute_on = 'timestep_end'
[]
[massfrac_H2O]
type = ParsedAux
coupled_variables = 'transported_H2O transported_mass'
variable = massfrac_H2O
expression = 'transported_H2O * 18.0152 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_Na]
type = ParsedAux
coupled_variables = 'transported_Na transported_mass'
variable = massfrac_Na
expression = 'transported_Na * 22.9898 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_Cl]
type = ParsedAux
coupled_variables = 'transported_Cl transported_mass'
variable = massfrac_Cl
expression = 'transported_Cl * 35.453 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_SiO2]
type = ParsedAux
coupled_variables = 'transported_SiO2 transported_mass'
variable = massfrac_SiO2
expression = 'transported_SiO2 * 60.0843 / transported_mass'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[cm3_quartz]
type = PointValue
variable = free_cm3_QuartzLike
[]
[porosity]
type = PointValue
variable = porosity
[]
[solution_temperature]
type = PointValue
variable = solution_temperature
[]
[massfrac_H2O]
type = PointValue
variable = massfrac_H2O
[]
[massfrac_Na]
type = PointValue
variable = massfrac_Na
[]
[massfrac_Cl]
type = PointValue
variable = massfrac_Cl
[]
[massfrac_SiO2]
type = PointValue
variable = massfrac_SiO2
[]
[]
[Outputs]
exodus = true
csv = true
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/aquifer_geochemistry.i)
# Simulates geochemistry in the aquifer. This input file may be run in standalone fashion but it does not do anything of interest. To simulate something interesting, run the porous_flow.i simulation which couples to this input file using MultiApps.
# This file receives pf_rate_H2O, pf_rate_Na, pf_rate_Cl, pf_rate_SiO2 and temperature as AuxVariables from porous_flow.i.
# The pf_rate quantities are kg/s changes of fluid-component mass at each node, but the geochemistry module expects rates-of-changes of moles at every node. Secondly, since this input file considers just 1 litre of aqueous solution at every node, the nodal_void_volume is used to convert pf_rate_* into rate_*_per_1l, which is measured in mol/s/1_litre_of_aqueous_solution.
# This file sends massfrac_Na, massfrac_Cl and massfrac_SiO2 to porous_flow.i. These are computed from the corresponding transported_* quantities.
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[]
[GlobalParams]
point = '0 0 0'
reactor = reactor
[]
[SpatialReactionSolver]
model_definition = definition
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
constraint_species = "H2O Na+ Cl- SiO2(aq)"
# ASSUME that 1 litre of solution contains:
constraint_value = " 1.0 0.1 0.1 0.000555052386"
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_concentration"
constraint_unit = " kg moles moles molal"
initial_temperature = 50.0
kinetic_species_name = QuartzLike
# Per 1 litre (1000cm^3) of aqueous solution (1kg of solvent water), there is 9000cm^3 of QuartzLike, which means the initial porosity is 0.1.
kinetic_species_initial_value = 9000
kinetic_species_unit = cm3
temperature = temperature
source_species_names = 'H2O Na+ Cl- SiO2(aq)'
source_species_rates = 'rate_H2O_per_1l rate_Na_per_1l rate_Cl_per_1l rate_SiO2_per_1l'
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
evaluate_kinetic_rates_always = true # implicit time-marching used for stability
execute_console_output_on = ''
[]
[UserObjects]
[rate_quartz]
type = GeochemistryKineticRate
kinetic_species_name = QuartzLike
intrinsic_rate_constant = 1.0E-2
multiply_by_mass = true
area_quantity = 1
activation_energy = 72800.0
[]
[definition]
type = GeochemicalModelDefinition
database_file = "small_database.json"
basis_species = "H2O SiO2(aq) Na+ Cl-"
kinetic_minerals = "QuartzLike"
kinetic_rate_descriptions = "rate_quartz"
[]
[nodal_void_volume_uo]
type = NodalVoidVolume
porosity = porosity
execute_on = 'initial timestep_end' # "initial" means this is evaluated properly for the first timestep
[]
[]
[Executioner]
type = Transient
dt = 1E5
end_time = 7.76E6 # 90 days
[]
[AuxVariables]
[temperature]
initial_condition = 50.0
[]
[porosity]
initial_condition = 0.1
[]
[nodal_void_volume]
[]
[pf_rate_H2O] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_Na] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_Cl] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_SiO2] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[rate_H2O_per_1l] # rate per 1 litre of aqueous solution that we consider at each node
[]
[rate_Na_per_1l]
[]
[rate_Cl_per_1l]
[]
[rate_SiO2_per_1l]
[]
[transported_H2O]
[]
[transported_Na]
[]
[transported_Cl]
[]
[transported_SiO2]
[]
[transported_mass]
[]
[massfrac_Na]
[]
[massfrac_Cl]
[]
[massfrac_SiO2]
[]
[massfrac_H2O]
[]
[]
[AuxKernels]
[porosity]
type = ParsedAux
coupled_variables = free_cm3_QuartzLike
expression = '1000.0 / (1000.0 + free_cm3_QuartzLike)'
variable = porosity
execute_on = 'timestep_end'
[]
[nodal_void_volume_auxk]
type = NodalVoidVolumeAux
variable = nodal_void_volume
nodal_void_volume_uo = nodal_void_volume_uo
execute_on = 'initial timestep_end' # "initial" to ensure it is properly evaluated for the first timestep
[]
[rate_H2O_per_1l_auxk]
type = ParsedAux
coupled_variables = 'pf_rate_H2O nodal_void_volume'
variable = rate_H2O_per_1l
# pf_rate = change in kg at every node
# pf_rate * 1000 / molar_mass_in_g_per_mole = change in moles at every node
# pf_rate * 1000 / molar_mass / (nodal_void_volume_in_m^3 * 1000) = change in moles per litre of aqueous solution
expression = 'pf_rate_H2O / 18.0152 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_Na_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_Na nodal_void_volume'
variable = rate_Na_per_1l
expression = 'pf_rate_Na / 22.9898 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_Cl_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_Cl nodal_void_volume'
variable = rate_Cl_per_1l
expression = 'pf_rate_Cl / 35.453 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_SiO2_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_SiO2 nodal_void_volume'
variable = rate_SiO2_per_1l
expression = 'pf_rate_SiO2 / 60.0843 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[transported_H2O_auxk]
type = GeochemistryQuantityAux
variable = transported_H2O
species = H2O
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_Na]
type = GeochemistryQuantityAux
variable = transported_Na
species = Na+
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_Cl]
type = GeochemistryQuantityAux
variable = transported_Cl
species = Cl-
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_SiO2]
type = GeochemistryQuantityAux
variable = transported_SiO2
species = 'SiO2(aq)'
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_mass_auxk]
type = ParsedAux
coupled_variables = 'transported_H2O transported_Na transported_Cl transported_SiO2'
variable = transported_mass
expression = 'transported_H2O * 18.0152 + transported_Na * 22.9898 + transported_Cl * 35.453 + transported_SiO2 * 60.0843'
execute_on = 'timestep_end'
[]
[massfrac_H2O]
type = ParsedAux
coupled_variables = 'transported_H2O transported_mass'
variable = massfrac_H2O
expression = 'transported_H2O * 18.0152 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_Na]
type = ParsedAux
coupled_variables = 'transported_Na transported_mass'
variable = massfrac_Na
expression = 'transported_Na * 22.9898 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_Cl]
type = ParsedAux
coupled_variables = 'transported_Cl transported_mass'
variable = massfrac_Cl
expression = 'transported_Cl * 35.453 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_SiO2]
type = ParsedAux
coupled_variables = 'transported_SiO2 transported_mass'
variable = massfrac_SiO2
expression = 'transported_SiO2 * 60.0843 / transported_mass'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[cm3_quartz]
type = PointValue
variable = free_cm3_QuartzLike
[]
[porosity]
type = PointValue
variable = porosity
[]
[solution_temperature]
type = PointValue
variable = solution_temperature
[]
[massfrac_H2O]
type = PointValue
variable = massfrac_H2O
[]
[massfrac_Na]
type = PointValue
variable = massfrac_Na
[]
[massfrac_Cl]
type = PointValue
variable = massfrac_Cl
[]
[massfrac_SiO2]
type = PointValue
variable = massfrac_SiO2
[]
[]
[Outputs]
exodus = true
csv = true
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/aquifer_geochemistry.i)
# Simulates geochemistry in the aquifer. This input file may be run in standalone fashion but it does not do anything of interest. To simulate something interesting, run the porous_flow.i simulation which couples to this input file using MultiApps.
# This file receives pf_rate_H2O, pf_rate_Na, pf_rate_Cl, pf_rate_SiO2 and temperature as AuxVariables from porous_flow.i.
# The pf_rate quantities are kg/s changes of fluid-component mass at each node, but the geochemistry module expects rates-of-changes of moles at every node. Secondly, since this input file considers just 1 litre of aqueous solution at every node, the nodal_void_volume is used to convert pf_rate_* into rate_*_per_1l, which is measured in mol/s/1_litre_of_aqueous_solution.
# This file sends massfrac_Na, massfrac_Cl and massfrac_SiO2 to porous_flow.i. These are computed from the corresponding transported_* quantities.
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[]
[GlobalParams]
point = '0 0 0'
reactor = reactor
[]
[SpatialReactionSolver]
model_definition = definition
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
constraint_species = "H2O Na+ Cl- SiO2(aq)"
# ASSUME that 1 litre of solution contains:
constraint_value = " 1.0 0.1 0.1 0.000555052386"
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_concentration"
constraint_unit = " kg moles moles molal"
initial_temperature = 50.0
kinetic_species_name = QuartzLike
# Per 1 litre (1000cm^3) of aqueous solution (1kg of solvent water), there is 9000cm^3 of QuartzLike, which means the initial porosity is 0.1.
kinetic_species_initial_value = 9000
kinetic_species_unit = cm3
temperature = temperature
source_species_names = 'H2O Na+ Cl- SiO2(aq)'
source_species_rates = 'rate_H2O_per_1l rate_Na_per_1l rate_Cl_per_1l rate_SiO2_per_1l'
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
evaluate_kinetic_rates_always = true # implicit time-marching used for stability
execute_console_output_on = ''
[]
[UserObjects]
[rate_quartz]
type = GeochemistryKineticRate
kinetic_species_name = QuartzLike
intrinsic_rate_constant = 1.0E-2
multiply_by_mass = true
area_quantity = 1
activation_energy = 72800.0
[]
[definition]
type = GeochemicalModelDefinition
database_file = "small_database.json"
basis_species = "H2O SiO2(aq) Na+ Cl-"
kinetic_minerals = "QuartzLike"
kinetic_rate_descriptions = "rate_quartz"
[]
[nodal_void_volume_uo]
type = NodalVoidVolume
porosity = porosity
execute_on = 'initial timestep_end' # "initial" means this is evaluated properly for the first timestep
[]
[]
[Executioner]
type = Transient
dt = 1E5
end_time = 7.76E6 # 90 days
[]
[AuxVariables]
[temperature]
initial_condition = 50.0
[]
[porosity]
initial_condition = 0.1
[]
[nodal_void_volume]
[]
[pf_rate_H2O] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_Na] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_Cl] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_SiO2] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[rate_H2O_per_1l] # rate per 1 litre of aqueous solution that we consider at each node
[]
[rate_Na_per_1l]
[]
[rate_Cl_per_1l]
[]
[rate_SiO2_per_1l]
[]
[transported_H2O]
[]
[transported_Na]
[]
[transported_Cl]
[]
[transported_SiO2]
[]
[transported_mass]
[]
[massfrac_Na]
[]
[massfrac_Cl]
[]
[massfrac_SiO2]
[]
[massfrac_H2O]
[]
[]
[AuxKernels]
[porosity]
type = ParsedAux
coupled_variables = free_cm3_QuartzLike
expression = '1000.0 / (1000.0 + free_cm3_QuartzLike)'
variable = porosity
execute_on = 'timestep_end'
[]
[nodal_void_volume_auxk]
type = NodalVoidVolumeAux
variable = nodal_void_volume
nodal_void_volume_uo = nodal_void_volume_uo
execute_on = 'initial timestep_end' # "initial" to ensure it is properly evaluated for the first timestep
[]
[rate_H2O_per_1l_auxk]
type = ParsedAux
coupled_variables = 'pf_rate_H2O nodal_void_volume'
variable = rate_H2O_per_1l
# pf_rate = change in kg at every node
# pf_rate * 1000 / molar_mass_in_g_per_mole = change in moles at every node
# pf_rate * 1000 / molar_mass / (nodal_void_volume_in_m^3 * 1000) = change in moles per litre of aqueous solution
expression = 'pf_rate_H2O / 18.0152 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_Na_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_Na nodal_void_volume'
variable = rate_Na_per_1l
expression = 'pf_rate_Na / 22.9898 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_Cl_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_Cl nodal_void_volume'
variable = rate_Cl_per_1l
expression = 'pf_rate_Cl / 35.453 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_SiO2_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_SiO2 nodal_void_volume'
variable = rate_SiO2_per_1l
expression = 'pf_rate_SiO2 / 60.0843 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[transported_H2O_auxk]
type = GeochemistryQuantityAux
variable = transported_H2O
species = H2O
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_Na]
type = GeochemistryQuantityAux
variable = transported_Na
species = Na+
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_Cl]
type = GeochemistryQuantityAux
variable = transported_Cl
species = Cl-
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_SiO2]
type = GeochemistryQuantityAux
variable = transported_SiO2
species = 'SiO2(aq)'
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_mass_auxk]
type = ParsedAux
coupled_variables = 'transported_H2O transported_Na transported_Cl transported_SiO2'
variable = transported_mass
expression = 'transported_H2O * 18.0152 + transported_Na * 22.9898 + transported_Cl * 35.453 + transported_SiO2 * 60.0843'
execute_on = 'timestep_end'
[]
[massfrac_H2O]
type = ParsedAux
coupled_variables = 'transported_H2O transported_mass'
variable = massfrac_H2O
expression = 'transported_H2O * 18.0152 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_Na]
type = ParsedAux
coupled_variables = 'transported_Na transported_mass'
variable = massfrac_Na
expression = 'transported_Na * 22.9898 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_Cl]
type = ParsedAux
coupled_variables = 'transported_Cl transported_mass'
variable = massfrac_Cl
expression = 'transported_Cl * 35.453 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_SiO2]
type = ParsedAux
coupled_variables = 'transported_SiO2 transported_mass'
variable = massfrac_SiO2
expression = 'transported_SiO2 * 60.0843 / transported_mass'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[cm3_quartz]
type = PointValue
variable = free_cm3_QuartzLike
[]
[porosity]
type = PointValue
variable = porosity
[]
[solution_temperature]
type = PointValue
variable = solution_temperature
[]
[massfrac_H2O]
type = PointValue
variable = massfrac_H2O
[]
[massfrac_Na]
type = PointValue
variable = massfrac_Na
[]
[massfrac_Cl]
type = PointValue
variable = massfrac_Cl
[]
[massfrac_SiO2]
type = PointValue
variable = massfrac_SiO2
[]
[]
[Outputs]
exodus = true
csv = true
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/aquifer_geochemistry.i)
# Simulates geochemistry in the aquifer. This input file may be run in standalone fashion but it does not do anything of interest. To simulate something interesting, run the porous_flow.i simulation which couples to this input file using MultiApps.
# This file receives pf_rate_H2O, pf_rate_Na, pf_rate_Cl, pf_rate_SiO2 and temperature as AuxVariables from porous_flow.i.
# The pf_rate quantities are kg/s changes of fluid-component mass at each node, but the geochemistry module expects rates-of-changes of moles at every node. Secondly, since this input file considers just 1 litre of aqueous solution at every node, the nodal_void_volume is used to convert pf_rate_* into rate_*_per_1l, which is measured in mol/s/1_litre_of_aqueous_solution.
# This file sends massfrac_Na, massfrac_Cl and massfrac_SiO2 to porous_flow.i. These are computed from the corresponding transported_* quantities.
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[]
[GlobalParams]
point = '0 0 0'
reactor = reactor
[]
[SpatialReactionSolver]
model_definition = definition
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
constraint_species = "H2O Na+ Cl- SiO2(aq)"
# ASSUME that 1 litre of solution contains:
constraint_value = " 1.0 0.1 0.1 0.000555052386"
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_concentration"
constraint_unit = " kg moles moles molal"
initial_temperature = 50.0
kinetic_species_name = QuartzLike
# Per 1 litre (1000cm^3) of aqueous solution (1kg of solvent water), there is 9000cm^3 of QuartzLike, which means the initial porosity is 0.1.
kinetic_species_initial_value = 9000
kinetic_species_unit = cm3
temperature = temperature
source_species_names = 'H2O Na+ Cl- SiO2(aq)'
source_species_rates = 'rate_H2O_per_1l rate_Na_per_1l rate_Cl_per_1l rate_SiO2_per_1l'
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
evaluate_kinetic_rates_always = true # implicit time-marching used for stability
execute_console_output_on = ''
[]
[UserObjects]
[rate_quartz]
type = GeochemistryKineticRate
kinetic_species_name = QuartzLike
intrinsic_rate_constant = 1.0E-2
multiply_by_mass = true
area_quantity = 1
activation_energy = 72800.0
[]
[definition]
type = GeochemicalModelDefinition
database_file = "small_database.json"
basis_species = "H2O SiO2(aq) Na+ Cl-"
kinetic_minerals = "QuartzLike"
kinetic_rate_descriptions = "rate_quartz"
[]
[nodal_void_volume_uo]
type = NodalVoidVolume
porosity = porosity
execute_on = 'initial timestep_end' # "initial" means this is evaluated properly for the first timestep
[]
[]
[Executioner]
type = Transient
dt = 1E5
end_time = 7.76E6 # 90 days
[]
[AuxVariables]
[temperature]
initial_condition = 50.0
[]
[porosity]
initial_condition = 0.1
[]
[nodal_void_volume]
[]
[pf_rate_H2O] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_Na] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_Cl] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_SiO2] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[rate_H2O_per_1l] # rate per 1 litre of aqueous solution that we consider at each node
[]
[rate_Na_per_1l]
[]
[rate_Cl_per_1l]
[]
[rate_SiO2_per_1l]
[]
[transported_H2O]
[]
[transported_Na]
[]
[transported_Cl]
[]
[transported_SiO2]
[]
[transported_mass]
[]
[massfrac_Na]
[]
[massfrac_Cl]
[]
[massfrac_SiO2]
[]
[massfrac_H2O]
[]
[]
[AuxKernels]
[porosity]
type = ParsedAux
coupled_variables = free_cm3_QuartzLike
expression = '1000.0 / (1000.0 + free_cm3_QuartzLike)'
variable = porosity
execute_on = 'timestep_end'
[]
[nodal_void_volume_auxk]
type = NodalVoidVolumeAux
variable = nodal_void_volume
nodal_void_volume_uo = nodal_void_volume_uo
execute_on = 'initial timestep_end' # "initial" to ensure it is properly evaluated for the first timestep
[]
[rate_H2O_per_1l_auxk]
type = ParsedAux
coupled_variables = 'pf_rate_H2O nodal_void_volume'
variable = rate_H2O_per_1l
# pf_rate = change in kg at every node
# pf_rate * 1000 / molar_mass_in_g_per_mole = change in moles at every node
# pf_rate * 1000 / molar_mass / (nodal_void_volume_in_m^3 * 1000) = change in moles per litre of aqueous solution
expression = 'pf_rate_H2O / 18.0152 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_Na_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_Na nodal_void_volume'
variable = rate_Na_per_1l
expression = 'pf_rate_Na / 22.9898 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_Cl_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_Cl nodal_void_volume'
variable = rate_Cl_per_1l
expression = 'pf_rate_Cl / 35.453 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_SiO2_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_SiO2 nodal_void_volume'
variable = rate_SiO2_per_1l
expression = 'pf_rate_SiO2 / 60.0843 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[transported_H2O_auxk]
type = GeochemistryQuantityAux
variable = transported_H2O
species = H2O
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_Na]
type = GeochemistryQuantityAux
variable = transported_Na
species = Na+
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_Cl]
type = GeochemistryQuantityAux
variable = transported_Cl
species = Cl-
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_SiO2]
type = GeochemistryQuantityAux
variable = transported_SiO2
species = 'SiO2(aq)'
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_mass_auxk]
type = ParsedAux
coupled_variables = 'transported_H2O transported_Na transported_Cl transported_SiO2'
variable = transported_mass
expression = 'transported_H2O * 18.0152 + transported_Na * 22.9898 + transported_Cl * 35.453 + transported_SiO2 * 60.0843'
execute_on = 'timestep_end'
[]
[massfrac_H2O]
type = ParsedAux
coupled_variables = 'transported_H2O transported_mass'
variable = massfrac_H2O
expression = 'transported_H2O * 18.0152 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_Na]
type = ParsedAux
coupled_variables = 'transported_Na transported_mass'
variable = massfrac_Na
expression = 'transported_Na * 22.9898 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_Cl]
type = ParsedAux
coupled_variables = 'transported_Cl transported_mass'
variable = massfrac_Cl
expression = 'transported_Cl * 35.453 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_SiO2]
type = ParsedAux
coupled_variables = 'transported_SiO2 transported_mass'
variable = massfrac_SiO2
expression = 'transported_SiO2 * 60.0843 / transported_mass'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[cm3_quartz]
type = PointValue
variable = free_cm3_QuartzLike
[]
[porosity]
type = PointValue
variable = porosity
[]
[solution_temperature]
type = PointValue
variable = solution_temperature
[]
[massfrac_H2O]
type = PointValue
variable = massfrac_H2O
[]
[massfrac_Na]
type = PointValue
variable = massfrac_Na
[]
[massfrac_Cl]
type = PointValue
variable = massfrac_Cl
[]
[massfrac_SiO2]
type = PointValue
variable = massfrac_SiO2
[]
[]
[Outputs]
exodus = true
csv = true
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/aquifer_geochemistry.i)
# Simulates geochemistry in the aquifer. This input file may be run in standalone fashion but it does not do anything of interest. To simulate something interesting, run the porous_flow.i simulation which couples to this input file using MultiApps.
# This file receives pf_rate_H2O, pf_rate_Na, pf_rate_Cl, pf_rate_SiO2 and temperature as AuxVariables from porous_flow.i.
# The pf_rate quantities are kg/s changes of fluid-component mass at each node, but the geochemistry module expects rates-of-changes of moles at every node. Secondly, since this input file considers just 1 litre of aqueous solution at every node, the nodal_void_volume is used to convert pf_rate_* into rate_*_per_1l, which is measured in mol/s/1_litre_of_aqueous_solution.
# This file sends massfrac_Na, massfrac_Cl and massfrac_SiO2 to porous_flow.i. These are computed from the corresponding transported_* quantities.
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[]
[GlobalParams]
point = '0 0 0'
reactor = reactor
[]
[SpatialReactionSolver]
model_definition = definition
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
constraint_species = "H2O Na+ Cl- SiO2(aq)"
# ASSUME that 1 litre of solution contains:
constraint_value = " 1.0 0.1 0.1 0.000555052386"
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_concentration"
constraint_unit = " kg moles moles molal"
initial_temperature = 50.0
kinetic_species_name = QuartzLike
# Per 1 litre (1000cm^3) of aqueous solution (1kg of solvent water), there is 9000cm^3 of QuartzLike, which means the initial porosity is 0.1.
kinetic_species_initial_value = 9000
kinetic_species_unit = cm3
temperature = temperature
source_species_names = 'H2O Na+ Cl- SiO2(aq)'
source_species_rates = 'rate_H2O_per_1l rate_Na_per_1l rate_Cl_per_1l rate_SiO2_per_1l'
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
evaluate_kinetic_rates_always = true # implicit time-marching used for stability
execute_console_output_on = ''
[]
[UserObjects]
[rate_quartz]
type = GeochemistryKineticRate
kinetic_species_name = QuartzLike
intrinsic_rate_constant = 1.0E-2
multiply_by_mass = true
area_quantity = 1
activation_energy = 72800.0
[]
[definition]
type = GeochemicalModelDefinition
database_file = "small_database.json"
basis_species = "H2O SiO2(aq) Na+ Cl-"
kinetic_minerals = "QuartzLike"
kinetic_rate_descriptions = "rate_quartz"
[]
[nodal_void_volume_uo]
type = NodalVoidVolume
porosity = porosity
execute_on = 'initial timestep_end' # "initial" means this is evaluated properly for the first timestep
[]
[]
[Executioner]
type = Transient
dt = 1E5
end_time = 7.76E6 # 90 days
[]
[AuxVariables]
[temperature]
initial_condition = 50.0
[]
[porosity]
initial_condition = 0.1
[]
[nodal_void_volume]
[]
[pf_rate_H2O] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_Na] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_Cl] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[pf_rate_SiO2] # change in H2O mass (kg/s) at each node provided by the porous-flow simulation
[]
[rate_H2O_per_1l] # rate per 1 litre of aqueous solution that we consider at each node
[]
[rate_Na_per_1l]
[]
[rate_Cl_per_1l]
[]
[rate_SiO2_per_1l]
[]
[transported_H2O]
[]
[transported_Na]
[]
[transported_Cl]
[]
[transported_SiO2]
[]
[transported_mass]
[]
[massfrac_Na]
[]
[massfrac_Cl]
[]
[massfrac_SiO2]
[]
[massfrac_H2O]
[]
[]
[AuxKernels]
[porosity]
type = ParsedAux
coupled_variables = free_cm3_QuartzLike
expression = '1000.0 / (1000.0 + free_cm3_QuartzLike)'
variable = porosity
execute_on = 'timestep_end'
[]
[nodal_void_volume_auxk]
type = NodalVoidVolumeAux
variable = nodal_void_volume
nodal_void_volume_uo = nodal_void_volume_uo
execute_on = 'initial timestep_end' # "initial" to ensure it is properly evaluated for the first timestep
[]
[rate_H2O_per_1l_auxk]
type = ParsedAux
coupled_variables = 'pf_rate_H2O nodal_void_volume'
variable = rate_H2O_per_1l
# pf_rate = change in kg at every node
# pf_rate * 1000 / molar_mass_in_g_per_mole = change in moles at every node
# pf_rate * 1000 / molar_mass / (nodal_void_volume_in_m^3 * 1000) = change in moles per litre of aqueous solution
expression = 'pf_rate_H2O / 18.0152 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_Na_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_Na nodal_void_volume'
variable = rate_Na_per_1l
expression = 'pf_rate_Na / 22.9898 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_Cl_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_Cl nodal_void_volume'
variable = rate_Cl_per_1l
expression = 'pf_rate_Cl / 35.453 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[rate_SiO2_per_1l]
type = ParsedAux
coupled_variables = 'pf_rate_SiO2 nodal_void_volume'
variable = rate_SiO2_per_1l
expression = 'pf_rate_SiO2 / 60.0843 / nodal_void_volume'
execute_on = 'timestep_begin'
[]
[transported_H2O_auxk]
type = GeochemistryQuantityAux
variable = transported_H2O
species = H2O
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_Na]
type = GeochemistryQuantityAux
variable = transported_Na
species = Na+
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_Cl]
type = GeochemistryQuantityAux
variable = transported_Cl
species = Cl-
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_SiO2]
type = GeochemistryQuantityAux
variable = transported_SiO2
species = 'SiO2(aq)'
quantity = transported_moles_in_original_basis
execute_on = 'timestep_end'
[]
[transported_mass_auxk]
type = ParsedAux
coupled_variables = 'transported_H2O transported_Na transported_Cl transported_SiO2'
variable = transported_mass
expression = 'transported_H2O * 18.0152 + transported_Na * 22.9898 + transported_Cl * 35.453 + transported_SiO2 * 60.0843'
execute_on = 'timestep_end'
[]
[massfrac_H2O]
type = ParsedAux
coupled_variables = 'transported_H2O transported_mass'
variable = massfrac_H2O
expression = 'transported_H2O * 18.0152 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_Na]
type = ParsedAux
coupled_variables = 'transported_Na transported_mass'
variable = massfrac_Na
expression = 'transported_Na * 22.9898 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_Cl]
type = ParsedAux
coupled_variables = 'transported_Cl transported_mass'
variable = massfrac_Cl
expression = 'transported_Cl * 35.453 / transported_mass'
execute_on = 'timestep_end'
[]
[massfrac_SiO2]
type = ParsedAux
coupled_variables = 'transported_SiO2 transported_mass'
variable = massfrac_SiO2
expression = 'transported_SiO2 * 60.0843 / transported_mass'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[cm3_quartz]
type = PointValue
variable = free_cm3_QuartzLike
[]
[porosity]
type = PointValue
variable = porosity
[]
[solution_temperature]
type = PointValue
variable = solution_temperature
[]
[massfrac_H2O]
type = PointValue
variable = massfrac_H2O
[]
[massfrac_Na]
type = PointValue
variable = massfrac_Na
[]
[massfrac_Cl]
type = PointValue
variable = massfrac_Cl
[]
[massfrac_SiO2]
type = PointValue
variable = massfrac_SiO2
[]
[]
[Outputs]
exodus = true
csv = true
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/porous_flow.i)
# PorousFlow simulation of injection and production in a 2D aquifer
# Much of this file is standard porous-flow stuff. The unusual aspects are:
# - transfer of the rates of changes of each species (kg/s) to the aquifer_geochemistry.i simulation. This is achieved by saving these changes from the PorousFlowMassTimeDerivative residuals
# - transfer of the temperature field to the aquifer_geochemistry.i simulation
# Interesting behaviour can be simulated by this file without its "parent" simulation, exchanger.i. exchanger.i provides mass-fractions injected via the injection_rate_massfrac_* variables, but since these are more-or-less constant throughout the duration of the exchanger.i simulation, the initial_conditions specified below may be used. Similar, exchanger.i provides injection_temperature, but that is also constant.
injection_rate = -1.0 # kg/s/m, negative because injection as a source
production_rate = 1.0 # kg/s/m
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[injection_node]
input = gen
type = ExtraNodesetGenerator
new_boundary = injection_node
coord = '-30 0 0'
[]
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[f0]
initial_condition = 0.002285946
[]
[f1]
initial_condition = 0.0035252
[]
[f2]
initial_condition = 1.3741E-05
[]
[porepressure]
initial_condition = 2E6
[]
[temperature]
initial_condition = 50
scaling = 1E-6 # fluid enthalpy is roughly 1E6
[]
[]
[BCs]
[injection_temperature]
type = MatchedValueBC
variable = temperature
v = injection_temperature
boundary = injection_node
[]
[]
[DiracKernels]
[inject_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Na
point_file = injection.bh
variable = f0
[]
[inject_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Cl
point_file = injection.bh
variable = f1
[]
[inject_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_SiO2
point_file = injection.bh
variable = f2
[]
[inject_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_H2O
point_file = injection.bh
variable = porepressure
[]
[produce_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Na
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 0
point_file = production.bh
variable = f0
[]
[produce_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Cl
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 1
point_file = production.bh
variable = f1
[]
[produce_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_SiO2
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 2
point_file = production.bh
variable = f2
[]
[produce_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_H2O
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 3
point_file = production.bh
variable = porepressure
[]
[produce_heat]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_heat
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
use_enthalpy = true
point_file = production.bh
variable = temperature
[]
[]
[UserObjects]
[injected_mass]
type = PorousFlowSumQuantity
[]
[produced_mass_Na]
type = PorousFlowSumQuantity
[]
[produced_mass_Cl]
type = PorousFlowSumQuantity
[]
[produced_mass_SiO2]
type = PorousFlowSumQuantity
[]
[produced_mass_H2O]
type = PorousFlowSumQuantity
[]
[produced_heat]
type = PorousFlowSumQuantity
[]
[]
[Postprocessors]
[dt]
type = TimestepSize
execute_on = TIMESTEP_BEGIN
[]
[tot_kg_injected_this_timestep]
type = PorousFlowPlotQuantity
uo = injected_mass
[]
[kg_Na_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Na
[]
[kg_Cl_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Cl
[]
[kg_SiO2_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_SiO2
[]
[kg_H2O_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_H2O
[]
[mole_rate_Na_produced]
type = FunctionValuePostprocessor
function = moles_Na
indirect_dependencies = 'kg_Na_produced_this_timestep dt'
[]
[mole_rate_Cl_produced]
type = FunctionValuePostprocessor
function = moles_Cl
indirect_dependencies = 'kg_Cl_produced_this_timestep dt'
[]
[mole_rate_SiO2_produced]
type = FunctionValuePostprocessor
function = moles_SiO2
indirect_dependencies = 'kg_SiO2_produced_this_timestep dt'
[]
[mole_rate_H2O_produced]
type = FunctionValuePostprocessor
function = moles_H2O
indirect_dependencies = 'kg_H2O_produced_this_timestep dt'
[]
[heat_joules_extracted_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_heat
[]
[production_temperature]
type = PointValue
point = '30 0 0'
variable = temperature
[]
[]
[Functions]
[moles_Na]
type = ParsedFunction
symbol_names = 'kg_Na dt'
symbol_values = 'kg_Na_produced_this_timestep dt'
expression = 'kg_Na * 1000 / 22.9898 / dt'
[]
[moles_Cl]
type = ParsedFunction
symbol_names = 'kg_Cl dt'
symbol_values = 'kg_Cl_produced_this_timestep dt'
expression = 'kg_Cl * 1000 / 35.453 / dt'
[]
[moles_SiO2]
type = ParsedFunction
symbol_names = 'kg_SiO2 dt'
symbol_values = 'kg_SiO2_produced_this_timestep dt'
expression = 'kg_SiO2 * 1000 / 60.0843 / dt'
[]
[moles_H2O]
type = ParsedFunction
symbol_names = 'kg_H2O dt'
symbol_values = 'kg_H2O_produced_this_timestep dt'
expression = 'kg_H2O * 1000 / 18.0152 / dt'
[]
[]
[FluidProperties]
[the_simple_fluid]
type = SimpleFluidProperties
thermal_expansion = 0
bulk_modulus = 2E9
viscosity = 1E-3
density0 = 1000
cv = 4000.0
cp = 4000.0
[]
[]
[PorousFlowFullySaturated]
coupling_type = ThermoHydro
porepressure = porepressure
temperature = temperature
mass_fraction_vars = 'f0 f1 f2'
save_component_rate_in = 'rate_Na rate_Cl rate_SiO2 rate_H2O' # change in kg at every node / dt
fp = the_simple_fluid
temperature_unit = Celsius
[]
[AuxVariables]
[injection_temperature]
initial_condition = 200
[]
[injection_rate_massfrac_Na]
initial_condition = 0.002285946
[]
[injection_rate_massfrac_Cl]
initial_condition = 0.0035252
[]
[injection_rate_massfrac_SiO2]
initial_condition = 1.3741E-05
[]
[injection_rate_massfrac_H2O]
initial_condition = 0.994175112
[]
[rate_H2O]
[]
[rate_Na]
[]
[rate_Cl]
[]
[rate_SiO2]
[]
[]
[Materials]
[porosity]
type = PorousFlowPorosityConst # this simulation has no porosity changes from dissolution
porosity = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-12 0 0 0 1E-12 0 0 0 1E-12'
[]
[thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '0 0 0 0 0 0 0 0 0'
[]
[rock_heat]
type = PorousFlowMatrixInternalEnergy
density = 2500.0
specific_heat_capacity = 1200.0
[]
[]
[Preconditioning]
active = typically_efficient
[typically_efficient]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = ' hypre boomeramg'
[]
[strong]
type = SMP
full = true
petsc_options = '-ksp_diagonal_scale -ksp_diagonal_scale_fix'
petsc_options_iname = '-pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = ' asm ilu NONZERO 2'
[]
[probably_too_strong]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = ' lu mumps'
[]
[]
[Executioner]
type = Transient
solve_type = Newton
end_time = 7.76E6 # 90 days
dt = 1E5
[]
[Outputs]
exodus = true
[]
[MultiApps]
[react]
type = TransientMultiApp
input_files = aquifer_geochemistry.i
clone_master_mesh = true
execute_on = 'timestep_end'
[]
[]
[Transfers]
[changes_due_to_flow]
type = MultiAppCopyTransfer
source_variable = 'rate_H2O rate_Na rate_Cl rate_SiO2 temperature'
variable = 'pf_rate_H2O pf_rate_Na pf_rate_Cl pf_rate_SiO2 temperature'
to_multi_app = react
[]
[massfrac_from_geochem]
type = MultiAppCopyTransfer
source_variable = 'massfrac_Na massfrac_Cl massfrac_SiO2'
variable = 'f0 f1 f2'
from_multi_app = react
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/production.bh)
1.0 30 0 0
(modules/combined/examples/geochem-porous_flow/geotes_2D/porous_flow.i)
# PorousFlow simulation of injection and production in a 2D aquifer
# Much of this file is standard porous-flow stuff. The unusual aspects are:
# - transfer of the rates of changes of each species (kg/s) to the aquifer_geochemistry.i simulation. This is achieved by saving these changes from the PorousFlowMassTimeDerivative residuals
# - transfer of the temperature field to the aquifer_geochemistry.i simulation
# Interesting behaviour can be simulated by this file without its "parent" simulation, exchanger.i. exchanger.i provides mass-fractions injected via the injection_rate_massfrac_* variables, but since these are more-or-less constant throughout the duration of the exchanger.i simulation, the initial_conditions specified below may be used. Similar, exchanger.i provides injection_temperature, but that is also constant.
injection_rate = -1.0 # kg/s/m, negative because injection as a source
production_rate = 1.0 # kg/s/m
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[injection_node]
input = gen
type = ExtraNodesetGenerator
new_boundary = injection_node
coord = '-30 0 0'
[]
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[f0]
initial_condition = 0.002285946
[]
[f1]
initial_condition = 0.0035252
[]
[f2]
initial_condition = 1.3741E-05
[]
[porepressure]
initial_condition = 2E6
[]
[temperature]
initial_condition = 50
scaling = 1E-6 # fluid enthalpy is roughly 1E6
[]
[]
[BCs]
[injection_temperature]
type = MatchedValueBC
variable = temperature
v = injection_temperature
boundary = injection_node
[]
[]
[DiracKernels]
[inject_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Na
point_file = injection.bh
variable = f0
[]
[inject_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Cl
point_file = injection.bh
variable = f1
[]
[inject_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_SiO2
point_file = injection.bh
variable = f2
[]
[inject_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_H2O
point_file = injection.bh
variable = porepressure
[]
[produce_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Na
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 0
point_file = production.bh
variable = f0
[]
[produce_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Cl
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 1
point_file = production.bh
variable = f1
[]
[produce_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_SiO2
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 2
point_file = production.bh
variable = f2
[]
[produce_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_H2O
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 3
point_file = production.bh
variable = porepressure
[]
[produce_heat]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_heat
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
use_enthalpy = true
point_file = production.bh
variable = temperature
[]
[]
[UserObjects]
[injected_mass]
type = PorousFlowSumQuantity
[]
[produced_mass_Na]
type = PorousFlowSumQuantity
[]
[produced_mass_Cl]
type = PorousFlowSumQuantity
[]
[produced_mass_SiO2]
type = PorousFlowSumQuantity
[]
[produced_mass_H2O]
type = PorousFlowSumQuantity
[]
[produced_heat]
type = PorousFlowSumQuantity
[]
[]
[Postprocessors]
[dt]
type = TimestepSize
execute_on = TIMESTEP_BEGIN
[]
[tot_kg_injected_this_timestep]
type = PorousFlowPlotQuantity
uo = injected_mass
[]
[kg_Na_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Na
[]
[kg_Cl_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Cl
[]
[kg_SiO2_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_SiO2
[]
[kg_H2O_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_H2O
[]
[mole_rate_Na_produced]
type = FunctionValuePostprocessor
function = moles_Na
indirect_dependencies = 'kg_Na_produced_this_timestep dt'
[]
[mole_rate_Cl_produced]
type = FunctionValuePostprocessor
function = moles_Cl
indirect_dependencies = 'kg_Cl_produced_this_timestep dt'
[]
[mole_rate_SiO2_produced]
type = FunctionValuePostprocessor
function = moles_SiO2
indirect_dependencies = 'kg_SiO2_produced_this_timestep dt'
[]
[mole_rate_H2O_produced]
type = FunctionValuePostprocessor
function = moles_H2O
indirect_dependencies = 'kg_H2O_produced_this_timestep dt'
[]
[heat_joules_extracted_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_heat
[]
[production_temperature]
type = PointValue
point = '30 0 0'
variable = temperature
[]
[]
[Functions]
[moles_Na]
type = ParsedFunction
symbol_names = 'kg_Na dt'
symbol_values = 'kg_Na_produced_this_timestep dt'
expression = 'kg_Na * 1000 / 22.9898 / dt'
[]
[moles_Cl]
type = ParsedFunction
symbol_names = 'kg_Cl dt'
symbol_values = 'kg_Cl_produced_this_timestep dt'
expression = 'kg_Cl * 1000 / 35.453 / dt'
[]
[moles_SiO2]
type = ParsedFunction
symbol_names = 'kg_SiO2 dt'
symbol_values = 'kg_SiO2_produced_this_timestep dt'
expression = 'kg_SiO2 * 1000 / 60.0843 / dt'
[]
[moles_H2O]
type = ParsedFunction
symbol_names = 'kg_H2O dt'
symbol_values = 'kg_H2O_produced_this_timestep dt'
expression = 'kg_H2O * 1000 / 18.0152 / dt'
[]
[]
[FluidProperties]
[the_simple_fluid]
type = SimpleFluidProperties
thermal_expansion = 0
bulk_modulus = 2E9
viscosity = 1E-3
density0 = 1000
cv = 4000.0
cp = 4000.0
[]
[]
[PorousFlowFullySaturated]
coupling_type = ThermoHydro
porepressure = porepressure
temperature = temperature
mass_fraction_vars = 'f0 f1 f2'
save_component_rate_in = 'rate_Na rate_Cl rate_SiO2 rate_H2O' # change in kg at every node / dt
fp = the_simple_fluid
temperature_unit = Celsius
[]
[AuxVariables]
[injection_temperature]
initial_condition = 200
[]
[injection_rate_massfrac_Na]
initial_condition = 0.002285946
[]
[injection_rate_massfrac_Cl]
initial_condition = 0.0035252
[]
[injection_rate_massfrac_SiO2]
initial_condition = 1.3741E-05
[]
[injection_rate_massfrac_H2O]
initial_condition = 0.994175112
[]
[rate_H2O]
[]
[rate_Na]
[]
[rate_Cl]
[]
[rate_SiO2]
[]
[]
[Materials]
[porosity]
type = PorousFlowPorosityConst # this simulation has no porosity changes from dissolution
porosity = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-12 0 0 0 1E-12 0 0 0 1E-12'
[]
[thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '0 0 0 0 0 0 0 0 0'
[]
[rock_heat]
type = PorousFlowMatrixInternalEnergy
density = 2500.0
specific_heat_capacity = 1200.0
[]
[]
[Preconditioning]
active = typically_efficient
[typically_efficient]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = ' hypre boomeramg'
[]
[strong]
type = SMP
full = true
petsc_options = '-ksp_diagonal_scale -ksp_diagonal_scale_fix'
petsc_options_iname = '-pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = ' asm ilu NONZERO 2'
[]
[probably_too_strong]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = ' lu mumps'
[]
[]
[Executioner]
type = Transient
solve_type = Newton
end_time = 7.76E6 # 90 days
dt = 1E5
[]
[Outputs]
exodus = true
[]
[MultiApps]
[react]
type = TransientMultiApp
input_files = aquifer_geochemistry.i
clone_master_mesh = true
execute_on = 'timestep_end'
[]
[]
[Transfers]
[changes_due_to_flow]
type = MultiAppCopyTransfer
source_variable = 'rate_H2O rate_Na rate_Cl rate_SiO2 temperature'
variable = 'pf_rate_H2O pf_rate_Na pf_rate_Cl pf_rate_SiO2 temperature'
to_multi_app = react
[]
[massfrac_from_geochem]
type = MultiAppCopyTransfer
source_variable = 'massfrac_Na massfrac_Cl massfrac_SiO2'
variable = 'f0 f1 f2'
from_multi_app = react
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/porous_flow.i)
# PorousFlow simulation of injection and production in a 2D aquifer
# Much of this file is standard porous-flow stuff. The unusual aspects are:
# - transfer of the rates of changes of each species (kg/s) to the aquifer_geochemistry.i simulation. This is achieved by saving these changes from the PorousFlowMassTimeDerivative residuals
# - transfer of the temperature field to the aquifer_geochemistry.i simulation
# Interesting behaviour can be simulated by this file without its "parent" simulation, exchanger.i. exchanger.i provides mass-fractions injected via the injection_rate_massfrac_* variables, but since these are more-or-less constant throughout the duration of the exchanger.i simulation, the initial_conditions specified below may be used. Similar, exchanger.i provides injection_temperature, but that is also constant.
injection_rate = -1.0 # kg/s/m, negative because injection as a source
production_rate = 1.0 # kg/s/m
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[injection_node]
input = gen
type = ExtraNodesetGenerator
new_boundary = injection_node
coord = '-30 0 0'
[]
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[f0]
initial_condition = 0.002285946
[]
[f1]
initial_condition = 0.0035252
[]
[f2]
initial_condition = 1.3741E-05
[]
[porepressure]
initial_condition = 2E6
[]
[temperature]
initial_condition = 50
scaling = 1E-6 # fluid enthalpy is roughly 1E6
[]
[]
[BCs]
[injection_temperature]
type = MatchedValueBC
variable = temperature
v = injection_temperature
boundary = injection_node
[]
[]
[DiracKernels]
[inject_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Na
point_file = injection.bh
variable = f0
[]
[inject_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Cl
point_file = injection.bh
variable = f1
[]
[inject_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_SiO2
point_file = injection.bh
variable = f2
[]
[inject_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_H2O
point_file = injection.bh
variable = porepressure
[]
[produce_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Na
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 0
point_file = production.bh
variable = f0
[]
[produce_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Cl
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 1
point_file = production.bh
variable = f1
[]
[produce_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_SiO2
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 2
point_file = production.bh
variable = f2
[]
[produce_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_H2O
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 3
point_file = production.bh
variable = porepressure
[]
[produce_heat]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_heat
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
use_enthalpy = true
point_file = production.bh
variable = temperature
[]
[]
[UserObjects]
[injected_mass]
type = PorousFlowSumQuantity
[]
[produced_mass_Na]
type = PorousFlowSumQuantity
[]
[produced_mass_Cl]
type = PorousFlowSumQuantity
[]
[produced_mass_SiO2]
type = PorousFlowSumQuantity
[]
[produced_mass_H2O]
type = PorousFlowSumQuantity
[]
[produced_heat]
type = PorousFlowSumQuantity
[]
[]
[Postprocessors]
[dt]
type = TimestepSize
execute_on = TIMESTEP_BEGIN
[]
[tot_kg_injected_this_timestep]
type = PorousFlowPlotQuantity
uo = injected_mass
[]
[kg_Na_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Na
[]
[kg_Cl_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Cl
[]
[kg_SiO2_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_SiO2
[]
[kg_H2O_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_H2O
[]
[mole_rate_Na_produced]
type = FunctionValuePostprocessor
function = moles_Na
indirect_dependencies = 'kg_Na_produced_this_timestep dt'
[]
[mole_rate_Cl_produced]
type = FunctionValuePostprocessor
function = moles_Cl
indirect_dependencies = 'kg_Cl_produced_this_timestep dt'
[]
[mole_rate_SiO2_produced]
type = FunctionValuePostprocessor
function = moles_SiO2
indirect_dependencies = 'kg_SiO2_produced_this_timestep dt'
[]
[mole_rate_H2O_produced]
type = FunctionValuePostprocessor
function = moles_H2O
indirect_dependencies = 'kg_H2O_produced_this_timestep dt'
[]
[heat_joules_extracted_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_heat
[]
[production_temperature]
type = PointValue
point = '30 0 0'
variable = temperature
[]
[]
[Functions]
[moles_Na]
type = ParsedFunction
symbol_names = 'kg_Na dt'
symbol_values = 'kg_Na_produced_this_timestep dt'
expression = 'kg_Na * 1000 / 22.9898 / dt'
[]
[moles_Cl]
type = ParsedFunction
symbol_names = 'kg_Cl dt'
symbol_values = 'kg_Cl_produced_this_timestep dt'
expression = 'kg_Cl * 1000 / 35.453 / dt'
[]
[moles_SiO2]
type = ParsedFunction
symbol_names = 'kg_SiO2 dt'
symbol_values = 'kg_SiO2_produced_this_timestep dt'
expression = 'kg_SiO2 * 1000 / 60.0843 / dt'
[]
[moles_H2O]
type = ParsedFunction
symbol_names = 'kg_H2O dt'
symbol_values = 'kg_H2O_produced_this_timestep dt'
expression = 'kg_H2O * 1000 / 18.0152 / dt'
[]
[]
[FluidProperties]
[the_simple_fluid]
type = SimpleFluidProperties
thermal_expansion = 0
bulk_modulus = 2E9
viscosity = 1E-3
density0 = 1000
cv = 4000.0
cp = 4000.0
[]
[]
[PorousFlowFullySaturated]
coupling_type = ThermoHydro
porepressure = porepressure
temperature = temperature
mass_fraction_vars = 'f0 f1 f2'
save_component_rate_in = 'rate_Na rate_Cl rate_SiO2 rate_H2O' # change in kg at every node / dt
fp = the_simple_fluid
temperature_unit = Celsius
[]
[AuxVariables]
[injection_temperature]
initial_condition = 200
[]
[injection_rate_massfrac_Na]
initial_condition = 0.002285946
[]
[injection_rate_massfrac_Cl]
initial_condition = 0.0035252
[]
[injection_rate_massfrac_SiO2]
initial_condition = 1.3741E-05
[]
[injection_rate_massfrac_H2O]
initial_condition = 0.994175112
[]
[rate_H2O]
[]
[rate_Na]
[]
[rate_Cl]
[]
[rate_SiO2]
[]
[]
[Materials]
[porosity]
type = PorousFlowPorosityConst # this simulation has no porosity changes from dissolution
porosity = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-12 0 0 0 1E-12 0 0 0 1E-12'
[]
[thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '0 0 0 0 0 0 0 0 0'
[]
[rock_heat]
type = PorousFlowMatrixInternalEnergy
density = 2500.0
specific_heat_capacity = 1200.0
[]
[]
[Preconditioning]
active = typically_efficient
[typically_efficient]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = ' hypre boomeramg'
[]
[strong]
type = SMP
full = true
petsc_options = '-ksp_diagonal_scale -ksp_diagonal_scale_fix'
petsc_options_iname = '-pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = ' asm ilu NONZERO 2'
[]
[probably_too_strong]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = ' lu mumps'
[]
[]
[Executioner]
type = Transient
solve_type = Newton
end_time = 7.76E6 # 90 days
dt = 1E5
[]
[Outputs]
exodus = true
[]
[MultiApps]
[react]
type = TransientMultiApp
input_files = aquifer_geochemistry.i
clone_master_mesh = true
execute_on = 'timestep_end'
[]
[]
[Transfers]
[changes_due_to_flow]
type = MultiAppCopyTransfer
source_variable = 'rate_H2O rate_Na rate_Cl rate_SiO2 temperature'
variable = 'pf_rate_H2O pf_rate_Na pf_rate_Cl pf_rate_SiO2 temperature'
to_multi_app = react
[]
[massfrac_from_geochem]
type = MultiAppCopyTransfer
source_variable = 'massfrac_Na massfrac_Cl massfrac_SiO2'
variable = 'f0 f1 f2'
from_multi_app = react
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/porous_flow.i)
# PorousFlow simulation of injection and production in a 2D aquifer
# Much of this file is standard porous-flow stuff. The unusual aspects are:
# - transfer of the rates of changes of each species (kg/s) to the aquifer_geochemistry.i simulation. This is achieved by saving these changes from the PorousFlowMassTimeDerivative residuals
# - transfer of the temperature field to the aquifer_geochemistry.i simulation
# Interesting behaviour can be simulated by this file without its "parent" simulation, exchanger.i. exchanger.i provides mass-fractions injected via the injection_rate_massfrac_* variables, but since these are more-or-less constant throughout the duration of the exchanger.i simulation, the initial_conditions specified below may be used. Similar, exchanger.i provides injection_temperature, but that is also constant.
injection_rate = -1.0 # kg/s/m, negative because injection as a source
production_rate = 1.0 # kg/s/m
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[injection_node]
input = gen
type = ExtraNodesetGenerator
new_boundary = injection_node
coord = '-30 0 0'
[]
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[f0]
initial_condition = 0.002285946
[]
[f1]
initial_condition = 0.0035252
[]
[f2]
initial_condition = 1.3741E-05
[]
[porepressure]
initial_condition = 2E6
[]
[temperature]
initial_condition = 50
scaling = 1E-6 # fluid enthalpy is roughly 1E6
[]
[]
[BCs]
[injection_temperature]
type = MatchedValueBC
variable = temperature
v = injection_temperature
boundary = injection_node
[]
[]
[DiracKernels]
[inject_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Na
point_file = injection.bh
variable = f0
[]
[inject_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Cl
point_file = injection.bh
variable = f1
[]
[inject_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_SiO2
point_file = injection.bh
variable = f2
[]
[inject_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_H2O
point_file = injection.bh
variable = porepressure
[]
[produce_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Na
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 0
point_file = production.bh
variable = f0
[]
[produce_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Cl
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 1
point_file = production.bh
variable = f1
[]
[produce_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_SiO2
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 2
point_file = production.bh
variable = f2
[]
[produce_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_H2O
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 3
point_file = production.bh
variable = porepressure
[]
[produce_heat]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_heat
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
use_enthalpy = true
point_file = production.bh
variable = temperature
[]
[]
[UserObjects]
[injected_mass]
type = PorousFlowSumQuantity
[]
[produced_mass_Na]
type = PorousFlowSumQuantity
[]
[produced_mass_Cl]
type = PorousFlowSumQuantity
[]
[produced_mass_SiO2]
type = PorousFlowSumQuantity
[]
[produced_mass_H2O]
type = PorousFlowSumQuantity
[]
[produced_heat]
type = PorousFlowSumQuantity
[]
[]
[Postprocessors]
[dt]
type = TimestepSize
execute_on = TIMESTEP_BEGIN
[]
[tot_kg_injected_this_timestep]
type = PorousFlowPlotQuantity
uo = injected_mass
[]
[kg_Na_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Na
[]
[kg_Cl_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Cl
[]
[kg_SiO2_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_SiO2
[]
[kg_H2O_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_H2O
[]
[mole_rate_Na_produced]
type = FunctionValuePostprocessor
function = moles_Na
indirect_dependencies = 'kg_Na_produced_this_timestep dt'
[]
[mole_rate_Cl_produced]
type = FunctionValuePostprocessor
function = moles_Cl
indirect_dependencies = 'kg_Cl_produced_this_timestep dt'
[]
[mole_rate_SiO2_produced]
type = FunctionValuePostprocessor
function = moles_SiO2
indirect_dependencies = 'kg_SiO2_produced_this_timestep dt'
[]
[mole_rate_H2O_produced]
type = FunctionValuePostprocessor
function = moles_H2O
indirect_dependencies = 'kg_H2O_produced_this_timestep dt'
[]
[heat_joules_extracted_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_heat
[]
[production_temperature]
type = PointValue
point = '30 0 0'
variable = temperature
[]
[]
[Functions]
[moles_Na]
type = ParsedFunction
symbol_names = 'kg_Na dt'
symbol_values = 'kg_Na_produced_this_timestep dt'
expression = 'kg_Na * 1000 / 22.9898 / dt'
[]
[moles_Cl]
type = ParsedFunction
symbol_names = 'kg_Cl dt'
symbol_values = 'kg_Cl_produced_this_timestep dt'
expression = 'kg_Cl * 1000 / 35.453 / dt'
[]
[moles_SiO2]
type = ParsedFunction
symbol_names = 'kg_SiO2 dt'
symbol_values = 'kg_SiO2_produced_this_timestep dt'
expression = 'kg_SiO2 * 1000 / 60.0843 / dt'
[]
[moles_H2O]
type = ParsedFunction
symbol_names = 'kg_H2O dt'
symbol_values = 'kg_H2O_produced_this_timestep dt'
expression = 'kg_H2O * 1000 / 18.0152 / dt'
[]
[]
[FluidProperties]
[the_simple_fluid]
type = SimpleFluidProperties
thermal_expansion = 0
bulk_modulus = 2E9
viscosity = 1E-3
density0 = 1000
cv = 4000.0
cp = 4000.0
[]
[]
[PorousFlowFullySaturated]
coupling_type = ThermoHydro
porepressure = porepressure
temperature = temperature
mass_fraction_vars = 'f0 f1 f2'
save_component_rate_in = 'rate_Na rate_Cl rate_SiO2 rate_H2O' # change in kg at every node / dt
fp = the_simple_fluid
temperature_unit = Celsius
[]
[AuxVariables]
[injection_temperature]
initial_condition = 200
[]
[injection_rate_massfrac_Na]
initial_condition = 0.002285946
[]
[injection_rate_massfrac_Cl]
initial_condition = 0.0035252
[]
[injection_rate_massfrac_SiO2]
initial_condition = 1.3741E-05
[]
[injection_rate_massfrac_H2O]
initial_condition = 0.994175112
[]
[rate_H2O]
[]
[rate_Na]
[]
[rate_Cl]
[]
[rate_SiO2]
[]
[]
[Materials]
[porosity]
type = PorousFlowPorosityConst # this simulation has no porosity changes from dissolution
porosity = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-12 0 0 0 1E-12 0 0 0 1E-12'
[]
[thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '0 0 0 0 0 0 0 0 0'
[]
[rock_heat]
type = PorousFlowMatrixInternalEnergy
density = 2500.0
specific_heat_capacity = 1200.0
[]
[]
[Preconditioning]
active = typically_efficient
[typically_efficient]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = ' hypre boomeramg'
[]
[strong]
type = SMP
full = true
petsc_options = '-ksp_diagonal_scale -ksp_diagonal_scale_fix'
petsc_options_iname = '-pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = ' asm ilu NONZERO 2'
[]
[probably_too_strong]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = ' lu mumps'
[]
[]
[Executioner]
type = Transient
solve_type = Newton
end_time = 7.76E6 # 90 days
dt = 1E5
[]
[Outputs]
exodus = true
[]
[MultiApps]
[react]
type = TransientMultiApp
input_files = aquifer_geochemistry.i
clone_master_mesh = true
execute_on = 'timestep_end'
[]
[]
[Transfers]
[changes_due_to_flow]
type = MultiAppCopyTransfer
source_variable = 'rate_H2O rate_Na rate_Cl rate_SiO2 temperature'
variable = 'pf_rate_H2O pf_rate_Na pf_rate_Cl pf_rate_SiO2 temperature'
to_multi_app = react
[]
[massfrac_from_geochem]
type = MultiAppCopyTransfer
source_variable = 'massfrac_Na massfrac_Cl massfrac_SiO2'
variable = 'f0 f1 f2'
from_multi_app = react
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/porous_flow.i)
# PorousFlow simulation of injection and production in a 2D aquifer
# Much of this file is standard porous-flow stuff. The unusual aspects are:
# - transfer of the rates of changes of each species (kg/s) to the aquifer_geochemistry.i simulation. This is achieved by saving these changes from the PorousFlowMassTimeDerivative residuals
# - transfer of the temperature field to the aquifer_geochemistry.i simulation
# Interesting behaviour can be simulated by this file without its "parent" simulation, exchanger.i. exchanger.i provides mass-fractions injected via the injection_rate_massfrac_* variables, but since these are more-or-less constant throughout the duration of the exchanger.i simulation, the initial_conditions specified below may be used. Similar, exchanger.i provides injection_temperature, but that is also constant.
injection_rate = -1.0 # kg/s/m, negative because injection as a source
production_rate = 1.0 # kg/s/m
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[injection_node]
input = gen
type = ExtraNodesetGenerator
new_boundary = injection_node
coord = '-30 0 0'
[]
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[f0]
initial_condition = 0.002285946
[]
[f1]
initial_condition = 0.0035252
[]
[f2]
initial_condition = 1.3741E-05
[]
[porepressure]
initial_condition = 2E6
[]
[temperature]
initial_condition = 50
scaling = 1E-6 # fluid enthalpy is roughly 1E6
[]
[]
[BCs]
[injection_temperature]
type = MatchedValueBC
variable = temperature
v = injection_temperature
boundary = injection_node
[]
[]
[DiracKernels]
[inject_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Na
point_file = injection.bh
variable = f0
[]
[inject_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Cl
point_file = injection.bh
variable = f1
[]
[inject_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_SiO2
point_file = injection.bh
variable = f2
[]
[inject_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_H2O
point_file = injection.bh
variable = porepressure
[]
[produce_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Na
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 0
point_file = production.bh
variable = f0
[]
[produce_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Cl
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 1
point_file = production.bh
variable = f1
[]
[produce_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_SiO2
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 2
point_file = production.bh
variable = f2
[]
[produce_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_H2O
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 3
point_file = production.bh
variable = porepressure
[]
[produce_heat]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_heat
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
use_enthalpy = true
point_file = production.bh
variable = temperature
[]
[]
[UserObjects]
[injected_mass]
type = PorousFlowSumQuantity
[]
[produced_mass_Na]
type = PorousFlowSumQuantity
[]
[produced_mass_Cl]
type = PorousFlowSumQuantity
[]
[produced_mass_SiO2]
type = PorousFlowSumQuantity
[]
[produced_mass_H2O]
type = PorousFlowSumQuantity
[]
[produced_heat]
type = PorousFlowSumQuantity
[]
[]
[Postprocessors]
[dt]
type = TimestepSize
execute_on = TIMESTEP_BEGIN
[]
[tot_kg_injected_this_timestep]
type = PorousFlowPlotQuantity
uo = injected_mass
[]
[kg_Na_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Na
[]
[kg_Cl_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Cl
[]
[kg_SiO2_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_SiO2
[]
[kg_H2O_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_H2O
[]
[mole_rate_Na_produced]
type = FunctionValuePostprocessor
function = moles_Na
indirect_dependencies = 'kg_Na_produced_this_timestep dt'
[]
[mole_rate_Cl_produced]
type = FunctionValuePostprocessor
function = moles_Cl
indirect_dependencies = 'kg_Cl_produced_this_timestep dt'
[]
[mole_rate_SiO2_produced]
type = FunctionValuePostprocessor
function = moles_SiO2
indirect_dependencies = 'kg_SiO2_produced_this_timestep dt'
[]
[mole_rate_H2O_produced]
type = FunctionValuePostprocessor
function = moles_H2O
indirect_dependencies = 'kg_H2O_produced_this_timestep dt'
[]
[heat_joules_extracted_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_heat
[]
[production_temperature]
type = PointValue
point = '30 0 0'
variable = temperature
[]
[]
[Functions]
[moles_Na]
type = ParsedFunction
symbol_names = 'kg_Na dt'
symbol_values = 'kg_Na_produced_this_timestep dt'
expression = 'kg_Na * 1000 / 22.9898 / dt'
[]
[moles_Cl]
type = ParsedFunction
symbol_names = 'kg_Cl dt'
symbol_values = 'kg_Cl_produced_this_timestep dt'
expression = 'kg_Cl * 1000 / 35.453 / dt'
[]
[moles_SiO2]
type = ParsedFunction
symbol_names = 'kg_SiO2 dt'
symbol_values = 'kg_SiO2_produced_this_timestep dt'
expression = 'kg_SiO2 * 1000 / 60.0843 / dt'
[]
[moles_H2O]
type = ParsedFunction
symbol_names = 'kg_H2O dt'
symbol_values = 'kg_H2O_produced_this_timestep dt'
expression = 'kg_H2O * 1000 / 18.0152 / dt'
[]
[]
[FluidProperties]
[the_simple_fluid]
type = SimpleFluidProperties
thermal_expansion = 0
bulk_modulus = 2E9
viscosity = 1E-3
density0 = 1000
cv = 4000.0
cp = 4000.0
[]
[]
[PorousFlowFullySaturated]
coupling_type = ThermoHydro
porepressure = porepressure
temperature = temperature
mass_fraction_vars = 'f0 f1 f2'
save_component_rate_in = 'rate_Na rate_Cl rate_SiO2 rate_H2O' # change in kg at every node / dt
fp = the_simple_fluid
temperature_unit = Celsius
[]
[AuxVariables]
[injection_temperature]
initial_condition = 200
[]
[injection_rate_massfrac_Na]
initial_condition = 0.002285946
[]
[injection_rate_massfrac_Cl]
initial_condition = 0.0035252
[]
[injection_rate_massfrac_SiO2]
initial_condition = 1.3741E-05
[]
[injection_rate_massfrac_H2O]
initial_condition = 0.994175112
[]
[rate_H2O]
[]
[rate_Na]
[]
[rate_Cl]
[]
[rate_SiO2]
[]
[]
[Materials]
[porosity]
type = PorousFlowPorosityConst # this simulation has no porosity changes from dissolution
porosity = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-12 0 0 0 1E-12 0 0 0 1E-12'
[]
[thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '0 0 0 0 0 0 0 0 0'
[]
[rock_heat]
type = PorousFlowMatrixInternalEnergy
density = 2500.0
specific_heat_capacity = 1200.0
[]
[]
[Preconditioning]
active = typically_efficient
[typically_efficient]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = ' hypre boomeramg'
[]
[strong]
type = SMP
full = true
petsc_options = '-ksp_diagonal_scale -ksp_diagonal_scale_fix'
petsc_options_iname = '-pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = ' asm ilu NONZERO 2'
[]
[probably_too_strong]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = ' lu mumps'
[]
[]
[Executioner]
type = Transient
solve_type = Newton
end_time = 7.76E6 # 90 days
dt = 1E5
[]
[Outputs]
exodus = true
[]
[MultiApps]
[react]
type = TransientMultiApp
input_files = aquifer_geochemistry.i
clone_master_mesh = true
execute_on = 'timestep_end'
[]
[]
[Transfers]
[changes_due_to_flow]
type = MultiAppCopyTransfer
source_variable = 'rate_H2O rate_Na rate_Cl rate_SiO2 temperature'
variable = 'pf_rate_H2O pf_rate_Na pf_rate_Cl pf_rate_SiO2 temperature'
to_multi_app = react
[]
[massfrac_from_geochem]
type = MultiAppCopyTransfer
source_variable = 'massfrac_Na massfrac_Cl massfrac_SiO2'
variable = 'f0 f1 f2'
from_multi_app = react
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/porous_flow.i)
# PorousFlow simulation of injection and production in a 2D aquifer
# Much of this file is standard porous-flow stuff. The unusual aspects are:
# - transfer of the rates of changes of each species (kg/s) to the aquifer_geochemistry.i simulation. This is achieved by saving these changes from the PorousFlowMassTimeDerivative residuals
# - transfer of the temperature field to the aquifer_geochemistry.i simulation
# Interesting behaviour can be simulated by this file without its "parent" simulation, exchanger.i. exchanger.i provides mass-fractions injected via the injection_rate_massfrac_* variables, but since these are more-or-less constant throughout the duration of the exchanger.i simulation, the initial_conditions specified below may be used. Similar, exchanger.i provides injection_temperature, but that is also constant.
injection_rate = -1.0 # kg/s/m, negative because injection as a source
production_rate = 1.0 # kg/s/m
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[injection_node]
input = gen
type = ExtraNodesetGenerator
new_boundary = injection_node
coord = '-30 0 0'
[]
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[f0]
initial_condition = 0.002285946
[]
[f1]
initial_condition = 0.0035252
[]
[f2]
initial_condition = 1.3741E-05
[]
[porepressure]
initial_condition = 2E6
[]
[temperature]
initial_condition = 50
scaling = 1E-6 # fluid enthalpy is roughly 1E6
[]
[]
[BCs]
[injection_temperature]
type = MatchedValueBC
variable = temperature
v = injection_temperature
boundary = injection_node
[]
[]
[DiracKernels]
[inject_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Na
point_file = injection.bh
variable = f0
[]
[inject_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Cl
point_file = injection.bh
variable = f1
[]
[inject_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_SiO2
point_file = injection.bh
variable = f2
[]
[inject_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_H2O
point_file = injection.bh
variable = porepressure
[]
[produce_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Na
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 0
point_file = production.bh
variable = f0
[]
[produce_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Cl
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 1
point_file = production.bh
variable = f1
[]
[produce_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_SiO2
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 2
point_file = production.bh
variable = f2
[]
[produce_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_H2O
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 3
point_file = production.bh
variable = porepressure
[]
[produce_heat]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_heat
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
use_enthalpy = true
point_file = production.bh
variable = temperature
[]
[]
[UserObjects]
[injected_mass]
type = PorousFlowSumQuantity
[]
[produced_mass_Na]
type = PorousFlowSumQuantity
[]
[produced_mass_Cl]
type = PorousFlowSumQuantity
[]
[produced_mass_SiO2]
type = PorousFlowSumQuantity
[]
[produced_mass_H2O]
type = PorousFlowSumQuantity
[]
[produced_heat]
type = PorousFlowSumQuantity
[]
[]
[Postprocessors]
[dt]
type = TimestepSize
execute_on = TIMESTEP_BEGIN
[]
[tot_kg_injected_this_timestep]
type = PorousFlowPlotQuantity
uo = injected_mass
[]
[kg_Na_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Na
[]
[kg_Cl_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Cl
[]
[kg_SiO2_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_SiO2
[]
[kg_H2O_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_H2O
[]
[mole_rate_Na_produced]
type = FunctionValuePostprocessor
function = moles_Na
indirect_dependencies = 'kg_Na_produced_this_timestep dt'
[]
[mole_rate_Cl_produced]
type = FunctionValuePostprocessor
function = moles_Cl
indirect_dependencies = 'kg_Cl_produced_this_timestep dt'
[]
[mole_rate_SiO2_produced]
type = FunctionValuePostprocessor
function = moles_SiO2
indirect_dependencies = 'kg_SiO2_produced_this_timestep dt'
[]
[mole_rate_H2O_produced]
type = FunctionValuePostprocessor
function = moles_H2O
indirect_dependencies = 'kg_H2O_produced_this_timestep dt'
[]
[heat_joules_extracted_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_heat
[]
[production_temperature]
type = PointValue
point = '30 0 0'
variable = temperature
[]
[]
[Functions]
[moles_Na]
type = ParsedFunction
symbol_names = 'kg_Na dt'
symbol_values = 'kg_Na_produced_this_timestep dt'
expression = 'kg_Na * 1000 / 22.9898 / dt'
[]
[moles_Cl]
type = ParsedFunction
symbol_names = 'kg_Cl dt'
symbol_values = 'kg_Cl_produced_this_timestep dt'
expression = 'kg_Cl * 1000 / 35.453 / dt'
[]
[moles_SiO2]
type = ParsedFunction
symbol_names = 'kg_SiO2 dt'
symbol_values = 'kg_SiO2_produced_this_timestep dt'
expression = 'kg_SiO2 * 1000 / 60.0843 / dt'
[]
[moles_H2O]
type = ParsedFunction
symbol_names = 'kg_H2O dt'
symbol_values = 'kg_H2O_produced_this_timestep dt'
expression = 'kg_H2O * 1000 / 18.0152 / dt'
[]
[]
[FluidProperties]
[the_simple_fluid]
type = SimpleFluidProperties
thermal_expansion = 0
bulk_modulus = 2E9
viscosity = 1E-3
density0 = 1000
cv = 4000.0
cp = 4000.0
[]
[]
[PorousFlowFullySaturated]
coupling_type = ThermoHydro
porepressure = porepressure
temperature = temperature
mass_fraction_vars = 'f0 f1 f2'
save_component_rate_in = 'rate_Na rate_Cl rate_SiO2 rate_H2O' # change in kg at every node / dt
fp = the_simple_fluid
temperature_unit = Celsius
[]
[AuxVariables]
[injection_temperature]
initial_condition = 200
[]
[injection_rate_massfrac_Na]
initial_condition = 0.002285946
[]
[injection_rate_massfrac_Cl]
initial_condition = 0.0035252
[]
[injection_rate_massfrac_SiO2]
initial_condition = 1.3741E-05
[]
[injection_rate_massfrac_H2O]
initial_condition = 0.994175112
[]
[rate_H2O]
[]
[rate_Na]
[]
[rate_Cl]
[]
[rate_SiO2]
[]
[]
[Materials]
[porosity]
type = PorousFlowPorosityConst # this simulation has no porosity changes from dissolution
porosity = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-12 0 0 0 1E-12 0 0 0 1E-12'
[]
[thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '0 0 0 0 0 0 0 0 0'
[]
[rock_heat]
type = PorousFlowMatrixInternalEnergy
density = 2500.0
specific_heat_capacity = 1200.0
[]
[]
[Preconditioning]
active = typically_efficient
[typically_efficient]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = ' hypre boomeramg'
[]
[strong]
type = SMP
full = true
petsc_options = '-ksp_diagonal_scale -ksp_diagonal_scale_fix'
petsc_options_iname = '-pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = ' asm ilu NONZERO 2'
[]
[probably_too_strong]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = ' lu mumps'
[]
[]
[Executioner]
type = Transient
solve_type = Newton
end_time = 7.76E6 # 90 days
dt = 1E5
[]
[Outputs]
exodus = true
[]
[MultiApps]
[react]
type = TransientMultiApp
input_files = aquifer_geochemistry.i
clone_master_mesh = true
execute_on = 'timestep_end'
[]
[]
[Transfers]
[changes_due_to_flow]
type = MultiAppCopyTransfer
source_variable = 'rate_H2O rate_Na rate_Cl rate_SiO2 temperature'
variable = 'pf_rate_H2O pf_rate_Na pf_rate_Cl pf_rate_SiO2 temperature'
to_multi_app = react
[]
[massfrac_from_geochem]
type = MultiAppCopyTransfer
source_variable = 'massfrac_Na massfrac_Cl massfrac_SiO2'
variable = 'f0 f1 f2'
from_multi_app = react
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/porous_flow.i)
# PorousFlow simulation of injection and production in a 2D aquifer
# Much of this file is standard porous-flow stuff. The unusual aspects are:
# - transfer of the rates of changes of each species (kg/s) to the aquifer_geochemistry.i simulation. This is achieved by saving these changes from the PorousFlowMassTimeDerivative residuals
# - transfer of the temperature field to the aquifer_geochemistry.i simulation
# Interesting behaviour can be simulated by this file without its "parent" simulation, exchanger.i. exchanger.i provides mass-fractions injected via the injection_rate_massfrac_* variables, but since these are more-or-less constant throughout the duration of the exchanger.i simulation, the initial_conditions specified below may be used. Similar, exchanger.i provides injection_temperature, but that is also constant.
injection_rate = -1.0 # kg/s/m, negative because injection as a source
production_rate = 1.0 # kg/s/m
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[injection_node]
input = gen
type = ExtraNodesetGenerator
new_boundary = injection_node
coord = '-30 0 0'
[]
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[f0]
initial_condition = 0.002285946
[]
[f1]
initial_condition = 0.0035252
[]
[f2]
initial_condition = 1.3741E-05
[]
[porepressure]
initial_condition = 2E6
[]
[temperature]
initial_condition = 50
scaling = 1E-6 # fluid enthalpy is roughly 1E6
[]
[]
[BCs]
[injection_temperature]
type = MatchedValueBC
variable = temperature
v = injection_temperature
boundary = injection_node
[]
[]
[DiracKernels]
[inject_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Na
point_file = injection.bh
variable = f0
[]
[inject_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Cl
point_file = injection.bh
variable = f1
[]
[inject_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_SiO2
point_file = injection.bh
variable = f2
[]
[inject_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_H2O
point_file = injection.bh
variable = porepressure
[]
[produce_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Na
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 0
point_file = production.bh
variable = f0
[]
[produce_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Cl
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 1
point_file = production.bh
variable = f1
[]
[produce_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_SiO2
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 2
point_file = production.bh
variable = f2
[]
[produce_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_H2O
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 3
point_file = production.bh
variable = porepressure
[]
[produce_heat]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_heat
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
use_enthalpy = true
point_file = production.bh
variable = temperature
[]
[]
[UserObjects]
[injected_mass]
type = PorousFlowSumQuantity
[]
[produced_mass_Na]
type = PorousFlowSumQuantity
[]
[produced_mass_Cl]
type = PorousFlowSumQuantity
[]
[produced_mass_SiO2]
type = PorousFlowSumQuantity
[]
[produced_mass_H2O]
type = PorousFlowSumQuantity
[]
[produced_heat]
type = PorousFlowSumQuantity
[]
[]
[Postprocessors]
[dt]
type = TimestepSize
execute_on = TIMESTEP_BEGIN
[]
[tot_kg_injected_this_timestep]
type = PorousFlowPlotQuantity
uo = injected_mass
[]
[kg_Na_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Na
[]
[kg_Cl_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Cl
[]
[kg_SiO2_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_SiO2
[]
[kg_H2O_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_H2O
[]
[mole_rate_Na_produced]
type = FunctionValuePostprocessor
function = moles_Na
indirect_dependencies = 'kg_Na_produced_this_timestep dt'
[]
[mole_rate_Cl_produced]
type = FunctionValuePostprocessor
function = moles_Cl
indirect_dependencies = 'kg_Cl_produced_this_timestep dt'
[]
[mole_rate_SiO2_produced]
type = FunctionValuePostprocessor
function = moles_SiO2
indirect_dependencies = 'kg_SiO2_produced_this_timestep dt'
[]
[mole_rate_H2O_produced]
type = FunctionValuePostprocessor
function = moles_H2O
indirect_dependencies = 'kg_H2O_produced_this_timestep dt'
[]
[heat_joules_extracted_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_heat
[]
[production_temperature]
type = PointValue
point = '30 0 0'
variable = temperature
[]
[]
[Functions]
[moles_Na]
type = ParsedFunction
symbol_names = 'kg_Na dt'
symbol_values = 'kg_Na_produced_this_timestep dt'
expression = 'kg_Na * 1000 / 22.9898 / dt'
[]
[moles_Cl]
type = ParsedFunction
symbol_names = 'kg_Cl dt'
symbol_values = 'kg_Cl_produced_this_timestep dt'
expression = 'kg_Cl * 1000 / 35.453 / dt'
[]
[moles_SiO2]
type = ParsedFunction
symbol_names = 'kg_SiO2 dt'
symbol_values = 'kg_SiO2_produced_this_timestep dt'
expression = 'kg_SiO2 * 1000 / 60.0843 / dt'
[]
[moles_H2O]
type = ParsedFunction
symbol_names = 'kg_H2O dt'
symbol_values = 'kg_H2O_produced_this_timestep dt'
expression = 'kg_H2O * 1000 / 18.0152 / dt'
[]
[]
[FluidProperties]
[the_simple_fluid]
type = SimpleFluidProperties
thermal_expansion = 0
bulk_modulus = 2E9
viscosity = 1E-3
density0 = 1000
cv = 4000.0
cp = 4000.0
[]
[]
[PorousFlowFullySaturated]
coupling_type = ThermoHydro
porepressure = porepressure
temperature = temperature
mass_fraction_vars = 'f0 f1 f2'
save_component_rate_in = 'rate_Na rate_Cl rate_SiO2 rate_H2O' # change in kg at every node / dt
fp = the_simple_fluid
temperature_unit = Celsius
[]
[AuxVariables]
[injection_temperature]
initial_condition = 200
[]
[injection_rate_massfrac_Na]
initial_condition = 0.002285946
[]
[injection_rate_massfrac_Cl]
initial_condition = 0.0035252
[]
[injection_rate_massfrac_SiO2]
initial_condition = 1.3741E-05
[]
[injection_rate_massfrac_H2O]
initial_condition = 0.994175112
[]
[rate_H2O]
[]
[rate_Na]
[]
[rate_Cl]
[]
[rate_SiO2]
[]
[]
[Materials]
[porosity]
type = PorousFlowPorosityConst # this simulation has no porosity changes from dissolution
porosity = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-12 0 0 0 1E-12 0 0 0 1E-12'
[]
[thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '0 0 0 0 0 0 0 0 0'
[]
[rock_heat]
type = PorousFlowMatrixInternalEnergy
density = 2500.0
specific_heat_capacity = 1200.0
[]
[]
[Preconditioning]
active = typically_efficient
[typically_efficient]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = ' hypre boomeramg'
[]
[strong]
type = SMP
full = true
petsc_options = '-ksp_diagonal_scale -ksp_diagonal_scale_fix'
petsc_options_iname = '-pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = ' asm ilu NONZERO 2'
[]
[probably_too_strong]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = ' lu mumps'
[]
[]
[Executioner]
type = Transient
solve_type = Newton
end_time = 7.76E6 # 90 days
dt = 1E5
[]
[Outputs]
exodus = true
[]
[MultiApps]
[react]
type = TransientMultiApp
input_files = aquifer_geochemistry.i
clone_master_mesh = true
execute_on = 'timestep_end'
[]
[]
[Transfers]
[changes_due_to_flow]
type = MultiAppCopyTransfer
source_variable = 'rate_H2O rate_Na rate_Cl rate_SiO2 temperature'
variable = 'pf_rate_H2O pf_rate_Na pf_rate_Cl pf_rate_SiO2 temperature'
to_multi_app = react
[]
[massfrac_from_geochem]
type = MultiAppCopyTransfer
source_variable = 'massfrac_Na massfrac_Cl massfrac_SiO2'
variable = 'f0 f1 f2'
from_multi_app = react
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/porous_flow.i)
# PorousFlow simulation of injection and production in a 2D aquifer
# Much of this file is standard porous-flow stuff. The unusual aspects are:
# - transfer of the rates of changes of each species (kg/s) to the aquifer_geochemistry.i simulation. This is achieved by saving these changes from the PorousFlowMassTimeDerivative residuals
# - transfer of the temperature field to the aquifer_geochemistry.i simulation
# Interesting behaviour can be simulated by this file without its "parent" simulation, exchanger.i. exchanger.i provides mass-fractions injected via the injection_rate_massfrac_* variables, but since these are more-or-less constant throughout the duration of the exchanger.i simulation, the initial_conditions specified below may be used. Similar, exchanger.i provides injection_temperature, but that is also constant.
injection_rate = -1.0 # kg/s/m, negative because injection as a source
production_rate = 1.0 # kg/s/m
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[injection_node]
input = gen
type = ExtraNodesetGenerator
new_boundary = injection_node
coord = '-30 0 0'
[]
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[f0]
initial_condition = 0.002285946
[]
[f1]
initial_condition = 0.0035252
[]
[f2]
initial_condition = 1.3741E-05
[]
[porepressure]
initial_condition = 2E6
[]
[temperature]
initial_condition = 50
scaling = 1E-6 # fluid enthalpy is roughly 1E6
[]
[]
[BCs]
[injection_temperature]
type = MatchedValueBC
variable = temperature
v = injection_temperature
boundary = injection_node
[]
[]
[DiracKernels]
[inject_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Na
point_file = injection.bh
variable = f0
[]
[inject_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Cl
point_file = injection.bh
variable = f1
[]
[inject_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_SiO2
point_file = injection.bh
variable = f2
[]
[inject_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_H2O
point_file = injection.bh
variable = porepressure
[]
[produce_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Na
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 0
point_file = production.bh
variable = f0
[]
[produce_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Cl
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 1
point_file = production.bh
variable = f1
[]
[produce_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_SiO2
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 2
point_file = production.bh
variable = f2
[]
[produce_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_H2O
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 3
point_file = production.bh
variable = porepressure
[]
[produce_heat]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_heat
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
use_enthalpy = true
point_file = production.bh
variable = temperature
[]
[]
[UserObjects]
[injected_mass]
type = PorousFlowSumQuantity
[]
[produced_mass_Na]
type = PorousFlowSumQuantity
[]
[produced_mass_Cl]
type = PorousFlowSumQuantity
[]
[produced_mass_SiO2]
type = PorousFlowSumQuantity
[]
[produced_mass_H2O]
type = PorousFlowSumQuantity
[]
[produced_heat]
type = PorousFlowSumQuantity
[]
[]
[Postprocessors]
[dt]
type = TimestepSize
execute_on = TIMESTEP_BEGIN
[]
[tot_kg_injected_this_timestep]
type = PorousFlowPlotQuantity
uo = injected_mass
[]
[kg_Na_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Na
[]
[kg_Cl_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Cl
[]
[kg_SiO2_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_SiO2
[]
[kg_H2O_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_H2O
[]
[mole_rate_Na_produced]
type = FunctionValuePostprocessor
function = moles_Na
indirect_dependencies = 'kg_Na_produced_this_timestep dt'
[]
[mole_rate_Cl_produced]
type = FunctionValuePostprocessor
function = moles_Cl
indirect_dependencies = 'kg_Cl_produced_this_timestep dt'
[]
[mole_rate_SiO2_produced]
type = FunctionValuePostprocessor
function = moles_SiO2
indirect_dependencies = 'kg_SiO2_produced_this_timestep dt'
[]
[mole_rate_H2O_produced]
type = FunctionValuePostprocessor
function = moles_H2O
indirect_dependencies = 'kg_H2O_produced_this_timestep dt'
[]
[heat_joules_extracted_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_heat
[]
[production_temperature]
type = PointValue
point = '30 0 0'
variable = temperature
[]
[]
[Functions]
[moles_Na]
type = ParsedFunction
symbol_names = 'kg_Na dt'
symbol_values = 'kg_Na_produced_this_timestep dt'
expression = 'kg_Na * 1000 / 22.9898 / dt'
[]
[moles_Cl]
type = ParsedFunction
symbol_names = 'kg_Cl dt'
symbol_values = 'kg_Cl_produced_this_timestep dt'
expression = 'kg_Cl * 1000 / 35.453 / dt'
[]
[moles_SiO2]
type = ParsedFunction
symbol_names = 'kg_SiO2 dt'
symbol_values = 'kg_SiO2_produced_this_timestep dt'
expression = 'kg_SiO2 * 1000 / 60.0843 / dt'
[]
[moles_H2O]
type = ParsedFunction
symbol_names = 'kg_H2O dt'
symbol_values = 'kg_H2O_produced_this_timestep dt'
expression = 'kg_H2O * 1000 / 18.0152 / dt'
[]
[]
[FluidProperties]
[the_simple_fluid]
type = SimpleFluidProperties
thermal_expansion = 0
bulk_modulus = 2E9
viscosity = 1E-3
density0 = 1000
cv = 4000.0
cp = 4000.0
[]
[]
[PorousFlowFullySaturated]
coupling_type = ThermoHydro
porepressure = porepressure
temperature = temperature
mass_fraction_vars = 'f0 f1 f2'
save_component_rate_in = 'rate_Na rate_Cl rate_SiO2 rate_H2O' # change in kg at every node / dt
fp = the_simple_fluid
temperature_unit = Celsius
[]
[AuxVariables]
[injection_temperature]
initial_condition = 200
[]
[injection_rate_massfrac_Na]
initial_condition = 0.002285946
[]
[injection_rate_massfrac_Cl]
initial_condition = 0.0035252
[]
[injection_rate_massfrac_SiO2]
initial_condition = 1.3741E-05
[]
[injection_rate_massfrac_H2O]
initial_condition = 0.994175112
[]
[rate_H2O]
[]
[rate_Na]
[]
[rate_Cl]
[]
[rate_SiO2]
[]
[]
[Materials]
[porosity]
type = PorousFlowPorosityConst # this simulation has no porosity changes from dissolution
porosity = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-12 0 0 0 1E-12 0 0 0 1E-12'
[]
[thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '0 0 0 0 0 0 0 0 0'
[]
[rock_heat]
type = PorousFlowMatrixInternalEnergy
density = 2500.0
specific_heat_capacity = 1200.0
[]
[]
[Preconditioning]
active = typically_efficient
[typically_efficient]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = ' hypre boomeramg'
[]
[strong]
type = SMP
full = true
petsc_options = '-ksp_diagonal_scale -ksp_diagonal_scale_fix'
petsc_options_iname = '-pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = ' asm ilu NONZERO 2'
[]
[probably_too_strong]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = ' lu mumps'
[]
[]
[Executioner]
type = Transient
solve_type = Newton
end_time = 7.76E6 # 90 days
dt = 1E5
[]
[Outputs]
exodus = true
[]
[MultiApps]
[react]
type = TransientMultiApp
input_files = aquifer_geochemistry.i
clone_master_mesh = true
execute_on = 'timestep_end'
[]
[]
[Transfers]
[changes_due_to_flow]
type = MultiAppCopyTransfer
source_variable = 'rate_H2O rate_Na rate_Cl rate_SiO2 temperature'
variable = 'pf_rate_H2O pf_rate_Na pf_rate_Cl pf_rate_SiO2 temperature'
to_multi_app = react
[]
[massfrac_from_geochem]
type = MultiAppCopyTransfer
source_variable = 'massfrac_Na massfrac_Cl massfrac_SiO2'
variable = 'f0 f1 f2'
from_multi_app = react
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/porous_flow.i)
# PorousFlow simulation of injection and production in a 2D aquifer
# Much of this file is standard porous-flow stuff. The unusual aspects are:
# - transfer of the rates of changes of each species (kg/s) to the aquifer_geochemistry.i simulation. This is achieved by saving these changes from the PorousFlowMassTimeDerivative residuals
# - transfer of the temperature field to the aquifer_geochemistry.i simulation
# Interesting behaviour can be simulated by this file without its "parent" simulation, exchanger.i. exchanger.i provides mass-fractions injected via the injection_rate_massfrac_* variables, but since these are more-or-less constant throughout the duration of the exchanger.i simulation, the initial_conditions specified below may be used. Similar, exchanger.i provides injection_temperature, but that is also constant.
injection_rate = -1.0 # kg/s/m, negative because injection as a source
production_rate = 1.0 # kg/s/m
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[injection_node]
input = gen
type = ExtraNodesetGenerator
new_boundary = injection_node
coord = '-30 0 0'
[]
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[f0]
initial_condition = 0.002285946
[]
[f1]
initial_condition = 0.0035252
[]
[f2]
initial_condition = 1.3741E-05
[]
[porepressure]
initial_condition = 2E6
[]
[temperature]
initial_condition = 50
scaling = 1E-6 # fluid enthalpy is roughly 1E6
[]
[]
[BCs]
[injection_temperature]
type = MatchedValueBC
variable = temperature
v = injection_temperature
boundary = injection_node
[]
[]
[DiracKernels]
[inject_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Na
point_file = injection.bh
variable = f0
[]
[inject_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Cl
point_file = injection.bh
variable = f1
[]
[inject_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_SiO2
point_file = injection.bh
variable = f2
[]
[inject_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_H2O
point_file = injection.bh
variable = porepressure
[]
[produce_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Na
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 0
point_file = production.bh
variable = f0
[]
[produce_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Cl
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 1
point_file = production.bh
variable = f1
[]
[produce_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_SiO2
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 2
point_file = production.bh
variable = f2
[]
[produce_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_H2O
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 3
point_file = production.bh
variable = porepressure
[]
[produce_heat]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_heat
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
use_enthalpy = true
point_file = production.bh
variable = temperature
[]
[]
[UserObjects]
[injected_mass]
type = PorousFlowSumQuantity
[]
[produced_mass_Na]
type = PorousFlowSumQuantity
[]
[produced_mass_Cl]
type = PorousFlowSumQuantity
[]
[produced_mass_SiO2]
type = PorousFlowSumQuantity
[]
[produced_mass_H2O]
type = PorousFlowSumQuantity
[]
[produced_heat]
type = PorousFlowSumQuantity
[]
[]
[Postprocessors]
[dt]
type = TimestepSize
execute_on = TIMESTEP_BEGIN
[]
[tot_kg_injected_this_timestep]
type = PorousFlowPlotQuantity
uo = injected_mass
[]
[kg_Na_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Na
[]
[kg_Cl_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Cl
[]
[kg_SiO2_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_SiO2
[]
[kg_H2O_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_H2O
[]
[mole_rate_Na_produced]
type = FunctionValuePostprocessor
function = moles_Na
indirect_dependencies = 'kg_Na_produced_this_timestep dt'
[]
[mole_rate_Cl_produced]
type = FunctionValuePostprocessor
function = moles_Cl
indirect_dependencies = 'kg_Cl_produced_this_timestep dt'
[]
[mole_rate_SiO2_produced]
type = FunctionValuePostprocessor
function = moles_SiO2
indirect_dependencies = 'kg_SiO2_produced_this_timestep dt'
[]
[mole_rate_H2O_produced]
type = FunctionValuePostprocessor
function = moles_H2O
indirect_dependencies = 'kg_H2O_produced_this_timestep dt'
[]
[heat_joules_extracted_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_heat
[]
[production_temperature]
type = PointValue
point = '30 0 0'
variable = temperature
[]
[]
[Functions]
[moles_Na]
type = ParsedFunction
symbol_names = 'kg_Na dt'
symbol_values = 'kg_Na_produced_this_timestep dt'
expression = 'kg_Na * 1000 / 22.9898 / dt'
[]
[moles_Cl]
type = ParsedFunction
symbol_names = 'kg_Cl dt'
symbol_values = 'kg_Cl_produced_this_timestep dt'
expression = 'kg_Cl * 1000 / 35.453 / dt'
[]
[moles_SiO2]
type = ParsedFunction
symbol_names = 'kg_SiO2 dt'
symbol_values = 'kg_SiO2_produced_this_timestep dt'
expression = 'kg_SiO2 * 1000 / 60.0843 / dt'
[]
[moles_H2O]
type = ParsedFunction
symbol_names = 'kg_H2O dt'
symbol_values = 'kg_H2O_produced_this_timestep dt'
expression = 'kg_H2O * 1000 / 18.0152 / dt'
[]
[]
[FluidProperties]
[the_simple_fluid]
type = SimpleFluidProperties
thermal_expansion = 0
bulk_modulus = 2E9
viscosity = 1E-3
density0 = 1000
cv = 4000.0
cp = 4000.0
[]
[]
[PorousFlowFullySaturated]
coupling_type = ThermoHydro
porepressure = porepressure
temperature = temperature
mass_fraction_vars = 'f0 f1 f2'
save_component_rate_in = 'rate_Na rate_Cl rate_SiO2 rate_H2O' # change in kg at every node / dt
fp = the_simple_fluid
temperature_unit = Celsius
[]
[AuxVariables]
[injection_temperature]
initial_condition = 200
[]
[injection_rate_massfrac_Na]
initial_condition = 0.002285946
[]
[injection_rate_massfrac_Cl]
initial_condition = 0.0035252
[]
[injection_rate_massfrac_SiO2]
initial_condition = 1.3741E-05
[]
[injection_rate_massfrac_H2O]
initial_condition = 0.994175112
[]
[rate_H2O]
[]
[rate_Na]
[]
[rate_Cl]
[]
[rate_SiO2]
[]
[]
[Materials]
[porosity]
type = PorousFlowPorosityConst # this simulation has no porosity changes from dissolution
porosity = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-12 0 0 0 1E-12 0 0 0 1E-12'
[]
[thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '0 0 0 0 0 0 0 0 0'
[]
[rock_heat]
type = PorousFlowMatrixInternalEnergy
density = 2500.0
specific_heat_capacity = 1200.0
[]
[]
[Preconditioning]
active = typically_efficient
[typically_efficient]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = ' hypre boomeramg'
[]
[strong]
type = SMP
full = true
petsc_options = '-ksp_diagonal_scale -ksp_diagonal_scale_fix'
petsc_options_iname = '-pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = ' asm ilu NONZERO 2'
[]
[probably_too_strong]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = ' lu mumps'
[]
[]
[Executioner]
type = Transient
solve_type = Newton
end_time = 7.76E6 # 90 days
dt = 1E5
[]
[Outputs]
exodus = true
[]
[MultiApps]
[react]
type = TransientMultiApp
input_files = aquifer_geochemistry.i
clone_master_mesh = true
execute_on = 'timestep_end'
[]
[]
[Transfers]
[changes_due_to_flow]
type = MultiAppCopyTransfer
source_variable = 'rate_H2O rate_Na rate_Cl rate_SiO2 temperature'
variable = 'pf_rate_H2O pf_rate_Na pf_rate_Cl pf_rate_SiO2 temperature'
to_multi_app = react
[]
[massfrac_from_geochem]
type = MultiAppCopyTransfer
source_variable = 'massfrac_Na massfrac_Cl massfrac_SiO2'
variable = 'f0 f1 f2'
from_multi_app = react
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/porous_flow.i)
# PorousFlow simulation of injection and production in a 2D aquifer
# Much of this file is standard porous-flow stuff. The unusual aspects are:
# - transfer of the rates of changes of each species (kg/s) to the aquifer_geochemistry.i simulation. This is achieved by saving these changes from the PorousFlowMassTimeDerivative residuals
# - transfer of the temperature field to the aquifer_geochemistry.i simulation
# Interesting behaviour can be simulated by this file without its "parent" simulation, exchanger.i. exchanger.i provides mass-fractions injected via the injection_rate_massfrac_* variables, but since these are more-or-less constant throughout the duration of the exchanger.i simulation, the initial_conditions specified below may be used. Similar, exchanger.i provides injection_temperature, but that is also constant.
injection_rate = -1.0 # kg/s/m, negative because injection as a source
production_rate = 1.0 # kg/s/m
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[injection_node]
input = gen
type = ExtraNodesetGenerator
new_boundary = injection_node
coord = '-30 0 0'
[]
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[f0]
initial_condition = 0.002285946
[]
[f1]
initial_condition = 0.0035252
[]
[f2]
initial_condition = 1.3741E-05
[]
[porepressure]
initial_condition = 2E6
[]
[temperature]
initial_condition = 50
scaling = 1E-6 # fluid enthalpy is roughly 1E6
[]
[]
[BCs]
[injection_temperature]
type = MatchedValueBC
variable = temperature
v = injection_temperature
boundary = injection_node
[]
[]
[DiracKernels]
[inject_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Na
point_file = injection.bh
variable = f0
[]
[inject_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Cl
point_file = injection.bh
variable = f1
[]
[inject_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_SiO2
point_file = injection.bh
variable = f2
[]
[inject_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_H2O
point_file = injection.bh
variable = porepressure
[]
[produce_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Na
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 0
point_file = production.bh
variable = f0
[]
[produce_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Cl
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 1
point_file = production.bh
variable = f1
[]
[produce_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_SiO2
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 2
point_file = production.bh
variable = f2
[]
[produce_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_H2O
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 3
point_file = production.bh
variable = porepressure
[]
[produce_heat]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_heat
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
use_enthalpy = true
point_file = production.bh
variable = temperature
[]
[]
[UserObjects]
[injected_mass]
type = PorousFlowSumQuantity
[]
[produced_mass_Na]
type = PorousFlowSumQuantity
[]
[produced_mass_Cl]
type = PorousFlowSumQuantity
[]
[produced_mass_SiO2]
type = PorousFlowSumQuantity
[]
[produced_mass_H2O]
type = PorousFlowSumQuantity
[]
[produced_heat]
type = PorousFlowSumQuantity
[]
[]
[Postprocessors]
[dt]
type = TimestepSize
execute_on = TIMESTEP_BEGIN
[]
[tot_kg_injected_this_timestep]
type = PorousFlowPlotQuantity
uo = injected_mass
[]
[kg_Na_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Na
[]
[kg_Cl_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Cl
[]
[kg_SiO2_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_SiO2
[]
[kg_H2O_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_H2O
[]
[mole_rate_Na_produced]
type = FunctionValuePostprocessor
function = moles_Na
indirect_dependencies = 'kg_Na_produced_this_timestep dt'
[]
[mole_rate_Cl_produced]
type = FunctionValuePostprocessor
function = moles_Cl
indirect_dependencies = 'kg_Cl_produced_this_timestep dt'
[]
[mole_rate_SiO2_produced]
type = FunctionValuePostprocessor
function = moles_SiO2
indirect_dependencies = 'kg_SiO2_produced_this_timestep dt'
[]
[mole_rate_H2O_produced]
type = FunctionValuePostprocessor
function = moles_H2O
indirect_dependencies = 'kg_H2O_produced_this_timestep dt'
[]
[heat_joules_extracted_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_heat
[]
[production_temperature]
type = PointValue
point = '30 0 0'
variable = temperature
[]
[]
[Functions]
[moles_Na]
type = ParsedFunction
symbol_names = 'kg_Na dt'
symbol_values = 'kg_Na_produced_this_timestep dt'
expression = 'kg_Na * 1000 / 22.9898 / dt'
[]
[moles_Cl]
type = ParsedFunction
symbol_names = 'kg_Cl dt'
symbol_values = 'kg_Cl_produced_this_timestep dt'
expression = 'kg_Cl * 1000 / 35.453 / dt'
[]
[moles_SiO2]
type = ParsedFunction
symbol_names = 'kg_SiO2 dt'
symbol_values = 'kg_SiO2_produced_this_timestep dt'
expression = 'kg_SiO2 * 1000 / 60.0843 / dt'
[]
[moles_H2O]
type = ParsedFunction
symbol_names = 'kg_H2O dt'
symbol_values = 'kg_H2O_produced_this_timestep dt'
expression = 'kg_H2O * 1000 / 18.0152 / dt'
[]
[]
[FluidProperties]
[the_simple_fluid]
type = SimpleFluidProperties
thermal_expansion = 0
bulk_modulus = 2E9
viscosity = 1E-3
density0 = 1000
cv = 4000.0
cp = 4000.0
[]
[]
[PorousFlowFullySaturated]
coupling_type = ThermoHydro
porepressure = porepressure
temperature = temperature
mass_fraction_vars = 'f0 f1 f2'
save_component_rate_in = 'rate_Na rate_Cl rate_SiO2 rate_H2O' # change in kg at every node / dt
fp = the_simple_fluid
temperature_unit = Celsius
[]
[AuxVariables]
[injection_temperature]
initial_condition = 200
[]
[injection_rate_massfrac_Na]
initial_condition = 0.002285946
[]
[injection_rate_massfrac_Cl]
initial_condition = 0.0035252
[]
[injection_rate_massfrac_SiO2]
initial_condition = 1.3741E-05
[]
[injection_rate_massfrac_H2O]
initial_condition = 0.994175112
[]
[rate_H2O]
[]
[rate_Na]
[]
[rate_Cl]
[]
[rate_SiO2]
[]
[]
[Materials]
[porosity]
type = PorousFlowPorosityConst # this simulation has no porosity changes from dissolution
porosity = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-12 0 0 0 1E-12 0 0 0 1E-12'
[]
[thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '0 0 0 0 0 0 0 0 0'
[]
[rock_heat]
type = PorousFlowMatrixInternalEnergy
density = 2500.0
specific_heat_capacity = 1200.0
[]
[]
[Preconditioning]
active = typically_efficient
[typically_efficient]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = ' hypre boomeramg'
[]
[strong]
type = SMP
full = true
petsc_options = '-ksp_diagonal_scale -ksp_diagonal_scale_fix'
petsc_options_iname = '-pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = ' asm ilu NONZERO 2'
[]
[probably_too_strong]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = ' lu mumps'
[]
[]
[Executioner]
type = Transient
solve_type = Newton
end_time = 7.76E6 # 90 days
dt = 1E5
[]
[Outputs]
exodus = true
[]
[MultiApps]
[react]
type = TransientMultiApp
input_files = aquifer_geochemistry.i
clone_master_mesh = true
execute_on = 'timestep_end'
[]
[]
[Transfers]
[changes_due_to_flow]
type = MultiAppCopyTransfer
source_variable = 'rate_H2O rate_Na rate_Cl rate_SiO2 temperature'
variable = 'pf_rate_H2O pf_rate_Na pf_rate_Cl pf_rate_SiO2 temperature'
to_multi_app = react
[]
[massfrac_from_geochem]
type = MultiAppCopyTransfer
source_variable = 'massfrac_Na massfrac_Cl massfrac_SiO2'
variable = 'f0 f1 f2'
from_multi_app = react
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/porous_flow.i)
# PorousFlow simulation of injection and production in a 2D aquifer
# Much of this file is standard porous-flow stuff. The unusual aspects are:
# - transfer of the rates of changes of each species (kg/s) to the aquifer_geochemistry.i simulation. This is achieved by saving these changes from the PorousFlowMassTimeDerivative residuals
# - transfer of the temperature field to the aquifer_geochemistry.i simulation
# Interesting behaviour can be simulated by this file without its "parent" simulation, exchanger.i. exchanger.i provides mass-fractions injected via the injection_rate_massfrac_* variables, but since these are more-or-less constant throughout the duration of the exchanger.i simulation, the initial_conditions specified below may be used. Similar, exchanger.i provides injection_temperature, but that is also constant.
injection_rate = -1.0 # kg/s/m, negative because injection as a source
production_rate = 1.0 # kg/s/m
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 14 # for better resolution, use 56 or 112
ny = 8 # for better resolution, use 32 or 64
xmin = -70
xmax = 70
ymin = -40
ymax = 40
[]
[injection_node]
input = gen
type = ExtraNodesetGenerator
new_boundary = injection_node
coord = '-30 0 0'
[]
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[f0]
initial_condition = 0.002285946
[]
[f1]
initial_condition = 0.0035252
[]
[f2]
initial_condition = 1.3741E-05
[]
[porepressure]
initial_condition = 2E6
[]
[temperature]
initial_condition = 50
scaling = 1E-6 # fluid enthalpy is roughly 1E6
[]
[]
[BCs]
[injection_temperature]
type = MatchedValueBC
variable = temperature
v = injection_temperature
boundary = injection_node
[]
[]
[DiracKernels]
[inject_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Na
point_file = injection.bh
variable = f0
[]
[inject_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_Cl
point_file = injection.bh
variable = f1
[]
[inject_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_SiO2
point_file = injection.bh
variable = f2
[]
[inject_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = injected_mass
fluxes = ${injection_rate}
p_or_t_vals = 0.0
line_length = 1.0
multiplying_var = injection_rate_massfrac_H2O
point_file = injection.bh
variable = porepressure
[]
[produce_Na]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Na
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 0
point_file = production.bh
variable = f0
[]
[produce_Cl]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_Cl
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 1
point_file = production.bh
variable = f1
[]
[produce_SiO2]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_SiO2
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 2
point_file = production.bh
variable = f2
[]
[produce_H2O]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_mass_H2O
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
mass_fraction_component = 3
point_file = production.bh
variable = porepressure
[]
[produce_heat]
type = PorousFlowPolyLineSink
SumQuantityUO = produced_heat
fluxes = ${production_rate}
p_or_t_vals = 0.0
line_length = 1.0
use_enthalpy = true
point_file = production.bh
variable = temperature
[]
[]
[UserObjects]
[injected_mass]
type = PorousFlowSumQuantity
[]
[produced_mass_Na]
type = PorousFlowSumQuantity
[]
[produced_mass_Cl]
type = PorousFlowSumQuantity
[]
[produced_mass_SiO2]
type = PorousFlowSumQuantity
[]
[produced_mass_H2O]
type = PorousFlowSumQuantity
[]
[produced_heat]
type = PorousFlowSumQuantity
[]
[]
[Postprocessors]
[dt]
type = TimestepSize
execute_on = TIMESTEP_BEGIN
[]
[tot_kg_injected_this_timestep]
type = PorousFlowPlotQuantity
uo = injected_mass
[]
[kg_Na_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Na
[]
[kg_Cl_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_Cl
[]
[kg_SiO2_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_SiO2
[]
[kg_H2O_produced_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_mass_H2O
[]
[mole_rate_Na_produced]
type = FunctionValuePostprocessor
function = moles_Na
indirect_dependencies = 'kg_Na_produced_this_timestep dt'
[]
[mole_rate_Cl_produced]
type = FunctionValuePostprocessor
function = moles_Cl
indirect_dependencies = 'kg_Cl_produced_this_timestep dt'
[]
[mole_rate_SiO2_produced]
type = FunctionValuePostprocessor
function = moles_SiO2
indirect_dependencies = 'kg_SiO2_produced_this_timestep dt'
[]
[mole_rate_H2O_produced]
type = FunctionValuePostprocessor
function = moles_H2O
indirect_dependencies = 'kg_H2O_produced_this_timestep dt'
[]
[heat_joules_extracted_this_timestep]
type = PorousFlowPlotQuantity
uo = produced_heat
[]
[production_temperature]
type = PointValue
point = '30 0 0'
variable = temperature
[]
[]
[Functions]
[moles_Na]
type = ParsedFunction
symbol_names = 'kg_Na dt'
symbol_values = 'kg_Na_produced_this_timestep dt'
expression = 'kg_Na * 1000 / 22.9898 / dt'
[]
[moles_Cl]
type = ParsedFunction
symbol_names = 'kg_Cl dt'
symbol_values = 'kg_Cl_produced_this_timestep dt'
expression = 'kg_Cl * 1000 / 35.453 / dt'
[]
[moles_SiO2]
type = ParsedFunction
symbol_names = 'kg_SiO2 dt'
symbol_values = 'kg_SiO2_produced_this_timestep dt'
expression = 'kg_SiO2 * 1000 / 60.0843 / dt'
[]
[moles_H2O]
type = ParsedFunction
symbol_names = 'kg_H2O dt'
symbol_values = 'kg_H2O_produced_this_timestep dt'
expression = 'kg_H2O * 1000 / 18.0152 / dt'
[]
[]
[FluidProperties]
[the_simple_fluid]
type = SimpleFluidProperties
thermal_expansion = 0
bulk_modulus = 2E9
viscosity = 1E-3
density0 = 1000
cv = 4000.0
cp = 4000.0
[]
[]
[PorousFlowFullySaturated]
coupling_type = ThermoHydro
porepressure = porepressure
temperature = temperature
mass_fraction_vars = 'f0 f1 f2'
save_component_rate_in = 'rate_Na rate_Cl rate_SiO2 rate_H2O' # change in kg at every node / dt
fp = the_simple_fluid
temperature_unit = Celsius
[]
[AuxVariables]
[injection_temperature]
initial_condition = 200
[]
[injection_rate_massfrac_Na]
initial_condition = 0.002285946
[]
[injection_rate_massfrac_Cl]
initial_condition = 0.0035252
[]
[injection_rate_massfrac_SiO2]
initial_condition = 1.3741E-05
[]
[injection_rate_massfrac_H2O]
initial_condition = 0.994175112
[]
[rate_H2O]
[]
[rate_Na]
[]
[rate_Cl]
[]
[rate_SiO2]
[]
[]
[Materials]
[porosity]
type = PorousFlowPorosityConst # this simulation has no porosity changes from dissolution
porosity = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-12 0 0 0 1E-12 0 0 0 1E-12'
[]
[thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '0 0 0 0 0 0 0 0 0'
[]
[rock_heat]
type = PorousFlowMatrixInternalEnergy
density = 2500.0
specific_heat_capacity = 1200.0
[]
[]
[Preconditioning]
active = typically_efficient
[typically_efficient]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = ' hypre boomeramg'
[]
[strong]
type = SMP
full = true
petsc_options = '-ksp_diagonal_scale -ksp_diagonal_scale_fix'
petsc_options_iname = '-pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = ' asm ilu NONZERO 2'
[]
[probably_too_strong]
type = SMP
full = true
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = ' lu mumps'
[]
[]
[Executioner]
type = Transient
solve_type = Newton
end_time = 7.76E6 # 90 days
dt = 1E5
[]
[Outputs]
exodus = true
[]
[MultiApps]
[react]
type = TransientMultiApp
input_files = aquifer_geochemistry.i
clone_master_mesh = true
execute_on = 'timestep_end'
[]
[]
[Transfers]
[changes_due_to_flow]
type = MultiAppCopyTransfer
source_variable = 'rate_H2O rate_Na rate_Cl rate_SiO2 temperature'
variable = 'pf_rate_H2O pf_rate_Na pf_rate_Cl pf_rate_SiO2 temperature'
to_multi_app = react
[]
[massfrac_from_geochem]
type = MultiAppCopyTransfer
source_variable = 'massfrac_Na massfrac_Cl massfrac_SiO2'
variable = 'f0 f1 f2'
from_multi_app = react
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/exchanger.i)
# Model of the heat-exchanger
# The input fluid to the heat exchanger is determined by AuxVariables called production_temperature, production_rate_Na, production_rate_Cl, production_rate_SiO2 and production_rate_H2O. These come from Postprocessors in the porous-flow simulation that measure the fluid composition at the production well.
# Given the input fluid, the exchanger cools/heats the fluid, removing any precipitates, and injects fluid back to the porous-flow simulation at temperature output_temperature and composition given by massfrac_Na, etc.
# In the absence of data concerning Quartz precipitation rates in heat exchangers, do not treat Quartz as kinetic
[GlobalParams]
point = '0 0 0'
reactor = reactor
[]
[TimeDependentReactionSolver]
model_definition = definition
include_moose_solve = false
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
swap_out_of_basis = "SiO2(aq)"
swap_into_basis = "QuartzLike"
constraint_species = "H2O Na+ Cl- QuartzLike"
constraint_value = " 1.0E-2 0.1E-2 0.1E-2 1E-10"
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_mineral"
constraint_unit = " kg moles moles moles"
initial_temperature = 50.0
mode = 4
temperature = 200
cold_temperature = 40.0
source_species_names = 'H2O Na+ Cl- SiO2(aq)'
source_species_rates = 'production_rate_H2O production_rate_Na production_rate_Cl production_rate_SiO2'
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
evaluate_kinetic_rates_always = true # implicit time-marching used for stability
execute_console_output_on = '' # only CSV output used in this example
[]
[UserObjects]
[definition]
type = GeochemicalModelDefinition
database_file = "small_database.json"
basis_species = "H2O SiO2(aq) Na+ Cl-"
equilibrium_minerals = "QuartzLike"
[]
[]
[Executioner]
type = Transient
dt = 1E5
end_time = 2E6 #7.76E6 # 90 days
[]
[AuxVariables]
[production_temperature]
initial_condition = 50 # the production_T Transfer lags one timestep behind for some reason, so give this a reasonable initial condition
[]
[transported_H2O]
[]
[transported_Na]
[]
[transported_Cl]
[]
[transported_SiO2]
[]
[transported_mass]
[]
[massfrac_H2O]
[]
[massfrac_Na]
[]
[massfrac_Cl]
[]
[massfrac_SiO2]
[]
[dumped_quartz]
[]
[production_rate_H2O]
initial_condition = 5.518533e+01 # the production_H2O Transfer lags one timestep behind for some reason (when the porous_flow simulation has finished, it correctly computes mole_rate_H2O_produced, but the Transfer gets the mole_rate_H2O_produced from the previous timestep), so give this a reasonable initial condition, otherwise this will be zero at the start of the simulation!
[]
[production_rate_Na]
initial_condition = 9.943302e-02
[]
[production_rate_Cl]
initial_condition = 9.943302e-02
[]
[production_rate_SiO2]
initial_condition = 2.340931e-04
[]
[]
[AuxKernels]
[transported_H2O_auxk]
type = GeochemistryQuantityAux
variable = transported_H2O
species = H2O
quantity = transported_moles_in_original_basis
[]
[transported_Na]
type = GeochemistryQuantityAux
variable = transported_Na
species = Na+
quantity = transported_moles_in_original_basis
[]
[transported_Cl]
type = GeochemistryQuantityAux
variable = transported_Cl
species = Cl-
quantity = transported_moles_in_original_basis
[]
[transported_SiO2]
type = GeochemistryQuantityAux
variable = transported_SiO2
species = 'SiO2(aq)'
quantity = transported_moles_in_original_basis
[]
[transported_mass_auxk]
type = ParsedAux
coupled_variables = 'transported_H2O transported_Na transported_Cl transported_SiO2'
variable = transported_mass
expression = 'transported_H2O * 18.0152 + transported_Na * 22.9898 + transported_Cl * 35.453 + transported_SiO2 * 60.0843'
[]
[massfrac_H2O]
type = ParsedAux
coupled_variables = 'transported_mass transported_H2O'
variable = massfrac_H2O
expression = '18.0152 * transported_H2O / transported_mass'
[]
[massfrac_Na]
type = ParsedAux
coupled_variables = 'transported_mass transported_Na'
variable = massfrac_Na
expression = '22.9898 * transported_Na / transported_mass'
[]
[massfrac_Cl]
type = ParsedAux
coupled_variables = 'transported_mass transported_Cl'
variable = massfrac_Cl
expression = '35.453 * transported_Cl / transported_mass'
[]
[massfrac_SiO2]
type = ParsedAux
coupled_variables = 'transported_mass transported_SiO2'
variable = massfrac_SiO2
expression = '60.0843 * transported_SiO2 / transported_mass'
[]
[dumped_quartz]
type = GeochemistryQuantityAux
variable = dumped_quartz
species = QuartzLike
quantity = moles_dumped
[]
[]
[Postprocessors]
[cumulative_moles_precipitated_quartz]
type = PointValue
variable = dumped_quartz
[]
[production_temperature]
type = PointValue
variable = production_temperature
[]
[mass_heated_this_timestep]
type = PointValue
variable = transported_mass
[]
[]
[Outputs]
csv = true
[]
[MultiApps]
[porous_flow_sim]
type = TransientMultiApp
input_files = porous_flow.i
execute_on = 'timestep_end'
[]
[]
[Transfers]
[injection_T]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'solution_temperature'
variable = 'injection_temperature'
[]
[injection_Na]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_Na'
variable = 'injection_rate_massfrac_Na'
[]
[injection_Cl]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_Cl'
variable = 'injection_rate_massfrac_Cl'
[]
[injection_SiO2]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_SiO2'
variable = 'injection_rate_massfrac_SiO2'
[]
[injection_H2O]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_H2O'
variable = 'injection_rate_massfrac_H2O'
[]
[production_T]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = production_temperature
variable = production_temperature
[]
[production_Na]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_Na_produced
variable = production_rate_Na
[]
[production_Cl]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_Cl_produced
variable = production_rate_Cl
[]
[production_SiO2]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_SiO2_produced
variable = production_rate_SiO2
[]
[production_H2O]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_H2O_produced
variable = production_rate_H2O
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/exchanger.i)
# Model of the heat-exchanger
# The input fluid to the heat exchanger is determined by AuxVariables called production_temperature, production_rate_Na, production_rate_Cl, production_rate_SiO2 and production_rate_H2O. These come from Postprocessors in the porous-flow simulation that measure the fluid composition at the production well.
# Given the input fluid, the exchanger cools/heats the fluid, removing any precipitates, and injects fluid back to the porous-flow simulation at temperature output_temperature and composition given by massfrac_Na, etc.
# In the absence of data concerning Quartz precipitation rates in heat exchangers, do not treat Quartz as kinetic
[GlobalParams]
point = '0 0 0'
reactor = reactor
[]
[TimeDependentReactionSolver]
model_definition = definition
include_moose_solve = false
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
swap_out_of_basis = "SiO2(aq)"
swap_into_basis = "QuartzLike"
constraint_species = "H2O Na+ Cl- QuartzLike"
constraint_value = " 1.0E-2 0.1E-2 0.1E-2 1E-10"
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_mineral"
constraint_unit = " kg moles moles moles"
initial_temperature = 50.0
mode = 4
temperature = 200
cold_temperature = 40.0
source_species_names = 'H2O Na+ Cl- SiO2(aq)'
source_species_rates = 'production_rate_H2O production_rate_Na production_rate_Cl production_rate_SiO2'
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
evaluate_kinetic_rates_always = true # implicit time-marching used for stability
execute_console_output_on = '' # only CSV output used in this example
[]
[UserObjects]
[definition]
type = GeochemicalModelDefinition
database_file = "small_database.json"
basis_species = "H2O SiO2(aq) Na+ Cl-"
equilibrium_minerals = "QuartzLike"
[]
[]
[Executioner]
type = Transient
dt = 1E5
end_time = 2E6 #7.76E6 # 90 days
[]
[AuxVariables]
[production_temperature]
initial_condition = 50 # the production_T Transfer lags one timestep behind for some reason, so give this a reasonable initial condition
[]
[transported_H2O]
[]
[transported_Na]
[]
[transported_Cl]
[]
[transported_SiO2]
[]
[transported_mass]
[]
[massfrac_H2O]
[]
[massfrac_Na]
[]
[massfrac_Cl]
[]
[massfrac_SiO2]
[]
[dumped_quartz]
[]
[production_rate_H2O]
initial_condition = 5.518533e+01 # the production_H2O Transfer lags one timestep behind for some reason (when the porous_flow simulation has finished, it correctly computes mole_rate_H2O_produced, but the Transfer gets the mole_rate_H2O_produced from the previous timestep), so give this a reasonable initial condition, otherwise this will be zero at the start of the simulation!
[]
[production_rate_Na]
initial_condition = 9.943302e-02
[]
[production_rate_Cl]
initial_condition = 9.943302e-02
[]
[production_rate_SiO2]
initial_condition = 2.340931e-04
[]
[]
[AuxKernels]
[transported_H2O_auxk]
type = GeochemistryQuantityAux
variable = transported_H2O
species = H2O
quantity = transported_moles_in_original_basis
[]
[transported_Na]
type = GeochemistryQuantityAux
variable = transported_Na
species = Na+
quantity = transported_moles_in_original_basis
[]
[transported_Cl]
type = GeochemistryQuantityAux
variable = transported_Cl
species = Cl-
quantity = transported_moles_in_original_basis
[]
[transported_SiO2]
type = GeochemistryQuantityAux
variable = transported_SiO2
species = 'SiO2(aq)'
quantity = transported_moles_in_original_basis
[]
[transported_mass_auxk]
type = ParsedAux
coupled_variables = 'transported_H2O transported_Na transported_Cl transported_SiO2'
variable = transported_mass
expression = 'transported_H2O * 18.0152 + transported_Na * 22.9898 + transported_Cl * 35.453 + transported_SiO2 * 60.0843'
[]
[massfrac_H2O]
type = ParsedAux
coupled_variables = 'transported_mass transported_H2O'
variable = massfrac_H2O
expression = '18.0152 * transported_H2O / transported_mass'
[]
[massfrac_Na]
type = ParsedAux
coupled_variables = 'transported_mass transported_Na'
variable = massfrac_Na
expression = '22.9898 * transported_Na / transported_mass'
[]
[massfrac_Cl]
type = ParsedAux
coupled_variables = 'transported_mass transported_Cl'
variable = massfrac_Cl
expression = '35.453 * transported_Cl / transported_mass'
[]
[massfrac_SiO2]
type = ParsedAux
coupled_variables = 'transported_mass transported_SiO2'
variable = massfrac_SiO2
expression = '60.0843 * transported_SiO2 / transported_mass'
[]
[dumped_quartz]
type = GeochemistryQuantityAux
variable = dumped_quartz
species = QuartzLike
quantity = moles_dumped
[]
[]
[Postprocessors]
[cumulative_moles_precipitated_quartz]
type = PointValue
variable = dumped_quartz
[]
[production_temperature]
type = PointValue
variable = production_temperature
[]
[mass_heated_this_timestep]
type = PointValue
variable = transported_mass
[]
[]
[Outputs]
csv = true
[]
[MultiApps]
[porous_flow_sim]
type = TransientMultiApp
input_files = porous_flow.i
execute_on = 'timestep_end'
[]
[]
[Transfers]
[injection_T]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'solution_temperature'
variable = 'injection_temperature'
[]
[injection_Na]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_Na'
variable = 'injection_rate_massfrac_Na'
[]
[injection_Cl]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_Cl'
variable = 'injection_rate_massfrac_Cl'
[]
[injection_SiO2]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_SiO2'
variable = 'injection_rate_massfrac_SiO2'
[]
[injection_H2O]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_H2O'
variable = 'injection_rate_massfrac_H2O'
[]
[production_T]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = production_temperature
variable = production_temperature
[]
[production_Na]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_Na_produced
variable = production_rate_Na
[]
[production_Cl]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_Cl_produced
variable = production_rate_Cl
[]
[production_SiO2]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_SiO2_produced
variable = production_rate_SiO2
[]
[production_H2O]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_H2O_produced
variable = production_rate_H2O
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/exchanger.i)
# Model of the heat-exchanger
# The input fluid to the heat exchanger is determined by AuxVariables called production_temperature, production_rate_Na, production_rate_Cl, production_rate_SiO2 and production_rate_H2O. These come from Postprocessors in the porous-flow simulation that measure the fluid composition at the production well.
# Given the input fluid, the exchanger cools/heats the fluid, removing any precipitates, and injects fluid back to the porous-flow simulation at temperature output_temperature and composition given by massfrac_Na, etc.
# In the absence of data concerning Quartz precipitation rates in heat exchangers, do not treat Quartz as kinetic
[GlobalParams]
point = '0 0 0'
reactor = reactor
[]
[TimeDependentReactionSolver]
model_definition = definition
include_moose_solve = false
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
swap_out_of_basis = "SiO2(aq)"
swap_into_basis = "QuartzLike"
constraint_species = "H2O Na+ Cl- QuartzLike"
constraint_value = " 1.0E-2 0.1E-2 0.1E-2 1E-10"
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_mineral"
constraint_unit = " kg moles moles moles"
initial_temperature = 50.0
mode = 4
temperature = 200
cold_temperature = 40.0
source_species_names = 'H2O Na+ Cl- SiO2(aq)'
source_species_rates = 'production_rate_H2O production_rate_Na production_rate_Cl production_rate_SiO2'
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
evaluate_kinetic_rates_always = true # implicit time-marching used for stability
execute_console_output_on = '' # only CSV output used in this example
[]
[UserObjects]
[definition]
type = GeochemicalModelDefinition
database_file = "small_database.json"
basis_species = "H2O SiO2(aq) Na+ Cl-"
equilibrium_minerals = "QuartzLike"
[]
[]
[Executioner]
type = Transient
dt = 1E5
end_time = 2E6 #7.76E6 # 90 days
[]
[AuxVariables]
[production_temperature]
initial_condition = 50 # the production_T Transfer lags one timestep behind for some reason, so give this a reasonable initial condition
[]
[transported_H2O]
[]
[transported_Na]
[]
[transported_Cl]
[]
[transported_SiO2]
[]
[transported_mass]
[]
[massfrac_H2O]
[]
[massfrac_Na]
[]
[massfrac_Cl]
[]
[massfrac_SiO2]
[]
[dumped_quartz]
[]
[production_rate_H2O]
initial_condition = 5.518533e+01 # the production_H2O Transfer lags one timestep behind for some reason (when the porous_flow simulation has finished, it correctly computes mole_rate_H2O_produced, but the Transfer gets the mole_rate_H2O_produced from the previous timestep), so give this a reasonable initial condition, otherwise this will be zero at the start of the simulation!
[]
[production_rate_Na]
initial_condition = 9.943302e-02
[]
[production_rate_Cl]
initial_condition = 9.943302e-02
[]
[production_rate_SiO2]
initial_condition = 2.340931e-04
[]
[]
[AuxKernels]
[transported_H2O_auxk]
type = GeochemistryQuantityAux
variable = transported_H2O
species = H2O
quantity = transported_moles_in_original_basis
[]
[transported_Na]
type = GeochemistryQuantityAux
variable = transported_Na
species = Na+
quantity = transported_moles_in_original_basis
[]
[transported_Cl]
type = GeochemistryQuantityAux
variable = transported_Cl
species = Cl-
quantity = transported_moles_in_original_basis
[]
[transported_SiO2]
type = GeochemistryQuantityAux
variable = transported_SiO2
species = 'SiO2(aq)'
quantity = transported_moles_in_original_basis
[]
[transported_mass_auxk]
type = ParsedAux
coupled_variables = 'transported_H2O transported_Na transported_Cl transported_SiO2'
variable = transported_mass
expression = 'transported_H2O * 18.0152 + transported_Na * 22.9898 + transported_Cl * 35.453 + transported_SiO2 * 60.0843'
[]
[massfrac_H2O]
type = ParsedAux
coupled_variables = 'transported_mass transported_H2O'
variable = massfrac_H2O
expression = '18.0152 * transported_H2O / transported_mass'
[]
[massfrac_Na]
type = ParsedAux
coupled_variables = 'transported_mass transported_Na'
variable = massfrac_Na
expression = '22.9898 * transported_Na / transported_mass'
[]
[massfrac_Cl]
type = ParsedAux
coupled_variables = 'transported_mass transported_Cl'
variable = massfrac_Cl
expression = '35.453 * transported_Cl / transported_mass'
[]
[massfrac_SiO2]
type = ParsedAux
coupled_variables = 'transported_mass transported_SiO2'
variable = massfrac_SiO2
expression = '60.0843 * transported_SiO2 / transported_mass'
[]
[dumped_quartz]
type = GeochemistryQuantityAux
variable = dumped_quartz
species = QuartzLike
quantity = moles_dumped
[]
[]
[Postprocessors]
[cumulative_moles_precipitated_quartz]
type = PointValue
variable = dumped_quartz
[]
[production_temperature]
type = PointValue
variable = production_temperature
[]
[mass_heated_this_timestep]
type = PointValue
variable = transported_mass
[]
[]
[Outputs]
csv = true
[]
[MultiApps]
[porous_flow_sim]
type = TransientMultiApp
input_files = porous_flow.i
execute_on = 'timestep_end'
[]
[]
[Transfers]
[injection_T]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'solution_temperature'
variable = 'injection_temperature'
[]
[injection_Na]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_Na'
variable = 'injection_rate_massfrac_Na'
[]
[injection_Cl]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_Cl'
variable = 'injection_rate_massfrac_Cl'
[]
[injection_SiO2]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_SiO2'
variable = 'injection_rate_massfrac_SiO2'
[]
[injection_H2O]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_H2O'
variable = 'injection_rate_massfrac_H2O'
[]
[production_T]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = production_temperature
variable = production_temperature
[]
[production_Na]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_Na_produced
variable = production_rate_Na
[]
[production_Cl]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_Cl_produced
variable = production_rate_Cl
[]
[production_SiO2]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_SiO2_produced
variable = production_rate_SiO2
[]
[production_H2O]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_H2O_produced
variable = production_rate_H2O
[]
[]
(modules/combined/examples/geochem-porous_flow/geotes_2D/exchanger.i)
# Model of the heat-exchanger
# The input fluid to the heat exchanger is determined by AuxVariables called production_temperature, production_rate_Na, production_rate_Cl, production_rate_SiO2 and production_rate_H2O. These come from Postprocessors in the porous-flow simulation that measure the fluid composition at the production well.
# Given the input fluid, the exchanger cools/heats the fluid, removing any precipitates, and injects fluid back to the porous-flow simulation at temperature output_temperature and composition given by massfrac_Na, etc.
# In the absence of data concerning Quartz precipitation rates in heat exchangers, do not treat Quartz as kinetic
[GlobalParams]
point = '0 0 0'
reactor = reactor
[]
[TimeDependentReactionSolver]
model_definition = definition
include_moose_solve = false
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
swap_out_of_basis = "SiO2(aq)"
swap_into_basis = "QuartzLike"
constraint_species = "H2O Na+ Cl- QuartzLike"
constraint_value = " 1.0E-2 0.1E-2 0.1E-2 1E-10"
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_mineral"
constraint_unit = " kg moles moles moles"
initial_temperature = 50.0
mode = 4
temperature = 200
cold_temperature = 40.0
source_species_names = 'H2O Na+ Cl- SiO2(aq)'
source_species_rates = 'production_rate_H2O production_rate_Na production_rate_Cl production_rate_SiO2'
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
evaluate_kinetic_rates_always = true # implicit time-marching used for stability
execute_console_output_on = '' # only CSV output used in this example
[]
[UserObjects]
[definition]
type = GeochemicalModelDefinition
database_file = "small_database.json"
basis_species = "H2O SiO2(aq) Na+ Cl-"
equilibrium_minerals = "QuartzLike"
[]
[]
[Executioner]
type = Transient
dt = 1E5
end_time = 2E6 #7.76E6 # 90 days
[]
[AuxVariables]
[production_temperature]
initial_condition = 50 # the production_T Transfer lags one timestep behind for some reason, so give this a reasonable initial condition
[]
[transported_H2O]
[]
[transported_Na]
[]
[transported_Cl]
[]
[transported_SiO2]
[]
[transported_mass]
[]
[massfrac_H2O]
[]
[massfrac_Na]
[]
[massfrac_Cl]
[]
[massfrac_SiO2]
[]
[dumped_quartz]
[]
[production_rate_H2O]
initial_condition = 5.518533e+01 # the production_H2O Transfer lags one timestep behind for some reason (when the porous_flow simulation has finished, it correctly computes mole_rate_H2O_produced, but the Transfer gets the mole_rate_H2O_produced from the previous timestep), so give this a reasonable initial condition, otherwise this will be zero at the start of the simulation!
[]
[production_rate_Na]
initial_condition = 9.943302e-02
[]
[production_rate_Cl]
initial_condition = 9.943302e-02
[]
[production_rate_SiO2]
initial_condition = 2.340931e-04
[]
[]
[AuxKernels]
[transported_H2O_auxk]
type = GeochemistryQuantityAux
variable = transported_H2O
species = H2O
quantity = transported_moles_in_original_basis
[]
[transported_Na]
type = GeochemistryQuantityAux
variable = transported_Na
species = Na+
quantity = transported_moles_in_original_basis
[]
[transported_Cl]
type = GeochemistryQuantityAux
variable = transported_Cl
species = Cl-
quantity = transported_moles_in_original_basis
[]
[transported_SiO2]
type = GeochemistryQuantityAux
variable = transported_SiO2
species = 'SiO2(aq)'
quantity = transported_moles_in_original_basis
[]
[transported_mass_auxk]
type = ParsedAux
coupled_variables = 'transported_H2O transported_Na transported_Cl transported_SiO2'
variable = transported_mass
expression = 'transported_H2O * 18.0152 + transported_Na * 22.9898 + transported_Cl * 35.453 + transported_SiO2 * 60.0843'
[]
[massfrac_H2O]
type = ParsedAux
coupled_variables = 'transported_mass transported_H2O'
variable = massfrac_H2O
expression = '18.0152 * transported_H2O / transported_mass'
[]
[massfrac_Na]
type = ParsedAux
coupled_variables = 'transported_mass transported_Na'
variable = massfrac_Na
expression = '22.9898 * transported_Na / transported_mass'
[]
[massfrac_Cl]
type = ParsedAux
coupled_variables = 'transported_mass transported_Cl'
variable = massfrac_Cl
expression = '35.453 * transported_Cl / transported_mass'
[]
[massfrac_SiO2]
type = ParsedAux
coupled_variables = 'transported_mass transported_SiO2'
variable = massfrac_SiO2
expression = '60.0843 * transported_SiO2 / transported_mass'
[]
[dumped_quartz]
type = GeochemistryQuantityAux
variable = dumped_quartz
species = QuartzLike
quantity = moles_dumped
[]
[]
[Postprocessors]
[cumulative_moles_precipitated_quartz]
type = PointValue
variable = dumped_quartz
[]
[production_temperature]
type = PointValue
variable = production_temperature
[]
[mass_heated_this_timestep]
type = PointValue
variable = transported_mass
[]
[]
[Outputs]
csv = true
[]
[MultiApps]
[porous_flow_sim]
type = TransientMultiApp
input_files = porous_flow.i
execute_on = 'timestep_end'
[]
[]
[Transfers]
[injection_T]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'solution_temperature'
variable = 'injection_temperature'
[]
[injection_Na]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_Na'
variable = 'injection_rate_massfrac_Na'
[]
[injection_Cl]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_Cl'
variable = 'injection_rate_massfrac_Cl'
[]
[injection_SiO2]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_SiO2'
variable = 'injection_rate_massfrac_SiO2'
[]
[injection_H2O]
type = MultiAppNearestNodeTransfer
direction = TO_MULTIAPP
multi_app = porous_flow_sim
fixed_meshes = true
source_variable = 'massfrac_H2O'
variable = 'injection_rate_massfrac_H2O'
[]
[production_T]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = production_temperature
variable = production_temperature
[]
[production_Na]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_Na_produced
variable = production_rate_Na
[]
[production_Cl]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_Cl_produced
variable = production_rate_Cl
[]
[production_SiO2]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_SiO2_produced
variable = production_rate_SiO2
[]
[production_H2O]
type = MultiAppPostprocessorInterpolationTransfer
direction = FROM_MULTIAPP
multi_app = porous_flow_sim
postprocessor = mole_rate_H2O_produced
variable = production_rate_H2O
[]
[]