Quartz deposition in a fracture
Section 26.2 of Bethke (2007) describes quartz deposition in a hydrothermal fracture. The setup is similar to quartz dissolution but with a different form of the reaction rate. The reaction is with rate It is assumed that:
there is 1kg of water;
the initial temperature is 300C and this steadily reduces to 25C over the course of 1 year;
the mineral quartz is used instead of SiO(aq) in the basis initially while quartz is an equilibrium mineral (before it is kinetically-controlled);
initially 400g (6.657313mol) of quartz is added to the water;
the specific surface area is cm/g(quartz);
the activation energy is J.mol;
all other silica-containing minerals are prevented from precipitating.
MOOSE input file: stage 1
The MOOSE simulation is in 2 stages. The first determines the molality of SiO2(aq) that is in equilibrium with the quartz. This is necessary because the problem description assumes that the water has had enough time to equilibrate with the quartz mineral at 300C, and in this stage the quartz mineral is not governed by a kinetic rate.
The system described in the input file also includes very small amounts of Na and Cl. These do not impact the results but are necessary because the geochemistry module requires a charge-balance species to be defined.
# Finds the equilibrium free-concentration of SiO2(aq) in contact with Quartz at 300degC
[TimeIndependentReactionSolver]
model_definition = definition
geochemistry_reactor_name = reactor
swap_into_basis = "Quartz"
swap_out_of_basis = "SiO2(aq)"
charge_balance_species = "Cl-"
constraint_species = "H2O Na+ Cl- Quartz"
# the amount of free quartz is irrelevant to the equilibrium system, provided it is large enough, but here 400g is used to make the connection with quartz_deposition.i
constraint_value = " 1.0 1E-10 1E-10 0.4"
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_mineral"
constraint_unit = " kg moles moles kg"
temperature = 300.0
add_aux_pH = false # there is no H+ in this system
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
[]
[UserObjects]
[definition]
type = GeochemicalModelDefinition
database_file = "../../../database/moose_geochemdb.json"
basis_species = "H2O SiO2(aq) Na+ Cl-"
equilibrium_minerals = "Quartz"
[]
[]
The output of this simulation is that the molality of SiO2(aq) is 0.009723mol.
MOOSE input file: stage 2
The second stage uses this molality and performs the time-dependent simulation, as the temperature is reduced. The GeochemistryKineticRate is defined:
[rate_quartz]
type = GeochemistryKineticRate
kinetic_species_name = Quartz
intrinsic_rate_constant = 7.4112E2 # 2.35E-5mol/s/cm^2 = 7.411E2mol/yr/cm^2
multiply_by_mass = true
area_quantity = 1
activation_energy = 72800.0
[]
The TimeDependentReactionSolver defines the free molality of SiO2(aq) at the initial time, the initial mole number of quartz and that the temperature is controlled using the temp_controller AuxVariable:
[TimeDependentReactionSolver]
model_definition = definition
geochemistry_reactor_name = reactor
charge_balance_species = "Cl-"
constraint_species = "H2O Na+ Cl- SiO2(aq)"
constraint_value = " 1.0 1E-10 1E-10 0.009722905"
constraint_meaning = "kg_solvent_water bulk_composition bulk_composition free_concentration"
constraint_unit = " kg moles moles molal"
initial_temperature = 300.0
temperature = temp_controller
kinetic_species_name = Quartz
kinetic_species_initial_value = 400
kinetic_species_unit = g
ramp_max_ionic_strength_initial = 0 # max_ionic_strength in such a simple problem does not need ramping
add_aux_pH = false # there is no H+ in this system
evaluate_kinetic_rates_always = true # implicit time-marching used for stability
execute_console_output_on = '' # only CSV output used in this example
[]
The temperature controller is:
[temp_controller_auxk]
type = FunctionAux
function = '300 - 275 * t'
variable = temp_controller
execute_on = 'timestep_begin'
[]
with time defined through:
[Executioner]
type = Transient
dt = 0.02
end_time = 1 # measured in years
[]
The figures below were generated using a time-step of 0.001yr. A set of AuxVariables and Postprocessors define the desired output using the mg_per_kg_SiO2(aq) variable automatically included by the TimeDependentReactionSolver:
[AuxVariables]
[temp_controller]
[]
[diss_rate]
[]
[]
[AuxKernels]
[temp_controller_auxk]
type = FunctionAux
function = '300 - 275 * t'
variable = temp_controller
execute_on = 'timestep_begin'
[]
[diss_rate]
type = ParsedAux
coupled_variables = mol_change_Quartz
expression = '-mol_change_Quartz / 0.02' # 0.02 = timestep size
variable = diss_rate
[]
[]
[Postprocessors]
[mg_per_kg_sio2]
type = PointValue
variable = "mg_per_kg_SiO2(aq)"
[]
[rate_mole_per_year]
type = PointValue
variable = diss_rate
[]
[temperature]
type = PointValue
variable = "solution_temperature"
[]
[]
[Outputs]
csv = true
[]
GWB input file
The equivalent Geochemists Workbench file is
# React script that is equivalent to quartz_deposition.i
time end = 1 year
T initial = 300, final = 25
swap Quartz for SiO2(aq)
400 free grams Quartz
kinetic Quartz surface = 1
kinetic Quartz pre-exp = 2.35e-5, act_eng = 72800
suppress Tridymite Chalcedony Cristobalite Amrph^silica
delxi = 0.001
go
Results
Bethke (2007) presents results in Figures 26.3 and 26.4, which look like:
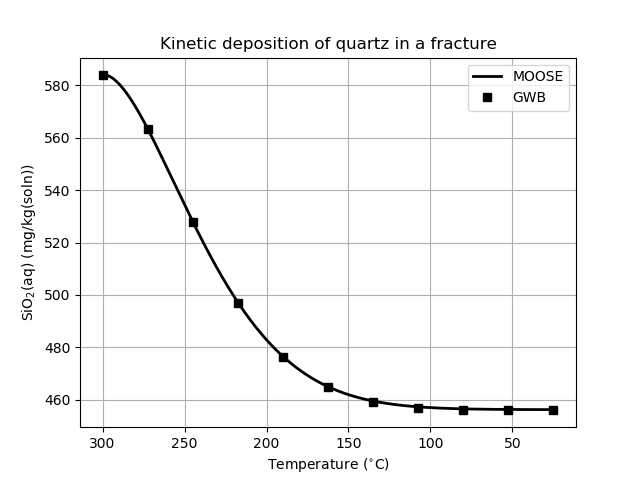
Figure 1: Change in free mass of SiO2(aq) as fluid flows through a fracture, changing temperature as it does so. Compare with Bethke's Figure 26.3
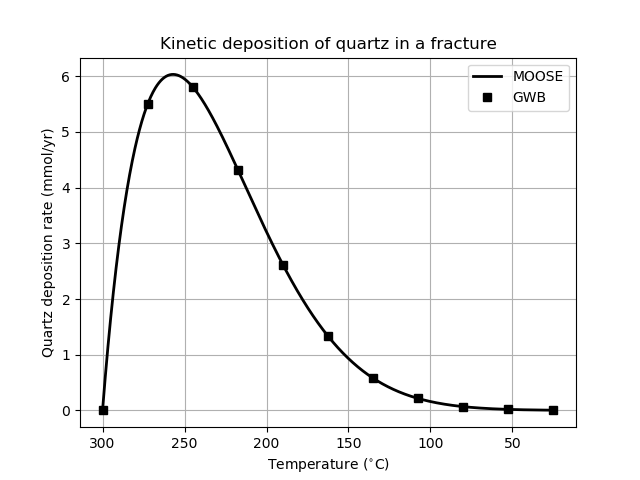
Figure 2: Quartz reaction rate as fluid flows through a fracture, changing temperature as it does so. Compare with Bethke's Figure 26.4
The accuracy of the geochemistry simulation depends on the time-step size. The above figures were generated using a step size of 0.001yr.
References
- Craig M. Bethke.
Geochemical and Biogeochemical Reaction Modeling.
Cambridge University Press, 2 edition, 2007.
doi:10.1017/CBO9780511619670.[BibTeX]