Three-dimensional (Berkovich) frictional spherical indenter
A three-dimensional problem is used to model the penetration of a Berkovich indenter into a crystal-plasticity base material.
Background
Indentation tests are often used to characterize the behavior of materials at small scales. In this example, we use a Berkovich indenter driven by a prescribed displacement as a boundary condition. Frictional contact with a node-on-face formulation is employed to drive the base material deformation. As a result, a load displacement curve can be obtained.
Creating contact input
This example represents an extension of Two-dimensional frictional spherical indenter (node-face) to three dimensions.
primary and secondary surfaces are created from mesh sidesets. The formulation is tangential_penalty which employs a kinematic approach in the normal direction and a penalty one in the tangential directions.
[Contact]
[./ind_base]
primary = 202
secondary = 102
model = coulomb
friction_coefficient = 0.4
normalize_penalty = true
formulation = tangential_penalty
penalty = 1e7
capture_tolerance = 0.0001
[../]
Fig. 1: Indentation animation (indenter represented as a cyan wireframe). Pile-up takes place causing deformation along the positive Z direction, see dark color in animation.
Critical to the convergence of this frictional problem is the use of ContactSlipDamper, which controls the stick-slip behavior of the many nodes in contact at nonlinear iterations.
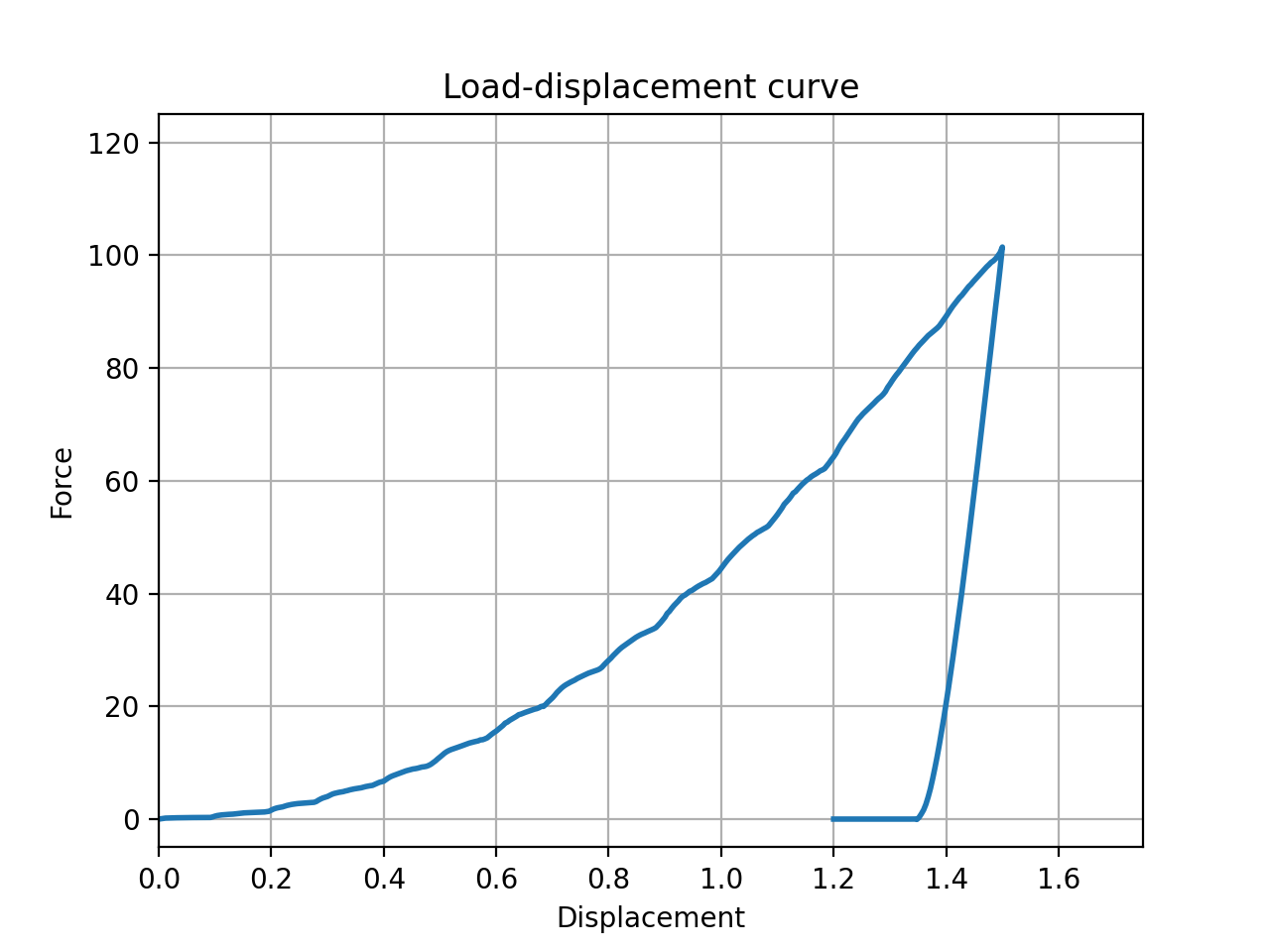
Fig. 2: Load-displacement curve.
Numerical results
The resulting force exerted as material resistance on the indenter may be plotted against the vertical displacement. In this problem, the base material is a monocrystal with body-centered cubic (bcc) unit cell with arbitrary parameters.
Crystal plasticity parameters can be calibrated to match a given experimental nano-indentation test. For this example, the load-displacement curve is shown in Fig. 2.
Note:
Element distortions become large. This may have some impact on the numerical results.