Two-dimensional frictional spherical indenter (node-face)
A two-dimensional problem with RZ symmetry is used to model the penetration of a spherical indenter into an inelastic base material.
Background
Indentation tests are often used to characterize the behavior of materials at small scales. In this example, we use a spherical indenter driven by a prescribed displacement imposed as a boundary condition. Frictional contact with a node-on-face formulation is employed to drive base material deformation. As a result, a load displacement curve can be obtained.
An example of the use of two-dimensional mortar mechanical contact can be consulted in Two-dimensional spherical indenter (mortar).
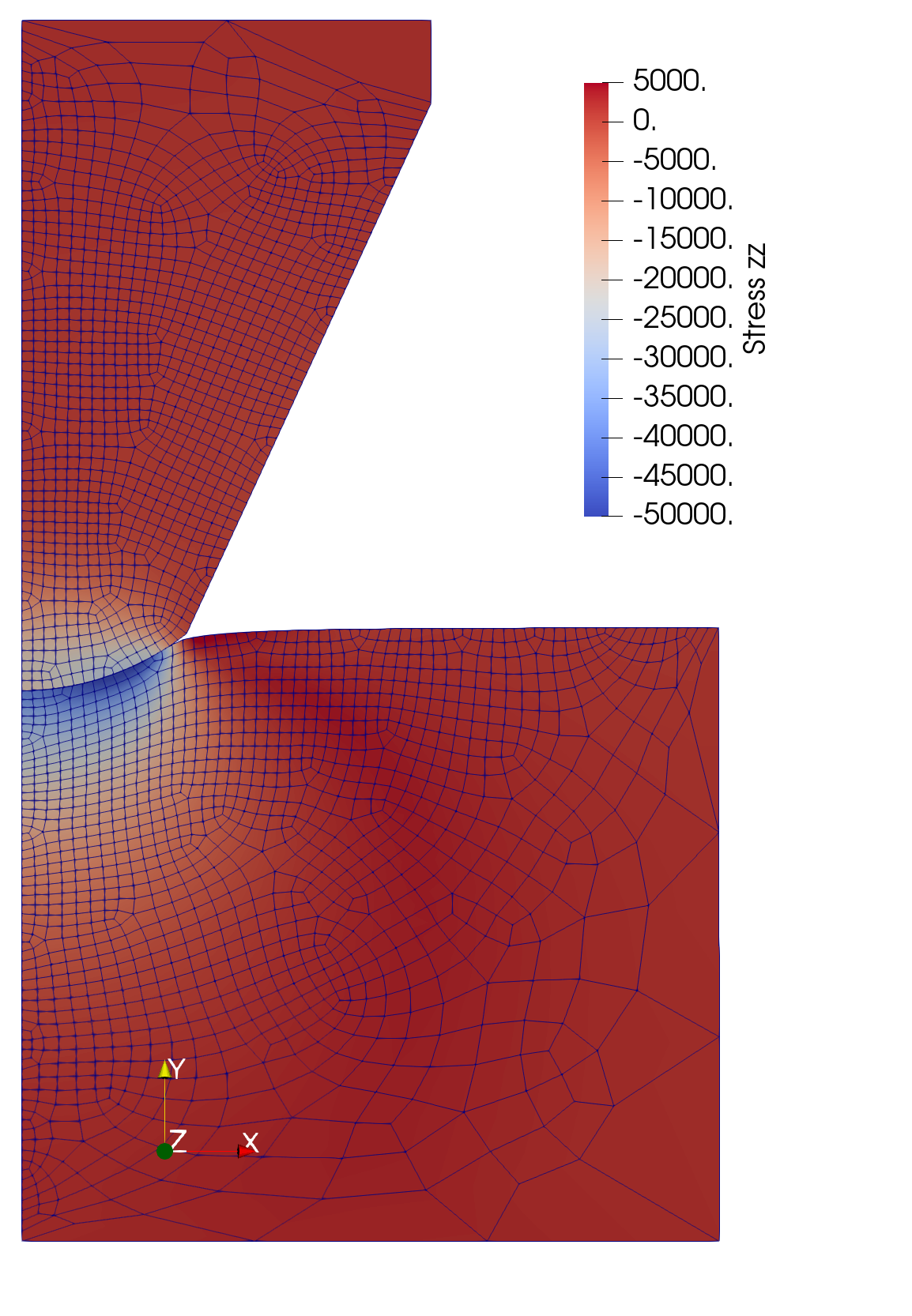
Fig. 1: Snapshot of indentation process.
Creating contact input
The Contact input block allows the user to select the primary and secondary surfaces; the formulation type: kinematic, penalty, and tangential_penalty; and the penalty_factor. This input parameter will determine the amount of interpenetration between the contacting surfaces. In order to make the penalty factor consistent among all the element surfaces into contact, it is recommended to select normalize_penalty = true, which ensures the penalty factor per area unit is constant throughout the simulation. Finally, tangential_tolerance is a real number that represents an additional length to be considered during the contact search. This value is usually taken to be a fraction of a characteristic element length, and ensures edge contact is not missed.
[Contact]
[./dummy_name]
primary = 6
secondary = 4
model = coulomb
formulation = penalty
normalize_penalty = true
friction_coefficient = 0.5
penalty = 8e6
tangential_tolerance = 0.005
[../]
The use of friction introduces complexity in the states of the nodes in contact. Namely, if a node tangential forces surpasses its frictional capacity, it will slip; otherwise, it will stick to the primary surface. This behavior hinders convergence because a node state can change from one iteration to the next, preventing the system residual from reaching reasonable tolerance values. A heuristic countermeasure is implemented in ContactSlipDamper. Based on some optional parameters, the slip damper controls the stick/slip state changes such that this ping-ponging is dampened. In this problem, the use of the ContactSlipDamper significantly helps convergence.
[Dampers]
[./contact_slip]
type = ContactSlipDamper
secondary = 4
primary = 6
[../]
Other input
The problem is axisymmetric Compute Axisymmetric RZ Finite Strain and symmetric boundary conditions are used.
Numerical results
The resulting force exerted as material resistance on the indenter may be plotted against the vertical displacement. In this problem, the base material behaves according to a creep law. The maximum material deformation is relatively low which allows for a smooth load-displacement curve, as depicted in Fig. 2.
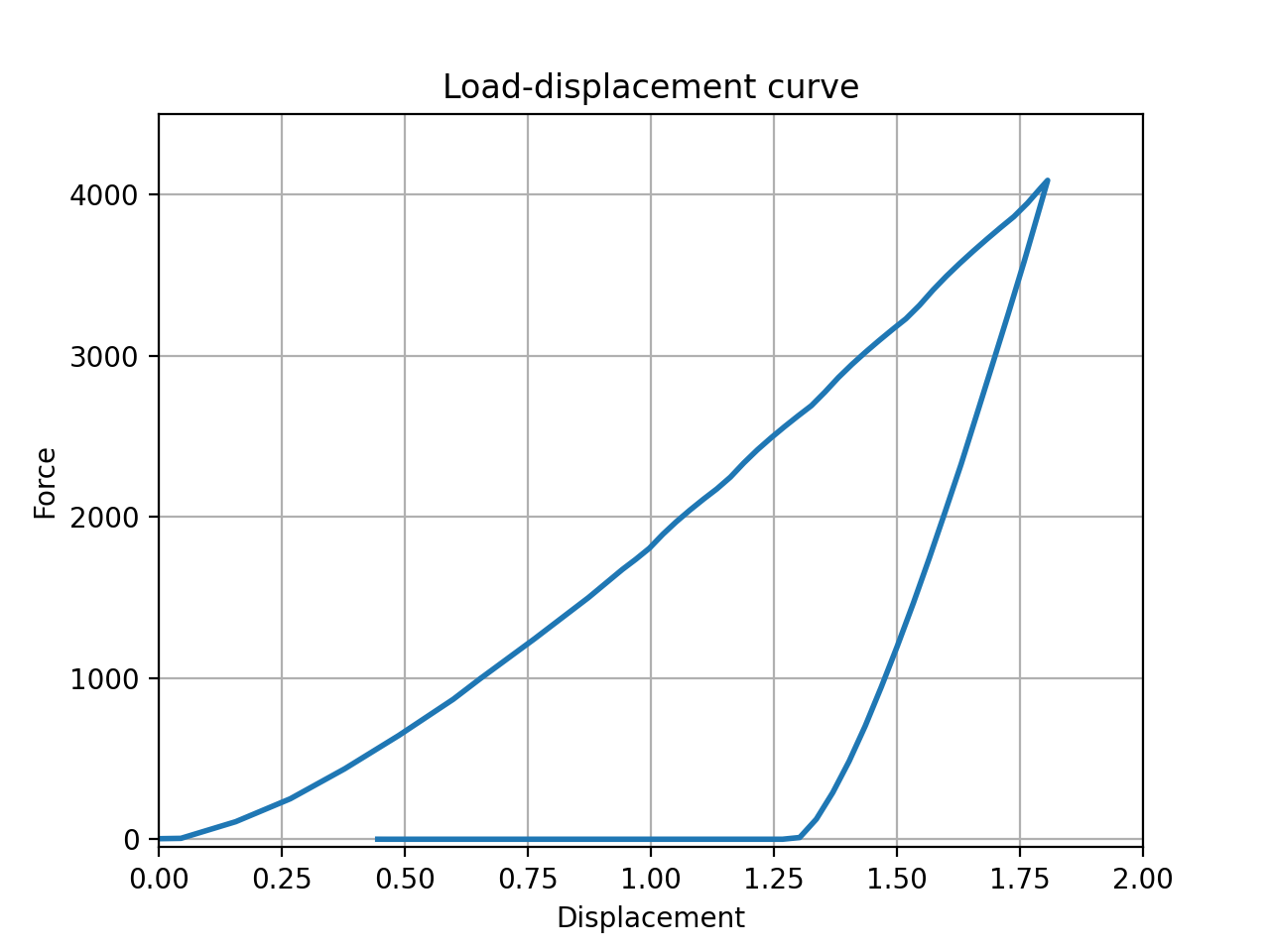
Fig. 2: Load-displacement curve.
Creep material model parameters can be calibrated to match a given experimental nano-indentation test.
Notes:
Indenter geometry does not reproduce that of a real problem's. Its geometry can be modified in the journal file.
Element distortions may become large