Fracture flow using a MultiApp approach: Primer
Background
PorousFlow can be used to simulate flow through fractured porous media in the case when the fracture network is so complicated it cannot be incorporated into the porous-media mesh. The fundamental premise is the fractures can be considered as lower dimensional entities within the higher-dimensional porous media. This page is part of a set that describes a MOOSE MultiApp approach to simulating such models:
MultiApp primer: the diffusion equation with no fractures, and quantifying the errors introduced by the MultiApp approach
Primer using the diffusion equation with no fractures
Before considering porous flow in a mixed-dimensional fracture-matrix system, consider the simpler situation involving two coupled diffusion equations in 1D. Hence there is no "fracture" and "matrix" in this section: the labels "f" and "m" simply distinguish two different variables, and the dimensionality is all one dimensional. Assume physical parameters have been chosen appropriately so that (see the page desribing mathematics and physics of heat transfer)
It is important that the same numerical value of is used in both formulae, otherwise heat energy would not be conserved in this system.
In this section, assume the boundary conditions are and the initial conditions are where is the Dirac delta functions. These conditions make the analytic solution easy to derive.
Physically, this system represents the situation in which the system is initially provided with a unit of heat energy at , and that heat energy is allowed to disperse under diffusion, and transfer to the system, which also disperses it. To derive the solution, the sum of the two governing equations yields the standard diffusion equation (which may be solved using the fundamental solution), while the difference yields the diffusion equation augmented with a decay term. The final result is: (1)
A single variable (no heat transfer)
When , the system becomes decoupled and no heat will be transferred from the fracture to the matrix. The solution is , and given by the fundamental solution. This may be solved by MOOSE without any MultiApp system using the following input file
# No heat transfer between matrix and fracture, with the matrix and fracture being identical spatial domains
[Mesh]
[generate]
type = GeneratedMeshGenerator
dim = 1
nx = 100
xmin = 0
xmax = 50.0
[]
[]
[Variables]
[T]
[]
[]
[ICs]
[T]
type = FunctionIC
variable = T
function = 'if(x<0.5, 2, 0)' # delta function
[]
[]
[Kernels]
[dot]
type = TimeDerivative
variable = T
[]
[fracture_diffusion]
type = Diffusion
variable = T
[]
[]
[Preconditioning]
[entire_jacobian]
type = SMP
full = true
[]
[]
[Executioner]
type = Transient
solve_type = NEWTON
dt = 100
end_time = 100
[]
[VectorPostprocessors]
[final_results]
type = LineValueSampler
start_point = '0 0 0'
end_point = '50 0 0'
num_points = 11
sort_by = x
variable = T
outputs = final_csv
[]
[]
[Outputs]
print_linear_residuals = false
[final_csv]
type = CSV
sync_times = 100
sync_only = true
[]
[]
The result depends on the spatial and temporal discretisation. The temporal-discretisation dependence of is shown in Figure 1
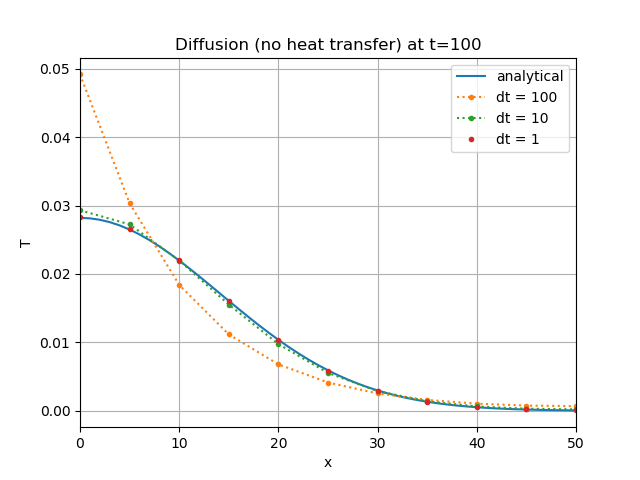
Figure 1: Decoupled case fracture temperature: comparison of the analytical solution with the MOOSE results as computed using no MultiApp
Two coupled variables (no MultiApp)
The system is coupled when . A MultiApp approach is not strictly needed in this case, because there are no meshing problems: the domain is just the real line. Hence, the system may be solved by MOOSE using the following input file
# Heat transfer between matrix and fracture, with the matrix and fracture being identical spatial domains, but a multiapp approach is not used
[Mesh]
[generate]
type = GeneratedMeshGenerator
dim = 1
nx = 100
xmin = 0
xmax = 50.0
[]
[]
[Variables]
[frac_T]
[]
[matrix_T]
[]
[]
[ICs]
[frac_T]
type = FunctionIC
variable = frac_T
function = 'if(x<0.5, 2, 0)' # delta function
[]
[]
[Kernels]
[dot_frac]
type = TimeDerivative
variable = frac_T
[]
[frac_diffusion]
type = Diffusion
variable = frac_T
[]
[toMatrix]
type = PorousFlowHeatMassTransfer
variable = frac_T
v = matrix_T
transfer_coefficient = 0.004
[]
[dot_matrix]
type = TimeDerivative
variable = matrix_T
[]
[matrix_diffusion]
type = Diffusion
variable = matrix_T
[]
[toFrac]
type = PorousFlowHeatMassTransfer
variable = matrix_T
v = frac_T
transfer_coefficient = 0.004
[]
[]
[Preconditioning]
[entire_jacobian]
type = SMP
full = true
[]
[]
[Executioner]
type = Transient
solve_type = NEWTON
dt = 100
end_time = 100
[]
[VectorPostprocessors]
[final_results]
type = LineValueSampler
start_point = '0 0 0'
end_point = '50 0 0'
num_points = 11
sort_by = x
variable = 'frac_T matrix_T'
outputs = final_csv
[]
[]
[Outputs]
print_linear_residuals = false
[final_csv]
type = CSV
sync_times = 100
sync_only = true
[]
[]
The result for depends on the spatial and temporal discretisation. The temporal-discretisation dependence is shown in Figure 2. Notice that the matrix has removed heat from the fracture, so the temperature is decreased compared with the case (i.e. in Figure 2 which is lower than it was for the uncoulpled case with shown in Figure 1 where ).
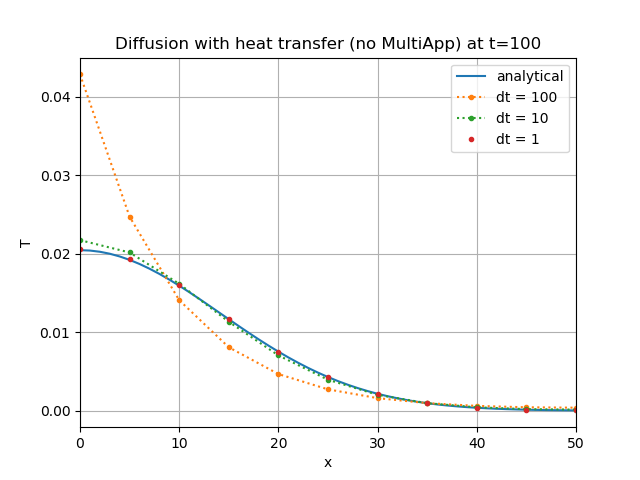
Figure 2: Coupled case fracture temperature: comparison of the analytical solution with the MOOSE results as computed using no MultiApp
A MultiApp approach
Using a MultiApp approach for the case yields similar results. The MultiApp methodology used throughout this set of pages is as follows. One timestep involves:
One timestep of the fracture physics is solved, holding the matrix variables fixed.
Transfers from the fracture system to the matrix system are performed.
One timestep of the matrix system is solved, holding the fracture variables fixed.
Transfers from the matrix system to the fracture system are performed.
Upon reflection, the reader will realise there are many potential ways of actually implementing this. In the case at hand, the fracture physics () is governed by the "main" App, and the matrix physics () by the "sub" App. On the other hand, in the pages describing diffusion in mixed dimensions and PorousFlow models in 2D and 3D, the matrix physics is controlled by the main App and the fracture by the sub App. This latter approach is probably advantageous in most situations because it easily allows the fracture App to take smaller time-steps.
The MultiApp approach typically breaks the unconditional stability of MOOSE's implicit time-stepping scheme. See the discussion at the end of this page.
Transfer of heat energy ("heat" MultiApp)
In order to conserve heat energy, the following approach may be used
One timestep of the fracture App is solved, holding the fixed, using PorousFlowHeatMassTransfer Kernel to implement the term, and recording the heat lost to the matrix, into an
AuxVariable.The heat lost to the matrix is transferred to the matrix App.
One timestep of the matrix system is solved, using a
CoupledForceKernel to inject the heat gained from the fracture at each node.The resulting is transferred to the fracture App.
This is implemented using the following AuxKernel in the fracture App:
[AuxKernels]
[heat_to_matrix]
type = ParsedAux
variable = heat_to_matrix
args = 'frac_T transferred_matrix_T'
function = '0.004 * (frac_T - transferred_matrix_T)'
[]
[]
along with the following Transfers:
[Transfers]
[heat_to_matrix]
type = MultiAppCopyTransfer
to_multi_app = matrix_app
source_variable = heat_to_matrix
variable = heat_from_frac
[]
[T_from_matrix]
type = MultiAppCopyTransfer
from_multi_app = matrix_app
source_variable = matrix_T
variable = transferred_matrix_T
[]
[]
and the Kernel in the matrix App:
[fromFrac]
type = CoupledForce
variable = matrix_T
v = heat_from_frac
A couple of subtleties are that the CoupledForce Kernel will smooth the nodal heat_to_matrix AuxVariable (since it uses quad-point values) and that a save_in cannot be employed in the frac_app_heat.i input file PorousFlowHeatMassTransfer Kernel, since that would include the nodal volume. (The inclusion of nodal volume is exactly what is required in the diffusion, 2D and 3D cases, since the amount of heat energy (measured in Joules) is transferred between the Apps in those cases, but in the current situation CoupledForce requires an energy density measured in Joules.m.) The results are shown in Figure 3.
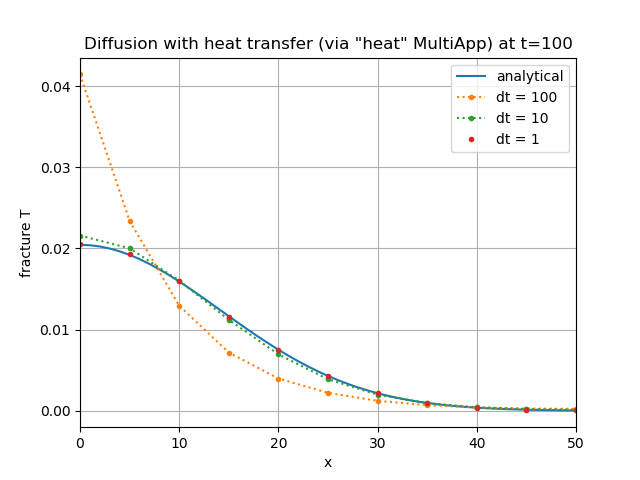
Figure 3: Coupled case: comparison of the analytical solution with the MOOSE results as computed using a "heat" MultiApp
Transfer of temperature ("T" MultiApp)
An alternative approach is to transfer and :
One timestep of the fracture App is solved, holding fixed, using PorousFlowHeatMassTransfer Kernel to implement the term.
The resulting is transferred to the matrix App.
One timestep of the matrix system is solved, holding fixed, using PorousFlowHeatMassTransfer Kernel to implement the term (using the same as the fracture App).
The resulting is transferred to the fracture App.
The disadvantage of this approach is that it doesn't conserve heat energy, however, the advantage is that the original differential equations are clearly evident. Given that the error of using a MultiApp is irrespective of the type of Transfer implemented, the non-conservation of heat energy, which is also proportional to , is probably not of critical importance. This idea is implemented using the following Kernel in the fracture App:
[toMatrix]
type = PorousFlowHeatMassTransfer
variable = frac_T
v = transferred_matrix_T
transfer_coefficient = 0.004
along with the following Transfers:
[Transfers]
[T_to_matrix]
type = MultiAppCopyTransfer
to_multi_app = matrix_app
source_variable = frac_T
variable = transferred_frac_T
[]
[T_from_matrix]
type = MultiAppCopyTransfer
from_multi_app = matrix_app
source_variable = matrix_T
variable = transferred_matrix_T
[]
[]
and the Kernel in the matrix App:
[fromFrac]
type = PorousFlowHeatMassTransfer
variable = matrix_T
v = transferred_frac_T
transfer_coefficient = 0.004
The results are shown in Figure 4.
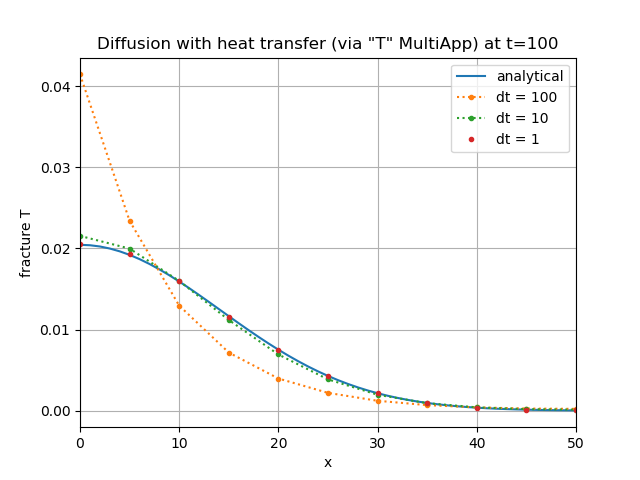
Figure 4: Coupled case: comparison of the analytical solution with the MOOSE results as computed using a "T" MultiApp
Error in each approach
The L2 error in each approach (square-root of the sum of squares of differences between the MOOSE result and the analytical result) is plotted in Figure 5. The errors are very similar for each of the models explored in this section. The magnitude of the error is largely unimportant: the scaling with time-step size is more crucial, and in this case it follows the expected first-order result.
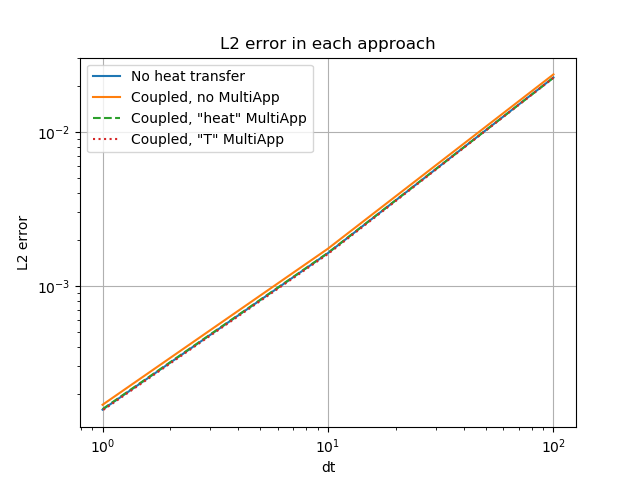
Figure 5: L2 error of each approach as a function of time-step size
Final remarks on stability
One aspect that is not captured in this analysis is stability. The non-MultiApp approaches ("No heat transfer" and "Coupled, no MultiApp") use fully-implicit time-stepping, so are unconditionally stable. Conversely, the MultiApp approaches break this unconditional stability, which could be important in PorousFlow applications. For instance, the matrix temperature is "frozen" while the fracture App is solving. If a very large time-step is taken before the matrix App is allowed to evolve, this would lead to huge, unphysical heat losses to the matrix system. The fracture temperature could reduce to the matrix temperature during fracture evolution, and then the matrix temperature could rise significantly during its evolution when it receives the large quantity of heat from the fracture. This oscillation is unlikely to become unstable, but is clearly unphysical.