Fracture flow using a MultiApp approach: Porous flow in a single matrix system
Background
PorousFlow can be used to simulate flow through fractured porous media in the case when the fracture network is so complicated it cannot be incorporated into the porous-media mesh. The fundamental premise is the fractures can be considered as lower dimensional entities within the higher-dimensional porous media. This page is part of a set that describes a MOOSE MultiApp approach to simulating such models:
MultiApp primer: the diffusion equation with no fractures, and quantifying the errors introduced by the MultiApp approach
Porous flow in a single matrix system
Consider a single 1D planar fracture within a 2D mesh. Fluid flows along the fracture according to Darcy's equation, so may be modelled using PorousFlowFullySaturated
[PorousFlowFullySaturated]
coupling_type = ThermoHydro
porepressure = frac_P
temperature = frac_T
fp = simple_fluid
stabilization = KT
flux_limiter_type = minmod
gravity = '0 0 0'
pressure_unit = MPa
temperature_unit = Celsius
time_unit = seconds
[]
Kuzmin-Turek stabilization cannot typically be used for the fracture flow. This is because multiple fracture elements will meet along a single finite-element edge when fracture planes intersect, while for performance reasons, libMesh assumes only one or two elements share an edge. This prevents the KT approach from quantifying flows in all neighboring elements, which prevents the scheme from working. In the case at hand, KT stabilization is possible because there is just a single fracture.
The following assumptions are used (see Mathematics and physical interpretation).
The fracture aperture is m, and its porosity is . Therefore, the porosity required by PorousFlow is .
The permeability is given by the formula, modified by a roughness coefficient, , so the permeability required by PorousFlow (which includes the extra factor of ) is .
The fracture is basically filled with water, so the internal energy of any rock material within it may be ignored.
The thermal conductivity in the fracture is dominated by the water (which has thermal conductivity 0.6W.m.K), so the thermal conductivity required by PorousFlow is .
Hence, the Materials are
[Materials]
[porosity]
type = PorousFlowPorosityConst
porosity = 1E-2 # includes fracture aperture of 1E-2
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-8 0 0 0 1E-8 0 0 0 1E-8' # roughness times a^3/12
[]
[internal_energy]
type = PorousFlowMatrixInternalEnergy
density = 1
specific_heat_capacity = 0 # basically no rock inside the fracture
[]
[aq_thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '0.6E-2 0 0 0 0.6E-2 0 0 0 0.6E-2' # thermal conductivity of water times fracture aperture
[]
[]
The heat transfer between the fracture and matrix is encoded in the usual way (see the primer and the diffusion pages). The heat transfer coefficient is chosen to be 100, just so that an appreciable amount of heat energy is transferred, not because this is a realistic transfer coefficient for this case:
[Kernels]
[toMatrix]
type = PorousFlowHeatMassTransfer
variable = frac_T
v = transferred_matrix_T
transfer_coefficient = 1E2
save_in = joules_per_s
[]
[]
The boundary conditions correspond to injection of 100C water at a rate of 10kg.s at the left side of the model, and withdrawal of water at the same rate (and whatever temperature it is extracted at) at the right side:
[left_injection]
type = PorousFlowSinkBC
boundary = left
fluid_phase = 0
T_in = 373 # Kelvin!
fp = simple_fluid
flux_function = -10 # 10 kg/s
[BCs]
[mass_production]
type = PorousFlowSink
boundary = right
variable = frac_P
flux_function = 10
[]
[heat_production]
type = PorousFlowSink
boundary = right
variable = frac_T
flux_function = 10
fluid_phase = 0
use_enthalpy = true
[]
[]
The physics in the matrix is assumed to be the simple heat equation. Note that this has no stabilization, so there are overshoots and undershoots in the solution.
[Kernels]
[dot]
type = CoefTimeDerivative
variable = matrix_T
Coefficient = 1E5
[]
[matrix_diffusion]
type = AnisotropicDiffusion
variable = matrix_T
tensor_coeff = '1 0 0 0 1 0 0 0 1'
[]
[]
The Transfers are identical to those used in the diffusion-equation case:
[Transfers]
[T_to_fracture]
type = MultiAppInterpolationTransfer
to_multi_app = fracture_app
source_variable = matrix_T
variable = transferred_matrix_T
[]
[heat_from_fracture]
type = MultiAppReporterTransfer
from_multi_app = fracture_app
from_reporters = 'heat_transfer_rate/joules_per_s heat_transfer_rate/x heat_transfer_rate/y heat_transfer_rate/z'
to_reporters = 'heat_transfer_rate/transferred_joules_per_s heat_transfer_rate/x heat_transfer_rate/y heat_transfer_rate/z'
[]
[]
The fracture-matrix-fracture-matrix-etc time-stepping procedure is the same as described in the primer. Remember that the MultiApp approach typically breaks the unconditional stability of MOOSE's implicit time-stepping scheme. This is because usually the fracture physics is "frozen" while the matrix physics is evolving, and vice-versa. This can easily lead to oscillations if the time-step is too big. For example, start with a cold matrix and hot fracture. When the fracture evolves, it could transfer a huge amount of heat energy to the cold matrix, since the matrix temperature is fixed. During its evolution, the matrix starts hot, so transfers the heat back to the fracture. This cycle continues.
After 100s of simulation, the matrix temperature is shown in Figure 1. The evolution of the temperatures is shown in Figure 2. Without any heat transfer, the fracture heats up to 100C, but when the fracture transfers heat energy to the matrix, the temperature evolution is retarded.
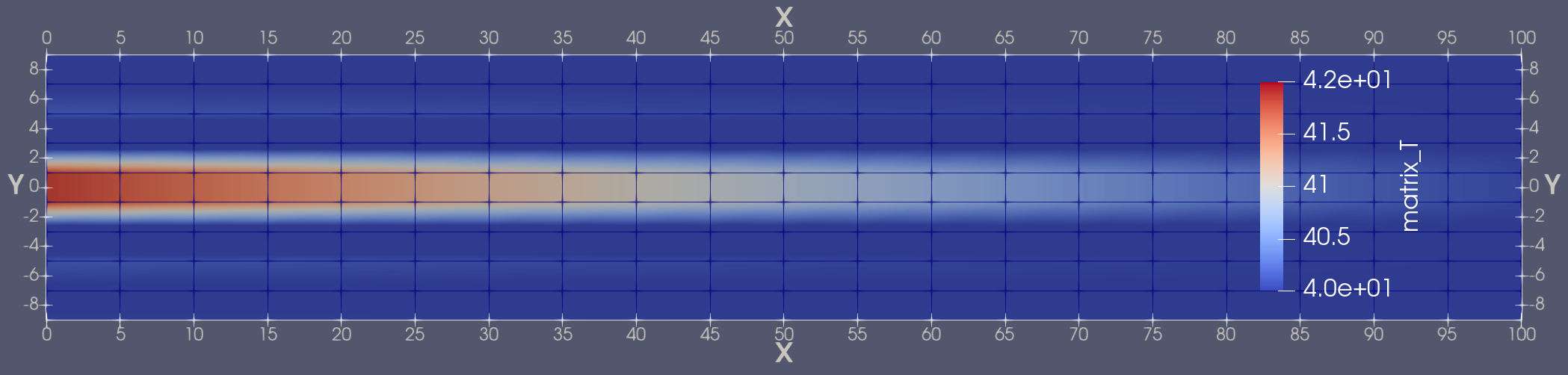
Figure 1: Heat conduction into the matrix (the matrix mesh is shown)
Figure 2: Temperature along the fracture, with heat transfer to the matrix and without heat transfer to the matrix. Fluid at 100degC is injected into the fracture at its left end, and fluid is withdrawn at the right end. With heat transfer, the matrix heats up a little.