Porous Flow Tutorial Page 04. Adding solid mechanics

In this Page, solid mechanics is added to the thermo-hydro simulation of previous Pages. The equations are discussed in governing equations. Only quasi-static solid mechanics is considered here, without gravity, so the equations read (1) As described previously, is the porepressure, the temperature and is the Biot coefficient. The additional nomenclature used here is

• is the effective stress tensor

• is the total stress tensor

• is the elasticity tensor of the drained porous skeleton

• is the linear thermal expansion coefficient. Note that this is the linear version, in contrast to the volumetric coefficients introduced in Page 1.

Once again, before attempting to write an input file, a rough estimate of the expected nonlinear residuals must be performed, as discussed in convergence criteria. The residual for the Eq. (1) is approximately Corresponding to the choice Pa.m made in Page 02 the choice Pa.m may be made here. This means which is significantly greater than for the fluid equation. Therefore, the displacement variables are scaled by .

Some mechanically-related MOOSE objects (Kernels, BCs, etc) accept the use_displaced_mesh input parameter. For virtually all PorousFlow simulations, it is appropriate to set this to false: use_displaced_mesh = false. This means that the Kernel's residual (or BC's residual, Postprocessor's value, etc) will be evaluated using the undisplaced mesh. This has the great numerical advantage that the solid-mechanics elasticity equations remain linear.

Also, some mechanically-related MOOSE objects require the displacements input parameter. Therefore, it is convenient to put this parameter into the GlobalParams block:

[GlobalParams<<<{"href": "../../syntax/GlobalParams/index.html"}>>>]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  biot_coefficient = 1.0
[]

To model this thermo-hydro-mechanical system, the PorousFlowBasicTHM action needs to be enhanced to read:

[Variables<<<{"href": "../../syntax/Variables/index.html"}>>>]
  [porepressure]
  []
  [temperature]
    initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 293
    scaling<<<{"description": "Specifies a scaling factor to apply to this variable"}>>> = 1E-8
  []
  [disp_x]
    scaling<<<{"description": "Specifies a scaling factor to apply to this variable"}>>> = 1E-10
  []
  [disp_y]
    scaling<<<{"description": "Specifies a scaling factor to apply to this variable"}>>> = 1E-10
  []
  [disp_z]
    scaling<<<{"description": "Specifies a scaling factor to apply to this variable"}>>> = 1E-10
  []
[]

[PorousFlowBasicTHM<<<{"href": "../../syntax/PorousFlowBasicTHM/index.html"}>>>]
  porepressure<<<{"description": "The name of the porepressure variable"}>>> = porepressure
  temperature<<<{"description": "For isothermal simulations, this is the temperature at which fluid properties (and stress-free strains) are evaluated at.  Otherwise, this is the name of the temperature variable.  Units = Kelvin"}>>> = temperature
  coupling_type<<<{"description": "The type of simulation.  For simulations involving Mechanical deformations, you will need to supply the correct Biot coefficient.  For simulations involving Thermal flows, you will need an associated ConstantThermalExpansionCoefficient Material"}>>> = ThermoHydroMechanical
  gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
  fp<<<{"description": "The name of the user object for fluid properties. Only needed if fluid_properties_type = PorousFlowSingleComponentFluid"}>>> = the_simple_fluid
  eigenstrain_names<<<{"description": "List of all eigenstrain models used in mechanics calculations. Typically the eigenstrain_name used in ComputeThermalExpansionEigenstrain.  Only needed for thermally-coupled simulations with thermal expansion."}>>> = thermal_contribution
  use_displaced_mesh<<<{"description": "Use displaced mesh computations in mechanical kernels"}>>> = false
[]

The boundary conditions used here are roller boundary conditions, as well as boundary conditions that model the effect of the fluid porepressure on the injection area:

[BCs<<<{"href": "../../syntax/BCs/index.html"}>>>]
  [constant_injection_porepressure]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    value<<<{"description": "Value of the BC"}>>> = 1E6
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = injection_area
  []
  [constant_injection_temperature]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temperature
    value<<<{"description": "Value of the BC"}>>> = 313
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = injection_area
  []

  [roller_tmax]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = dmax
  []
  [roller_tmin]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = dmin
  []
  [roller_top_bottom]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'top bottom'
  []
  [cavity_pressure_x]
    type = Pressure<<<{"description": "Applies a pressure on a given boundary in a given direction", "href": "../../source/bcs/Pressure.html"}>>>
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = injection_area
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    factor<<<{"description": "The magnitude to use in computing the pressure"}>>> = 1E6
    use_displaced_mesh<<<{"description": "Whether to use the displaced mesh."}>>> = false
  []
  [cavity_pressure_y]
    type = Pressure<<<{"description": "Applies a pressure on a given boundary in a given direction", "href": "../../source/bcs/Pressure.html"}>>>
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = injection_area
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    factor<<<{"description": "The magnitude to use in computing the pressure"}>>> = 1E6
    use_displaced_mesh<<<{"description": "Whether to use the displaced mesh."}>>> = false
  []
[]

The SolidMechanics module of MOOSE provides some useful AuxKernels for extracting effective stresses of interest to this problem (the effective radial stress and the effective hoop stress)

[AuxVariables<<<{"href": "../../syntax/AuxVariables/index.html"}>>>]
  [stress_rr]
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
  []
  [stress_pp]
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
  []
[]

[AuxKernels<<<{"href": "../../syntax/AuxKernels/index.html"}>>>]
  [stress_rr]
    type = RankTwoScalarAux<<<{"description": "Compute a scalar property of a RankTwoTensor", "href": "../../source/auxscalarkernels/RankTwoScalarAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_rr
    scalar_type<<<{"description": "Type of scalar output"}>>> = RadialStress
    point1<<<{"description": "Start point for axis used to calculate some cylindrical material tensor quantities"}>>> = '0 0 0'
    point2<<<{"description": "End point for axis used to calculate some material tensor quantities"}>>> = '0 0 1'
  []
  [stress_pp]
    type = RankTwoScalarAux<<<{"description": "Compute a scalar property of a RankTwoTensor", "href": "../../source/auxscalarkernels/RankTwoScalarAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_pp
    scalar_type<<<{"description": "Type of scalar output"}>>> = HoopStress
    point1<<<{"description": "Start point for axis used to calculate some cylindrical material tensor quantities"}>>> = '0 0 0'
    point2<<<{"description": "End point for axis used to calculate some material tensor quantities"}>>> = '0 0 1'
  []
[]

Finally, some mechanics-related Materials need to be defined

  [elasticity_tensor]
    type = ComputeIsotropicElasticityTensor
    youngs_modulus = 5E9
    poissons_ratio = 0.0
  []
  [strain]
    type = ComputeSmallStrain
    eigenstrain_names = thermal_contribution
  []
  [thermal_contribution]
    type = ComputeThermalExpansionEigenstrain
    temperature = temperature
    thermal_expansion_coeff = 0.001 # this is the linear thermal expansion coefficient
    eigenstrain_name = thermal_contribution
    stress_free_temperature = 293
  []
  [stress]
    type = ComputeLinearElasticStress
  []
[]

An animation of the results is shown in Figure 1.

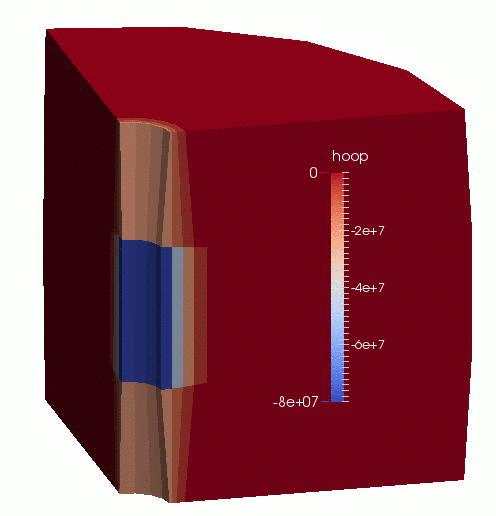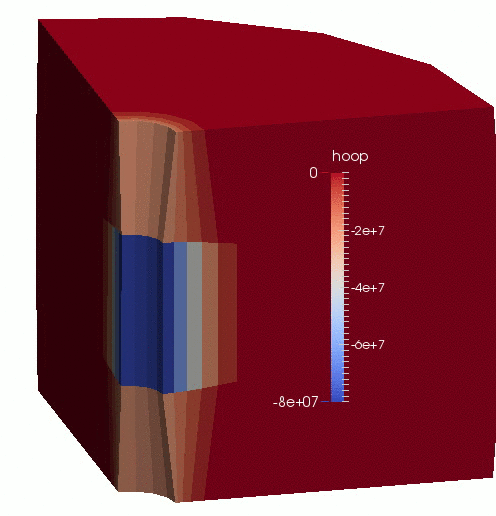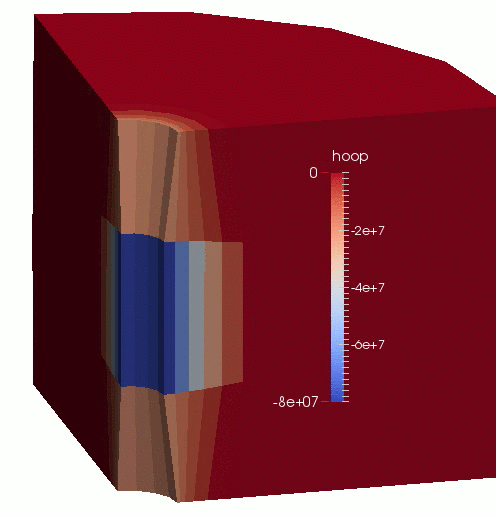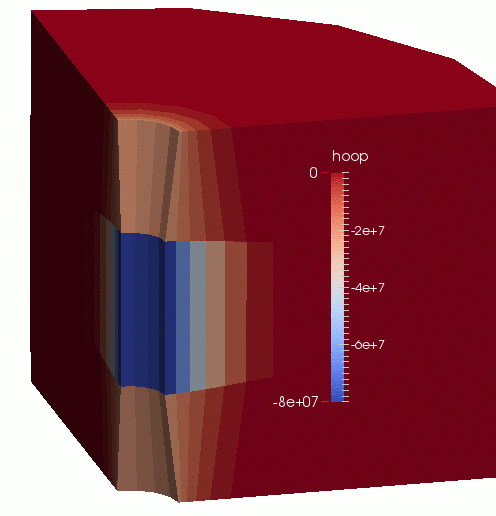
Figure 1: Displacement (magnified by 100 times) and effective hoop-stress evolution in the borehole-aquifer-caprock system.

The dynamics of this model are fascinating, and readers are encouraged to pause and play with parameters to explore how they effect the final result. In fact, this model is very similar to the "THM Rehbinder" test in PorousFlow's test suite. Rehbinder (Rehbinder, 1995) derived analytical solutions for a similar THM problem, and MOOSE replicates his result exactly:

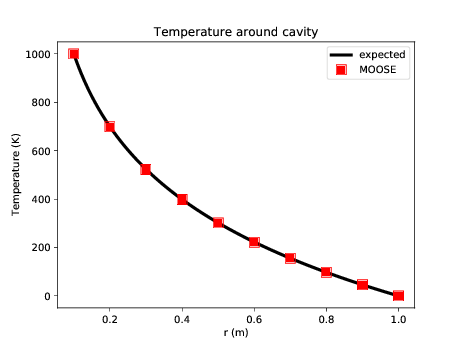
Figure 2: Comparison between MOOSE and Rehbinder's analytical solution.

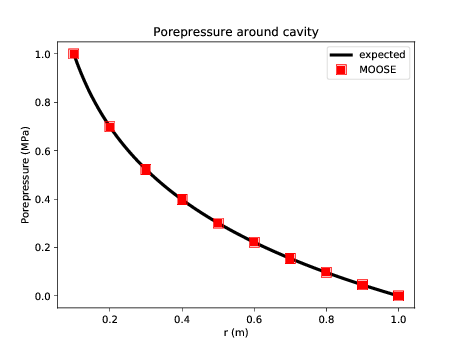
Figure 3: Comparison between MOOSE and Rehbinder's analytical solution.

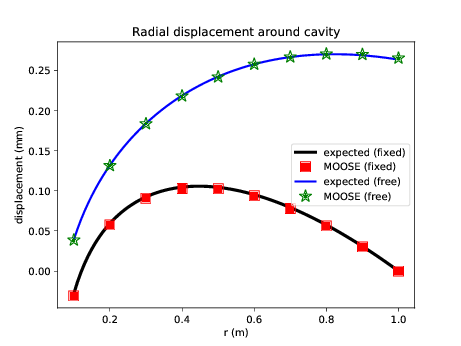
Figure 4: Comparison between MOOSE and Rehbinder's analytical solution.