Heat and fluid responses in 1D bars
Classic Newton cooling in a bar
Without fluids, mechanical deformation and sinks, the heat equation is where is the porosity, is the rock grain density (kg.m), is the rock grain specific heat capacity (J.kg.K), is the temperature, and is the tensorial thermal conductivity of the porous material (J.s.K.m).
Below, the dynamics of this equation is explored, while this section concentrates on the steady-state situation. Consider the one-dimensional case where a bar sits between and with a fixed temperature at : and a sink flux at the other end: (1) Here is a fixed quantity ("e" stands for "external"), and is a constant conductance (J.m.s.K).
The solution is the linear function The heat sink in Eq. (1) is a linear function of , so the PorousFlowPiecewiseLinearSink may be employed.
The simulation is run in MOOSE using , , , and . The solution is shown in Figure 1

Figure 1: The steady-state temperature in the bar. MOOSE agrees well with theory illustrating that piecewise-linear heat sinks/sources and heat conduction are correctly implemented in MOOSE.
# Newton cooling from a bar. Heat conduction
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
type = GeneratedMesh
dim = 2
nx = 100
ny = 1
xmin = 0
xmax = 100
ymin = 0
ymax = 1
[]
[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
PorousFlowDictator = dictator
[]
[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
[dictator]
type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation. Jacobian entries involving derivatives wrt these variables will be computed. In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'temp'
number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 0
number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 0
[]
[]
[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
[temp]
[]
[]
[ICs<<<{"href": "../../../../syntax/ICs/index.html"}>>>]
[temp]
type = FunctionIC<<<{"description": "An initial condition that uses a normal function of x, y, z to produce values (and optionally gradients) for a field variable.", "href": "../../../../source/ics/FunctionIC.html"}>>>
variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = temp
function<<<{"description": "The initial condition function."}>>> = '2-x/100'
[]
[]
[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
[conduction]
type = PorousFlowHeatConduction<<<{"description": "Heat conduction in the Porous Flow module", "href": "../../../../source/kernels/PorousFlowHeatConduction.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temp
[]
[]
[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
[temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
temperature<<<{"description": "Fluid temperature variable. Note, the default is suitable if your simulation is using Kelvin units, but probably not for Celsius"}>>> = temp
[]
[thermal_conductivity_irrelevant]
type = PorousFlowThermalConductivityIdeal<<<{"description": "This Material calculates rock-fluid combined thermal conductivity by using a weighted sum. Thermal conductivity = dry_thermal_conductivity + S^exponent * (wet_thermal_conductivity - dry_thermal_conductivity), where S is the aqueous saturation", "href": "../../../../source/materials/PorousFlowThermalConductivityIdeal.html"}>>>
dry_thermal_conductivity<<<{"description": "The thermal conductivity of the rock matrix when the aqueous saturation is zero"}>>> = '1E2 0 0 0 1E2 0 0 0 1E2'
[]
[]
[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
[left]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temp
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
value<<<{"description": "Value of the BC"}>>> = 2
[]
[newton]
type = PorousFlowPiecewiseLinearSink<<<{"description": "Applies a flux sink to a boundary. The base flux defined by PorousFlowSink is multiplied by a piecewise linear function.", "href": "../../../../source/bcs/PorousFlowPiecewiseLinearSink.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temp
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
pt_vals<<<{"description": "Tuple of pressure values (for the fluid_phase specified). Must be monotonically increasing. For heat fluxes that don't involve fluids, these are temperature values"}>>> = '0 1 2'
multipliers<<<{"description": "Tuple of multiplying values. The flux values are multiplied by these."}>>> = '-1 0 1'
flux_function<<<{"description": "The flux. The flux is OUT of the medium: hence positive values of this function means this BC will act as a SINK, while negative values indicate this flux will be a SOURCE. The functional form is useful for spatially or temporally varying sinks. Without any use_*, this function is measured in kg.m^-2.s^-1 (or J.m^-2.s^-1 for the case with only heat and no fluids)"}>>> = 1
[]
[]
[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
[temp]
type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = temp
start_point<<<{"description": "The beginning of the line"}>>> = '0 0.5 0'
end_point<<<{"description": "The ending of the line"}>>> = '100 0.5 0'
sort_by<<<{"description": "What to sort the samples by"}>>> = x
num_points<<<{"description": "The number of points to sample along the line"}>>> = 11
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[]
[]
[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
[andy]
type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
petsc_options<<<{"description": "Singleton PETSc options"}>>> = '-snes_converged_reason'
petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol '
petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu 100 NONZERO 2 1E-14 1E-12'
[]
[]
[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
type = Steady
[]
[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = nc04
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
exodus<<<{"description": "Output the results using the default settings for Exodus output."}>>> = false
[along_line]
type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
execute_vector_postprocessors_on<<<{"description": "Enable/disable the output of VectorPostprocessors"}>>> = timestep_end
[]
[]Porepressure sink in a bar
These tests demonstrate that MOOSE behaves correctly when a simulation contains a sink. The sink is a piecewise linear function of pressure.
Darcy's equation for (single-phase) flow through a fully saturated medium without gravity and without sources is with the following notation:
is the medium's porosity;
is the fluid density;
is the permeability tensor;
is the fluid viscosity;
and denote the time and spatial derivatives, respectively.
Using , where is the fluid bulk modulus, Darcy's equation becomes with Here the porosity and bulk modulus are assumed to be constant in space and time.
Consider the one-dimensional case where a bar sits between and with initial pressure distribution so . Maintain the end at constant pressure, so that . At the end , prescribe a sink flux where is a fixed quantity ("e" stands for "external"), and is a constant conductance. This corresponds to the flux which can easily be coded into a MOOSE input file: the flux is , and this may be represented by a piecewise linear function of pressure.
The solution of this problem is well known and is where is the positive root of the equation ( is a little bigger than ), and is determined from which may be solved numerically (Mathematica is used to generate the solution in Figure 2).
The problem is solved in MOOSE using the following parameters:
Table 1: Parameter values used in the porepressure evolution tests
| Parameter | Value |
|---|---|
| Bar length | m |
| Bar porosity | 0.1 |
| Bar permeability | m |
| Gravity | 0 |
| Water density | 1000kg.m |
| Water viscosity | 0.001Pa.s |
| Water bulk modulus | 1MPa |
| Initial porepressure | 2MPa |
| Environmental pressure | 0 |
| Conductance | 0.05389m |
This conductance is chosen so at steadystate kg.m.
The problem is solved using 1000 elements along the direction (m), and using 100 time-steps of size s. Using fewer elements or fewer timesteps means the agreement with the theory is marginally poorer. Two tests are performed: one with transient flow, and one using the steadystate solver. In steady-state case the initial condition is MPa, since the uniform MPa does not converge. The results are shown in Figure 2.
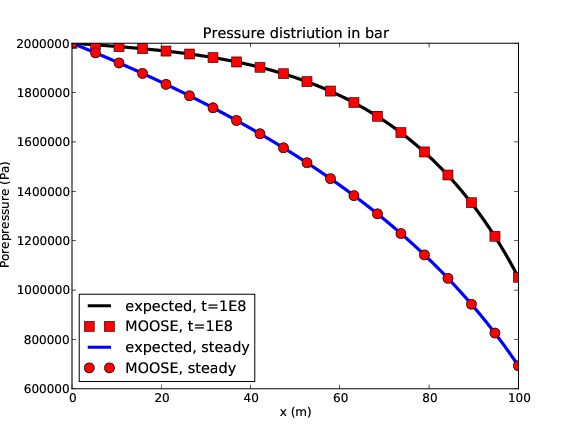
Figure 2: The porepressure in the bar at 1E8s, and at steadystate. The pressure at is held fixed on the left-hand end, while the sink is applied at the right end. MOOSE agrees well with theory demonstrating that piecewise-linear sinks/sources and single-phase Darcy fluid flow are correctly implemented in MOOSE.
The transient simulation:
# Newton cooling from a bar. 1-phase transient
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
type = GeneratedMesh
dim = 2
nx = 1000
ny = 1
xmin = 0
xmax = 100
ymin = 0
ymax = 1
[]
[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
PorousFlowDictator = dictator
[]
[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
[dictator]
type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation. Jacobian entries involving derivatives wrt these variables will be computed. In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'pressure'
number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
[]
[pc]
type = PorousFlowCapillaryPressureVG<<<{"description": "van Genuchten capillary pressure", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureVG.html"}>>>
m<<<{"description": "van Genuchten exponent m. Must be between 0 and 1, and optimally should be set to >0.5"}>>> = 0.8
alpha<<<{"description": "van Genuchten parameter alpha. Must be positive"}>>> = 1e-5
[]
[]
[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
[pressure]
initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 2E6
[]
[]
[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
[mass0]
type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time. Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[flux]
type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[]
[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
[simple_fluid]
type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 1e6
density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1000
thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1e-3
[]
[]
[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
[temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
[]
[ppss]
type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = pressure
capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
[]
[massfrac]
type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
[]
[simple_fluid]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
phase<<<{"description": "The phase number"}>>> = 0
[]
[porosity]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>>
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1E-15 0 0 0 1E-15 0 0 0 1E-15'
[]
[relperm]
type = PorousFlowRelativePermeabilityCorey<<<{"description": "This Material calculates relative permeability of the fluid phase, using the simple Corey model ((S-S_res)/(1-sum(S_res)))^n", "href": "../../../../source/materials/PorousFlowRelativePermeabilityCorey.html"}>>> # irrelevant in this fully-saturated situation
n<<<{"description": "The Corey exponent of the phase."}>>> = 2
phase<<<{"description": "The phase number"}>>> = 0
[]
[]
[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
[left]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
value<<<{"description": "Value of the BC"}>>> = 2E6
[]
[newton]
type = PorousFlowPiecewiseLinearSink<<<{"description": "Applies a flux sink to a boundary. The base flux defined by PorousFlowSink is multiplied by a piecewise linear function.", "href": "../../../../source/bcs/PorousFlowPiecewiseLinearSink.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
pt_vals<<<{"description": "Tuple of pressure values (for the fluid_phase specified). Must be monotonically increasing. For heat fluxes that don't involve fluids, these are temperature values"}>>> = '0 100000 200000 300000 400000 500000 600000 700000 800000 900000 1000000 1100000 1200000 1300000 1400000 1500000 1600000 1700000 1800000 1900000 2000000'
multipliers<<<{"description": "Tuple of multiplying values. The flux values are multiplied by these."}>>> = '0. 5.6677197748570516e-6 0.000011931518841831313 0.00001885408740732065 0.000026504708864284114 0.000034959953203725676 0.000044304443352900224 0.00005463170211001232 0.00006604508815181467 0.00007865883048198513 0.00009259917167338928 0.00010800563134618119 0.00012503240252705603 0.00014384989486488752 0.00016464644014777016 0.00018763017719085535 0.0002130311349595711 0.00024110353477682344 0.00027212833465544285 0.00030641604122040985 0.00034430981736352295'
use_mobility<<<{"description": "If true, then fluxes are multiplied by (density*permeability_nn/viscosity), where the '_nn' indicates the component normal to the boundary. In this case bare_flux is measured in Pa.m^-1. This can be used in conjunction with other use_*"}>>> = false
use_relperm<<<{"description": "If true, then fluxes are multiplied by relative permeability. This can be used in conjunction with other use_*"}>>> = false
fluid_phase<<<{"description": "If supplied, then this BC will potentially be a function of fluid pressure, and you can use mass_fraction_component, use_mobility, use_relperm, use_enthalpy and use_energy. If not supplied, then this BC can only be a function of temperature"}>>> = 0
flux_function<<<{"description": "The flux. The flux is OUT of the medium: hence positive values of this function means this BC will act as a SINK, while negative values indicate this flux will be a SOURCE. The functional form is useful for spatially or temporally varying sinks. Without any use_*, this function is measured in kg.m^-2.s^-1 (or J.m^-2.s^-1 for the case with only heat and no fluids)"}>>> = 1
[]
[]
[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
[porepressure]
type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = pressure
start_point<<<{"description": "The beginning of the line"}>>> = '0 0.5 0'
end_point<<<{"description": "The ending of the line"}>>> = '100 0.5 0'
sort_by<<<{"description": "What to sort the samples by"}>>> = x
num_points<<<{"description": "The number of points to sample along the line"}>>> = 20
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[]
[]
[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
[andy]
type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
petsc_options<<<{"description": "Singleton PETSc options"}>>> = '-snes_converged_reason'
petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'bcgs bjacobi 1E-12 1E-15 10000'
[]
[]
[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
type = Transient
solve_type = Newton
end_time = 1E8
dt = 1E6
[]
[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = nc01
[along_line]
type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
execute_vector_postprocessors_on<<<{"description": "Enable/disable the output of VectorPostprocessors"}>>> = final
[]
[]The steady-state simulation:
# Newton cooling from a bar. 1-phase steady
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
type = GeneratedMesh
dim = 2
nx = 1000
ny = 1
xmin = 0
xmax = 100
ymin = 0
ymax = 1
[]
[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
PorousFlowDictator = dictator
[]
[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
[dictator]
type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation. Jacobian entries involving derivatives wrt these variables will be computed. In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'pressure'
number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
[]
[pc]
type = PorousFlowCapillaryPressureVG<<<{"description": "van Genuchten capillary pressure", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureVG.html"}>>>
m<<<{"description": "van Genuchten exponent m. Must be between 0 and 1, and optimally should be set to >0.5"}>>> = 0.8
alpha<<<{"description": "van Genuchten parameter alpha. Must be positive"}>>> = 1e-5
[]
[]
[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
[pressure]
[]
[]
[ICs<<<{"href": "../../../../syntax/ICs/index.html"}>>>]
[pressure]
type = FunctionIC<<<{"description": "An initial condition that uses a normal function of x, y, z to produce values (and optionally gradients) for a field variable.", "href": "../../../../source/ics/FunctionIC.html"}>>>
variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = pressure
function<<<{"description": "The initial condition function."}>>> = '(2-x/100)*1E6'
[]
[]
[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
[flux]
type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[]
[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
[simple_fluid]
type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 1e6
density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1000
thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1e-3
[]
[]
[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
[temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
[]
[ppss]
type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = pressure
capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
[]
[massfrac]
type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
[]
[simple_fluid]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
phase<<<{"description": "The phase number"}>>> = 0
[]
[porosity]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>>
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1E-15 0 0 0 1E-15 0 0 0 1E-15'
[]
[relperm]
type = PorousFlowRelativePermeabilityCorey<<<{"description": "This Material calculates relative permeability of the fluid phase, using the simple Corey model ((S-S_res)/(1-sum(S_res)))^n", "href": "../../../../source/materials/PorousFlowRelativePermeabilityCorey.html"}>>> # irrelevant in this fully-saturated situation
n<<<{"description": "The Corey exponent of the phase."}>>> = 2
phase<<<{"description": "The phase number"}>>> = 0
[]
[]
[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
[left]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
value<<<{"description": "Value of the BC"}>>> = 2E6
[]
[newton]
type = PorousFlowPiecewiseLinearSink<<<{"description": "Applies a flux sink to a boundary. The base flux defined by PorousFlowSink is multiplied by a piecewise linear function.", "href": "../../../../source/bcs/PorousFlowPiecewiseLinearSink.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
pt_vals<<<{"description": "Tuple of pressure values (for the fluid_phase specified). Must be monotonically increasing. For heat fluxes that don't involve fluids, these are temperature values"}>>> = '0 100000 200000 300000 400000 500000 600000 700000 800000 900000 1000000 1100000 1200000 1300000 1400000 1500000 1600000 1700000 1800000 1900000 2000000'
multipliers<<<{"description": "Tuple of multiplying values. The flux values are multiplied by these."}>>> = '0. 5.6677197748570516e-6 0.000011931518841831313 0.00001885408740732065 0.000026504708864284114 0.000034959953203725676 0.000044304443352900224 0.00005463170211001232 0.00006604508815181467 0.00007865883048198513 0.00009259917167338928 0.00010800563134618119 0.00012503240252705603 0.00014384989486488752 0.00016464644014777016 0.00018763017719085535 0.0002130311349595711 0.00024110353477682344 0.00027212833465544285 0.00030641604122040985 0.00034430981736352295'
use_mobility<<<{"description": "If true, then fluxes are multiplied by (density*permeability_nn/viscosity), where the '_nn' indicates the component normal to the boundary. In this case bare_flux is measured in Pa.m^-1. This can be used in conjunction with other use_*"}>>> = false
use_relperm<<<{"description": "If true, then fluxes are multiplied by relative permeability. This can be used in conjunction with other use_*"}>>> = false
fluid_phase<<<{"description": "If supplied, then this BC will potentially be a function of fluid pressure, and you can use mass_fraction_component, use_mobility, use_relperm, use_enthalpy and use_energy. If not supplied, then this BC can only be a function of temperature"}>>> = 0
flux_function<<<{"description": "The flux. The flux is OUT of the medium: hence positive values of this function means this BC will act as a SINK, while negative values indicate this flux will be a SOURCE. The functional form is useful for spatially or temporally varying sinks. Without any use_*, this function is measured in kg.m^-2.s^-1 (or J.m^-2.s^-1 for the case with only heat and no fluids)"}>>> = 1
[]
[]
[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
[porepressure]
type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = pressure
start_point<<<{"description": "The beginning of the line"}>>> = '0 0.5 0'
end_point<<<{"description": "The ending of the line"}>>> = '100 0.5 0'
sort_by<<<{"description": "What to sort the samples by"}>>> = x
num_points<<<{"description": "The number of points to sample along the line"}>>> = 20
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[]
[]
[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
active<<<{"description": "If specified only the blocks named will be visited and made active"}>>> = 'andy'
[andy]
type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
petsc_options<<<{"description": "Singleton PETSc options"}>>> = '-snes_converged_reason'
petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol '
petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu 100 NONZERO 2 1E-12 1E-15'
[]
[]
[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
type = Steady
[]
[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = nc02
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
exodus<<<{"description": "Output the results using the default settings for Exodus output."}>>> = false
[along_line]
type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
execute_vector_postprocessors_on<<<{"description": "Enable/disable the output of VectorPostprocessors"}>>> = timestep_end
[]
[]Porepressure sink in a bar with heat
The simulation of the previous section is re-run, but this time heat flow is included. In this section it is assumed that the fluid specific enthalpy (J.kg) is exactly equal to the fluid internal energy, and that internal energy is ideal: This makes the arguments below simple without having to consider real fluids with complicated enthalpy and density expressions.
At the left end of the bar, the temperature is kept fixed: At the other end of the bar, heat is removed only by the fluid flowing out of the system (see sink documentation). That is, there is a heat sink: No other sinks or sources are applied to the heat equation.
With this setup, the steady-state temperature in the bar must be exactly For consider the fluid flowing from to in order to assume steady-state. At it must have temperature because that temperature is fixed at . It advects this temperature with it as it moves, so therefore at , this temperature has permeated throughout the entire bar. This occurs even without heat conduction, and is independent of the initial temperature of the bar.
MOOSE produces this result exactly. The input file is
# Newton cooling from a bar. 1-phase and heat, steady
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
type = GeneratedMesh
dim = 2
nx = 100
ny = 1
xmin = 0
xmax = 100
ymin = 0
ymax = 1
[]
[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
PorousFlowDictator = dictator
[]
[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
[dictator]
type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation. Jacobian entries involving derivatives wrt these variables will be computed. In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'pressure temp'
number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
[]
[pc]
type = PorousFlowCapillaryPressureVG<<<{"description": "van Genuchten capillary pressure", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureVG.html"}>>>
m<<<{"description": "van Genuchten exponent m. Must be between 0 and 1, and optimally should be set to >0.5"}>>> = 0.8
alpha<<<{"description": "van Genuchten parameter alpha. Must be positive"}>>> = 1e-5
[]
[]
[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
[pressure]
[]
[temp]
[]
[]
[ICs<<<{"href": "../../../../syntax/ICs/index.html"}>>>]
# have to start these reasonably close to their steady-state values
[pressure]
type = FunctionIC<<<{"description": "An initial condition that uses a normal function of x, y, z to produce values (and optionally gradients) for a field variable.", "href": "../../../../source/ics/FunctionIC.html"}>>>
variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = pressure
function<<<{"description": "The initial condition function."}>>> = '(2-x/100)*1E6'
[]
[temperature]
type = FunctionIC<<<{"description": "An initial condition that uses a normal function of x, y, z to produce values (and optionally gradients) for a field variable.", "href": "../../../../source/ics/FunctionIC.html"}>>>
variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = temp
function<<<{"description": "The initial condition function."}>>> = 100+0.1*x
[]
[]
[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
[flux]
type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[heat_advection]
type = PorousFlowHeatAdvection<<<{"description": "Fully-upwinded heat flux, advected by the fluid", "href": "../../../../source/kernels/PorousFlowHeatAdvection.html"}>>>
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temp
[]
[]
[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
[simple_fluid]
type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 1e6
density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1000
thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1e-3
cv<<<{"description": "Constant specific heat capacity at constant volume (J/kg/K)"}>>> = 1e6
porepressure_coefficient<<<{"description": "The enthalpy is internal_energy + P / density * porepressure_coefficient. Physically this should be 1.0, but analytic solutions are simplified when it is zero"}>>> = 0
[]
[]
[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
[temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
temperature<<<{"description": "Fluid temperature variable. Note, the default is suitable if your simulation is using Kelvin units, but probably not for Celsius"}>>> = temp
[]
[ppss]
type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = pressure
capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
[]
[massfrac]
type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
[]
[simple_fluid]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
phase<<<{"description": "The phase number"}>>> = 0
[]
[permeability]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1E-15 0 0 0 1E-15 0 0 0 1E-15'
[]
[relperm]
type = PorousFlowRelativePermeabilityCorey<<<{"description": "This Material calculates relative permeability of the fluid phase, using the simple Corey model ((S-S_res)/(1-sum(S_res)))^n", "href": "../../../../source/materials/PorousFlowRelativePermeabilityCorey.html"}>>> # irrelevant in this fully-saturated situation
n<<<{"description": "The Corey exponent of the phase."}>>> = 2
phase<<<{"description": "The phase number"}>>> = 0
[]
[]
[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
[leftp]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
value<<<{"description": "Value of the BC"}>>> = 2E6
[]
[leftt]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temp
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
value<<<{"description": "Value of the BC"}>>> = 100
[]
[newtonp]
type = PorousFlowPiecewiseLinearSink<<<{"description": "Applies a flux sink to a boundary. The base flux defined by PorousFlowSink is multiplied by a piecewise linear function.", "href": "../../../../source/bcs/PorousFlowPiecewiseLinearSink.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
pt_vals<<<{"description": "Tuple of pressure values (for the fluid_phase specified). Must be monotonically increasing. For heat fluxes that don't involve fluids, these are temperature values"}>>> = '0 100000 200000 300000 400000 500000 600000 700000 800000 900000 1000000 1100000 1200000 1300000 1400000 1500000 1600000 1700000 1800000 1900000 2000000'
multipliers<<<{"description": "Tuple of multiplying values. The flux values are multiplied by these."}>>> = '0. 5.6677197748570516e-6 0.000011931518841831313 0.00001885408740732065 0.000026504708864284114 0.000034959953203725676 0.000044304443352900224 0.00005463170211001232 0.00006604508815181467 0.00007865883048198513 0.00009259917167338928 0.00010800563134618119 0.00012503240252705603 0.00014384989486488752 0.00016464644014777016 0.00018763017719085535 0.0002130311349595711 0.00024110353477682344 0.00027212833465544285 0.00030641604122040985 0.00034430981736352295'
use_mobility<<<{"description": "If true, then fluxes are multiplied by (density*permeability_nn/viscosity), where the '_nn' indicates the component normal to the boundary. In this case bare_flux is measured in Pa.m^-1. This can be used in conjunction with other use_*"}>>> = false
use_relperm<<<{"description": "If true, then fluxes are multiplied by relative permeability. This can be used in conjunction with other use_*"}>>> = false
fluid_phase<<<{"description": "If supplied, then this BC will potentially be a function of fluid pressure, and you can use mass_fraction_component, use_mobility, use_relperm, use_enthalpy and use_energy. If not supplied, then this BC can only be a function of temperature"}>>> = 0
flux_function<<<{"description": "The flux. The flux is OUT of the medium: hence positive values of this function means this BC will act as a SINK, while negative values indicate this flux will be a SOURCE. The functional form is useful for spatially or temporally varying sinks. Without any use_*, this function is measured in kg.m^-2.s^-1 (or J.m^-2.s^-1 for the case with only heat and no fluids)"}>>> = 1
[]
[newton]
type = PorousFlowPiecewiseLinearSink<<<{"description": "Applies a flux sink to a boundary. The base flux defined by PorousFlowSink is multiplied by a piecewise linear function.", "href": "../../../../source/bcs/PorousFlowPiecewiseLinearSink.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temp
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
pt_vals<<<{"description": "Tuple of pressure values (for the fluid_phase specified). Must be monotonically increasing. For heat fluxes that don't involve fluids, these are temperature values"}>>> = '0 100000 200000 300000 400000 500000 600000 700000 800000 900000 1000000 1100000 1200000 1300000 1400000 1500000 1600000 1700000 1800000 1900000 2000000'
multipliers<<<{"description": "Tuple of multiplying values. The flux values are multiplied by these."}>>> = '0. 5.6677197748570516e-6 0.000011931518841831313 0.00001885408740732065 0.000026504708864284114 0.000034959953203725676 0.000044304443352900224 0.00005463170211001232 0.00006604508815181467 0.00007865883048198513 0.00009259917167338928 0.00010800563134618119 0.00012503240252705603 0.00014384989486488752 0.00016464644014777016 0.00018763017719085535 0.0002130311349595711 0.00024110353477682344 0.00027212833465544285 0.00030641604122040985 0.00034430981736352295'
use_mobility<<<{"description": "If true, then fluxes are multiplied by (density*permeability_nn/viscosity), where the '_nn' indicates the component normal to the boundary. In this case bare_flux is measured in Pa.m^-1. This can be used in conjunction with other use_*"}>>> = false
use_relperm<<<{"description": "If true, then fluxes are multiplied by relative permeability. This can be used in conjunction with other use_*"}>>> = false
use_internal_energy<<<{"description": "If true, then fluxes are multiplied by fluid internal energy. In this case bare_flux is measured in kg.m^-2.s^-1 / (J.kg). This can be used in conjunction with other use_*"}>>> = true
fluid_phase<<<{"description": "If supplied, then this BC will potentially be a function of fluid pressure, and you can use mass_fraction_component, use_mobility, use_relperm, use_enthalpy and use_energy. If not supplied, then this BC can only be a function of temperature"}>>> = 0
flux_function<<<{"description": "The flux. The flux is OUT of the medium: hence positive values of this function means this BC will act as a SINK, while negative values indicate this flux will be a SOURCE. The functional form is useful for spatially or temporally varying sinks. Without any use_*, this function is measured in kg.m^-2.s^-1 (or J.m^-2.s^-1 for the case with only heat and no fluids)"}>>> = 1
[]
[]
[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
[porepressure]
type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = pressure
start_point<<<{"description": "The beginning of the line"}>>> = '0 0.5 0'
end_point<<<{"description": "The ending of the line"}>>> = '100 0.5 0'
sort_by<<<{"description": "What to sort the samples by"}>>> = x
num_points<<<{"description": "The number of points to sample along the line"}>>> = 11
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[]
[temperature]
type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = temp
start_point<<<{"description": "The beginning of the line"}>>> = '0 0.5 0'
end_point<<<{"description": "The ending of the line"}>>> = '100 0.5 0'
sort_by<<<{"description": "What to sort the samples by"}>>> = x
num_points<<<{"description": "The number of points to sample along the line"}>>> = 11
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[]
[]
[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
[andy]
type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
petsc_options<<<{"description": "Singleton PETSc options"}>>> = '-snes_converged_reason'
petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol '
petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu 100 NONZERO 2 1E-8 1E-15'
[]
[]
[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
type = Steady
solve_type = Newton
[]
[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = nc06
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[along_line]
type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
execute_vector_postprocessors_on<<<{"description": "Enable/disable the output of VectorPostprocessors"}>>> = timestep_end
[]
[]Hot ideal fluid in a bar
This test uses a similar setup to the previous section, except that here an ideal fluid is used. The use of an ideal gas simplifies the equations. Only the steady-state is studied in this section.
The governing equation for the fluid's porepressure is It is assumed that and are constant, and that holds (this is the ideal gas equation of state). In this formula is the gas molar mass, is the gas constant and is the temperature.
The equation governing the temperature is assumed to be just the fluid advection equation As in the previous section, heat conduction could be added, but it is actually irrelevant since the solution to the problem below is constant . The enthalpy, , for an ideal gas is
The boundary conditions at the left-hand end are Physically these correspond to fluid and heat being removed or added to the left-hand end by some external source in order to keep the porepressure and temperature fixed.
The porepressure boundary condition at the right-hand end of the bar is (2) Physically this corresponds to the mass-flow through the boundary being proportional to . Here is a fixed "environmental" porepressure, and this acts as a source or sink of fluid. is the "conductance" of the boundary. Notice the appearance of in the LHS of this equation means that this is truly a flux of fluid mass (measured in kg.m.s), and the appearance of on the RHS means that a PorousFlowPiecewiseLinearFlux may be used with use_mobility=true.
The temperature boundary condition at the right-hand end of the bar is Comparing this with Eq. (2), it is seen that this is exactly the heat loss (or gain) at the boundary corresponding to the loss (or gain) of the fluid. Notice the appearance of in the LHS of this equation means that this is truly a flux of fluid mass (measured in J.m.s), and the appearance of on the RHS means that a PorousFlowPiecewiseLinearFlux may be used with use_mobility=true and use_enthalpy=true.
There is a clear similarity between the fluid and heat equations. The heat equation does not actually depend on temperature, and is simply which is solved by The fluid equation then yields The constant may be determined from the either of the boundary conditions. For the special case of and , the solution is MOOSE produces this result exactly, as illustrated in Figure 3
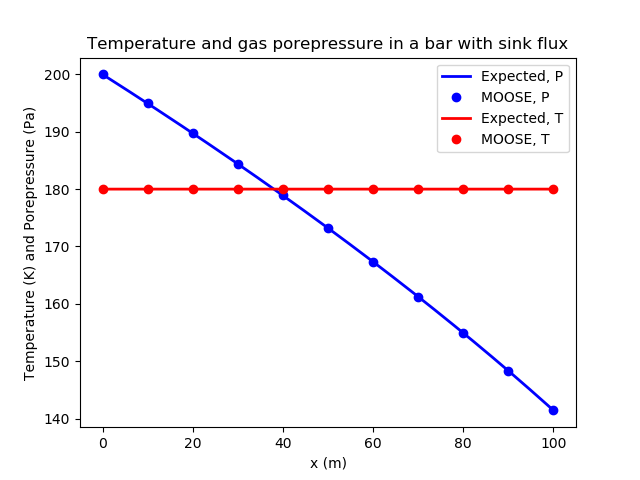
Figure 3: The steady-state porepressure and temperature distributions in the bar. MOOSE agrees well with theory illustrating that piecewise-linear fluid and heat sinks/sources as well as ideal fluids are correctly implemented in MOOSE.
# Newton cooling from a bar. 1-phase ideal fluid and heat, steady
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
type = GeneratedMesh
dim = 2
nx = 100
ny = 1
xmin = 0
xmax = 100
ymin = 0
ymax = 1
[]
[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
PorousFlowDictator = dictator
[]
[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
[dictator]
type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation. Jacobian entries involving derivatives wrt these variables will be computed. In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'pressure temp'
number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
[]
[pc]
type = PorousFlowCapillaryPressureVG<<<{"description": "van Genuchten capillary pressure", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureVG.html"}>>>
m<<<{"description": "van Genuchten exponent m. Must be between 0 and 1, and optimally should be set to >0.5"}>>> = 0.8
alpha<<<{"description": "van Genuchten parameter alpha. Must be positive"}>>> = 1e-5
[]
[]
[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
[pressure]
[]
[temp]
[]
[]
[ICs<<<{"href": "../../../../syntax/ICs/index.html"}>>>]
# have to start these reasonably close to their steady-state values
[pressure]
type = FunctionIC<<<{"description": "An initial condition that uses a normal function of x, y, z to produce values (and optionally gradients) for a field variable.", "href": "../../../../source/ics/FunctionIC.html"}>>>
variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = pressure
function<<<{"description": "The initial condition function."}>>> = '200-0.5*x'
[]
[temperature]
type = FunctionIC<<<{"description": "An initial condition that uses a normal function of x, y, z to produce values (and optionally gradients) for a field variable.", "href": "../../../../source/ics/FunctionIC.html"}>>>
variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = temp
function<<<{"description": "The initial condition function."}>>> = 180+0.1*x
[]
[]
[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
[flux]
type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[heat_advection]
type = PorousFlowHeatAdvection<<<{"description": "Fully-upwinded heat flux, advected by the fluid", "href": "../../../../source/kernels/PorousFlowHeatAdvection.html"}>>>
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temp
[]
[]
[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
[idealgas]
type = IdealGasFluidProperties<<<{"description": "Fluid properties for an ideal gas", "href": "../../../../source/fluidproperties/IdealGasFluidProperties.html"}>>>
molar_mass<<<{"description": "Constant molar mass of the fluid (kg/mol)"}>>> = 1.4
gamma<<<{"description": "gamma value (cp/cv)"}>>> = 1.2
mu<<<{"description": "Dynamic viscosity, Pa.s"}>>> = 1.2
[]
[]
[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
[temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
temperature<<<{"description": "Fluid temperature variable. Note, the default is suitable if your simulation is using Kelvin units, but probably not for Celsius"}>>> = temp
[]
[ppss]
type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = pressure
capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
[]
[massfrac]
type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
[]
[dens0]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = idealgas
phase<<<{"description": "The phase number"}>>> = 0
[]
[permeability]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1.1 0 0 0 1.1 0 0 0 1.1'
[]
[relperm]
type = PorousFlowRelativePermeabilityCorey<<<{"description": "This Material calculates relative permeability of the fluid phase, using the simple Corey model ((S-S_res)/(1-sum(S_res)))^n", "href": "../../../../source/materials/PorousFlowRelativePermeabilityCorey.html"}>>> # irrelevant in this fully-saturated situation
n<<<{"description": "The Corey exponent of the phase."}>>> = 2
phase<<<{"description": "The phase number"}>>> = 0
[]
[]
[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
[leftp]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
value<<<{"description": "Value of the BC"}>>> = 200
[]
[leftt]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temp
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
value<<<{"description": "Value of the BC"}>>> = 180
[]
[newtonp]
type = PorousFlowPiecewiseLinearSink<<<{"description": "Applies a flux sink to a boundary. The base flux defined by PorousFlowSink is multiplied by a piecewise linear function.", "href": "../../../../source/bcs/PorousFlowPiecewiseLinearSink.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
pt_vals<<<{"description": "Tuple of pressure values (for the fluid_phase specified). Must be monotonically increasing. For heat fluxes that don't involve fluids, these are temperature values"}>>> = '-200 0 200'
multipliers<<<{"description": "Tuple of multiplying values. The flux values are multiplied by these."}>>> = '-200 0 200'
use_mobility<<<{"description": "If true, then fluxes are multiplied by (density*permeability_nn/viscosity), where the '_nn' indicates the component normal to the boundary. In this case bare_flux is measured in Pa.m^-1. This can be used in conjunction with other use_*"}>>> = true
use_relperm<<<{"description": "If true, then fluxes are multiplied by relative permeability. This can be used in conjunction with other use_*"}>>> = true
fluid_phase<<<{"description": "If supplied, then this BC will potentially be a function of fluid pressure, and you can use mass_fraction_component, use_mobility, use_relperm, use_enthalpy and use_energy. If not supplied, then this BC can only be a function of temperature"}>>> = 0
flux_function<<<{"description": "The flux. The flux is OUT of the medium: hence positive values of this function means this BC will act as a SINK, while negative values indicate this flux will be a SOURCE. The functional form is useful for spatially or temporally varying sinks. Without any use_*, this function is measured in kg.m^-2.s^-1 (or J.m^-2.s^-1 for the case with only heat and no fluids)"}>>> = 0.005 # 1/2/L
[]
[newtont]
type = PorousFlowPiecewiseLinearSink<<<{"description": "Applies a flux sink to a boundary. The base flux defined by PorousFlowSink is multiplied by a piecewise linear function.", "href": "../../../../source/bcs/PorousFlowPiecewiseLinearSink.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temp
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
pt_vals<<<{"description": "Tuple of pressure values (for the fluid_phase specified). Must be monotonically increasing. For heat fluxes that don't involve fluids, these are temperature values"}>>> = '-200 0 200'
multipliers<<<{"description": "Tuple of multiplying values. The flux values are multiplied by these."}>>> = '-200 0 200'
use_mobility<<<{"description": "If true, then fluxes are multiplied by (density*permeability_nn/viscosity), where the '_nn' indicates the component normal to the boundary. In this case bare_flux is measured in Pa.m^-1. This can be used in conjunction with other use_*"}>>> = true
use_relperm<<<{"description": "If true, then fluxes are multiplied by relative permeability. This can be used in conjunction with other use_*"}>>> = true
use_enthalpy<<<{"description": "If true, then fluxes are multiplied by enthalpy. In this case bare_flux is measured in kg.m^-2.s^-1 / (J.kg). This can be used in conjunction with other use_*"}>>> = true
fluid_phase<<<{"description": "If supplied, then this BC will potentially be a function of fluid pressure, and you can use mass_fraction_component, use_mobility, use_relperm, use_enthalpy and use_energy. If not supplied, then this BC can only be a function of temperature"}>>> = 0
flux_function<<<{"description": "The flux. The flux is OUT of the medium: hence positive values of this function means this BC will act as a SINK, while negative values indicate this flux will be a SOURCE. The functional form is useful for spatially or temporally varying sinks. Without any use_*, this function is measured in kg.m^-2.s^-1 (or J.m^-2.s^-1 for the case with only heat and no fluids)"}>>> = 0.005 # 1/2/L
[]
[]
[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
[porepressure]
type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = pressure
start_point<<<{"description": "The beginning of the line"}>>> = '0 0.5 0'
end_point<<<{"description": "The ending of the line"}>>> = '100 0.5 0'
sort_by<<<{"description": "What to sort the samples by"}>>> = x
num_points<<<{"description": "The number of points to sample along the line"}>>> = 11
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[]
[temperature]
type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = temp
start_point<<<{"description": "The beginning of the line"}>>> = '0 0.5 0'
end_point<<<{"description": "The ending of the line"}>>> = '100 0.5 0'
sort_by<<<{"description": "What to sort the samples by"}>>> = x
num_points<<<{"description": "The number of points to sample along the line"}>>> = 11
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[]
[]
[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
[andy]
type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
[]
[]
[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
type = Steady
solve_type = Newton
nl_rel_tol = 1E-10
nl_abs_tol = 1E-15
[]
[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = nc08
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[along_line]
type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
execute_vector_postprocessors_on<<<{"description": "Enable/disable the output of VectorPostprocessors"}>>> = timestep_end
[]
[]