Radial flow from an injection well
This problem was presented in Pruess et al. (2002) and Pruess et al. (2004) as intercomparison problem 3. It serves as a useful test as injection into a one dimensional radial reservoir admits a similarity solution , where is the radial distance from the injection well, and is time. This similarity solution holds even when complicated physics, such as mutual solubility of fluid components, is included.
Model
Reservoir properties
The properties of the reservoir used in the model are summarized in Table 1.
Table 1: Reservoir properties
| Property | Value |
|---|---|
| Pressure | 12 MPa |
| Temperature | 45 C |
| Permeability | m (100 md) |
| Porosity | 0.12 |
| NaCl mass fraction | 0.15 |
Relative permeability of the aqueous phase is represented by a van Genuchten model, with exponent and residual saturation . Gas phase relative permeability is represented using a Corey model, with exponent and residual saturation . Capillary pressure is given by a van Genuchten model, again with exponent , but this time with zero residual saturation.
Unlike other simulators used in the intercomparison study, PorousFlow is able to model this problem using a one-dimensional mesh that is rotated about the vertical axis to represent a true 1D radial model. TOUGH2, in contrast, uses a 2D mesh rotated about the vertical axis, which is why the model presented in Pruess et al. (2004) has a height of 100m. For this problem, we use a 1D mesh, and reduce the rate of injection accordingly so that 1 kg/s of CO is injected at the origin.
Results
Figure 1 shows the evolution of the saturation front of the CO-rich gas phase in this problem. It is interesting to observe the presence of a fully gas saturated region near the injection point that emerges after sufficient time. In the model, the residual saturation of the liquid phase is set to 0.3. For liquid saturations below this, the relative permeability is zero, and no advection of the liquid phase is possible. However, in this miscible model, the brine below residual saturation is slowly evaporated into the gas phase as it is injected, whereby the liquid fluid component is advected as part of the gas phase. This drying out process continues until all of the aqueous phase is removed.
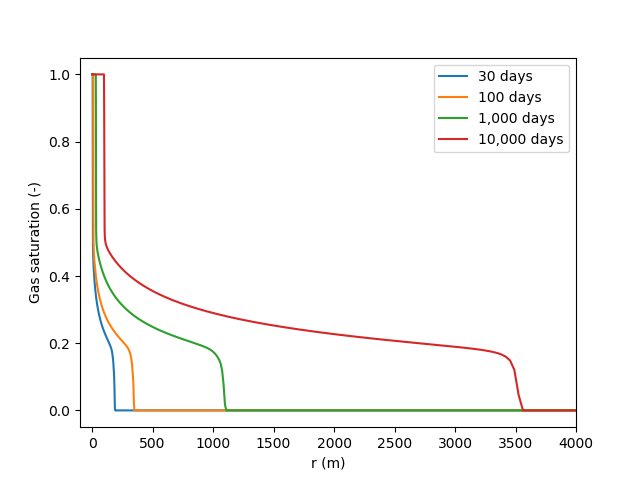
Figure 1: Gas saturation profile at various times
As previously stated, this one-dimensional radial model admits a similarity solution. Figure 2 shows a comparison of the four profiles presented in Figure 1 as a function of the similarity variable . As this figure shows, all four profiles are essentially coincident. As discussed in Pruess et al. (2002), three distinct regions can be observed. For , no aqueous phase is present (note that some liquid fluid component can be present in the gas phase, as discussed earlier). This region corresponds to small radial distances and long times. For , both gas and liquid phases coexist, while for , only a liquid phase is present (the gas phase hasn't reached this radial distance yet).
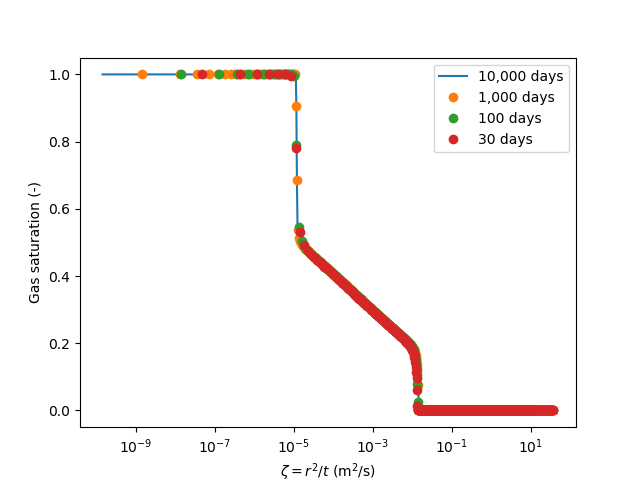
Figure 2: Gas saturation profile vs similarity variable
The similarity solution can also be verified by comparing the spatial results at a fixed time with the temporal results at a fixed radial distance. Examples of this are presented in Figure 3 and Figure 4 for the mass fraction of CO in the liquid phase (dissolved) and the mass fraction of HO in the gas phase (evaporation). In the two-phase region , each of these mass fractions are given by their equilibrium value. Outside the two-phase region, these mass fractions are zero, as expected. We observe good agreement between the two results (spatial profile and temporal profile), which provides further evidence of the presence of a similarity solution (some minor oscillation is observed in the temporal profile due to the finite grid size).
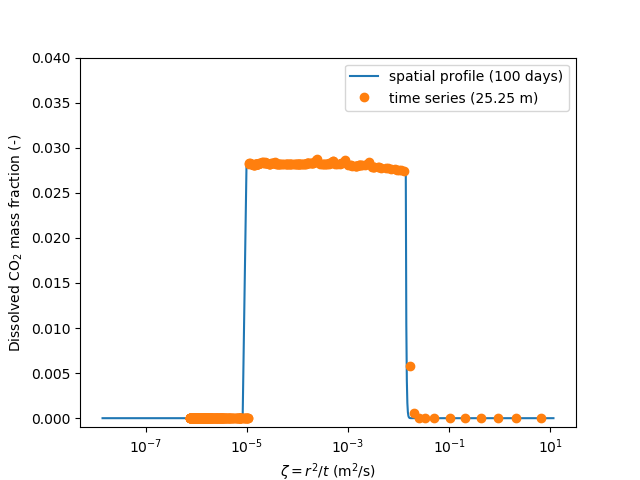
Figure 3: Mass fraction of CO in the liquid phase vs similarity variable
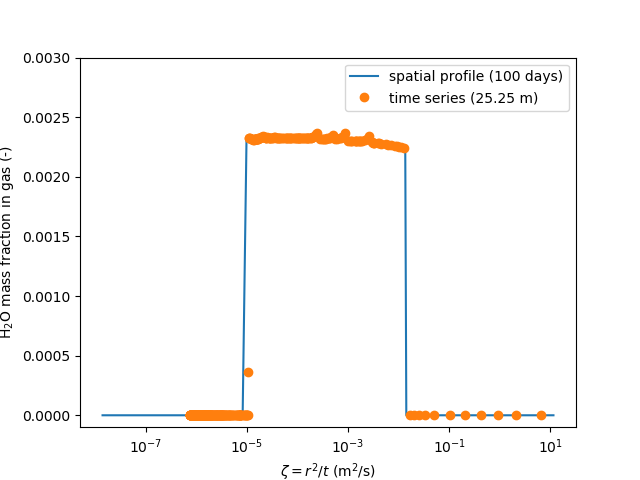
Figure 4: Mass fraction of HO in the liquid phase vs similarity variable
Note that these results are slightly different to the results presented in Pruess et al. (2002) and Pruess et al. (2004). This is because PorousFlow features an updated equation of state which was not available when the intercomparison results were first published. However, they do exhibit excellent agreement with the results presented in Pruess (2005) for a version of TOUGH2 that uses the updated equation of state.
The second part of this intercomparison problem was to compare thermophysical properties of the fluids between codes. Phase densities and viscosities, as well as equilibrium solubilities, were compared for various pressures at a specified temperature of C. The results obtained using PorousFlow are summarized in Table 2 and Table 3 for water and brine, respectively.
Table 2: Phase properties and equilibrium solubilities for water (zero salinity)
| Pressure (MPa) | (kg m) | ( kg m s) | (kg m) | ( kg m s) | ||
|---|---|---|---|---|---|---|
| 12 | 1006.35 | 5.978 | 657.87 | 5.127 | 0.052 | 0.0021 |
| 16 | 1008.72 | 5.986 | 759.86 | 6.470 | 0.055 | 0.0024 |
| 20 | 1010.90 | 5.993 | 812.65 | 7.336 | 0.058 | 0.0025 |
| 24 | 1012.73 | 6.001 | 849.38 | 8.030 | 0.059 | 0.0026 |
The phase properties for water and CO are nearly identical to the results presented in Pruess et al. (2002) for the TOUGH2 simulator (Pruess et al., 1999), as expected. This is because the mutual solubility model implemented in PorousFlow is the same as that used in TOUGH2, see the brine-co2 documentation for details.
Table 3: Phase properties and equilibrium solubilities for brine ()
| Pressure (MPa) | (kg m) | ( kg m s) | (kg m) | ( kg m s) | ||
|---|---|---|---|---|---|---|
| 12 | 1102.96 | 8.286 | 657.87 | 5.127 | 0.025 | 0.0019 |
| 16 | 1104.72 | 8.296 | 759.86 | 6.470 | 0.027 | 0.0022 |
| 20 | 1106.39 | 8.307 | 812.65 | 7.336 | 0.028 | 0.0023 |
| 24 | 1108.02 | 8.317 | 849.38 | 8.030 | 0.029 | 0.0024 |
Similarly, the phase properties for brine and CO are very similar to those obtained using TOUGH2 (Pruess et al., 2002), again as expected.
References
- K. Pruess, C. Oldenburg, and G. Moridis.
TOUGH2 User's Guide, Version 2.0.
Technical Report LBNL-43134, Lawrence Berkeley National Laboratory, Berkeley CA, USA, 1999.[BibTeX]
- Karsten Pruess.
ECO2N: A TOUGH2 fluid property module for mixtures of water, NaCl, and CO2.
Technical Report LBNL-57952, Lawrence Berkeley National Laboratory, Berkeley CA, USA, 2005.[BibTeX]
- Karsten Pruess, Julio García, Tony Kovscek, Curt Oldenburg, Jonny Rutqvist, Carl Steefel, and Tianfu Xu.
Intercomparison of numerical simulation codes for geologic disposal of co2.
Technical Report LBNL-51813, Lawrence Berkeley National Laboratory, Berkeley CA, USA, 2002.[BibTeX]
- Karsten Pruess, Julio García, Tony Kovscek, Curt Oldenburg, Jonny Rutqvist, Carl Steefel, and Tianfu Xu.
Code intercomparison builds confidence in numerical simulation models for geologic disposal of co2.
Energy, 29(9-10):1431–1444, 2004.[BibTeX]