Rotating Circle

The second example is a typical benchmark problem for the level set equation: a rotating bubble. The problem involves initializing $var element = document.getElementById("moose-equation-19cf37a4-6ab7-453a-a433-7d79993b7413");katex.render("u_h", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ (see Theory) with a "bubble" of radius 0.15 at $var element = document.getElementById("moose-equation-137faecb-72cb-4168-9921-10c88065fc89");katex.render("(0.0, 0.5)", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ for $var element = document.getElementById("moose-equation-563a0ebf-1a7c-4a57-bfdb-cd0a1af37739");katex.render("\\Omega = [-1,1]^2", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ . This bubble is then advected with the given velocity field $var element = document.getElementById("moose-equation-cbc34b50-605b-4cdf-83f6-c020f3524055");katex.render("\\vec{v}=(4y,-4x)", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , so that, at $var element = document.getElementById("moose-equation-f281c963-08a0-4292-88c0-3fde62985b48");katex.render("t=\\pi/2", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , the bubble should return to its original position.

Level Set Equation

Figure 1 show the results of solving the rotating bubble problem with the level set equation alone, which initially behaves in a consistent manner. However, near the end of the simulation node-to-node oscillations appear in the solution, which is evident in the contour lines shown in Figure 1. As expected, these oscillations influence the area of the region encapsulated by the 0.5 level set contour as shown in Figure 4 and discussed in the Area Comparison section.

The complete input file for running this portion of the example is included below and it may be executed as follows.


cd ~/projects/moose/module/level_set/examples/rotating_circle
../../level_set-opt -i rotating_circle.i

[Mesh<<<{"href": "../../syntax/Mesh/index.html"}>>>]
  type = GeneratedMesh
  dim = 2
  xmin = -1
  xmax = 1
  ymin = -1
  ymax = 1
  nx = 32
  ny = 32
  uniform_refine<<<{"description": "Specify the level of uniform refinement applied to the initial mesh"}>>> = 2
[]

[AuxVariables<<<{"href": "../../syntax/AuxVariables/index.html"}>>>]
  [./velocity]
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = LAGRANGE_VEC
  [../]
[]

[Variables<<<{"href": "../../syntax/Variables/index.html"}>>>]
  [./phi]
  [../]
[]

[Functions<<<{"href": "../../syntax/Functions/index.html"}>>>]
  [./phi_exact]
    type = LevelSetOlssonBubble<<<{"description": "Implementation of 'bubble' ranging from 0 to 1.", "href": "../../source/functions/LevelSetOlssonBubble.html"}>>>
    epsilon<<<{"description": "The interface thickness."}>>> = 0.03
    center<<<{"description": "The center of the bubble."}>>> = '0 0.5 0'
    radius<<<{"description": "The radius of the bubble."}>>> = 0.15
  [../]
  [./velocity_func]
    type = ParsedVectorFunction<<<{"description": "Returns a vector function based on string descriptions for each component.", "href": "../../source/functions/MooseParsedVectorFunction.html"}>>>
    expression_x<<<{"description": "x-component of function."}>>> = '4*y'
    expression_y<<<{"description": "y-component of function."}>>> = '-4*x'
  [../]
[]

[ICs<<<{"href": "../../syntax/ICs/index.html"}>>>]
  [./phi_ic]
    type = FunctionIC<<<{"description": "An initial condition that uses a normal function of x, y, z to produce values (and optionally gradients) for a field variable.", "href": "../../source/ics/FunctionIC.html"}>>>
    function<<<{"description": "The initial condition function."}>>> = phi_exact
    variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = phi
  [../]
  [./vel_ic]
    type = VectorFunctionIC<<<{"description": "Sets component values for a vector field variable based on a vector function.", "href": "../../source/ics/VectorFunctionIC.html"}>>>
    variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = velocity
    function<<<{"description": "The initial condition vector function. This cannot be supplied with the component parameters."}>>> = velocity_func
  []
[]

[Kernels<<<{"href": "../../syntax/Kernels/index.html"}>>>]
  [./time]
    type = TimeDerivative<<<{"description": "The time derivative operator with the weak form of $(\\psi_i, \\frac{\\partial u_h}{\\partial t})$.", "href": "../../source/kernels/TimeDerivative.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = phi
  [../]

  [./advection]
    type = LevelSetAdvection<<<{"description": "Implements the level set advection equation: $\\vec{v}\\cdot\\nabla u = 0$, where the weak form is $(\\psi_i, \\vec{v}\\cdot\\nabla u) = 0$.", "href": "../../source/kernels/LevelSetAdvection.html"}>>>
    velocity<<<{"description": "Velocity vector variable."}>>> = velocity
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = phi
  [../]
[]

[Postprocessors<<<{"href": "../../syntax/Postprocessors/index.html"}>>>]
  [./area]
    type = LevelSetVolume<<<{"description": "Compute the area or volume of the region inside or outside of a level set contour.", "href": "../../source/postprocessors/LevelSetVolume.html"}>>>
    threshold<<<{"description": "The level set threshold to consider for computing area/volume."}>>> = 0.5
    variable<<<{"description": "The name of the variable that this postprocessor operates on"}>>> = phi
    location<<<{"description": "The location of the area/volume to be computed."}>>> = outside
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'initial timestep_end'
  [../]
  [./cfl]
    type = LevelSetCFLCondition<<<{"description": "Compute the minimum timestep from the Courant-Friedrichs-Lewy (CFL) condition for the level-set equation.", "href": "../../source/postprocessors/LevelSetCFLCondition.html"}>>>
    velocity<<<{"description": "Velocity vector variable."}>>> = velocity
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'initial' #timestep_end'
  [../]
[]

[Executioner<<<{"href": "../../syntax/Executioner/index.html"}>>>]
  type = Transient
  solve_type = PJFNK
  start_time = 0
  end_time = 1.570796
  scheme = crank-nicolson
  petsc_options_iname = '-pc_type -sub_pc_type'
  petsc_options_value = 'asm      ilu'
  [./TimeStepper<<<{"href": "../../syntax/Executioner/TimeStepper/index.html"}>>>]
    type = PostprocessorDT
    postprocessor = cfl
    scale = 0.8
  [../]
[]

[Outputs<<<{"href": "../../syntax/Outputs/index.html"}>>>]
  csv<<<{"description": "Output the scalar variable and postprocessors to a *.csv file using the default CSV output."}>>> = true
  exodus<<<{"description": "Output the results using the default settings for Exodus output."}>>> = true
[]

Level Set Equation with SUPG

Adding SUPG stabilization—set the theory for details—mitigates the oscillations present in the first step, as shown in Figure 2. Adding the SUPG stabilization is trivial simply add the time and advection SUPG kernels to the input file ((modules/level_set/examples/rotating_circle/circle_rotate_supg.i)) shown previously, the kernels block will then appear as:

[Kernels<<<{"href": "../../syntax/Kernels/index.html"}>>>]
  [./time]
    type = TimeDerivative<<<{"description": "The time derivative operator with the weak form of $(\\psi_i, \\frac{\\partial u_h}{\\partial t})$.", "href": "../../source/kernels/TimeDerivative.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = phi
  [../]
  [./advection]
    type = LevelSetAdvection<<<{"description": "Implements the level set advection equation: $\\vec{v}\\cdot\\nabla u = 0$, where the weak form is $(\\psi_i, \\vec{v}\\cdot\\nabla u) = 0$.", "href": "../../source/kernels/LevelSetAdvection.html"}>>>
    velocity<<<{"description": "Velocity vector variable."}>>> = velocity
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = phi
  [../]
  [./advection_supg]
    type = LevelSetAdvectionSUPG<<<{"description": "SUPG stablization term for the advection portion of the level set equation.", "href": "../../source/kernels/LevelSetAdvectionSUPG.html"}>>>
    velocity<<<{"description": "Velocity vector variable."}>>> = velocity
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = phi
  [../]
  [./time_supg]
    type = LevelSetTimeDerivativeSUPG<<<{"description": "SUPG stablization terms for the time derivative of the level set equation.", "href": "../../source/kernels/LevelSetTimeDerivativeSUPG.html"}>>>
    velocity<<<{"description": "Velocity vector variable."}>>> = velocity
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = phi
  [../]
[]

Adding the stabilization improve the numerical solution but it suffers from a loss of conservation of the phase field variable, as discussed in the Area Comparison section and shown in Figure 4.

Level Set Equation with Reinitialization

Adding reinitialization, in this case the scheme proposed by Olsson et al. (2007), requires the use of the MOOSE MultiApp. The enable reinitialization two input files are required: a parent and sub-application.

The parent input file must add the necessary MultiApps and Transfers blocks. For the problem at hand ((modules/level_set/examples/rotating_circle/circle_rotate_parent.i)) this easily accomplished by adding the following to the input file from the first step (i.e., do not include the SUPG kernels).

[MultiApps<<<{"href": "../../syntax/MultiApps/index.html"}>>>]
  [./reinit]
    type = LevelSetReinitializationMultiApp<<<{"description": "MultiApp capable of performing repeated complete solves for level set reinitialization.", "href": "../../source/multiapps/LevelSetReinitializationMultiApp.html"}>>>
    input_files<<<{"description": "The input file for each App.  If this parameter only contains one input file it will be used for all of the Apps.  When using 'positions_from_file' it is also admissable to provide one input_file per file."}>>> = 'circle_rotate_sub.i'
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'timestep_end'
  [../]
[]

[Transfers<<<{"href": "../../syntax/Transfers/index.html"}>>>]
  [./to_sub]
    type = MultiAppCopyTransfer<<<{"description": "Copies variables (nonlinear and auxiliary) between multiapps that have identical meshes.", "href": "../../source/transfers/MultiAppCopyTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = phi
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = phi
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = reinit
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'timestep_end'
  [../]
  [./to_sub_init]
    type = MultiAppCopyTransfer<<<{"description": "Copies variables (nonlinear and auxiliary) between multiapps that have identical meshes.", "href": "../../source/transfers/MultiAppCopyTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = phi
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = phi_0
    to_multi_app<<<{"description": "The name of the MultiApp to transfer the data to"}>>> = reinit
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'timestep_end'
  [../]
  [./from_sub]
    type = MultiAppCopyTransfer<<<{"description": "Copies variables (nonlinear and auxiliary) between multiapps that have identical meshes.", "href": "../../source/transfers/MultiAppCopyTransfer.html"}>>>
    source_variable<<<{"description": "The variable to transfer from."}>>> = phi
    variable<<<{"description": "The auxiliary variable to store the transferred values in."}>>> = phi
    from_multi_app<<<{"description": "The name of the MultiApp to receive data from"}>>> = reinit
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'timestep_end'
  [../]
[]

Next, the sub-application input file must be created, which is shown below. This input file mimics the parent input file closely, with three notable exceptions. First, the Kernels block utilize the time derivative and a new object, LevelSetOlssonReinitialization, that implements the reinitialization scheme of Olsson et al. (2007). Second, the Problem is set to use the LevelSetReinitializationProblem. Finally, the UserObjects block includes a terminator, LevelSetOlssonTerminator, which is responsible for stopping the reinitialization solve when steady-state is achieved according to the criteria defined by Olsson et al. (2007).

[Mesh<<<{"href": "../../syntax/Mesh/index.html"}>>>]
  type = GeneratedMesh
  dim = 2
  xmin = -1
  xmax = 1
  ymin = -1
  ymax = 1
  nx = 32
  ny = 32
  uniform_refine<<<{"description": "Specify the level of uniform refinement applied to the initial mesh"}>>> = 2
[]

[Variables<<<{"href": "../../syntax/Variables/index.html"}>>>]
  [./phi]
  [../]
[]

[AuxVariables<<<{"href": "../../syntax/AuxVariables/index.html"}>>>]
  [./phi_0]
  [../]
  [./marker]
  [../]
[]

[Kernels<<<{"href": "../../syntax/Kernels/index.html"}>>>]
  [./time]
    type = TimeDerivative<<<{"description": "The time derivative operator with the weak form of $(\\psi_i, \\frac{\\partial u_h}{\\partial t})$.", "href": "../../source/kernels/TimeDerivative.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = phi
  [../]
  [./reinit]
    type = LevelSetOlssonReinitialization<<<{"description": "The re-initialization equation defined by Olsson et. al. (2007).", "href": "../../source/kernels/LevelSetOlssonReinitialization.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = phi
    phi_0<<<{"description": "The level set variable to be reinitialized as signed distance function."}>>> = phi_0
    epsilon<<<{"description": "The epsilon coefficient to be used in the reinitialization calculation."}>>> = 0.03
  [../]
[]

[Problem<<<{"href": "../../syntax/Problem/index.html"}>>>]
  type = LevelSetReinitializationProblem
[]

[UserObjects<<<{"href": "../../syntax/UserObjects/index.html"}>>>]
  [./arnold]
    type = LevelSetOlssonTerminator<<<{"description": "Tool for terminating the reinitialization of the level set equation based on the criteria defined by Olsson et. al. (2007).", "href": "../../source/userobjects/LevelSetOlssonTerminator.html"}>>>
    tol<<<{"description": "The limit at which the reinitialization problem is considered converged."}>>> = 1
    min_steps<<<{"description": "The minimum number of time steps to consider."}>>> = 3
  [../]
[]

[Executioner<<<{"href": "../../syntax/Executioner/index.html"}>>>]
  type = Transient
  solve_type = NEWTON
  start_time = 0
  num_steps = 100
  nl_abs_tol = 1e-14
  scheme = crank-nicolson
  line_search = none
  petsc_options_iname = '-pc_type -sub_pc_type'
  petsc_options_value = 'asm      ilu'
  dt = 0.003
[]

[Outputs<<<{"href": "../../syntax/Outputs/index.html"}>>>]
[]

Figure 3 shows the results of the bubble problem with reinitialization, the result looks similar to the SUPG result. However, if you consider the area conservation discussed in the Area Comparison section, the reinitialization scheme yields the superior solution for this problem.

Figure 1: Results from solving the rotating circle problem with the level set equation alone.

Figure 2: Results from solving the rotating circle problem with the level set equation using SUPG stabilization.

Figure 3: Results from solving the rotating circle problem with the level set equation with reinitialization.

Area Comparison

Figure 4 is a plot of the area of the circle during the three simulations. Note that in the unstabilized, un-reinitialized level set equation, both area conservation and stability issues are readily apparent. The instabilities are especially obvious in Figure 4, where the drastic area changes are due to numerical oscillations in the solution field. Adding SUPG stabilization helps ameliorate the stability concern but it suffers from loss of area conservation. The re-initialization scheme is both stable and area-conserving.

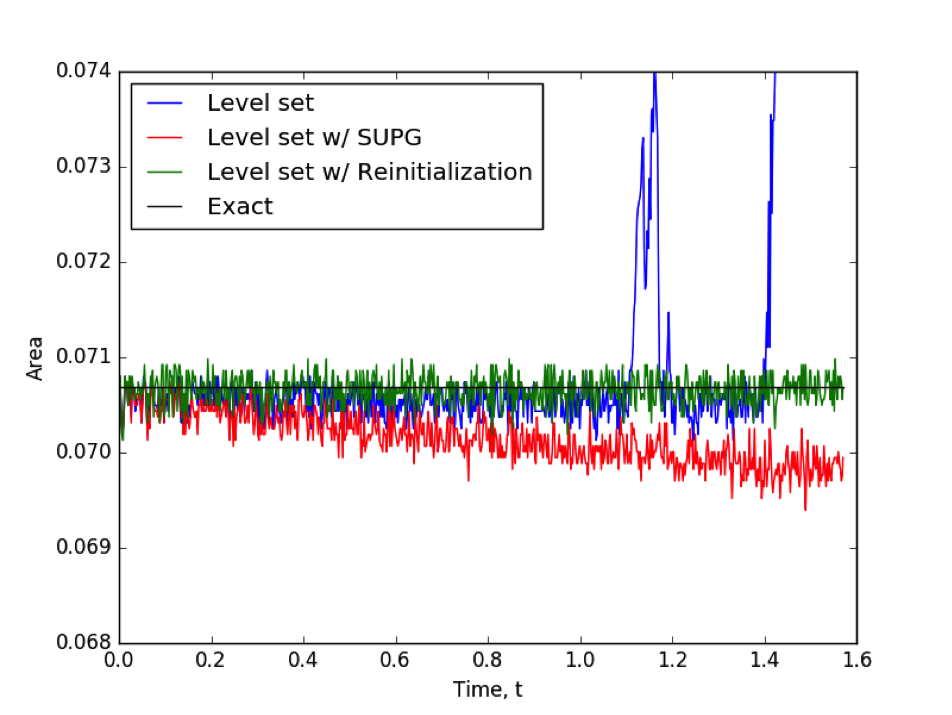
Figure 4: Comparison of area inside the bubble during simulations.

The re-initialization methods performs well, but it is computationally expensive and picking the pseudo timestep size $var element = document.getElementById("moose-equation-23a1d2f0-1073-4d31-8748-d4704bdb434d");katex.render("\\Delta \\tau", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , steady-state criteria $var element = document.getElementById("moose-equation-56e7a89b-a421-45bb-bcf6-f69fb23e3df2");katex.render("\\delta", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , and interface thickness $var element = document.getElementById("moose-equation-df487d4d-37e3-41a5-a2ad-8303000ad62d");katex.render("\\epsilon", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ correctly for the re-initialization problem is a non-trivial difficulty. Nevertheless, the level set module provides a valuable starting point and proof-of-concept for other researchers interested in the method, and the existing algorithm can no doubt be tuned to the needs of specific applications in terms of conservation and computational cost requirements.

References

Elin Olsson, Gunilla Kreiss, and Sara Zahedi. A conservative level set method for two phase flow ii. Journal of Computational Physics, 225(1):785–807, 2007. URL: http://dx.doi.org/10.1016/j.jcp.2006.12.027.

@article{olsson2007conservative,
    author = "Olsson, Elin and Kreiss, Gunilla and Zahedi, Sara",
    title = "A conservative level set method for two phase flow II",
    journal = "Journal of Computational Physics",
    volume = "225",
    number = "1",
    pages = "785--807",
    year = "2007",
    publisher = "Elsevier",
    url = "http://dx.doi.org/10.1016/j.jcp.2006.12.027"
}

(modules/level_set/examples/rotating_circle/circle_rotate.i)

[Mesh]
  type = GeneratedMesh
  dim = 2
  xmin = -1
  xmax = 1
  ymin = -1
  ymax = 1
  nx = 32
  ny = 32
  uniform_refine = 2
[]

[AuxVariables]
  [./velocity]
    family = LAGRANGE_VEC
  [../]
[]

[Variables]
  [./phi]
  [../]
[]

[Functions]
  [./phi_exact]
    type = LevelSetOlssonBubble
    epsilon = 0.03
    center = '0 0.5 0'
    radius = 0.15
  [../]
  [./velocity_func]
    type = ParsedVectorFunction
    expression_x = '4*y'
    expression_y = '-4*x'
  [../]
[]

[ICs]
  [./phi_ic]
    type = FunctionIC
    function = phi_exact
    variable = phi
  [../]
  [./vel_ic]
    type = VectorFunctionIC
    variable = velocity
    function = velocity_func
  []
[]

[Kernels]
  [./time]
    type = TimeDerivative
    variable = phi
  [../]

  [./advection]
    type = LevelSetAdvection
    velocity = velocity
    variable = phi
  [../]
[]

[Postprocessors]
  [./area]
    type = LevelSetVolume
    threshold = 0.5
    variable = phi
    location = outside
    execute_on = 'initial timestep_end'
  [../]
  [./cfl]
    type = LevelSetCFLCondition
    velocity = velocity
    execute_on = 'initial' #timestep_end'
  [../]
[]

[Executioner]
  type = Transient
  solve_type = PJFNK
  start_time = 0
  end_time = 1.570796
  scheme = crank-nicolson
  petsc_options_iname = '-pc_type -sub_pc_type'
  petsc_options_value = 'asm      ilu'
  [./TimeStepper]
    type = PostprocessorDT
    postprocessor = cfl
    scale = 0.8
  [../]
[]

[Outputs]
  csv = true
  exodus = true
[]

(modules/level_set/examples/rotating_circle/circle_rotate_supg.i)

[Mesh]
  type = GeneratedMesh
  dim = 2
  xmin = -1
  xmax = 1
  ymin = -1
  ymax = 1
  nx = 32
  ny = 32
  uniform_refine = 2
[]

[AuxVariables]
  [./velocity]
    family = LAGRANGE_VEC
  [../]
[]

[Variables]
  [./phi]
  [../]
[]

[Functions]
  [./phi_exact]
    type = LevelSetOlssonBubble
    epsilon = 0.03
    center = '0 0.5 0'
    radius = 0.15
  [../]
  [./velocity_func]
    type = ParsedVectorFunction
    expression_x = '4*y'
    expression_y = '-4*x'
  [../]
[]

[ICs]
  [./phi_ic]
    type = FunctionIC
    function = phi_exact
    variable = phi
  [../]
  [./vel_ic]
    type = VectorFunctionIC
    variable = velocity
    function = velocity_func
  []
[]

[Kernels]
  [./time]
    type = TimeDerivative
    variable = phi
  [../]
  [./advection]
    type = LevelSetAdvection
    velocity = velocity
    variable = phi
  [../]
  [./advection_supg]
    type = LevelSetAdvectionSUPG
    velocity = velocity
    variable = phi
  [../]
  [./time_supg]
    type = LevelSetTimeDerivativeSUPG
    velocity = velocity
    variable = phi
  [../]
[]

[Postprocessors]
  [./area]
    type = LevelSetVolume
    threshold = 0.5
    variable = phi
    location = outside
    execute_on = 'initial timestep_end'
  [../]
  [./cfl]
    type = LevelSetCFLCondition
    velocity = velocity
    execute_on = 'initial'
  [../]
[]

[Executioner]
  type = Transient
  solve_type = PJFNK
  start_time = 0
  end_time = 1.570796
  scheme = crank-nicolson
  petsc_options_iname = '-pc_type -sub_pc_type'
  petsc_options_value = 'asm      ilu'
  [./TimeStepper]
    type = PostprocessorDT
    postprocessor = cfl
    scale = 0.8
  [../]
[]

[Outputs]
  csv = true
  exodus = true
[]

(modules/level_set/examples/rotating_circle/circle_rotate_supg.i)

[Mesh]
  type = GeneratedMesh
  dim = 2
  xmin = -1
  xmax = 1
  ymin = -1
  ymax = 1
  nx = 32
  ny = 32
  uniform_refine = 2
[]

[AuxVariables]
  [./velocity]
    family = LAGRANGE_VEC
  [../]
[]

[Variables]
  [./phi]
  [../]
[]

[Functions]
  [./phi_exact]
    type = LevelSetOlssonBubble
    epsilon = 0.03
    center = '0 0.5 0'
    radius = 0.15
  [../]
  [./velocity_func]
    type = ParsedVectorFunction
    expression_x = '4*y'
    expression_y = '-4*x'
  [../]
[]

[ICs]
  [./phi_ic]
    type = FunctionIC
    function = phi_exact
    variable = phi
  [../]
  [./vel_ic]
    type = VectorFunctionIC
    variable = velocity
    function = velocity_func
  []
[]

[Kernels]
  [./time]
    type = TimeDerivative
    variable = phi
  [../]
  [./advection]
    type = LevelSetAdvection
    velocity = velocity
    variable = phi
  [../]
  [./advection_supg]
    type = LevelSetAdvectionSUPG
    velocity = velocity
    variable = phi
  [../]
  [./time_supg]
    type = LevelSetTimeDerivativeSUPG
    velocity = velocity
    variable = phi
  [../]
[]

[Postprocessors]
  [./area]
    type = LevelSetVolume
    threshold = 0.5
    variable = phi
    location = outside
    execute_on = 'initial timestep_end'
  [../]
  [./cfl]
    type = LevelSetCFLCondition
    velocity = velocity
    execute_on = 'initial'
  [../]
[]

[Executioner]
  type = Transient
  solve_type = PJFNK
  start_time = 0
  end_time = 1.570796
  scheme = crank-nicolson
  petsc_options_iname = '-pc_type -sub_pc_type'
  petsc_options_value = 'asm      ilu'
  [./TimeStepper]
    type = PostprocessorDT
    postprocessor = cfl
    scale = 0.8
  [../]
[]

[Outputs]
  csv = true
  exodus = true
[]

(modules/level_set/examples/rotating_circle/circle_rotate_parent.i)

[Mesh]
  type = GeneratedMesh
  dim = 2
  xmin = -1
  xmax = 1
  ymin = -1
  ymax = 1
  nx = 32
  ny = 32
  uniform_refine = 2
[]

[AuxVariables]
  [./velocity]
    family = LAGRANGE_VEC
  [../]
[]

[Variables]
  [./phi]
  [../]
[]

[BCs]
  [./all]
    type = DirichletBC
    variable = phi
    boundary = 'top bottom left right'
    value = 0
  [../]
[]

[Functions]
  [./phi_exact]
    type = LevelSetOlssonBubble
    epsilon = 0.03
    center = '0 0.5 0'
    radius = 0.15
  [../]
  [./velocity_func]
    type = ParsedVectorFunction
    expression_x = '4*y'
    expression_y = '-4*x'
  [../]
[]

[ICs]
  [./phi_ic]
    type = FunctionIC
    function = phi_exact
    variable = phi
  [../]
  [./vel_ic]
    type = VectorFunctionIC
    variable = velocity
    function = velocity_func
  []
[]

[Kernels]
  [./time]
    type = TimeDerivative
    variable = phi
  [../]

  [./advection]
    type = LevelSetAdvection
    velocity = velocity
    variable = phi
  [../]
[]

[Postprocessors]
  [./area]
    type = LevelSetVolume
    threshold = 0.5
    variable = phi
    location = outside
    execute_on = 'initial timestep_end'
  [../]
  [./cfl]
    type = LevelSetCFLCondition
    velocity = velocity
    execute_on = 'initial timestep_end'
  [../]
[]

[Executioner]
  type = Transient
  solve_type = PJFNK
  start_time = 0
  end_time = 1.570796
  scheme = crank-nicolson
  petsc_options_iname = '-pc_type -sub_pc_type'
  petsc_options_value = 'asm      ilu'
  [./TimeStepper]
    type = PostprocessorDT
    postprocessor = cfl
    scale = 0.8
  [../]
[]

[MultiApps]
  [./reinit]
    type = LevelSetReinitializationMultiApp
    input_files = 'circle_rotate_sub.i'
    execute_on = 'timestep_end'
  [../]
[]

[Transfers]
  [./to_sub]
    type = MultiAppCopyTransfer
    source_variable = phi
    variable = phi
    to_multi_app = reinit
    execute_on = 'timestep_end'
  [../]
  [./to_sub_init]
    type = MultiAppCopyTransfer
    source_variable = phi
    variable = phi_0
    to_multi_app = reinit
    execute_on = 'timestep_end'
  [../]
  [./from_sub]
    type = MultiAppCopyTransfer
    source_variable = phi
    variable = phi
    from_multi_app = reinit
    execute_on = 'timestep_end'
  [../]
[]

[Outputs]
  csv = true
  exodus = true
[]

(modules/level_set/examples/rotating_circle/circle_rotate_parent.i)

[Mesh]
  type = GeneratedMesh
  dim = 2
  xmin = -1
  xmax = 1
  ymin = -1
  ymax = 1
  nx = 32
  ny = 32
  uniform_refine = 2
[]

[AuxVariables]
  [./velocity]
    family = LAGRANGE_VEC
  [../]
[]

[Variables]
  [./phi]
  [../]
[]

[BCs]
  [./all]
    type = DirichletBC
    variable = phi
    boundary = 'top bottom left right'
    value = 0
  [../]
[]

[Functions]
  [./phi_exact]
    type = LevelSetOlssonBubble
    epsilon = 0.03
    center = '0 0.5 0'
    radius = 0.15
  [../]
  [./velocity_func]
    type = ParsedVectorFunction
    expression_x = '4*y'
    expression_y = '-4*x'
  [../]
[]

[ICs]
  [./phi_ic]
    type = FunctionIC
    function = phi_exact
    variable = phi
  [../]
  [./vel_ic]
    type = VectorFunctionIC
    variable = velocity
    function = velocity_func
  []
[]

[Kernels]
  [./time]
    type = TimeDerivative
    variable = phi
  [../]

  [./advection]
    type = LevelSetAdvection
    velocity = velocity
    variable = phi
  [../]
[]

[Postprocessors]
  [./area]
    type = LevelSetVolume
    threshold = 0.5
    variable = phi
    location = outside
    execute_on = 'initial timestep_end'
  [../]
  [./cfl]
    type = LevelSetCFLCondition
    velocity = velocity
    execute_on = 'initial timestep_end'
  [../]
[]

[Executioner]
  type = Transient
  solve_type = PJFNK
  start_time = 0
  end_time = 1.570796
  scheme = crank-nicolson
  petsc_options_iname = '-pc_type -sub_pc_type'
  petsc_options_value = 'asm      ilu'
  [./TimeStepper]
    type = PostprocessorDT
    postprocessor = cfl
    scale = 0.8
  [../]
[]

[MultiApps]
  [./reinit]
    type = LevelSetReinitializationMultiApp
    input_files = 'circle_rotate_sub.i'
    execute_on = 'timestep_end'
  [../]
[]

[Transfers]
  [./to_sub]
    type = MultiAppCopyTransfer
    source_variable = phi
    variable = phi
    to_multi_app = reinit
    execute_on = 'timestep_end'
  [../]
  [./to_sub_init]
    type = MultiAppCopyTransfer
    source_variable = phi
    variable = phi_0
    to_multi_app = reinit
    execute_on = 'timestep_end'
  [../]
  [./from_sub]
    type = MultiAppCopyTransfer
    source_variable = phi
    variable = phi
    from_multi_app = reinit
    execute_on = 'timestep_end'
  [../]
[]

[Outputs]
  csv = true
  exodus = true
[]

(modules/level_set/examples/rotating_circle/circle_rotate_sub.i)

[Mesh]
  type = GeneratedMesh
  dim = 2
  xmin = -1
  xmax = 1
  ymin = -1
  ymax = 1
  nx = 32
  ny = 32
  uniform_refine = 2
[]

[Variables]
  [./phi]
  [../]
[]

[AuxVariables]
  [./phi_0]
  [../]
  [./marker]
  [../]
[]

[Kernels]
  [./time]
    type = TimeDerivative
    variable = phi
  [../]
  [./reinit]
    type = LevelSetOlssonReinitialization
    variable = phi
    phi_0 = phi_0
    epsilon = 0.03
  [../]
[]

[Problem]
  type = LevelSetReinitializationProblem
[]

[UserObjects]
  [./arnold]
    type = LevelSetOlssonTerminator
    tol = 1
    min_steps = 3
  [../]
[]

[Executioner]
  type = Transient
  solve_type = NEWTON
  start_time = 0
  num_steps = 100
  nl_abs_tol = 1e-14
  scheme = crank-nicolson
  line_search = none
  petsc_options_iname = '-pc_type -sub_pc_type'
  petsc_options_value = 'asm      ilu'
  dt = 0.003
[]

[Outputs]
[]

Level Set Equation
Level Set Equation with SUPG
Level Set Equation with Reinitialization
Area Comparison
References