ver-1kd

Sieverts’ Law Boundaries with Chemical Reactions and Volumetric Source

General Case Description

Two enclosures are separated by a membrane that allows diffusion according to Sieverts' law and chemical reactions, with a volumetric source in Enclosure 1. Enclosure 2 has twice the volume of Enclosure 1.

Case Set Up

This verification problem is taken from Ambrosek and Longhurst (2008).

This setup describes a diffusion system in which tritium T $var element = document.getElementById("moose-equation-62760171-d1f1-467a-9219-ad0d5eb564e4");katex.render("_2", element, {displayMode:false,throwOnError:false});$ , dihydrogen H $var element = document.getElementById("moose-equation-3909ff34-4b0e-4d8f-be14-5897196da5c4");katex.render("_2", element, {displayMode:false,throwOnError:false});$ and HT are modeled across a one-dimensional domain split into two enclosures. Compared to the ver-1kc-2 case, we now incorporate a T $var element = document.getElementById("moose-equation-c50dc906-8c1f-4fd9-88cc-877ff6346d01");katex.render("_2", element, {displayMode:false,throwOnError:false});$ tritium volumetric source in Enclosure 1. The volumetric source rate is set to $var element = document.getElementById("moose-equation-7f38ae4a-ef03-4b74-989b-c6c4dc2c698c");katex.render("S_{\\text{T}_2} = 10^{23}/N_A", element, {displayMode:false,throwOnError:false});$ mol/m $var element = document.getElementById("moose-equation-b3b46ca7-bfb0-4ef8-9185-295ae85d2c53");katex.render("^3", element, {displayMode:false,throwOnError:false});$ /s with $var element = document.getElementById("moose-equation-bafec4f1-d67f-40b2-8ebf-91ac250e0cd4");katex.render("N_A = 6.02214076 \\times 10^{23}", element, {displayMode:false,throwOnError:false});$ 1/mol. The total system length is $var element = document.getElementById("moose-equation-7bf16980-b7c9-4182-b303-fbcd5fb5c40b");katex.render("2.5 \\times 10^{-4}", element, {displayMode:false,throwOnError:false});$ m, divided into 100 segments. The system operates at a constant temperature of 500 Kelvin. Initial tritium T $var element = document.getElementById("moose-equation-5da70a46-e130-450b-bcf8-1ad8ca8d1c4b");katex.render("_2", element, {displayMode:false,throwOnError:false});$ and dihydrogen H $var element = document.getElementById("moose-equation-69373a98-b676-4d29-a769-438dfe8cc4f9");katex.render("_2", element, {displayMode:false,throwOnError:false});$ pressures are specified as $var element = document.getElementById("moose-equation-89562b4f-9590-4ba2-bf27-aa89bc267baa");katex.render("10^{5}", element, {displayMode:false,throwOnError:false});$ Pa for Enclosure 1 and $var element = document.getElementById("moose-equation-39c41b0b-e8c4-46bd-98fd-387a76afeb13");katex.render("10^{-10}", element, {displayMode:false,throwOnError:false});$ Pa for Enclosure 2. Initially, there is no HT in either enclosure.

The reaction between the species is described as follows

$var element = document.getElementById("moose-equation-fb008794-a0e5-4503-adc0-59b12efa4227");katex.render("\\text{H}_2 + \\text{T}_2 \\leftrightarrow 2\\text{HT}", element, {displayMode:true,throwOnError:false});$

The kinematic evolutions of the species are given by the following equations

$var element = document.getElementById("moose-equation-bca36236-19d1-4e86-805a-4034e02e3b1d");katex.render("\\frac{d C_{\\text{HT}}}{dt} = 2K_1 C_{\\text{H}_2} C_{\\text{T}_2} - K_2 C_{\\text{HT}}^2", element, {displayMode:true,throwOnError:false});$

$var element = document.getElementById("moose-equation-076aaa93-6b7a-405b-b0fb-0952fcf2d937");katex.render("\\frac{d C_{\\text{H}_2}}{dt} = -K_1 C_{\\text{H}_2} C_{\\text{T}_2} + \\frac{1}{2} K_2 C_{\\text{HT}}^2", element, {displayMode:true,throwOnError:false});$

$var element = document.getElementById("moose-equation-29677f40-874f-47bf-8b9c-e268cf58edad");katex.render("\\frac{d C_{\\text{T}_2}}{dt} = -K_1 c_{\\text{H}_2} C_{\\text{T}_2} + \\frac{1}{2} K_2 C_{\\text{HT}}^2", element, {displayMode:true,throwOnError:false});$

where $var element = document.getElementById("moose-equation-8d8d109a-6f17-43a0-9d35-52bc93250dbd");katex.render("K_1", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-0d56c43a-10a3-4702-b8ff-14803b0ae294");katex.render("K_2", element, {displayMode:false,throwOnError:false});$ represent the reaction rates for the forward and reverse reactions, respectively.

At equilibrium, the time derivatives are zero

$var element = document.getElementById("moose-equation-2118b528-3c8d-4cb7-92e5-47b2e5bbe813");katex.render("2K_1 C_{\\text{H}_2} C_{\\text{T}_2} - K_2 C_{\\text{HT}}^2 = 0", element, {displayMode:true,throwOnError:false});$

From this, we can derive the same equilibrium condition as used in TMAP7:

$var element = document.getElementById("moose-equation-b818bd97-905a-4c46-a65e-fdb8e8f5bfc0");katex.render("P_{\\text{HT}} = \\eta \\sqrt{P_{\\text{H}_2} P_{\\text{T}_2}}", element, {displayMode:true,throwOnError:false});$

where the equilibrium constant $var element = document.getElementById("moose-equation-a4e72192-0236-4e71-a390-0f5ada0ba66f");katex.render("\\eta", element, {displayMode:false,throwOnError:false});$ is defined as

$(1)var element = document.getElementById("moose-equation-62868b8a-0c3f-4124-a30b-53bf3a548bb0");katex.render(" \\eta = \\sqrt{\\frac{2K_1}{K_2}}", element, {displayMode:true,throwOnError:false});$

Similarly to TMAP7, the equilibrium constant $var element = document.getElementById("moose-equation-a51a1efa-0a97-4e6a-abd5-0a3c85f3cbbf");katex.render("\\eta", element, {displayMode:false,throwOnError:false});$ has been set to a fixed value of $var element = document.getElementById("moose-equation-91a313bf-10da-4ed6-9f50-123c4d97a7a5");katex.render("\\eta = 2", element, {displayMode:false,throwOnError:false});$ .

The diffusion and generation processes for each species in the two enclosures can be expressed by

$var element = document.getElementById("moose-equation-8c2a7a7c-696d-4bab-8f28-815fd9c95050");katex.render("\\frac{\\partial C_1}{\\partial t} = \\nabla D \\nabla C_1 + S_1,", element, {displayMode:true,throwOnError:false});$ and $var element = document.getElementById("moose-equation-bde6d7c7-9d68-4989-b077-f49645f9fcf8");katex.render("\\frac{\\partial C_2}{\\partial t} = \\nabla D \\nabla C_2,", element, {displayMode:true,throwOnError:false});$

where $var element = document.getElementById("moose-equation-36b7af3f-de56-41e5-9229-7e74d4d9c44d");katex.render("C_1", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-ef1c30f1-b1a1-42c4-9107-f1894d48fd13");katex.render("C_2", element, {displayMode:false,throwOnError:false});$ represent the concentration fields in enclosures 1 and 2 respectively, $var element = document.getElementById("moose-equation-13db59af-a88d-431e-8e9e-0cf810c127c5");katex.render("t", element, {displayMode:false,throwOnError:false});$ is the time, $var element = document.getElementById("moose-equation-10507950-867e-4fce-9d0c-857bbe4fb746");katex.render("D", element, {displayMode:false,throwOnError:false});$ denotes the diffusivity, $var element = document.getElementById("moose-equation-5e6c1f95-0ce4-4429-b072-09084605295f");katex.render("S", element, {displayMode:false,throwOnError:false});$ the volumetric source rate, $var element = document.getElementById("moose-equation-a7a93794-f1af-4d10-82af-e34538e40cbd");katex.render("V_1", element, {displayMode:false,throwOnError:false});$ the volume of enclosure 1, $var element = document.getElementById("moose-equation-8065857b-caea-4bb4-b5d2-e05b4928b2dd");katex.render("k", element, {displayMode:false,throwOnError:false});$ the Boltzmann constant and $var element = document.getElementById("moose-equation-5b0c1919-e5ed-4772-9def-7bcb248298ec");katex.render("T", element, {displayMode:false,throwOnError:false});$ the temperature. Note that the diffusivity may vary across different species and enclosures. However, in this case, it is assumed to be identical for all.

The concentration in Enclosure 1 is related to the partial pressure and concentration in Enclosure 2 via the interface sorption law:

$var element = document.getElementById("moose-equation-07499596-93bd-47c6-b552-26d7fe0220ea");katex.render("C_1 = K P_2^n = K \\left( C_2 RT \\right)^n", element, {displayMode:true,throwOnError:false});$

where $var element = document.getElementById("moose-equation-20e6f769-f0c5-478e-8f1a-0172db4e40b3");katex.render("R", element, {displayMode:false,throwOnError:false});$ is the ideal gas constant in J/mol/K, $var element = document.getElementById("moose-equation-0b309d74-f8df-4f40-bde0-dd20a8460581");katex.render("T", element, {displayMode:false,throwOnError:false});$ is the temperature in K, $var element = document.getElementById("moose-equation-d13ada84-bb70-4718-affb-647e8fee2b60");katex.render("K", element, {displayMode:false,throwOnError:false});$ is the solubility, and $var element = document.getElementById("moose-equation-cc9e053a-7787-4819-a766-42954508e5bd");katex.render("n", element, {displayMode:false,throwOnError:false});$ is the exponent of the sorption law. For Sieverts' law, $var element = document.getElementById("moose-equation-371d7148-adee-4785-a74f-a028a427b63a");katex.render("n=0.5", element, {displayMode:false,throwOnError:false});$ .

Results

We assume that $var element = document.getElementById("moose-equation-d4a80206-2a54-473b-9d85-e52f0b7a66e4");katex.render("K = 10/\\sqrt{RT}", element, {displayMode:false,throwOnError:false});$ , which is expected to result in $var element = document.getElementById("moose-equation-a540406b-3b76-4a76-b3c9-bc1d87ac9ef9");katex.render("C_1 = 10 \\sqrt{C_2}", element, {displayMode:false,throwOnError:false});$ at equilibrium.

As illustrated in Figure 1, since the chemical reactions occur immediately, an initial quantity of HT is present in Enclosure 1, while T $var element = document.getElementById("moose-equation-3d2d1281-986a-4c8c-9000-f60914710f52");katex.render("_2", element, {displayMode:false,throwOnError:false});$ and H $var element = document.getElementById("moose-equation-f71f163e-c4be-4928-9b58-aef0a4ac6c36");katex.render("_2", element, {displayMode:false,throwOnError:false});$ initially drop to half their original amounts.

The pressures of T $var element = document.getElementById("moose-equation-9c8b08e7-534b-424a-83cd-dbf819756d5c");katex.render("_2", element, {displayMode:false,throwOnError:false});$ and H $var element = document.getElementById("moose-equation-347d205b-dfdb-4389-b894-48650f099181");katex.render("_2", element, {displayMode:false,throwOnError:false});$ in Enclosure 1 decrease due to diffusion into Enclosure 2. The constant flow rate of the T $var element = document.getElementById("moose-equation-73f7cdaf-93c9-4a1e-b8f2-5eab9d320426");katex.render("_2", element, {displayMode:false,throwOnError:false});$ source slows down the pressure drop of T $var element = document.getElementById("moose-equation-4dbfa3ac-6dad-4251-94aa-e017bb4b4368");katex.render("_2", element, {displayMode:false,throwOnError:false});$ in Enclosure 2. Moreover, the volumetric source increases the amount of T $var element = document.getElementById("moose-equation-39684340-50a0-4505-a543-7c555c5a4286");katex.render("_2", element, {displayMode:false,throwOnError:false});$ in Enclosure 1, thereby enhancing its chemical reactions with H $var element = document.getElementById("moose-equation-822462c5-f42a-4808-9498-9e49839c520a");katex.render("_2", element, {displayMode:false,throwOnError:false});$ . Consequently, in Enclosure 1, H $var element = document.getElementById("moose-equation-d867c7ff-b8f4-4a84-bc5d-a8770710998a");katex.render("_2", element, {displayMode:false,throwOnError:false});$ pressure gradually decreases over time, while HT pressure rises.

Similarly, in Enclosure 2, the pressures of T $var element = document.getElementById("moose-equation-cd916bd3-62d4-4900-a049-890aed236274");katex.render("_2", element, {displayMode:false,throwOnError:false});$ and H $var element = document.getElementById("moose-equation-76cbfaca-9b23-4c75-9eec-df7f81b8841a");katex.render("_2", element, {displayMode:false,throwOnError:false});$ increase, with the rise being more pronounced for T $var element = document.getElementById("moose-equation-7f0e4d4e-ce5a-46d6-bf6d-cbac5967e2fb");katex.render("_2", element, {displayMode:false,throwOnError:false});$ due to the continuous supply from the source. As a result, more H $var element = document.getElementById("moose-equation-35ab0e69-6210-4bd3-9824-27082ea3ba55");katex.render("_2", element, {displayMode:false,throwOnError:false});$ reacts with T $var element = document.getElementById("moose-equation-681b95f8-d988-417f-99e5-f71ad2f50295");katex.render("_2", element, {displayMode:false,throwOnError:false});$ , further contributing to the increase in HT pressure.

For verification purposes, it is crucial to ensure that the chemical equilibrium between HT, T $var element = document.getElementById("moose-equation-097770a4-6755-4256-99f2-574443edc0bb");katex.render("_2", element, {displayMode:false,throwOnError:false});$ and H $var element = document.getElementById("moose-equation-4c3ed4df-3237-4951-9218-6f6d1017daa9");katex.render("_2", element, {displayMode:false,throwOnError:false});$ is achieved. This can be verified in both enclosures by examining the ratio between $var element = document.getElementById("moose-equation-5206f5eb-268e-41e2-90c9-73911f817c8e");katex.render("P_{\\text{HT}}", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-6e770395-74d6-44ab-8b9d-239d325614bb");katex.render("\\sqrt{P_{\\text{H}_2} P_{\\text{T}_2}}", element, {displayMode:false,throwOnError:false});$ , which must equal $var element = document.getElementById("moose-equation-a5dfdc53-c1db-4447-ac7f-665f275e635c");katex.render("\\eta=2", element, {displayMode:false,throwOnError:false});$ . As shown in Figure 2, this ratio approaches $var element = document.getElementById("moose-equation-11abaa4a-2a9d-4394-938f-ec9072aca05a");katex.render("\\eta=2", element, {displayMode:false,throwOnError:false});$ for both enclosures at equilibrium. To reach this equilibrium, the ratio of $var element = document.getElementById("moose-equation-29cb1c7a-1699-4a78-bb3e-0a2636d60bc4");katex.render("K_1", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-1154ce41-dad3-498d-8e48-9a17e427e5c1");katex.render("K_2", element, {displayMode:false,throwOnError:false});$ must respect Eq. (1). The values of $var element = document.getElementById("moose-equation-30397ef4-d8d1-4ecd-b90d-127ccf552078");katex.render("K_1", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-12e51b1d-b4b2-437a-ae70-6cbf391a327f");katex.render("K_2", element, {displayMode:false,throwOnError:false});$ must also be large enough to ensure that the kinetics of chemical reactions are faster than diffusion or surface permeation to be closer to the equilibrium assumption imposed in TMAP7. Here, the equilibrium in enclosure 1 is achieved rapidly. Increasing $var element = document.getElementById("moose-equation-b38b4798-05fe-4a84-9094-937bc73944c1");katex.render("K_1", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-1ab42c66-7a44-45f6-acb3-a4d983af7cb7");katex.render("K_2", element, {displayMode:false,throwOnError:false});$ would also enable a quicker attainment of equilibrium in enclosure 2. However, using very high values for $var element = document.getElementById("moose-equation-5e3fe1bd-9f23-4548-a5fd-b631d4d33ea1");katex.render("K_1", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-48665226-0c8e-4c1d-a28e-c97168cb6c21");katex.render("K_2", element, {displayMode:false,throwOnError:false});$ would lead to an unnecessary increase in computational costs.

The concentration ratios for T $var element = document.getElementById("moose-equation-eb3d0679-d164-466b-81aa-5065e2fc5c4b");katex.render("_2", element, {displayMode:false,throwOnError:false});$ , H $var element = document.getElementById("moose-equation-cf4da368-d071-407c-8df0-4c93a09a8995");katex.render("_2", element, {displayMode:false,throwOnError:false});$ , and HT between enclosures 1 and 2, shown in Figure 3, Figure 4, and Figure 5, demonstrate that the results obtained with TMAP8 are consistent with the analytical results derived from the sorption law for $var element = document.getElementById("moose-equation-911a0190-48e2-4175-a968-493ee3163e87");katex.render("K \\sqrt{RT} = 10", element, {displayMode:false,throwOnError:false});$ .

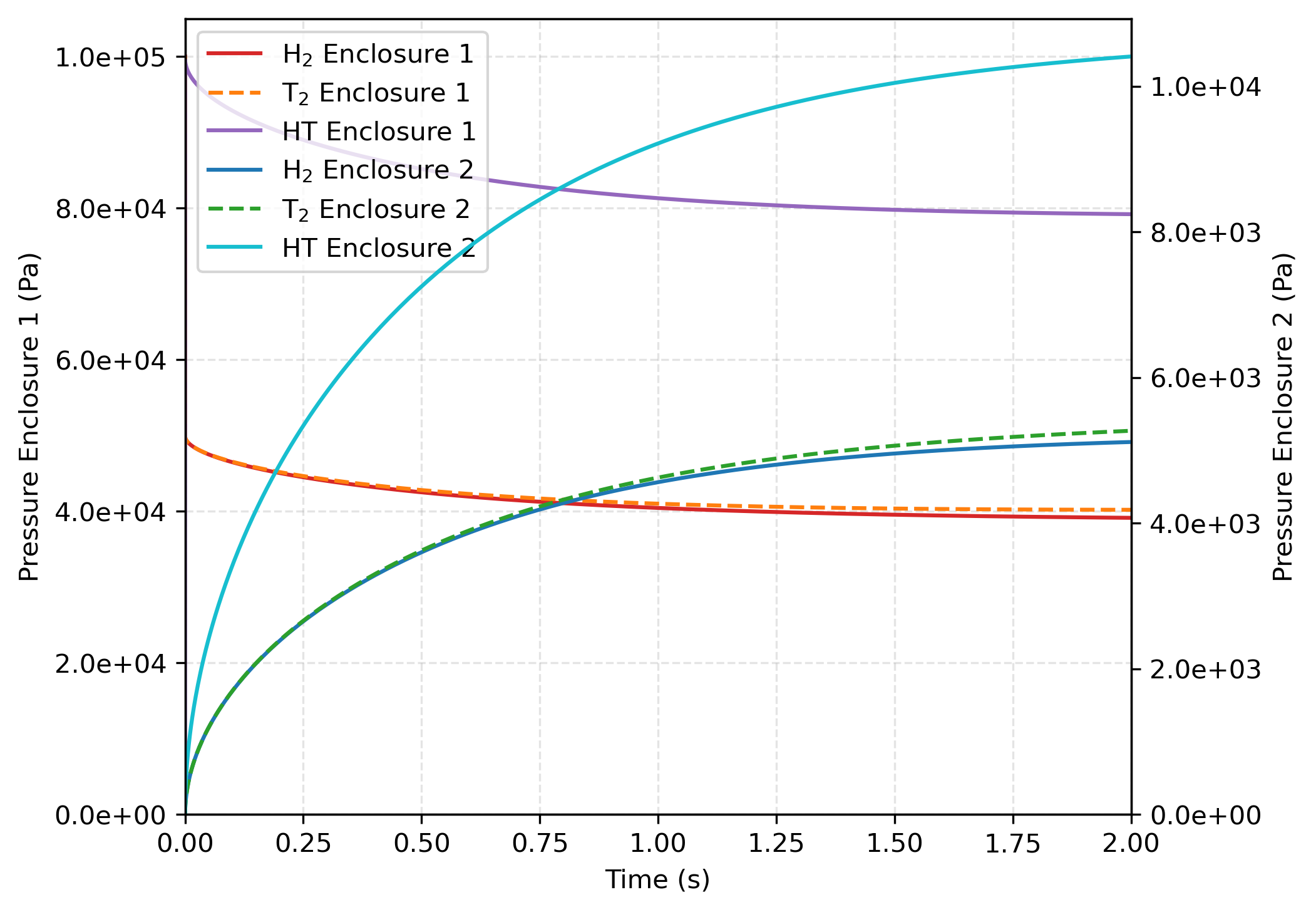
Figure 1: Evolution of species concentration over time governed by Sieverts' law with $var element = document.getElementById("moose-equation-190fc95b-3b41-4cf4-8e61-73e1569a8958");katex.render("K = 10/\\sqrt{RT}", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-ecc7544f-165e-4b6d-b6c4-a39777e3f217");katex.render("\\eta = \\sqrt{2K_1/K_2}", element, {displayMode:false,throwOnError:false});$ .

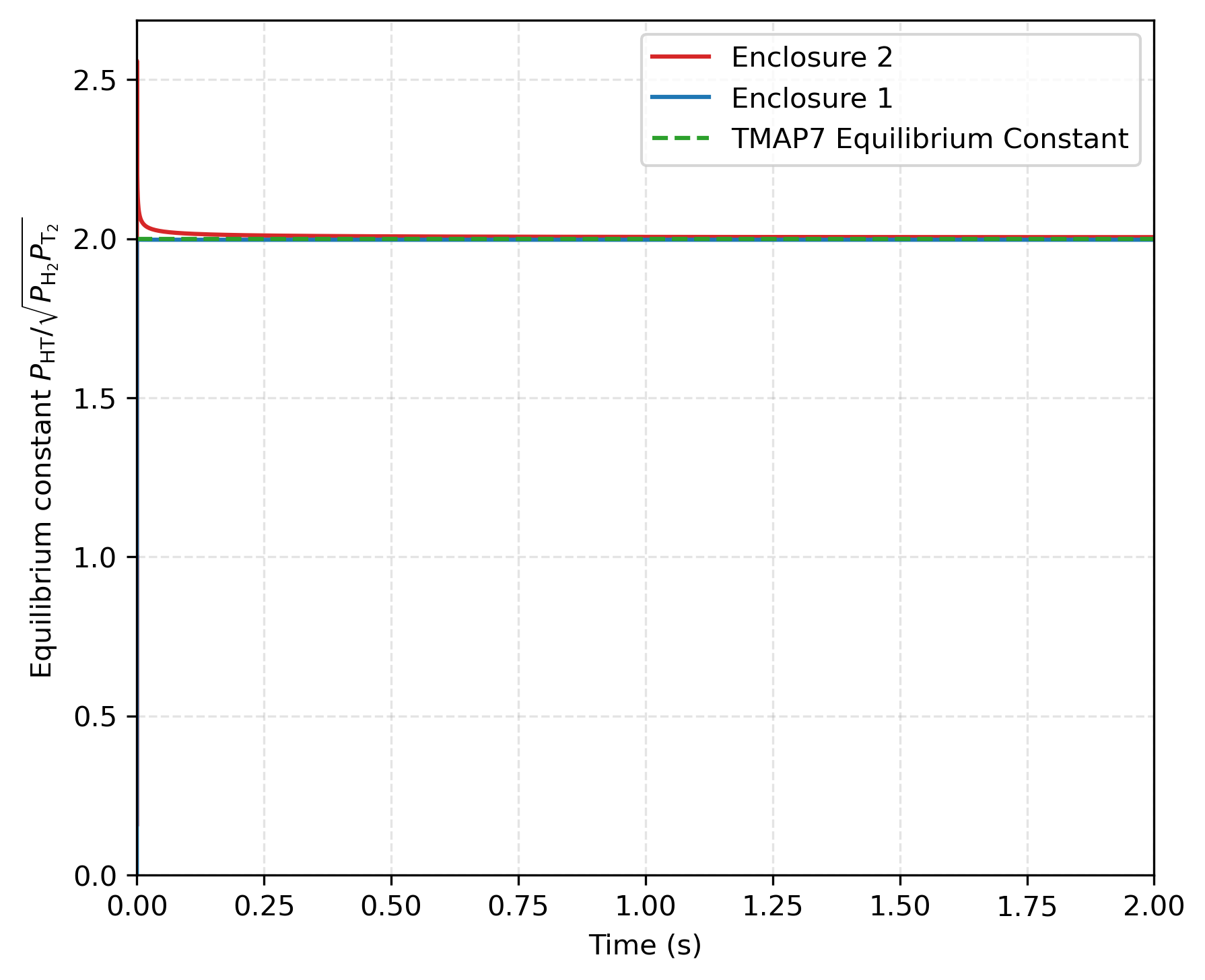
Figure 2: Equilibrium constant as a function of time for $var element = document.getElementById("moose-equation-74242684-6813-4e9d-8fc7-59957477d974");katex.render("\\eta = \\sqrt{2K_1/K_2}=2", element, {displayMode:false,throwOnError:false});$ .

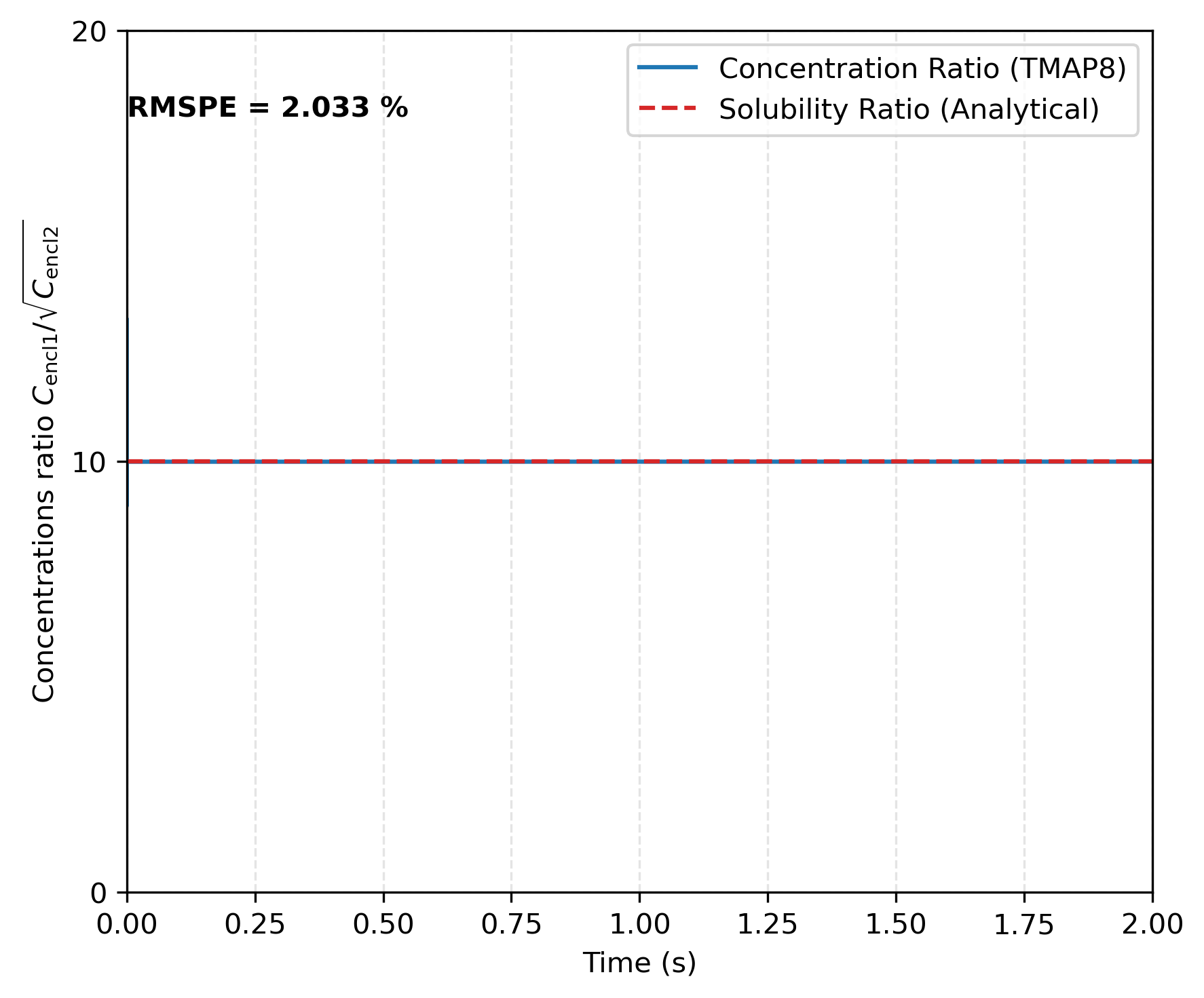
Figure 3: T $var element = document.getElementById("moose-equation-fd145101-2599-4c81-8269-a00af78bda34");katex.render("_2", element, {displayMode:false,throwOnError:false});$ concentration ratio between enclosures 1 and 2 at the interface for $var element = document.getElementById("moose-equation-bb13a179-4571-4f1c-9b2a-ab54df27b2dc");katex.render("K = 10/\\sqrt{RT}", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-c21cce87-7b47-4117-a0ba-abea7395c3c1");katex.render("\\eta = \\sqrt{2K_1/K_2}", element, {displayMode:false,throwOnError:false});$ . This verifies TMAP8's ability to apply Sieverts' law across the interface.

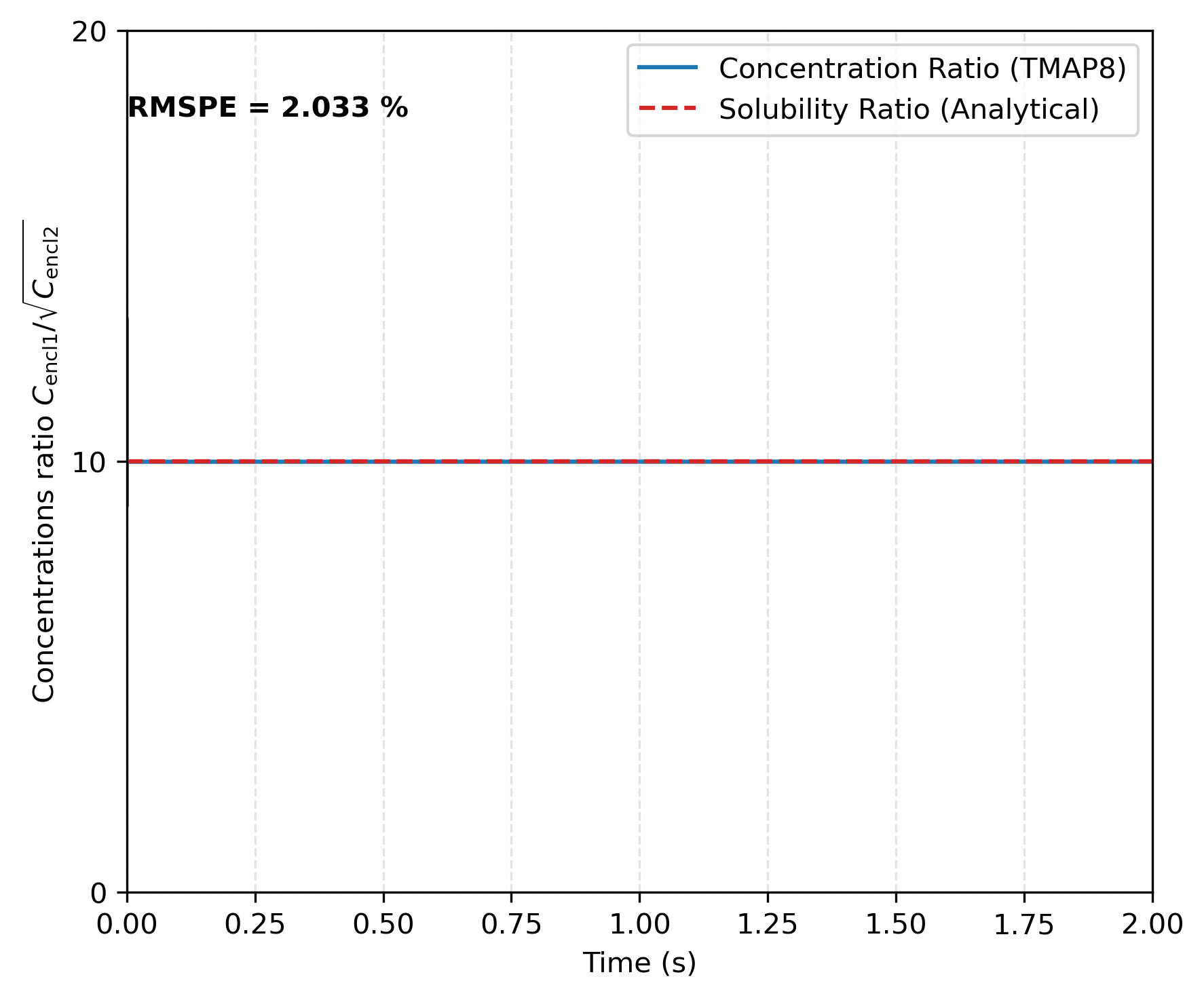
Figure 4: H $var element = document.getElementById("moose-equation-41a6f2f3-51f4-4e11-80e9-a6722d966dba");katex.render("_2", element, {displayMode:false,throwOnError:false});$ concentration ratio between enclosures 1 and 2 at the interface for $var element = document.getElementById("moose-equation-4c845bd7-c213-4bf6-a013-ca29c38d2aec");katex.render("K = 10/\\sqrt{RT}", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-f6103747-1248-4cf4-9633-4f05f72b0a81");katex.render("\\eta = \\sqrt{2K_1/K_2}", element, {displayMode:false,throwOnError:false});$ . This verifies TMAP8's ability to apply Sieverts' law across the interface.

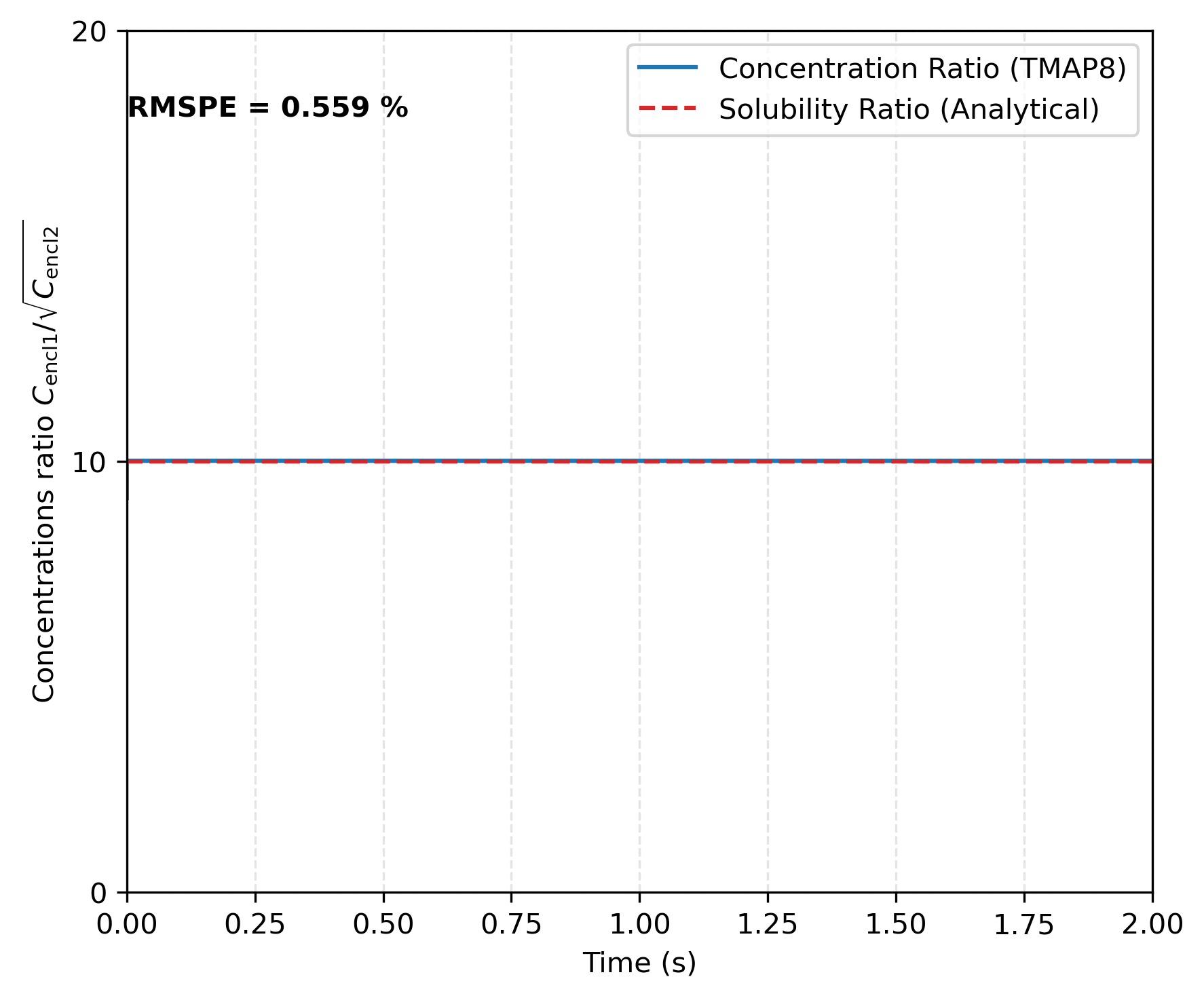
Figure 5: HT concentration ratio between enclosures 1 and 2 at the interface for $var element = document.getElementById("moose-equation-8e94df1b-b2c4-4ecd-a02b-c1b6fc8df079");katex.render("K = 10/\\sqrt{RT}", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-c7f6bfa0-7716-41bb-ba7c-27f09b2add71");katex.render("\\eta = \\sqrt{2K_1/K_2}", element, {displayMode:false,throwOnError:false});$ . This verifies TMAP8's ability to apply Sieverts' law across the interface.

Input files

The input file for this case can be found at (test/tests/ver-1kd/ver-1kd.i).

References

James Ambrosek and GR Longhurst. Verification and Validation of TMAP7. Technical Report INEEL/EXT-04-01657, Idaho National Engineering and Environmental Laboratory, December 2008.

@techreport{ambrosek2008verification,
    author = "Ambrosek, James and Longhurst, GR",
    title = "{Verification and Validation of TMAP7}",
    year = "2008",
    number = "INEEL/EXT-04-01657",
    month = "December",
    institution = "Idaho National Engineering and Environmental Laboratory"
}

(test/tests/ver-1kd/ver-1kd.i)

nb_segments_TMAP7 = 20
node_size_TMAP7 = '${units 1.25e-5 m}'
long_total = '${units ${fparse nb_segments_TMAP7 * node_size_TMAP7} m}'
nb_segments_TMAP8 = 1e2
simulation_time = '${units 2 s}'
N_a = '${units 6.02214076e23 1/mol}' # Avogadro's number from PhysicalConstants.h
source = '${units ${fparse 1e23 / N_a} mol/m^3/s}' # Source term for T2 in enclosure 1
temperature = '${units 500 K}'
R = '${units 8.31446261815324 J/mol/K}' # ideal gas constant from PhysicalConstants.h
initial_pressure_1 = '${units 1e5 Pa}'
initial_pressure_2 = '${units 1e-10 Pa}'
initial_concentration_1 = '${units ${fparse initial_pressure_1 / (R*temperature)} mol/m^3}'
initial_concentration_2 = '${units ${fparse initial_pressure_2 / (R*temperature)} mol/m^3}'
solubility = '${units ${fparse 10/sqrt(R*temperature)} mol/m^3/Pa^(1/2)}' # Sieverts' law solubility
diffusivity = '${units ${fparse 4.31e-6 * exp(-2818/temperature)} m^2/s}'
n_sorption = 0.5 # Sieverts' Law
K1 = '${units 4000 mol/m^3/s}' # reaction rate for H2+T2->2HT
equilibrium_constant = 2.0
K2 = '${units ${fparse (2*K1) / (equilibrium_constant)^2} mol/m^3/s}' # reaction rate for 2HT->H2+T2
unit_scale = 1
unit_scale_neighbor = 1

[Mesh]
  [generated]
    type = GeneratedMeshGenerator
    dim = 1
    nx = ${nb_segments_TMAP8}
    xmax = ${long_total}
  []
  [enclosure_1]
    type = SubdomainBoundingBoxGenerator
    input = generated
    block_id = 1
    bottom_left = '0 0 0'
    top_right = '${fparse 1/3 * long_total} 0 0'
  []
  [enclosure_2]
    type = SubdomainBoundingBoxGenerator
    input = enclosure_1
    block_id = 2
    bottom_left = '${fparse 1/3 * long_total} 0 0'
    top_right = '${fparse long_total} 0 0'
  []
  [interface]
    type = SideSetsBetweenSubdomainsGenerator
    input = enclosure_2
    primary_block = 1
    paired_block = 2
    new_boundary = interface
  []
  [interface2]
    type = SideSetsBetweenSubdomainsGenerator
    input = interface
    primary_block = 2
    paired_block = 1
    new_boundary = interface2
  []
[]

[Variables]

  # Variables for H2, T2, and HT in enclosure 1
  [concentration_H2_enclosure_1]
    block = 1
    initial_condition = '${initial_concentration_1}'
  []
  [concentration_T2_enclosure_1]
    block = 1
    initial_condition = '${initial_concentration_1}'
  []
  [concentration_HT_enclosure_1]
    block = 1
    initial_condition = '${initial_concentration_2}'
  []

  # Variables for H2, T2, and HT in enclosure 2
  [concentration_H2_enclosure_2]
    block = 2
    initial_condition = '${initial_concentration_2}'
  []
  [concentration_T2_enclosure_2]
    block = 2
    initial_condition = '${initial_concentration_2}'
  []
  [concentration_HT_enclosure_2]
    block = 2
    initial_condition = '${initial_concentration_2}'
  []
[]

[AuxVariables]

  # Auxiliary variables for H2, T2, and HT in enclosure 1
  [pressure_H2_enclosure_1]
    order = CONSTANT
    family = MONOMIAL
    block = 1
    initial_condition = '${initial_pressure_1}'
  []
  [pressure_T2_enclosure_1]
    order = CONSTANT
    family = MONOMIAL
    block = 1
    initial_condition = '${initial_pressure_1}'
  []
  [pressure_HT_enclosure_1]
    order = CONSTANT
    family = MONOMIAL
    block = 1
    initial_condition = '${initial_pressure_2}'
  []

  # Auxiliary variables for H2, T2, and HT in enclosure 2
  [pressure_H2_enclosure_2]
    order = CONSTANT
    family = MONOMIAL
    block = 2
    initial_condition = '${initial_pressure_2}'
  []
  [pressure_T2_enclosure_2]
    order = CONSTANT
    family = MONOMIAL
    block = 2
    initial_condition = '${initial_pressure_2}'
  []
  [pressure_HT_enclosure_2]
    order = CONSTANT
    family = MONOMIAL
    block = 2
    initial_condition = '${initial_pressure_2}'
  []
[]

[Kernels]
  # Source term for T2 in enclosure 1
  [T2_source_term_enclosure_1]
    type = BodyForce
    variable = concentration_T2_enclosure_1
    block = '1'
    value = ${source}
  []

  # Diffusion equation for H2
  [H2_diffusion_enclosure_1]
    type = MatDiffusion
    variable = concentration_H2_enclosure_1
    diffusivity = ${diffusivity}
    block = '1'
  []
  [H2_time_derivative_enclosure_1]
    type = TimeDerivative
    variable = concentration_H2_enclosure_1
    block = '1'
  []
  [H2_diffusion_enclosure_2]
    type = MatDiffusion
    variable = concentration_H2_enclosure_2
    diffusivity = ${diffusivity}
    block = '2'
  []
  [H2_time_derivative_enclosure_2]
    type = TimeDerivative
    variable = concentration_H2_enclosure_2
    block = '2'
  []

  # Diffusion equation for T2
  [T2_diffusion_enclosure_1]
    type = MatDiffusion
    variable = concentration_T2_enclosure_1
    diffusivity = ${diffusivity}
    block = '1'
  []
  [T2_time_derivative_enclosure_1]
    type = TimeDerivative
    variable = concentration_T2_enclosure_1
    block = '1'
  []
  [T2_diffusion_enclosure_2]
    type = MatDiffusion
    variable = concentration_T2_enclosure_2
    diffusivity = ${diffusivity}
    block = '2'
  []
  [T2_time_derivative_enclosure_2]
    type = TimeDerivative
    variable = concentration_T2_enclosure_2
    block = '2'
  []

  # Diffusion equation for HT
  [HT_diffusion_enclosure_1]
    type = MatDiffusion
    variable = concentration_HT_enclosure_1
    diffusivity = ${diffusivity}
    block = '1'
  []
  [HT_time_derivative_enclosure_1]
    type = TimeDerivative
    variable = concentration_HT_enclosure_1
    block = '1'
  []
  [HT_diffusion_enclosure_2]
    type = MatDiffusion
    variable = concentration_HT_enclosure_2
    diffusivity = ${diffusivity}
    block = '2'
  []
  [HT_time_derivative_enclosure_2]
    type = TimeDerivative
    variable = concentration_HT_enclosure_2
    block = '2'
  []

  # Reaction H2+T2->2HT in enclosure 1
  [reaction_H2_encl_1_1]
    type = ADMatReactionFlexible
    variable = concentration_H2_enclosure_1
    vs = 'concentration_H2_enclosure_1 concentration_T2_enclosure_1'
    block = 1
    coeff = -1
    reaction_rate_name = ${K1}
  []
  [reaction_T2_encl_1_1]
    type = ADMatReactionFlexible
    variable = concentration_T2_enclosure_1
    vs = 'concentration_H2_enclosure_1 concentration_T2_enclosure_1'
    block = 1
    coeff = -1
    reaction_rate_name = ${K1}
  []
  [reaction_HT_encl_1_1]
    type = ADMatReactionFlexible
    variable = concentration_HT_enclosure_1
    vs = 'concentration_H2_enclosure_1 concentration_T2_enclosure_1'
    block = 1
    coeff = 2
    reaction_rate_name = ${K1}
  []

  # Reaction 2HT->H2+T2 in enclosure 1
  [reaction_H2_encl_1_2]
    type = ADMatReactionFlexible
    variable = concentration_H2_enclosure_1
    vs = 'concentration_HT_enclosure_1 concentration_HT_enclosure_1'
    block = 1
    coeff = 0.5
    reaction_rate_name = ${K2}
  []
  [reaction_T2_encl_1_2]
    type = ADMatReactionFlexible
    variable = concentration_T2_enclosure_1
    vs = 'concentration_HT_enclosure_1 concentration_HT_enclosure_1'
    block = 1
    coeff = 0.5
    reaction_rate_name = ${K2}
  []
  [reaction_HT_encl_1_2]
    type = ADMatReactionFlexible
    variable = concentration_HT_enclosure_1
    vs = 'concentration_HT_enclosure_1 concentration_HT_enclosure_1'
    block = 1
    coeff = -1
    reaction_rate_name = ${K2}
  []

  # Reaction H2+T2->2HT in enclosure 2
  [reaction_H2_encl_2_1]
    type = ADMatReactionFlexible
    variable = concentration_H2_enclosure_2
    vs = 'concentration_H2_enclosure_2 concentration_T2_enclosure_2'
    block = 2
    coeff = -1
    reaction_rate_name = ${K1}
  []
  [reaction_T2_encl_2_1]
    type = ADMatReactionFlexible
    variable = concentration_T2_enclosure_2
    vs = 'concentration_H2_enclosure_2 concentration_T2_enclosure_2'
    block = 2
    coeff = -1
    reaction_rate_name = ${K1}
  []
  [reaction_HT_encl_2_1]
    type = ADMatReactionFlexible
    variable = concentration_HT_enclosure_2
    vs = 'concentration_H2_enclosure_2 concentration_T2_enclosure_2'
    block = 2
    coeff = 2
    reaction_rate_name = ${K1}
  []

  # Reaction 2HT->H2+T2 in enclosure 2
  [reaction_H2_encl_2_2]
    type = ADMatReactionFlexible
    variable = concentration_H2_enclosure_2
    vs = 'concentration_HT_enclosure_2 concentration_HT_enclosure_2'
    block = 2
    coeff = 0.5
    reaction_rate_name = ${K2}
  []
  [reaction_T2_encl_2_2]
    type = ADMatReactionFlexible
    variable = concentration_T2_enclosure_2
    vs = 'concentration_HT_enclosure_2 concentration_HT_enclosure_2'
    block = 2
    coeff = 0.5
    reaction_rate_name = ${K2}
  []
  [reaction_HT_encl_2_2]
    type = ADMatReactionFlexible
    variable = concentration_HT_enclosure_2
    vs = 'concentration_HT_enclosure_2 concentration_HT_enclosure_2'
    block = 2
    coeff = -1
    reaction_rate_name = ${K2}
  []
[]

[AuxKernels]

  # Auxiliary kernels for H2, T2, and HT in enclosure 1
  [pressure_H2_enclosure_1]
    type = ParsedAux
    variable = pressure_H2_enclosure_1
    coupled_variables = 'concentration_H2_enclosure_1'
    expression = '${fparse R*temperature}*concentration_H2_enclosure_1'
    block = 1
    execute_on = 'initial timestep_end'
  []
  [pressure_T2_enclosure_1]
    type = ParsedAux
    variable = pressure_T2_enclosure_1
    coupled_variables = 'concentration_T2_enclosure_1'
    expression = '${fparse R*temperature}*concentration_T2_enclosure_1'
    block = 1
    execute_on = 'initial timestep_end'
  []
  [pressure_HT_enclosure_1]
    type = ParsedAux
    variable = pressure_HT_enclosure_1
    coupled_variables = 'concentration_HT_enclosure_1'
    expression = '${fparse R*temperature}*concentration_HT_enclosure_1'
    block = 1
    execute_on = 'initial timestep_end'
  []

  # Auxiliary kernels for H2, T2, and HT in enclosure 2
  [pressure_H2_enclosure_2]
    type = ParsedAux
    variable = pressure_H2_enclosure_2
    coupled_variables = 'concentration_H2_enclosure_2'
    expression = '${fparse R*temperature}*concentration_H2_enclosure_2'
    block = 2
    execute_on = 'initial timestep_end'
  []
  [pressure_T2_enclosure_2]
    type = ParsedAux
    variable = pressure_T2_enclosure_2
    coupled_variables = 'concentration_T2_enclosure_2'
    expression = '${fparse R*temperature}*concentration_T2_enclosure_2'
    block = 2
    execute_on = 'initial timestep_end'
  []
  [pressure_HT_enclosure_2]
    type = ParsedAux
    variable = pressure_HT_enclosure_2
    coupled_variables = 'concentration_HT_enclosure_2'
    expression = '${fparse R*temperature}*concentration_HT_enclosure_2'
    block = 2
    execute_on = 'initial timestep_end'
  []
[]

[InterfaceKernels]
  [interface_sorption_H2]
    type = InterfaceSorption
    K0 = ${solubility}
    Ea = 0
    n_sorption = ${n_sorption}
    diffusivity = ${diffusivity}
    unit_scale = ${unit_scale}
    unit_scale_neighbor = ${unit_scale_neighbor}
    temperature = ${temperature}
    variable = concentration_H2_enclosure_1
    neighbor_var = concentration_H2_enclosure_2
    sorption_penalty = 1e1
    boundary = interface
  []
  [interface_sorption_T2]
    type = InterfaceSorption
    K0 = ${solubility}
    Ea = 0
    n_sorption = ${n_sorption}
    diffusivity = ${diffusivity}
    unit_scale = ${unit_scale}
    unit_scale_neighbor = ${unit_scale_neighbor}
    temperature = ${temperature}
    variable = concentration_T2_enclosure_1
    neighbor_var = concentration_T2_enclosure_2
    sorption_penalty = 1e1
    boundary = interface
  []
  [interface_sorption_HT]
    type = InterfaceSorption
    K0 = ${solubility}
    Ea = 0
    n_sorption = ${n_sorption}
    diffusivity = ${diffusivity}
    unit_scale = ${unit_scale}
    unit_scale_neighbor = ${unit_scale_neighbor}
    temperature = ${temperature}
    variable = concentration_HT_enclosure_1
    neighbor_var = concentration_HT_enclosure_2
    sorption_penalty = 1e1
    boundary = interface
  []
[]

[Postprocessors]

  # postprocessors for H2
  [pressure_H2_enclosure_1]
    type = ElementAverageValue
    variable = pressure_H2_enclosure_1
    block = 1
    execute_on = 'initial timestep_end'
  []
  [pressure_H2_enclosure_2]
    type = ElementAverageValue
    variable = pressure_H2_enclosure_2
    block = 2
    execute_on = 'initial timestep_end'
  []
  [concentration_H2_enclosure_1_at_interface]
    type = SideAverageValue
    boundary = interface
    variable = concentration_H2_enclosure_1
    outputs = 'csv console'
    execute_on = 'initial timestep_end'
  []
  [concentration_H2_enclosure_2_at_interface]
    type = SideAverageValue
    boundary = interface2
    variable = concentration_H2_enclosure_2
    outputs = 'csv console'
    execute_on = 'initial timestep_end'
  []
  [concentration_ratio_H2]
    type = ParsedPostprocessor
    expression = 'concentration_H2_enclosure_1_at_interface / sqrt(concentration_H2_enclosure_2_at_interface)'
    pp_names = 'concentration_H2_enclosure_1_at_interface concentration_H2_enclosure_2_at_interface'
    execute_on = 'initial timestep_end'
    outputs = 'csv console'
  []
  [pressure_H2_enclosure_1_at_interface]
    type = SideAverageValue
    boundary = interface
    variable = pressure_H2_enclosure_1
    outputs = 'csv console'
    execute_on = 'initial timestep_end'
  []
  [pressure_H2_enclosure_2_at_interface]
    type = SideAverageValue
    boundary = interface2
    variable = pressure_H2_enclosure_2
    outputs = 'csv console'
    execute_on = 'initial timestep_end'
  []
  [concentration_H2_encl_1_inventory]
    type = ElementIntegralVariablePostprocessor
    variable = concentration_H2_enclosure_1
    block = 1
    execute_on = 'initial timestep_end'
  []
  [concentration_H2_encl_2_inventory]
    type = ElementIntegralVariablePostprocessor
    variable = concentration_H2_enclosure_2
    block = 2
    execute_on = 'initial timestep_end'
  []

  # postprocessors for T2
  [pressure_T2_enclosure_1]
    type = ElementAverageValue
    variable = pressure_T2_enclosure_1
    block = 1
    execute_on = 'initial timestep_end'
  []
  [pressure_T2_enclosure_2]
    type = ElementAverageValue
    variable = pressure_T2_enclosure_2
    block = 2
    execute_on = 'initial timestep_end'
  []
  [concentration_T2_enclosure_1_at_interface]
    type = SideAverageValue
    boundary = interface
    variable = concentration_T2_enclosure_1
    outputs = 'csv console'
    execute_on = 'initial timestep_end'
  []
  [concentration_T2_enclosure_2_at_interface]
    type = SideAverageValue
    boundary = interface2
    variable = concentration_T2_enclosure_2
    outputs = 'csv console'
    execute_on = 'initial timestep_end'
  []
  [concentration_ratio_T2]
    type = ParsedPostprocessor
    expression = 'concentration_T2_enclosure_1_at_interface / sqrt(concentration_T2_enclosure_2_at_interface)'
    pp_names = 'concentration_T2_enclosure_1_at_interface concentration_T2_enclosure_2_at_interface'
    execute_on = 'initial timestep_end'
    outputs = 'csv console'
  []
  [concentration_T2_encl_1_inventory]
    type = ElementIntegralVariablePostprocessor
    variable = concentration_T2_enclosure_1
    block = 1
    execute_on = 'initial timestep_end'
  []
  [concentration_T2_encl_2_inventory]
    type = ElementIntegralVariablePostprocessor
    variable = concentration_T2_enclosure_2
    block = 2
    execute_on = 'initial timestep_end'
  []

  # postprocessors for HT
  [pressure_HT_enclosure_1]
    type = ElementAverageValue
    variable = pressure_HT_enclosure_1
    block = 1
    execute_on = 'initial timestep_end'
  []
  [pressure_HT_enclosure_2]
    type = ElementAverageValue
    variable = pressure_HT_enclosure_2
    block = 2
    execute_on = 'initial timestep_end'
  []
  [concentration_HT_enclosure_1_at_interface]
    type = SideAverageValue
    boundary = interface
    variable = concentration_HT_enclosure_1
    outputs = 'csv console'
    execute_on = 'initial timestep_end'
  []
  [concentration_HT_enclosure_2_at_interface]
    type = SideAverageValue
    boundary = interface2
    variable = concentration_HT_enclosure_2
    outputs = 'csv console'
    execute_on = 'initial timestep_end'
  []
  [concentration_ratio_HT]
    type = ParsedPostprocessor
    expression = 'concentration_HT_enclosure_1_at_interface / sqrt(concentration_HT_enclosure_2_at_interface)'
    pp_names = 'concentration_HT_enclosure_1_at_interface concentration_HT_enclosure_2_at_interface'
    execute_on = 'initial timestep_end'
    outputs = 'csv console'
  []
  [concentration_HT_encl_1_inventory]
    type = ElementIntegralVariablePostprocessor
    variable = concentration_HT_enclosure_1
    block = 1
    execute_on = 'initial timestep_end'
  []
  [concentration_HT_encl_2_inventory]
    type = ElementIntegralVariablePostprocessor
    variable = concentration_HT_enclosure_2
    block = 2
    execute_on = 'initial timestep_end'
  []

  # postprocessors for mass conservation
  [mass_conservation_sum_encl1_encl2]
    type = LinearCombinationPostprocessor
    pp_names = 'concentration_HT_encl_1_inventory concentration_HT_encl_2_inventory concentration_H2_encl_1_inventory concentration_H2_encl_2_inventory concentration_T2_encl_1_inventory concentration_T2_encl_2_inventory'
    pp_coefs = '1            1           1            1            1            1'
    execute_on = 'initial timestep_end'
  []

  # postprocessors for equilibrium constant
  [equilibrium_constant_encl_1]
    type = ParsedPostprocessor
    expression = 'pressure_HT_enclosure_1 / sqrt(pressure_H2_enclosure_1 * pressure_T2_enclosure_1)'
    pp_names = 'pressure_HT_enclosure_1 pressure_H2_enclosure_1 pressure_T2_enclosure_1'
    execute_on = 'initial timestep_end'
    outputs = 'csv console'
  []
  [equilibrium_constant_encl_2]
    type = ParsedPostprocessor
    expression = 'pressure_HT_enclosure_2 / sqrt(pressure_H2_enclosure_2 * pressure_T2_enclosure_2)'
    pp_names = 'pressure_HT_enclosure_2 pressure_H2_enclosure_2 pressure_T2_enclosure_2'
    execute_on = 'initial timestep_end'
    outputs = 'csv console'
  []
[]

[Preconditioning]
  [smp]
    type = SMP
    full = true
  []
[]

[Executioner]
  type = Transient
  end_time = ${simulation_time}
  dtmax = 1e-2
  nl_max_its = 9
  l_max_its = 30
  scheme = 'bdf2'
  solve_type = 'PJFNK'
  petsc_options_iname = '-pc_type'
  petsc_options_value = 'lu'
  [TimeStepper]
    type = IterationAdaptiveDT
    dt = 1e-6
    optimal_iterations = 7
    iteration_window = 1
    growth_factor = 1.1
    cutback_factor = 0.9
    cutback_factor_at_failure = 0.9
  []
[]

[Outputs]
  file_base = 'ver-1kd_out_k10'
  csv = true
  exodus = true
  execute_on = 'initial timestep_end'
[]

General Case Description
Case Set Up
Results
Input files
References