ver-1g

A Simple Forward Chemical Reaction

This verification problem is taken from Longhurst et al. (1992) and Ambrosek and Longhurst (2008), and it has been updated and extended in Simon et al. (2025). A simple time-dependent chemical reaction given by

$var element = document.getElementById("moose-equation-458f4827-cf90-444a-8641-80cb54c86d91");katex.render("A + B \\Rightarrow AB", element, {displayMode:true,throwOnError:false});$

is modeled in a functional enclosure. The reaction rate, $var element = document.getElementById("moose-equation-696c642a-6f9c-4ef1-8050-9720a48a661d");katex.render("R", element, {displayMode:false,throwOnError:false});$ , is positive if the species AB is being produced in the reaction and negative if it is being consumed. The forward rate coefficient, $var element = document.getElementById("moose-equation-f02d0396-fdde-40fd-bbbb-f69a18d7be9c");katex.render("K", element, {displayMode:false,throwOnError:false});$ , for the reaction has no spatial or time dependence. The reaction rate is:

$var element = document.getElementById("moose-equation-c0331904-cc99-46a8-802b-81d3cdb9cea1");katex.render("R = K C_A C_B", element, {displayMode:true,throwOnError:false});$

where $var element = document.getElementById("moose-equation-b8d9a632-df1f-4ce8-8b94-8a806fa595d4");katex.render("C_A", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-8157bfc7-f342-4840-b63d-a865d5b20176");katex.render("C_B", element, {displayMode:false,throwOnError:false});$ are the concentrations of A and B, respectively. The reaction rate in terms of the concentrations of the reactants and product is given as:

$var element = document.getElementById("moose-equation-9f736b10-dc9f-45f9-a73c-ea31fb3af164");katex.render("R = -\\frac{d[C_A]}{dt} = -\\frac{d[C_B]}{dt} = \\frac{d[C_{AB}]}{dt} = K C_A C_B", element, {displayMode:true,throwOnError:false});$

where $var element = document.getElementById("moose-equation-b07dff74-b752-4991-91af-f165e6f85f0f");katex.render("C_{AB}", element, {displayMode:false,throwOnError:false});$ is the concentration of species AB. The analytical solution for the concentration of species AB as a function of time ( $var element = document.getElementById("moose-equation-d71589e4-0b56-4538-a8b2-19df2e6070c8");katex.render("t", element, {displayMode:false,throwOnError:false});$ ) is given as:

$(1)var element = document.getElementById("moose-equation-519b9fae-282d-4b8a-b7d7-2e09d34b8f42");katex.render("C_{AB} = C_{B_0} \\frac{1 - exp{[K t (C_{B_0} - C_{A_0})]}}{1 - \\frac{C_{B_0}}{C_{A_0}}exp{[K t (C_{B_0} - C_{A_0})]}} ", element, {displayMode:true,throwOnError:false});$

where $var element = document.getElementById("moose-equation-5dc7ad5e-97f7-4173-8e99-f6bfee6fb9bb");katex.render("C_{A_0}", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-629a7abb-9e54-439a-8f3a-e48941e07715");katex.render("C_{B_0}", element, {displayMode:false,throwOnError:false});$ are the initial concentrations of A and B, respectively. For the special case when $var element = document.getElementById("moose-equation-430aae18-fe5e-46ec-af87-c4be90f5e47b");katex.render("C_{A_0}", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-42097d8a-e881-4a8e-bc29-0a9fe326b67d");katex.render("C_{B_0}", element, {displayMode:false,throwOnError:false});$ are equal, Eq. (1) becomes: $var element = document.getElementById("moose-equation-e71638ae-67b2-4da7-953d-e39bb6461322");katex.render("C_{AB} = C_{A_0} - \\frac{1}{\\frac{1}{C_{A_0}} + Kt}", element, {displayMode:true,throwOnError:false});$

For this verification exercise, three cases were considered: (a) the initial concentrations of A and B are equal, (b) the initial concentrations of A and B are different and use the TMAP4 verification case values, and (c) the initial concentrations of A and B are different and use the TMAP7 verification case values. The equal concentration case is the same in TMAP4 and TMAP7, and is used for verification of TMAP8 here. While both TMAP4 and TMAP7 verification cases ((b) and (c) respectively) have the same analytical solution, the different initial conditions produce different $var element = document.getElementById("moose-equation-d3a054da-149a-4878-b68e-cce5adec6f5f");katex.render("C_{AB}", element, {displayMode:false,throwOnError:false});$ values over time, and we replicate both results here.

For case (a), the initial pressures of A and B were 1 $var element = document.getElementById("moose-equation-186bc599-dce4-43b2-b527-790d27d868f5");katex.render("\\mu", element, {displayMode:false,throwOnError:false});$ Pa, and the reaction rate $var element = document.getElementById("moose-equation-1deb5e59-307f-45da-9bc1-0b7c66e9ae60");katex.render("K", element, {displayMode:false,throwOnError:false});$ is 4.14 $var element = document.getElementById("moose-equation-b6f807cf-b5a3-48c8-838c-01aa4435130b");katex.render("\\times", element, {displayMode:false,throwOnError:false});$ 10 $var element = document.getElementById("moose-equation-97831508-1d74-4676-bcc4-42e215c67c39");katex.render("^3", element, {displayMode:false,throwOnError:false});$ $var element = document.getElementById("moose-equation-2bd5df3e-1839-487e-8bd1-6492566cfa19");katex.render("\\mu", element, {displayMode:false,throwOnError:false});$ m $var element = document.getElementById("moose-equation-bc7c1fe1-3f2d-4c78-a8f1-04e0c3a56c3d");katex.render("^3", element, {displayMode:false,throwOnError:false});$ / atom $var element = document.getElementById("moose-equation-de470d10-008e-4a13-8279-22c03c5b2273");katex.render("\\cdot", element, {displayMode:false,throwOnError:false});$ s. For case (b) the initial pressure of A was same as in case (a) while the initial pressure of B is 0.1 $var element = document.getElementById("moose-equation-ef9a97ba-9694-457a-834f-30e14ccb1e97");katex.render("\\mu", element, {displayMode:false,throwOnError:false});$ Pa as per TMAP4. For case (c) the initial pressure of A was same as in case (a) while the initial pressure of B is 0.5 $var element = document.getElementById("moose-equation-07285ed9-f103-42c8-9fff-1b99bfc191d2");katex.render("\\mu", element, {displayMode:false,throwOnError:false});$ Pa. In all cases, the initial pressures of A and B are first converted to their initial concentrations $var element = document.getElementById("moose-equation-c42a241f-b2c7-4757-a57e-91615a0812d5");katex.render("C_{A_0}", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-307ae09b-e378-4f40-b58e-b2d2fdba200b");katex.render("C_{B_0}", element, {displayMode:false,throwOnError:false});$ using the ideal gas law to be used in the TMAP8 simulations and analytical solutions. The initial concentration $var element = document.getElementById("moose-equation-4570029e-7224-483b-bdaf-0fcd8627f388");katex.render("C_{i_0}", element, {displayMode:false,throwOnError:false});$ of component $var element = document.getElementById("moose-equation-835d4ada-bbb1-4426-95c0-02771eaa8496");katex.render("i", element, {displayMode:false,throwOnError:false});$ is

$var element = document.getElementById("moose-equation-b6007542-022f-44d2-9deb-a4b2fd50fd92");katex.render("C_{i_0} = 10^{-18} \\frac{P_{i_0} N_a}{R T},", element, {displayMode:true,throwOnError:false});$

where $var element = document.getElementById("moose-equation-d75e4c7f-f3c1-4d13-b58f-21ae11a77160");katex.render("P_{i_0}", element, {displayMode:false,throwOnError:false});$ is the initial pressure, $var element = document.getElementById("moose-equation-47d4658f-e3ca-47fa-9655-8d115e429436");katex.render("N_a", element, {displayMode:false,throwOnError:false});$ is Avogardro's constant, $var element = document.getElementById("moose-equation-27ba20ab-d803-4630-adce-7014e514b13d");katex.render("R", element, {displayMode:false,throwOnError:false});$ is the gas constant (from PhysicalConstants), and $var element = document.getElementById("moose-equation-14730903-26a2-479d-b925-dbca7c5b5268");katex.render("T", element, {displayMode:false,throwOnError:false});$ = 298.15 K (25 $var element = document.getElementById("moose-equation-d56daf76-6ef6-455f-ba14-109a23bf2256");katex.render("\\deg", element, {displayMode:false,throwOnError:false});$ C) is the temperature. The factor $var element = document.getElementById("moose-equation-5c9d6043-76c2-4c72-b822-980c247a7a83");katex.render("10^{-18}", element, {displayMode:false,throwOnError:false});$ converts the concentration from atoms/m $var element = document.getElementById("moose-equation-c05ae438-7978-415d-8438-84669c52c2ad");katex.render("^3", element, {displayMode:false,throwOnError:false});$ to atoms/ $var element = document.getElementById("moose-equation-0ec8763c-ad3d-4ecb-a2b7-cc1637b8aa96");katex.render("\\mu", element, {displayMode:false,throwOnError:false});$ m $var element = document.getElementById("moose-equation-ae247ccc-86d4-4521-be04-51e5f3d3fcd1");katex.render("^3", element, {displayMode:false,throwOnError:false});$ .

A comparison of the concentration of AB as a function of time is plotted in Figure 1 for case (a), and Figure 2 for the cases (b) and (c), respectively. The TMAP8 calculations are found to be in good agreement with the analytical solution with the root mean square percentage errors of (a) RMSPE = 0.27 %, (b) RMSPE = 0.22 %, and (c) RMSPE = 0.24 %.

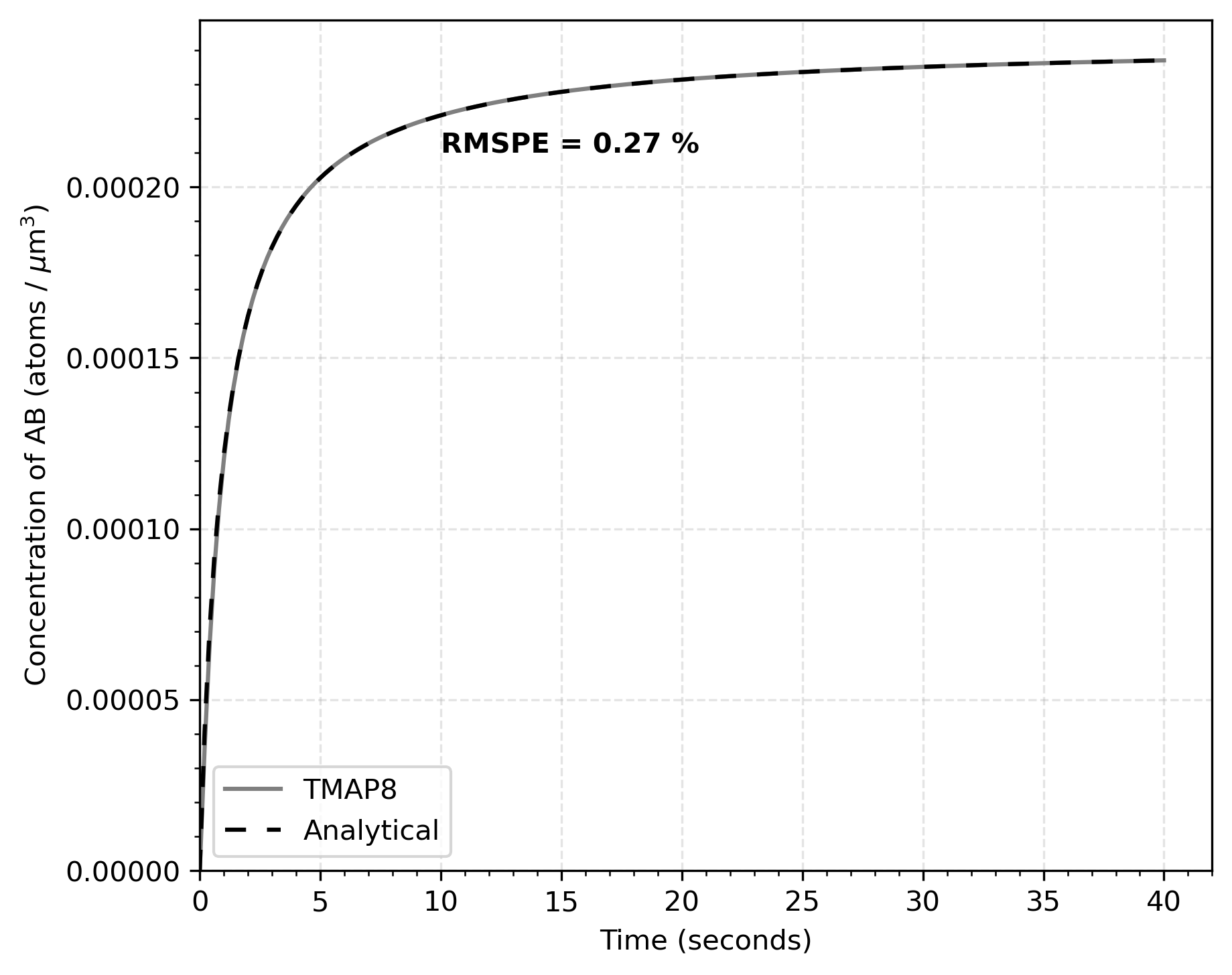
Figure 1: Comparison of concentration of AB as a function of time calculated through TMAP8 and analytically for the case when A and B have equal concentrations.

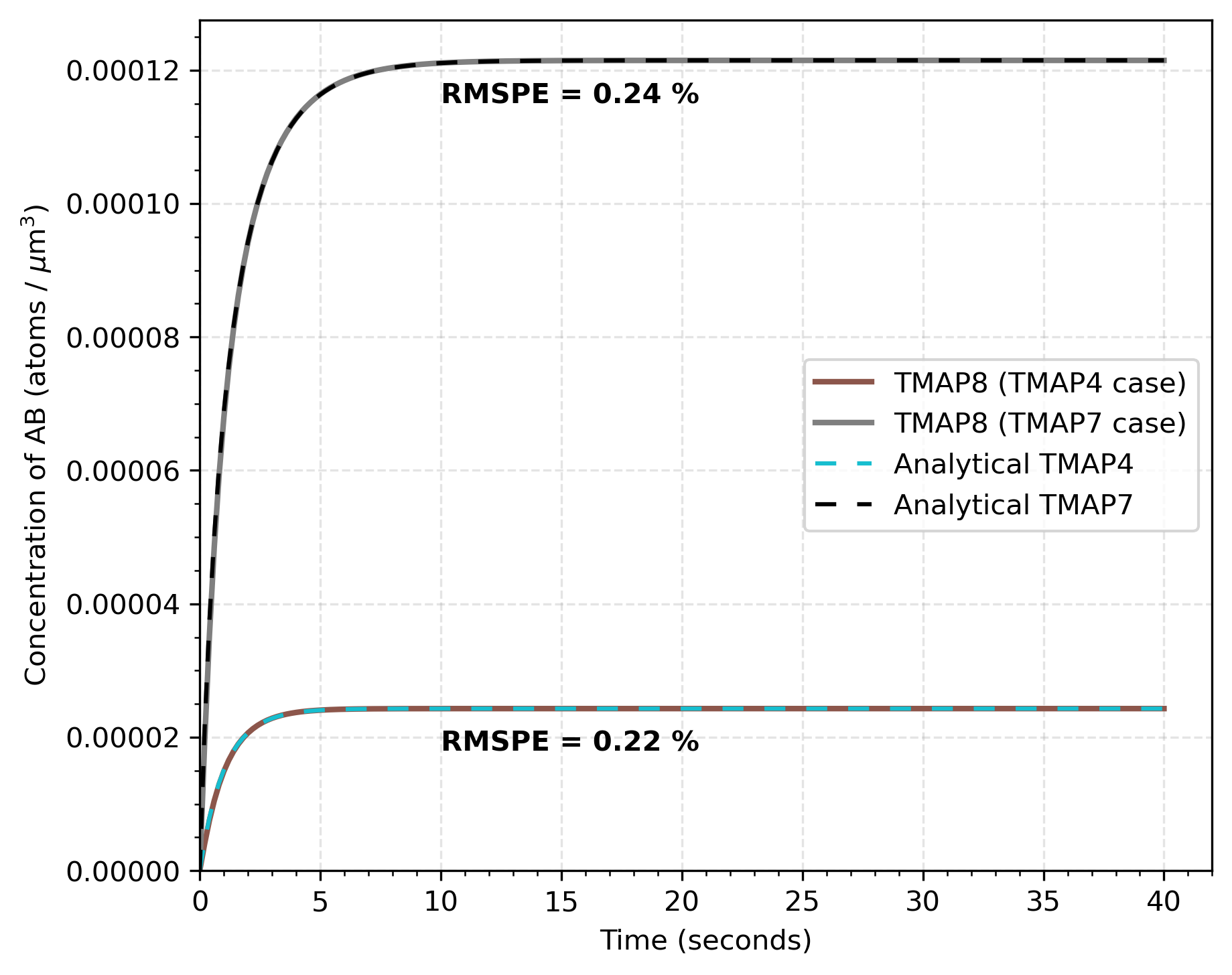
Figure 2: Comparison of concentration of AB as a function of time calculated through TMAP8 and analytically for the case when A and B have different concentrations. The plot shows comparisons for the initial conditions specified in both TMAP4 (case (b)) and TMAP7 (case (c)).

Input files

The input file for these cases can be found at (test/tests/ver-1g/ver-1g.i), which is also used as tests in TMAP8 at (test/tests/ver-1g/tests). The initial conditions of three cases (a), (b), and (c) can be found at (test/tests/ver-1g/equal_conc.i), (test/tests/ver-1g/diff_conc_TMAP4.i), and (test/tests/ver-1g/diff_conc_TMAP7.i), respectively.

References

James Ambrosek and GR Longhurst. Verification and Validation of TMAP7. Technical Report INEEL/EXT-04-01657, Idaho National Engineering and Environmental Laboratory, December 2008.

@techreport{ambrosek2008verification,
    author = "Ambrosek, James and Longhurst, GR",
    title = "{Verification and Validation of TMAP7}",
    year = "2008",
    number = "INEEL/EXT-04-01657",
    month = "December",
    institution = "Idaho National Engineering and Environmental Laboratory"
}

GR Longhurst, SL Harms, ES Marwil, and BG Miller. Verification and Validation of TMAP4. Technical Report EGG-FSP-10347, Idaho National Engineering Laboratory, Idaho Falls, ID (United States), 1992.

@techreport{longhurst1992verification,
    author = "Longhurst, GR and Harms, SL and Marwil, ES and Miller, BG",
    title = "{Verification and Validation of TMAP4}",
    year = "1992",
    institution = "Idaho National Engineering Laboratory, Idaho Falls, ID (United States)",
    number = "EGG-FSP-10347"
}

Pierre-Clément A. Simon, Casey T. Icenhour, Gyanender Singh, Alexander D Lindsay, Chaitanya Vivek Bhave, Lin Yang, Adriaan Anthony Riet, Yifeng Che, Paul Humrickhouse, Masashi Shimada, and Pattrick Calderoni. MOOSE-based tritium migration analysis program, version 8 (TMAP8) for advanced open-source tritium transport and fuel cycle modeling. Fusion Engineering and Design, 214:114874, May 2025. doi:10.1016/j.fusengdes.2025.114874.

@article{Simon2025,
    author = "Simon, Pierre-Clément A. and Icenhour, Casey T. and Singh, Gyanender and Lindsay, Alexander D and Bhave, Chaitanya Vivek and Yang, Lin and Riet, Adriaan Anthony and Che, Yifeng and Humrickhouse, Paul and Shimada, Masashi and Calderoni, Pattrick",
    title = "{MOOSE}-based Tritium Migration Analysis Program, Version 8 ({TMAP8}) for Advanced Open-Source Tritium Transport and Fuel Cycle Modeling",
    journal = "Fusion Engineering and Design",
    publisher = "Elsevier",
    volume = "214",
    pages = "114874",
    year = "2025",
    month = "May",
    issn = "0920-3796",
    doi = "10.1016/j.fusengdes.2025.114874"
}

(test/tests/ver-1g/ver-1g.i)

## Run this file with one of three input files to simulate various verification cases
## a. equal_conc.i        -> TMAP4 and TMAP7 equal concentration case
## b. diff_conc_TMAP4.i  -> TMAP4 different concentration case
## c. diff_conc_TMAP7.i  -> TMAP7 different concentration case
## Example: ~/projects/TMAP8/tmap8-opt -i ver-1g.i equal_conc.i

R = 8.31446261815324 # Gas constant (from PhysicalConstants.h - https://physics.nist.gov/cgi-bin/cuu/Value?r)
T = '${units 25 degC -> K}' # Temperature
Na = 6.02214076E23 # Avogadro's constant (from PhysicalConstants.h - https://physics.nist.gov/cgi-bin/cuu/Value?na)

[Mesh]
    type = GeneratedMesh
    dim = 2
[]

[Variables]
    [c_a]
    []
    [c_b]
    []
    [c_ab]
        initial_condition = 0
    []
[]

[Kernels]
    [timeDerivative_c_a]
        type = ADTimeDerivative
        variable = c_a
    []
    [timeDerivative_c_b]
        type = TimeDerivative
        variable = c_b
    []
    [timeDerivative_c_ab]
        type = TimeDerivative
        variable = c_ab
    []
    [MatReaction_b]
        type = ADMatReactionFlexible
        variable = c_b
        vs = 'c_a c_b'
        coeff = -1
        reaction_rate_name = K
    []
    [MatReaction_a]
        type = ADMatReactionFlexible
        variable = c_a
        vs = 'c_b c_a'
        coeff = -1
        reaction_rate_name = K
    []
    [MatReaction_ab]
        type = ADMatReactionFlexible
        variable = c_ab
        vs = 'c_b c_a'
        coeff = 1
        reaction_rate_name = K
    []
[]

[Materials]
    [K]
      type = ADParsedMaterial
      property_name = 'K'
      expression = '4.14e3' # units: molecule.micrometer^3/atom/second
    []
[]

[BCs]
    [c_a_neumann] # No flux on the sides
        type = NeumannBC
        variable = c_a
        boundary = 'left right bottom top'
        value = 0
    []
    [c_b_neumann] # No flux on the sides
        type = NeumannBC
        variable = c_b
        boundary = 'left right bottom top'
        value = 0
    []
    [c_ab_neumann] # No flux on the sides
        type = NeumannBC
        variable = c_ab
        boundary = 'left right bottom top'
        value = 0
    []
[]

[Postprocessors]
    [conc_a]
        type = ElementAverageValue
        variable = c_a
    []
    [conc_b]
        type = ElementAverageValue
        variable = c_b
    []
    [conc_ab]
        type = ElementAverageValue
        variable = c_ab
    []
[]

[Executioner]
    type = Transient
    scheme = bdf2
    nl_rel_tol = 1e-10
    nl_abs_tol = 1e-15

    solve_type = 'NEWTON'

    petsc_options = '-snes_ksp_ew'
    petsc_options_iname = '-pc_type'
    petsc_options_value = 'lu'

    start_time = 0.0
    end_time = 40
    num_steps = 60000
    dt = .2
    n_startup_steps = 0
[]

[Outputs]
    exodus = true
    csv = true
[]

(test/tests/ver-1g/tests)

[Tests]
  design = 'ADMatReactionFlexible.md'
  issues = '#12'
  verification = 'ver-1g.md'
  [binary_reaction_equal_concentrations]
    type = Exodiff
    input = 'ver-1g.i equal_conc.i'
    exodiff = equal_conc_out.e
    requirement = 'The system shall be able to model a chemical reaction between two species with the same concentrations and calculate the concentrations of reactants and product as a function of time'
  []
  [binary_reaction_diff_concentrations_TMAP4]
    type = Exodiff
    input = 'ver-1g.i diff_conc_TMAP4.i'
    exodiff = diff_conc_TMAP4_out.e
    requirement = 'The system shall be able to model a chemical reaction between two species with different concentrations and calculate the concentrations of reactants and product as a function of time using the initial conditions from the TMAP4 case'
  []
  [binary_reaction_diff_concentrations_TMAP7]
    type = Exodiff
    input = 'ver-1g.i diff_conc_TMAP7.i'
    exodiff = diff_conc_TMAP7_out.e
    requirement = 'The system shall be able to model a chemical reaction between two species with different concentrations and calculate the concentrations of reactants and product as a function of time using the initial conditions from the TMAP7 case'
  []
  [binary_reaction_equal_concentrations_csv_diff]
    type = CSVDiff
    input = 'ver-1g.i equal_conc.i'
    should_execute = False # this test relies on the output files from binary_reaction_equal_concentrations, so it shouldn't be run twice
    csvdiff = equal_conc_out.csv
    requirement = 'The system shall be able to model a chemical reaction between two species with the same concentrations and calculate the concentrations of reactants and product as a function of time, to match the analytical solution to generate CSV data for use in comparisons with the analytic solution over time.'
    prereq = binary_reaction_equal_concentrations
  []
  [binary_reaction_diff_concentrations_csv_diff_TMAP4]
    type = CSVDiff
    input = 'ver-1g.i diff_conc_TMAP4.i'
    should_execute = False # this test relies on the output files from binary_reaction_equal_concentrations, so it shouldn't be run twice
    csvdiff = diff_conc_TMAP4_out.csv
    requirement = 'The system shall be able to model a chemical reaction between two species with different concentrations using the initial conditions from the TMAP4 case and calculate the concentrations of reactants and product as a function of time to generate CSV data for use in comparisons with the analytic solution over time.'
    prereq = binary_reaction_diff_concentrations_TMAP4
  []
  [binary_reaction_diff_concentrations_csv_diff_TMAP7]
    type = CSVDiff
    input = 'ver-1g.i diff_conc_TMAP7.i'
    should_execute = False # this test relies on the output files from binary_reaction_equal_concentrations, so it shouldn't be run twice
    csvdiff = diff_conc_TMAP7_out.csv
    requirement = 'The system shall be able to model a chemical reaction between two species with different concentrations using the initial conditions from the TMAP7 case and calculate the concentrations of reactants and product as a function of time to generate CSV data for use in comparisons with the analytic solution over time.'
    prereq = binary_reaction_diff_concentrations_TMAP7
  []
  [ver-1g_comparison]
    type = RunCommand
    command = 'python3 comparison_ver-1g.py'
    requirement = 'The system shall be able to generate comparison plots between the analytical solution and simulated solution of a chemical reaction between two species with same or different concentrations, using the initial conditions from both TMAP4 and TMAP7 cases.'
    required_python_packages = 'matplotlib numpy pandas os'
  []
[]

(test/tests/ver-1g/equal_conc.i)

[ICs]
    ca_IC = '${fparse ${units 1 muPa -> Pa} * ${Na} / ( ${R} * ${T} ) }'
    cb_IC = '${fparse ${units 1 muPa -> Pa} * ${Na} / ( ${R} * ${T} ) }'
    [ca_same_conc_IC]
        type = ConstantIC
        variable = c_a
        value = '${units ${ca_IC} at/m^3 -> at/mum^3 }'
    []
    [cb_same_conc_IC]
        type = ConstantIC
        variable = c_b
        value = '${units ${cb_IC} at/m^3 -> at/mum^3 }'
    []
[]

(test/tests/ver-1g/diff_conc_TMAP4.i)

[ICs]
    ca_IC = '${fparse ${units 1 muPa -> Pa}   * ${Na} / ( ${R} * ${T} ) }'
    cb_IC = '${fparse ${units 0.1 muPa -> Pa} * ${Na} / ( ${R} * ${T} ) }'
    [ca_same_conc_IC]
        type = ConstantIC
        variable = c_a
        value = '${units ${ca_IC} at/m^3 -> at/mum^3 }'
    []
    [cb_same_conc_IC]
        type = ConstantIC
        variable = c_b
        value = '${units ${cb_IC} at/m^3 -> at/mum^3 }'
    []
[]

(test/tests/ver-1g/diff_conc_TMAP7.i)

[ICs]
    ca_IC = '${fparse ${units 1 muPa -> Pa}   * ${Na} / ( ${R} * ${T} ) }'
    cb_IC = '${fparse ${units 0.5 muPa -> Pa} * ${Na} / ( ${R} * ${T} ) }'
    [ca_same_conc_IC]
        type = ConstantIC
        variable = c_a
        value = '${units ${ca_IC} at/m^3 -> at/mum^3 }'
    []
    [cb_same_conc_IC]
        type = ConstantIC
        variable = c_b
        value = '${units ${cb_IC} at/m^3 -> at/mum^3 }'
    []
[]

Input files
References