ver-1b

Diffusion Problem with Constant Source Boundary Condition

This verification problem is taken from Longhurst et al. (1992), and it has been updated and extended in Simon et al. (2025). Diffusion of tritium through a semi-infinite SiC layer is modeled with a constant source located on one boundary. No solubility or trapping is included. The concentration as a function of time and position is given by $var element = document.getElementById("moose-equation-f28bef9a-5611-4c86-9b53-50af547d43bd");katex.render("C = C_0 \\; erfc \\left(\\frac{x}{2\\sqrt{Dt}}\\right),", element, {displayMode:true,throwOnError:false});$ where $var element = document.getElementById("moose-equation-ca6d9608-08b3-4a88-bfab-c28ce8083bb0");katex.render("C_0", element, {displayMode:false,throwOnError:false});$ the constant source concentration, erfc is the error function, $var element = document.getElementById("moose-equation-f561b039-2be9-431a-9e87-307d230ac164");katex.render("x", element, {displayMode:false,throwOnError:false});$ is the distance from the boundary, $var element = document.getElementById("moose-equation-0e4d19af-4176-423f-9f37-733eb0b70deb");katex.render("D", element, {displayMode:false,throwOnError:false});$ is the diffusion coefficient, and $var element = document.getElementById("moose-equation-e601167e-6432-4c41-b2e3-ab5cbb1da41f");katex.render("t", element, {displayMode:false,throwOnError:false});$ is the time.

Comparison of the TMAP8 results and the analytical solution is shown in Figure 1 as a function of time at $var element = document.getElementById("moose-equation-b60f6f0a-a67e-408a-a515-d9df55c39455");katex.render("x = 0.2", element, {displayMode:false,throwOnError:false});$ mm. For simplicity, both the diffusion coefficient and the initial concentration were set to unity. The TMAP8 code predictions match the analytical solution very well.

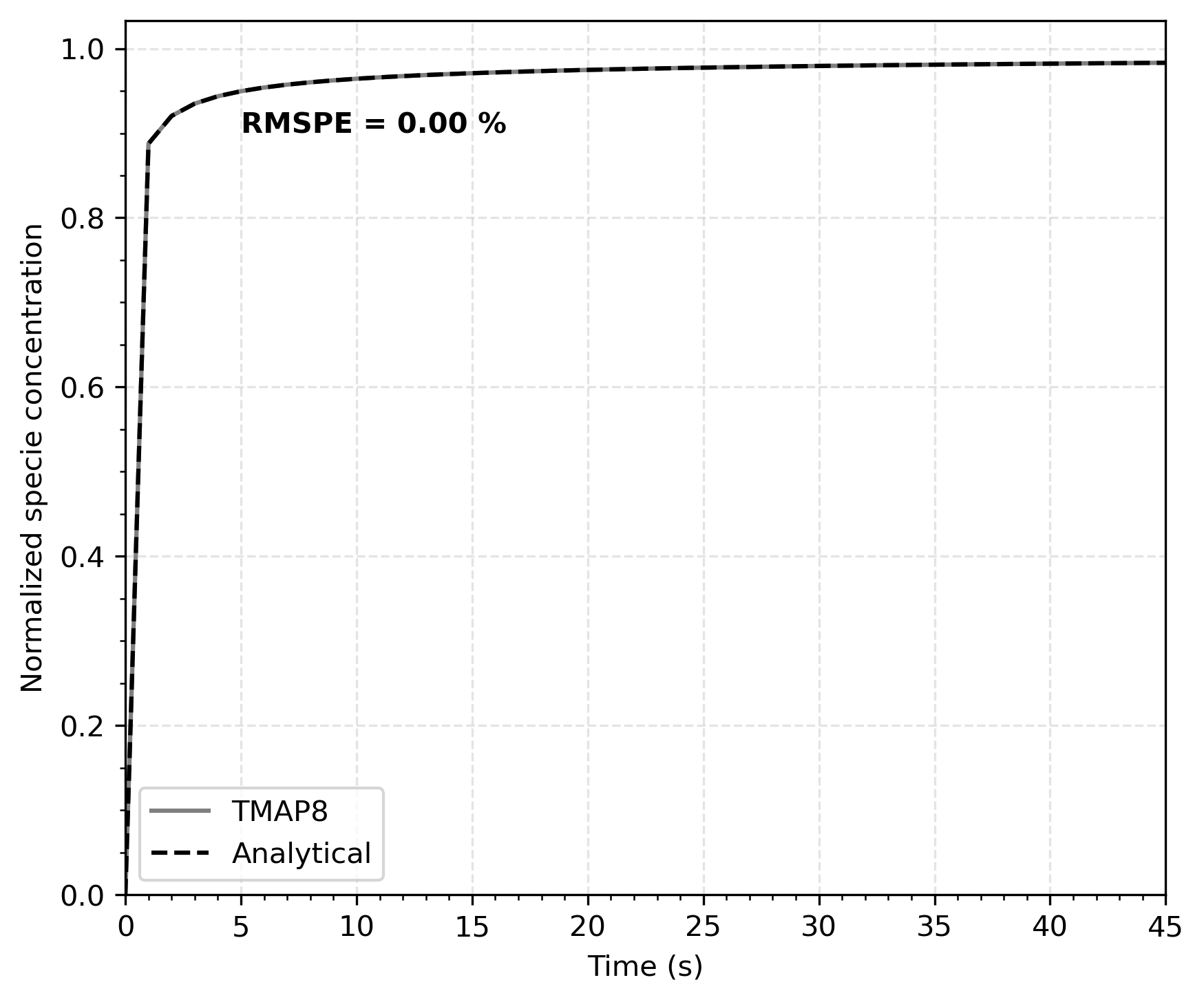
Figure 1: Comparison of concentration as function of time at $var element = document.getElementById("moose-equation-6e20dca2-8be6-4b33-b57b-4ddad04ad8e9");katex.render("x = 0.2", element, {displayMode:false,throwOnError:false});$ m calculated through TMAP8 and analytically.

As a second check, the concentration as a function of position at a given time $var element = document.getElementById("moose-equation-c1bd356d-aad0-4f02-9653-6fe8a794bad6");katex.render("t = 25", element, {displayMode:false,throwOnError:false});$ s calculated by TMAP8 was compared with the analytical solution as shown in Figure 2. The predicted concentration profile from TMAP8 is in good agreement with the analytical solution.

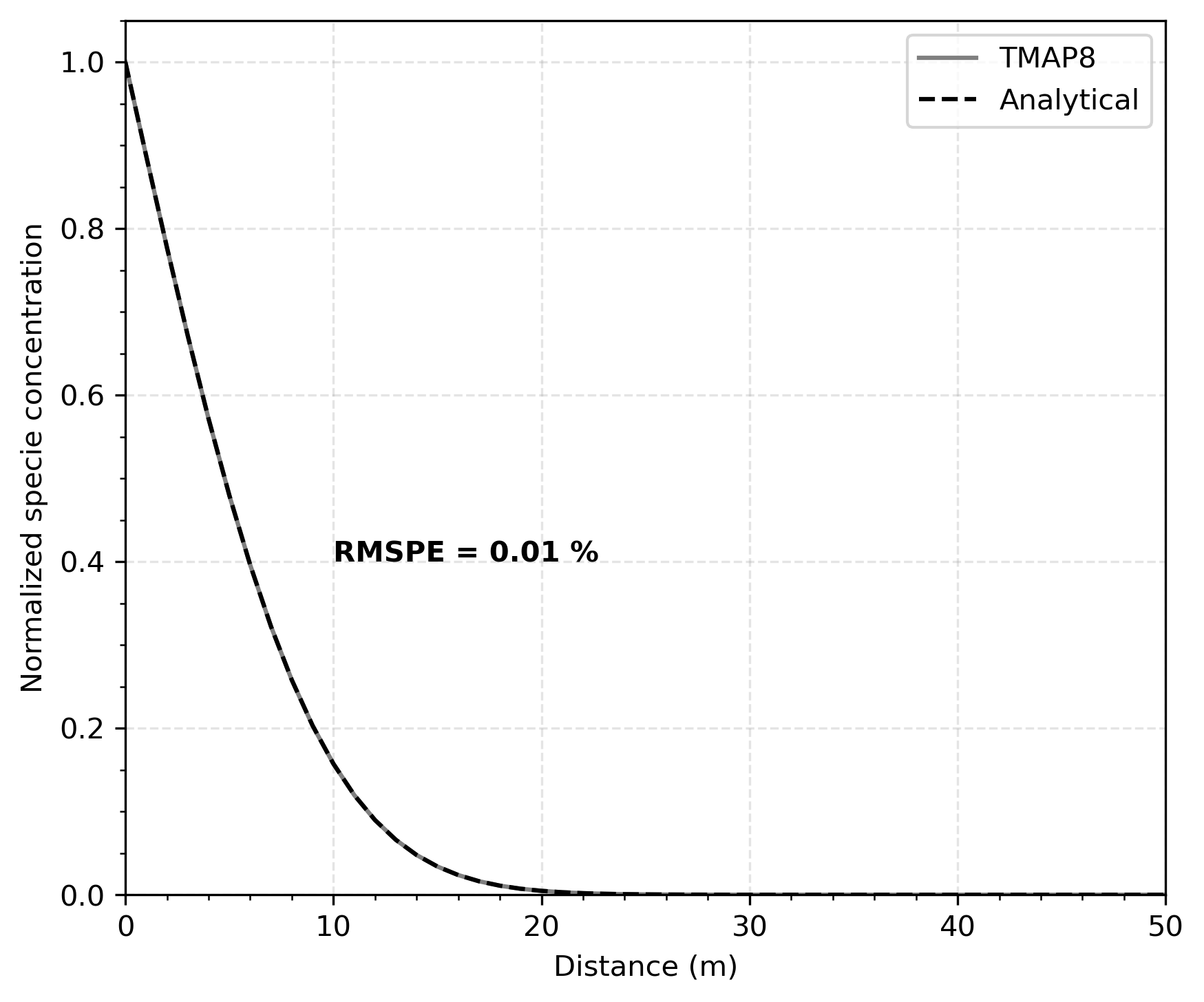
Figure 2: Comparison of concentration as function of distance from the source at $var element = document.getElementById("moose-equation-d7c3fab8-ce93-4904-a646-11eb0a0bf8df");katex.render("t = 25", element, {displayMode:false,throwOnError:false});$ s calculated through TMAP8 and analytically.

Finally, the diffusive flux ( $var element = document.getElementById("moose-equation-8daa1651-ce98-4d2a-850d-2da5b7509509");katex.render("J", element, {displayMode:false,throwOnError:false});$ ) was compared with the analytic solution where the flux is proportional to the derivative of the concentration with respect to $var element = document.getElementById("moose-equation-e6d4fc93-1a5a-4f02-aa47-6021a43bf76b");katex.render("x", element, {displayMode:false,throwOnError:false});$ and is given by $(1)var element = document.getElementById("moose-equation-f5005986-66ec-4bdc-82f9-c6bb70e8e763");katex.render(" J = C_0 \\; \\sqrt{\\frac{D}{t\\pi}} \\; exp \\left(\\frac{x}{2\\sqrt{Dt}}\\right).", element, {displayMode:true,throwOnError:false});$

The flux as given by Eq. (1) is compared with values calculated by TMAP8. The diffusivity, D, and the initial concentration, $var element = document.getElementById("moose-equation-28b25bc0-2601-428f-afd8-0cf0eb26d570");katex.render("C_0", element, {displayMode:false,throwOnError:false});$ , were both taken as unity, and the distance, $var element = document.getElementById("moose-equation-e3f3c7b8-36c4-4062-b26c-fddddf1766f9");katex.render("x", element, {displayMode:false,throwOnError:false});$ , was taken as 0.5 in this comparison. TMAP8 initially underpredicts but the results match well subsequently. Comparison results are shown in Figure 3 with a root mean square percentage error of RMSPE = 6.03 %. The error is calculated for $var element = document.getElementById("moose-equation-10816471-6e45-4fd0-9704-f5e52467b8ac");katex.render("t \\geq 10", element, {displayMode:false,throwOnError:false});$ s due to infinite value at small $var element = document.getElementById("moose-equation-2cb70675-0096-471a-bba1-a114aeae7b7b");katex.render("t", element, {displayMode:false,throwOnError:false});$ .

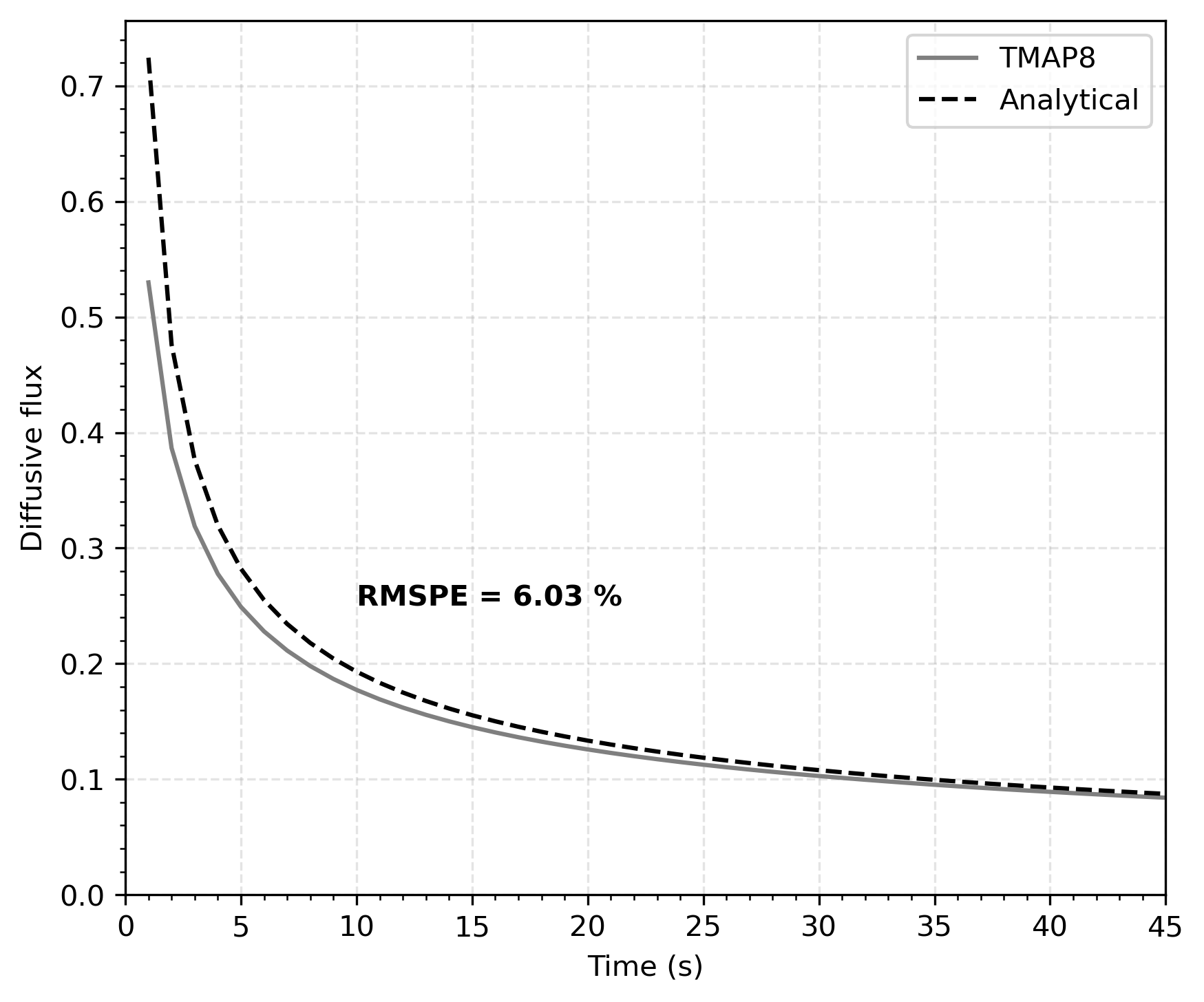
Figure 3: Comparison of flux as function of time at x=0.5m calculated through TMAP8 and analytically.

The oscillations in the permeation graph go away with increasing fineness in the mesh and in the time step dt.

Input files

The input file for this case can be found at (test/tests/ver-1b/ver-1b.i), which is different from the input file used as test in TMAP8. To limit the computational costs of the test cases, the tests run a version of the file with a coarser mesh and larger time steps. More information about the changes can be found in the test specification file for this case (test/tests/ver-1b/tests).

References

GR Longhurst, SL Harms, ES Marwil, and BG Miller. Verification and Validation of TMAP4. Technical Report EGG-FSP-10347, Idaho National Engineering Laboratory, Idaho Falls, ID (United States), 1992.

@techreport{longhurst1992verification,
    author = "Longhurst, GR and Harms, SL and Marwil, ES and Miller, BG",
    title = "{Verification and Validation of TMAP4}",
    year = "1992",
    institution = "Idaho National Engineering Laboratory, Idaho Falls, ID (United States)",
    number = "EGG-FSP-10347"
}

Pierre-Clément A. Simon, Casey T. Icenhour, Gyanender Singh, Alexander D Lindsay, Chaitanya Vivek Bhave, Lin Yang, Adriaan Anthony Riet, Yifeng Che, Paul Humrickhouse, Masashi Shimada, and Pattrick Calderoni. MOOSE-based tritium migration analysis program, version 8 (TMAP8) for advanced open-source tritium transport and fuel cycle modeling. Fusion Engineering and Design, 214:114874, May 2025. doi:10.1016/j.fusengdes.2025.114874.

@article{Simon2025,
    author = "Simon, Pierre-Clément A. and Icenhour, Casey T. and Singh, Gyanender and Lindsay, Alexander D and Bhave, Chaitanya Vivek and Yang, Lin and Riet, Adriaan Anthony and Che, Yifeng and Humrickhouse, Paul and Shimada, Masashi and Calderoni, Pattrick",
    title = "{MOOSE}-based Tritium Migration Analysis Program, Version 8 ({TMAP8}) for Advanced Open-Source Tritium Transport and Fuel Cycle Modeling",
    journal = "Fusion Engineering and Design",
    publisher = "Elsevier",
    volume = "214",
    pages = "114874",
    year = "2025",
    month = "May",
    issn = "0920-3796",
    doi = "10.1016/j.fusengdes.2025.114874"
}

(test/tests/ver-1b/ver-1b.i)

[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = 5000
  xmax = 200
[]

[Variables]
  [./u]
  [../]
[]

[AuxVariables]
  [./flux_x]
    order = FIRST
    family = MONOMIAL
  [../]
[]

[Kernels]
  [./diff]
    type = Diffusion
    variable = u
  [../]
  [./time]
    type = TimeDerivative
    variable = u
  [../]
[]

[AuxKernels]
  [./flux_x]
    type = DiffusionFluxAux
    diffusivity = ${fparse 1.0}
    variable = flux_x
    diffusion_variable = u
    component = x
  [../]
[]

[BCs]
  [./left]
    type = DirichletBC
    variable = u
    boundary = left
    value = 1
  [../]
  [./right]
    type = DirichletBC
    variable = u
    boundary = right
    value = 0
  [../]
[]

[VectorPostprocessors]
  [line]
    type = LineValueSampler
    start_point = '0 0 0'
    end_point = '50 0 0'
    num_points = 51
    sort_by = 'x'
    variable = u
    outputs = 'vector_postproc'
  []
[]

[Postprocessors]
  [conc_point1]
    type = PointValue
    variable = u
    point = '.2 0 0'
    outputs = 'csv'
  []
  [flux_point2]
    type = PointValue
    variable = flux_x
    point = '.5 0 0'
    outputs = 'csv'
  []
[]

[Executioner]
  type = Transient
  end_time = 50
  dt = .1
  solve_type = NEWTON
  petsc_options_iname = '-pc_type '
  petsc_options_value = 'lu '
  scheme = 'bdf2'
[]

[Outputs]
  [exodus]
    type = Exodus
    file_base = 'ver-1b_out'
  []
  [csv]
    type = CSV
    time_step_interval = 10
  []
  [vector_postproc]
    type = CSV
    sync_times = '25'
    sync_only = true
  []
  perf_graph = true
[]

(test/tests/ver-1b/tests)

[Tests]
  design = 'Diffusion.md TimeDerivative.md DirichletBC.md'
  issues = '#12'
  verification = 'ver-1b.md'
    [ver-1b]
      type = Exodiff
      input = ver-1b.i
      exodiff = ver-1b_test_out.e
      cli_args = 'Executioner/dt=10 Mesh/nx=100 Outputs/exodus/file_base=ver-1b_test_out'
      requirement = 'The system shall be able to model transient diffusion through a slab with a constant concentration boundary condition as the species source.'
    []
    [ver-1b_heavy]
      type = Exodiff
      input = ver-1b.i
      exodiff = ver-1b_out.e
      heavy = true
      requirement = 'The system shall be able to model transient diffusion through a slab with a constant concentration boundary condition as the species source with the fine mesh and time step required to match the analytical solution.'
    []
    [ver-1b_heavy_csvdiff]
      type = CSVDiff
      input = ver-1b.i
      should_execute = False  # this test relies on the output files from ver-1b_heavy, so it shouldn't be run twice
      csvdiff = ver-1b_csv.csv
      requirement = 'The system shall be able to model transient diffusion through a slab with a constant concentration boundary condition as the species source, with the fine mesh and time step required to match the analytical solution to generate CSV data for use in comparisons with the analytic solution over time.'
      heavy = true
      prereq = ver-1b_heavy
    []
    [ver-1b_heavy_lineplot]
      type = CSVDiff
      input = ver-1b.i
      should_execute = False  # this test relies on the output files from ver-1b_heavy, so it shouldn't be run twice
      csvdiff = ver-1b_vector_postproc_line_0250.csv
      requirement = 'The system shall be able to model transient diffusion through a slab with a constant concentration boundary condition as the species source, with the fine mesh and timestep required to match the analytical solution to generate CSV data for use in comparisons with the analytic solution for the profile concentration.'
      heavy = true
      prereq = ver-1b_heavy
    []
    [ver-1b_comparison]
      type = RunCommand
      command = 'python3 comparison_ver-1b.py'
      requirement = 'The system shall be able to generate comparison plots between the analytical solution and simulated solution of verification case 1b, modeling transient diffusion through a slab with a constant concentration boundary condition as the species source.'
      required_python_packages = 'matplotlib numpy pandas scipy os'
    []
[]

Input files
References