ver-1a
Depleting Source Problem
General Case Description
This verification case consists of an enclosure containing a finite concentration of atoms which are allowed to thermally diffuse through a SiC layer over time. No Soret effects, solubility, or trapping effects are included.
This is one of the original problems introduced in Longhurst et al. (1992) for TMAP4 and adapted in Ambrosek and Longhurst (2008) for TMAP7. This case has been updated and extended in the context of TMAP8 in Simon et al. (2025). Note, however, that the verification cases for TMAP4 and TMAP7, although using the exact same setup, use different quantities to verify their implementation (see Figure 2, Figure 3, and Figure 4). In TMAP8, for completeness, we perform verification on all these quantities and show agreement with analytical solutions from both TMAP4 and TMAP7.
Case Set up
Figure 1 shows a schematic of the ver-1a case, along with an illustration of the quantities used for verification. It consists of an enclosure that is pre-charged with a fixed quantity of tritium in gaseous form and a finite SiC slab. At time t > 0, the tritium is allowed to thermally diffuse through the SiC slab, initially at zero concentration. The surface of the slab in contact with the source is assumed to be in equilibrium with the source enclosure, assuming a temperature-dependent solubility . As a boundary condition, the concentration at the outer surface of the SiC slab is kept at zero for all time. The diffusion of the tritium through the SiC slab is calculated by neglecting Soret and trapping effects. Different aspects of the diffusion are compared against analytical solutions, as described below. The values used to characterize the necessary material properties and the case geometry are provided in Table 1.
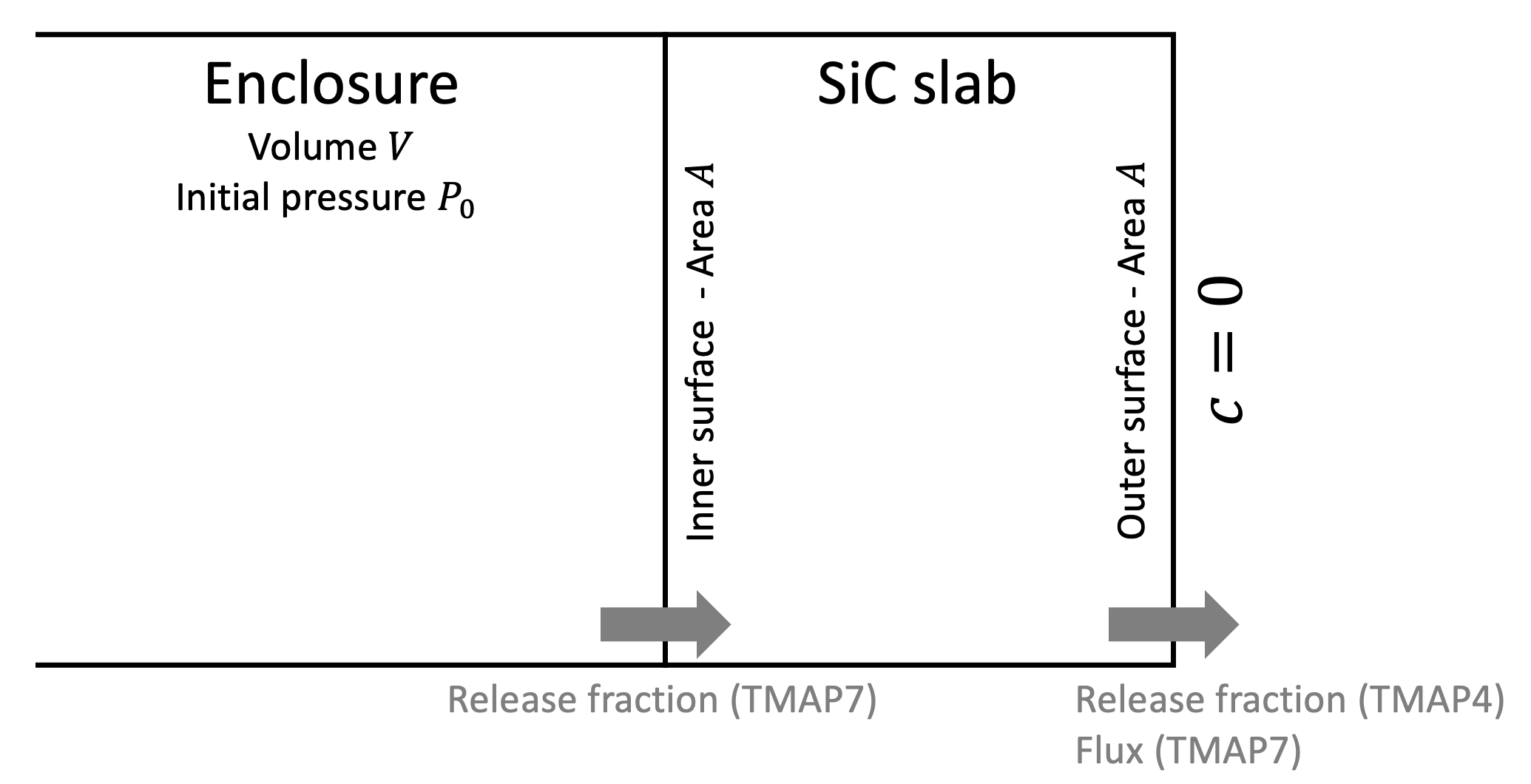
Figure 1: Schematic of the ver-1a case and illustration of the quantities used for verification.
Table 1: Values of material properties and case geometry with , the gas constant, as defined in PhysicalConstants.
| Parameter | Description | Value | Units |
|---|---|---|---|
| Enclosure volume | 5.20e-11 | m | |
| SiC slab surface area | 2.16e-6 | m | |
| Initial enclosure pressure | 1e6 | Pa | |
| Temperature | 2373 | K | |
| Tritium diffusivity in SiC | 1.58e-4 | m/2 | |
| Tritium solubility in SiC | 7.244e22 / | 1/m/Pa | |
| Slab thickness | 3.30e-5 | m |
Verification of the release fraction on the outer surface of the SiC slab (TMAP4)
Analytical solution
In Longhurst et al. (1992), i.e., TMAP4, the verification test focused on the fractional release from the outside of the slab. The analytical solution for this quantity is given by
where
with
where the "source concentration" is the concentration in the enclosure (), is the Boltzmann constant (as defined in PhysicalConstants), and "layer concentration" is the concentration in the slab at the interface with the enclosure (). is constant in time, and are the roots of
The expression in Eq. (1) of Longhurst et al. (1992) writes instead of the correct in the exponential. If the interested reader needs convincing, analyze the units in the original report for consistency. Despite this typo, their results are accurate.
Results
Figure 2 shows the comparison of the TMAP8 calculation and the analytical solution provided in Longhurst et al. (1992). There is agreement between the two plots with a root mean square percentage error of RMSPE = 0.19 % for s.
Figure 2: Comparison of TMAP8 calculation with the analytical solution for the release fraction on the outer surface of the SiC slab Longhurst et al. (1992).
Verification of the release fraction on the inner surface of the SiC slab (TMAP7)
Analytical solution
In Ambrosek and Longhurst (2008), i.e., TMAP7, the verification test focuses on the fractional release as determined by the amount of gas release from the enclosure. It is therefore defined as where is the pressure at the surface of the enclosure over time.
To derive , Ambrosek and Longhurst (2008) first references the analytical solution for an analogous heat transfer problem Carslaw and Jaeger (1959), which provides the solute concentration profile in the membrane as
where is the position of the surface in contact with the enclosure, and is the position of the outer surface (as defined in Ambrosek and Longhurst (2008) - see note below), and are the roots of
By linking the concentration on the surface of the slab in contact with the enclosure ( as used in Ambrosek and Longhurst (2008)) with the pressure of the enclosure, Henry's law provides which leads to
The units and expression of the solubility provided in Ambrosek and Longhurst (2008) have typos. The correct values and units are provided above in Table 1. The value provided in Ambrosek and Longhurst (2008) is kg m /s instead of 1/m/Pa when K. The correct value of is used in the input file decks in Longhurst et al. (1992) and Ambrosek and Longhurst (2008).
The release fraction in Ambrosek and Longhurst (2008) is described as in their Eq. (5) but is actually plotted as in Figure 1 of that report.
Not a typo, per se, but a potential source of confusion for users is that in Ambrosek and Longhurst (2008), represents the surface not exposed to the enclosure (where ), and represents the surface exposed to the enclosure. In the TMAP8 documentation, we have kept this convention to correspond to the TMAP7 case, but note that the TMAP8 input file fixes at the enclosure surface and for the outer surface.
Results
Figure 3 shows the comparison of the TMAP8 calculation and the analytical solution for release fraction provided in Ambrosek and Longhurst (2008). There is agreement between the two plots with a root mean square percentage error of RMSPE = 0.07 % for s.
Figure 3: Comparison of TMAP8 calculation with the analytical solution for the release fraction on the inner surface of the SiC slab Ambrosek and Longhurst (2008).
Verification of the tritium flux at the outer surface of the SiC slab (TMAP7)
Analytical solution
In Ambrosek and Longhurst (2008), i.e., TMAP7, the verification test also tests the model's accuracy in determining the tritium flux across the outer surface of the SiC slab. Using the expression of the concentration provided above, the flux on the outer surface of the SiC slab can be derived as
which can be compared to TMAP8 predictions.
Again, be aware of the typos in Ambrosek and Longhurst (2008) and the different coordinates used in TMAP8 and TMAP7 discussed above.
Results
Figure 4 shows the comparison of the TMAP8 calculation and the analytical solution for flux at the outer surface of the SiC slab in Ambrosek and Longhurst (2008). There is agreement between the two plots with a root mean square percentage error of RMSPE = 0.26 % for s.
Figure 4: Comparison of TMAP8 calculation with the analytical solution for the tritium flux at the outer surface of the SiC slab Ambrosek and Longhurst (2008).
Input files
It is important to note that the input file used to reproduce these results and the input file used as test in TMAP8 are different. Indeed, the input file (test/tests/ver-1a/ver-1a.i) has a fine mesh and uses small time steps to accurately match the analytical solutions and reproduce the figures above. To limit the computational costs of the tests, however, the tests run a version of the file with a coarser mesh and larger time steps. More information about the changes can be found in the test specification file for this case (test/tests/ver-1a/tests).
References
- James Ambrosek and GR Longhurst.
Verification and Validation of TMAP7.
Technical Report INEEL/EXT-04-01657, Idaho National Engineering and Environmental Laboratory, December 2008.[BibTeX]
- H. S. Carslaw and J. C. Jaeger.
Conduction of Heat in Solids.
2nd Edition, Oxford University Press, 1959.[BibTeX]
- GR Longhurst, SL Harms, ES Marwil, and BG Miller.
Verification and Validation of TMAP4.
Technical Report EGG-FSP-10347, Idaho National Engineering Laboratory, Idaho Falls, ID (United States), 1992.[BibTeX]
- Pierre-Clément A. Simon, Casey T. Icenhour, Gyanender Singh, Alexander D Lindsay, Chaitanya Vivek Bhave, Lin Yang, Adriaan Anthony Riet, Yifeng Che, Paul Humrickhouse, Masashi Shimada, and Pattrick Calderoni.
MOOSE-based tritium migration analysis program, version 8 (TMAP8) for advanced open-source tritium transport and fuel cycle modeling.
Fusion Engineering and Design, 214:114874, May 2025.
doi:10.1016/j.fusengdes.2025.114874.[BibTeX]