val-2a
Ion Implantation Experiment
Case Description
This validation problem is taken from Anderl et al. (1985). This paper describes an ion implantation experiment on a modified 316 stainless steel called Primary Candidate Alloy (PCA). This case is part of the validation suite of TMAP4 and TMAP7 as val-2a (Longhurst et al., 1992; Ambrosek and Longhurst, 2008), and it has been updated and extended in Simon et al. (2025). The PCA sample is a 0.5 mm thick disk with a diameter of 2.5 cm. It is exposed to a deuterium ion beam on the left side (also called the upstream side of the sample). The TRIM code (Biersack and Ziegler, 1982) was used in Longhurst et al. (1992) and Ambrosek and Longhurst (2008) to determine that the average implantation depth for the ions is 11 nm 5.4 nm. Reemission data from the TRIM calculation shows that only 75 % of the incident flux remained in the metal and other 25 % is re-emitted.
This model considers the diffusion in PCA and the recombination of deuterium on both sides. First, the diffusion of deuterium in PCA is described as:
(1)
where is the concentration of deuterium in PCA, is the time, is the diffusivity of deuterium in PCA, and is the source term in PCA due to the deuterium ion implantation.
Second, the deuterium recombines into gas on both sides of the PCA sample. By assuming that the recombination process is at steady state (which is not a necessary assumption in TMAP8, but appropriate in this case), it is described as the following surface flux:
(2)
where is the recombination flux out of the sample sides, is the area on the upstream or downstream side, is the pressure on the corresponding side, and and are the recombination and dissociation coefficients, respectively. The coefficient of 2 accounts for the fact that 2 deuterium atoms form one D molecule.
The objective of this simulation is to determine the permeation flux on the downstream side and match the experimental data published in Anderl et al. (1985) and reproduced in Figure 2.
Model Description
In this case, TMAP8 simulates a one-dimensional domain to represent the deuterium implantation, diffusion, and recombination. Note that this case can easily be extended to a two- or three-dimensional case.
The source term in the model is described as a normal distribution instead of the piecewise function from TMAP4 (Longhurst et al., 1992). The source term of deuterium from ion beam implantation is defined as:
(3)
where is the implantation flux provided in Table 1, m is the characteristic width of the normal distribution, and m is the depth of the normal distribution from the upstream side. Eq. (3) uses the same factor of 1.5 from Longhurst et al. (1992) to better correspond to implantation of experiment from Anderl et al. (1985). The comparison between the normal distribution from TMAP8 and piecewise function from TMAP4 is shown in Figure 1. The normal distribution has a similar distribution to the piecewise function, but the distribution profile is closer to the expected implantation profile.
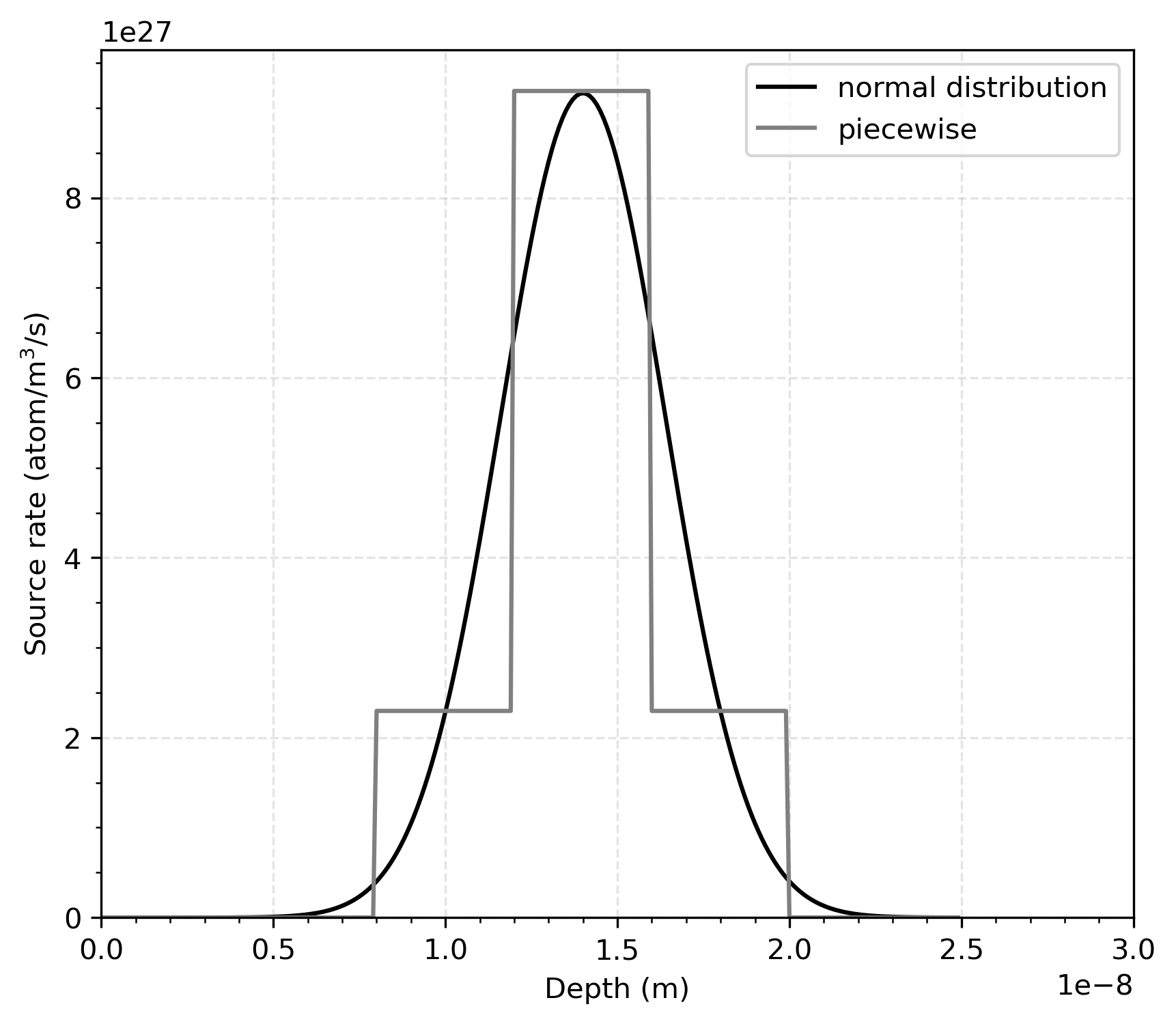
Figure 1: Comparison between the normal distribution from TMAP8 and piecewise function from TMAP4 for the source term due to deuterium ion beam implantation.
The pressures on the upstream and downstream sides are close to vacuum pressures, and have only little impact for the recombination on both sides (Longhurst et al., 1992; Ambrosek and Longhurst, 2008). Thus, TMAP8 ignores the impact of pressure on the boundary conditions to simplify the model. The recombination is described as a simplified version of Eq. (2):
(4)
Case and Model Parameters
The beam flux on the upstream side of the sample during the experiment is presented in Table 1, and only 75% of the flux remains in the sample. Other case and model parameters used in TMAP8 are listed in Table 2.
Table 1: Values of beam flux on the upstream side of the sample during the experiment (Anderl et al., 1985; Longhurst et al., 1992).
| time (s) | Beam flux (atom/m/s) |
|---|---|
| 0 - 5820 | 4.9 |
| 5820 - 9056 | 0 |
| 9056 - 12062 | 4.9 |
| 12062 - 14572 | 0 |
| 14572 - 17678 | 4.9 |
| 17678 - 20000 | 0 |
The times listed in Longhurst et al. (1992) for TMAP8 for the start and end times of the beam are not accurate. Instead, TMAP8 uses the times directly from Anderl et al. (1985) to better correspond to experimental conditions.
Table 2: Values of material properties. Note that are currently not used in the input file since the upstream and downstream pressure do not noticeably influence the results.
| Parameter | Description | Value | Units | Reference |
|---|---|---|---|---|
| upstream dissociation coefficient | 8.959 | at/m/s/Pa | Longhurst et al. (1992) | |
| downstream dissociation coefficient | 1.7918 | at/m/s/Pa | Longhurst et al. (1992) | |
| upstream recombination coefficient | 1 | m/at/s | Inspired from Longhurst et al. (1992) | |
| downstream recombination coefficient | 2 | m/at/s | Anderl et al. (1985) | |
| upstream pressure | 0 | Pa | Anderl et al. (1985) | |
| downstream pressure | 0 | Pa | Anderl et al. (1985) | |
| deuterium diffusivity in PCA | 3 | m/s | Anderl et al. (1985) | |
| diameter of PCA | 0.025 | m | Anderl et al. (1985) | |
| thickness of PCA | 5 | m | Anderl et al. (1985) | |
| temperature | 703 | K | Anderl et al. (1985) |
TMAP4 (Longhurst et al., 1992) and TMAP7 (Ambrosek and Longhurst, 2008) both replicate this validation case. However, they use different model parameters and configurations, and the experimental data presented in (Ambrosek and Longhurst, 2008) for TMAP7 do not correspond to the data published in Anderl et al. (1985). We therefore replicate only the data from TMAP4 and Anderl et al. (1985) in this TMAP8 validation case.
Both TMAP4 (Longhurst et al., 1992) and TMAP7 (Ambrosek and Longhurst, 2008) describe the upstream recombination and dissociation coefficients as time-dependent exponentials rather than mechanistically capture the influence of ion irradiation on material performance. TMAP8 uses the same expressions.
Results
Figure 2 shows the comparison of the TMAP8 calculation and the experimental data from Anderl et al. (1985). There is reasonable agreement between the TMAP predictions and the experimental data with a root mean square percentage error of RMSPE = 25.95 %. Note that the agreement could be improved by adjusting the model parameters. It is also possible to perform this optimization with MOOSE's stochastic tools module.
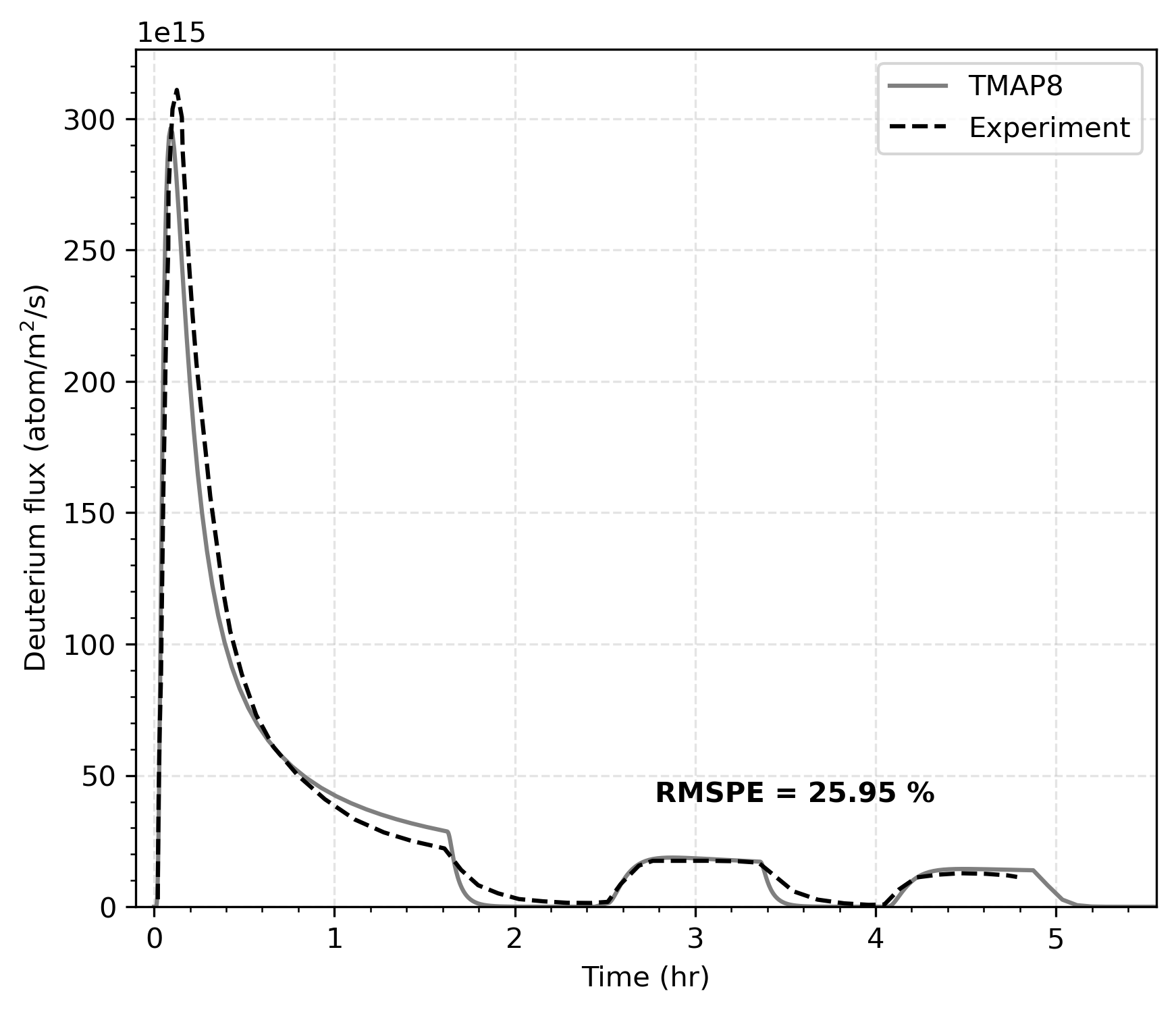
Figure 2: Comparison of TMAP8 calculation with the experimental data on the downstream side of the sample. TMAP8 accurately replicates the experimental data.
Input files
The input file for this case can be generated by (test/tests/val-2a/val-2a.i). The file are also used as test in TMAP8 at (test/tests/val-2a/tests).
References
- James Ambrosek and GR Longhurst.
Verification and Validation of TMAP7.
Technical Report INEEL/EXT-04-01657, Idaho National Engineering and Environmental Laboratory, December 2008.[BibTeX]
- RA Anderl, DF Holland, DA Struttmann, GR Longhurst, and BJ Merrill.
Tritium permeation in stainless-steel structures exposed to plasma ions.
Technical Report, Idaho National Engineering Lab., Idaho Falls (USA), 1985.[BibTeX]
- JP Biersack and JF Ziegler.
The stopping and range of ions in solids.
In Ion Implantation Techniques: Lectures given at the Ion Implantation School in Connection with Fourth International Conference on Ion Implantation: Equipment and Techniques Berchtesgaden, Fed. Rep. of Germany, September 13–15, 1982, 122–156. Springer, 1982.[BibTeX]
- GR Longhurst, SL Harms, ES Marwil, and BG Miller.
Verification and Validation of TMAP4.
Technical Report EGG-FSP-10347, Idaho National Engineering Laboratory, Idaho Falls, ID (United States), 1992.[BibTeX]
- Pierre-Clément A. Simon, Casey T. Icenhour, Gyanender Singh, Alexander D Lindsay, Chaitanya Vivek Bhave, Lin Yang, Adriaan Anthony Riet, Yifeng Che, Paul Humrickhouse, Masashi Shimada, and Pattrick Calderoni.
MOOSE-based tritium migration analysis program, version 8 (TMAP8) for advanced open-source tritium transport and fuel cycle modeling.
Fusion Engineering and Design, 214:114874, May 2025.
doi:10.1016/j.fusengdes.2025.114874.[BibTeX]