Griffin-BISON Multiphysics 30 Ȼ Reactivity Insertion Test
This document outlines the efforts on modeling the 30 Ȼ reactivity insertion tests conducted in the KRUSTY warm critical experiments. This model is developed based on the 15 Ȼ Reactivity Insertion Test model.
Overview
Similar to the 15 Ȼ reactivity insertion transient, KRUSTY was operated at a zero-power critical state (fission power negligible) at room temperatures prior to the transient. The 30 Ȼ test started by repeating the 15 Ȼ test with roughly 15 Ȼ reactivity inserted in a single step to initiate the transient (Poston et al., 2020). Fission heat generated in the UMo fuel region increased as the radial reflector of KRUSTY was lifted upwards, covering more portion of the fuel disk. The fuel region heated up and thermally expanded, creating negative reactivity feedback to reduce the power. The power peaked at 3.65 kW and was brought down due to increased neutron leakages. An additional 15 Ȼ reactivity was added to the core incrementally when the reactor power dropped at about 3 kW. With small reactivity inserted to the core, the reactor power was maintained around 3 kW for about 150 s. During this period, the fuel temperature increased continuously which led to more negative reactivity feedback. With no additional reactivity added to the core, the reactor power dropped again due to the increased negative reactivity feedback. The total excess reactivity inserted to the core was estimated to be about 29.9 Ȼ. The β_eff was assumed to be 650 pm (Poston et al., 2020).
Griffin-BISON Multiphysics Model
The Multiphysics model to simulate the 30 Ȼ run are very similar to the model developed for the 15 Ȼ test (Poston et al., 2020). Specifically, a two-level MOOSE MultiApp hierarchy with Griffin for neutronics and BISON for thermo-mechanics was used to couple the two codes. Fission power was calculated using the DFEM-SN(2,3) solver accelerated with the CMFD technique. Anisotropic scattering of neutrons in the reflectors were modeled by setting NA=3 and adopting a hybrid cross section set. BISON read the fission power from Griffin to solve for core temperatures and displacement fields. Griffin neutronic calculations were then repeated with the updated temperature fields and displacement fields and provided updated fission power to BISON.
The approach to model the first 15 Ȼ reactivity insertion for starting up the 30 Ȼ transient is the same as those in the 15 Ȼ model (Poston et al., 2020), except that the radial reflector displacement was slightly reduced (1.447 mm instead of the 1.48 mm) considering the measured peak power was 3.65 kW instead of 3.75 kW. To model the control mechanism used in KRUSTY for maintaining a constant power, an automatic reactivity insertion mechanism was implemented. The radial reflector was raised by about 0.126 mm whenever the quarter-core power passed below 750 W. With this mechanism, the reactor power was successfully maintained between 750 ∼760 W window for approximately 150 seconds in the simulation. The total displacement of the radial reflector during the second stage is 1.638 mm, resulting in a total of 3.085 mm reflector insertion throughout the simulation of the 30 Ȼ test. The total reactivity added in the numerical model was estimated to be about 29.7 Ȼ, which is close to the 29.9 Ȼ from experiments. The displacements were created by applying a Dirichlet boundary condition to the bottom surface of the solid assembly in BISON. Figure 1 presents the calculated displacement fields before the transient, after the startup and after all 29.7 Ȼ inserted to the core.
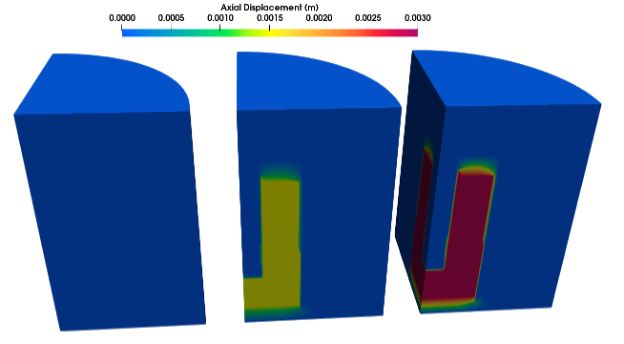
Figure 1: Displacement field prior the 30 Ȼ transient (left), at the beginning of the transient (middle) and after the transient (right).
The steps of modeling the 30 Ȼ transient are like the steps for 15 Ȼ test. Griffin was the main application which calculates the fission power, controls the time steps, and calls the BISON sub-application to calculate the temperature distributions as well as the displacement fields. Listing 1-6 include the key blocks that were unique for modeling the 30 Ȼ tests, in particular for modeling the second step of the transient.
Listing 1: Input block in Griffin main application to control the time step based on the number of iterations and power evolution.
[Executioner]
[TimeStepper]
type = IterationAdaptiveDT
dt = 1e-2
timestep_limiting_postprocessor = power_driven_dt
[]
[]The upper limit for the current time step length between 755 seconds and 900 s is determined by the Postprocessor “power_driven_dt” which is defined in Listing 2.
Listing 2: Input block which defines the postprocessor power_driven_dt, which is utilized to control the time step size.
[Postprocessors]
[power_driven_dt]
type = ParsedPostprocessor
pp_names = 'integrated_power power_limited_dt'
constant_names = 'low_pw hi_pw ldt hdt'
constant_expressions = '754 760 1 1'
function = 'pddt:=if(integrated_power<low_pw,ldt,if(integrated_power>hi_pw,hdt,ldt+(hdt-ldt)*(integrated_power-low_pw)/(hi_pw-low_pw)));
min(power_limited_dt,pddt)'
[]
[]These Postprocessors help make it possible to control the time step size during the insertion of the second 15 Ȼ.
Listing 3: Input blocks to transfer the displacement positions between BISON and Griffin for modeling the second step of the experiment.
[Transfers]
[from_bison_disp]
type = MultiAppPostprocessorTransfer
from_multi_app = bison
from_postprocessor = disp_old_origin
to_postprocessor = disp_old_medium
reduction_type = average
[]
[to_bison_disp]
type = MultiAppPostprocessorTransfer
to_multi_app = bison
from_postprocessor = disp_old_medium
to_postprocessor = disp_old_target
[]
[]As an essential part of the control approach used for the second stage of reactivity insertion, the shift value of the radial reflector at the last time step must be accessible by the control algorithm. To simplify the setup which already includes fixed point iterations between multiple solves, this value is transferred to the main application and transferred back into another Postprocessor. The input blocks for the three postprocessor, in which the disp_old_medium is defined in the Griffin input and the other two defined in BISON input are included in the Listing 4.
Listing 4: Input blocks for defining the Postprocessors in transferring the displacements.
[Postprocessors]
[disp_old_origin]
type = FunctionValuePostprocessor
function = ref_mov
execute_on = 'initial timestep_end'
[]
[disp_old_target]
type = Receiver
default = '${fparse reflector_disp_init+reflector_disp_increment_1}'
[]
[]Listing 5: Input blocks that define the function “ref_mov” in Listing 4.
[Functions]
[ref_mov]
type = ParsedFunction
symbol_names = 'reflector_disp_0 reflector_disp_increment_1 reflector_disp_increment_2 rdi2_scale_factor t_first_15c_insertion t_start_power_monitoring existing_reflector_disp unit_increment_fraction pw pw_ref'
symbol_values = '${reflector_disp_init} ${reflector_disp_increment_1} ${reflector_disp_increment_2} 1.1 0.5 697 disp_old_target 0.09 total_power 750'
expression = 'reflector_disp_15c:=reflector_disp_0+reflector_disp_increment_1;
if(t<0,reflector_disp_0,
if(t<t_first_15c_insertion,reflector_disp_0+reflector_disp_increment_1/t_first_15c_insertion*t,
if(t<t_start_power_monitoring,reflector_disp_15c,
if(pw<pw_ref&existing_reflector_disp<reflector_disp_15c+reflector_disp_increment_2*rdi2_scale_factor,existing_reflector_disp+reflector_disp_increment_2*unit_increment_fraction,
existing_reflector_disp))))'
[]
[]The definitions for each of the variables and symbols were listed in Table 1 below:
Table 1: Definition of the constant values in the ref_mov function that used to describe the radial reflector movement in the second step of the 30 Ȼ test.
| Constant Name | Description |
|---|---|
reflector_disp_init | initial reflector displacement at the start of the test |
reflector_disp_increment_1 | increment of the reflector displacement at the first 15 Ȼ insertion |
reflector_disp_increment_2 | nominal total increment of the reflector displacement at the second 15 Ȼ insertion |
rdi2_scale_factor | scale factor for the second 15 Ȼ insertion that is tuned to achieve ~150 second power maintenance |
t_first_15c_insertion | time at which the first 15 Ȼ insertion is completed (starting from t = 0) |
t_start_power_monitoring | time at which the power starts to be monitored for power maintenance during the second 15 Ȼ insertion |
existing_reflector_disp | existing reflector displacement recorded by a post-processor |
unit_increment_fraction | fraction of the nominal total increment of the reflector displacement at the second 15 Ȼ insertion that is applied during each insertion step; the value is obtained by tuning to limit the power jump during each step of the insertion |
pw | total current power of the microreactor |
pw_ref | reference power for power maintenance during the second 15 Ȼ insertion |
The Function “Ref_mov” has also been used to prescribe the boundary condition for generating the displacement mesh as its input block is included in Listing 6.
Listing 6: Input block for defining the BISON boundary condition at the bottom surface the comet
[BCs]
[BottomSSFixZ]
type = FunctionDirichletBC
variable = disp_z
boundary = 'ss_bot'
function = ref_mov
[]
[]Simulation Results
Figure 2 compares the total power calculated by Griffin with the measured total power from neutron detectors. Overall, the calculated power history matches experimental history well. The multiphysics model predicted the power peaking accurately. In experiment, the experiment achieved a peak power of 3.65 kW, or a quarter-core power of 913 W, and the numerical model calculated a peak quarter-core power of 913.5 W. After the peaking, when the quarter-core power drops to 750 W, the automatic reactivity insertion mechanism was proved to be able to maintain the quarter-core power within the 750~760 W window for approximately 150 seconds, which agrees also well with the experimental data. Finally, in the absence of additional reactivity insertion, reactor power started to decrease continuously. Figure 2 also shows that the multiphysics model predicts the power decreasing rate correctly.
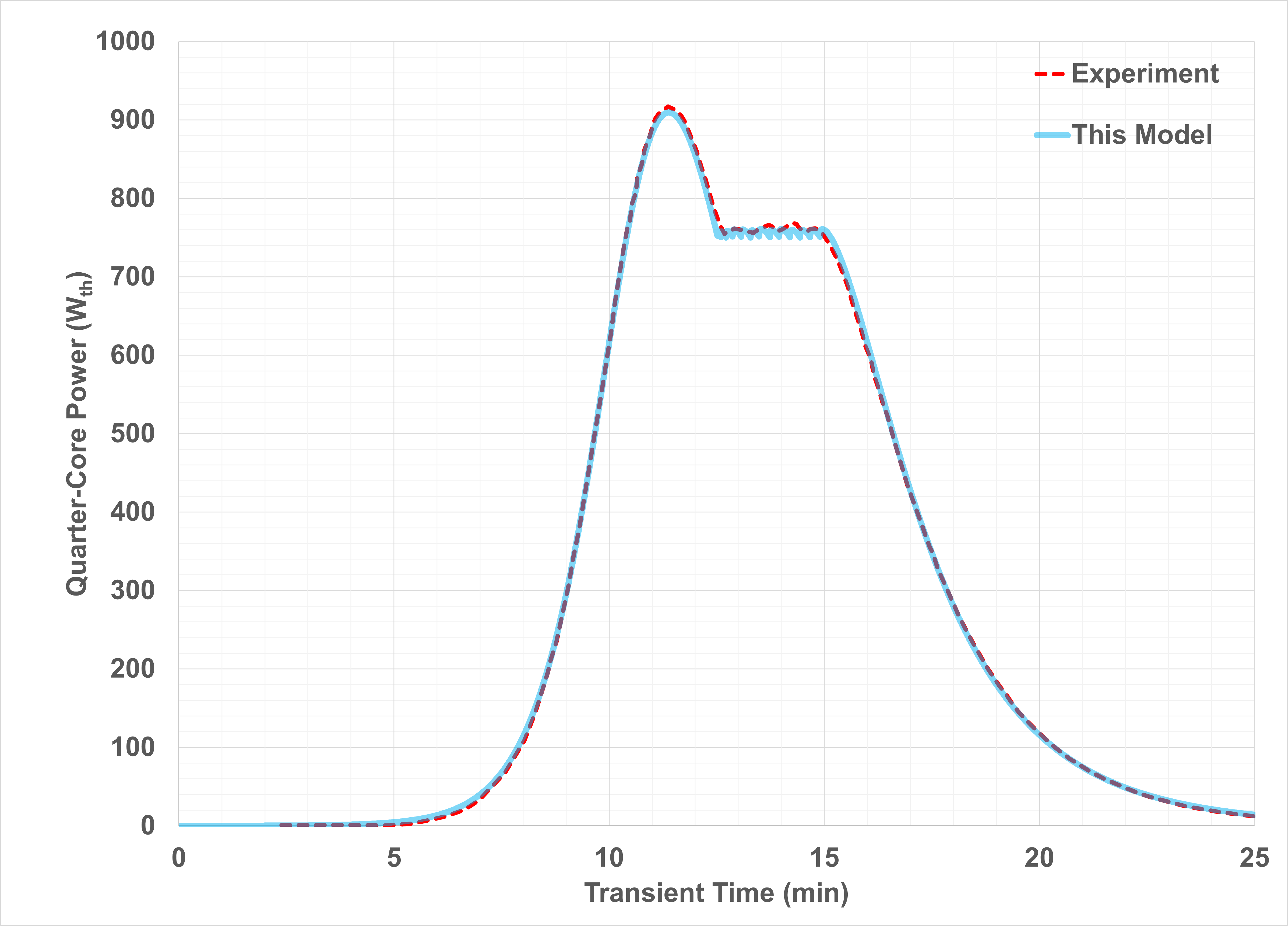
Figure 2: Predicted power evolution vs measurement (30 ₵ test)
References
- David I Poston, Marc A Gibson, Patrick R McClure, and Rene G Sanchez.
Results of the krusty warm critical experiments.
Nuclear Technology, 206(sup1):S78–S88, 2020.[BibTeX]
@article{Poston2020_1, author = "Poston, David I and Gibson, Marc A and McClure, Patrick R and Sanchez, Rene G", title = "Results of the KRUSTY warm critical experiments", journal = "Nuclear Technology", volume = "206", number = "sup1", pages = "S78--S88", year = "2020", publisher = "Taylor \\& Francis" }
(microreactors/KRUSTY/Multiphysics_30C_RIT/KRUSTY_Griffin_SN23_NA23_CMFD_TR.i)
################################################################################
## NEAMS Micro-Reactor Application Driver ##
## KRUSTY Multiphysics 30-Cent Reactivity Insertion ##
## Griffin neutronics input file (Main App) ##
## DFEM-SN (2, 3) NA = 3 with CMFD acceleration ##
################################################################################
max_power_increment = 10
min_dt = 0.01
mesh_file = '../gold/MESH/Griffin_mesh.e'
[Mesh]
[fmg]
# This simulation relies on the steady state KRUSTY simulation
# with zero reflector insertion as the initial condition
# Refer to the mesh setup in the steady state simulation
type = FileMeshGenerator
file = ${mesh_file}
# file = 'griffin_mesh.cpr'
[]
[rot]
type = TransformGenerator
input = fmg
transform = ROTATE
vector_value = '-90 0 0'
[]
[id]
type=SubdomainExtraElementIDGenerator
input = rot
subdomains = '1 2 3 4 5 6
64 71 72 73
8 9 10 11
12 1212
13 14 15 16 17 18 19
20 21 22 23 24
2081 2091 2101 2111 2121 2131 2141
2082 2092 2102 2112 2122 2132 2142
3081 3091 3101 3111 3121 3131 3141
3082 3092 3102 3112 3122 3132 3142
4081 4091 4101 4111 4121 4131 4141
4082 4092 4102 4112 4122 4132 4142'
extra_element_id_names = 'material_id'
extra_element_ids ='99 17 11 15 70 18
99 6 6 60
8 5 10 40
51 52
4 20 18 40 50 14 13
6 7 12 11 9
300 310 320 330 340 350 360
301 311 321 331 341 351 361
202 212 222 232 242 252 262
203 213 223 233 243 253 263
104 114 124 134 144 154 164
105 115 125 135 145 155 165'
[]
[coarse_mesh]
type = GeneratedMeshGenerator
dim= 3
nx = 20 # about 2 cm may need to adjust
ny = 20 # about 2 cm may need to adjust
nz = 40 # about 5 cm may need to adjust to test convergence or performance
xmin = -2
xmax = 52
ymin = -2
ymax = 52
zmin = -1
zmax = 135
[]
[assign_coarse_id]
type = CoarseMeshExtraElementIDGenerator
input = id
coarse_mesh = coarse_mesh
extra_element_id_name = coarse_element_id
[]
parallel_type = distributed
displacements = 'disp_x disp_y disp_z'
[]
# No initial value needed as this is restarting
[AuxVariables]
[Tf]
order = CONSTANT
family = MONOMIAL
[]
[Ts]
order = CONSTANT
family = MONOMIAL
[]
[disp_x]
[]
[disp_y]
[]
[disp_z]
[]
[]
[TransportSystems]
particle = neutron
equation_type = transient
G = 22
VacuumBoundary = '9527 9528 9529'
ReflectingBoundary = '1982 1983'
[sn]
scheme = DFEM-SN
family = MONOMIAL
order = FIRST
AQtype = Gauss-Chebyshev
NPolar = 2
NAzmthl = 3
NA = 3
sweep_type = asynchronous_parallel_sweeper
using_array_variable = true
collapse_scattering = true
n_delay_groups = 6
use_displaced_mesh = true
[]
[]
[PowerDensity]
power = 0.01
power_density_variable = power_density
integrated_power_postprocessor = integrated_power
[]
[Postprocessors]
[_dt]
type = TimestepSize
execute_on = 'initial timestep_end'
[]
[power_increment]
type = ChangeOverTimePostprocessor
postprocessor = integrated_power
change_with_respect_to_initial = false
execute_on = 'initial timestep_end'
take_absolute_value = true
[]
# A postprocessor to limit the timestep based on the absolute power increment
[power_limited_dt]
type = ParsedPostprocessor
pp_names = 'power_increment _dt'
constant_names = 'max_increment min_dt'
constant_expressions = '${max_power_increment} ${min_dt}'
function = 't_lim:=_dt*max_increment/power_increment;
max(min_dt,t_lim)'
[]
[power_driven_dt]
type = ParsedPostprocessor
pp_names = 'integrated_power power_limited_dt'
constant_names = 'low_pw hi_pw ldt hdt'
constant_expressions = '754 760 1 1'
function = 'pddt:=if(integrated_power<low_pw,ldt,if(integrated_power>hi_pw,hdt,ldt+(hdt-ldt)*(integrated_power-low_pw)/(hi_pw-low_pw)));
min(power_limited_dt,pddt)'
[]
[disp_old_medium]
type = Receiver
default = 0.0 # should be the same as `reflector_disp_init` in subapp
[]
[]
[Executioner]
type = TransientSweepUpdate
verbose = true
richardson_abs_tol = 1e-6
richardson_rel_tol = 1e-15
richardson_max_its = 30
inner_solve_type = GMRes
max_inner_its = 100
cmfd_acceleration = true
coarse_element_id = coarse_element_id
max_diffusion_coefficient = 10.0
diffusion_prec_type = lu
prolongation_type = multiplicative
end_time = 7200
dtmin = ${min_dt}
dtmax = 10
[TimeStepper]
type = IterationAdaptiveDT
dt = 1e-2
timestep_limiting_postprocessor = power_driven_dt
[]
[]
[Materials]
[all]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = '1 2 3 4 5 6
64 71 72 73
8 9 10 11
12 1212
13 14 15 16 17 18 19
20 21 22 23 24
2081 2091 2101 2111 2121 2131 2141
2082 2092 2102 2112 2122 2132 2142
3081 3091 3101 3111 3121 3131 3141
3082 3092 3102 3112 3122 3132 3142
4081 4091 4101 4111 4121 4131 4141
4082 4092 4102 4112 4122 4132 4142'
library_file ='../Neutronics/Serp_hbrid_reflector_updated.xml'
library_name ='krusty_serpent_ANL_endf70_g22'
isotopes = 'pseudo'
densities = '1.0'
grid_names = 'Tfuel Tsteel'
grid_variables = 'Tf Ts'
plus = 1
is_meter = true
dbgmat = false
displacements = 'disp_x disp_y disp_z'
[]
[]
[Outputs]
csv = true
exodus = true
[pgraph]
type = PerfGraphOutput
level = 2
[]
[cp]
type = Checkpoint
num_files = 2
[]
[]
[MultiApps]
[bison]
type = TransientMultiApp
input_files = KRUSTY_BISON_THERMOMECHANICS_TR.i
execute_on = 'initial timestep_end'
[]
[]
[Transfers]
[to_sub_power_density]
type = MultiAppGeneralFieldShapeEvaluationTransfer
to_multi_app = bison
source_variable = power_density
variable = power_density
from_postprocessors_to_be_preserved = integrated_power
to_postprocessors_to_be_preserved = total_power
execute_on = 'timestep_end'
[]
[from_sub_tempf]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = Tf
source_variable = Tfuel
[]
[from_sub_tempm]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = Ts
source_variable = Tsteel
[]
[from_sub_disp_x]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = disp_x
source_variable = disp_x
[]
[from_sub_disp_y]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = disp_y
source_variable = disp_y
[]
[from_sub_disp_z]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = disp_z
source_variable = disp_z
[]
## transfer and store the reflector displacement at the main app to facilitate the control mechanism
[from_bison_disp]
type = MultiAppPostprocessorTransfer
from_multi_app = bison
from_postprocessor = disp_old_origin
to_postprocessor = disp_old_medium
reduction_type = average
[]
[to_bison_disp]
type = MultiAppPostprocessorTransfer
to_multi_app = bison
from_postprocessor = disp_old_medium
to_postprocessor = disp_old_target
[]
[]
[UserObjects]
[ss]
type = TransportSolutionVectorFile
transport_system = sn
writing = false
execute_on = initial
[]
[]
(microreactors/KRUSTY/Multiphysics_30C_RIT/KRUSTY_Griffin_SN23_NA23_CMFD_TR.i)
################################################################################
## NEAMS Micro-Reactor Application Driver ##
## KRUSTY Multiphysics 30-Cent Reactivity Insertion ##
## Griffin neutronics input file (Main App) ##
## DFEM-SN (2, 3) NA = 3 with CMFD acceleration ##
################################################################################
max_power_increment = 10
min_dt = 0.01
mesh_file = '../gold/MESH/Griffin_mesh.e'
[Mesh]
[fmg]
# This simulation relies on the steady state KRUSTY simulation
# with zero reflector insertion as the initial condition
# Refer to the mesh setup in the steady state simulation
type = FileMeshGenerator
file = ${mesh_file}
# file = 'griffin_mesh.cpr'
[]
[rot]
type = TransformGenerator
input = fmg
transform = ROTATE
vector_value = '-90 0 0'
[]
[id]
type=SubdomainExtraElementIDGenerator
input = rot
subdomains = '1 2 3 4 5 6
64 71 72 73
8 9 10 11
12 1212
13 14 15 16 17 18 19
20 21 22 23 24
2081 2091 2101 2111 2121 2131 2141
2082 2092 2102 2112 2122 2132 2142
3081 3091 3101 3111 3121 3131 3141
3082 3092 3102 3112 3122 3132 3142
4081 4091 4101 4111 4121 4131 4141
4082 4092 4102 4112 4122 4132 4142'
extra_element_id_names = 'material_id'
extra_element_ids ='99 17 11 15 70 18
99 6 6 60
8 5 10 40
51 52
4 20 18 40 50 14 13
6 7 12 11 9
300 310 320 330 340 350 360
301 311 321 331 341 351 361
202 212 222 232 242 252 262
203 213 223 233 243 253 263
104 114 124 134 144 154 164
105 115 125 135 145 155 165'
[]
[coarse_mesh]
type = GeneratedMeshGenerator
dim= 3
nx = 20 # about 2 cm may need to adjust
ny = 20 # about 2 cm may need to adjust
nz = 40 # about 5 cm may need to adjust to test convergence or performance
xmin = -2
xmax = 52
ymin = -2
ymax = 52
zmin = -1
zmax = 135
[]
[assign_coarse_id]
type = CoarseMeshExtraElementIDGenerator
input = id
coarse_mesh = coarse_mesh
extra_element_id_name = coarse_element_id
[]
parallel_type = distributed
displacements = 'disp_x disp_y disp_z'
[]
# No initial value needed as this is restarting
[AuxVariables]
[Tf]
order = CONSTANT
family = MONOMIAL
[]
[Ts]
order = CONSTANT
family = MONOMIAL
[]
[disp_x]
[]
[disp_y]
[]
[disp_z]
[]
[]
[TransportSystems]
particle = neutron
equation_type = transient
G = 22
VacuumBoundary = '9527 9528 9529'
ReflectingBoundary = '1982 1983'
[sn]
scheme = DFEM-SN
family = MONOMIAL
order = FIRST
AQtype = Gauss-Chebyshev
NPolar = 2
NAzmthl = 3
NA = 3
sweep_type = asynchronous_parallel_sweeper
using_array_variable = true
collapse_scattering = true
n_delay_groups = 6
use_displaced_mesh = true
[]
[]
[PowerDensity]
power = 0.01
power_density_variable = power_density
integrated_power_postprocessor = integrated_power
[]
[Postprocessors]
[_dt]
type = TimestepSize
execute_on = 'initial timestep_end'
[]
[power_increment]
type = ChangeOverTimePostprocessor
postprocessor = integrated_power
change_with_respect_to_initial = false
execute_on = 'initial timestep_end'
take_absolute_value = true
[]
# A postprocessor to limit the timestep based on the absolute power increment
[power_limited_dt]
type = ParsedPostprocessor
pp_names = 'power_increment _dt'
constant_names = 'max_increment min_dt'
constant_expressions = '${max_power_increment} ${min_dt}'
function = 't_lim:=_dt*max_increment/power_increment;
max(min_dt,t_lim)'
[]
[power_driven_dt]
type = ParsedPostprocessor
pp_names = 'integrated_power power_limited_dt'
constant_names = 'low_pw hi_pw ldt hdt'
constant_expressions = '754 760 1 1'
function = 'pddt:=if(integrated_power<low_pw,ldt,if(integrated_power>hi_pw,hdt,ldt+(hdt-ldt)*(integrated_power-low_pw)/(hi_pw-low_pw)));
min(power_limited_dt,pddt)'
[]
[disp_old_medium]
type = Receiver
default = 0.0 # should be the same as `reflector_disp_init` in subapp
[]
[]
[Executioner]
type = TransientSweepUpdate
verbose = true
richardson_abs_tol = 1e-6
richardson_rel_tol = 1e-15
richardson_max_its = 30
inner_solve_type = GMRes
max_inner_its = 100
cmfd_acceleration = true
coarse_element_id = coarse_element_id
max_diffusion_coefficient = 10.0
diffusion_prec_type = lu
prolongation_type = multiplicative
end_time = 7200
dtmin = ${min_dt}
dtmax = 10
[TimeStepper]
type = IterationAdaptiveDT
dt = 1e-2
timestep_limiting_postprocessor = power_driven_dt
[]
[]
[Materials]
[all]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = '1 2 3 4 5 6
64 71 72 73
8 9 10 11
12 1212
13 14 15 16 17 18 19
20 21 22 23 24
2081 2091 2101 2111 2121 2131 2141
2082 2092 2102 2112 2122 2132 2142
3081 3091 3101 3111 3121 3131 3141
3082 3092 3102 3112 3122 3132 3142
4081 4091 4101 4111 4121 4131 4141
4082 4092 4102 4112 4122 4132 4142'
library_file ='../Neutronics/Serp_hbrid_reflector_updated.xml'
library_name ='krusty_serpent_ANL_endf70_g22'
isotopes = 'pseudo'
densities = '1.0'
grid_names = 'Tfuel Tsteel'
grid_variables = 'Tf Ts'
plus = 1
is_meter = true
dbgmat = false
displacements = 'disp_x disp_y disp_z'
[]
[]
[Outputs]
csv = true
exodus = true
[pgraph]
type = PerfGraphOutput
level = 2
[]
[cp]
type = Checkpoint
num_files = 2
[]
[]
[MultiApps]
[bison]
type = TransientMultiApp
input_files = KRUSTY_BISON_THERMOMECHANICS_TR.i
execute_on = 'initial timestep_end'
[]
[]
[Transfers]
[to_sub_power_density]
type = MultiAppGeneralFieldShapeEvaluationTransfer
to_multi_app = bison
source_variable = power_density
variable = power_density
from_postprocessors_to_be_preserved = integrated_power
to_postprocessors_to_be_preserved = total_power
execute_on = 'timestep_end'
[]
[from_sub_tempf]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = Tf
source_variable = Tfuel
[]
[from_sub_tempm]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = Ts
source_variable = Tsteel
[]
[from_sub_disp_x]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = disp_x
source_variable = disp_x
[]
[from_sub_disp_y]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = disp_y
source_variable = disp_y
[]
[from_sub_disp_z]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = disp_z
source_variable = disp_z
[]
## transfer and store the reflector displacement at the main app to facilitate the control mechanism
[from_bison_disp]
type = MultiAppPostprocessorTransfer
from_multi_app = bison
from_postprocessor = disp_old_origin
to_postprocessor = disp_old_medium
reduction_type = average
[]
[to_bison_disp]
type = MultiAppPostprocessorTransfer
to_multi_app = bison
from_postprocessor = disp_old_medium
to_postprocessor = disp_old_target
[]
[]
[UserObjects]
[ss]
type = TransportSolutionVectorFile
transport_system = sn
writing = false
execute_on = initial
[]
[]
(microreactors/KRUSTY/Multiphysics_30C_RIT/KRUSTY_Griffin_SN23_NA23_CMFD_TR.i)
################################################################################
## NEAMS Micro-Reactor Application Driver ##
## KRUSTY Multiphysics 30-Cent Reactivity Insertion ##
## Griffin neutronics input file (Main App) ##
## DFEM-SN (2, 3) NA = 3 with CMFD acceleration ##
################################################################################
max_power_increment = 10
min_dt = 0.01
mesh_file = '../gold/MESH/Griffin_mesh.e'
[Mesh]
[fmg]
# This simulation relies on the steady state KRUSTY simulation
# with zero reflector insertion as the initial condition
# Refer to the mesh setup in the steady state simulation
type = FileMeshGenerator
file = ${mesh_file}
# file = 'griffin_mesh.cpr'
[]
[rot]
type = TransformGenerator
input = fmg
transform = ROTATE
vector_value = '-90 0 0'
[]
[id]
type=SubdomainExtraElementIDGenerator
input = rot
subdomains = '1 2 3 4 5 6
64 71 72 73
8 9 10 11
12 1212
13 14 15 16 17 18 19
20 21 22 23 24
2081 2091 2101 2111 2121 2131 2141
2082 2092 2102 2112 2122 2132 2142
3081 3091 3101 3111 3121 3131 3141
3082 3092 3102 3112 3122 3132 3142
4081 4091 4101 4111 4121 4131 4141
4082 4092 4102 4112 4122 4132 4142'
extra_element_id_names = 'material_id'
extra_element_ids ='99 17 11 15 70 18
99 6 6 60
8 5 10 40
51 52
4 20 18 40 50 14 13
6 7 12 11 9
300 310 320 330 340 350 360
301 311 321 331 341 351 361
202 212 222 232 242 252 262
203 213 223 233 243 253 263
104 114 124 134 144 154 164
105 115 125 135 145 155 165'
[]
[coarse_mesh]
type = GeneratedMeshGenerator
dim= 3
nx = 20 # about 2 cm may need to adjust
ny = 20 # about 2 cm may need to adjust
nz = 40 # about 5 cm may need to adjust to test convergence or performance
xmin = -2
xmax = 52
ymin = -2
ymax = 52
zmin = -1
zmax = 135
[]
[assign_coarse_id]
type = CoarseMeshExtraElementIDGenerator
input = id
coarse_mesh = coarse_mesh
extra_element_id_name = coarse_element_id
[]
parallel_type = distributed
displacements = 'disp_x disp_y disp_z'
[]
# No initial value needed as this is restarting
[AuxVariables]
[Tf]
order = CONSTANT
family = MONOMIAL
[]
[Ts]
order = CONSTANT
family = MONOMIAL
[]
[disp_x]
[]
[disp_y]
[]
[disp_z]
[]
[]
[TransportSystems]
particle = neutron
equation_type = transient
G = 22
VacuumBoundary = '9527 9528 9529'
ReflectingBoundary = '1982 1983'
[sn]
scheme = DFEM-SN
family = MONOMIAL
order = FIRST
AQtype = Gauss-Chebyshev
NPolar = 2
NAzmthl = 3
NA = 3
sweep_type = asynchronous_parallel_sweeper
using_array_variable = true
collapse_scattering = true
n_delay_groups = 6
use_displaced_mesh = true
[]
[]
[PowerDensity]
power = 0.01
power_density_variable = power_density
integrated_power_postprocessor = integrated_power
[]
[Postprocessors]
[_dt]
type = TimestepSize
execute_on = 'initial timestep_end'
[]
[power_increment]
type = ChangeOverTimePostprocessor
postprocessor = integrated_power
change_with_respect_to_initial = false
execute_on = 'initial timestep_end'
take_absolute_value = true
[]
# A postprocessor to limit the timestep based on the absolute power increment
[power_limited_dt]
type = ParsedPostprocessor
pp_names = 'power_increment _dt'
constant_names = 'max_increment min_dt'
constant_expressions = '${max_power_increment} ${min_dt}'
function = 't_lim:=_dt*max_increment/power_increment;
max(min_dt,t_lim)'
[]
[power_driven_dt]
type = ParsedPostprocessor
pp_names = 'integrated_power power_limited_dt'
constant_names = 'low_pw hi_pw ldt hdt'
constant_expressions = '754 760 1 1'
function = 'pddt:=if(integrated_power<low_pw,ldt,if(integrated_power>hi_pw,hdt,ldt+(hdt-ldt)*(integrated_power-low_pw)/(hi_pw-low_pw)));
min(power_limited_dt,pddt)'
[]
[disp_old_medium]
type = Receiver
default = 0.0 # should be the same as `reflector_disp_init` in subapp
[]
[]
[Executioner]
type = TransientSweepUpdate
verbose = true
richardson_abs_tol = 1e-6
richardson_rel_tol = 1e-15
richardson_max_its = 30
inner_solve_type = GMRes
max_inner_its = 100
cmfd_acceleration = true
coarse_element_id = coarse_element_id
max_diffusion_coefficient = 10.0
diffusion_prec_type = lu
prolongation_type = multiplicative
end_time = 7200
dtmin = ${min_dt}
dtmax = 10
[TimeStepper]
type = IterationAdaptiveDT
dt = 1e-2
timestep_limiting_postprocessor = power_driven_dt
[]
[]
[Materials]
[all]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = '1 2 3 4 5 6
64 71 72 73
8 9 10 11
12 1212
13 14 15 16 17 18 19
20 21 22 23 24
2081 2091 2101 2111 2121 2131 2141
2082 2092 2102 2112 2122 2132 2142
3081 3091 3101 3111 3121 3131 3141
3082 3092 3102 3112 3122 3132 3142
4081 4091 4101 4111 4121 4131 4141
4082 4092 4102 4112 4122 4132 4142'
library_file ='../Neutronics/Serp_hbrid_reflector_updated.xml'
library_name ='krusty_serpent_ANL_endf70_g22'
isotopes = 'pseudo'
densities = '1.0'
grid_names = 'Tfuel Tsteel'
grid_variables = 'Tf Ts'
plus = 1
is_meter = true
dbgmat = false
displacements = 'disp_x disp_y disp_z'
[]
[]
[Outputs]
csv = true
exodus = true
[pgraph]
type = PerfGraphOutput
level = 2
[]
[cp]
type = Checkpoint
num_files = 2
[]
[]
[MultiApps]
[bison]
type = TransientMultiApp
input_files = KRUSTY_BISON_THERMOMECHANICS_TR.i
execute_on = 'initial timestep_end'
[]
[]
[Transfers]
[to_sub_power_density]
type = MultiAppGeneralFieldShapeEvaluationTransfer
to_multi_app = bison
source_variable = power_density
variable = power_density
from_postprocessors_to_be_preserved = integrated_power
to_postprocessors_to_be_preserved = total_power
execute_on = 'timestep_end'
[]
[from_sub_tempf]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = Tf
source_variable = Tfuel
[]
[from_sub_tempm]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = Ts
source_variable = Tsteel
[]
[from_sub_disp_x]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = disp_x
source_variable = disp_x
[]
[from_sub_disp_y]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = disp_y
source_variable = disp_y
[]
[from_sub_disp_z]
type = MultiAppGeneralFieldShapeEvaluationTransfer
from_multi_app = bison
variable = disp_z
source_variable = disp_z
[]
## transfer and store the reflector displacement at the main app to facilitate the control mechanism
[from_bison_disp]
type = MultiAppPostprocessorTransfer
from_multi_app = bison
from_postprocessor = disp_old_origin
to_postprocessor = disp_old_medium
reduction_type = average
[]
[to_bison_disp]
type = MultiAppPostprocessorTransfer
to_multi_app = bison
from_postprocessor = disp_old_medium
to_postprocessor = disp_old_target
[]
[]
[UserObjects]
[ss]
type = TransportSolutionVectorFile
transport_system = sn
writing = false
execute_on = initial
[]
[]
(microreactors/KRUSTY/Multiphysics_30C_RIT/KRUSTY_BISON_THERMOMECHANICS_TR.i)
################################################################################
## NEAMS Micro-Reactor Application Driver ##
## KRUSTY Multiphysics 30-Cent Reactivity Insertion ##
## BISON thermomechanics main input file (Child App) ##
## Heat Conduction, Thermal Expansion, Thermal Stress ##
################################################################################
!include ../Multiphysics_SS/KRUSTY_BISON_PARAMS.i
restart_cp_file = '../Multiphysics_SS/KRUSTY_Griffin_SN23_NA23_CMFD_out_bison0_checkpoint_cp/LATEST'
reflector_disp_init = 0
reflector_disp_increment_1 = 1.447e-3 # Corresponding to the first 15 cents reactivity insertion
reflector_disp_increment_2 = 1.400e-3 # Corresponding to the nominal second 15 cents reactivity insertion
[GlobalParams]
temperature = temp
displacements = 'disp_x disp_y disp_z'
stress_free_temperature = 298
[]
[Problem]
type = ReferenceResidualProblem
reference_vector = 'ref'
extra_tag_vectors = 'ref'
group_variables = 'disp_x disp_y disp_z'
restart_file_base = ${restart_cp_file}
[]
[Mesh]
file = ${restart_cp_file}
parallel_type = distributed
[]
# No initial value needed as this is restarting
# For both Variables and AuxVariables
[Variables]
# We have two temperature variables, one for the fuel and one for the non-fuel
# This is to allow discontinuity on the fuel surface so that the insulation
# can be better simulated using `InterfaceKernels`
[temp]
block = ${nonfuel_all}
[]
[temp_f]
block = ${fuel_all}
[]
[]
[AuxVariables]
[power_density]
block = ${fuel_all}
family = L2_LAGRANGE
order = FIRST
[]
[Tfuel]
order = CONSTANT
family = MONOMIAL
[]
[Tsteel]
order = CONSTANT
family = MONOMIAL
[]
[external_power]
[]
[hp_temp_aux]
[]
[]
[UserObjects]
[temp_f_avg]
type = LayeredAverage
variable = temp_f
direction = z
num_layers = 100
block = ${fuel_all}
[]
[temp_s_avg]
type = LayeredAverage
variable = temp
direction = z
num_layers = 100
block = '${ss_all} 998'
[]
[]
[AuxKernels]
[assign_tfuel_f]
type = NormalizationAux
variable = Tfuel
source_variable = temp_f
execute_on = 'timestep_end'
block = ${fuel_all}
[]
[assign_tfuel_nf]
type = SpatialUserObjectAux
variable = Tfuel
user_object = temp_f_avg
execute_on = 'timestep_end'
block = ${nonfuel_all}
[]
[assign_tsteel_s]
type = NormalizationAux
variable = Tsteel
source_variable = temp
execute_on = 'timestep_end'
block = '${ss_all} 998'
[]
[assign_tsteel_ns]
type = SpatialUserObjectAux
variable = Tsteel
user_object = temp_s_avg
execute_on = 'timestep_end'
block = ${non_ss_998_all}
[]
[]
# A small materials block for thin layers
[Materials]
[thermal_cond_mli]
type = GenericConstantMaterial
prop_names = 'thermal_conductivity_mli'
prop_values = '${hp_mli_cond}'
boundary = 'fuel_top fuel_bottom fuel_side_1'
[]
[thermal_cond_center]
type = GenericConstantMaterial
prop_names = 'thermal_conductivity_center'
prop_values = '0.20'
boundary = 'fuel_inside'
[]
[thermal_cond_other]
type = GenericConstantMaterial
prop_names = 'thermal_conductivity_other'
prop_values = '15.0'
boundary = 'fuel_side_2'
[]
[]
[InterfaceKernels]
[fuel_ref]
type = ThinLayerHeatTransfer
thermal_conductivity = thermal_conductivity_mli
thickness = 0.005
variable = temp_f
neighbor_var = temp
boundary = 'fuel_top fuel_bottom fuel_side_1'
[]
[fuel_center]
type = ThinLayerHeatTransfer
thermal_conductivity = thermal_conductivity_center
thickness = 0.001
variable = temp_f
neighbor_var = temp
boundary = 'fuel_inside'
[]
[fuel_other]
type = ThinLayerHeatTransfer
thermal_conductivity = thermal_conductivity_other
thickness = 0.0001
variable = temp_f
neighbor_var = temp
boundary = 'fuel_side_2'
[]
[]
[Kernels]
[heat]
type = HeatConduction
variable = temp
extra_vector_tags = 'ref'
block = ${nonfuel_all}
[]
[heat_f]
type = HeatConduction
variable = temp_f
extra_vector_tags = 'ref'
block = ${fuel_all}
[]
[heat_ie]
type = HeatConductionTimeDerivative
variable = temp
extra_vector_tags = 'ref'
block = ${nonfuel_all}
[]
[heat_ie_f]
type = HeatConductionTimeDerivative
variable = temp_f
extra_vector_tags = 'ref'
block = ${fuel_all}
[]
[heatsource]
type = CoupledForce
variable = temp_f
block = ${fuel_all}
v = power_density
extra_vector_tags = 'ref'
[]
# These diffusion kernels evenly disperse the displacement across the void
[diff_x]
type = MatDiffusion
block = '${air_all} ${hp_fuel_gap_all} ${hp_mli_all}'
variable = disp_x
diffusivity = 1e5
extra_vector_tags = 'ref'
[]
[diff_y]
type = MatDiffusion
block = '${air_all} ${hp_fuel_gap_all} ${hp_mli_all}'
variable = disp_y
diffusivity = 1e5
extra_vector_tags = 'ref'
[]
[diff_z]
type = MatDiffusion
block = '${air_all} ${hp_fuel_gap_all} ${hp_mli_all}'
variable = disp_z
diffusivity = 1e5
extra_vector_tags = 'ref'
[]
[]
# We create variables separately because Air density requires displacement variables
# but the solid mechanics equations would only create these variables on blocks we solve equations
# for displacements on
# Note: not creating the displacement variables on the air blocks would likely be more efficient
[Variables]
[disp_x]
[]
[disp_y]
[]
[disp_z]
[]
[]
[Physics/SolidMechanics/QuasiStatic]
add_variables = false
[mech_parts_fuel]
block = '${fuel_all}'
temperature = temp_f
strain = SMALL # Small strain should work, but finite may have better performance
add_variables = true
eigenstrain_names = 'thermal_strain'
generate_output = 'vonmises_stress strain_xx strain_yy strain_zz stress_xx stress_yy stress_zz hydrostatic_stress'
extra_vector_tags = 'ref'
use_automatic_differentiation = false
[]
[mech_parts_non_fuel]
block = '${nonfuel_mech}'
strain = SMALL # Small strain should work, but finite may have better performance
add_variables = true
eigenstrain_names = 'thermal_strain'
generate_output = 'vonmises_stress strain_xx strain_yy strain_zz stress_xx stress_yy stress_zz hydrostatic_stress'
extra_vector_tags = 'ref'
use_automatic_differentiation = false
[]
[]
[Materials]
[stress]
type = ComputeLinearElasticStress
block = '${no_void} ${hp_all}'
[]
[UMoDens]
type = Density
block = ${fuel_all}
density = ${umo_dens}
[]
[UMoMech]
type = ComputeIsotropicElasticityTensor
block = ${fuel_all}
youngs_modulus = ${umo_ym}
poissons_ratio = ${umo_pr}
[]
[UMoExp]
type = U10MoThermalExpansionEigenstrain
block = ${fuel_all}
temperature = temp_f
eigenstrain_name = thermal_strain
stress_free_temperature = 298
model_option = Rest
[]
[fission_density]
type = GenericConstantMaterial
prop_names = 'fission_density'
prop_values = 0.0
block = ${fuel_all}
[]
[UMo_thermal]
type = HeatConductionMaterial
block = ${fuel_all}
temp = temp_f
specific_heat_temperature_function = umo_heat_cap
thermal_conductivity_temperature_function = umo_tc
[]
[BeODens]
type = Density
block = ${beo_all}
density = ${beo_dens}
[]
[BeOMech]
type = BeOElasticityTensor
temperature = temp
block = ${beo_all}
porosity = 0.01
[]
[BeOExp]
type = BeOThermalExpansionEigenstrain
eigenstrain_name = thermal_strain
stress_free_temperature = 298
temperature = temp
block = ${beo_all}
[]
[BeO_thermal]
type = BeOThermal
block = ${beo_all}
fluence_conversion_factor = 1
temperature = temp
outputs = all
porosity = 0
fast_neutron_fluence = 0
[]
[AirDens]
type = Density
block = ${air_all}
density = ${air_dens}
[]
[AirTherm]
type = HeatConductionMaterial
block = ${air_all}
thermal_conductivity = ${air_cond}
specific_heat = ${air_sph}
[]
# HP Fuel Coupling Material
# Note HP was replaced with steel rods
[HPFDens]
type = Density
block = ${hp_fuel_gap_names}
density = ${hp_fuel_couple_dens}
[]
[HPFTherm]
type = HeatConductionMaterial
block = ${hp_fuel_gap_names}
thermal_conductivity = ${hp_fuel_couple_cond}
specific_heat = ${hp_fuel_couple_sph}
[]
[HPMLIDens]
type = Density
block = ${hp_mli_names}
density = ${hp_mli_dens}
[]
[HPMLIherm]
type = HeatConductionMaterial
block = ${hp_mli_names}
thermal_conductivity = ${hp_mli_cond}
specific_heat = ${hp_mli_sph}
[]
#Stainless Steel; Assuming all the stuctures are SS316
[SS316Dens]
type = Density
block = '${ss_all} ${hp_all}'
density = ${ss_dens}
[]
[SS316Mech]
type = SS316ElasticityTensor
elastic_constants_model = legacy_ifr
block = '${ss_all} ${hp_all}'
temperature = temp
[]
[SS316Exp]
type = SS316ThermalExpansionEigenstrain
block = '${ss_all} ${hp_all}'
temperature = temp
eigenstrain_name = thermal_strain
stress_free_temperature = 298
[]
[SS316Therm]
type = SS316Thermal
block = '${ss_all} ${hp_all}'
temperature = temp
[]
#Aluminium
[Al6061Dens]
type = Density
block = ${Al_all}
density = ${al_dens}
[]
[Al6061Mech]
type = Al6061ElasticityTensor
block = ${Al_all}
temperature = temp
youngs_modulus_model = Kaufman
[]
[Al6061Exp]
type = Al6061ThermalExpansionEigenstrain
block = ${Al_all}
temperature = temp
eigenstrain_name = thermal_strain
stress_free_temperature = 298
[]
[Al6061Therm]
type = SS316Thermal
block = ${Al_all}
temperature = temp
[]
#Natural Boron Carbide (Not enriched boron)
[B4CDens]
type = Density
block = ${b4c_all}
density = ${b4c_dens}
[]
[B4CMech]
type = ComputeIsotropicElasticityTensor
block = ${b4c_all}
youngs_modulus = ${b4c_ym}
poissons_ratio = ${b4c_pr}
[]
[B4CExp]
type = ComputeThermalExpansionEigenstrain
block = ${b4c_all}
thermal_expansion_coeff = ${b4c_exp}
eigenstrain_name = thermal_strain
[]
[B4CTherm]
type = HeatConductionMaterial
block = ${b4c_all}
thermal_conductivity = ${b4c_cond}
specific_heat = ${b4c_sph}
[]
#Pure Beryllium
[BeDens]
type = Density
block = ${Be_all}
density = ${Be_dens}
[]
[BeMech]
type = ComputeIsotropicElasticityTensor
block = ${Be_all}
youngs_modulus = ${Be_ym}
poissons_ratio = ${Be_pr}
[]
[BeExp]
type = ComputeThermalExpansionEigenstrain
block = ${Be_all}
thermal_expansion_coeff = ${Be_exp}
eigenstrain_name = thermal_strain
[]
[BeTherm]
type = HeatConductionMaterial
block = ${Be_all}
thermal_conductivity = ${Be_cond}
specific_heat = ${Be_sph}
[]
[]
[Functions]
[umo_heat_cap]
# https://doi.org/10.1016/S0022-3697(00)00219-5.
type = ParsedFunction
expression = 'M:=210.4243/1000;
dHdT:=20.8+1.174e-2*t+0.4715e5/t/t;
dHdT/M'
[]
[umo_tc]
type = ParsedFunction
expression = '0.606+0.0351*t'
[]
# The function that controls the displacement of the reflector
# Used to control the reactivity insertion
[ref_mov]
type = ParsedFunction
symbol_names = 'reflector_disp_0 reflector_disp_increment_1 reflector_disp_increment_2 rdi2_scale_factor t_first_15c_insertion t_start_power_monitoring existing_reflector_disp unit_increment_fraction pw pw_ref'
symbol_values = '${reflector_disp_init} ${reflector_disp_increment_1} ${reflector_disp_increment_2} 1.1 0.5 697 disp_old_target 0.09 total_power 750'
expression = 'reflector_disp_15c:=reflector_disp_0+reflector_disp_increment_1;
if(t<0,reflector_disp_0,
if(t<t_first_15c_insertion,reflector_disp_0+reflector_disp_increment_1/t_first_15c_insertion*t,
if(t<t_start_power_monitoring,reflector_disp_15c,
if(pw<pw_ref&existing_reflector_disp<reflector_disp_15c+reflector_disp_increment_2*rdi2_scale_factor,existing_reflector_disp+reflector_disp_increment_2*unit_increment_fraction,
existing_reflector_disp))))'
[]
[]
[BCs]
[OuterWall]
type = ConvectiveHeatFluxBC
variable = temp
boundary = '9531 Core_bottom Core_outer_boundary' #outer wall sideset
heat_transfer_coefficient = 5 # free convection in dry air W/m2/K
T_infinity = 300 # room temperature
[]
[BottomFixZ]
type = DirichletBC
variable = disp_z
boundary = 'Core_bottom'
value = 0.0
[]
# The BC that controls the displacement of the reflector
[BottomSSFixZ]
type = FunctionDirichletBC
variable = disp_z
boundary = 'ss_bot'
function = ref_mov
[]
[TopFixZ]
type = DirichletBC
variable = disp_z
boundary = 'Core_top'
value = 0.0
[]
[MirrorOneFixX]
type = DirichletBC
variable = disp_y
boundary = 'Mirror_Y_surf'
value = 0.0
[]
[MirrorOneFixY]
type = DirichletBC
variable = disp_x
boundary = 'Mirror_X_surf'
value = 0.0
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Transient
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package -ksp_gmres_restart'
petsc_options_value = 'lu superlu_dist 51'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-7
l_tol = 1e-4
l_max_its = 25
automatic_scaling = true
compute_scaling_once = false
start_time = 0
end_time = 7200
# Let main app to control the time step
dt = 10
[]
[Postprocessors]
[_dt]
type = TimestepSize
[]
[total_power]
type = ElementIntegralVariablePostprocessor
block = ${fuel_all}
variable = power_density
execute_on = 'initial TIMESTEP_END transfer'
[]
[avg_fuel_temp]
type = ElementAverageValue
block = ${fuel_all}
variable = temp_f
execute_on = 'initial TIMESTEP_END'
[]
[max_fuel_temp]
type = ElementExtremeValue
block = ${fuel_all}
variable = temp_f
value_type = max
execute_on = 'initial TIMESTEP_END'
[]
[min_fuel_temp]
type = ElementExtremeValue
block = ${fuel_all}
variable = temp_f
value_type = min
execute_on = 'initial TIMESTEP_END'
[]
[avg_nonfuel_temp]
type = ElementAverageValue
block = ${nonfuel_all}
variable = temp
execute_on = 'initial TIMESTEP_END'
[]
[max_nonfuel_temp]
type = ElementExtremeValue
block = ${nonfuel_all}
variable = temp
value_type = max
execute_on = 'initial TIMESTEP_END'
[]
[min_nonfuel_temp]
type = ElementExtremeValue
block = ${nonfuel_all}
variable = temp
value_type = min
execute_on = 'initial TIMESTEP_END'
[]
[avg_fuel_cond]
type = ElementAverageValue
block = ${fuel_all}
variable = thermal_conductivity
execute_on = 'initial TIMESTEP_END'
[]
[fuel_volume]
type = VolumePostprocessor
block = ${fuel_all}
use_displaced_mesh = true
execute_on = 'initial TIMESTEP_END'
[]
[power_density_avg_everywhere]
type = ElementAverageValue
variable = power_density
block = ${fuel_all}
[]
[power_density_avg]
type = ElementAverageValue
variable = power_density
block = ${fuel_all}
[]
[power_density_max]
type = ElementExtremeValue
variable = power_density
block = ${fuel_all}
[]
[power_density_min]
type = ElementExtremeValue
variable = power_density
block = ${fuel_all}
value_type = min
[]
[disp_old_origin]
type = FunctionValuePostprocessor
function = ref_mov
execute_on = 'initial timestep_end'
[]
[disp_old_target]
type = Receiver
default = ${fparse reflector_disp_init+reflector_disp_increment_1}
[]
[]
[Outputs]
csv = true
[exodus]
type = Exodus
enable = false
[]
[checkpoint]
type = Checkpoint
enable = false
[]
perf_graph = true
color = true
[]
(microreactors/KRUSTY/Multiphysics_30C_RIT/KRUSTY_BISON_THERMOMECHANICS_TR.i)
################################################################################
## NEAMS Micro-Reactor Application Driver ##
## KRUSTY Multiphysics 30-Cent Reactivity Insertion ##
## BISON thermomechanics main input file (Child App) ##
## Heat Conduction, Thermal Expansion, Thermal Stress ##
################################################################################
!include ../Multiphysics_SS/KRUSTY_BISON_PARAMS.i
restart_cp_file = '../Multiphysics_SS/KRUSTY_Griffin_SN23_NA23_CMFD_out_bison0_checkpoint_cp/LATEST'
reflector_disp_init = 0
reflector_disp_increment_1 = 1.447e-3 # Corresponding to the first 15 cents reactivity insertion
reflector_disp_increment_2 = 1.400e-3 # Corresponding to the nominal second 15 cents reactivity insertion
[GlobalParams]
temperature = temp
displacements = 'disp_x disp_y disp_z'
stress_free_temperature = 298
[]
[Problem]
type = ReferenceResidualProblem
reference_vector = 'ref'
extra_tag_vectors = 'ref'
group_variables = 'disp_x disp_y disp_z'
restart_file_base = ${restart_cp_file}
[]
[Mesh]
file = ${restart_cp_file}
parallel_type = distributed
[]
# No initial value needed as this is restarting
# For both Variables and AuxVariables
[Variables]
# We have two temperature variables, one for the fuel and one for the non-fuel
# This is to allow discontinuity on the fuel surface so that the insulation
# can be better simulated using `InterfaceKernels`
[temp]
block = ${nonfuel_all}
[]
[temp_f]
block = ${fuel_all}
[]
[]
[AuxVariables]
[power_density]
block = ${fuel_all}
family = L2_LAGRANGE
order = FIRST
[]
[Tfuel]
order = CONSTANT
family = MONOMIAL
[]
[Tsteel]
order = CONSTANT
family = MONOMIAL
[]
[external_power]
[]
[hp_temp_aux]
[]
[]
[UserObjects]
[temp_f_avg]
type = LayeredAverage
variable = temp_f
direction = z
num_layers = 100
block = ${fuel_all}
[]
[temp_s_avg]
type = LayeredAverage
variable = temp
direction = z
num_layers = 100
block = '${ss_all} 998'
[]
[]
[AuxKernels]
[assign_tfuel_f]
type = NormalizationAux
variable = Tfuel
source_variable = temp_f
execute_on = 'timestep_end'
block = ${fuel_all}
[]
[assign_tfuel_nf]
type = SpatialUserObjectAux
variable = Tfuel
user_object = temp_f_avg
execute_on = 'timestep_end'
block = ${nonfuel_all}
[]
[assign_tsteel_s]
type = NormalizationAux
variable = Tsteel
source_variable = temp
execute_on = 'timestep_end'
block = '${ss_all} 998'
[]
[assign_tsteel_ns]
type = SpatialUserObjectAux
variable = Tsteel
user_object = temp_s_avg
execute_on = 'timestep_end'
block = ${non_ss_998_all}
[]
[]
# A small materials block for thin layers
[Materials]
[thermal_cond_mli]
type = GenericConstantMaterial
prop_names = 'thermal_conductivity_mli'
prop_values = '${hp_mli_cond}'
boundary = 'fuel_top fuel_bottom fuel_side_1'
[]
[thermal_cond_center]
type = GenericConstantMaterial
prop_names = 'thermal_conductivity_center'
prop_values = '0.20'
boundary = 'fuel_inside'
[]
[thermal_cond_other]
type = GenericConstantMaterial
prop_names = 'thermal_conductivity_other'
prop_values = '15.0'
boundary = 'fuel_side_2'
[]
[]
[InterfaceKernels]
[fuel_ref]
type = ThinLayerHeatTransfer
thermal_conductivity = thermal_conductivity_mli
thickness = 0.005
variable = temp_f
neighbor_var = temp
boundary = 'fuel_top fuel_bottom fuel_side_1'
[]
[fuel_center]
type = ThinLayerHeatTransfer
thermal_conductivity = thermal_conductivity_center
thickness = 0.001
variable = temp_f
neighbor_var = temp
boundary = 'fuel_inside'
[]
[fuel_other]
type = ThinLayerHeatTransfer
thermal_conductivity = thermal_conductivity_other
thickness = 0.0001
variable = temp_f
neighbor_var = temp
boundary = 'fuel_side_2'
[]
[]
[Kernels]
[heat]
type = HeatConduction
variable = temp
extra_vector_tags = 'ref'
block = ${nonfuel_all}
[]
[heat_f]
type = HeatConduction
variable = temp_f
extra_vector_tags = 'ref'
block = ${fuel_all}
[]
[heat_ie]
type = HeatConductionTimeDerivative
variable = temp
extra_vector_tags = 'ref'
block = ${nonfuel_all}
[]
[heat_ie_f]
type = HeatConductionTimeDerivative
variable = temp_f
extra_vector_tags = 'ref'
block = ${fuel_all}
[]
[heatsource]
type = CoupledForce
variable = temp_f
block = ${fuel_all}
v = power_density
extra_vector_tags = 'ref'
[]
# These diffusion kernels evenly disperse the displacement across the void
[diff_x]
type = MatDiffusion
block = '${air_all} ${hp_fuel_gap_all} ${hp_mli_all}'
variable = disp_x
diffusivity = 1e5
extra_vector_tags = 'ref'
[]
[diff_y]
type = MatDiffusion
block = '${air_all} ${hp_fuel_gap_all} ${hp_mli_all}'
variable = disp_y
diffusivity = 1e5
extra_vector_tags = 'ref'
[]
[diff_z]
type = MatDiffusion
block = '${air_all} ${hp_fuel_gap_all} ${hp_mli_all}'
variable = disp_z
diffusivity = 1e5
extra_vector_tags = 'ref'
[]
[]
# We create variables separately because Air density requires displacement variables
# but the solid mechanics equations would only create these variables on blocks we solve equations
# for displacements on
# Note: not creating the displacement variables on the air blocks would likely be more efficient
[Variables]
[disp_x]
[]
[disp_y]
[]
[disp_z]
[]
[]
[Physics/SolidMechanics/QuasiStatic]
add_variables = false
[mech_parts_fuel]
block = '${fuel_all}'
temperature = temp_f
strain = SMALL # Small strain should work, but finite may have better performance
add_variables = true
eigenstrain_names = 'thermal_strain'
generate_output = 'vonmises_stress strain_xx strain_yy strain_zz stress_xx stress_yy stress_zz hydrostatic_stress'
extra_vector_tags = 'ref'
use_automatic_differentiation = false
[]
[mech_parts_non_fuel]
block = '${nonfuel_mech}'
strain = SMALL # Small strain should work, but finite may have better performance
add_variables = true
eigenstrain_names = 'thermal_strain'
generate_output = 'vonmises_stress strain_xx strain_yy strain_zz stress_xx stress_yy stress_zz hydrostatic_stress'
extra_vector_tags = 'ref'
use_automatic_differentiation = false
[]
[]
[Materials]
[stress]
type = ComputeLinearElasticStress
block = '${no_void} ${hp_all}'
[]
[UMoDens]
type = Density
block = ${fuel_all}
density = ${umo_dens}
[]
[UMoMech]
type = ComputeIsotropicElasticityTensor
block = ${fuel_all}
youngs_modulus = ${umo_ym}
poissons_ratio = ${umo_pr}
[]
[UMoExp]
type = U10MoThermalExpansionEigenstrain
block = ${fuel_all}
temperature = temp_f
eigenstrain_name = thermal_strain
stress_free_temperature = 298
model_option = Rest
[]
[fission_density]
type = GenericConstantMaterial
prop_names = 'fission_density'
prop_values = 0.0
block = ${fuel_all}
[]
[UMo_thermal]
type = HeatConductionMaterial
block = ${fuel_all}
temp = temp_f
specific_heat_temperature_function = umo_heat_cap
thermal_conductivity_temperature_function = umo_tc
[]
[BeODens]
type = Density
block = ${beo_all}
density = ${beo_dens}
[]
[BeOMech]
type = BeOElasticityTensor
temperature = temp
block = ${beo_all}
porosity = 0.01
[]
[BeOExp]
type = BeOThermalExpansionEigenstrain
eigenstrain_name = thermal_strain
stress_free_temperature = 298
temperature = temp
block = ${beo_all}
[]
[BeO_thermal]
type = BeOThermal
block = ${beo_all}
fluence_conversion_factor = 1
temperature = temp
outputs = all
porosity = 0
fast_neutron_fluence = 0
[]
[AirDens]
type = Density
block = ${air_all}
density = ${air_dens}
[]
[AirTherm]
type = HeatConductionMaterial
block = ${air_all}
thermal_conductivity = ${air_cond}
specific_heat = ${air_sph}
[]
# HP Fuel Coupling Material
# Note HP was replaced with steel rods
[HPFDens]
type = Density
block = ${hp_fuel_gap_names}
density = ${hp_fuel_couple_dens}
[]
[HPFTherm]
type = HeatConductionMaterial
block = ${hp_fuel_gap_names}
thermal_conductivity = ${hp_fuel_couple_cond}
specific_heat = ${hp_fuel_couple_sph}
[]
[HPMLIDens]
type = Density
block = ${hp_mli_names}
density = ${hp_mli_dens}
[]
[HPMLIherm]
type = HeatConductionMaterial
block = ${hp_mli_names}
thermal_conductivity = ${hp_mli_cond}
specific_heat = ${hp_mli_sph}
[]
#Stainless Steel; Assuming all the stuctures are SS316
[SS316Dens]
type = Density
block = '${ss_all} ${hp_all}'
density = ${ss_dens}
[]
[SS316Mech]
type = SS316ElasticityTensor
elastic_constants_model = legacy_ifr
block = '${ss_all} ${hp_all}'
temperature = temp
[]
[SS316Exp]
type = SS316ThermalExpansionEigenstrain
block = '${ss_all} ${hp_all}'
temperature = temp
eigenstrain_name = thermal_strain
stress_free_temperature = 298
[]
[SS316Therm]
type = SS316Thermal
block = '${ss_all} ${hp_all}'
temperature = temp
[]
#Aluminium
[Al6061Dens]
type = Density
block = ${Al_all}
density = ${al_dens}
[]
[Al6061Mech]
type = Al6061ElasticityTensor
block = ${Al_all}
temperature = temp
youngs_modulus_model = Kaufman
[]
[Al6061Exp]
type = Al6061ThermalExpansionEigenstrain
block = ${Al_all}
temperature = temp
eigenstrain_name = thermal_strain
stress_free_temperature = 298
[]
[Al6061Therm]
type = SS316Thermal
block = ${Al_all}
temperature = temp
[]
#Natural Boron Carbide (Not enriched boron)
[B4CDens]
type = Density
block = ${b4c_all}
density = ${b4c_dens}
[]
[B4CMech]
type = ComputeIsotropicElasticityTensor
block = ${b4c_all}
youngs_modulus = ${b4c_ym}
poissons_ratio = ${b4c_pr}
[]
[B4CExp]
type = ComputeThermalExpansionEigenstrain
block = ${b4c_all}
thermal_expansion_coeff = ${b4c_exp}
eigenstrain_name = thermal_strain
[]
[B4CTherm]
type = HeatConductionMaterial
block = ${b4c_all}
thermal_conductivity = ${b4c_cond}
specific_heat = ${b4c_sph}
[]
#Pure Beryllium
[BeDens]
type = Density
block = ${Be_all}
density = ${Be_dens}
[]
[BeMech]
type = ComputeIsotropicElasticityTensor
block = ${Be_all}
youngs_modulus = ${Be_ym}
poissons_ratio = ${Be_pr}
[]
[BeExp]
type = ComputeThermalExpansionEigenstrain
block = ${Be_all}
thermal_expansion_coeff = ${Be_exp}
eigenstrain_name = thermal_strain
[]
[BeTherm]
type = HeatConductionMaterial
block = ${Be_all}
thermal_conductivity = ${Be_cond}
specific_heat = ${Be_sph}
[]
[]
[Functions]
[umo_heat_cap]
# https://doi.org/10.1016/S0022-3697(00)00219-5.
type = ParsedFunction
expression = 'M:=210.4243/1000;
dHdT:=20.8+1.174e-2*t+0.4715e5/t/t;
dHdT/M'
[]
[umo_tc]
type = ParsedFunction
expression = '0.606+0.0351*t'
[]
# The function that controls the displacement of the reflector
# Used to control the reactivity insertion
[ref_mov]
type = ParsedFunction
symbol_names = 'reflector_disp_0 reflector_disp_increment_1 reflector_disp_increment_2 rdi2_scale_factor t_first_15c_insertion t_start_power_monitoring existing_reflector_disp unit_increment_fraction pw pw_ref'
symbol_values = '${reflector_disp_init} ${reflector_disp_increment_1} ${reflector_disp_increment_2} 1.1 0.5 697 disp_old_target 0.09 total_power 750'
expression = 'reflector_disp_15c:=reflector_disp_0+reflector_disp_increment_1;
if(t<0,reflector_disp_0,
if(t<t_first_15c_insertion,reflector_disp_0+reflector_disp_increment_1/t_first_15c_insertion*t,
if(t<t_start_power_monitoring,reflector_disp_15c,
if(pw<pw_ref&existing_reflector_disp<reflector_disp_15c+reflector_disp_increment_2*rdi2_scale_factor,existing_reflector_disp+reflector_disp_increment_2*unit_increment_fraction,
existing_reflector_disp))))'
[]
[]
[BCs]
[OuterWall]
type = ConvectiveHeatFluxBC
variable = temp
boundary = '9531 Core_bottom Core_outer_boundary' #outer wall sideset
heat_transfer_coefficient = 5 # free convection in dry air W/m2/K
T_infinity = 300 # room temperature
[]
[BottomFixZ]
type = DirichletBC
variable = disp_z
boundary = 'Core_bottom'
value = 0.0
[]
# The BC that controls the displacement of the reflector
[BottomSSFixZ]
type = FunctionDirichletBC
variable = disp_z
boundary = 'ss_bot'
function = ref_mov
[]
[TopFixZ]
type = DirichletBC
variable = disp_z
boundary = 'Core_top'
value = 0.0
[]
[MirrorOneFixX]
type = DirichletBC
variable = disp_y
boundary = 'Mirror_Y_surf'
value = 0.0
[]
[MirrorOneFixY]
type = DirichletBC
variable = disp_x
boundary = 'Mirror_X_surf'
value = 0.0
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Transient
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package -ksp_gmres_restart'
petsc_options_value = 'lu superlu_dist 51'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-7
l_tol = 1e-4
l_max_its = 25
automatic_scaling = true
compute_scaling_once = false
start_time = 0
end_time = 7200
# Let main app to control the time step
dt = 10
[]
[Postprocessors]
[_dt]
type = TimestepSize
[]
[total_power]
type = ElementIntegralVariablePostprocessor
block = ${fuel_all}
variable = power_density
execute_on = 'initial TIMESTEP_END transfer'
[]
[avg_fuel_temp]
type = ElementAverageValue
block = ${fuel_all}
variable = temp_f
execute_on = 'initial TIMESTEP_END'
[]
[max_fuel_temp]
type = ElementExtremeValue
block = ${fuel_all}
variable = temp_f
value_type = max
execute_on = 'initial TIMESTEP_END'
[]
[min_fuel_temp]
type = ElementExtremeValue
block = ${fuel_all}
variable = temp_f
value_type = min
execute_on = 'initial TIMESTEP_END'
[]
[avg_nonfuel_temp]
type = ElementAverageValue
block = ${nonfuel_all}
variable = temp
execute_on = 'initial TIMESTEP_END'
[]
[max_nonfuel_temp]
type = ElementExtremeValue
block = ${nonfuel_all}
variable = temp
value_type = max
execute_on = 'initial TIMESTEP_END'
[]
[min_nonfuel_temp]
type = ElementExtremeValue
block = ${nonfuel_all}
variable = temp
value_type = min
execute_on = 'initial TIMESTEP_END'
[]
[avg_fuel_cond]
type = ElementAverageValue
block = ${fuel_all}
variable = thermal_conductivity
execute_on = 'initial TIMESTEP_END'
[]
[fuel_volume]
type = VolumePostprocessor
block = ${fuel_all}
use_displaced_mesh = true
execute_on = 'initial TIMESTEP_END'
[]
[power_density_avg_everywhere]
type = ElementAverageValue
variable = power_density
block = ${fuel_all}
[]
[power_density_avg]
type = ElementAverageValue
variable = power_density
block = ${fuel_all}
[]
[power_density_max]
type = ElementExtremeValue
variable = power_density
block = ${fuel_all}
[]
[power_density_min]
type = ElementExtremeValue
variable = power_density
block = ${fuel_all}
value_type = min
[]
[disp_old_origin]
type = FunctionValuePostprocessor
function = ref_mov
execute_on = 'initial timestep_end'
[]
[disp_old_target]
type = Receiver
default = ${fparse reflector_disp_init+reflector_disp_increment_1}
[]
[]
[Outputs]
csv = true
[exodus]
type = Exodus
enable = false
[]
[checkpoint]
type = Checkpoint
enable = false
[]
perf_graph = true
color = true
[]
(microreactors/KRUSTY/Multiphysics_30C_RIT/KRUSTY_BISON_THERMOMECHANICS_TR.i)
################################################################################
## NEAMS Micro-Reactor Application Driver ##
## KRUSTY Multiphysics 30-Cent Reactivity Insertion ##
## BISON thermomechanics main input file (Child App) ##
## Heat Conduction, Thermal Expansion, Thermal Stress ##
################################################################################
!include ../Multiphysics_SS/KRUSTY_BISON_PARAMS.i
restart_cp_file = '../Multiphysics_SS/KRUSTY_Griffin_SN23_NA23_CMFD_out_bison0_checkpoint_cp/LATEST'
reflector_disp_init = 0
reflector_disp_increment_1 = 1.447e-3 # Corresponding to the first 15 cents reactivity insertion
reflector_disp_increment_2 = 1.400e-3 # Corresponding to the nominal second 15 cents reactivity insertion
[GlobalParams]
temperature = temp
displacements = 'disp_x disp_y disp_z'
stress_free_temperature = 298
[]
[Problem]
type = ReferenceResidualProblem
reference_vector = 'ref'
extra_tag_vectors = 'ref'
group_variables = 'disp_x disp_y disp_z'
restart_file_base = ${restart_cp_file}
[]
[Mesh]
file = ${restart_cp_file}
parallel_type = distributed
[]
# No initial value needed as this is restarting
# For both Variables and AuxVariables
[Variables]
# We have two temperature variables, one for the fuel and one for the non-fuel
# This is to allow discontinuity on the fuel surface so that the insulation
# can be better simulated using `InterfaceKernels`
[temp]
block = ${nonfuel_all}
[]
[temp_f]
block = ${fuel_all}
[]
[]
[AuxVariables]
[power_density]
block = ${fuel_all}
family = L2_LAGRANGE
order = FIRST
[]
[Tfuel]
order = CONSTANT
family = MONOMIAL
[]
[Tsteel]
order = CONSTANT
family = MONOMIAL
[]
[external_power]
[]
[hp_temp_aux]
[]
[]
[UserObjects]
[temp_f_avg]
type = LayeredAverage
variable = temp_f
direction = z
num_layers = 100
block = ${fuel_all}
[]
[temp_s_avg]
type = LayeredAverage
variable = temp
direction = z
num_layers = 100
block = '${ss_all} 998'
[]
[]
[AuxKernels]
[assign_tfuel_f]
type = NormalizationAux
variable = Tfuel
source_variable = temp_f
execute_on = 'timestep_end'
block = ${fuel_all}
[]
[assign_tfuel_nf]
type = SpatialUserObjectAux
variable = Tfuel
user_object = temp_f_avg
execute_on = 'timestep_end'
block = ${nonfuel_all}
[]
[assign_tsteel_s]
type = NormalizationAux
variable = Tsteel
source_variable = temp
execute_on = 'timestep_end'
block = '${ss_all} 998'
[]
[assign_tsteel_ns]
type = SpatialUserObjectAux
variable = Tsteel
user_object = temp_s_avg
execute_on = 'timestep_end'
block = ${non_ss_998_all}
[]
[]
# A small materials block for thin layers
[Materials]
[thermal_cond_mli]
type = GenericConstantMaterial
prop_names = 'thermal_conductivity_mli'
prop_values = '${hp_mli_cond}'
boundary = 'fuel_top fuel_bottom fuel_side_1'
[]
[thermal_cond_center]
type = GenericConstantMaterial
prop_names = 'thermal_conductivity_center'
prop_values = '0.20'
boundary = 'fuel_inside'
[]
[thermal_cond_other]
type = GenericConstantMaterial
prop_names = 'thermal_conductivity_other'
prop_values = '15.0'
boundary = 'fuel_side_2'
[]
[]
[InterfaceKernels]
[fuel_ref]
type = ThinLayerHeatTransfer
thermal_conductivity = thermal_conductivity_mli
thickness = 0.005
variable = temp_f
neighbor_var = temp
boundary = 'fuel_top fuel_bottom fuel_side_1'
[]
[fuel_center]
type = ThinLayerHeatTransfer
thermal_conductivity = thermal_conductivity_center
thickness = 0.001
variable = temp_f
neighbor_var = temp
boundary = 'fuel_inside'
[]
[fuel_other]
type = ThinLayerHeatTransfer
thermal_conductivity = thermal_conductivity_other
thickness = 0.0001
variable = temp_f
neighbor_var = temp
boundary = 'fuel_side_2'
[]
[]
[Kernels]
[heat]
type = HeatConduction
variable = temp
extra_vector_tags = 'ref'
block = ${nonfuel_all}
[]
[heat_f]
type = HeatConduction
variable = temp_f
extra_vector_tags = 'ref'
block = ${fuel_all}
[]
[heat_ie]
type = HeatConductionTimeDerivative
variable = temp
extra_vector_tags = 'ref'
block = ${nonfuel_all}
[]
[heat_ie_f]
type = HeatConductionTimeDerivative
variable = temp_f
extra_vector_tags = 'ref'
block = ${fuel_all}
[]
[heatsource]
type = CoupledForce
variable = temp_f
block = ${fuel_all}
v = power_density
extra_vector_tags = 'ref'
[]
# These diffusion kernels evenly disperse the displacement across the void
[diff_x]
type = MatDiffusion
block = '${air_all} ${hp_fuel_gap_all} ${hp_mli_all}'
variable = disp_x
diffusivity = 1e5
extra_vector_tags = 'ref'
[]
[diff_y]
type = MatDiffusion
block = '${air_all} ${hp_fuel_gap_all} ${hp_mli_all}'
variable = disp_y
diffusivity = 1e5
extra_vector_tags = 'ref'
[]
[diff_z]
type = MatDiffusion
block = '${air_all} ${hp_fuel_gap_all} ${hp_mli_all}'
variable = disp_z
diffusivity = 1e5
extra_vector_tags = 'ref'
[]
[]
# We create variables separately because Air density requires displacement variables
# but the solid mechanics equations would only create these variables on blocks we solve equations
# for displacements on
# Note: not creating the displacement variables on the air blocks would likely be more efficient
[Variables]
[disp_x]
[]
[disp_y]
[]
[disp_z]
[]
[]
[Physics/SolidMechanics/QuasiStatic]
add_variables = false
[mech_parts_fuel]
block = '${fuel_all}'
temperature = temp_f
strain = SMALL # Small strain should work, but finite may have better performance
add_variables = true
eigenstrain_names = 'thermal_strain'
generate_output = 'vonmises_stress strain_xx strain_yy strain_zz stress_xx stress_yy stress_zz hydrostatic_stress'
extra_vector_tags = 'ref'
use_automatic_differentiation = false
[]
[mech_parts_non_fuel]
block = '${nonfuel_mech}'
strain = SMALL # Small strain should work, but finite may have better performance
add_variables = true
eigenstrain_names = 'thermal_strain'
generate_output = 'vonmises_stress strain_xx strain_yy strain_zz stress_xx stress_yy stress_zz hydrostatic_stress'
extra_vector_tags = 'ref'
use_automatic_differentiation = false
[]
[]
[Materials]
[stress]
type = ComputeLinearElasticStress
block = '${no_void} ${hp_all}'
[]
[UMoDens]
type = Density
block = ${fuel_all}
density = ${umo_dens}
[]
[UMoMech]
type = ComputeIsotropicElasticityTensor
block = ${fuel_all}
youngs_modulus = ${umo_ym}
poissons_ratio = ${umo_pr}
[]
[UMoExp]
type = U10MoThermalExpansionEigenstrain
block = ${fuel_all}
temperature = temp_f
eigenstrain_name = thermal_strain
stress_free_temperature = 298
model_option = Rest
[]
[fission_density]
type = GenericConstantMaterial
prop_names = 'fission_density'
prop_values = 0.0
block = ${fuel_all}
[]
[UMo_thermal]
type = HeatConductionMaterial
block = ${fuel_all}
temp = temp_f
specific_heat_temperature_function = umo_heat_cap
thermal_conductivity_temperature_function = umo_tc
[]
[BeODens]
type = Density
block = ${beo_all}
density = ${beo_dens}
[]
[BeOMech]
type = BeOElasticityTensor
temperature = temp
block = ${beo_all}
porosity = 0.01
[]
[BeOExp]
type = BeOThermalExpansionEigenstrain
eigenstrain_name = thermal_strain
stress_free_temperature = 298
temperature = temp
block = ${beo_all}
[]
[BeO_thermal]
type = BeOThermal
block = ${beo_all}
fluence_conversion_factor = 1
temperature = temp
outputs = all
porosity = 0
fast_neutron_fluence = 0
[]
[AirDens]
type = Density
block = ${air_all}
density = ${air_dens}
[]
[AirTherm]
type = HeatConductionMaterial
block = ${air_all}
thermal_conductivity = ${air_cond}
specific_heat = ${air_sph}
[]
# HP Fuel Coupling Material
# Note HP was replaced with steel rods
[HPFDens]
type = Density
block = ${hp_fuel_gap_names}
density = ${hp_fuel_couple_dens}
[]
[HPFTherm]
type = HeatConductionMaterial
block = ${hp_fuel_gap_names}
thermal_conductivity = ${hp_fuel_couple_cond}
specific_heat = ${hp_fuel_couple_sph}
[]
[HPMLIDens]
type = Density
block = ${hp_mli_names}
density = ${hp_mli_dens}
[]
[HPMLIherm]
type = HeatConductionMaterial
block = ${hp_mli_names}
thermal_conductivity = ${hp_mli_cond}
specific_heat = ${hp_mli_sph}
[]
#Stainless Steel; Assuming all the stuctures are SS316
[SS316Dens]
type = Density
block = '${ss_all} ${hp_all}'
density = ${ss_dens}
[]
[SS316Mech]
type = SS316ElasticityTensor
elastic_constants_model = legacy_ifr
block = '${ss_all} ${hp_all}'
temperature = temp
[]
[SS316Exp]
type = SS316ThermalExpansionEigenstrain
block = '${ss_all} ${hp_all}'
temperature = temp
eigenstrain_name = thermal_strain
stress_free_temperature = 298
[]
[SS316Therm]
type = SS316Thermal
block = '${ss_all} ${hp_all}'
temperature = temp
[]
#Aluminium
[Al6061Dens]
type = Density
block = ${Al_all}
density = ${al_dens}
[]
[Al6061Mech]
type = Al6061ElasticityTensor
block = ${Al_all}
temperature = temp
youngs_modulus_model = Kaufman
[]
[Al6061Exp]
type = Al6061ThermalExpansionEigenstrain
block = ${Al_all}
temperature = temp
eigenstrain_name = thermal_strain
stress_free_temperature = 298
[]
[Al6061Therm]
type = SS316Thermal
block = ${Al_all}
temperature = temp
[]
#Natural Boron Carbide (Not enriched boron)
[B4CDens]
type = Density
block = ${b4c_all}
density = ${b4c_dens}
[]
[B4CMech]
type = ComputeIsotropicElasticityTensor
block = ${b4c_all}
youngs_modulus = ${b4c_ym}
poissons_ratio = ${b4c_pr}
[]
[B4CExp]
type = ComputeThermalExpansionEigenstrain
block = ${b4c_all}
thermal_expansion_coeff = ${b4c_exp}
eigenstrain_name = thermal_strain
[]
[B4CTherm]
type = HeatConductionMaterial
block = ${b4c_all}
thermal_conductivity = ${b4c_cond}
specific_heat = ${b4c_sph}
[]
#Pure Beryllium
[BeDens]
type = Density
block = ${Be_all}
density = ${Be_dens}
[]
[BeMech]
type = ComputeIsotropicElasticityTensor
block = ${Be_all}
youngs_modulus = ${Be_ym}
poissons_ratio = ${Be_pr}
[]
[BeExp]
type = ComputeThermalExpansionEigenstrain
block = ${Be_all}
thermal_expansion_coeff = ${Be_exp}
eigenstrain_name = thermal_strain
[]
[BeTherm]
type = HeatConductionMaterial
block = ${Be_all}
thermal_conductivity = ${Be_cond}
specific_heat = ${Be_sph}
[]
[]
[Functions]
[umo_heat_cap]
# https://doi.org/10.1016/S0022-3697(00)00219-5.
type = ParsedFunction
expression = 'M:=210.4243/1000;
dHdT:=20.8+1.174e-2*t+0.4715e5/t/t;
dHdT/M'
[]
[umo_tc]
type = ParsedFunction
expression = '0.606+0.0351*t'
[]
# The function that controls the displacement of the reflector
# Used to control the reactivity insertion
[ref_mov]
type = ParsedFunction
symbol_names = 'reflector_disp_0 reflector_disp_increment_1 reflector_disp_increment_2 rdi2_scale_factor t_first_15c_insertion t_start_power_monitoring existing_reflector_disp unit_increment_fraction pw pw_ref'
symbol_values = '${reflector_disp_init} ${reflector_disp_increment_1} ${reflector_disp_increment_2} 1.1 0.5 697 disp_old_target 0.09 total_power 750'
expression = 'reflector_disp_15c:=reflector_disp_0+reflector_disp_increment_1;
if(t<0,reflector_disp_0,
if(t<t_first_15c_insertion,reflector_disp_0+reflector_disp_increment_1/t_first_15c_insertion*t,
if(t<t_start_power_monitoring,reflector_disp_15c,
if(pw<pw_ref&existing_reflector_disp<reflector_disp_15c+reflector_disp_increment_2*rdi2_scale_factor,existing_reflector_disp+reflector_disp_increment_2*unit_increment_fraction,
existing_reflector_disp))))'
[]
[]
[BCs]
[OuterWall]
type = ConvectiveHeatFluxBC
variable = temp
boundary = '9531 Core_bottom Core_outer_boundary' #outer wall sideset
heat_transfer_coefficient = 5 # free convection in dry air W/m2/K
T_infinity = 300 # room temperature
[]
[BottomFixZ]
type = DirichletBC
variable = disp_z
boundary = 'Core_bottom'
value = 0.0
[]
# The BC that controls the displacement of the reflector
[BottomSSFixZ]
type = FunctionDirichletBC
variable = disp_z
boundary = 'ss_bot'
function = ref_mov
[]
[TopFixZ]
type = DirichletBC
variable = disp_z
boundary = 'Core_top'
value = 0.0
[]
[MirrorOneFixX]
type = DirichletBC
variable = disp_y
boundary = 'Mirror_Y_surf'
value = 0.0
[]
[MirrorOneFixY]
type = DirichletBC
variable = disp_x
boundary = 'Mirror_X_surf'
value = 0.0
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Transient
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package -ksp_gmres_restart'
petsc_options_value = 'lu superlu_dist 51'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-7
l_tol = 1e-4
l_max_its = 25
automatic_scaling = true
compute_scaling_once = false
start_time = 0
end_time = 7200
# Let main app to control the time step
dt = 10
[]
[Postprocessors]
[_dt]
type = TimestepSize
[]
[total_power]
type = ElementIntegralVariablePostprocessor
block = ${fuel_all}
variable = power_density
execute_on = 'initial TIMESTEP_END transfer'
[]
[avg_fuel_temp]
type = ElementAverageValue
block = ${fuel_all}
variable = temp_f
execute_on = 'initial TIMESTEP_END'
[]
[max_fuel_temp]
type = ElementExtremeValue
block = ${fuel_all}
variable = temp_f
value_type = max
execute_on = 'initial TIMESTEP_END'
[]
[min_fuel_temp]
type = ElementExtremeValue
block = ${fuel_all}
variable = temp_f
value_type = min
execute_on = 'initial TIMESTEP_END'
[]
[avg_nonfuel_temp]
type = ElementAverageValue
block = ${nonfuel_all}
variable = temp
execute_on = 'initial TIMESTEP_END'
[]
[max_nonfuel_temp]
type = ElementExtremeValue
block = ${nonfuel_all}
variable = temp
value_type = max
execute_on = 'initial TIMESTEP_END'
[]
[min_nonfuel_temp]
type = ElementExtremeValue
block = ${nonfuel_all}
variable = temp
value_type = min
execute_on = 'initial TIMESTEP_END'
[]
[avg_fuel_cond]
type = ElementAverageValue
block = ${fuel_all}
variable = thermal_conductivity
execute_on = 'initial TIMESTEP_END'
[]
[fuel_volume]
type = VolumePostprocessor
block = ${fuel_all}
use_displaced_mesh = true
execute_on = 'initial TIMESTEP_END'
[]
[power_density_avg_everywhere]
type = ElementAverageValue
variable = power_density
block = ${fuel_all}
[]
[power_density_avg]
type = ElementAverageValue
variable = power_density
block = ${fuel_all}
[]
[power_density_max]
type = ElementExtremeValue
variable = power_density
block = ${fuel_all}
[]
[power_density_min]
type = ElementExtremeValue
variable = power_density
block = ${fuel_all}
value_type = min
[]
[disp_old_origin]
type = FunctionValuePostprocessor
function = ref_mov
execute_on = 'initial timestep_end'
[]
[disp_old_target]
type = Receiver
default = ${fparse reflector_disp_init+reflector_disp_increment_1}
[]
[]
[Outputs]
csv = true
[exodus]
type = Exodus
enable = false
[]
[checkpoint]
type = Checkpoint
enable = false
[]
perf_graph = true
color = true
[]