- blockBlock IDs for the coordinate systems
C++ Type:std::vector
Description:Block IDs for the coordinate systems
- coord_typeXYZType of the coordinate system per block param
Default:XYZ
C++ Type:MultiMooseEnum
Description:Type of the coordinate system per block param
- error_on_jacobian_nonzero_reallocationFalseThis causes PETSc to error if it had to reallocate memory in the Jacobian matrix due to not having enough nonzeros
Default:False
C++ Type:bool
Description:This causes PETSc to error if it had to reallocate memory in the Jacobian matrix due to not having enough nonzeros
- extra_tag_matricesExtra matrices to add to the system that can be filled by objects which compute residuals and Jacobians (Kernels, BCs, etc.) by setting tags on them.
C++ Type:std::vector
Description:Extra matrices to add to the system that can be filled by objects which compute residuals and Jacobians (Kernels, BCs, etc.) by setting tags on them.
- extra_tag_vectorsExtra vectors to add to the system that can be filled by objects which compute residuals and Jacobians (Kernels, BCs, etc.) by setting tags on them.
C++ Type:std::vector
Description:Extra vectors to add to the system that can be filled by objects which compute residuals and Jacobians (Kernels, BCs, etc.) by setting tags on them.
- force_restartFalseEXPERIMENTAL: If true, a sub_app may use a restart file instead of using of using the master backup file
Default:False
C++ Type:bool
Description:EXPERIMENTAL: If true, a sub_app may use a restart file instead of using of using the master backup file
- ignore_zeros_in_jacobianFalseDo not explicitly store zero values in the Jacobian matrix if true
Default:False
C++ Type:bool
Description:Do not explicitly store zero values in the Jacobian matrix if true
- kernel_coverage_checkTrueSet to false to disable kernel->subdomain coverage check
Default:True
C++ Type:bool
Description:Set to false to disable kernel->subdomain coverage check
- material_coverage_checkTrueSet to false to disable material->subdomain coverage check
Default:True
C++ Type:bool
Description:Set to false to disable material->subdomain coverage check
- near_null_space_dimension0The dimension of the near nullspace
Default:0
C++ Type:unsigned int
Description:The dimension of the near nullspace
- null_space_dimension0The dimension of the nullspace
Default:0
C++ Type:unsigned int
Description:The dimension of the nullspace
- parallel_barrier_messagingFalseDisplays messaging from parallel barrier notifications when executing or transferring to/from Multiapps (default: false)
Default:False
C++ Type:bool
Description:Displays messaging from parallel barrier notifications when executing or transferring to/from Multiapps (default: false)
- restart_file_baseFile base name used for restart (e.g.
/ or /LATEST to grab the latest file available) C++ Type:FileNameNoExtension
Description:File base name used for restart (e.g.
/ or /LATEST to grab the latest file available) - rz_coord_axisYThe rotation axis (X | Y) for axisymetric coordinates
Default:Y
C++ Type:MooseEnum
Description:The rotation axis (X | Y) for axisymetric coordinates
- skip_additional_restart_dataFalseTrue to skip additional data in equation system for restart. It is useful for starting a transient calculation with a steady-state solution
Default:False
C++ Type:bool
Description:True to skip additional data in equation system for restart. It is useful for starting a transient calculation with a steady-state solution
- skip_nl_system_checkFalseTrue to skip the NonlinearSystem check for work to do (e.g. Make sure that there are variables to solve for).
Default:False
C++ Type:bool
Description:True to skip the NonlinearSystem check for work to do (e.g. Make sure that there are variables to solve for).
- solveTrueWhether or not to actually solve the Nonlinear system. This is handy in the case that all you want to do is execute AuxKernels, Transfers, etc. without actually solving anything
Default:True
C++ Type:bool
Description:Whether or not to actually solve the Nonlinear system. This is handy in the case that all you want to do is execute AuxKernels, Transfers, etc. without actually solving anything
- transpose_null_space_dimension0The dimension of the transpose nullspace
Default:0
C++ Type:unsigned int
Description:The dimension of the transpose nullspace
- use_nonlinearTrueDetermines whether to use a Nonlinear vs a Eigenvalue system (Automatically determined based on executioner)
Default:True
C++ Type:bool
Description:Determines whether to use a Nonlinear vs a Eigenvalue system (Automatically determined based on executioner)
FEProblemBase
The FEProblemBase class is an intermediate base class containing all of the common logic for running the various MOOSE simulations. MOOSE has two built-in types of problems FEProblem for solving "normal" physics problems and EigenProblem for solving Eigenvalue problems. Additionally, MOOSE contains an ExternalProblem problem useful for creating "MOOSE-wrapped Apps".
Convenience Zeros
One of the advantages of the MOOSE framework is the ease at building up Multiphysics simulations. Coupling is a first-class feature and filling out residuals, or materials properties with coupling is very natural. When coupling is optional, it is often handy to have access to valid data structures that may be used in-place of the actual coupled variables. This makes it possible to avoid branch statements inside of your residual statements and other computationally intensive areas of code. One of the ways MOOSE makes this possible is by making several different types of "zero" variables available. The following statements illustrate how optional coupling may be implemented with these zeros.
// In the constructor initialization list of a Kernel
_velocity_vector(isParamValid("velocity_vector") ? coupledGradient("velocity_vector") : _grad_zero)
// The residual statement
return _test[_i][_qp] * (_velocity_vector[_qp] * _grad_u[_qp]);
Selective Reinit
The system automatically determines which variables should be made available for use on the current element ("reinit"-ed). Each variable is tracked on calls through the coupling interface. Variables that are not needed are simply not prepared. This can save significant amounts of time on systems that have several active variables.
Finite Element Concepts
Shape Functions
While the weak form is essentially what you need for adding physics to MOOSE, in traditional finite element software more work is necessary.
We need to discretize our weak form and select a set of simple "basis functions" amenable for manipulation by a computer.

Example of linear Lagrange shape function associated with single node on triangular mesh
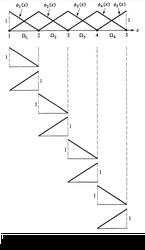
1D linear Lagrange shape functions
Our discretized expansion of u takes on the following form:
The here are called "basis functions"
These form the basis for the "trial function",
Analogous to the we used earlier
The gradient of can be expanded similarly:
In the Galerkin finite element method, the same basis functions are used for both the trial and test functions:
Substituting these expansions back into our weak form, we get:
The left-hand side of the equation above is what we generally refer to as the component of our "Residual Vector" and write as .
Shape Functions are the functions that get multiplied by coefficients and summed to form the solution.
Individual shape functions are restrictions of the global basis functions to individual elements.
They are analogous to the functions from polynomial fitting (in fact, you can use those as shape functions).
Typical shape function families: Lagrange, Hermite, Hierarchic, Monomial, Clough-Toucher - MOOSE has support for all of these.
Lagrange shape functions are the most common. - They are interpolary at the nodes, i.e., the coefficients correspond to the values of the functions at the nodes.
Example 1D Shape Functions
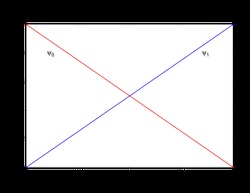
Linear Lagrange
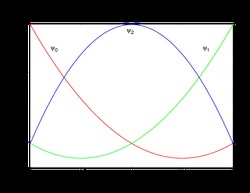
Quadratic Lagrange
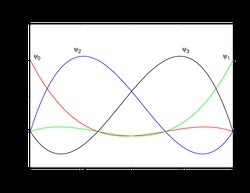
Cubic Lagrange
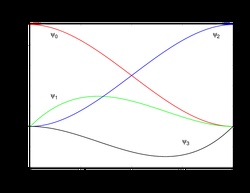
Cubic Hermite
2D Lagrange Shape Functions
Example bi-quadratic basis functions defined on the Quad9 element:
is associated to a "corner" node, it is zero on the opposite edges.
is associated to a "mid-edge" node, it is zero on all other edges.
is associated to the "center" node, it is symmetric and on the element.
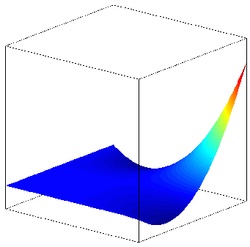
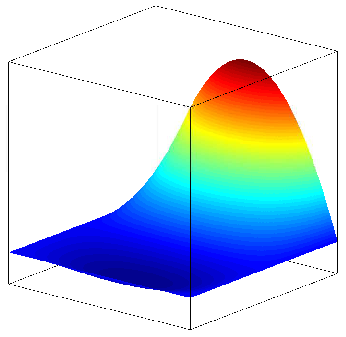
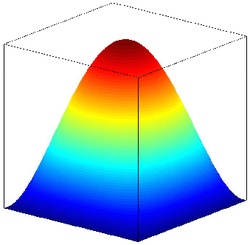
Numerical Integration
The only remaining non-discretized parts of the weak form are the integrals.
We split the domain integral into a sum of integrals over elements:
Through a change of variables, the element integrals are mapped to integrals over the "reference" elements .
is the Jacobian of the map from the physical element to the reference element.
To approximate the reference element integrals numerically, we use quadrature (typically "Gaussian Quadrature"):
is the spatial location of the th quadrature point and is its associated weight.
MOOSE handles multiplication by the Jacobian and the weight automatically, thus your
Kernelis only responsible for computing the part of the integrand.Under certain common situations, the quadrature approximation is exact! - For example, in 1 dimension, Gaussian Quadrature can exactly integrate polynomials of order with quadrature points.
Note that sampling at the quadrature points yields:
And our weak form becomes:
The second sum is over boundary faces, .
MOOSE
Kernelsmust provide each of the terms in square brackets (evaluated at or as necessary).
A normal (default) Problem object that contains a single NonlinearSystem and a single AuxiliarySystem object.
Input Parameters
- control_tagsAdds user-defined labels for accessing object parameters via control logic.
C++ Type:std::vector
Options:
Description:Adds user-defined labels for accessing object parameters via control logic.
- default_ghostingFalseWhether or not to use libMesh's default amount of algebraic and geometric ghosting
Default:False
C++ Type:bool
Options:
Description:Whether or not to use libMesh's default amount of algebraic and geometric ghosting
- enableTrueSet the enabled status of the MooseObject.
Default:True
C++ Type:bool
Options:
Description:Set the enabled status of the MooseObject.
Advanced Parameters
Input Files
- test/tests/auxkernels/grad_component/grad_component_monomial.i
- tutorials/darcy_thermo_mech/step05_heat_conduction/tests/bcs/outflow/outflow.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_4/ring4_mu_0_2_pen_sm.i
- test/tests/multiapps/command_line/master_common.i
- test/tests/mesh/distributed_generated_mesh/distributed_generated_mesh.i
- test/tests/meshgenerators/subdomain_bounding_box_generator/oriented_subdomain_bounding_box_generator.i
- tutorials/darcy_thermo_mech/step06_coupled_darcy_heat_conduction/tests/kernels/darcy_advection/darcy_advection.i
- tutorials/darcy_thermo_mech/step04_velocity_aux/tests/auxkernels/velocity_aux/velocity_aux.i
- test/tests/markers/q_point_marker/q_point_marker.i
- test/tests/geomsearch/patch_update_strategy/never.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_1/ring1_template1.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_3/cyl3_template1_sm.i
- tutorials/darcy_thermo_mech/step03_darcy_material/problems/step3.i
- test/tests/restart/pointer_restart_errors/pointer_store_error.i
- test/tests/transfers/multiapp_copy_transfer/third_monomial_from_sub/sub.i
- modules/phase_field/test/tests/initial_conditions/MultiSmoothSuperellipsoidIC_3D.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_4/ring4_template1.i
- test/tests/mesh_modifiers/image_subdomain/image_2d.i
- test/tests/functions/image_function/error/threshold_values.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_3/ring3_template1.i
- modules/stochastic_tools/test/tests/multiapps/commandline_control/master_wrong_size.i
- test/tests/functions/image_function/component.i
- modules/porous_flow/test/tests/fluidstate/theis_tabulated.i
- test/tests/controls/restrict_exec_flag/exec_flag_error.i
- test/tests/auxkernels/element_length/element_length.i
- test/tests/geomsearch/patch_update_strategy/always.i
- test/tests/functions/image_function/threshold.i
- modules/porous_flow/test/tests/fluidstate/theis_brineco2_nonisothermal.i
- tutorials/darcy_thermo_mech/step01_diffusion/tests/kernels/simple_diffusion/simple_diffusion.i
- modules/phase_field/test/tests/initial_conditions/PolycrystalVoronoiVoidIC_moregrains.i
- test/tests/quadrature/gauss_lobatto/gauss_lobatto.i
- modules/phase_field/test/tests/initial_conditions/PolycrystalVoronoi_fromfile.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_1/cyl1_mu_0_2_pen.i
- test/tests/userobjects/shape_element_user_object/shape_side_uo_jac_test.i
- modules/phase_field/test/tests/initial_conditions/PolycrystalVoronoiVoidIC_periodic.i
- modules/phase_field/test/tests/grain_tracker_test/grain_tracker_volume_changing.i
- modules/stochastic_tools/test/tests/multiapps/commandline_control/master_single.i
- tutorials/darcy_thermo_mech/step02_darcy_pressure/tests/kernels/darcy_pressure/darcy_pressure.i
- test/tests/functions/image_function/image_3d.i
- modules/stochastic_tools/test/tests/multiapps/commandline_control/sub.i
- test/tests/restart/restartable_types/restartable_types2.i
- modules/phase_field/test/tests/reconstruction/2phase_reconstruction.i
- tutorials/darcy_thermo_mech/step03_darcy_material/tests/kernels/darcy_pressure/darcy_pressure.i
- tutorials/darcy_thermo_mech/step06_coupled_darcy_heat_conduction/problems/step6a_coupled.i
- modules/porous_flow/test/tests/fluidstate/theis_brineco2.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_1/ring1_template1_sm.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_2/ring2_template1_sm.i
- test/tests/transfers/multiapp_copy_transfer/aux_to_aux/sub.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_1/ring1_mu_0_2_pen_sm.i
- tutorials/darcy_thermo_mech/step07_adaptivity/problems/step7d_adapt_blocks.i
- test/tests/multiapps/command_line/sub.i
- test/tests/auxkernels/pp_depend/pp_depend.i
- test/tests/restart/pointer_restart_errors/pointer_load_error.i
- test/tests/transfers/multiapp_copy_transfer/constant_monomial_from_sub/master.i
- tutorials/darcy_thermo_mech/step10_multiapps/tests/auxkernels/corrosion/corrosion.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_1/ring1_mu_0_2_pen.i
- tutorials/darcy_thermo_mech/step05_heat_conduction/problems/step5b_transient.i
- modules/phase_field/test/tests/initial_conditions/ClosePackIC_3D.i
- modules/phase_field/test/tests/feature_flood_test/parallel_feature_count.i
- tutorials/darcy_thermo_mech/step06_coupled_darcy_heat_conduction/problems/step6b_transient_inflow.i
- test/tests/functions/image_function/flip_dual.i
- test/tests/mesh_modifiers/subdomain_bounding_box/oriented_subdomain_bounding_box_outside.i
- test/tests/restart/pointer_restart_errors/pointer_load_error2.i
- test/tests/mesh_modifiers/assign_subdomain_id/assign_subdomain_id.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_2/cyl2_template1_sm.i
- test/tests/postprocessors/difference_pps/difference_depend_check.i
- test/tests/tag/2d_diffusion_tag_matrix.i
- test/tests/indicators/value_jump_indicator/value_jump_indicator_test.i
- test/tests/markers/block_restricted/marker_block.i
- test/tests/controls/restrict_exec_flag/sub.i
- tutorials/darcy_thermo_mech/step03_darcy_material/tests/materials/packed_column/packed_column.i
- modules/phase_field/test/tests/phase_field_crystal/PFC_IC/PFC_IC_FCC_test.i
- test/tests/transfers/multiapp_userobject_transfer/sub.i
- test/tests/transfers/multiapp_copy_transfer/linear_lagrange_from_sub/master.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_4/ring4_mu_0_2_pen.i
- modules/phase_field/test/tests/initial_conditions/PolycrystalVoronoiVoidIC_periodic_fromfile.i
- test/tests/markers/oriented_box_marker/obm.i
- test/tests/functions/image_function/image_2d.i
- test/tests/functions/image_function/image_2d_elemental.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_2/cyl2_template1.i
- test/tests/geomsearch/patch_update_strategy/auto.i
- test/tests/functions/image_function/flip.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_3/cyl3_template1.i
- test/tests/misc/block_boundary_material_check/dgkernel_check_boundary.i
- modules/solid_mechanics/test/tests/interaction_integral_benchmark/input.i
- modules/phase_field/test/tests/initial_conditions/RampIC.i
- test/tests/problems/no_solve/no_solve.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_3/cyl3_mu_0_2_pen_sm.i
- tutorials/darcy_thermo_mech/step06_coupled_darcy_heat_conduction/tests/materials/packed_column/packed_column.i
- tutorials/darcy_thermo_mech/step07_adaptivity/problems/step7c_adapt.i
- modules/stochastic_tools/test/tests/multiapps/commandline_control/master_wrong_num_params.i
- test/tests/transfers/multiapp_copy_transfer/multivariable_copy/master.i
- modules/stochastic_tools/test/tests/multiapps/batch_commandline_control/master_wrong_size.i
- test/tests/misc/block_user_object_check/coupled_check.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_2/cyl2_mu_0_2_pen_sm.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_2/ring2_mu_0_2_pen.i
- test/tests/functions/image_function/image_mesh_2d.i
- tutorials/darcy_thermo_mech/step06_coupled_darcy_heat_conduction/problems/step6c_decoupled.i
- test/tests/misc/block_boundary_material_check/dgkernel_check_block.i
- test/tests/functions/image_function/threshold_adapt_parallel.i
- modules/phase_field/test/tests/reconstruction/2phase_reconstruction4.i
- modules/phase_field/test/tests/MultiSmoothCircleIC/test_problem.i
- test/tests/functions/image_function/image_mesh_3d.i
- tutorials/darcy_thermo_mech/step01_diffusion/problems/step1.i
- test/tests/multiapps/command_line/master.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_4/cyl4_template1_sm.i
- modules/phase_field/test/tests/initial_conditions/ClosePackIC.i
- test/tests/functions/image_function/subset.i
- test/tests/tag/2d_diffusion_tag_vector.i
- test/tests/functions/image_function/threshold_adapt.i
- modules/heat_conduction/test/tests/meshed_gap_thermal_contact/meshed_gap_thermal_contact.i
- modules/porous_flow/test/tests/recover/theis.i
- modules/porous_flow/test/tests/dirackernels/theis3.i
- modules/phase_field/test/tests/grain_tracker_test/grain_tracker_remapping_test.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_2/ring2_template1.i
- test/tests/transfers/multiapp_userobject_transfer/tosub_displaced_sub.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_3/ring3_mu_0_2_pen.i
- modules/phase_field/test/tests/reconstruction/2phase_reconstruction2.i
- test/tests/mesh_modifiers/image_subdomain/image_3d.i
- test/tests/coord_type/coord_type_rz.i
- test/tests/misc/block_boundary_material_check/bc_check.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_3/ring3_template1_sm.i
- tutorials/darcy_thermo_mech/step09_mechanics/problems/step9.i
- modules/stochastic_tools/test/tests/multiapps/commandline_control/master_multiple.i
- test/tests/transfers/multiapp_userobject_transfer/tosub_sub.i
- test/tests/misc/stop_for_debugger/stop_for_debugger.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_1/cyl1_template1_sm.i
- test/tests/restart/restartable_types/restartable_types.i
- modules/phase_field/test/tests/reconstruction/1phase_reconstruction.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_1/cyl1_mu_0_2_pen_sm.i
- modules/phase_field/test/tests/initial_conditions/PolycrystalVoronoiVoidIC_notperiodic.i
- modules/porous_flow/test/tests/fluidstate/theis_nonisothermal.i
- tutorials/darcy_thermo_mech/step08_postprocessors/problems/step8.i
- modules/stochastic_tools/test/tests/multiapps/batch_commandline_control/master_single.i
- test/tests/transfers/multiapp_copy_transfer/second_lagrange_from_sub/master.i
- tutorials/darcy_thermo_mech/step07_adaptivity/problems/step7b_fine.i
- modules/porous_flow/test/tests/fluidstate/theis.i
- test/tests/coord_type/coord_type_rz_integrated.i
- modules/stochastic_tools/test/tests/multiapps/batch_commandline_control/master_wrong_num_params.i
- test/tests/transfers/multiapp_copy_transfer/linear_lagrange_to_sub/sub.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_2/ring2_mu_0_2_pen_sm.i
- test/tests/userobjects/shape_element_user_object/shape_side_uo_physics_test.i
- test/tests/transfers/multiapp_copy_transfer/second_lagrange_to_sub/sub.i
- test/tests/mesh_modifiers/subdomain_bounding_box/oriented_subdomain_bounding_box_inside.i
- test/tests/transfers/multiapp_conservative_transfer/sub_userobject.i
- test/tests/multiapps/command_line/master_wrong_size.i
- test/tests/functions/image_function/image_3d_subset.i
- test/tests/functions/image_function/image.i
- modules/phase_field/test/tests/initial_conditions/MultiSmoothSuperellipsoidIC_2D.i
- test/tests/transfers/multiapp_copy_transfer/errors/sub.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_4/cyl4_template1.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_4/cyl4_mu_0_2_pen.i
- modules/stochastic_tools/test/tests/multiapps/batch_commandline_control/sub.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_1/cyl1_template1.i
- tutorials/darcy_thermo_mech/step02_darcy_pressure/problems/step2.i
- tutorials/darcy_thermo_mech/step05_heat_conduction/problems/step5a_steady.i
- modules/stochastic_tools/examples/batch/sub.i
- tutorials/darcy_thermo_mech/step07_adaptivity/problems/step7a_coarse.i
- modules/stochastic_tools/test/tests/multiapps/batch_commandline_control/master_multiple.i
- test/tests/preconditioners/fsp/fsp_test_image.i
- test/tests/mesh_modifiers/subdomain_bounding_box/oriented_subdomain_bounding_box.i
- test/tests/misc/block_user_object_check/block_check.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_4/cyl4_mu_0_2_pen_sm.i
- modules/phase_field/test/tests/phase_field_crystal/PFC_IC/PFC_IC_BCC_test.i
- test/tests/auxkernels/vector_function_aux/vector_function_aux.i
- test/tests/transfers/transfer_on_final/master.i
- test/tests/transfers/multiapp_copy_transfer/array_variable_transfer/master.i
- test/tests/executioners/pp_binding/pp_binding_check.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_3/cyl3_mu_0_2_pen.i
- test/tests/functions/image_function/error/check_error.i
- test/tests/postprocessors/cumulative_value_postprocessor/cumulative_value_postprocessor.i
- test/tests/functions/image_function/flip_quad.i
- test/tests/transfers/multiapp_copy_transfer/constant_monomial_from_sub/sub.i
- tutorials/darcy_thermo_mech/step05_heat_conduction/problems/step5c_outflow.i
- test/tests/transfers/multiapp_copy_transfer/constant_monomial_to_sub/sub.i
- modules/solid_mechanics/test/tests/crack_loop/crack_loop.i
- modules/combined/test/tests/contact_verification/patch_tests/cyl_2/cyl2_mu_0_2_pen.i
- modules/heat_conduction/test/tests/meshed_gap_thermal_contact/meshed_gap_thermal_contact_constant_conductance.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_3/ring3_mu_0_2_pen_sm.i
- tutorials/darcy_thermo_mech/step04_velocity_aux/problems/step4.i
- test/tests/functions/image_function/shift_and_scale.i
- modules/phase_field/test/tests/reconstruction/2phase_reconstruction3.i
- test/tests/transfers/multiapp_copy_transfer/third_monomial_from_sub/master.i
- test/tests/transfers/multiapp_conservative_transfer/sub_conservative_transfer.i
- tutorials/darcy_thermo_mech/step11_action/problems/step11.i
- tutorials/darcy_thermo_mech/step03_darcy_material/problems/step3b.i
- test/tests/quadrature/order/elem5_side7.i
- modules/combined/test/tests/contact_verification/patch_tests/ring_4/ring4_template1_sm.i
- test/tests/transfers/multiapp_copy_transfer/third_monomial_to_sub/sub.i
- modules/porous_flow/examples/co2_intercomparison/1Dradial/1Dradial.i
- test/tests/quadrature/order/order5.i
- modules/heat_conduction/test/tests/meshed_gap_thermal_contact/meshed_annulus_thermal_contact.i
- test/tests/misc/block_boundary_material_check/side_uo_check.i
- test/tests/functions/image_function/crop.i
- test/tests/parser/vector_range_checking/all_pass.i
- test/tests/preconditioners/pbp/pbp_test.i
- test/tests/preconditioners/pbp/pbp_dg_test.i
- modules/tensor_mechanics/test/tests/interaction_integral_benchmark/input.i
- modules/phase_field/test/tests/boundary_intersecting_features/boundary_intersecting_features.i
test/tests/auxkernels/grad_component/grad_component_monomial.i
[Mesh]
type = GeneratedMesh
dim = 2
xmax = 2
nx = 20
ny = 10
[]
[Variables]
[./not_u]
[../]
[]
[AuxVariables]
[./u]
family = MONOMIAL
order = FIRST
[../]
[./grad_u_x]
order = CONSTANT
family = MONOMIAL
[../]
[]
[ICs]
[./u]
type = FunctionIC
variable = u
function = 'if(x>0.5,if(x<1.5,2*x,3),0)'
[../]
[]
[AuxKernels]
[./grad_u_x_aux]
type = VariableGradientComponent
variable = grad_u_x
component = x
gradient_variable = u
execute_on = initial
[../]
[]
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Executioner]
type = Steady
[]
[Outputs]
exodus = true
[]
tutorials/darcy_thermo_mech/step05_heat_conduction/tests/bcs/outflow/outflow.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 30
ny = 5
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[Kernels]
[heat_conduction]
type = HeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = SpecificHeatConductionTimeDerivative
variable = temperature
[]
[]
[BCs]
[inlet_temperature]
type = DirichletBC
variable = temperature
boundary = left
value = 350 # (K)
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[steel]
type = GenericConstantMaterial
prop_names = 'thermal_conductivity specific_heat density'
prop_values = '18 466 8000' # W/m*K, J/kg-K, kg/m^3 @ 296K
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
num_steps = 2
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_4/ring4_mu_0_2_pen_sm.i
[Mesh]
file = ring4_mesh.e
[]
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x16]
type = NodalVariableValue
nodeid = 15
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y16]
type = NodalVariableValue
nodeid = 15
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-9
nl_rel_tol = 1e-8
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-3
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = ring4_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = ring4_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x9 disp_y9 disp_x16 disp_y16 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
friction_coefficient = 0.2
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
test/tests/multiapps/command_line/master_common.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[MultiApps]
[sub]
type = FullSolveMultiApp
positions = '0 0 0
1 1 1'
input_files = 'sub.i'
cli_args = 'Mesh/nx=42'
[]
[]
test/tests/mesh/distributed_generated_mesh/distributed_generated_mesh.i
# Note: The gold files for this test were generated using GeneratedMesh
[Mesh]
#type = GeneratedMesh
type = DistributedGeneratedMesh
nx = 10
ny = 10
nz = 10
dim = 3
verbose = false
[]
[Variables]
[u]
[]
[]
[AuxVariables]
[x]
[]
[]
[Kernels]
[diff]
type = Diffusion
variable = u
[]
[]
[AuxKernels]
[f]
type = FunctionAux
variable = x
function = x
[]
[]
[BCs]
[left]
type = DirichletBC
variable = u
boundary = 'left'
value = 0
[]
[right]
type = DirichletBC
variable = u
boundary = 'right'
value = 1
[]
[]
[Problem]
solve = false
type = FEProblem
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
# exodus = true
perf_graph = true
[]
test/tests/meshgenerators/subdomain_bounding_box_generator/oriented_subdomain_bounding_box_generator.i
[Mesh]
[./gmg]
type = GeneratedMeshGenerator
dim = 3
xmin = -6
xmax = 4
nx = 10
ymin = -2
ymax = 10
ny = 12
zmin = -5
zmax = 7
nz = 12
[]
[./subdomains]
type = OrientedSubdomainBoundingBoxGenerator
input = gmg
center = '-1 4 1'
width = 5
length = 10
height = 4
width_direction = '2 1 0'
length_direction = '-1 2 2'
block_id = 10
[]
[]
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Variables]
[./u]
[../]
[]
[Executioner]
type = Steady
solve_type = PJFNK
[]
[Outputs]
exodus = true
[]
tutorials/darcy_thermo_mech/step06_coupled_darcy_heat_conduction/tests/kernels/darcy_advection/darcy_advection.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 200
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[pressure]
initial_condition = 10000
[]
[]
[Kernels]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[BCs]
[inlet_temperature]
type = DirichletBC
variable = temperature
boundary = left
value = 350
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
temperature = temperature
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
num_steps = 10
dt = 0.1
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
tutorials/darcy_thermo_mech/step04_velocity_aux/tests/auxkernels/velocity_aux/velocity_aux.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 2
ny = 2
[]
[Variables]
[pressure]
[]
[]
[AuxVariables]
[velocity_x]
order = CONSTANT
family = MONOMIAL
[]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[velocity_x]
type = VectorVariableComponentAux
variable = velocity_x
component = x
execute_on = timestep_end
vector_variable = velocity
[]
[]
[Functions]
[pressure_ic_func]
type = ParsedFunction
value = 2000*x*y*x*y
[]
[]
[ICs]
[pressure_ic]
type = FunctionIC
variable = pressure
function = pressure_ic_func
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
solve = false
[]
[Materials]
[pressure]
type = GenericConstantMaterial
prop_values = '0.8451e-9 7.98e-4'
prop_names = 'permeability viscosity'
[]
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
test/tests/markers/q_point_marker/q_point_marker.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
nz = 0
zmax = 0
elem_type = QUAD4
[]
[Variables]
[./u]
order = FIRST
family = LAGRANGE
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = 1
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = 2
value = 1
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
solve_type = PJFNK
[]
[Adaptivity]
[./Markers]
[./marker]
type = QPointMarker
variable = u
[../]
[../]
[]
[Outputs]
exodus = true
[]
test/tests/geomsearch/patch_update_strategy/never.i
[Mesh]
type = FileMesh
file = long_range.e
dim = 2
patch_update_strategy = never
displacements = 'disp_x disp_y'
[]
[Variables]
[./u]
block = right
[../]
[]
[AuxVariables]
[./linear_field]
[../]
[./receiver]
# The field to transfer into
[../]
[./disp_x]
[../]
[./disp_y]
[../]
[./elemental_reciever]
order = CONSTANT
family = MONOMIAL
[../]
[]
[Kernels]
[./diff]
type = CoefDiffusion
variable = u
coef = 1
[../]
[./time]
type = TimeDerivative
variable = u
[../]
[]
[AuxKernels]
[./linear_in_y]
# This just gives us something to transfer that varies in y so we can ensure the transfer is working properly...
type = FunctionAux
variable = linear_field
function = y
execute_on = initial
[../]
[./right_to_left]
type = GapValueAux
variable = receiver
paired_variable = linear_field
paired_boundary = rightleft
execute_on = timestep_end
boundary = leftright
[../]
[./y_displacement]
type = FunctionAux
variable = disp_y
function = t
execute_on = 'linear timestep_begin'
block = left
[../]
[./elemental_right_to_left]
type = GapValueAux
variable = elemental_reciever
paired_variable = linear_field
paired_boundary = rightleft
boundary = leftright
[../]
[]
[BCs]
[./top]
type = DirichletBC
variable = u
boundary = righttop
value = 1
[../]
[./bottom]
type = DirichletBC
variable = u
boundary = rightbottom
value = 0
[../]
[]
[Problem]
type = FEProblem
kernel_coverage_check = false
[]
[Executioner]
type = Transient
num_steps = 30
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_1/ring1_template1.i
[GlobalParams]
order = FIRST
family = LAGRANGE
volumetric_locking_correction = true
displacements = 'disp_x disp_y'
[]
[Mesh]
file = ring1_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x7]
type = NodalVariableValue
nodeid = 6
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y7]
type = NodalVariableValue
nodeid = 6
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-10
nl_rel_tol = 1e-9
l_max_its = 100
nl_max_its = 200
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x7 disp_y7 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
normalize_penalty = true
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_3/cyl3_template1_sm.i
#
# This input file is a template for both the frictionless and glued test
# variations for the current problem geometry. In order to create an input
# file to run outside the runtest framework, look at the tests file and add the
# appropriate input file lines from the cli_args line.
#
[Mesh]
file = cyl3_mesh.e
[]
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x11]
type = NodalVariableValue
nodeid = 10
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y11]
type = NodalVariableValue
nodeid = 10
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x11 disp_y11 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
tutorials/darcy_thermo_mech/step03_darcy_material/problems/step3.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables/pressure]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Materials]
[column]
type = PackedColumn
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
test/tests/restart/pointer_restart_errors/pointer_store_error.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[UserObjects]
[./restartable_types]
type = PointerStoreError
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[./checkpoint]
type = Checkpoint
num_files = 1
[../]
[]
test/tests/transfers/multiapp_copy_transfer/third_monomial_from_sub/sub.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[AuxVariables]
[./aux]
family = MONOMIAL
order = THIRD
[../]
[]
[AuxKernels]
[./aux]
type = FunctionAux
variable = aux
execute_on = initial
function = 10*x*y
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Variables]
[./u]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 1
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 2
[../]
[]
[Executioner]
type = Transient
num_steps = 1
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
hide = 'u'
exodus = true
[]
modules/phase_field/test/tests/initial_conditions/MultiSmoothSuperellipsoidIC_3D.i
[Mesh]
type = GeneratedMesh
dim = 3
nx = 22
ny = 22
nz = 22
xmin = 0
xmax = 100
ymin = 0
ymax = 100
zmin = 0
zmax = 100
elem_type = HEX8
[]
[Variables]
[./c]
order = FIRST
family = LAGRANGE
[../]
[]
[ICs]
[./c]
type = MultiSmoothSuperellipsoidIC
variable = c
invalue = 1.0
outvalue = 0.1
bubspac = '10 5'
numbub = '5 5'
semiaxis_b_variation = '0.25 0.35'
semiaxis_variation_type = uniform
semiaxis_a_variation = '0.2 0.3'
semiaxis_a = '7 5'
semiaxis_c_variation = '0.3 0.5'
semiaxis_b = '10 8'
semiaxis_c = '15 5'
exponent = '2 3'
prevent_overlap = true
check_extremes = true
[../]
[]
[Executioner]
type = Transient
scheme = bdf2
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type -ksp_gmres_restart -mat_mffd_type'
petsc_options_value = 'hypre boomeramg 31 ds'
l_max_its = 20
l_tol = 1e-4
nl_max_its = 20
nl_rel_tol = 1e-9
nl_abs_tol = 1e-11
start_time = 0.0
num_steps = 1
dt = 100.0
enable = false
[./Adaptivity]
refine_fraction = .5
[../]
[]
[Outputs]
exodus = true
[]
[Problem]
type = FEProblem
solve = false
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_4/ring4_template1.i
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Mesh]
file = ring4_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x16]
type = NodalVariableValue
nodeid = 15
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y16]
type = NodalVariableValue
nodeid = 15
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-10
nl_rel_tol = 1e-9
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x9 disp_y9 disp_x16 disp_y16 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
normalize_penalty = true
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
test/tests/mesh_modifiers/image_subdomain/image_2d.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 176
ny = 287
[]
[Variables]
[./u]
[../]
[]
[MeshModifiers]
[./image]
type = ImageSubdomain
file = kitten.png #../../functions/image_function/stack/test
threshold = 100
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Steady
[]
[Outputs]
execute_on = 'timestep_end'
exodus = true
[]
test/tests/functions/image_function/error/threshold_values.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 20
ny = 20
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./tif]
type = ImageFunction
file_base = ../stack/test
file_suffix = png
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
threshold = 30000
upper_value = 1
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = tif
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_3/ring3_template1.i
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Mesh]
file = ring3_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x11]
type = NodalVariableValue
nodeid = 10
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y11]
type = NodalVariableValue
nodeid = 10
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
petsc_options = '-mat_superlu_dist_iterrefine -mat_superlu_dist_replacetinypivot'
line_search = 'none'
nl_abs_tol = 1e-10
nl_rel_tol = 1e-9
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x11 disp_y11 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
normalize_penalty = true
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
modules/stochastic_tools/test/tests/multiapps/commandline_control/master_wrong_size.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[MultiApps]
[sub]
type = FullSolveMultiApp
positions = '0 0 0
1 1 1'
input_files = 'sub.i'
[]
[]
[Distributions]
[uniform]
type = UniformDistribution
lower_bound = 5
upper_bound = 10
[]
[]
[Samplers]
[sample]
type = MonteCarloSampler
num_rows = 10
distributions = 'uniform'
execute_on = PRE_MULTIAPP_SETUP
[]
[]
[Controls]
[cmdline]
type = MultiAppCommandLineControl
multi_app = sub
sampler = sample
arguments = 'Mesh/nx'
[]
[]
test/tests/functions/image_function/component.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 20
ny = 20
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
type = ImageFunction
file_base = stack/test
file_suffix = png
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
component = 0
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
modules/porous_flow/test/tests/fluidstate/theis_tabulated.i
# Two phase Theis problem: Flow from single source using WaterNCG fluidstate.
# Constant rate injection 2 kg/s
# 1D cylindrical mesh
# Initially, system has only a liquid phase, until enough gas is injected
# to form a gas phase, in which case the system becomes two phase.
# Note: this test is the same as theis.i, but uses the tabulated version of the CO2FluidProperties
[Mesh]
type = GeneratedMesh
dim = 1
nx = 80
xmax = 200
bias_x = 1.05
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = Y
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[AuxVariables]
[./saturation_gas]
order = CONSTANT
family = MONOMIAL
[../]
[./x1]
order = CONSTANT
family = MONOMIAL
[../]
[./y0]
order = CONSTANT
family = MONOMIAL
[../]
[]
[AuxKernels]
[./saturation_gas]
type = PorousFlowPropertyAux
variable = saturation_gas
property = saturation
phase = 1
execute_on = timestep_end
[../]
[./x1]
type = PorousFlowPropertyAux
variable = x1
property = mass_fraction
phase = 0
fluid_component = 1
execute_on = timestep_end
[../]
[./y0]
type = PorousFlowPropertyAux
variable = y0
property = mass_fraction
phase = 1
fluid_component = 0
execute_on = timestep_end
[../]
[]
[Variables]
[./pgas]
initial_condition = 20e6
[../]
[./zi]
initial_condition = 0
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pgas
[../]
[./flux0]
type = PorousFlowAdvectiveFlux
fluid_component = 0
variable = pgas
[../]
[./mass1]
type = PorousFlowMassTimeDerivative
fluid_component = 1
variable = zi
[../]
[./flux1]
type = PorousFlowAdvectiveFlux
fluid_component = 1
variable = zi
[../]
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pgas zi'
number_fluid_phases = 2
number_fluid_components = 2
[../]
[./pc]
type = PorousFlowCapillaryPressureConst
pc = 0
[../]
[./fs]
type = PorousFlowWaterNCG
water_fp = water
gas_fp = tabulated
capillary_pressure = pc
[../]
[]
[Modules]
[./FluidProperties]
[./co2]
type = CO2FluidProperties
[../]
[./tabulated]
type = TabulatedFluidProperties
fp = co2
fluid_property_file = fluid_properties.csv
[../]
[./water]
type = Water97FluidProperties
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./waterncg]
type = PorousFlowFluidState
gas_porepressure = pgas
z = zi
temperature_unit = Celsius
capillary_pressure = pc
fluid_state = fs
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.2
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1e-12 0 0 0 1e-12 0 0 0 1e-12'
[../]
[./relperm_water]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
s_res = 0.1
sum_s_res = 0.1
[../]
[./relperm_gas]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 1
[../]
[]
[BCs]
[./rightwater]
type = DirichletBC
boundary = right
value = 20e6
variable = pgas
[../]
[]
[DiracKernels]
[./source]
type = PorousFlowSquarePulsePointSource
point = '0 0 0'
mass_flux = 2
variable = zi
[../]
[]
[Preconditioning]
[./smp]
type = SMP
full = true
petsc_options = '-snes_converged_reason -ksp_diagonal_scale -ksp_diagonal_scale_fix -ksp_gmres_modifiedgramschmidt -snes_linesearch_monitor'
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol -snes_max_it'
petsc_options_value = 'gmres asm lu NONZERO 2 1E-8 1E-10 20'
[../]
[]
[Executioner]
type = Transient
solve_type = NEWTON
end_time = 8e2
[./TimeStepper]
type = IterationAdaptiveDT
dt = 2
growth_factor = 2
[../]
[]
[VectorPostprocessors]
[./line]
type = LineValueSampler
sort_by = x
start_point = '0 0 0'
end_point = '200 0 0'
num_points = 1000
variable = 'pgas zi x1 saturation_gas'
execute_on = 'timestep_end'
[../]
[]
[Postprocessors]
[./pgas]
type = PointValue
point = '1 0 0'
variable = pgas
[../]
[./sgas]
type = PointValue
point = '1 0 0'
variable = saturation_gas
[../]
[./zi]
type = PointValue
point = '1 0 0'
variable = zi
[../]
[./massgas]
type = PorousFlowFluidMass
fluid_component = 1
[../]
[./x1]
type = PointValue
point = '1 0 0'
variable = x1
[../]
[./y0]
type = PointValue
point = '1 0 0'
variable = y0
[../]
[]
[Outputs]
print_linear_residuals = false
perf_graph = true
[./csvout]
type = CSV
file_base = theis_tabulated_csvout
execute_on = timestep_end
execute_vector_postprocessors_on = final
[../]
[]
test/tests/controls/restrict_exec_flag/exec_flag_error.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[MultiApps]
[sub]
type = FullSolveMultiApp
positions = '0 0 0'
input_files = sub.i
[]
[]
[Controls]
[test]
type = TestControl
test_type = 'execflag_error'
[]
[]
test/tests/auxkernels/element_length/element_length.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 100
[]
[AuxVariables]
[./min]
[../]
[./max]
order = CONSTANT
family = MONOMIAL
[../]
[]
[AuxKernels]
[./min]
type = ElementLengthAux
variable = min
method = min
execute_on = initial
[../]
[./max]
type = ElementLengthAux
variable = max
method = max
execute_on = initial
[../]
[../]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Outputs]
execute_on = 'TIMESTEP_END'
exodus = true
[]
test/tests/geomsearch/patch_update_strategy/always.i
[Mesh]
type = FileMesh
file = long_range.e
dim = 2
patch_update_strategy = always
displacements = 'disp_x disp_y'
[]
[Variables]
[./u]
block = right
[../]
[]
[AuxVariables]
[./linear_field]
[../]
[./receiver]
# The field to transfer into
[../]
[./disp_x]
[../]
[./disp_y]
[../]
[./elemental_reciever]
order = CONSTANT
family = MONOMIAL
[../]
[]
[Kernels]
[./diff]
type = CoefDiffusion
variable = u
coef = 1
[../]
[./time]
type = TimeDerivative
variable = u
[../]
[]
[AuxKernels]
[./linear_in_y]
# This just gives us something to transfer that varies in y so we can ensure the transfer is working properly...
type = FunctionAux
variable = linear_field
function = y
execute_on = initial
[../]
[./right_to_left]
type = GapValueAux
variable = receiver
paired_variable = linear_field
paired_boundary = rightleft
execute_on = timestep_end
boundary = leftright
[../]
[./y_displacement]
type = FunctionAux
variable = disp_y
function = t
execute_on = 'linear timestep_begin'
block = left
[../]
[./elemental_right_to_left]
type = GapValueAux
variable = elemental_reciever
paired_variable = linear_field
paired_boundary = rightleft
boundary = leftright
[../]
[]
[BCs]
[./top]
type = DirichletBC
variable = u
boundary = righttop
value = 1
[../]
[./bottom]
type = DirichletBC
variable = u
boundary = rightbottom
value = 0
[../]
[]
[Problem]
type = FEProblem
kernel_coverage_check = false
[]
[Executioner]
type = Transient
num_steps = 30
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
test/tests/functions/image_function/threshold.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 20
ny = 20
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
type = ImageFunction
file_base = stack/test
file_suffix = png
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
threshold = 2.7e4
upper_value = 1
lower_value = -1
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
modules/porous_flow/test/tests/fluidstate/theis_brineco2_nonisothermal.i
# Two phase nonisothermal Theis problem: Flow from single source.
# Constant rate injection 2 kg/s of cold CO2 into warm reservoir
# 1D cylindrical mesh
# Initially, system has only a liquid phase, until enough gas is injected
# to form a gas phase, in which case the system becomes two phase.
[Mesh]
[./mesh]
type = GeneratedMeshGenerator
dim = 1
nx = 40
xmin = 0.1
xmax = 200
bias_x = 1.05
[../]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = Y
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[AuxVariables]
[./saturation_gas]
order = CONSTANT
family = MONOMIAL
[../]
[./x1]
order = CONSTANT
family = MONOMIAL
[../]
[./y0]
order = CONSTANT
family = MONOMIAL
[../]
[]
[AuxKernels]
[./saturation_gas]
type = PorousFlowPropertyAux
variable = saturation_gas
property = saturation
phase = 1
execute_on = timestep_end
[../]
[./x1]
type = PorousFlowPropertyAux
variable = x1
property = mass_fraction
phase = 0
fluid_component = 1
execute_on = timestep_end
[../]
[./y0]
type = PorousFlowPropertyAux
variable = y0
property = mass_fraction
phase = 1
fluid_component = 0
execute_on = timestep_end
[../]
[]
[Variables]
[./pgas]
initial_condition = 20e6
[../]
[./zi]
initial_condition = 0
[../]
[./xnacl]
initial_condition = 0.1
[../]
[./temperature]
initial_condition = 70
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pgas
[../]
[./flux0]
type = PorousFlowAdvectiveFlux
fluid_component = 0
variable = pgas
[../]
[./mass1]
type = PorousFlowMassTimeDerivative
fluid_component = 1
variable = zi
[../]
[./flux1]
type = PorousFlowAdvectiveFlux
fluid_component = 1
variable = zi
[../]
[./mass2]
type = PorousFlowMassTimeDerivative
fluid_component = 2
variable = xnacl
[../]
[./flux2]
type = PorousFlowAdvectiveFlux
fluid_component = 2
variable = xnacl
[../]
[./energy]
type = PorousFlowEnergyTimeDerivative
variable = temperature
[../]
[./heatadv]
type = PorousFlowHeatAdvection
variable = temperature
[../]
[./conduction]
type = PorousFlowHeatConduction
variable = temperature
[../]
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pgas zi xnacl temperature'
number_fluid_phases = 2
number_fluid_components = 3
[../]
[./pc]
type = PorousFlowCapillaryPressureConst
pc = 0
[../]
[./fs]
type = PorousFlowBrineCO2
brine_fp = brine
co2_fp = co2
capillary_pressure = pc
[../]
[]
[Modules]
[./FluidProperties]
[./co2]
type = CO2FluidProperties
[../]
[./brine]
type = BrineFluidProperties
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
temperature = temperature
[../]
[./brineco2]
type = PorousFlowFluidState
gas_porepressure = pgas
z = zi
temperature = temperature
temperature_unit = Celsius
xnacl = xnacl
capillary_pressure = pc
fluid_state = fs
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.2
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1e-12 0 0 0 1e-12 0 0 0 1e-12'
[../]
[./relperm_water]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
s_res = 0.1
sum_s_res = 0.1
[../]
[./relperm_gas]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 1
[../]
[./rockheat]
type = PorousFlowMatrixInternalEnergy
specific_heat_capacity = 1000
density = 2500
[../]
[./rock_thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '50 0 0 0 50 0 0 0 50'
[../]
[]
[BCs]
[./cold_gas]
type = DirichletBC
boundary = left
variable = temperature
value = 20
[../]
[./gas_injecton]
type = PorousFlowSink
boundary = left
variable = zi
flux_function = -0.159155
[../]
[./rightwater]
type = DirichletBC
boundary = right
value = 20e6
variable = pgas
[../]
[./righttemp]
type = DirichletBC
boundary = right
value = 70
variable = temperature
[../]
[]
[Preconditioning]
[./smp]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = 'gmres asm lu NONZERO 2'
[../]
[]
[Executioner]
type = Transient
solve_type = NEWTON
end_time = 1e4
automatic_scaling = true
nl_abs_tol = 1e-7
nl_rel_tol = 1e-5
[./TimeStepper]
type = IterationAdaptiveDT
dt = 1
growth_factor = 1.5
[../]
[]
[Postprocessors]
[./pgas]
type = PointValue
point = '2 0 0'
variable = pgas
[../]
[./sgas]
type = PointValue
point = '2 0 0'
variable = saturation_gas
[../]
[./zi]
type = PointValue
point = '2 0 0'
variable = zi
[../]
[./temperature]
type = PointValue
point = '2 0 0'
variable = temperature
[../]
[./massgas]
type = PorousFlowFluidMass
fluid_component = 1
[../]
[./x1]
type = PointValue
point = '2 0 0'
variable = x1
[../]
[./y0]
type = PointValue
point = '2 0 0'
variable = y0
[../]
[]
[Outputs]
print_linear_residuals = false
perf_graph = true
csv = true
[]
tutorials/darcy_thermo_mech/step01_diffusion/tests/kernels/simple_diffusion/simple_diffusion.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[u]
[]
[]
[Kernels]
[diff]
type = Diffusion
variable = u
[]
[]
[BCs]
[left]
type = DirichletBC
variable = u
boundary = left
value = 0
[]
[right]
type = DirichletBC
variable = u
boundary = right
value = 1
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
modules/phase_field/test/tests/initial_conditions/PolycrystalVoronoiVoidIC_moregrains.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 40
ny = 40
nz = 0
xmax = 250
ymax = 250
zmax = 0
elem_type = QUAD4
[]
[GlobalParams]
op_num = 12
grain_num = 25
var_name_base = gr
numbub = 15
bubspac = 22
radius = 8
int_width = 10
invalue = 1
outvalue = 0.1
[]
[Variables]
[./c]
[../]
[./PolycrystalVariables]
[../]
[]
[ICs]
[./PolycrystalICs]
[./PolycrystalVoronoiVoidIC]
polycrystal_ic_uo = voronoi
[../]
[../]
[./c_IC]
variable = c
type = PolycrystalVoronoiVoidIC
structure_type = voids
polycrystal_ic_uo = voronoi
[../]
[]
[UserObjects]
[./voronoi]
type = PolycrystalVoronoi
int_width = 0
[../]
[]
[BCs]
[./Periodic]
[./all]
auto_direction = 'x y'
[../]
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 0
[]
[Outputs]
exodus = true
[]
test/tests/quadrature/gauss_lobatto/gauss_lobatto.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 1
ny = 1
nz = 0
elem_type = QUAD4
[]
[Postprocessors]
[./num_elem_qps]
type = NumElemQPs
block = 0
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
# In 1D, 5th-order Gauss-Lobatto quadrature has 4 points, so in 2D
# it should have 16.
[./Quadrature]
type = GAUSS_LOBATTO
order = FIFTH
[../]
[]
[Outputs]
execute_on = 'timestep_end'
exodus = false
csv = true
[]
modules/phase_field/test/tests/initial_conditions/PolycrystalVoronoi_fromfile.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 40
ny = 40
nz = 0
xmax = 250
ymax = 250
zmax = 0
elem_type = QUAD4
[]
[GlobalParams]
op_num = 8
var_name_base = gr
[]
[Variables]
[./PolycrystalVariables]
[../]
[]
[ICs]
[./PolycrystalICs]
[./PolycrystalColoringIC]
polycrystal_ic_uo = voronoi
[../]
[../]
[]
[UserObjects]
[./voronoi]
type = PolycrystalVoronoi
coloring_algorithm = jp
file_name = 'grains.txt'
[../]
[]
[BCs]
[./Periodic]
[./all]
auto_direction = 'x y'
[../]
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 0
[]
[Outputs]
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_1/cyl1_mu_0_2_pen.i
[GlobalParams]
volumetric_locking_correction = true
displacements = 'disp_x disp_y'
[]
[Mesh]
file = cyl1_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x7]
type = NodalVariableValue
nodeid = 6
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y7]
type = NodalVariableValue
nodeid = 6
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = cyl1_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = cyl1_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x7 disp_y7 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
tangential_tolerance = 1e-3
friction_coefficient = 0.2
penalty = 1e+9
[../]
[]
test/tests/userobjects/shape_element_user_object/shape_side_uo_jac_test.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 2
ny = 2
parallel_type = replicated
[]
[Variables]
[./u]
order = FIRST
family = LAGRANGE
[../]
[./pot]
[../]
[]
[Kernels]
[]
[BCs]
[./left_pot]
boundary = left
type = ExampleShapeSideIntegratedBC
variable = pot
num_user_object = num_user_object
denom_user_object = denom_user_object
v = u
Vb = 1
[../]
[]
[UserObjects]
[./num_user_object]
type = NumShapeSideUserObject
u = u
boundary = left
execute_on = 'linear nonlinear'
[../]
[./denom_user_object]
type = DenomShapeSideUserObject
u = u
boundary = left
execute_on = 'linear nonlinear'
[../]
[]
[Problem]
type = FEProblem
kernel_coverage_check = false
[]
[Preconditioning]
[./smp]
type = SMP
full = true
[../]
[]
[Executioner]
type = Steady
solve_type = NEWTON
petsc_options = '-snes_test_display'
petsc_options_iname = '-snes_type'
petsc_options_value = 'test'
[]
[Outputs]
exodus = true
perf_graph = true
[]
[ICs]
[./u]
type = RandomIC
variable = u
[../]
[./pot]
type = RandomIC
variable = pot
[../]
[]
modules/phase_field/test/tests/initial_conditions/PolycrystalVoronoiVoidIC_periodic.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 85
ny = 85
nz = 0
xmax = 250
ymax = 250
zmax = 0
elem_type = QUAD4
[]
[GlobalParams]
op_num = 5
grain_num = 5
var_name_base = gr
numbub = 15
bubspac = 22
radius = 8
int_width = 10
invalue = 1
outvalue = 0.1
[]
[Variables]
[./c]
[../]
[./w]
scaling = 1.0e4
[../]
[./PolycrystalVariables]
[../]
[]
[ICs]
[./PolycrystalICs]
[./PolycrystalVoronoiVoidIC]
polycrystal_ic_uo = voronoi
[../]
[../]
[./c_IC]
variable = c
type = PolycrystalVoronoiVoidIC
structure_type = voids
polycrystal_ic_uo = voronoi
[../]
[]
[UserObjects]
[./voronoi]
type = PolycrystalVoronoi
rand_seed = 10
int_width = 0
[../]
[]
[BCs]
[./Periodic]
[./all]
auto_direction = 'x y'
[../]
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 0
[]
[Outputs]
exodus = true
[]
modules/phase_field/test/tests/grain_tracker_test/grain_tracker_volume_changing.i
# This simulation predicts GB migration of a 2D copper polycrystal with 100 grains represented with 18 order parameters
# Mesh adaptivity and time step adaptivity are used
# An AuxVariable is used to calculate the grain boundary locations
# Postprocessors are used to record time step and the number of grains
[Mesh]
# Mesh block. Meshes can be read in or automatically generated
type = GeneratedMesh
dim = 2 # Problem dimension
nx = 12 # Number of elements in the x-direction
ny = 12 # Number of elements in the y-direction
xmax = 1000 # maximum x-coordinate of the mesh
ymax = 1000 # maximum y-coordinate of the mesh
elem_type = QUAD4 # Type of elements used in the mesh
uniform_refine = 1 # Initial uniform refinement of the mesh
[]
[GlobalParams]
# Parameters used by several kernels that are defined globally to simplify input file
op_num = 8 # Number of order parameters used
var_name_base = gr # Base name of grains
order = CONSTANT
family = MONOMIAL
[]
[Variables]
# Variable block, where all variables in the simulation are declared
[./PolycrystalVariables]
order = FIRST
family = LAGRANGE
[../]
[]
[UserObjects]
[./voronoi]
type = PolycrystalVoronoi
grain_num = 12 # Number of grains
coloring_algorithm = jp
rand_seed = 15
output_adjacency_matrix = true
[../]
[./grain_tracker]
type = GrainTracker
threshold = 0.2
verbosity_level = 1
connecting_threshold = 0.08
compute_var_to_feature_map = true
compute_halo_maps = true # For displaying HALO fields
polycrystal_ic_uo = voronoi
execute_on = 'initial timestep_end'
[../]
[]
[ICs]
[./PolycrystalICs]
[./PolycrystalColoringIC]
polycrystal_ic_uo = voronoi
[../]
[../]
[]
[AuxVariables]
# Dependent variables
[./bnds]
# Variable used to visualize the grain boundaries in the simulation
order = FIRST
family = LAGRANGE
[../]
[./unique_grains]
[../]
[./var_indices]
[../]
[./ghost_regions]
[../]
[./halos]
[../]
[./halo0]
[../]
[./halo1]
[../]
[./halo2]
[../]
[./halo3]
[../]
[./halo4]
[../]
[./halo5]
[../]
[./halo6]
[../]
[./halo7]
[../]
[./centroids]
order = CONSTANT
family = MONOMIAL
[../]
[]
[Kernels]
# Kernel block, where the kernels defining the residual equations are set up.
[./PolycrystalKernel]
# Custom action creating all necessary kernels for grain growth. All input parameters are up in GlobalParams
[../]
[]
[AuxKernels]
# AuxKernel block, defining the equations used to calculate the auxvars
[./bnds_aux]
# AuxKernel that calculates the GB term
type = BndsCalcAux
variable = bnds
execute_on = 'initial timestep_end'
[../]
[./unique_grains]
type = FeatureFloodCountAux
variable = unique_grains
flood_counter = grain_tracker
field_display = UNIQUE_REGION
execute_on = 'initial timestep_end'
[../]
[./var_indices]
type = FeatureFloodCountAux
variable = var_indices
flood_counter = grain_tracker
field_display = VARIABLE_COLORING
execute_on = 'initial timestep_end'
[../]
[./ghosted_entities]
type = FeatureFloodCountAux
variable = ghost_regions
flood_counter = grain_tracker
field_display = GHOSTED_ENTITIES
execute_on = 'initial timestep_end'
[../]
[./halos]
type = FeatureFloodCountAux
variable = halos
flood_counter = grain_tracker
field_display = HALOS
execute_on = 'initial timestep_end'
[../]
[./halo0]
type = FeatureFloodCountAux
variable = halo0
map_index = 0
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo1]
type = FeatureFloodCountAux
variable = halo1
map_index = 1
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo2]
type = FeatureFloodCountAux
variable = halo2
map_index = 2
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo3]
type = FeatureFloodCountAux
variable = halo3
map_index = 3
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo4]
type = FeatureFloodCountAux
variable = halo4
map_index = 4
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo5]
type = FeatureFloodCountAux
variable = halo5
map_index = 5
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo6]
type = FeatureFloodCountAux
variable = halo6
map_index = 6
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo7]
type = FeatureFloodCountAux
variable = halo7
map_index = 7
field_display = HALOS
flood_counter = grain_tracker
[../]
[./centroids]
type = FeatureFloodCountAux
variable = centroids
execute_on = timestep_end
field_display = CENTROID
flood_counter = grain_tracker
[../]
[]
[BCs]
# Boundary Condition block
[]
[Materials]
[./CuGrGr]
# Material properties
type = GBEvolution
T = 450 # Constant temperature of the simulation (for mobility calculation)
wGB = 125 # Width of the diffuse GB
GBmob0 = 2.5e-6 # m^4(Js) for copper from Schoenfelder1997
Q = 0.23 # eV for copper from Schoenfelder1997
GBenergy = 0.708 # J/m^2 from Schoenfelder1997
[../]
[]
[Postprocessors]
# Scalar postprocessors
[./dt]
# Outputs the current time step
type = TimestepSize
[../]
[./avg_grain_volumes]
type = AverageGrainVolume
feature_counter = grain_tracker
execute_on = 'initial timestep_end'
[../]
[]
[Executioner]
# Uses newton iteration to solve the problem.
type = Transient # Type of executioner, here it is transient with an adaptive time step
scheme = bdf2 # Type of time integration (2nd order backward euler), defaults to 1st order backward euler
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type -ksp_gmres_restart -mat_mffd_type'
petsc_options_value = 'hypre boomeramg 101 ds'
l_max_its = 30 # Max number of linear iterations
l_tol = 1e-4 # Relative tolerance for linear solves
nl_max_its = 40 # Max number of nonlinear iterations
nl_rel_tol = 1e-10 # Absolute tolerance for nonlienar solves
start_time = 0.0
num_steps = 15
dt = 300
[]
[Problem]
type = FEProblem
[]
[Outputs]
csv = true
exodus = true
[]
modules/stochastic_tools/test/tests/multiapps/commandline_control/master_single.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Distributions]
[uniform]
type = UniformDistribution
lower_bound = 5
upper_bound = 10
[]
[]
[Samplers]
[sample]
type = MonteCarloSampler
num_rows = 3
distributions = 'uniform'
execute_on = 'PRE_MULTIAPP_SETUP'
[]
[]
[MultiApps]
[sub]
type = FullSolveMultiApp
positions = '0 0 0
1 1 1
2 2 2'
input_files = 'sub.i'
[]
[]
[Controls]
[cmdline]
type = MultiAppCommandLineControl
multi_app = sub
sampler = sample
param_names = 'Mesh/xmax'
[]
[]
tutorials/darcy_thermo_mech/step02_darcy_pressure/tests/kernels/darcy_pressure/darcy_pressure.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
permeability = 0.8451e-9 # (m^2) 1mm spheres.
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First dot for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
test/tests/functions/image_function/image_3d.i
[Mesh]
type = GeneratedMesh
dim = 3
nx = 20
ny = 20
nz = 20
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
type = ImageFunction
file_base = stack/test
file_suffix = png
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
modules/stochastic_tools/test/tests/multiapps/commandline_control/sub.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Variables]
[u]
initial_condition = 1980
[]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Postprocessors]
[size]
type = AverageElementSize
execute_on = 'initial'
[]
[]
[Outputs]
csv = true
[]
test/tests/restart/restartable_types/restartable_types2.i
###########################################################
# This is a simple test of the restart/recover capability.
# The test object "RestartableTypesChecker" is used
# to reload data from a previous simulation written out
# with the object "RestartableTypes".
#
# See "restartable_types.i"
#
# @Requirement F1.60
###########################################################
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[UserObjects]
[./restartable_types]
type = RestartableTypesChecker
[../]
[]
[Problem]
type = FEProblem
solve = false
restart_file_base = restartable_types_out_cp/LATEST
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
modules/phase_field/test/tests/reconstruction/2phase_reconstruction.i
#
# In this test we set the initial condition of two variables
# based on solely the phase information in a given EBSD data file,
# ignoring the feature IDs entirely
#
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
# The following sections are extracted in the documentation in
# moose/docs/content/modules/phase_field/ICs/EBSD.md
[Mesh]
# Create a mesh representing the EBSD data
type = EBSDMesh
filename = 'Ti_2Phase_28x28_ebsd.txt'
[]
[UserObjects]
[./ebsd]
# Read in the EBSD data. Uses the filename given in the mesh block.
type = EBSDReader
[../]
[]
[Variables]
# Creates the two variables being initialized
[./c1]
[../]
[./c2]
[../]
[]
[ICs]
[./phase1_recon]
# Initializes the variable info from the ebsd data
type = ReconPhaseVarIC
ebsd_reader = ebsd
phase = 1
variable = c1
[../]
[./phase2_recon]
type = ReconPhaseVarIC
ebsd_reader = ebsd
phase = 2
variable = c2
[../]
[]
#ENDDOC - End of the file section that is included in the documentation. Do not change this line!
[AuxVariables]
[./PHI1]
family = MONOMIAL
order = CONSTANT
[../]
[./PHI]
family = MONOMIAL
order = CONSTANT
[../]
[./APHI2]
family = MONOMIAL
order = CONSTANT
[../]
[./PHI2]
family = MONOMIAL
order = CONSTANT
[../]
[./PHASE]
family = MONOMIAL
order = CONSTANT
[../]
[]
[AuxKernels]
[./phi1_aux]
type = EBSDReaderPointDataAux
variable = PHI1
ebsd_reader = ebsd
data_name = 'phi1'
execute_on = 'initial'
[../]
[./phi_aux]
type = EBSDReaderPointDataAux
variable = PHI
ebsd_reader = ebsd
data_name = 'phi'
execute_on = 'initial'
[../]
[./phi2_aux]
type = EBSDReaderPointDataAux
variable = PHI2
ebsd_reader = ebsd
data_name = 'phi2'
execute_on = 'initial'
[../]
[./phase_aux]
type = EBSDReaderPointDataAux
variable = PHASE
ebsd_reader = ebsd
data_name = 'phase'
execute_on = 'initial'
[../]
[]
[Executioner]
type = Transient
num_steps = 0
[]
[Outputs]
exodus = true
[]
tutorials/darcy_thermo_mech/step03_darcy_material/tests/kernels/darcy_pressure/darcy_pressure.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First dot for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Materials]
[pressure]
type = GenericConstantMaterial
prop_values = '0.8451e-9 7.98e-4'
prop_names = 'permeability viscosity'
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
tutorials/darcy_thermo_mech/step06_coupled_darcy_heat_conduction/problems/step6a_coupled.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 200
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
temperature = temperature
radius = 1
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
exodus = true
[]
modules/porous_flow/test/tests/fluidstate/theis_brineco2.i
# Two phase Theis problem: Flow from single source.
# Constant rate injection 2 kg/s
# 1D cylindrical mesh
# Initially, system has only a liquid phase, until enough gas is injected
# to form a gas phase, in which case the system becomes two phase.
#
# This test takes a few minutes to run, so is marked heavy
[Mesh]
type = GeneratedMesh
dim = 1
nx = 2000
xmax = 2000
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = Y
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[AuxVariables]
[./saturation_gas]
order = CONSTANT
family = MONOMIAL
[../]
[./x1]
order = CONSTANT
family = MONOMIAL
[../]
[./y0]
order = CONSTANT
family = MONOMIAL
[../]
[]
[AuxKernels]
[./saturation_gas]
type = PorousFlowPropertyAux
variable = saturation_gas
property = saturation
phase = 1
execute_on = timestep_end
[../]
[./x1]
type = PorousFlowPropertyAux
variable = x1
property = mass_fraction
phase = 0
fluid_component = 1
execute_on = timestep_end
[../]
[./y0]
type = PorousFlowPropertyAux
variable = y0
property = mass_fraction
phase = 1
fluid_component = 0
execute_on = timestep_end
[../]
[]
[Variables]
[./pgas]
initial_condition = 20e6
[../]
[./zi]
initial_condition = 0
[../]
[./xnacl]
initial_condition = 0.1
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pgas
[../]
[./flux0]
type = PorousFlowAdvectiveFlux
fluid_component = 0
variable = pgas
[../]
[./mass1]
type = PorousFlowMassTimeDerivative
fluid_component = 1
variable = zi
[../]
[./flux1]
type = PorousFlowAdvectiveFlux
fluid_component = 1
variable = zi
[../]
[./mass2]
type = PorousFlowMassTimeDerivative
fluid_component = 2
variable = xnacl
[../]
[./flux2]
type = PorousFlowAdvectiveFlux
fluid_component = 2
variable = xnacl
[../]
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pgas zi xnacl'
number_fluid_phases = 2
number_fluid_components = 3
[../]
[./pc]
type = PorousFlowCapillaryPressureConst
pc = 0
[../]
[./fs]
type = PorousFlowBrineCO2
brine_fp = brine
co2_fp = co2
capillary_pressure = pc
[../]
[]
[Modules]
[./FluidProperties]
[./co2sw]
type = CO2FluidProperties
[../]
[./co2]
type = TabulatedFluidProperties
fp = co2sw
[../]
[./water]
type = Water97FluidProperties
[../]
[./watertab]
type = TabulatedFluidProperties
fp = water
temperature_min = 273.15
temperature_max = 573.15
fluid_property_file = water_fluid_properties.csv
save_file = false
[../]
[./brine]
type = BrineFluidProperties
water_fp = watertab
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./brineco2]
type = PorousFlowFluidState
gas_porepressure = pgas
z = zi
temperature_unit = Celsius
xnacl = xnacl
capillary_pressure = pc
fluid_state = fs
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.2
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1e-12 0 0 0 1e-12 0 0 0 1e-12'
[../]
[./relperm_water]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
s_res = 0.1
sum_s_res = 0.1
[../]
[./relperm_gas]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 1
[../]
[]
[BCs]
[./rightwater]
type = DirichletBC
boundary = right
value = 20e6
variable = pgas
[../]
[]
[DiracKernels]
[./source]
type = PorousFlowSquarePulsePointSource
point = '0 0 0'
mass_flux = 2
variable = zi
[../]
[]
[Preconditioning]
[./smp]
type = SMP
full = true
[../]
[]
[Executioner]
type = Transient
solve_type = NEWTON
end_time = 1e5
[./TimeStepper]
type = IterationAdaptiveDT
dt = 1
growth_factor = 1.5
[../]
[]
[VectorPostprocessors]
[./line]
type = LineValueSampler
sort_by = x
start_point = '0 0 0'
end_point = '2000 0 0'
num_points = 10000
variable = 'pgas zi xnacl x1 saturation_gas'
execute_on = 'timestep_end'
[../]
[]
[Postprocessors]
[./pgas]
type = PointValue
point = '4 0 0'
variable = pgas
[../]
[./sgas]
type = PointValue
point = '4 0 0'
variable = saturation_gas
[../]
[./zi]
type = PointValue
point = '4 0 0'
variable = zi
[../]
[./massgas]
type = PorousFlowFluidMass
fluid_component = 1
[../]
[./x1]
type = PointValue
point = '4 0 0'
variable = x1
[../]
[./y0]
type = PointValue
point = '4 0 0'
variable = y0
[../]
[./xnacl]
type = PointValue
point = '4 0 0'
variable = xnacl
[../]
[]
[Outputs]
print_linear_residuals = false
perf_graph = true
[./csvout]
type = CSV
execute_on = timestep_end
execute_vector_postprocessors_on = final
[../]
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_1/ring1_template1_sm.i
[Mesh]
file = ring1_mesh.e
[]
[GlobalParams]
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x7]
type = NodalVariableValue
nodeid = 6
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y7]
type = NodalVariableValue
nodeid = 6
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-10
nl_rel_tol = 1e-9
l_max_its = 100
nl_max_its = 200
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x7 disp_y7 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
normalize_penalty = true
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_2/ring2_template1_sm.i
[Mesh]
file = ring2_mesh.e
[]
[GlobalParams]
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x5]
type = NodalVariableValue
nodeid = 4
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y5]
type = NodalVariableValue
nodeid = 4
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-9
nl_rel_tol = 1e-8
l_max_its = 100
nl_max_its = 200
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x5 disp_y5 disp_x9 disp_y9 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
normalize_penalty = true
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
test/tests/transfers/multiapp_copy_transfer/aux_to_aux/sub.i
[Problem]
type = FEProblem
solve = false
[]
[Mesh]
type = GeneratedMesh
dim = 2
[]
[AuxVariables/aux]
initial_condition = 1980
[]
[Executioner]
type = Transient
[]
[Outputs]
execute_on = 'FINAL'
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_1/ring1_mu_0_2_pen_sm.i
[Mesh]
file = ring1_mesh.e
[]
[GlobalParams]
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x7]
type = NodalVariableValue
nodeid = 6
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y7]
type = NodalVariableValue
nodeid = 6
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-10
nl_rel_tol = 1e-9
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = ring1_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = ring1_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x7 disp_y7 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
tangential_tolerance = 1e-3
friction_coefficient = 0.2
penalty = 1e+9
[../]
[]
tutorials/darcy_thermo_mech/step07_adaptivity/problems/step7d_adapt_blocks.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 40
ny = 4
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
uniform_refine = 3
[]
[MeshModifiers]
[bottom]
type = SubdomainBoundingBox
location = inside
bottom_left = '0 0 0'
top_right = '0.304 0.01285 0'
block_id = 1
[]
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
viscosity_file = data/water_viscosity.csv
density_file = data/water_density.csv
thermal_conductivity_file = data/water_thermal_conductivity.csv
specific_heat_file = data/water_specific_heat.csv
[column_bottom]
type = PackedColumn
block = 1
radius = 1.15
temperature = temperature
fluid_viscosity_file = ${viscosity_file}
fluid_density_file = ${density_file}
fluid_thermal_conductivity_file = ${thermal_conductivity_file}
fluid_specific_heat_file = ${specific_heat_file}
[]
[column_top]
type = PackedColumn
block = 0
radius = 1
temperature = temperature
porosity = '0.25952 + 0.7*x/0.304'
fluid_viscosity_file = ${viscosity_file}
fluid_density_file = ${density_file}
fluid_thermal_conductivity_file = ${thermal_conductivity_file}
fluid_specific_heat_file = ${specific_heat_file}
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Adaptivity]
marker = error_frac
max_h_level = 3
[Indicators]
[temperature_jump]
type = GradientJumpIndicator
variable = temperature
scale_by_flux_faces = true
[]
[]
[Markers]
[error_frac]
type = ErrorFractionMarker
coarsen = 0.025
indicator = temperature_jump
refine = 0.9
[]
[]
[]
[Outputs]
[out]
type = Exodus
output_material_properties = true
[]
[]
test/tests/multiapps/command_line/sub.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Variables]
[u]
initial_condition = 1980
[]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Outputs]
exodus = true
[]
test/tests/auxkernels/pp_depend/pp_depend.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
[../]
[]
[AuxVariables]
[./pp_aux]
[../]
[]
[Functions]
[./t_func]
type = ParsedFunction
value = t
[../]
[]
[Kernels]
[./diff]
type = CoefDiffusion
variable = u
coef = 0.01
[../]
[]
[AuxKernels]
[./pp_aux]
type = PostprocessorAux
variable = pp_aux
execute_on = timestep_end
pp = t_pp
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[Postprocessors]
[./t_pp]
type = FunctionValuePostprocessor
function = t_func
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
solve_type = PJFNK
dt = 1
num_steps = 5
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
test/tests/restart/pointer_restart_errors/pointer_load_error.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[UserObjects]
[./restartable_types]
type = PointerLoadError
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
checkpoint = true
[]
test/tests/transfers/multiapp_copy_transfer/constant_monomial_from_sub/master.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
family = MONOMIAL
order = CONSTANT
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[MultiApps]
[./sub]
type = FullSolveMultiApp
input_files = sub.i
execute_on = initial
[../]
[]
[Transfers]
[./from_sub]
type = MultiAppCopyTransfer
direction = from_multiapp
source_variable = aux
variable = u
multi_app = sub
[../]
[]
[Outputs]
exodus = true
[]
tutorials/darcy_thermo_mech/step10_multiapps/tests/auxkernels/corrosion/corrosion.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
ymax = 0.1
xmax = 0.1
uniform_refine = 0
[]
[Adaptivity]
max_h_level = 3
initial_steps = 5
cycles_per_step = 2
initial_marker = error_marker
marker = error_marker
[Indicators]
[phi_jump]
type = GradientJumpIndicator
variable = phi
[]
[]
[Markers]
[error_marker]
type = ErrorFractionMarker
indicator = phi_jump
refine = 0.9
[]
[]
[]
[Variables]
[temperature]
initial_condition = 300
[]
[]
[AuxVariables]
[phi]
[]
[]
[AuxKernels]
[corrosion]
type = RandomCorrosion
execute_on = 'timestep_end'
variable = phi
reference_temperature = 300
temperature = 301
[]
[]
[Kernels]
[heat_conduction]
type = HeatConduction
variable = temperature
[]
[]
[BCs]
[left]
type = PostprocessorDirichletBC
variable = temperature
boundary = left
postprocessor = 301
[]
[right]
type = NeumannBC
variable = temperature
boundary = right
value = 100 # prescribed flux
[]
[]
[Materials]
[column]
type = PackedColumn
temperature = temperature
radius = 1 # mm
phase = phi
outputs = exodus
output_properties = porosity
[]
[]
[Problem]
type = FEProblem
[]
[Postprocessors]
[k_eff]
type = ThermalConductivity
variable = temperature
T_hot = 301
flux = 100
dx = 0.1
boundary = right
length_scale = 1
[]
[]
[Executioner]
type = Transient
num_steps = 5
dt = 0.5
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
execute_on = 'initial timestep_end'
exodus = true
[console]
type = Console
execute_postprocessors_on = 'timestep_begin timestep_end'
[]
[]
[ICs]
[close_pack]
radius = 0.01
outvalue = 0 # water
variable = phi
invalue = 1 #steel
type = ClosePackIC
[]
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_1/ring1_mu_0_2_pen.i
[GlobalParams]
volumetric_locking_correction = true
displacements = 'disp_x disp_y'
[]
[Mesh]
file = ring1_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x7]
type = NodalVariableValue
nodeid = 6
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y7]
type = NodalVariableValue
nodeid = 6
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-10
nl_rel_tol = 1e-9
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = ring1_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = ring1_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x7 disp_y7 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
tangential_tolerance = 1e-3
friction_coefficient = 0.2
penalty = 1e+9
[../]
[]
tutorials/darcy_thermo_mech/step05_heat_conduction/problems/step5b_transient.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[Kernels]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[]
[BCs]
[inlet_temperature]
type = DirichletBC
variable = temperature
boundary = left
value = 350 # (K)
[]
[outlet_temperature]
type = DirichletBC
variable = temperature
boundary = right
value = 300 # (K)
[]
[]
[Materials]
[steel]
type = GenericConstantMaterial
prop_names = 'thermal_conductivity specific_heat density'
prop_values = '18 0.466 8000' # W/m*K, J/kg-K, kg/m^3 @ 296K
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
num_steps = 10
solve_type = NEWTON
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
modules/phase_field/test/tests/initial_conditions/ClosePackIC_3D.i
[Mesh]
type = GeneratedMesh
dim = 3
nx = 5
ny = 5
nz = 5
xmax = 0.5
ymax = .5
zmax = 0.5
uniform_refine = 3
[]
[Variables]
[./u]
[../]
[]
[AuxVariables]
[./phi]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
execute_on = 'timestep_end'
exodus = true
[]
[ICs]
[./close_pack]
radius = 0.1
outvalue = 0
variable = phi
invalue = 1
type = ClosePackIC
[../]
[]
modules/phase_field/test/tests/feature_flood_test/parallel_feature_count.i
[Mesh]
type = ImageMesh
dim = 2
file = spiral_16x16.png
scale_to_one = false
[]
[Variables]
[./u]
order = CONSTANT
family = MONOMIAL
[../]
[]
[AuxVariables]
[./feature]
order = CONSTANT
family = MONOMIAL
[../]
[./proc_id]
order = CONSTANT
family = MONOMIAL
[../]
[./feature_ghost]
order = CONSTANT
family = MONOMIAL
[../]
[]
[AuxKernels]
[./nodal_flood_aux]
type = FeatureFloodCountAux
variable = feature
flood_counter = flood_count_pp
execute_on = 'initial timestep_end'
[../]
[./proc_id]
type = ProcessorIDAux
variable = proc_id
execute_on = 'initial timestep_end'
[../]
[./ghost]
type = FeatureFloodCountAux
variable = feature_ghost
field_display = GHOSTED_ENTITIES
flood_counter = flood_count_pp
execute_on = 'initial timestep_end'
[../]
[]
[Functions]
[./tif]
type = ImageFunction
component = 0
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = tif
variable = u
[../]
[]
[Postprocessors]
[./flood_count_pp]
type = FeatureFloodCount
variable = u
threshold = 1.0
execute_on = 'initial timestep_end'
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Outputs]
csv = true
[]
tutorials/darcy_thermo_mech/step06_coupled_darcy_heat_conduction/problems/step6b_transient_inflow.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 200
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[Functions]
[inlet_function]
type = ParsedFunction
value = 2000*sin(0.466*pi*t) # Inlet signal from Fig. 3
[]
[outlet_function]
type = ParsedFunction
value = 2000*cos(0.466*pi*t) # Outlet signal from Fig. 3
[]
[]
[BCs]
[inlet]
type = FunctionDirichletBC
variable = pressure
boundary = left
function = inlet_function
[]
[outlet]
type = FunctionDirichletBC
variable = pressure
boundary = right
function = outlet_function
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
temperature = temperature
fluid_viscosity_file = data/water_viscosity.csv
fluid_density_file = data/water_density.csv
fluid_thermal_conductivity_file = data/water_thermal_conductivity.csv
fluid_specific_heat_file = data/water_specific_heat.csv
outputs = exodus
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,(2*pi/(0.466*pi))/16)' # dt to always hit the peaks of sine/cosine BC
[]
[]
[Outputs]
exodus = true
[]
test/tests/functions/image_function/flip_dual.i
[Mesh]
uniform_refine = 1
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 20
ny = 40
ymax = 2
[]
[./top]
type = SubdomainBoundingBoxGenerator
input = gen
top_right = '1 2 0'
bottom_left = '0 1 0'
block_id = 1
[../]
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./top]
type = ImageFunction
origin = '0 1 0'
file_base = stack/test
file_suffix = png
flip_y = true
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
dimensions = '1 1 0'
[../]
[./bottom]
type = ImageFunction
origin = '0 0 0'
file_base = stack/test
file_suffix = png
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
dimensions = '1 1 0'
[../]
[]
[ICs]
[./top_ic]
function = top
variable = u
type = FunctionIC
block = 1
[../]
[./bottom_ic]
function = bottom
variable = u
type = FunctionIC
block = 0
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
test/tests/mesh_modifiers/subdomain_bounding_box/oriented_subdomain_bounding_box_outside.i
[Mesh]
type = GeneratedMesh
dim = 3
xmin = -6
xmax = 4
nx = 10
ymin = -2
ymax = 10
ny = 12
zmin = -5
zmax = 7
nz = 12
[]
[MeshModifiers]
[./subdomains]
type = OrientedSubdomainBoundingBox
center = '-1 4 1'
width = 5
length = 10
height = 4
width_direction = '2 1 0'
length_direction = '-1 2 2'
block_id = 10
location = OUTSIDE
[../]
[]
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Variables]
[./u]
[../]
[]
[Materials]
[./mat10]
type = GenericConstantMaterial
block = 10
outputs = all
prop_values = 6.24
prop_names = prop
[../]
[./mat0]
type = GenericConstantMaterial
block = 0
prop_names = prop
prop_values = 0
[../]
[]
[Executioner]
type = Steady
solve_type = PJFNK
[]
[Outputs]
exodus = true
[]
test/tests/restart/pointer_restart_errors/pointer_load_error2.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[UserObjects]
[./restartable_types]
type = PointerLoadError
[../]
[]
[Problem]
type = FEProblem
solve = false
restart_file_base = pointer_load_error_out_cp/0001
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[./out]
type = Checkpoint
num_files = 1
[../]
[]
test/tests/mesh_modifiers/assign_subdomain_id/assign_subdomain_id.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[MeshModifiers]
[./assign_id]
type = AssignSubdomainID
subdomain_id = 3
[../]
[]
[Variables]
[./u]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_2/cyl2_template1_sm.i
#
# This input file is a template for both the frictionless and glued test
# variations for the current problem geometry. In order to create an input
# file to run outside the runtest framework, look at the tests file and add the
# appropriate input file lines from the cli_args line.
#
[Mesh]
file = cyl2_mesh.e
[]
[GlobalParams]
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x5]
type = NodalVariableValue
nodeid = 4
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y5]
type = NodalVariableValue
nodeid = 4
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
#Preconditioned JFNK (default)
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x5 disp_y5 disp_x9 disp_y9 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
normalize_penalty = true
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
test/tests/postprocessors/difference_pps/difference_depend_check.i
[Mesh]
type = GeneratedMesh
dim = 2
xmin = 0
xmax = 1
ymin = 0
ymax = 1
nx = 2
ny = 2
[]
[Variables]
[./u]
[../]
[]
[AuxVariables]
[./v]
[../]
[]
[AuxKernels]
[./one]
type = ConstantAux
variable = v
value = 1
[../]
[]
[Postprocessors]
# This postprocessor is listed first on purpose to give the resolver something to do
[./diff]
type = DifferencePostprocessor
value1 = nodes
value2 = elems
execute_on = 'initial timestep_end'
[../]
[./nodes]
type = NumNodes
execute_on = 'initial timestep_end'
[../]
[./elems]
type = NumElems
execute_on = 'initial timestep_end'
[../]
[]
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Executioner]
type = Steady
[]
[Outputs]
csv = true
[]
test/tests/tag/2d_diffusion_tag_matrix.i
[Mesh]
file = square.e
[]
[Variables]
[./u]
order = FIRST
family = LAGRANGE
[../]
[]
[AuxVariables]
[./tag_variable1]
order = FIRST
family = LAGRANGE
[../]
[./tag_variable2]
order = FIRST
family = LAGRANGE
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
extra_matrix_tags = 'mat_tag1 mat_tag2'
[../]
[]
[AuxKernels]
[./TagMatrixAux1]
type = TagMatrixAux
variable = tag_variable1
v = u
matrix_tag = mat_tag1
[../]
[./TagMatrixAux2]
type = TagMatrixAux
variable = tag_variable2
v = u
matrix_tag = mat_tag2
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = 1
value = 0
extra_matrix_tags = mat_tag1
[../]
[./right]
type = DirichletBC
variable = u
boundary = 2
value = 1
extra_matrix_tags = mat_tag2
[../]
[]
[Problem]
type = FEProblem
extra_tag_matrices = 'mat_tag1 mat_tag2'
[]
[Executioner]
type = Steady
solve_type = 'NEWTON'
[]
[Outputs]
file_base = tag_matrix_out
exodus = true
[]
test/tests/indicators/value_jump_indicator/value_jump_indicator_test.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Adaptivity]
[./Indicators]
[./error]
type = ValueJumpIndicator
variable = something
[../]
[../]
[]
[Variables]
[./u]
order = FIRST
family = LAGRANGE
[../]
[]
[ICs]
[./leftright]
type = BoundingBoxIC
variable = something
inside = 1
y2 = 1
y1 = 0
x2 = 0.5
x1 = 0
[../]
[]
[AuxVariables]
[./something]
order = CONSTANT
family = MONOMIAL
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = 'left'
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = 'right'
value = 1
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
solve_type = PJFNK
[]
[Outputs]
exodus = true
[]
test/tests/markers/block_restricted/marker_block.i
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 2
ny = 2
xmax = 5
ymax = 5
[]
[./lower_block]
input = gen
type = SubdomainBoundingBoxGenerator
top_right = '5 3 0'
bottom_left = '0 0 0'
block_id = 0
[../]
[./upper_block]
input = lower_block
type = SubdomainBoundingBoxGenerator
top_right = '5 5 0'
bottom_left = '0 3 0'
block_id = 1
[../]
[]
[Adaptivity]
initial_steps = 2
initial_marker = marker
[./Markers]
[./marker]
type = UniformMarker
block = 0
mark = REFINE
[../]
[../]
[]
[Variables]
[./u]
initial_condition = 0
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Outputs]
exodus = true
[]
test/tests/controls/restrict_exec_flag/sub.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Variables]
[u]
initial_condition = 1980
[]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Outputs]
exodus = true
[]
tutorials/darcy_thermo_mech/step03_darcy_material/tests/materials/packed_column/packed_column.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
# No parameters necessary because the values will come from the material system
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First dot for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Materials]
[column]
type = PackedColumn
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
modules/phase_field/test/tests/phase_field_crystal/PFC_IC/PFC_IC_FCC_test.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 100
xmax = 10
ymax = 10
[]
[Variables]
[./rho]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = rho
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 0
[]
[Outputs]
exodus = true
[]
[ICs]
[./rho_IC]
y2 = 8.75
lc = 5
y1 = 1.25
x2 = 8.75
crystal_structure = FCC
variable = rho
x1 = 1.25
type = PFCFreezingIC
min = .3
max = .7
[../]
[]
test/tests/transfers/multiapp_userobject_transfer/sub.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 4
ny = 8
xmax = 0.1
ymax = 0.5
[]
[Variables]
[./u]
initial_condition = 1
[../]
[]
[AuxVariables]
[./layered_average_value]
order = CONSTANT
family = MONOMIAL
[../]
[]
[Functions]
[./axial_force]
type = ParsedFunction
value = 1000*y
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[./td]
type = TimeDerivative
variable = u
[../]
[./force]
type = BodyForce
variable = u
function = axial_force
[../]
[]
[AuxKernels]
[./layered_aux]
type = SpatialUserObjectAux
variable = layered_average_value
execute_on = timestep_end
user_object = layered_average
[../]
[]
[BCs]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[UserObjects]
[./layered_average]
type = LayeredAverage
variable = u
direction = y
num_layers = 4
[../]
[]
[Executioner]
type = Transient
num_steps = 1
dt = 0.001
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
[Problem]
coord_type = rz
type = FEProblem
[]
test/tests/transfers/multiapp_copy_transfer/linear_lagrange_from_sub/master.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[MultiApps]
[./sub]
type = FullSolveMultiApp
input_files = sub.i
execute_on = initial
[../]
[]
[Transfers]
[./from_sub]
type = MultiAppCopyTransfer
direction = from_multiapp
source_variable = u
variable = u
multi_app = sub
[../]
[]
[Outputs]
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_4/ring4_mu_0_2_pen.i
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Mesh]
file = ring4_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x16]
type = NodalVariableValue
nodeid = 15
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y16]
type = NodalVariableValue
nodeid = 15
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-9
nl_rel_tol = 1e-8
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-3
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = ring4_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = ring4_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x9 disp_y9 disp_x16 disp_y16 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
friction_coefficient = 0.2
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
modules/phase_field/test/tests/initial_conditions/PolycrystalVoronoiVoidIC_periodic_fromfile.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 85
ny = 85
nz = 0
xmax = 250
ymax = 250
zmax = 0
elem_type = QUAD4
[]
[GlobalParams]
op_num = 8
var_name_base = gr
numbub = 15
bubspac = 22
radius = 8
int_width = 10
invalue = 1
outvalue = 0.1
file_name = 'grains.txt'
[]
[Variables]
[./c]
[../]
[./w]
scaling = 1.0e4
[../]
[./PolycrystalVariables]
[../]
[]
[ICs]
[./PolycrystalICs]
[./PolycrystalVoronoiVoidIC]
polycrystal_ic_uo = voronoi
[../]
[../]
[./c_IC]
variable = c
type = PolycrystalVoronoiVoidIC
structure_type = voids
polycrystal_ic_uo = voronoi
[../]
[]
[UserObjects]
[./voronoi]
type = PolycrystalVoronoi
rand_seed = 12444
int_width = 0
[../]
[]
[BCs]
[./Periodic]
[./all]
auto_direction = 'x y'
[../]
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 0
[]
[Outputs]
exodus = true
[]
test/tests/markers/oriented_box_marker/obm.i
# checks that OrientedBoxMarker behaves as desired
[Mesh]
type = GeneratedMesh
dim = 3
xmin = -6
xmax = 4
nx = 10
ymin = -2
ymax = 10
ny = 12
zmin = -5
zmax = 7
nz = 12
[]
[Variables]
[./u]
[../]
[]
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Executioner]
type = Transient
solve_type = PJFNK
end_time = 1
[]
[Adaptivity]
marker = obm
[./Markers]
[./obm]
type = OrientedBoxMarker
center = '-1 4 1'
width = 5
length = 10
height = 4
width_direction = '2 1 0'
length_direction = '-1 2 2'
inside = refine
outside = do_nothing
[../]
[../]
[]
[Outputs]
exodus = true
[]
test/tests/functions/image_function/image_2d.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 20
ny = 20
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
type = ImageFunction
file_base = stack/test
file_suffix = png
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
test/tests/functions/image_function/image_2d_elemental.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 20
ny = 20
[]
[Variables]
[./u]
order = CONSTANT
family = MONOMIAL
[../]
[]
[Functions]
[./image_func]
type = ImageFunction
file_base = stack/test
file_suffix = png
# file range is parsed as a vector of unsigned. If it only has 1
# entry, only a single file is read.
file_range = '0'
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Steady
[]
[Outputs]
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_2/cyl2_template1.i
#
# This input file is a template for both the frictionless and glued test
# variations for the current problem geometry. In order to create an input
# file to run outside the runtest framework, look at the tests file and add the
# appropriate input file lines from the cli_args line.
#
[GlobalParams]
volumetric_locking_correction = true
displacements = 'disp_x disp_y'
[]
[Mesh]
file = cyl2_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x5]
type = NodalVariableValue
nodeid = 4
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y5]
type = NodalVariableValue
nodeid = 4
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x5 disp_y5 disp_x9 disp_y9 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
normalize_penalty = true
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
test/tests/geomsearch/patch_update_strategy/auto.i
[Mesh]
type = FileMesh
file = long_range.e
dim = 2
patch_update_strategy = auto
displacements = 'disp_x disp_y'
[]
[Variables]
[./u]
block = right
[../]
[]
[AuxVariables]
[./linear_field]
[../]
[./receiver]
# The field to transfer into
[../]
[./disp_x]
[../]
[./disp_y]
[../]
[./elemental_reciever]
order = CONSTANT
family = MONOMIAL
[../]
[]
[Kernels]
[./diff]
type = CoefDiffusion
variable = u
coef = 1
[../]
[./time]
type = TimeDerivative
variable = u
[../]
[]
[AuxKernels]
[./linear_in_y]
# This just gives us something to transfer that varies in y so we can ensure the transfer is working properly...
type = FunctionAux
variable = linear_field
function = y
execute_on = initial
[../]
[./right_to_left]
type = GapValueAux
variable = receiver
paired_variable = linear_field
paired_boundary = rightleft
execute_on = timestep_end
boundary = leftright
[../]
[./y_displacement]
type = FunctionAux
variable = disp_y
function = t
execute_on = 'linear timestep_begin'
block = left
[../]
[./elemental_right_to_left]
type = GapValueAux
variable = elemental_reciever
paired_variable = linear_field
paired_boundary = rightleft
boundary = leftright
[../]
[]
[BCs]
[./top]
type = DirichletBC
variable = u
boundary = righttop
value = 1
[../]
[./bottom]
type = DirichletBC
variable = u
boundary = rightbottom
value = 0
[../]
[]
[Problem]
type = FEProblem
kernel_coverage_check = false
[]
[Executioner]
type = Transient
num_steps = 30
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
test/tests/functions/image_function/flip.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 20
ny = 20
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
type = ImageFunction
file_base = stack/test
file_suffix = png
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
flip_x = true
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_3/cyl3_template1.i
#
# This input file is a template for both the frictionless and glued test
# variations for the current problem geometry. In order to create an input
# file to run outside the runtest framework, look at the tests file and add the
# appropriate input file lines from the cli_args line.
#
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Mesh]
file = cyl3_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x11]
type = NodalVariableValue
nodeid = 10
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y11]
type = NodalVariableValue
nodeid = 10
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x11 disp_y11 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
test/tests/misc/block_boundary_material_check/dgkernel_check_boundary.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Variables]
[./u]
[../]
[]
[DGKernels]
[./dg]
type = MatDGKernel
mat_prop = 'foo'
variable = u
boundary = 1
[../]
[]
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Executioner]
type = Steady
[]
[Outputs]
[]
modules/solid_mechanics/test/tests/interaction_integral_benchmark/input.i
# Uses InteractionIntegralBenchmarkBC to test the mixed-mode stress intensity
# factor capability. InteractionIntegralBenchmarkBC applies a displacement
# field for which KI = KII = KIII = 1.0. Using the option 2d = true gives a
# q field that is constant along the tangent and returns Ki = 1.0 for all i.
# To get the correct value for all nodes with 2d = false, the mesh around the
# crack tip must be refined and the q-function radii must be reduced by at
# least two orders of magnitude.
[GlobalParams]
order = FIRST
family = LAGRANGE
disp_x = disp_x
disp_y = disp_y
disp_z = disp_z
displacements = 'disp_x disp_y disp_z'
[]
[Mesh]
file = 360degree_model.e
[]
[Problem]
type = FEProblem
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[./disp_z]
[../]
[]
[Functions]
[./kifunc]
type = PiecewiseLinear
x = '0.0 1.0 2.0'
y = '0.0 1.0 2.0'
[../]
[]
[DomainIntegral]
integrals = 'JIntegral InteractionIntegralKI InteractionIntegralKII InteractionIntegralKIII'
boundary = 1001
crack_direction_method = CrackDirectionVector
crack_direction_vector = '1 0 0'
radius_inner = '0.5 1.0 1.5 2.0'
radius_outer = '1.0 1.5 2.0 2.5'
youngs_modulus = 30000
poissons_ratio = 0.3
block = 1
2d = true
axis_2d = 2
equivalent_k = True
incremental = true
solid_mechanics = true
[]
[AuxVariables]
[./stress_xx] # stress aux variables are defined for output; this is a way to get integration point variables to the output file
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./vonmises]
order = CONSTANT
family = MONOMIAL
[../]
[./dq_x]
order = CONSTANT
family = MONOMIAL
[../]
[./dq_y]
order = CONSTANT
family = MONOMIAL
[../]
[./dq_z]
order = CONSTANT
family = MONOMIAL
[../]
[]
[SolidMechanics]
[./solid]
[../]
[]
[AuxKernels]
[./stress_xx] # computes stress components for output
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = MaterialTensorAux
tensor = stress
variable = stress_zz
index = 2
execute_on = timestep_end
[../]
[./vonmises]
type = MaterialTensorAux
tensor = stress
variable = vonmises
quantity = vonmises
execute_on = timestep_end
[../]
[]
[BCs]
[./all_x]
type = InteractionIntegralBenchmarkBC
variable = disp_x
component = x
boundary = 1
KI_function = kifunc
KII_function = 1.0
KIII_function = 1.0
youngs_modulus = 30000
poissons_ratio = 0.3
crack_front_definition = crackFrontDefinition
crack_front_point_index = 0
[../]
[./all_y]
type = InteractionIntegralBenchmarkBC
variable = disp_y
component = y
boundary = 1
KI_function = kifunc
KII_function = 1.0
KIII_function = 1.0
youngs_modulus = 30000
poissons_ratio = 0.3
crack_front_definition = crackFrontDefinition
crack_front_point_index = 0
[../]
[./all_z]
type = InteractionIntegralBenchmarkBC
variable = disp_z
component = z
boundary = 1
KI_function = kifunc
KII_function = 1.0
KIII_function = 1.0
youngs_modulus = 30000
poissons_ratio = 0.3
crack_front_definition = crackFrontDefinition
crack_front_point_index = 0
[../]
[] # BCs
[Materials]
[./stiffStuff]
type = Elastic
block = 1
disp_x = disp_x
disp_y = disp_y
disp_z = disp_z
youngs_modulus = 30000
poissons_ratio = 0.3
compute_JIntegral = true
[../]
[]
[Executioner]
type = Transient
# Two sets of linesearch options are for petsc 3.1 and 3.3 respectively
#Preconditioned JFNK (default)
solve_type = 'PJFNK'
petsc_options = '-snes_ksp_ew'
petsc_options_iname = '-ksp_gmres_restart'
petsc_options_value = '101'
line_search = 'none'
l_max_its = 50
nl_max_its = 20
nl_abs_tol = 1e-3
l_tol = 1e-2
start_time = 0.0
dt = 1
end_time = 2
num_steps = 2
[]
[Postprocessors]
[./_dt]
type = TimestepSize
[../]
[./nl_its]
type = NumNonlinearIterations
[../]
[./lin_its]
type = NumLinearIterations
[../]
[]
[Outputs]
execute_on = 'timestep_end'
file_base = 360degree_model_out
exodus = true
csv = true
[]
modules/phase_field/test/tests/initial_conditions/RampIC.i
[Mesh]
type = GeneratedMesh
dim = 1
nx = 30
xmax = 13
xmin = -5
elem_type = EDGE
[]
[Variables]
[./c]
order = FIRST
family = LAGRANGE
scaling = 1e1
[./InitialCondition]
type = RampIC
variable = c
value_left = -0.2
value_right = 1.3
[../]
[../]
[]
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
execute_on = 'timestep_end'
exodus = true
[]
test/tests/problems/no_solve/no_solve.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[AuxVariables]
[./t]
[../]
[]
[AuxKernels]
[./t]
type = FunctionAux
variable = t
function = t
execute_on = timestep_end
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 5
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_3/cyl3_mu_0_2_pen_sm.i
[Mesh]
file = cyl3_mesh.e
[]
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x11]
type = NodalVariableValue
nodeid = 10
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y11]
type = NodalVariableValue
nodeid = 10
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = cyl3_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = cyl3_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x11 disp_y11 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
tangential_tolerance = 1e-3
friction_coefficient = 0.2
penalty = 1e+9
[../]
[]
tutorials/darcy_thermo_mech/step06_coupled_darcy_heat_conduction/tests/materials/packed_column/packed_column.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First dot for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Materials]
[column]
type = PackedColumn
temperature = 303
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
tutorials/darcy_thermo_mech/step07_adaptivity/problems/step7c_adapt.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 30
ny = 3
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
uniform_refine = 3
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
temperature = temperature
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
exodus = true
[]
[Adaptivity]
marker = error_frac
max_h_level = 3
[Indicators]
[temperature_jump]
type = GradientJumpIndicator
variable = temperature
scale_by_flux_faces = true
[]
[]
[Markers]
[error_frac]
type = ErrorFractionMarker
coarsen = 0.15
indicator = temperature_jump
refine = 0.7
[]
[]
[]
modules/stochastic_tools/test/tests/multiapps/commandline_control/master_wrong_num_params.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Distributions]
[uniform]
type = UniformDistribution
lower_bound = 5
upper_bound = 10
[]
[]
[Samplers]
[sample]
type = MonteCarloSampler
num_rows = 3
distributions = 'uniform uniform'
execute_on = PRE_MULTIAPP_SETUP
[]
[]
[MultiApps]
[sub]
type = FullSolveMultiApp
positions = '0 0 0
1 1 1
2 2 2'
input_files = 'sub.i'
[]
[]
[Controls]
[cmdline]
type = MultiAppCommandLineControl
multi_app = sub
sampler = sample
param_names = 'Mesh/xmax Mesh/ymax Mesh/zmax'
[]
[]
test/tests/transfers/multiapp_copy_transfer/multivariable_copy/master.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
# Create two variables
[./u]
[../]
[./v]
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[MultiApps]
[./sub]
type = FullSolveMultiApp
input_files = sub.i
execute_on = initial
[../]
[]
[Transfers]
# Transfer both variables by inputting a vector of their names
[./from_sub]
type = MultiAppCopyTransfer
direction = from_multiapp
source_variable = 'u v'
variable = 'u v'
multi_app = sub
[../]
[]
[Outputs]
exodus = true
[]
modules/stochastic_tools/test/tests/multiapps/batch_commandline_control/master_wrong_size.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[MultiApps]
[sub]
type = FullSolveMultiApp
positions = '0 0 0
1 1 1'
input_files = 'sub.i'
[]
[]
[Distributions]
[uniform]
type = UniformDistribution
lower_bound = 5
upper_bound = 10
[]
[]
[Samplers]
[sample]
type = MonteCarloSampler
num_rows = 10
distributions = 'uniform'
execute_on = 'initial timestep_end'
[]
[]
[Controls]
[cmdline]
type = MultiAppCommandLineControl
multi_app = sub
sampler = sample
arguments = 'Mesh/nx'
[]
[]
test/tests/misc/block_user_object_check/coupled_check.i
[Mesh]
[./generator]
type = GeneratedMeshGenerator
dim = 2
nx = 10
ny = 5
[../]
[./left_block]
type = SubdomainBoundingBoxGenerator
input = generator
block_id = 1
bottom_left = '0 0 0'
top_right = '0.5 1 0'
[../]
[./right_block]
type = SubdomainBoundingBoxGenerator
input = left_block
block_id = 2
bottom_left = '0.5 0 0'
top_right = '1 1 0'
[../]
[]
[Variables]
[./var_0]
[../]
[./var_1]
block = 1
initial_condition = 100
[../]
[./var_2]
block = 2
initial_condition = 200
[../]
[]
[Kernels]
[./obj]
type = CoupledConvection
variable = var_0
velocity_vector = var_1
#block = 1 # this is being tested
[../]
[]
[Problem]
type = FEProblem
kernel_coverage_check = true
solve = false
[]
[Executioner]
type = Steady
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_2/cyl2_mu_0_2_pen_sm.i
[Mesh]
file = cyl2_mesh.e
[]
[GlobalParams]
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x5]
type = NodalVariableValue
nodeid = 4
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y5]
type = NodalVariableValue
nodeid = 4
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
#Preconditioned JFNK (default)
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = cyl2_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = cyl2_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x5 disp_y5 disp_x9 disp_y9 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
tangential_tolerance = 1e-3
friction_coefficient = 0.2
penalty = 1e+9
[../]
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_2/ring2_mu_0_2_pen.i
[GlobalParams]
volumetric_locking_correction = true
displacements = 'disp_x disp_y'
[]
[Mesh]
file = ring2_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x5]
type = NodalVariableValue
nodeid = 4
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y5]
type = NodalVariableValue
nodeid = 4
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-10
nl_rel_tol = 1e-8
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = ring2_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = ring2_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x5 disp_y5 disp_x9 disp_y9 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
friction_coefficient = 0.2
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
test/tests/functions/image_function/image_mesh_2d.i
[Mesh]
type = ImageMesh
dim = 2
file = stack/test_00.png
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
# ImageFunction gets its file range parameters from ImageMesh,
# when it is present. This prevents duplicating information in
# input files.
type = ImageFunction
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
tutorials/darcy_thermo_mech/step06_coupled_darcy_heat_conduction/problems/step6c_decoupled.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 200
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[pressure]
[]
[]
[AuxKernels]
[pressure]
type = FunctionAux
variable = pressure
function = 't*x*x*y'
execute_on = timestep_end
[]
[]
[Kernels]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[BCs]
[inlet_temperature]
type = DirichletBC
variable = temperature
boundary = left
value = 350
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
temperature = 293.15 # 20C
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
num_steps = 300
dt = 0.1
solve_type = NEWTON
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
test/tests/misc/block_boundary_material_check/dgkernel_check_block.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Variables]
[./u]
[../]
[]
[DGKernels]
[./dg]
type = MatDGKernel
mat_prop = 'foo'
variable = u
block = 0
[../]
[]
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Executioner]
type = Steady
[]
[Outputs]
[]
test/tests/functions/image_function/threshold_adapt_parallel.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 2
ny = 2
parallel_type = distributed
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
type = ImageFunction
file_base = stack/test
file_suffix = png
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
threshold = 2.7e4
upper_value = 1
lower_value = -1
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Adaptivity]
max_h_level = 5
initial_steps = 5
initial_marker = marker
[./Indicators]
[./indicator]
type = GradientJumpIndicator
variable = u
[../]
[../]
[./Markers]
[./marker]
type = ErrorFractionMarker
indicator = indicator
refine = 0.9
[../]
[../]
[]
[Outputs]
[]
modules/phase_field/test/tests/reconstruction/2phase_reconstruction4.i
#
# In this test we set the initial condition of a set of order parameters
# by pulling out the only grains from given EBSD data file that belong to a specified phase
#
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Mesh]
type = EBSDMesh
filename = ebsd_40x40_2_phase.txt
[]
[GlobalParams]
op_num = 6
var_name_base = gr
[]
[UserObjects]
[./ebsd_reader]
type = EBSDReader
[../]
[./ebsd]
type = PolycrystalEBSD
coloring_algorithm = bt
ebsd_reader = ebsd_reader
phase = 2
output_adjacency_matrix = true
[../]
[./grain_tracker]
type = GrainTracker
polycrystal_ic_uo = ebsd
remap_grains = false
[../]
[]
[AuxVariables]
[./var_indices]
family = MONOMIAL
order = CONSTANT
[../]
[]
[AuxKernels]
[./var_indices]
type = FeatureFloodCountAux
variable = var_indices
flood_counter = grain_tracker
field_display = VARIABLE_COLORING
[../]
[]
[ICs]
[./PolycrystalICs]
[./PolycrystalColoringIC]
polycrystal_ic_uo = ebsd
[../]
[../]
[]
[Variables]
[./PolycrystalVariables]
[../]
[]
[Executioner]
type = Transient
num_steps = 0
[]
[Outputs]
exodus = true
[]
modules/phase_field/test/tests/MultiSmoothCircleIC/test_problem.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 20
ny = 20
xmin = 0
xmax = 50
ymin = 0
ymax = 50
elem_type = QUAD4
[]
[Variables]
[./c]
order = FIRST
family = LAGRANGE
[../]
[]
[AuxVariables]
[./features]
order = CONSTANT
family = MONOMIAL
[../]
[./ghosts]
order = CONSTANT
family = MONOMIAL
[../]
[./halos]
order = CONSTANT
family = MONOMIAL
[../]
[./proc_id]
order = CONSTANT
family = MONOMIAL
[../]
[]
[ICs]
[./c]
type = LatticeSmoothCircleIC
variable = c
invalue = 1.0
outvalue = 0.0001
circles_per_side = '2 2'
pos_variation = 10.0
radius = 8.0
int_width = 5.0
radius_variation_type = uniform
avoid_bounds = false
[../]
[]
[BCs]
[./Periodic]
[./c]
variable = c
auto_direction = 'x y'
[../]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = c
[../]
[]
[AuxKernels]
[./features]
type = FeatureFloodCountAux
variable = features
execute_on = 'initial timestep_end'
flood_counter = features
[../]
[./ghosts]
type = FeatureFloodCountAux
variable = ghosts
field_display = GHOSTED_ENTITIES
execute_on = 'initial timestep_end'
flood_counter = features
[../]
[./halos]
type = FeatureFloodCountAux
variable = halos
field_display = HALOS
execute_on = 'initial timestep_end'
flood_counter = features
[../]
[./proc_id]
type = ProcessorIDAux
variable = proc_id
execute_on = 'initial timestep_end'
[../]
[]
[Postprocessors]
[./features]
type = FeatureFloodCount
variable = c
flood_entity_type = ELEMENTAL
execute_on = 'initial timestep_end'
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Outputs]
exodus = true
[]
test/tests/functions/image_function/image_mesh_3d.i
[Mesh]
type = ImageMesh
dim = 3
file_base = stack/test
file_suffix = png
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
# ImageFunction gets its file range parameters from ImageMesh,
# when it is present. This prevents duplicating information in
# input files.
type = ImageFunction
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
tutorials/darcy_thermo_mech/step01_diffusion/problems/step1.i
[Mesh]
type = GeneratedMesh # Can generate simple lines, rectangles and rectangular prisms
dim = 2 # Dimension of the mesh
nx = 100 # Number of elements in the x direction
ny = 10 # Number of elements in the y direction
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
# Adds a Linear Lagrange variable by default
[]
[]
[Kernels]
[diffusion]
type = ADDiffusion # Laplacian operator using automatic differentiation
variable = pressure # Operate on the "pressure" variable from above
[]
[]
[BCs]
[inlet]
type = DirichletBC # Simple u=value BC
variable = pressure # Variable to be set
boundary = left # Name of a sideset in the mesh
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Problem]
type = FEProblem # This is the "normal" type of Finite Element Problem in MOOSE
coord_type = RZ # Axisymmetric RZ
rz_coord_axis = X # Which axis the symmetry is around
[]
[Executioner]
type = Steady # Steady state problem
solve_type = NEWTON # Perform a Newton solve, uses AD to compute Jacobian terms
petsc_options_iname = '-pc_type -pc_hypre_type' # PETSc option pairs with values below
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true # Output Exodus format
[]
test/tests/multiapps/command_line/master.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[MultiApps]
[sub]
type = FullSolveMultiApp
positions = '0 0 0
1 1 1'
input_files = 'sub.i'
cli_args = 'Mesh/nx=10 Mesh/nx=100'
[]
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_4/cyl4_template1_sm.i
[Mesh]
file = cyl4_mesh.e
[]
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./stress_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./stress_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x16]
type = NodalVariableValue
nodeid = 15
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y16]
type = NodalVariableValue
nodeid = 15
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x9 disp_y9 disp_x16 disp_y16 stress_yy stress_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
modules/phase_field/test/tests/initial_conditions/ClosePackIC.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 5
ymax = .5
uniform_refine = 5
[]
[Variables]
[./u]
[../]
[]
[AuxVariables]
[./phi]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
execute_on = 'timestep_end'
exodus = true
[]
[ICs]
[./close_pack]
radius = 0.07
outvalue = 0
variable = phi
invalue = 1
type = ClosePackIC
[../]
[]
test/tests/functions/image_function/subset.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
uniform_refine = 2
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
type = ImageFunction
file_base = stack/test
file_suffix = png
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
origin = '0.25 0.25 0'
dimensions = '0.5 0.5 0'
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
test/tests/tag/2d_diffusion_tag_vector.i
[Mesh]
file = square.e
[]
[Variables]
[./u]
order = FIRST
family = LAGRANGE
[../]
[]
[AuxVariables]
[./tag_variable1]
order = FIRST
family = LAGRANGE
[../]
[./tag_variable2]
order = FIRST
family = LAGRANGE
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
extra_vector_tags = 'vec_tag1 vec_tag2'
[../]
[]
[AuxKernels]
[./TagVectorAux1]
type = TagVectorAux
variable = tag_variable1
v = u
vector_tag = vec_tag1
[../]
[./TagVectorAux2]
type = TagVectorAux
variable = tag_variable2
v = u
vector_tag = vec_tag2
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = 1
value = 0
extra_vector_tags = vec_tag1
[../]
[./right]
type = DirichletBC
variable = u
boundary = 2
value = 1
extra_vector_tags = vec_tag2
[../]
[]
[Problem]
type = FEProblem
extra_tag_vectors = 'vec_tag1 vec_tag2'
[]
[Executioner]
type = Steady
solve_type = 'NEWTON'
[]
[Outputs]
file_base = tag_vector_out
exodus = true
[]
test/tests/functions/image_function/threshold_adapt.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 2
ny = 2
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
type = ImageFunction
file_base = stack/test
file_suffix = png
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
threshold = 2.7e4
upper_value = 1
lower_value = -1
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Adaptivity]
max_h_level = 5
initial_steps = 5
initial_marker = marker
[./Indicators]
[./indicator]
type = GradientJumpIndicator
variable = u
[../]
[../]
[./Markers]
[./marker]
type = ErrorFractionMarker
indicator = indicator
refine = 0.9
[../]
[../]
[]
[Outputs]
exodus = true
[]
modules/heat_conduction/test/tests/meshed_gap_thermal_contact/meshed_gap_thermal_contact.i
[Mesh]
[fmesh]
type = FileMeshGenerator
file = meshed_gap.e
[]
[block0]
type = SubdomainBoundingBoxGenerator
input = fmesh
bottom_left = '.5 -.5 0'
top_right = '.7 .5 0'
block_id = 4
[]
[]
[Variables]
[./temp]
block = '1 3'
initial_condition = 1.0
[../]
[]
[Kernels]
[./hc]
type = HeatConduction
variable = temp
block = '1 3'
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = temp
boundary = 1
value = 1
[../]
[./right]
type = DirichletBC
variable = temp
boundary = 4
value = 2
[../]
[]
[ThermalContact]
[./gap_conductivity]
type = GapHeatTransfer
variable = temp
master = 2
slave = 3
gap_conductivity = 0.5
[../]
[]
[Materials]
[./hcm]
type = HeatConductionMaterial
block = '1 3'
temp = temp
thermal_conductivity = 1
[../]
[]
[Problem]
type = FEProblem
kernel_coverage_check = false
material_coverage_check = false
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
[./out]
type = Exodus
[../]
[]
modules/porous_flow/test/tests/recover/theis.i
# Tests that PorousFlow can successfully recover using a checkpoint file.
# This test contains stateful material properties, adaptivity and integrated
# boundary conditions with nodal-sized materials.
#
# This test file is run three times:
# 1) The full input file is run to completion
# 2) The input file is run for half the time and checkpointing is included
# 3) The input file is run in recovery using the checkpoint data
#
# The final output of test 3 is compared to the final output of test 1 to verify
# that recovery was successful.
[Mesh]
type = GeneratedMesh
dim = 1
nx = 20
xmax = 100
bias_x = 1.05
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = Y
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Adaptivity]
marker = marker
max_h_level = 4
[./Indicators]
[./front]
type = GradientJumpIndicator
variable = zi
[../]
[../]
[./Markers]
[./marker]
type = ErrorFractionMarker
indicator = front
refine = 0.8
coarsen = 0.2
[../]
[../]
[]
[AuxVariables]
[./saturation_gas]
order = CONSTANT
family = MONOMIAL
[../]
[./x1]
order = CONSTANT
family = MONOMIAL
[../]
[./y0]
order = CONSTANT
family = MONOMIAL
[../]
[]
[AuxKernels]
[./saturation_gas]
type = PorousFlowPropertyAux
variable = saturation_gas
property = saturation
phase = 1
execute_on = timestep_end
[../]
[./x1]
type = PorousFlowPropertyAux
variable = x1
property = mass_fraction
phase = 0
fluid_component = 1
execute_on = timestep_end
[../]
[./y0]
type = PorousFlowPropertyAux
variable = y0
property = mass_fraction
phase = 1
fluid_component = 0
execute_on = timestep_end
[../]
[]
[Variables]
[./pgas]
initial_condition = 20e6
[../]
[./zi]
initial_condition = 0
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pgas
[../]
[./flux0]
type = PorousFlowAdvectiveFlux
fluid_component = 0
variable = pgas
[../]
[./mass1]
type = PorousFlowMassTimeDerivative
fluid_component = 1
variable = zi
[../]
[./flux1]
type = PorousFlowAdvectiveFlux
fluid_component = 1
variable = zi
[../]
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pgas zi'
number_fluid_phases = 2
number_fluid_components = 2
[../]
[./pc]
type = PorousFlowCapillaryPressureConst
pc = 0
[../]
[./fs]
type = PorousFlowWaterNCG
water_fp = water
gas_fp = co2
capillary_pressure = pc
[../]
[]
[Modules]
[./FluidProperties]
[./co2]
type = CO2FluidProperties
[../]
[./water]
type = Water97FluidProperties
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./waterncg]
type = PorousFlowFluidState
gas_porepressure = pgas
z = zi
temperature_unit = Celsius
capillary_pressure = pc
fluid_state = fs
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.2
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1e-12 0 0 0 1e-12 0 0 0 1e-12'
[../]
[./relperm_water]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
s_res = 0.1
sum_s_res = 0.1
[../]
[./relperm_gas]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 1
[../]
[]
[BCs]
[./aquifer]
type = PorousFlowPiecewiseLinearSink
variable = pgas
boundary = right
pt_vals = '0 1e8'
multipliers = '0 1e8'
flux_function = 1e-6
PT_shift = 20e6
[../]
[]
[DiracKernels]
[./source]
type = PorousFlowSquarePulsePointSource
point = '0 0 0'
mass_flux = 2
variable = zi
[../]
[]
[Preconditioning]
[./smp]
type = SMP
full = true
[../]
[]
[Executioner]
type = Transient
solve_type = NEWTON
end_time = 2e2
dt = 50
[]
[VectorPostprocessors]
[./line]
type = NodalValueSampler
sort_by = x
variable = 'pgas zi'
[../]
[]
[Outputs]
print_linear_residuals = false
perf_graph = true
csv = true
[]
modules/porous_flow/test/tests/dirackernels/theis3.i
# Two phase Theis problem: Flow from single source
# Constant rate injection 0.5 kg/s
# 1D cylindrical mesh
[Mesh]
type = GeneratedMesh
dim = 1
nx = 100
xmax = 2000
bias_x = 1.05
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = Y
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[./ppwater]
initial_condition = 20e6
[../]
[./sgas]
initial_condition = 0
[../]
[]
[AuxVariables]
[./massfrac_ph0_sp0]
initial_condition = 1
[../]
[./massfrac_ph1_sp0]
initial_condition = 0
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = ppwater
[../]
[./flux0]
type = PorousFlowAdvectiveFlux
fluid_component = 0
variable = ppwater
[../]
[./mass1]
type = PorousFlowMassTimeDerivative
fluid_component = 1
variable = sgas
[../]
[./flux1]
type = PorousFlowAdvectiveFlux
fluid_component = 1
variable = sgas
[../]
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'ppwater sgas'
number_fluid_phases = 2
number_fluid_components = 2
[../]
[./pc]
type = PorousFlowCapillaryPressureConst
pc = 1e5
[../]
[]
[Modules]
[./FluidProperties]
[./simple_fluid0]
type = SimpleFluidProperties
bulk_modulus = 2e9
density0 = 1000
viscosity = 1e-3
thermal_expansion = 0
[../]
[./simple_fluid1]
type = SimpleFluidProperties
bulk_modulus = 2e9
density0 = 10
viscosity = 1e-4
thermal_expansion = 0
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./ppss]
type = PorousFlow2PhasePS
phase0_porepressure = ppwater
phase1_saturation = sgas
capillary_pressure = pc
[../]
[./massfrac]
type = PorousFlowMassFraction
mass_fraction_vars = 'massfrac_ph0_sp0 massfrac_ph1_sp0'
[../]
[./simple_fluid0]
type = PorousFlowSingleComponentFluid
fp = simple_fluid0
phase = 0
compute_enthalpy = false
compute_internal_energy = false
[../]
[./simple_fluid1]
type = PorousFlowSingleComponentFluid
fp = simple_fluid1
phase = 1
compute_enthalpy = false
compute_internal_energy = false
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.2
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1e-12 0 0 0 1e-12 0 0 0 1e-12'
[../]
[./relperm_water]
type = PorousFlowRelativePermeabilityCorey
n = 1
phase = 0
[../]
[./relperm_gas]
type = PorousFlowRelativePermeabilityCorey
n = 1
phase = 1
[../]
[]
[BCs]
[./rightwater]
type = DirichletBC
boundary = right
value = 20e6
variable = ppwater
[../]
[]
[DiracKernels]
[./source]
type = PorousFlowSquarePulsePointSource
point = '0 0 0'
mass_flux = 0.5
variable = sgas
[../]
[]
[Preconditioning]
[./smp]
type = SMP
full = true
petsc_options = '-snes_converged_reason -ksp_diagonal_scale -ksp_diagonal_scale_fix -ksp_gmres_modifiedgramschmidt -snes_linesearch_monitor'
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol -snes_max_it'
petsc_options_value = 'gmres asm lu NONZERO 2 1E-8 1E-10 20'
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
end_time = 1e4
[./TimeStepper]
type = IterationAdaptiveDT
dt = 10
growth_factor = 2
[../]
[]
[VectorPostprocessors]
[./line]
type = NodalValueSampler
sort_by = x
variable = 'ppwater sgas'
execute_on = 'timestep_end'
[../]
[]
[Postprocessors]
[./ppwater]
type = PointValue
point = '4 0 0'
variable = ppwater
[../]
[./sgas]
type = PointValue
point = '4 0 0'
variable = sgas
[../]
[./massgas]
type = PorousFlowFluidMass
fluid_component = 1
[../]
[]
[Outputs]
file_base = theis3
print_linear_residuals = false
perf_graph = true
[./csv]
type = CSV
execute_on = timestep_end
execute_vector_postprocessors_on = final
[../]
[]
modules/phase_field/test/tests/grain_tracker_test/grain_tracker_remapping_test.i
# This simulation predicts GB migration of a 2D copper polycrystal with 100 grains represented with 18 order parameters
# Mesh adaptivity and time step adaptivity are used
# An AuxVariable is used to calculate the grain boundary locations
# Postprocessors are used to record time step and the number of grains
[Mesh]
# Mesh block. Meshes can be read in or automatically generated
type = GeneratedMesh
dim = 2 # Problem dimension
nx = 12 # Number of elements in the x-direction
ny = 12 # Number of elements in the y-direction
xmax = 1000 # maximum x-coordinate of the mesh
ymax = 1000 # maximum y-coordinate of the mesh
elem_type = QUAD4 # Type of elements used in the mesh
uniform_refine = 1 # Initial uniform refinement of the mesh
[]
[GlobalParams]
# Parameters used by several kernels that are defined globally to simplify input file
op_num = 8 # Number of order parameters used
var_name_base = gr # Base name of grains
order = CONSTANT
family = MONOMIAL
[]
[Variables]
# Variable block, where all variables in the simulation are declared
[./PolycrystalVariables]
order = FIRST
family = LAGRANGE
[../]
[]
[UserObjects]
[./voronoi]
type = PolycrystalVoronoi
grain_num = 12 # Number of grains
coloring_algorithm = jp
rand_seed = 10
output_adjacency_matrix = true
[../]
[./grain_tracker]
type = GrainTracker
threshold = 0.2
verbosity_level = 1
connecting_threshold = 0.08
flood_entity_type = ELEMENTAL
compute_halo_maps = true # For displaying HALO fields
polycrystal_ic_uo = voronoi
error_on_grain_creation = true
execute_on = 'initial timestep_end'
[../]
[]
[ICs]
[./PolycrystalICs]
[./PolycrystalColoringIC]
polycrystal_ic_uo = voronoi
[../]
[../]
[]
[AuxVariables]
# Dependent variables
[./bnds]
# Variable used to visualize the grain boundaries in the simulation
order = FIRST
family = LAGRANGE
[../]
[./unique_grains]
[../]
[./var_indices]
[../]
[./ghost_regions]
[../]
[./halos]
[../]
[./halo0]
[../]
[./halo1]
[../]
[./halo2]
[../]
[./halo3]
[../]
[./halo4]
[../]
[./halo5]
[../]
[./halo6]
[../]
[./halo7]
[../]
[./centroids]
order = CONSTANT
family = MONOMIAL
[../]
[./proc_id]
[../]
[]
[Kernels]
# Kernel block, where the kernels defining the residual equations are set up.
[./PolycrystalKernel]
# Custom action creating all necessary kernels for grain growth. All input parameters are up in GlobalParams
[../]
[]
[AuxKernels]
# AuxKernel block, defining the equations used to calculate the auxvars
[./bnds_aux]
# AuxKernel that calculates the GB term
type = BndsCalcAux
variable = bnds
execute_on = 'initial timestep_end'
[../]
[./unique_grains]
type = FeatureFloodCountAux
variable = unique_grains
flood_counter = grain_tracker
field_display = UNIQUE_REGION
execute_on = 'initial timestep_end'
[../]
[./var_indices]
type = FeatureFloodCountAux
variable = var_indices
flood_counter = grain_tracker
field_display = VARIABLE_COLORING
execute_on = 'initial timestep_end'
[../]
[./ghosted_entities]
type = FeatureFloodCountAux
variable = ghost_regions
flood_counter = grain_tracker
field_display = GHOSTED_ENTITIES
execute_on = 'initial timestep_end'
[../]
[./halos]
type = FeatureFloodCountAux
variable = halos
flood_counter = grain_tracker
field_display = HALOS
execute_on = 'initial timestep_end'
[../]
[./halo0]
type = FeatureFloodCountAux
variable = halo0
map_index = 0
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo1]
type = FeatureFloodCountAux
variable = halo1
map_index = 1
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo2]
type = FeatureFloodCountAux
variable = halo2
map_index = 2
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo3]
type = FeatureFloodCountAux
variable = halo3
map_index = 3
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo4]
type = FeatureFloodCountAux
variable = halo4
map_index = 4
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo5]
type = FeatureFloodCountAux
variable = halo5
map_index = 5
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo6]
type = FeatureFloodCountAux
variable = halo6
map_index = 6
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo7]
type = FeatureFloodCountAux
variable = halo7
map_index = 7
field_display = HALOS
flood_counter = grain_tracker
[../]
[./centroids]
type = FeatureFloodCountAux
variable = centroids
execute_on = timestep_end
field_display = CENTROID
flood_counter = grain_tracker
[../]
[./proc_id]
type = ProcessorIDAux
variable = proc_id
execute_on = initial
[../]
[]
[BCs]
# Boundary Condition block
[]
[Materials]
[./CuGrGr]
# Material properties
type = GBEvolution
T = 450 # Constant temperature of the simulation (for mobility calculation)
wGB = 125 # Width of the diffuse GB
GBmob0 = 2.5e-6 # m^4(Js) for copper from Schoenfelder1997
Q = 0.23 # eV for copper from Schoenfelder1997
GBenergy = 0.708 # J/m^2 from Schoenfelder1997
[../]
[]
[Postprocessors]
# Scalar postprocessors
[./dt]
# Outputs the current time step
type = TimestepSize
[../]
[]
[Executioner]
# Uses newton iteration to solve the problem.
type = Transient # Type of executioner, here it is transient with an adaptive time step
scheme = bdf2 # Type of time integration (2nd order backward euler), defaults to 1st order backward euler
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type -ksp_gmres_restart -mat_mffd_type'
petsc_options_value = 'hypre boomeramg 101 ds'
l_max_its = 30 # Max number of linear iterations
l_tol = 1e-4 # Relative tolerance for linear solves
nl_max_its = 40 # Max number of nonlinear iterations
nl_rel_tol = 1e-10 # Absolute tolerance for nonlienar solves
start_time = 0.0
num_steps = 15
dt = 300
[]
[Problem]
type = FEProblem
[]
[Outputs]
csv = true
exodus = true
[./perf_graph]
type = PerfGraphOutput
level = 2 # Default is 1
[../]
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_2/ring2_template1.i
[GlobalParams]
volumetric_locking_correction = true
displacements = 'disp_x disp_y'
[]
[Mesh]
file = ring2_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x5]
type = NodalVariableValue
nodeid = 4
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y5]
type = NodalVariableValue
nodeid = 4
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-9
nl_rel_tol = 1e-8
l_max_its = 100
nl_max_its = 200
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x5 disp_y5 disp_x9 disp_y9 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
normalize_penalty = true
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
test/tests/transfers/multiapp_userobject_transfer/tosub_displaced_sub.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 4
ny = 8
xmax = 0.1
ymax = 0.5
displacements = 'disp_x disp_y'
[]
[Variables]
[./u]
initial_condition = 1
[../]
[]
[AuxVariables]
[./multi_layered_average]
[../]
[./element_multi_layered_average]
order = CONSTANT
family = MONOMIAL
[../]
[./disp_x]
initial_condition = 0.0
[../]
[./disp_y]
initial_condition = 0.5
[../]
[]
[Functions]
[./axial_force]
type = ParsedFunction
value = 1000*y
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[./td]
type = TimeDerivative
variable = u
[../]
[./force]
type = BodyForce
variable = u
function = axial_force
[../]
[]
[BCs]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[Executioner]
type = Transient
num_steps = 1
dt = 0.001
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
[Problem]
coord_type = rz
type = FEProblem
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_3/ring3_mu_0_2_pen.i
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Mesh]
file = ring3_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x11]
type = NodalVariableValue
nodeid = 10
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y11]
type = NodalVariableValue
nodeid = 10
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-10
nl_rel_tol = 1e-9
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = ring3_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = ring3_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x11 disp_y11 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
tangential_tolerance = 1e-3
friction_coefficient = 0.2
penalty = 1e+9
[../]
[]
modules/phase_field/test/tests/reconstruction/2phase_reconstruction2.i
#
# In this test we set the initial condition of a set of order parameters
# by pulling out the only grains from given EBSD data file that belong to a specified phase
#
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
# The following sections are extracted in the documentation in
# moose/docs/content/modules/phase_field/ICs/EBSD.md
[Mesh]
type = EBSDMesh
filename = Ti_2Phase_28x28_ebsd.txt
[]
[GlobalParams]
op_num = 2
var_name_base = gr
[]
[UserObjects]
[./ebsd_reader]
type = EBSDReader
[../]
[./ebsd]
type = PolycrystalEBSD
coloring_algorithm = bt
ebsd_reader = ebsd_reader
phase = 1
output_adjacency_matrix = true
[../]
[]
[Variables]
[./PolycrystalVariables]
[../]
[]
[ICs]
[./PolycrystalICs]
[./PolycrystalColoringIC]
# select only data for phase 1 from the EBSD file
polycrystal_ic_uo = ebsd
[../]
[../]
[]
#ENDDOC - End of the file section that is included in the documentation. Do not change this line!
[Executioner]
type = Transient
num_steps = 0
[]
[Outputs]
exodus = true
[]
test/tests/mesh_modifiers/image_subdomain/image_3d.i
[Mesh]
type = GeneratedMesh
dim = 3
nx = 20
ny = 20
nz = 20
[]
[Variables]
[./u]
[../]
[]
[MeshModifiers]
[./image]
type = ImageSubdomain
file_base = stack/test
file_suffix = png
threshold = 2.7e4
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Steady
[]
[Outputs]
execute_on = 'timestep_end'
exodus = true
[]
test/tests/coord_type/coord_type_rz.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
test/tests/misc/block_boundary_material_check/bc_check.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Variables]
[./u]
[../]
[]
[BCs]
[./bc_left]
type = MatTestNeumannBC
variable = u
boundary = left
mat_prop = 'prop'
[../]
[]
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Executioner]
type = Steady
[]
[Outputs]
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_3/ring3_template1_sm.i
[Mesh]
file = ring3_mesh.e
[]
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x11]
type = NodalVariableValue
nodeid = 10
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y11]
type = NodalVariableValue
nodeid = 10
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-10
nl_rel_tol = 1e-9
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x11 disp_y11 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
normalize_penalty = true
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
tutorials/darcy_thermo_mech/step09_mechanics/problems/step9.i
[GlobalParams]
displacements = 'disp_r disp_z'
[]
[Mesh]
type = GeneratedMesh
dim = 2
ny = 200
nx = 10
ymax = 0.304 # Length of test chamber
xmax = 0.0257 # Test chamber radius
[]
[MeshModifiers]
[bottom]
type = SubdomainBoundingBox
location = inside
bottom_left = '0 0 0'
top_right = '0.01285 0.304 0'
block_id = 1
[]
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Modules/TensorMechanics/Master]
[all]
# This block adds all of the proper Kernels, strain calculators, and Variables
# for TensorMechanics in the correct coordinate system (autodetected)
add_variables = true
strain = FINITE
eigenstrain_names = eigenstrain
use_automatic_differentiation = true
generate_output = 'vonmises_stress elastic_strain_xx elastic_strain_yy strain_xx strain_yy'
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = bottom
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = top
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = bottom
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = top
[]
[hold_inlet]
type = DirichletBC
variable = disp_z
boundary = bottom
value = 0
[]
[hold_center]
type = DirichletBC
variable = disp_r
boundary = left
value = 0
[]
[hold_outside]
type = DirichletBC
variable = disp_r
boundary = right
value = 0
[]
[]
[Materials]
viscosity_file = data/water_viscosity.csv
density_file = data/water_density.csv
thermal_conductivity_file = data/water_thermal_conductivity.csv
specific_heat_file = data/water_specific_heat.csv
thermal_expansion_file = data/water_thermal_expansion.csv
[column_top]
type = PackedColumn
block = 0
temperature = temperature
radius = 1.15
fluid_viscosity_file = ${viscosity_file}
fluid_density_file = ${density_file}
fluid_thermal_conductivity_file = ${thermal_conductivity_file}
fluid_specific_heat_file = ${specific_heat_file}
fluid_thermal_expansion_file = ${thermal_expansion_file}
[]
[column_bottom]
type = PackedColumn
block = 1
temperature = temperature
radius = 1
fluid_viscosity_file = ${viscosity_file}
fluid_density_file = ${density_file}
fluid_thermal_conductivity_file = ${thermal_conductivity_file}
fluid_specific_heat_file = ${specific_heat_file}
fluid_thermal_expansion_file = ${thermal_expansion_file}
[]
[elasticity_tensor]
type = ComputeIsotropicElasticityTensor
youngs_modulus = 200e9 # (Pa) from wikipedia
poissons_ratio = .3 # from wikipedia
[]
[elastic_stress]
type = ADComputeFiniteStrainElasticStress
[]
[thermal_strain]
type = ADComputeThermalExpansionEigenstrain
stress_free_temperature = 300
eigenstrain_name = eigenstrain
temperature = temperature
thermal_expansion_coeff = 1e-5 # TM modules doesn't support material property, but it will
[]
[]
[Postprocessors]
[average_temperature]
type = ElementAverageValue
variable = temperature
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Executioner]
type = Transient
start_time = -1
end_time = 200
steady_state_tolerance = 1e-7
steady_state_detection = true
dt = 0.25
solve_type = PJFNK
automatic_scaling = true
compute_scaling_once = false
petsc_options_iname = '-pc_type'
petsc_options_value = 'lu'
#petsc_options_iname = '-pc_type -pc_hypre_type -ksp_gmres_restart'
#petsc_options_value = 'hypre boomeramg 500'
line_search = none
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
[out]
type = Exodus
elemental_as_nodal = true
[]
[]
modules/stochastic_tools/test/tests/multiapps/commandline_control/master_multiple.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Distributions]
[uniform]
type = UniformDistribution
lower_bound = 5
upper_bound = 10
[]
[]
[Samplers]
[sample]
type = MonteCarloSampler
num_rows = 3
distributions = 'uniform uniform'
execute_on = 'PRE_MULTIAPP_SETUP'
[]
[]
[MultiApps]
[sub]
type = FullSolveMultiApp
positions = '0 0 0
1 1 1
2 2 2'
input_files = 'sub.i'
[]
[]
[Controls]
[cmdline]
type = MultiAppCommandLineControl
multi_app = sub
sampler = sample
param_names = 'Mesh/xmax Mesh/ymax'
[]
[]
test/tests/transfers/multiapp_userobject_transfer/tosub_sub.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 4
ny = 8
xmax = 0.1
ymax = 0.5
[]
[Variables]
[./u]
initial_condition = 1
[../]
[]
[AuxVariables]
[./multi_layered_average]
[../]
[./element_multi_layered_average]
order = CONSTANT
family = MONOMIAL
[../]
[]
[Functions]
[./axial_force]
type = ParsedFunction
value = 1000*y
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[./td]
type = TimeDerivative
variable = u
[../]
[./force]
type = BodyForce
variable = u
function = axial_force
[../]
[]
[BCs]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[Executioner]
type = Transient
num_steps = 1
dt = 0.001
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
[Problem]
coord_type = rz
type = FEProblem
[]
test/tests/misc/stop_for_debugger/stop_for_debugger.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_1/cyl1_template1_sm.i
#
# This input file is a template for both the frictionless and glued test
# variations for the current problem geometry. In order to create an input
# file to run outside the runtest framework, look at the tests file and add the
# appropriate input file lines from the cli_args line.
#
[Mesh]
file = cyl1_mesh.e
[]
[GlobalParams]
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x7]
type = NodalVariableValue
nodeid = 6
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y7]
type = NodalVariableValue
nodeid = 6
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x7 disp_y7 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
normalize_penalty = true
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
test/tests/restart/restartable_types/restartable_types.i
###########################################################
# This is a simple test of the restart/recover capability.
# The test object "RestartableTypesChecker" is used
# to reload data from a previous simulation written out
# with the object "RestartableTypes".
#
# See "restartable_types2.i"
#
# @Requirement F1.60
###########################################################
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[UserObjects]
[./restartable_types]
type = RestartableTypes
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[./out]
type = Checkpoint
num_files = 1
[../]
[]
modules/phase_field/test/tests/reconstruction/1phase_reconstruction.i
#
# In this test we set the initial condition of a set of order parameters
# by pulling out the grain data from given EBSD data file ignoring the phase completely.
#
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
# The following sections are extracted in the documentation in
# moose/docs/content/modules/phase_field/ICs/EBSD.md
[Mesh]
# Create a mesh representing the EBSD data
type = EBSDMesh
filename = IN100_001_28x28_Marmot.txt
[]
[GlobalParams]
# Define the number and names of the order parameters used to represent the grains
op_num = 4
var_name_base = gr
[]
[UserObjects]
[./ebsd_reader]
# Read in the EBSD data. Uses the filename given in the mesh block.
type = EBSDReader
[../]
[./ebsd]
type = PolycrystalEBSD
coloring_algorithm = bt
ebsd_reader = ebsd_reader
output_adjacency_matrix = true
[../]
[./grain_tracker]
type = GrainTracker
# For displaying HALO fields
compute_halo_maps = true
# Link in the ebsd userobject here so that grain tracker can extract info from it
polycrystal_ic_uo = ebsd
[../]
[]
[Variables]
[./PolycrystalVariables]
# Create all the order parameters
order = FIRST
family = LAGRANGE
[../]
[]
[ICs]
[./PolycrystalICs]
[./PolycrystalColoringIC]
# Uses the data from the user object 'ebsd' to initialize the variables for all the order parameters.
polycrystal_ic_uo = ebsd
[../]
[../]
[]
#ENDDOC - End of the file section that is included in the documentation. Do not change this line!
[GlobalParams]
execute_on = 'initial'
family = MONOMIAL
order = CONSTANT
[]
[AuxVariables]
[./PHI1]
[../]
[./PHI]
[../]
[./PHI2]
[../]
[./GRAIN]
[../]
[./unique_grains]
[../]
[./var_indices]
[../]
[./halo0]
[../]
[./halo1]
[../]
[./halo2]
[../]
[./halo3]
[../]
[]
[AuxKernels]
[./phi1_aux]
type = EBSDReaderPointDataAux
variable = PHI1
ebsd_reader = ebsd_reader
data_name = 'phi1'
[../]
[./phi_aux]
type = EBSDReaderPointDataAux
variable = PHI
ebsd_reader = ebsd_reader
data_name = 'phi'
[../]
[./phi2_aux]
type = EBSDReaderPointDataAux
variable = PHI2
ebsd_reader = ebsd_reader
data_name = 'phi2'
[../]
[./grain_aux]
type = EBSDReaderPointDataAux
variable = GRAIN
ebsd_reader = ebsd_reader
data_name = 'feature_id'
[../]
[./unique_grains]
type = FeatureFloodCountAux
variable = unique_grains
flood_counter = grain_tracker
field_display = UNIQUE_REGION
[../]
[./var_indices]
type = FeatureFloodCountAux
variable = var_indices
flood_counter = grain_tracker
field_display = VARIABLE_COLORING
[../]
[./halo0]
type = FeatureFloodCountAux
variable = halo0
map_index = 0
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo1]
type = FeatureFloodCountAux
variable = halo1
map_index = 1
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo2]
type = FeatureFloodCountAux
variable = halo2
map_index = 2
field_display = HALOS
flood_counter = grain_tracker
[../]
[./halo3]
type = FeatureFloodCountAux
variable = halo3
map_index = 3
field_display = HALOS
flood_counter = grain_tracker
[../]
[]
[Executioner]
type = Steady
[]
[Outputs]
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_1/cyl1_mu_0_2_pen_sm.i
[Mesh]
file = cyl1_mesh.e
[]
[GlobalParams]
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
order = FIRST
family = LAGRANGE
[../]
[./disp_y]
order = FIRST
family = LAGRANGE
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
order = FIRST
family = LAGRANGE
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x7]
type = NodalVariableValue
nodeid = 6
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y7]
type = NodalVariableValue
nodeid = 6
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = cyl1_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = cyl1_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x7 disp_y7 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
tangential_tolerance = 1e-3
friction_coefficient = 0.2
penalty = 1e+9
[../]
[]
modules/phase_field/test/tests/initial_conditions/PolycrystalVoronoiVoidIC_notperiodic.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 85
ny = 85
nz = 0
xmax = 250
ymax = 250
zmax = 0
elem_type = QUAD4
[]
[GlobalParams]
op_num = 5
grain_num = 5
var_name_base = gr
numbub = 20
bubspac = 22
radius = 8
int_width = 10
invalue = 1
outvalue = 0.1
[]
[Variables]
[./c]
[../]
[./w]
scaling = 1.0e4
[../]
[./PolycrystalVariables]
[../]
[]
[ICs]
[./PolycrystalICs]
[./PolycrystalVoronoiVoidIC]
polycrystal_ic_uo = voronoi
[../]
[../]
[./c_IC]
variable = c
type = PolycrystalVoronoiVoidIC
structure_type = voids
polycrystal_ic_uo = voronoi
[../]
[]
[UserObjects]
[./voronoi]
type = PolycrystalVoronoi
rand_seed = 12444
int_width = 0
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 0
[]
[Outputs]
exodus = true
[]
modules/porous_flow/test/tests/fluidstate/theis_nonisothermal.i
# Two-phase nonisothermal Theis problem: Flow from single source using WaterNCG fluidstate.
# Constant rate injection 2 kg/s of cold gas into warm reservoir
# 1D cylindrical mesh
# Initially, system has only a liquid phase, until enough gas is injected
# to form a gas phase, in which case the system becomes two phase.
[Mesh]
[./mesh]
type = GeneratedMeshGenerator
dim = 1
nx = 40
xmin = 0.1
xmax = 200
bias_x = 1.05
[../]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = Y
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[AuxVariables]
[./saturation_gas]
order = CONSTANT
family = MONOMIAL
[../]
[./x1]
order = CONSTANT
family = MONOMIAL
[../]
[./y0]
order = CONSTANT
family = MONOMIAL
[../]
[]
[AuxKernels]
[./saturation_gas]
type = PorousFlowPropertyAux
variable = saturation_gas
property = saturation
phase = 1
execute_on = timestep_end
[../]
[./x1]
type = PorousFlowPropertyAux
variable = x1
property = mass_fraction
phase = 0
fluid_component = 1
execute_on = timestep_end
[../]
[./y0]
type = PorousFlowPropertyAux
variable = y0
property = mass_fraction
phase = 1
fluid_component = 0
execute_on = timestep_end
[../]
[]
[Variables]
[./pgas]
initial_condition = 20e6
[../]
[./zi]
initial_condition = 0
[../]
[./temperature]
initial_condition = 70
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pgas
[../]
[./flux0]
type = PorousFlowAdvectiveFlux
fluid_component = 0
variable = pgas
[../]
[./mass1]
type = PorousFlowMassTimeDerivative
fluid_component = 1
variable = zi
[../]
[./flux1]
type = PorousFlowAdvectiveFlux
fluid_component = 1
variable = zi
[../]
[./energy]
type = PorousFlowEnergyTimeDerivative
variable = temperature
[../]
[./heatadv]
type = PorousFlowHeatAdvection
variable = temperature
[../]
[./conduction]
type = PorousFlowHeatConduction
variable = temperature
[../]
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pgas zi temperature'
number_fluid_phases = 2
number_fluid_components = 2
[../]
[./pc]
type = PorousFlowCapillaryPressureConst
pc = 0
[../]
[./fs]
type = PorousFlowWaterNCG
water_fp = water
gas_fp = methane
capillary_pressure = pc
[../]
[]
[Modules]
[./FluidProperties]
[./methane]
type = MethaneFluidProperties
[../]
[./water]
type = Water97FluidProperties
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
temperature = temperature
[../]
[./waterncg]
type = PorousFlowFluidState
gas_porepressure = pgas
z = zi
temperature = temperature
temperature_unit = Celsius
capillary_pressure = pc
fluid_state = fs
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.2
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1e-12 0 0 0 1e-12 0 0 0 1e-12'
[../]
[./relperm_water]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
s_res = 0.1
sum_s_res = 0.1
[../]
[./relperm_gas]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 1
[../]
[./rockheat]
type = PorousFlowMatrixInternalEnergy
specific_heat_capacity = 1000
density = 2500
[../]
[./rock_thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '50 0 0 0 50 0 0 0 50'
[../]
[]
[BCs]
[./cold_gas]
type = DirichletBC
boundary = left
variable = temperature
value = 20
[../]
[./gas_injecton]
type = PorousFlowSink
boundary = left
variable = zi
flux_function = -0.159155
[../]
[./rightwater]
type = DirichletBC
boundary = right
value = 20e6
variable = pgas
[../]
[./righttemp]
type = DirichletBC
boundary = right
value = 70
variable = temperature
[../]
[]
[Preconditioning]
[./smp]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = 'gmres asm lu NONZERO 2'
[../]
[]
[Executioner]
type = Transient
solve_type = NEWTON
end_time = 1e4
automatic_scaling = true
nl_abs_tol = 1e-7
nl_rel_tol = 1e-5
[./TimeStepper]
type = IterationAdaptiveDT
dt = 1
growth_factor = 1.5
[../]
[]
[Postprocessors]
[./pgas]
type = PointValue
point = '2 0 0'
variable = pgas
[../]
[./sgas]
type = PointValue
point = '2 0 0'
variable = saturation_gas
[../]
[./zi]
type = PointValue
point = '2 0 0'
variable = zi
[../]
[./temperature]
type = PointValue
point = '2 0 0'
variable = temperature
[../]
[./massgas]
type = PorousFlowFluidMass
fluid_component = 1
[../]
[./x1]
type = PointValue
point = '2 0 0'
variable = x1
[../]
[./y0]
type = PointValue
point = '2 0 0'
variable = y0
[../]
[]
[Outputs]
print_linear_residuals = false
perf_graph = true
csv = true
[]
tutorials/darcy_thermo_mech/step08_postprocessors/problems/step8.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 30
ny = 3
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
uniform_refine = 2
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
temperature = temperature
porosity = '0.25952 + 0.7*y/0.0257'
[]
[]
[Postprocessors]
[average_temperature]
type = ElementAverageValue
variable = temperature
[]
[outlet_heat_flux]
type = SideFluxIntegral
variable = temperature
boundary = right
diffusivity = thermal_conductivity
[]
[]
[VectorPostprocessors]
[temperature_sample]
type = LineValueSampler
num_points = 500
start_point = '0.1 0 0'
end_point = '0.1 0.0257 0'
variable = temperature
sort_by = y
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
exodus = true
csv = true
[]
modules/stochastic_tools/test/tests/multiapps/batch_commandline_control/master_single.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Distributions]
[uniform]
type = UniformDistribution
lower_bound = 5
upper_bound = 10
[]
[]
[Samplers]
[sample]
type = MonteCarloSampler
num_rows = 3
distributions = 'uniform'
execute_on = 'PRE_MULTIAPP_SETUP'
[]
[]
[MultiApps]
[sub]
type = SamplerFullSolveMultiApp
sampler = sample
input_files = 'sub.i'
mode = batch-reset
[]
[]
[Transfers]
[data]
type = SamplerPostprocessorTransfer
multi_app = sub
sampler = sample
to_vector_postprocessor = storage
from_postprocessor = size
[]
[]
[VectorPostprocessors]
[storage]
type = StochasticResults
samplers = sample
[]
[]
[Controls]
[cmdline]
type = MultiAppCommandLineControl
multi_app = sub
sampler = sample
param_names = 'Mesh/xmax'
[]
[]
[Outputs]
[out]
type = CSV
execute_on = FINAL
[]
[]
test/tests/transfers/multiapp_copy_transfer/second_lagrange_from_sub/master.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
elem_type = QUAD8
[]
[Variables]
[./u]
family = LAGRANGE
order = SECOND
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[MultiApps]
[./sub]
type = FullSolveMultiApp
input_files = sub.i
execute_on = initial
[../]
[]
[Transfers]
[./from_sub]
type = MultiAppCopyTransfer
direction = from_multiapp
source_variable = u
variable = u
multi_app = sub
[../]
[]
[Outputs]
exodus = true
[]
tutorials/darcy_thermo_mech/step07_adaptivity/problems/step7b_fine.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 30
ny = 3
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
uniform_refine = 3
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
temperature = temperature
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
exodus = true
[]
modules/porous_flow/test/tests/fluidstate/theis.i
# Two phase Theis problem: Flow from single source using WaterNCG fluidstate.
# Constant rate injection 2 kg/s
# 1D cylindrical mesh
# Initially, system has only a liquid phase, until enough gas is injected
# to form a gas phase, in which case the system becomes two phase.
[Mesh]
type = GeneratedMesh
dim = 1
nx = 40
xmax = 200
bias_x = 1.05
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = Y
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[AuxVariables]
[./saturation_gas]
order = CONSTANT
family = MONOMIAL
[../]
[./x1]
order = CONSTANT
family = MONOMIAL
[../]
[./y0]
order = CONSTANT
family = MONOMIAL
[../]
[]
[AuxKernels]
[./saturation_gas]
type = PorousFlowPropertyAux
variable = saturation_gas
property = saturation
phase = 1
execute_on = timestep_end
[../]
[./x1]
type = PorousFlowPropertyAux
variable = x1
property = mass_fraction
phase = 0
fluid_component = 1
execute_on = timestep_end
[../]
[./y0]
type = PorousFlowPropertyAux
variable = y0
property = mass_fraction
phase = 1
fluid_component = 0
execute_on = timestep_end
[../]
[]
[Variables]
[./pgas]
initial_condition = 20e6
[../]
[./zi]
initial_condition = 0
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pgas
[../]
[./flux0]
type = PorousFlowAdvectiveFlux
fluid_component = 0
variable = pgas
[../]
[./mass1]
type = PorousFlowMassTimeDerivative
fluid_component = 1
variable = zi
[../]
[./flux1]
type = PorousFlowAdvectiveFlux
fluid_component = 1
variable = zi
[../]
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pgas zi'
number_fluid_phases = 2
number_fluid_components = 2
[../]
[./pc]
type = PorousFlowCapillaryPressureConst
pc = 0
[../]
[./fs]
type = PorousFlowWaterNCG
water_fp = water
gas_fp = co2
capillary_pressure = pc
[../]
[]
[Modules]
[./FluidProperties]
[./co2]
type = CO2FluidProperties
[../]
[./water]
type = Water97FluidProperties
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./waterncg]
type = PorousFlowFluidState
gas_porepressure = pgas
z = zi
temperature_unit = Celsius
capillary_pressure = pc
fluid_state = fs
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.2
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1e-12 0 0 0 1e-12 0 0 0 1e-12'
[../]
[./relperm_water]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
s_res = 0.1
sum_s_res = 0.1
[../]
[./relperm_gas]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 1
[../]
[]
[BCs]
[./rightwater]
type = DirichletBC
boundary = right
value = 20e6
variable = pgas
[../]
[]
[DiracKernels]
[./source]
type = PorousFlowSquarePulsePointSource
point = '0 0 0'
mass_flux = 2
variable = zi
[../]
[]
[Preconditioning]
[./smp]
type = SMP
full = true
petsc_options = '-snes_converged_reason -ksp_diagonal_scale -ksp_diagonal_scale_fix -ksp_gmres_modifiedgramschmidt -snes_linesearch_monitor'
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol -snes_max_it'
petsc_options_value = 'gmres asm lu NONZERO 2 1E-8 1E-10 20'
[../]
[]
[Executioner]
type = Transient
solve_type = NEWTON
end_time = 2e2
[./TimeStepper]
type = IterationAdaptiveDT
dt = 10
growth_factor = 2
[../]
[]
[VectorPostprocessors]
[./line]
type = NodalValueSampler
sort_by = x
variable = 'pgas zi'
execute_on = 'timestep_end'
[../]
[]
[Postprocessors]
[./pgas]
type = PointValue
point = '1 0 0'
variable = pgas
[../]
[./sgas]
type = PointValue
point = '1 0 0'
variable = saturation_gas
[../]
[./zi]
type = PointValue
point = '1 0 0'
variable = zi
[../]
[./massgas]
type = PorousFlowFluidMass
fluid_component = 1
[../]
[./x1]
type = PointValue
point = '1 0 0'
variable = x1
[../]
[./y0]
type = PointValue
point = '1 0 0'
variable = y0
[../]
[]
[Outputs]
print_linear_residuals = false
perf_graph = true
[./csvout]
type = CSV
execute_on = timestep_end
execute_vector_postprocessors_on = final
[../]
[]
test/tests/coord_type/coord_type_rz_integrated.i
[Mesh]
type = GeneratedMesh
nx = 10
xmax = 1
ny = 10
ymax = 1
dim = 2
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Preconditioning]
[./smp]
type = SMP
full = true
[../]
[]
[Executioner]
type = Steady
solve_type = NEWTON
[]
[Outputs]
[./out]
type = Exodus
[../]
[]
[Kernels]
[./diff_u]
type = Diffusion
variable = u
[../]
[]
[DGKernels]
[./dg_diff]
type = DGDiffusion
variable = u
epsilon = -1
sigma = 6
[../]
[]
[Variables]
[./u]
order = FIRST
family = MONOMIAL
[../]
[]
[BCs]
[./source]
type = DGFunctionDiffusionDirichletBC
variable = u
boundary = 'right'
function = exact_fn
epsilon = -1
sigma = 6
[../]
[./vacuum]
boundary = 'top'
type = VacuumBC
variable = u
[../]
[]
[Functions]
[./exact_fn]
type = ConstantFunction
value = 1
[../]
[]
[ICs]
[./u]
type = ConstantIC
value = 1
variable = u
[../]
[]
modules/stochastic_tools/test/tests/multiapps/batch_commandline_control/master_wrong_num_params.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Distributions]
[uniform]
type = UniformDistribution
lower_bound = 5
upper_bound = 10
[]
[]
[Samplers]
[sample]
type = MonteCarloSampler
num_rows = 3
distributions = 'uniform uniform'
execute_on = 'initial timestep_end'
[]
[]
[MultiApps]
[sub]
type = FullSolveMultiApp
positions = '0 0 0
1 1 1
2 2 2'
input_files = 'sub.i'
[]
[]
[Controls]
[cmdline]
type = MultiAppCommandLineControl
multi_app = sub
sampler = sample
param_names = 'Mesh/xmax Mesh/ymax Mesh/zmax'
[]
[]
test/tests/transfers/multiapp_copy_transfer/linear_lagrange_to_sub/sub.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Outputs]
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_2/ring2_mu_0_2_pen_sm.i
[Mesh]
file = ring2_mesh.e
[]
[GlobalParams]
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x5]
type = NodalVariableValue
nodeid = 4
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y5]
type = NodalVariableValue
nodeid = 4
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
#Preconditioned JFNK (default)
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-10
nl_rel_tol = 1e-8
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = ring2_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = ring2_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x5 disp_y5 disp_x9 disp_y9 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
friction_coefficient = 0.2
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
test/tests/userobjects/shape_element_user_object/shape_side_uo_physics_test.i
u_left = 0.5
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
parallel_type = replicated
[]
[Variables]
[./u]
order = FIRST
family = LAGRANGE
[../]
[./pot]
[../]
[]
[Kernels]
[./diff_u]
type = Diffusion
variable = u
[../]
[./adv_u]
type = PotentialAdvection
variable = u
potential = pot
[../]
[./diff_pot]
type = Diffusion
variable = pot
[../]
[]
[BCs]
[./left]
boundary = left
type = DirichletBC
value = ${u_left}
variable = u
[../]
[./right]
boundary = right
type = DirichletBC
variable = u
value = 0
[../]
[./left_pot]
boundary = left
type = ExampleShapeSideIntegratedBC
variable = pot
num_user_object = num_user_object
denom_user_object = denom_user_object
v = u
Vb = 1
[../]
[./right_pot]
boundary = right
type = DirichletBC
variable = pot
value = 0
[../]
[]
[UserObjects]
[./num_user_object]
type = NumShapeSideUserObject
u = u
boundary = left
execute_on = 'linear nonlinear'
[../]
[./denom_user_object]
type = DenomShapeSideUserObject
u = u
boundary = left
execute_on = 'linear nonlinear'
[../]
[]
[AuxVariables]
[./u_flux]
family = MONOMIAL
order = CONSTANT
[../]
[]
[AuxKernels]
[./u_flux]
type = DriftDiffusionFluxAux
variable = u_flux
u = u
potential = pot
component = 0
[../]
[]
[Problem]
type = FEProblem
[]
[Preconditioning]
[./smp]
type = SMP
full = true
[../]
[]
[Executioner]
type = Steady
solve_type = NEWTON
petsc_options = '-snes_converged_reason -ksp_converged_reason -snes_linesearch_monitor'
petsc_options_iname = '-pc_type -sub_pc_type -sub_ksp_type'
petsc_options_value = 'asm lu preonly'
[]
[Outputs]
exodus = true
perf_graph = true
[]
[ICs]
[./u]
type = FunctionIC
variable = u
function = ic_u
[../]
[./pot]
type = FunctionIC
variable = pot
function = ic_pot
[../]
[]
[Functions]
[./ic_u]
type = ParsedFunction
value = '${u_left} * (1 - x)'
[../]
[./ic_pot]
type = ParsedFunction
value = '1 - x'
[../]
[]
test/tests/transfers/multiapp_copy_transfer/second_lagrange_to_sub/sub.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
elem_type = QUAD9
[]
[Variables]
[./u]
order = SECOND
family = LAGRANGE
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Outputs]
exodus = true
[]
test/tests/mesh_modifiers/subdomain_bounding_box/oriented_subdomain_bounding_box_inside.i
[Mesh]
type = GeneratedMesh
dim = 3
xmin = -6
xmax = 4
nx = 10
ymin = -2
ymax = 10
ny = 12
zmin = -5
zmax = 7
nz = 12
[]
[MeshModifiers]
[./subdomains]
type = OrientedSubdomainBoundingBox
center = '-1 4 1'
width = 5
length = 10
height = 4
width_direction = '2 1 0'
length_direction = '-1 2 2'
block_id = 10
location = INSIDE
[../]
[]
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Variables]
[./u]
[../]
[]
[Materials]
[./mat10]
type = GenericConstantMaterial
block = 10
outputs = all
prop_values = 6.24
prop_names = prop
[../]
[./mat0]
type = GenericConstantMaterial
block = 0
prop_names = prop
prop_values = 0
[../]
[]
[Executioner]
type = Steady
solve_type = PJFNK
[]
[Outputs]
exodus = true
[]
test/tests/transfers/multiapp_conservative_transfer/sub_userobject.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 4
ny = 8
xmax = 0.1
ymax = 0.5
[]
[Variables]
[./u]
initial_condition = 1
[../]
[]
[AuxVariables]
[./layered_average_value]
order = CONSTANT
family = MONOMIAL
[../]
[]
[Postprocessors]
[./from_postprocessor]
type = ElementIntegralVariablePostprocessor
variable = layered_average_value
execute_on = 'nonlinear TIMESTEP_END'
[../]
[]
[Functions]
[./axial_force]
type = ParsedFunction
value = 1000*y
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[./td]
type = TimeDerivative
variable = u
[../]
[./force]
type = BodyForce
variable = u
function = axial_force
[../]
[]
[AuxKernels]
[./layered_aux]
type = SpatialUserObjectAux
variable = layered_average_value
execute_on = 'nonlinear TIMESTEP_END'
user_object = layered_average
[../]
[]
[BCs]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[UserObjects]
[./layered_average]
type = LayeredAverage
variable = u
direction = y
num_layers = 4
[../]
[]
[Executioner]
type = Transient
num_steps = 1
dt = 0.001
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
[Problem]
coord_type = rz
type = FEProblem
[]
test/tests/multiapps/command_line/master_wrong_size.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[MultiApps]
[sub]
type = FullSolveMultiApp
positions = '0 0 0
1 1 1'
input_files = 'sub.i'
cli_args = 'Mesh/xmax=1.1 Mesh/xmax=1.2 Mesh/xmax=1.3'
[]
[]
test/tests/functions/image_function/image_3d_subset.i
[Mesh]
type = GeneratedMesh
dim = 3
nx = 20
ny = 20
nz = 6
zmax = 0.3
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
type = ImageFunction
file_base = stack/test
file_suffix = png
file_range = '0 5'
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
test/tests/functions/image_function/image.i
[Mesh]
type = GeneratedMesh
dim = 3
nx = 10
ny = 10
nz = 10
[]
[Adaptivity]
max_h_level = 5
initial_steps = 5
initial_marker = marker
[./Indicators]
[./indicator]
type = GradientJumpIndicator
variable = u
[../]
[../]
[./Markers]
[./marker]
type = ErrorFractionMarker
indicator = indicator
refine = 0.9
[../]
[../]
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
type = ImageFunction
file = stack/test_00.png
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
modules/phase_field/test/tests/initial_conditions/MultiSmoothSuperellipsoidIC_2D.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 50
ny = 50
nz = 0
xmax = 100
ymax = 100
zmax = 0
elem_type = QUAD4
[]
[Variables]
[./c]
order = FIRST
family = LAGRANGE
[../]
[]
[ICs]
[./c]
type = MultiSmoothSuperellipsoidIC
variable = c
invalue = 1.0
outvalue = 0.1
bubspac = '10 5'
numbub = '5 5'
semiaxis_b_variation = '0.25 0.35'
semiaxis_variation_type = uniform
semiaxis_a_variation = '0.2 0.3'
semiaxis_a = '7 5'
semiaxis_b = '10 8'
exponent = '2 3'
prevent_overlap = true
semiaxis_c_variation = '0 0'
semiaxis_c = '1 1'
[../]
[]
[Executioner]
type = Transient
scheme = bdf2
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type -ksp_gmres_restart -mat_mffd_type'
petsc_options_value = 'hypre boomeramg 31 ds'
l_max_its = 20
l_tol = 1e-4
nl_max_its = 20
nl_rel_tol = 1e-9
nl_abs_tol = 1e-11
start_time = 0.0
num_steps = 1
dt = 100.0
enable = false
[./Adaptivity]
refine_fraction = .5
[../]
[]
[Outputs]
exodus = true
[]
[Problem]
type = FEProblem
solve = false
[]
test/tests/transfers/multiapp_copy_transfer/errors/sub.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Outputs]
exodus = true
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_4/cyl4_template1.i
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Mesh]
file = cyl4_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./stress_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./stress_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x16]
type = NodalVariableValue
nodeid = 15
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y16]
type = NodalVariableValue
nodeid = 15
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x9 disp_y9 disp_x16 disp_y16 stress_yy stress_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_4/cyl4_mu_0_2_pen.i
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Mesh]
file = cyl4_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./stress_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./stress_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x16]
type = NodalVariableValue
nodeid = 15
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y16]
type = NodalVariableValue
nodeid = 15
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = cyl4_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = cyl4_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x9 disp_y9 disp_x16 disp_y16 stress_yy stress_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
friction_coefficient = 0.2
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
modules/stochastic_tools/test/tests/multiapps/batch_commandline_control/sub.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Variables]
[u]
initial_condition = 1980
[]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Postprocessors]
[size]
type = AverageElementSize
execute_on = 'initial'
[]
[]
[Outputs]
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_1/cyl1_template1.i
#
# This input file is a template for both the frictionless and glued test
# variations for the current problem geometry. In order to create an input
# file to run outside the runtest framework, look at the tests file and add the
# appropriate input file lines from the cli_args line.
#
[GlobalParams]
volumetric_locking_correction = true
displacements = 'disp_x disp_y'
[]
[Mesh]
file = cyl1_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x7]
type = NodalVariableValue
nodeid = 6
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y7]
type = NodalVariableValue
nodeid = 6
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x7 disp_y7 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
normalize_penalty = true
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
tutorials/darcy_thermo_mech/step02_darcy_pressure/problems/step2.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables/pressure]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
permeability = 0.8451e-9 # (m^2) 1mm spheres.
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
tutorials/darcy_thermo_mech/step05_heat_conduction/problems/step5a_steady.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[temperature]
[]
[]
[Kernels]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[]
[BCs]
[inlet_temperature]
type = DirichletBC
variable = temperature
boundary = left
value = 350 # (K)
[]
[outlet_temperature]
type = DirichletBC
variable = temperature
boundary = right
value = 300 # (K)
[]
[]
[Materials]
[steel]
type = GenericConstantMaterial
prop_names = thermal_conductivity
prop_values = 18 # K: (W/m*K) from wikipedia @296K
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = NEWTON
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
modules/stochastic_tools/examples/batch/sub.i
[Mesh]
type = GeneratedMesh
dim = 3
nx = 10
ny = 10
nz = 10
[]
[Variables]
[u]
[]
[]
[Kernels]
[diff]
type = ADDiffusion
variable = u
[]
[time]
type = ADTimeDerivative
variable = u
[]
[]
[BCs]
[left]
type = DirichletBC
variable = u
boundary = left
value = 0
[]
[right]
type = DirichletBC
variable = u
boundary = right
value = 1
[]
[]
[Postprocessors]
[average]
type = AverageNodalVariableValue
variable = u
[]
[]
[Problem]
type = FEProblem
[]
[Executioner]
type = Transient
num_steps = 1
dt = 0.25
solve_type = NEWTON
[]
[Controls]
[receiver]
type = SamplerReceiver
[]
[]
[Outputs]
[]
tutorials/darcy_thermo_mech/step07_adaptivity/problems/step7a_coarse.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 30
ny = 3
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
temperature = temperature
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
exodus = true
[]
modules/stochastic_tools/test/tests/multiapps/batch_commandline_control/master_multiple.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Distributions]
[uniform]
type = UniformDistribution
lower_bound = 5
upper_bound = 10
[]
[]
[Samplers]
[sample]
type = MonteCarloSampler
num_rows = 3
distributions = 'uniform uniform'
execute_on = 'PRE_MULTIAPP_SETUP'
[]
[]
[MultiApps]
[sub]
type = SamplerFullSolveMultiApp
sampler = sample
input_files = 'sub.i'
[]
[]
[Transfers]
[data]
type = SamplerPostprocessorTransfer
multi_app = sub
sampler = sample
to_vector_postprocessor = storage
from_postprocessor = size
[]
[]
[VectorPostprocessors]
[storage]
type = StochasticResults
samplers = sample
[]
[]
[Controls]
[cmdline]
type = MultiAppCommandLineControl
multi_app = sub
sampler = sample
param_names = 'Mesh/xmax Mesh/ymax'
[]
[]
[Outputs]
[out]
type = CSV
execute_on = FINAL
[]
[]
test/tests/preconditioners/fsp/fsp_test_image.i
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 41
ny = 41
[]
[./image]
input = gen
type = ImageSubdomainGenerator
file = kitten.png
threshold = 100
[../]
[]
[Variables]
[./u]
order = FIRST
family = LAGRANGE
block = 1
[../]
[./v]
order = FIRST
family = LAGRANGE
block = 1
[../]
[]
[Kernels]
[./diff_u]
type = Diffusion
variable = u
[../]
[./conv_v]
type = CoupledForce
variable = v
v = u
[../]
[./diff_v]
type = Diffusion
variable = v
[../]
[]
[BCs]
active = 'left_u left_v right_u'
[./left_u]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right_u]
type = DirichletBC
variable = u
boundary = right
value = 100
[../]
[./left_v]
type = DirichletBC
variable = v
boundary = left
value = 0
[../]
[./right_v]
type = DirichletBC
variable = v
boundary = right
value = 0
[../]
[]
[Problem]
type = FEProblem
material_coverage_check = false
kernel_coverage_check = false
[]
[Executioner]
# This is setup automatically in MOOSE (SetupPBPAction.C)
# petsc_options = '-snes_mf_operator'
# petsc_options_iname = '-pc_type'
# petsc_options_value = 'asm'
type = Steady
[]
[Preconditioning]
[./FSP]
# It is the starting point of splitting
type = FSP
topsplit = 'uv' # 'uv'
[./uv]
# Generally speaking, there are four types of splitting we could choose
# <additive,multiplicative,symmetric_multiplicative,schur>
# An approximate solution to the original system
# | A_uu A_uv | | u | _ |f_u|
# | 0 A_vv | | v | - |f_v|
# is obtained by solving the following subsystems
# A_uu u = f_u and A_vv v = f_v
# If splitting type is specified as schur, we may also want to set more options to
# control how schur works using PETSc options
# petsc_options_iname = '-pc_fieldsplit_schur_fact_type -pc_fieldsplit_schur_precondition'
# petsc_options_value = 'full selfp'
splitting = 'u v' # 'u' and 'v'
splitting_type = additive
[../]
[./u]
# PETSc options for this subsolver
# A prefix will be applied, so just put the options for this subsolver only
vars = u
petsc_options_iname = '-pc_type -ksp_type'
petsc_options_value = ' hypre preonly'
[../]
[./v]
# PETSc options for this subsolver
vars = v
petsc_options_iname = '-pc_type -ksp_type'
petsc_options_value = ' hypre preonly'
[../]
[../]
[]
[Outputs]
file_base = kitten_out
exodus = true
[]
test/tests/mesh_modifiers/subdomain_bounding_box/oriented_subdomain_bounding_box.i
[Mesh]
type = GeneratedMesh
dim = 3
xmin = -6
xmax = 4
nx = 10
ymin = -2
ymax = 10
ny = 12
zmin = -5
zmax = 7
nz = 12
[]
[MeshModifiers]
[./subdomains]
type = OrientedSubdomainBoundingBox
center = '-1 4 1'
width = 5
length = 10
height = 4
width_direction = '2 1 0'
length_direction = '-1 2 2'
block_id = 10
[../]
[]
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Variables]
[./u]
[../]
[]
[Executioner]
type = Steady
solve_type = PJFNK
[]
[Outputs]
exodus = true
[]
test/tests/misc/block_user_object_check/block_check.i
[Mesh]
[./generator]
type = GeneratedMeshGenerator
dim = 2
nx = 10
ny = 5
[../]
[./left_block]
type = SubdomainBoundingBoxGenerator
input = generator
block_id = 1
bottom_left = '0 0 0'
top_right = '0.5 1 0'
[../]
[./right_block]
type = SubdomainBoundingBoxGenerator
input = left_block
block_id = 2
bottom_left = '0.5 0 0'
top_right = '1 1 0'
[../]
[]
[Variables]
[./var_1]
block = 1
initial_condition = 100
[../]
[./var_2]
block = 2
initial_condition = 200
[../]
[]
[Problem]
type = FEProblem
kernel_coverage_check = true
solve = false
[]
[Executioner]
type = Steady
[]
[Postprocessors]
[./obj]
type = NodalMaxValue
variable = var_1
#block = 1 # this is what being tested, see the test spec
execute_on = 'initial'
[../]
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_4/cyl4_mu_0_2_pen_sm.i
[Mesh]
file = cyl4_mesh.e
[]
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./stress_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./stress_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x16]
type = NodalVariableValue
nodeid = 15
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y16]
type = NodalVariableValue
nodeid = 15
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = cyl4_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = cyl4_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x9 disp_y9 disp_x16 disp_y16 stress_yy stress_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
friction_coefficient = 0.2
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
modules/phase_field/test/tests/phase_field_crystal/PFC_IC/PFC_IC_BCC_test.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 100
xmax = 15
ymax = 15
[]
[Variables]
[./rho]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = rho
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 0
[]
[Outputs]
exodus = true
[]
[ICs]
[./rho_IC]
y2 = 12.5
lc = 5
y1 = 2.5
x2 = 12.5
crystal_structure = BCC
variable = rho
x1 = 2.5
type = PFCFreezingIC
min = .3
max = .7
[../]
[]
test/tests/auxkernels/vector_function_aux/vector_function_aux.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 2
ny = 2
[]
[AuxVariables]
[vec]
family = LAGRANGE_VEC
order = FIRST
[]
[]
[Variables]
[u][]
[]
[Functions]
[function]
type = ParsedVectorFunction
value_x = t*x
value_y = t*y
[]
[]
[AuxKernels]
[vec]
type = VectorFunctionAux
variable = vec
function = function
execute_on = 'INITIAL TIMESTEP_END'
[../]
[]
[Problem]
type = FEProblem
#solve = false
kernel_coverage_check = false
[]
[Executioner]
type = Transient
start_time = 0.0
num_steps = 5
dt = 1
[]
[Outputs]
exodus = true
[]
test/tests/transfers/transfer_on_final/master.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[u]
initial_condition = 1234
[]
[v]
initial_condition = 2458
[]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 4
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[MultiApps]
[sub]
type = TransientMultiApp
input_files = sub.i
execute_on = 'INITIAL TIMESTEP_END'
[]
[]
[Transfers]
[from_sub]
type = MultiAppCopyTransfer
direction = from_multiapp
source_variable = u
variable = u
multi_app = sub
check_multiapp_execute_on = false
execute_on = 'FINAL'
[]
[to_sub]
type = MultiAppCopyTransfer
direction = to_multiapp
source_variable = v
variable = v
multi_app = sub
check_multiapp_execute_on = false
execute_on = 'FINAL'
[]
[]
[Outputs]
exodus = true
[final]
type = Exodus
execute_on = 'FINAL'
execute_input_on = 'NONE' # This is needed to avoid problems with creating a file w/o data during --recover testing
[]
[]
test/tests/transfers/multiapp_copy_transfer/array_variable_transfer/master.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
# Array variable with two components
[v]
order = FIRST
family = LAGRANGE
components = 2
[]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[MultiApps]
[./sub]
type = FullSolveMultiApp
input_files = sub.i
execute_on = initial
[../]
[]
[Transfers]
# Transfers all components together on the same mesh.
[./from_sub]
type = MultiAppCopyTransfer
direction = from_multiapp
source_variable = u
variable = v
multi_app = sub
[../]
[]
[Outputs]
exodus = true
[]
test/tests/executioners/pp_binding/pp_binding_check.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Variables]
[./u]
[../]
[]
[Postprocessors]
[./ndofs]
type = NumDOFs
[../]
[]
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Executioner]
type = PPBindingSteady
postprocessor = ndofs
[]
[Outputs]
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_3/cyl3_mu_0_2_pen.i
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Mesh]
file = cyl3_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x11]
type = NodalVariableValue
nodeid = 10
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y11]
type = NodalVariableValue
nodeid = 10
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = cyl3_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = cyl3_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x11 disp_y11 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
tangential_tolerance = 1e-3
friction_coefficient = 0.2
penalty = 1e+9
[../]
[]
test/tests/functions/image_function/error/check_error.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 20
ny = 20
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./tif]
type = ImageFunction
file_base = stack/test
file_suffix = png
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = tif
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
test/tests/postprocessors/cumulative_value_postprocessor/cumulative_value_postprocessor.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
[../]
[]
[Kernels]
[./time_derivative]
type = TimeDerivative
variable = u
[../]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
scheme = implicit-euler
[./TimeStepper]
type = ConstantDT
dt = 0.01
[../]
start_time = 0.0
num_steps = 2
solve_type = 'NEWTON'
petsc_options_iname = '-pc_type'
petsc_options_value = 'lu'
[]
[Postprocessors]
[./nonlin_it]
type = NumNonlinearIterations
[../]
[./cumulative_nonlin_it]
type = CumulativeValuePostprocessor
postprocessor = nonlin_it
[../]
[]
[Outputs]
csv = true
[]
test/tests/functions/image_function/flip_quad.i
[Mesh]
uniform_refine = 1
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 20
ny = 20
xmax = 2
ymax = 2
[]
# Define block IDs for the four quadrants in CCW order:
# 1=top_right
# 2=top_left
# 3=bottom_left
# 4=bottom_right
[./top_right_modifier]
input = gen
type = SubdomainBoundingBoxGenerator
top_right = '2 2 0'
bottom_left = '1 1 0'
block_id = 1
[../]
[./top_left_modifier]
input = top_right_modifier
type = SubdomainBoundingBoxGenerator
top_right = '1 2 0'
bottom_left = '0 1 0'
block_id = 2
[../]
[./bottom_left_modifier]
input = top_left_modifier
type = SubdomainBoundingBoxGenerator
top_right = '1 1 0'
bottom_left = '0 0 0'
block_id = 3
[../]
[./bottom_right_modifier]
input = bottom_left_modifier
type = SubdomainBoundingBoxGenerator
top_right = '2 1 0'
bottom_left = '1 0 0'
block_id = 4
[../]
[]
[Variables]
[./u]
family = MONOMIAL
order = CONSTANT
[../]
[]
[Functions]
[./bottom_left_func]
type = ImageFunction
file_base = stack/test
flip_x = true
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
file_suffix = png
origin = '0 0 0'
dimensions = '1 1 0'
[../]
[./top_left_func]
type = ImageFunction
file_base = stack/test
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
file_suffix = png
origin = '0 1 0'
dimensions = '1 1 0'
flip_x = true
flip_y = true
[../]
[./top_right_func]
type = ImageFunction
origin = '1 1 0'
file_base = stack/test
file_suffix = png
flip_y = true
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
dimensions = '1 1 0'
[../]
[./bottom_right_func]
type = ImageFunction
origin = '1 0 0'
file_base = stack/test
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
file_suffix = png
dimensions = '1 1 0'
[../]
[]
[ICs]
# Defined the same way as the MeshGenerators
[./top_right_ic]
function = top_right_func
variable = u
type = FunctionIC
block = 1
[../]
[./top_left_ic]
function = top_left_func
variable = u
type = FunctionIC
block = 2
[../]
[./bottom_left_ic]
function = bottom_left_func
variable = u
type = FunctionIC
block = 3
[../]
[./bottom_right_ic]
function = bottom_right_func
variable = u
type = FunctionIC
block = 4
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
test/tests/transfers/multiapp_copy_transfer/constant_monomial_from_sub/sub.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[AuxVariables]
[./aux]
family = MONOMIAL
order = CONSTANT
[../]
[]
[AuxKernels]
[./aux]
type = FunctionAux
variable = aux
execute_on = initial
function = 10*x*y
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Variables]
[./u]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 1
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 2
[../]
[]
[Executioner]
type = Transient
num_steps = 1
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
hide = 'u'
exodus = true
[]
tutorials/darcy_thermo_mech/step05_heat_conduction/problems/step5c_outflow.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[Kernels]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[]
[BCs]
[inlet_temperature]
type = DirichletBC
variable = temperature
boundary = left
value = 350 # (K)
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[steel]
type = GenericConstantMaterial
prop_names = 'thermal_conductivity specific_heat density'
prop_values = '18 466 8000' # W/m*K, J/kg-K, kg/m^3 @ 296K
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
num_steps = 10
solve_type = NEWTON
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
test/tests/transfers/multiapp_copy_transfer/constant_monomial_to_sub/sub.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
family = MONOMIAL
order = CONSTANT
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Outputs]
exodus = true
[]
modules/solid_mechanics/test/tests/crack_loop/crack_loop.i
[Mesh]
file = crack_loop.e
[]
[Problem]
type = FEProblem
solve = false
[]
[UserObjects]
[./crack]
type = CrackFrontDefinition
crack_direction_method = CurvedCrackFront
boundary = 1001
[../]
[]
[Executioner]
type = Steady
[]
modules/combined/test/tests/contact_verification/patch_tests/cyl_2/cyl2_mu_0_2_pen.i
[GlobalParams]
volumetric_locking_correction = true
displacements = 'disp_x disp_y'
[]
[Mesh]
file = cyl2_mesh.e
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[Kernels]
[./TensorMechanics]
use_displaced_mesh = true
save_in = 'saved_x saved_y'
[../]
[]
[AuxKernels]
[./stress_xx]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xx
index_i = 0
index_j = 0
execute_on = timestep_end
[../]
[./stress_yy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_yy
index_i = 1
index_j = 1
execute_on = timestep_end
[../]
[./stress_xy]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_xy
index_i = 0
index_j = 1
execute_on = timestep_end
[../]
[./stress_zz]
type = RankTwoAux
rank_two_tensor = stress
variable = stress_zz
index_i = 2
index_j = 2
execute_on = timestep_end
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x5]
type = NodalVariableValue
nodeid = 4
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y5]
type = NodalVariableValue
nodeid = 4
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./side_x]
type = DirichletBC
variable = disp_x
boundary = 2
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '1'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./bot_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '1'
[../]
[./bot_stress]
type = ComputeFiniteStrainElasticStress
block = '1'
[../]
[./top_elas_tens]
type = ComputeIsotropicElasticityTensor
block = '2'
youngs_modulus = 1e6
poissons_ratio = 0.3
[../]
[./top_strain]
type = ComputeAxisymmetricRZIncrementalStrain
block = '2'
[../]
[./top_stress]
type = ComputeFiniteStrainElasticStress
block = '2'
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-7
nl_rel_tol = 1e-6
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-4
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = cyl2_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = cyl2_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x5 disp_y5 disp_x9 disp_y9 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
tangential_tolerance = 1e-3
friction_coefficient = 0.2
penalty = 1e+9
[../]
[]
modules/heat_conduction/test/tests/meshed_gap_thermal_contact/meshed_gap_thermal_contact_constant_conductance.i
[Mesh]
[fmesh]
type = FileMeshGenerator
file = meshed_gap.e
[]
[block0]
type = SubdomainBoundingBoxGenerator
input = fmesh
bottom_left = '.5 -.5 0'
top_right = '.7 .5 0'
block_id = 4
[]
[]
[Variables]
[./temp]
block = '1 3'
initial_condition = 1.0
[../]
[]
[Kernels]
[./hc]
type = HeatConduction
variable = temp
block = '1 3'
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = temp
boundary = 1
value = 1
[../]
[./right]
type = DirichletBC
variable = temp
boundary = 4
value = 2
[../]
[]
[ThermalContact]
[./gap_conductance]
type = GapHeatTransfer
variable = temp
master = 2
slave = 3
gap_conductance = 2.5
[../]
[]
[Materials]
[./hcm]
type = HeatConductionMaterial
block = '1 3'
temp = temp
thermal_conductivity = 1
[../]
[]
[Problem]
type = FEProblem
kernel_coverage_check = false
material_coverage_check = false
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
[./out]
type = Exodus
[../]
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_3/ring3_mu_0_2_pen_sm.i
[Mesh]
file = ring3_mesh.e
[]
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x2]
type = NodalVariableValue
nodeid = 1
variable = disp_x
[../]
[./disp_x11]
type = NodalVariableValue
nodeid = 10
variable = disp_x
[../]
[./disp_y2]
type = NodalVariableValue
nodeid = 1
variable = disp_y
[../]
[./disp_y11]
type = NodalVariableValue
nodeid = 10
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-10
nl_rel_tol = 1e-9
l_max_its = 100
nl_max_its = 1000
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
file_base = ring3_mu_0_2_pen_out
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
file_base = ring3_mu_0_2_pen_check
show = 'bot_react_x bot_react_y disp_x2 disp_y2 disp_x11 disp_y11 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
model = coulomb
formulation = penalty
normalize_penalty = true
tangential_tolerance = 1e-3
friction_coefficient = 0.2
penalty = 1e+9
[../]
[]
tutorials/darcy_thermo_mech/step04_velocity_aux/problems/step4.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables/pressure]
[]
[AuxVariables]
[velocity_x]
order = CONSTANT
family = MONOMIAL
[]
[velocity_y]
order = CONSTANT
family = MONOMIAL
[]
[velocity_z]
order = CONSTANT
family = MONOMIAL
[]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[velocity_x]
type = VectorVariableComponentAux
variable = velocity_x
component = x
execute_on = timestep_end
vector_variable = velocity
[]
[velocity_y]
type = VectorVariableComponentAux
variable = velocity_y
component = y
execute_on = timestep_end
vector_variable = velocity
[]
[velocity_z]
type = VectorVariableComponentAux
variable = velocity_z
component = z
execute_on = timestep_end
vector_variable = velocity
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = PJFNK
#nl_rel_tol = 1e-12
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
test/tests/functions/image_function/shift_and_scale.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 20
ny = 20
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
type = ImageFunction
file_base = stack/test
file_suffix = png
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
shift = -62735.0
scale = 0.0001
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
modules/phase_field/test/tests/reconstruction/2phase_reconstruction3.i
#
# In this test , which is set up similarly to 2phase_reconstruction_test2.i
# we demonstrate that the feature numbers in the EBSD file can be chosen arbitrarily.
# There is no need for then to start at a certain index or even to be contiguous!
# The EBSDReaderPointDataAux AuxKernel outputs the original feature IDs (grain numbers)
#
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Mesh]
type = EBSDMesh
filename = Renumbered.txt
[]
[GlobalParams]
op_num = 2
var_name_base = gr
[]
[UserObjects]
[./ebsd_reader]
type = EBSDReader
[../]
[./ebsd]
type = PolycrystalEBSD
coloring_algorithm = bt
ebsd_reader = ebsd_reader
phase = 1
output_adjacency_matrix = true
[../]
[]
[ICs]
[./PolycrystalICs]
[./PolycrystalColoringIC]
polycrystal_ic_uo = ebsd
[../]
[../]
[]
[AuxVariables]
[./GRAIN]
family = MONOMIAL
order = CONSTANT
[../]
[]
[AuxKernels]
[./grain_aux]
type = EBSDReaderPointDataAux
variable = GRAIN
ebsd_reader = ebsd_reader
data_name = 'feature_id'
execute_on = 'initial'
[../]
[]
[Variables]
[./PolycrystalVariables]
[../]
[]
[Executioner]
type = Transient
num_steps = 0
[]
[Outputs]
exodus = true
[]
test/tests/transfers/multiapp_copy_transfer/third_monomial_from_sub/master.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
family = MONOMIAL
order = THIRD
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[MultiApps]
[./sub]
type = FullSolveMultiApp
input_files = sub.i
execute_on = initial
[../]
[]
[Transfers]
[./from_sub]
type = MultiAppCopyTransfer
direction = from_multiapp
source_variable = aux
variable = u
multi_app = sub
[../]
[]
[Outputs]
exodus = true
[]
test/tests/transfers/multiapp_conservative_transfer/sub_conservative_transfer.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 20
ny = 20
xmin = 0.05
xmax = 1.2
ymin = 0.05
ymax = 1.1
[]
[Variables]
[./u]
[../]
[]
[Kernels]
[./diff]
type = Diffusion
variable = u
[../]
[./coupledforce]
type = CoupledForce
variable = u
v = aux_u
[../]
[]
[AuxVariables]
[./aux_u]
family = LAGRANGE
order = FIRST
[../]
[]
[BCs]
[./left]
type = DirichletBC
variable = u
boundary = left
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = right
value = 1
[../]
[]
[Postprocessors]
[./to_postprocessor]
type = ElementIntegralVariablePostprocessor
variable = aux_u
execute_on = 'transfer nonlinear TIMESTEP_END'
[../]
[]
[Problem]
type = FEProblem
[]
[Executioner]
type = Steady
solve_type = 'PJFNK'
nl_abs_tol = 1e-12
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
tutorials/darcy_thermo_mech/step11_action/problems/step11.i
[GlobalParams]
displacements = 'disp_r disp_z'
[]
[Mesh]
type = GeneratedMesh
dim = 2
ny = 200
nx = 10
ymax = 0.304 # Length of test chamber
xmax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[DarcyThermoMech]
[]
[Modules/TensorMechanics/Master]
[all]
# This block adds all of the proper Kernels, strain calculators, and Variables
# for TensorMechanics in the correct coordinate system (autodetected)
add_variables = true
strain = FINITE
eigenstrain_names = eigenstrain
use_automatic_differentiation = true
generate_output = 'vonmises_stress elastic_strain_xx elastic_strain_yy strain_xx strain_yy'
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = bottom
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = top
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = bottom
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = top
[]
[hold_inlet]
type = DirichletBC
variable = disp_z
boundary = bottom
value = 0
[]
[hold_center]
type = DirichletBC
variable = disp_r
boundary = left
value = 0
[]
[hold_outside]
type = DirichletBC
variable = disp_r
boundary = right
value = 0
[]
[]
[Materials]
viscosity_file = data/water_viscosity.csv
density_file = data/water_density.csv
thermal_conductivity_file = data/water_thermal_conductivity.csv
specific_heat_file = data/water_specific_heat.csv
thermal_expansion_file = data/water_thermal_expansion.csv
[column]
type = PackedColumn
block = 0
temperature = temperature
radius = 1.15
fluid_viscosity_file = ${viscosity_file}
fluid_density_file = ${density_file}
fluid_thermal_conductivity_file = ${thermal_conductivity_file}
fluid_specific_heat_file = ${specific_heat_file}
fluid_thermal_expansion_file = ${thermal_expansion_file}
[]
[elasticity_tensor]
type = ComputeIsotropicElasticityTensor
youngs_modulus = 200e9 # (Pa) from wikipedia
poissons_ratio = .3 # from wikipedia
[]
[elastic_stress]
type = ADComputeFiniteStrainElasticStress
[]
[thermal_strain]
type = ADComputeThermalExpansionEigenstrain
stress_free_temperature = 300
eigenstrain_name = eigenstrain
temperature = temperature
thermal_expansion_coeff = 1e-5
[]
[]
[Postprocessors]
[average_temperature]
type = ElementAverageValue
variable = temperature
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Executioner]
type = Transient
start_time = -1
end_time = 200
steady_state_tolerance = 1e-7
steady_state_detection = true
dt = 0.25
solve_type = PJFNK
automatic_scaling = true
compute_scaling_once = false
petsc_options_iname = '-pc_type -pc_hypre_type -ksp_gmres_restart'
petsc_options_value = 'hypre boomeramg 500'
line_search = none
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
[out]
type = Exodus
elemental_as_nodal = true
[]
[]
tutorials/darcy_thermo_mech/step03_darcy_material/problems/step3b.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables/pressure]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Materials]
[column]
type = PackedColumn
radius = '1 + 2/3.04*x'
outputs = exodus
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
test/tests/quadrature/order/elem5_side7.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 1
ny = 1
nz = 0
elem_type = QUAD4
[]
[Postprocessors]
[./numsideqps]
type = NumSideQPs
boundary = 0
[../]
[./numelemqps]
type = NumElemQPs
block = 0
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[./Quadrature]
order = third
element_order = fifth
side_order = seventh
[]
[]
[Outputs]
execute_on = 'timestep_end'
exodus = false
csv = true
[]
modules/combined/test/tests/contact_verification/patch_tests/ring_4/ring4_template1_sm.i
[Mesh]
file = ring4_mesh.e
[]
[GlobalParams]
order = SECOND
displacements = 'disp_x disp_y'
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Variables]
[./disp_x]
[../]
[./disp_y]
[../]
[]
[AuxVariables]
[./stress_xx]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_yy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_xy]
order = CONSTANT
family = MONOMIAL
[../]
[./stress_zz]
order = CONSTANT
family = MONOMIAL
[../]
[./penetration]
[../]
[./saved_x]
[../]
[./saved_y]
[../]
[./diag_saved_x]
[../]
[./diag_saved_y]
[../]
[./inc_slip_x]
[../]
[./inc_slip_y]
[../]
[./accum_slip_x]
[../]
[./accum_slip_y]
[../]
[./tang_force_x]
[../]
[./tang_force_y]
[../]
[]
[SolidMechanics]
[./solid]
disp_r = disp_x
disp_z = disp_y
save_in_disp_z = saved_y
save_in_disp_r = saved_x
diag_save_in_disp_z = diag_saved_y
diag_save_in_disp_r = diag_saved_x
[../]
[]
[AuxKernels]
[./stress_xx]
type = MaterialTensorAux
tensor = stress
variable = stress_xx
index = 0
[../]
[./stress_yy]
type = MaterialTensorAux
tensor = stress
variable = stress_yy
index = 1
[../]
[./stress_xy]
type = MaterialTensorAux
tensor = stress
variable = stress_xy
index = 3
[../]
[./inc_slip_x]
type = PenetrationAux
variable = inc_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./inc_slip_y]
type = PenetrationAux
variable = inc_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_x]
type = PenetrationAux
variable = accum_slip_x
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./accum_slip_y]
type = PenetrationAux
variable = accum_slip_y
execute_on = timestep_end
boundary = 3
paired_boundary = 4
[../]
[./penetration]
type = PenetrationAux
variable = penetration
boundary = 3
paired_boundary = 4
[../]
[./tang_force_x]
type = PenetrationAux
variable = tang_force_x
quantity = tangential_force_x
boundary = 3
paired_boundary = 4
[../]
[./tang_force_y]
type = PenetrationAux
variable = tang_force_y
quantity = tangential_force_y
boundary = 3
paired_boundary = 4
[../]
[] # AuxKernels
[Postprocessors]
[./bot_react_x]
type = NodalSum
variable = saved_x
boundary = 1
[../]
[./bot_react_y]
type = NodalSum
variable = saved_y
boundary = 1
[../]
[./top_react_x]
type = NodalSum
variable = saved_x
boundary = 5
[../]
[./top_react_y]
type = NodalSum
variable = saved_y
boundary = 5
[../]
[./ref_resid_x]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_x
[../]
[./ref_resid_y]
type = NodalL2Norm
execute_on = timestep_end
variable = saved_y
[../]
[./sigma_yy]
type = ElementAverageValue
variable = stress_yy
[../]
[./sigma_zz]
type = ElementAverageValue
variable = stress_zz
[../]
[./disp_x16]
type = NodalVariableValue
nodeid = 15
variable = disp_x
[../]
[./disp_x9]
type = NodalVariableValue
nodeid = 8
variable = disp_x
[../]
[./disp_y16]
type = NodalVariableValue
nodeid = 15
variable = disp_y
[../]
[./disp_y9]
type = NodalVariableValue
nodeid = 8
variable = disp_y
[../]
[./_dt]
type = TimestepSize
[../]
[./num_lin_it]
type = NumLinearIterations
[../]
[./num_nonlin_it]
type = NumNonlinearIterations
[../]
[]
[BCs]
[./bot_y]
type = DirichletBC
variable = disp_y
boundary = 1
value = 0.0
[../]
[./top_press]
type = Pressure
variable = disp_y
boundary = 5
component = 1
factor = 109.89
[../]
[]
[Materials]
[./bot]
type = Elastic
block = 1
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[./top]
type = Elastic
block = 2
disp_z = disp_y
disp_r = disp_x
poissons_ratio = 0.3
youngs_modulus = 1e6
[../]
[]
[Executioner]
type = Transient
#Preconditioned JFNK (default)
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist'
line_search = 'none'
nl_abs_tol = 1e-10
nl_rel_tol = 1e-9
l_max_its = 50
nl_max_its = 100
dt = 1.0
end_time = 1.0
num_steps = 10
dtmin = 1.0
l_tol = 1e-5
[]
[VectorPostprocessors]
[./x_disp]
type = NodalValueSampler
variable = disp_x
boundary = '1 3 4 5'
sort_by = x
[../]
[./cont_press]
type = NodalValueSampler
variable = contact_pressure
boundary = '3'
sort_by = x
[../]
[]
[Outputs]
print_linear_residuals = true
perf_graph = true
[./exodus]
type = Exodus
elemental_as_nodal = true
[../]
[./console]
type = Console
max_rows = 5
[../]
[./chkfile]
type = CSV
show = 'bot_react_x bot_react_y disp_x9 disp_y9 disp_x16 disp_y16 sigma_yy sigma_zz top_react_x top_react_y x_disp cont_press'
execute_vector_postprocessors_on = timestep_end
[../]
[./outfile]
type = CSV
delimiter = ' '
execute_vector_postprocessors_on = none
[../]
[]
[Contact]
[./leftright]
slave = 3
master = 4
system = constraint
normalize_penalty = true
tangential_tolerance = 1e-3
penalty = 1e+9
[../]
[]
test/tests/transfers/multiapp_copy_transfer/third_monomial_to_sub/sub.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
[]
[Variables]
[./u]
family = MONOMIAL
order = THIRD
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[]
[Outputs]
exodus = true
[]
modules/porous_flow/examples/co2_intercomparison/1Dradial/1Dradial.i
# Intercomparison problem 3: Radial flow from an injection well
#
# From Pruess et al, Code intercomparison builds confidence in
# numerical simulation models for geologic disposal of CO2, Energy 29 (2004)
#
# A variation with zero salinity can be run by changing the initial condition
# of the AuxVariable xnacl
[Mesh]
type = GeneratedMesh
dim = 1
nx = 500
xmax = 10000
bias_x = 1.01
[]
[Problem]
type = FEProblem
coord_type = 'RZ'
rz_coord_axis = Y
[]
[GlobalParams]
PorousFlowDictator = 'dictator'
gravity = '0 0 0'
[]
[AuxVariables]
[pressure_liquid]
order = CONSTANT
family = MONOMIAL
[]
[saturation_gas]
order = CONSTANT
family = MONOMIAL
[]
[x1]
order = CONSTANT
family = MONOMIAL
[]
[y0]
order = CONSTANT
family = MONOMIAL
[]
[xnacl]
initial_condition = 0.15
[]
[]
[AuxKernels]
[pressure_liquid]
type = PorousFlowPropertyAux
variable = pressure_liquid
property = pressure
phase = 0
execute_on = 'timestep_end'
[]
[saturation_gas]
type = PorousFlowPropertyAux
variable = saturation_gas
property = saturation
phase = 1
execute_on = 'timestep_end'
[]
[x1]
type = PorousFlowPropertyAux
variable = x1
property = mass_fraction
phase = 0
fluid_component = 1
execute_on = 'timestep_end'
[]
[y0]
type = PorousFlowPropertyAux
variable = y0
property = mass_fraction
phase = 1
fluid_component = 0
execute_on = 'timestep_end'
[]
[]
[Variables]
[pgas]
initial_condition = 12e6
[]
[zi]
initial_condition = 0
scaling = 1e4
[]
[]
[Kernels]
[mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pgas
[]
[flux0]
type = PorousFlowAdvectiveFlux
fluid_component = 0
variable = pgas
[]
[mass1]
type = PorousFlowMassTimeDerivative
fluid_component = 1
variable = zi
[]
[flux1]
type = PorousFlowAdvectiveFlux
fluid_component = 1
variable = zi
[]
[]
[UserObjects]
[dictator]
type = PorousFlowDictator
porous_flow_vars = 'pgas zi'
number_fluid_phases = 2
number_fluid_components = 3
[]
[pc]
type = PorousFlowCapillaryPressureVG
alpha = 5.099e-5
m = 0.457
sat_lr = 0.0
pc_max = 1e7
[]
[fs]
type = PorousFlowBrineCO2
brine_fp = brine
co2_fp = co2
capillary_pressure = pc
[]
[]
[Modules]
[FluidProperties]
[co2sw]
type = CO2FluidProperties
[]
[co2]
type = TabulatedFluidProperties
fp = co2sw
[]
[water]
type = Water97FluidProperties
[]
[watertab]
type = TabulatedFluidProperties
fp = water
temperature_min = 273.15
temperature_max = 573.15
fluid_property_file = water_fluid_properties.csv
save_file = false
[]
[brine]
type = BrineFluidProperties
water_fp = watertab
[]
[]
[]
[Materials]
[temperature]
type = PorousFlowTemperature
temperature = '45'
[]
[brineco2]
type = PorousFlowFluidState
gas_porepressure = 'pgas'
z = 'zi'
temperature_unit = Celsius
xnacl = 'xnacl'
capillary_pressure = pc
fluid_state = fs
[]
[porosity]
type = PorousFlowPorosityConst
porosity = '0.12'
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1e-13 0 0 0 1e-13 0 0 0 1e-13'
[]
[relperm_water]
type = PorousFlowRelativePermeabilityVG
m = 0.457
phase = 0
s_res = 0.3
sum_s_res = 0.35
[]
[relperm_gas]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 1
s_res = 0.05
sum_s_res = 0.35
[]
[]
[BCs]
[rightwater]
type = PorousFlowPiecewiseLinearSink
boundary = 'right'
variable = pgas
use_mobility = true
PorousFlowDictator = dictator
fluid_phase = 0
multipliers = '0 1e9'
PT_shift = '12e6'
pt_vals = '0 1e9'
mass_fraction_component = 0
use_relperm = true
[]
[rightco2]
type = PorousFlowPiecewiseLinearSink
variable = zi
boundary = 'right'
use_mobility = true
PorousFlowDictator = dictator
fluid_phase = 1
multipliers = '0 1e9'
PT_shift = '12e6'
pt_vals = '0 1e9'
mass_fraction_component = 1
use_relperm = true
[]
[]
[DiracKernels]
[source]
type = PorousFlowSquarePulsePointSource
point = '0 0 0'
mass_flux = 1
variable = zi
[]
[]
[Preconditioning]
[smp]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type'
petsc_options_value = 'gmres bjacobi lu NONZERO'
[]
[]
[Executioner]
type = Transient
solve_type = NEWTON
end_time = 8.64e8
nl_max_its = 25
l_max_its = 100
dtmax = 5e6
[TimeStepper]
type = IterationAdaptiveDT
dt = 100
[]
[]
[VectorPostprocessors]
[vars]
type = NodalValueSampler
sort_by = x
variable = 'pgas zi xnacl'
execute_on = 'timestep_end'
outputs = spatial
[]
[auxvars]
type = ElementValueSampler
sort_by = x
variable = 'saturation_gas x1 y0'
execute_on = 'timestep_end'
outputs = spatial
[]
[]
[Postprocessors]
[pgas]
type = PointValue
point = '25.25 0 0'
variable = pgas
outputs = time
[]
[sgas]
type = PointValue
point = '25.25 0 0'
variable = saturation_gas
outputs = time
[]
[zi]
type = PointValue
point = '25.25 0 0'
variable = zi
outputs = time
[]
[massgas]
type = PorousFlowFluidMass
fluid_component = 1
outputs = time
[]
[x1]
type = PointValue
point = '25.25 0 0'
variable = x1
outputs = time
[]
[y0]
type = PointValue
point = '25.25 0 0'
variable = y0
outputs = time
[]
[xnacl]
type = PointValue
point = '25.25 0 0'
variable = xnacl
outputs = time
[]
[]
[Outputs]
print_linear_residuals = false
perf_graph = true
sync_times = '2.592e6 8.64e6 8.64e7 8.64e8'
[time]
type = CSV
[]
[spatial]
type = CSV
sync_only = true
[]
[]
test/tests/quadrature/order/order5.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 1
ny = 1
nz = 0
elem_type = QUAD4
[]
[Postprocessors]
[./numsideqps]
type = NumSideQPs
boundary = 0
[../]
[./numelemqps]
type = NumElemQPs
block = 0
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Steady
[./Quadrature]
order = fifth
[]
[]
[Outputs]
execute_on = 'timestep_end'
exodus = false
csv = true
[]
modules/heat_conduction/test/tests/meshed_gap_thermal_contact/meshed_annulus_thermal_contact.i
[Mesh]
[fmesh]
type = FileMeshGenerator
file = meshed_annulus.e
[]
[rename]
type = RenameBlockGenerator
input = fmesh
old_block_id = '1 2 3'
new_block_id = '1 4 3'
[]
[]
[Variables]
[./temp]
block = '1 3'
initial_condition = 1.0
[../]
[]
[Kernels]
[./hc]
type = HeatConduction
variable = temp
block = '1 3'
[../]
[./source]
type = HeatSource
variable = temp
block = 3
value = 10.0
[../]
[]
[BCs]
[./outside]
type = DirichletBC
variable = temp
boundary = 1
value = 1.0
[../]
[]
[ThermalContact]
[./gap_conductivity]
type = GapHeatTransfer
variable = temp
master = 2
slave = 3
gap_conductivity = 0.5
[../]
[]
[Materials]
[./hcm]
type = HeatConductionMaterial
block = '1 3'
temp = temp
thermal_conductivity = 1
[../]
[]
[Problem]
type = FEProblem
kernel_coverage_check = false
material_coverage_check = false
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
[./out]
type = Exodus
[../]
[]
test/tests/misc/block_boundary_material_check/side_uo_check.i
[Mesh]
type = GeneratedMesh
dim = 1
[]
[Variables]
[./u]
[../]
[]
[UserObjects]
[./side_uo]
type = MatSideUserObject
mat_prop = 'foo'
boundary = 1
[../]
[]
[Problem]
type = FEProblem
solve = false
kernel_coverage_check = false
[]
[Executioner]
type = Steady
[]
[Outputs]
[]
test/tests/functions/image_function/crop.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
uniform_refine = 2
xmin = 0.5
ymin = 0.5
[]
[Variables]
[./u]
[../]
[]
[Functions]
[./image_func]
type = ImageFunction
file_base = stack/test
file_range = '0' # file_range is a vector input, a single entry means "read only 1 file"
file_suffix = png
origin = '0 0 0'
dimensions = '1 1 0'
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = image_func
variable = u
[../]
[]
[Problem]
type = FEProblem
solve = false
[]
[Executioner]
type = Transient
num_steps = 1
dt = 0.1
[]
[Outputs]
exodus = true
[]
test/tests/parser/vector_range_checking/all_pass.i
[Mesh]
type = GeneratedMesh
dim = 3
[]
[Materials]
[./vecrangecheck]
type = VecRangeCheckMaterial
block = 0
rv3 = '1.1 2.2 3.3'
iv3 = '1 2 3'
rvp = '0.1 0.2 0.3 0.4'
uvg = '2 1'
lvg = '2 1'
ivg = '2 1'
rvg = '2.0 1.0'
rvl = '0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3'
rve = ''
[../]
[]
[Problem]
type = FEProblem
solve = false
#kernel_check = false
[]
[Executioner]
type = Steady
[]
[Outputs]
execute_on = 'timestep_end'
[]
test/tests/preconditioners/pbp/pbp_test.i
[Mesh]
file = square.e
# init_unif_refine = 6
[]
[Variables]
active = 'u v'
[./u]
order = FIRST
family = LAGRANGE
[../]
[./v]
order = FIRST
family = LAGRANGE
[../]
[]
[Preconditioning]
[./PBP]
type = PBP
solve_order = 'u v'
preconditioner = 'LU LU'
off_diag_row = 'v'
off_diag_column = 'u'
petsc_options = '' # Test petsc options in PBP block
[../]
[]
[Problem]
type = FEProblem
error_on_jacobian_nonzero_reallocation = true
[]
[Kernels]
active = 'diff_u conv_v diff_v'
[./diff_u]
type = Diffusion
variable = u
[../]
[./conv_v]
type = CoupledForce
variable = v
v = u
[../]
[./diff_v]
type = Diffusion
variable = v
[../]
[]
[BCs]
active = 'left_u right_u left_v'
[./left_u]
type = DirichletBC
variable = u
boundary = 1
value = 0
[../]
[./right_u]
type = DirichletBC
variable = u
boundary = 2
value = 100
[../]
[./left_v]
type = DirichletBC
variable = v
boundary = 1
value = 0
[../]
[./right_v]
type = DirichletBC
variable = v
boundary = 2
value = 0
[../]
[]
[Executioner]
type = Steady
l_max_its = 10
nl_max_its = 10
solve_type = JFNK
[]
[Outputs]
file_base = out
exodus = true
[]
test/tests/preconditioners/pbp/pbp_dg_test.i
[Mesh]
type = GeneratedMesh
dim = 2
nx = 20
ny = 20
xmin = 0
xmax = 1
ymin = 0
ymax = 1
elem_type = QUAD4
[]
[Variables]
[./u]
order = FIRST
family = MONOMIAL
[../]
[./v]
order = FIRST
family = MONOMIAL
[../]
[]
[Preconditioning]
[./PBP]
type = PBP
solve_order = 'u v'
preconditioner = 'AMG AMG'
[../]
[]
[Kernels]
[./diff_u]
type = Diffusion
variable = u
[../]
[./abs_u]
type = Reaction
variable = u
[../]
[./forcing_u]
type = BodyForce
variable = u
function = forcing_fn
[../]
[./diff_v]
type = Diffusion
variable = v
[../]
[./abs_v]
type = Reaction
variable = v
[../]
[./forcing_v]
type = BodyForce
variable = v
function = forcing_fn
[../]
[./conv_v]
type = CoupledForce
variable = v
v = u
[../]
[]
[DGKernels]
[./dg_diff]
type = DGDiffusion
variable = u
epsilon = -1
sigma = 6
[../]
[./dg_diff_2]
type = DGDiffusion
variable = v
epsilon = -1
sigma = 6
[../]
[]
[Functions]
[./forcing_fn]
type = ParsedFunction
value = 2*pow(e,-x-(y*y))*(1-2*y*y)
[../]
[./exact_fn]
type = ParsedGradFunction
value = pow(e,-x-(y*y))
grad_x = -pow(e,-x-(y*y))
grad_y = -2*y*pow(e,-x-(y*y))
[../]
[]
[BCs]
[./all_u]
type = DGFunctionDiffusionDirichletBC
variable = u
boundary = '0 1 2 3'
function = exact_fn
epsilon = -1
sigma = 6
[../]
[./all_v]
type = DGFunctionDiffusionDirichletBC
variable = v
boundary = '0 1 2 3'
function = exact_fn
epsilon = -1
sigma = 6
[../]
[]
[Problem]
type = FEProblem
error_on_jacobian_nonzero_reallocation = true
[]
[Executioner]
type = Steady
l_max_its = 10
nl_max_its = 10
solve_type = JFNK
[]
[Outputs]
exodus = true
[]
modules/tensor_mechanics/test/tests/interaction_integral_benchmark/input.i
# Uses InteractionIntegralBenchmarkBC to test the mixed-mode stress intensity
# factor capability. InteractionIntegralBenchmarkBC applies a displacement
# field for which KI = KII = KIII = 1.0. Using the option 2d = true gives a
# q field that is constant along the tangent and returns Ki = 1.0 for all i.
# To get the correct value for all nodes with 2d = false, the mesh around the
# crack tip must be refined and the q-function radii must be reduced by at
# least two orders of magnitude.
[GlobalParams]
order = FIRST
family = LAGRANGE
displacements = 'disp_x disp_y disp_z'
volumetric_locking_correction = true
[]
[Mesh]
file = 360degree_model.e
displacements = 'disp_x disp_y disp_z'
[]
[Problem]
type = FEProblem
[]
[Functions]
[./kifunc]
type = PiecewiseLinear
x = '0.0 1.0 2.0'
y = '0.0 1.0 2.0'
[../]
[]
[DomainIntegral]
integrals = 'JIntegral InteractionIntegralKI InteractionIntegralKII InteractionIntegralKIII'
boundary = 1001
crack_direction_method = CrackDirectionVector
crack_direction_vector = '1 0 0'
radius_inner = '0.5 1.0 1.5 2.0'
radius_outer = '1.0 1.5 2.0 2.5'
youngs_modulus = 30000
poissons_ratio = 0.3
block = 1
2d = true
axis_2d = 2
equivalent_k = True
incremental = true
[]
[AuxVariables]
[./dq_x]
order = CONSTANT
family = MONOMIAL
[../]
[./dq_y]
order = CONSTANT
family = MONOMIAL
[../]
[./dq_z]
order = CONSTANT
family = MONOMIAL
[../]
[]
[Modules/TensorMechanics/Master]
[./master]
strain = FINITE
add_variables = true
incremental = true
generate_output = 'stress_xx stress_yy stress_zz vonmises_stress'
[../]
[]
[BCs]
[./all_x]
type = InteractionIntegralBenchmarkBC
variable = disp_x
component = x
boundary = 1
KI_function = kifunc
KII_function = 1.0
KIII_function = 1.0
youngs_modulus = 30000
poissons_ratio = 0.3
crack_front_definition = crackFrontDefinition
crack_front_point_index = 0
[../]
[./all_y]
type = InteractionIntegralBenchmarkBC
variable = disp_y
component = y
boundary = 1
KI_function = kifunc
KII_function = 1.0
KIII_function = 1.0
youngs_modulus = 30000
poissons_ratio = 0.3
crack_front_definition = crackFrontDefinition
crack_front_point_index = 0
[../]
[./all_z]
type = InteractionIntegralBenchmarkBC
variable = disp_z
component = z
boundary = 1
KI_function = kifunc
KII_function = 1.0
KIII_function = 1.0
youngs_modulus = 30000
poissons_ratio = 0.3
crack_front_definition = crackFrontDefinition
crack_front_point_index = 0
[../]
[]
[Materials]
[./elasticity_tensor]
type = ComputeIsotropicElasticityTensor
youngs_modulus = 30000
poissons_ratio = 0.3
[../]
[./elastic_stress]
type = ComputeFiniteStrainElasticStress
[../]
[]
[Executioner]
type = Transient
petsc_options = '-snes_ksp_ew'
petsc_options_iname = '-ksp_gmres_restart'
petsc_options_value = '101'
line_search = 'none'
l_max_its = 50
nl_max_its = 20
nl_abs_tol = 1e-3
l_tol = 1e-2
start_time = 0.0
dt = 1
end_time = 2
num_steps = 2
[]
[Postprocessors]
[./_dt]
type = TimestepSize
[../]
[./nl_its]
type = NumNonlinearIterations
[../]
[./lin_its]
type = NumLinearIterations
[../]
[]
[Outputs]
execute_on = 'timestep_end'
file_base = 360degree_model_out
exodus = true
csv = true
[]
modules/phase_field/test/tests/boundary_intersecting_features/boundary_intersecting_features.i
[Mesh]
# ImageMesh ignores nx, xmin, xmax (and similarly for y and z) and
# tries to read them from the image file...
type = ImageMesh
dim = 2
# Be sure to choose a corresponding image name below!
# file = image001_cropped3_closing_298.png # full size, 157 Mb Exodus file!
# file = eighth_image001_cropped3_closing_298.png # 1/8
file = sixteenth_image001_cropped3_closing_298.png # 1/16
# Uncomment to maintain 1:1 ratio between number of pixels and mesh size.
# scale_to_one = false
# Uncomment to set cells_per_pixel to something other than the default value of 1.0.
# Must be <= 1.
# cells_per_pixel = .75
# To crop an image to e.g. 1/8th size, install ImageMagick and run:
# convert image001_cropped3_closing_298.png -crop 230x198+100+100 eighth_image001_cropped3_closing_298.png
# Note: Do not use 'sips' on OSX to crop! It actually interpolates
# the colors in the image instead of just cropping.
[]
[Variables]
[./u]
order = CONSTANT
family = MONOMIAL
[../]
[]
[AuxVariables]
[./grain_auxvar]
order = CONSTANT
family = MONOMIAL
[../]
[./centroids]
order = CONSTANT
family = MONOMIAL
[../]
[]
[AuxKernels]
[./nodal_flood_aux]
variable = grain_auxvar
type = FeatureFloodCountAux
flood_counter = flood_count_pp
execute_on = 'initial timestep_end'
[../]
[./centroids]
type = FeatureFloodCountAux
variable = centroids
flood_counter = flood_count_pp
field_display = CENTROID
execute_on = 'initial timestep_end'
[../]
[]
[Functions]
[./tif]
# ImageFunction gets its file range parameters from ImageMesh,
# when it is present. This prevents duplicating information in
# input files.
type = ImageFunction
# In these sample images the features we want to analyze are RED (or close to pure red). The
# background is BLUE so we can easily distinguish between the two by selecting only the red channel.
component = 0
[../]
[]
[ICs]
[./u_ic]
type = FunctionIC
function = tif
variable = u
[../]
[]
[Postprocessors]
[./flood_count_pp]
type = FeatureFloodCount
variable = u
threshold = 1.0
compute_var_to_feature_map = true
execute_on = 'initial timestep_end'
[../]
[]
[VectorPostprocessors]
[./grain_volumes]
type = FeatureVolumeVectorPostprocessor
flood_counter = flood_count_pp
execute_on = 'initial timestep_end'
[../]
[]
[Problem]
type = FEProblem
solve = false
[../]
[Executioner]
type = Steady
[]
[Outputs]
exodus = true
csv = true
[]
Child Objects
- framework/include/problems/ReferenceResidualProblem.h
- test/include/problems/FailingProblem.h
- modules/richards/include/base/RichardsMultiphaseProblem.h
- modules/level_set/include/base/LevelSetReinitializationProblem.h
- test/include/problems/MooseTestProblem.h
- test/include/problems/FixedPointProblem.h
- modules/level_set/include/base/LevelSetProblem.h
- test/include/problems/TagTestProblem.h
framework/include/problems/ReferenceResidualProblem.h
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#pragma once
#include "FEProblem.h"
class ReferenceResidualProblem;
template <>
InputParameters validParams<ReferenceResidualProblem>();
/**
* FEProblemBase derived class to enable convergence checking relative to a user-specified
* postprocessor
*/
class ReferenceResidualProblem : public FEProblem
{
public:
static InputParameters validParams();
ReferenceResidualProblem(const InputParameters & params);
virtual ~ReferenceResidualProblem();
virtual void initialSetup() override;
virtual void timestepSetup() override;
void updateReferenceResidual();
virtual MooseNonlinearConvergenceReason
checkNonlinearConvergence(std::string & msg,
const PetscInt it,
const Real xnorm,
const Real snorm,
const Real fnorm,
const Real rtol,
const Real divtol,
const Real stol,
const Real abstol,
const PetscInt nfuncs,
const PetscInt max_funcs,
const PetscBool force_iteration,
const Real initial_residual_before_preset_bcs,
const Real div_threshold) override;
/**
* Check the convergence by comparing the norm of each variable separately against
* its reference variable's norm. Only consider the solution converged if all
* variables are converged individually using either a relative or absolute
* criterion.
* @param fnorm Function norm (norm of full residual vector)
* @param abstol Absolute convergence tolerance
* @param rtol Relative convergence tolerance
* @param initial_residual_before_preset_bcs Initial norm of full residual vector
* before applying preset bcs
* @return true if all variables are converged
*/
bool checkConvergenceIndividVars(const Real fnorm,
const Real abstol,
const Real rtol,
const Real initial_residual_before_preset_bcs);
/**
* Add solution variables to ReferenceResidualProblem.
* @param sol_vars A set of solution variables that need to be added to ReferenceResidualProblem.
*/
void addSolutionVariables(std::set<std::string> & sol_vars);
/**
* Add reference residual variables to ReferenceResidualProblem.
* @param ref_vars A set of reference residual variables that need to be added to
* ReferenceResidualProblem.
*/
void addReferenceResidualVariables(std::set<std::string> & ref_vars);
/**
* Add a set of variables that need to be grouped together.
* @param group_vars A set of solution variables that need to be grouped.
*/
void addGroupVariables(std::set<std::string> & group_vars);
protected:
///@{
/// List of solution variable names whose reference residuals will be stored,
/// and the residual variable names that will store them.
std::vector<std::string> _soln_var_names;
std::vector<std::string> _ref_resid_var_names;
///@}
///@{
/// List of grouped solution variable names whose reference residuals will be stored,
/// and the residual variable names that will store them.
std::vector<std::string> _group_soln_var_names;
std::vector<std::string> _group_ref_resid_var_names;
///@}
///@{
/// Variable numbers assoicated with the names in _soln_var_names and _ref_resid_var_names.
std::vector<unsigned int> _soln_vars;
std::vector<unsigned int> _ref_resid_vars;
///@}
///@{
/// "Acceptable" absolute and relative tolerance multiplier and
/// acceptable number of iterations. Used when checking the
/// convergence of individual variables.
Real _accept_mult;
int _accept_iters;
///@}
///@{
/// Local storage for *discrete L2 residual norms* of the variables listed in _ref_resid_var_names.
std::vector<Real> _ref_resid;
std::vector<Real> _resid;
///@}
///@{
/// Local storage for *discrete L2 residual norms* of the grouped variables listed in _group_ref_resid_var_names.
std::vector<Real> _group_ref_resid;
std::vector<Real> _group_resid;
///@}
/// Group number index for each variable
std::vector<unsigned int> _variable_group_num_index;
/// Local storage for the scaling factors applied to each of the variables to apply to _ref_resid_vars.
std::vector<Real> _scaling_factors;
/// Name of variables that are grouped together to check convergence
std::vector<std::vector<std::string>> _group_variables;
/// True if any variables are grouped
bool _use_group_variables;
/// The vector storing the reference residual values
const NumericVector<Number> * _reference_vector;
};
test/include/problems/FailingProblem.h
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#pragma once
#include "FEProblem.h"
/**
* FEProblemBase derived class that will fail a prescribed timestep for testing
* timestepping algorithms
*/
class FailingProblem : public FEProblem
{
public:
static InputParameters validParams();
FailingProblem(const InputParameters & params);
virtual bool converged();
protected:
bool _failed;
unsigned int _fail_step;
};
modules/richards/include/base/RichardsMultiphaseProblem.h
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#pragma once
#include "FEProblem.h"
class RichardsMultiphaseProblem;
template <>
InputParameters validParams<RichardsMultiphaseProblem>();
/**
* Allows a constraint u>=v to be enforced during
* the nonlinear iteration process. This is done
* by modifying u (which is called bounded_var below)
*/
class RichardsMultiphaseProblem : public FEProblem
{
public:
RichardsMultiphaseProblem(const InputParameters & params);
virtual ~RichardsMultiphaseProblem();
/**
* extracts the moose variable numbers associated with bounded_var and lower_var
*/
virtual void initialSetup();
/// returns true, indicating that updateSolution should be run
virtual bool shouldUpdateSolution();
/**
* Does the bounding by modifying vec_solution, and then ghosted_solution
* @param vec_solution is the solution that Petsc says we should use.
* @param ghosted_solution is a ghosted version of vec_solution.
* @return true if vec_solution was changed at a node in order to respect the bounds
*/
virtual bool updateSolution(NumericVector<Number> & vec_solution,
NumericVector<Number> & ghosted_solution);
protected:
/// name of the bounded variable (this is the variable that gets altered to respect bounded_var > lower_var)
NonlinearVariableName _bounded_var_name;
/// name of the variable that acts as the lower bound to bounded_var
NonlinearVariableName _lower_var_name;
/// internal moose variable number associated with _bounded_var
unsigned int _bounded_var_num;
/// internal moose variable number associated with _lower_var
unsigned int _lower_var_num;
};
modules/level_set/include/base/LevelSetReinitializationProblem.h
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#pragma once
#include "FEProblem.h"
class LevelSetReinitializationProblem;
template <>
InputParameters validParams<LevelSetReinitializationProblem>();
/**
* A Problem object to perform level set equation reinitialization implementation, mainly
* implementing
* a method to reset the state of the simulation so a solve can be performed again.
*/
class LevelSetReinitializationProblem : public FEProblem
{
public:
LevelSetReinitializationProblem(const InputParameters & parameters);
/**
* Resets the state of the simulation to allow for it to be re-executed.
*/
void resetTime();
};
test/include/problems/MooseTestProblem.h
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#pragma once
#include "FEProblem.h"
class AuxiliarySystem;
/**
* FEProblemBase derived class for customization of callbacks. In this instance we only print out
* something in the c-tor and d-tor, so we know the class was build and used properly.
*/
class MooseTestProblem : public FEProblem
{
public:
static InputParameters validParams();
MooseTestProblem(const InputParameters & params);
virtual ~MooseTestProblem();
private:
std::shared_ptr<AuxiliarySystem> _test_aux;
};
test/include/problems/FixedPointProblem.h
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#pragma once
#include "FEProblem.h"
/**
* FEProblem derived class for lagging a tagged residual.
*/
class FixedPointProblem : public FEProblem
{
public:
static InputParameters validParams();
FixedPointProblem(const InputParameters & params);
virtual void computeResidual(const NumericVector<Number> & soln,
NumericVector<Number> & residual) override;
virtual void computeFullResidual(const NumericVector<Number> & soln,
NumericVector<Number> & residual);
protected:
TagName _tag_previous;
TagID _tag_id;
NumericVector<Number> & _residual_previous;
};
modules/level_set/include/base/LevelSetProblem.h
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#pragma once
#include "FEProblem.h"
class LevelSetProblem;
template <>
InputParameters validParams<LevelSetProblem>();
/**
* Problem that defines a custom call to MultiAppTransfers to allow for
* adaptivity to be transferred from master to sub-application.
*/
class LevelSetProblem : public FEProblem
{
public:
LevelSetProblem(const InputParameters & parameters);
virtual bool adaptMesh() override;
virtual void computeMarkers() override;
};
test/include/problems/TagTestProblem.h
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#pragma once
#include "FEProblem.h"
/**
* FEProblem derived class for customization of callbacks. In this instance we only print out
* something in the c-tor and d-tor, so we know the class was build and used properly.
*/
class TagTestProblem : public FEProblem
{
public:
static InputParameters validParams();
TagTestProblem(const InputParameters & params);
virtual void computeResidual(const NumericVector<Number> & soln,
NumericVector<Number> & residual) override;
virtual void computeJacobian(const NumericVector<Number> & soln,
SparseMatrix<Number> & jacobian) override;
protected:
std::set<std::string> vtags;
std::set<std::string> mtags;
};