Heat and fluid responses in 1D bars
Classic Newton cooling in a bar
Without fluids, mechanical deformation and sinks, the heat equation is where is the porosity, is the rock grain density (kg.m), is the rock grain specific heat capacity (J.kg.K), is the temperature, and is the tensorial thermal conductivity of the porous material (J.s.K.m).
Below, the dynamics of this equation is explored, while this section concentrates on the steady-state situation. Consider the one-dimensional case where a bar sits between and with a fixed temperature at : and a sink flux at the other end: (1) Here is a fixed quantity ("e" stands for "external"), and is a constant conductance (J.m.s.K).
The solution is the linear function The heat sink in Eq. (1) is a linear function of , so the PorousFlowPiecewiseLinearSink may be employed.
The simulation is run in MOOSE using , , , and . The solution is shown in Figure 1
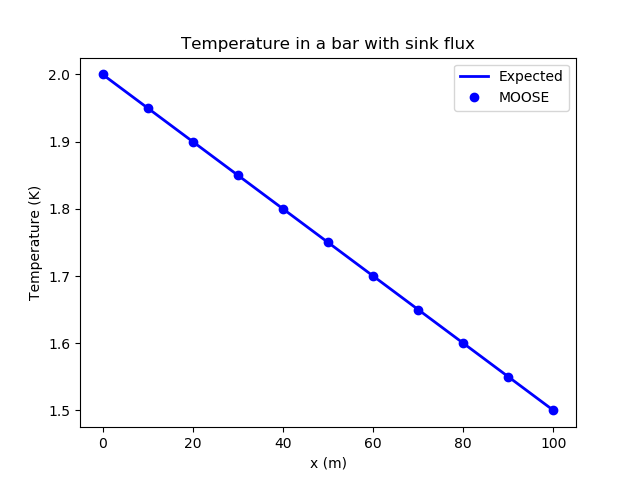
Figure 1: The steady-state temperature in the bar. MOOSE agrees well with theory illustrating that piecewise-linear heat sinks/sources and heat conduction are correctly implemented in MOOSE.
# Newton cooling from a bar. Heat conduction
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 1
xmin = 0
xmax = 100
ymin = 0
ymax = 1
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[dictator]
type = PorousFlowDictator
porous_flow_vars = 'temp'
number_fluid_phases = 0
number_fluid_components = 0
[]
[]
[Variables]
[temp]
[]
[]
[ICs]
[temp]
type = FunctionIC
variable = temp
function = '2-x/100'
[]
[]
[Kernels]
[conduction]
type = PorousFlowHeatConduction
variable = temp
[]
[]
[Materials]
[temperature]
type = PorousFlowTemperature
temperature = temp
[]
[thermal_conductivity_irrelevant]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '1E2 0 0 0 1E2 0 0 0 1E2'
[]
[]
[BCs]
[left]
type = DirichletBC
variable = temp
boundary = left
value = 2
[]
[newton]
type = PorousFlowPiecewiseLinearSink
variable = temp
boundary = right
pt_vals = '0 1 2'
multipliers = '-1 0 1'
flux_function = 1
[]
[]
[VectorPostprocessors]
[temp]
type = LineValueSampler
variable = temp
start_point = '0 0.5 0'
end_point = '100 0.5 0'
sort_by = x
num_points = 11
execute_on = timestep_end
[]
[]
[Preconditioning]
[andy]
type = SMP
full = true
petsc_options = '-snes_converged_reason'
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol '
petsc_options_value = 'gmres asm lu 100 NONZERO 2 1E-14 1E-12'
[]
[]
[Executioner]
type = Steady
[]
[Outputs]
file_base = nc04
execute_on = timestep_end
exodus = false
[along_line]
type = CSV
execute_vector_postprocessors_on = timestep_end
[]
[]
Porepressure sink in a bar
These tests demonstrate that MOOSE behaves correctly when a simulation contains a sink. The sink is a piecewise linear function of pressure.
Darcy's equation for (single-phase) flow through a fully saturated medium without gravity and without sources is with the following notation:
is the medium's porosity;
is the fluid density;
is the permeability tensor;
is the fluid viscosity;
and denote the time and spatial derivatives, respectively.
Using , where is the fluid bulk modulus, Darcy's equation becomes with Here the porosity and bulk modulus are assumed to be constant in space and time.
Consider the one-dimensional case where a bar sits between and with initial pressure distribution so . Maintain the end at constant pressure, so that . At the end , prescribe a sink flux where is a fixed quantity ("e" stands for "external"), and is a constant conductance. This corresponds to the flux which can easily be coded into a MOOSE input file: the flux is , and this may be represented by a piecewise linear function of pressure.
The solution of this problem is well known and is where is the positive root of the equation ( is a little bigger than ), and is determined from which may be solved numerically (Mathematica is used to generate the solution in Figure 2).
The problem is solved in MOOSE using the following parameters:
Table 1: Parameter values used in the porepressure evolution tests
| Parameter | Value |
|---|---|
| Bar length | m |
| Bar porosity | 0.1 |
| Bar permeability | m |
| Gravity | 0 |
| Water density | 1000kg.m |
| Water viscosity | 0.001Pa.s |
| Water bulk modulus | 1MPa |
| Initial porepressure | 2MPa |
| Environmental pressure | 0 |
| Conductance | 0.05389m |
This conductance is chosen so at steadystate kg.m.
The problem is solved using 1000 elements along the direction (m), and using 100 time-steps of size s. Using fewer elements or fewer timesteps means the agreement with the theory is marginally poorer. Two tests are performed: one with transient flow, and one using the steadystate solver. In steady-state case the initial condition is MPa, since the uniform MPa does not converge. The results are shown in Figure 2.
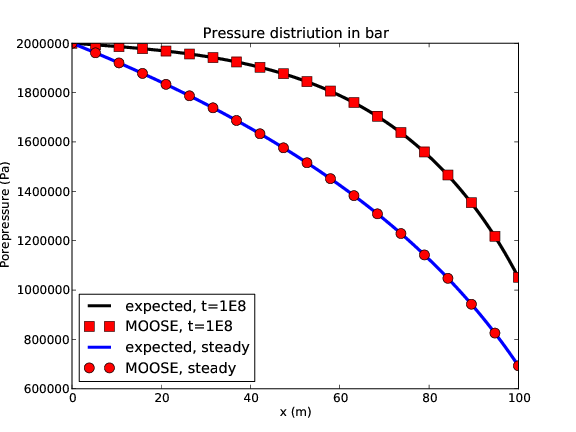
Figure 2: The porepressure in the bar at 1E8s, and at steadystate. The pressure at is held fixed on the left-hand end, while the sink is applied at the right end. MOOSE agrees well with theory demonstrating that piecewise-linear sinks/sources and single-phase Darcy fluid flow are correctly implemented in MOOSE.
The transient simulation:
# Newton cooling from a bar. 1-phase transient
[Mesh]
type = GeneratedMesh
dim = 2
nx = 1000
ny = 1
xmin = 0
xmax = 100
ymin = 0
ymax = 1
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[dictator]
type = PorousFlowDictator
porous_flow_vars = 'pressure'
number_fluid_phases = 1
number_fluid_components = 1
[]
[pc]
type = PorousFlowCapillaryPressureVG
m = 0.8
alpha = 1e-5
[]
[]
[Variables]
[pressure]
initial_condition = 2E6
[]
[]
[Kernels]
[mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pressure
[]
[flux]
type = PorousFlowAdvectiveFlux
fluid_component = 0
gravity = '0 0 0'
variable = pressure
[]
[]
[FluidProperties]
[simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 1e6
density0 = 1000
thermal_expansion = 0
viscosity = 1e-3
[]
[]
[Materials]
[temperature]
type = PorousFlowTemperature
[]
[ppss]
type = PorousFlow1PhaseP
porepressure = pressure
capillary_pressure = pc
[]
[massfrac]
type = PorousFlowMassFraction
[]
[simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[]
[porosity]
type = PorousFlowPorosityConst
porosity = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-15 0 0 0 1E-15 0 0 0 1E-15'
[]
[relperm]
type = PorousFlowRelativePermeabilityCorey # irrelevant in this fully-saturated situation
n = 2
phase = 0
[]
[]
[BCs]
[left]
type = DirichletBC
variable = pressure
boundary = left
value = 2E6
[]
[newton]
type = PorousFlowPiecewiseLinearSink
variable = pressure
boundary = right
pt_vals = '0 100000 200000 300000 400000 500000 600000 700000 800000 900000 1000000 1100000 1200000 1300000 1400000 1500000 1600000 1700000 1800000 1900000 2000000'
multipliers = '0. 5.6677197748570516e-6 0.000011931518841831313 0.00001885408740732065 0.000026504708864284114 0.000034959953203725676 0.000044304443352900224 0.00005463170211001232 0.00006604508815181467 0.00007865883048198513 0.00009259917167338928 0.00010800563134618119 0.00012503240252705603 0.00014384989486488752 0.00016464644014777016 0.00018763017719085535 0.0002130311349595711 0.00024110353477682344 0.00027212833465544285 0.00030641604122040985 0.00034430981736352295'
use_mobility = false
use_relperm = false
fluid_phase = 0
flux_function = 1
[]
[]
[VectorPostprocessors]
[porepressure]
type = LineValueSampler
variable = pressure
start_point = '0 0.5 0'
end_point = '100 0.5 0'
sort_by = x
num_points = 20
execute_on = timestep_end
[]
[]
[Preconditioning]
[andy]
type = SMP
full = true
petsc_options = '-snes_converged_reason'
petsc_options_iname = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
petsc_options_value = 'bcgs bjacobi 1E-12 1E-15 10000'
[]
[]
[Executioner]
type = Transient
solve_type = Newton
end_time = 1E8
dt = 1E6
[]
[Outputs]
file_base = nc01
[along_line]
type = CSV
execute_vector_postprocessors_on = final
[]
[]
The steady-state simulation:
# Newton cooling from a bar. 1-phase steady
[Mesh]
type = GeneratedMesh
dim = 2
nx = 1000
ny = 1
xmin = 0
xmax = 100
ymin = 0
ymax = 1
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[dictator]
type = PorousFlowDictator
porous_flow_vars = 'pressure'
number_fluid_phases = 1
number_fluid_components = 1
[]
[pc]
type = PorousFlowCapillaryPressureVG
m = 0.8
alpha = 1e-5
[]
[]
[Variables]
[pressure]
[]
[]
[ICs]
[pressure]
type = FunctionIC
variable = pressure
function = '(2-x/100)*1E6'
[]
[]
[Kernels]
[flux]
type = PorousFlowAdvectiveFlux
fluid_component = 0
gravity = '0 0 0'
variable = pressure
[]
[]
[FluidProperties]
[simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 1e6
density0 = 1000
thermal_expansion = 0
viscosity = 1e-3
[]
[]
[Materials]
[temperature]
type = PorousFlowTemperature
[]
[ppss]
type = PorousFlow1PhaseP
porepressure = pressure
capillary_pressure = pc
[]
[massfrac]
type = PorousFlowMassFraction
[]
[simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[]
[porosity]
type = PorousFlowPorosityConst
porosity = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-15 0 0 0 1E-15 0 0 0 1E-15'
[]
[relperm]
type = PorousFlowRelativePermeabilityCorey # irrelevant in this fully-saturated situation
n = 2
phase = 0
[]
[]
[BCs]
[left]
type = DirichletBC
variable = pressure
boundary = left
value = 2E6
[]
[newton]
type = PorousFlowPiecewiseLinearSink
variable = pressure
boundary = right
pt_vals = '0 100000 200000 300000 400000 500000 600000 700000 800000 900000 1000000 1100000 1200000 1300000 1400000 1500000 1600000 1700000 1800000 1900000 2000000'
multipliers = '0. 5.6677197748570516e-6 0.000011931518841831313 0.00001885408740732065 0.000026504708864284114 0.000034959953203725676 0.000044304443352900224 0.00005463170211001232 0.00006604508815181467 0.00007865883048198513 0.00009259917167338928 0.00010800563134618119 0.00012503240252705603 0.00014384989486488752 0.00016464644014777016 0.00018763017719085535 0.0002130311349595711 0.00024110353477682344 0.00027212833465544285 0.00030641604122040985 0.00034430981736352295'
use_mobility = false
use_relperm = false
fluid_phase = 0
flux_function = 1
[]
[]
[VectorPostprocessors]
[porepressure]
type = LineValueSampler
variable = pressure
start_point = '0 0.5 0'
end_point = '100 0.5 0'
sort_by = x
num_points = 20
execute_on = timestep_end
[]
[]
[Preconditioning]
active = 'andy'
[andy]
type = SMP
full = true
petsc_options = '-snes_converged_reason'
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol '
petsc_options_value = 'gmres asm lu 100 NONZERO 2 1E-12 1E-15'
[]
[]
[Executioner]
type = Steady
[]
[Outputs]
file_base = nc02
execute_on = timestep_end
exodus = false
[along_line]
type = CSV
execute_vector_postprocessors_on = timestep_end
[]
[]
Porepressure sink in a bar with heat
The simulation of the previous section is re-run, but this time heat flow is included. In this section it is assumed that the fluid specific enthalpy (J.kg) is exactly equal to the fluid internal energy, and that internal energy is ideal: This makes the arguments below simple without having to consider real fluids with complicated enthalpy and density expressions.
At the left end of the bar, the temperature is kept fixed: At the other end of the bar, heat is removed only by the fluid flowing out of the system (see sink documentation). That is, there is a heat sink: No other sinks or sources are applied to the heat equation.
With this setup, the steady-state temperature in the bar must be exactly For consider the fluid flowing from to in order to assume steady-state. At it must have temperature because that temperature is fixed at . It advects this temperature with it as it moves, so therefore at , this temperature has permeated throughout the entire bar. This occurs even without heat conduction, and is independent of the initial temperature of the bar.
MOOSE produces this result exactly. The input file is
# Newton cooling from a bar. 1-phase and heat, steady
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 1
xmin = 0
xmax = 100
ymin = 0
ymax = 1
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[dictator]
type = PorousFlowDictator
porous_flow_vars = 'pressure temp'
number_fluid_phases = 1
number_fluid_components = 1
[]
[pc]
type = PorousFlowCapillaryPressureVG
m = 0.8
alpha = 1e-5
[]
[]
[Variables]
[pressure]
[]
[temp]
[]
[]
[ICs]
# have to start these reasonably close to their steady-state values
[pressure]
type = FunctionIC
variable = pressure
function = '(2-x/100)*1E6'
[]
[temperature]
type = FunctionIC
variable = temp
function = 100+0.1*x
[]
[]
[Kernels]
[flux]
type = PorousFlowAdvectiveFlux
fluid_component = 0
gravity = '0 0 0'
variable = pressure
[]
[heat_advection]
type = PorousFlowHeatAdvection
gravity = '0 0 0'
variable = temp
[]
[]
[FluidProperties]
[simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 1e6
density0 = 1000
thermal_expansion = 0
viscosity = 1e-3
cv = 1e6
porepressure_coefficient = 0
[]
[]
[Materials]
[temperature]
type = PorousFlowTemperature
temperature = temp
[]
[ppss]
type = PorousFlow1PhaseP
porepressure = pressure
capillary_pressure = pc
[]
[massfrac]
type = PorousFlowMassFraction
[]
[simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-15 0 0 0 1E-15 0 0 0 1E-15'
[]
[relperm]
type = PorousFlowRelativePermeabilityCorey # irrelevant in this fully-saturated situation
n = 2
phase = 0
[]
[]
[BCs]
[leftp]
type = DirichletBC
variable = pressure
boundary = left
value = 2E6
[]
[leftt]
type = DirichletBC
variable = temp
boundary = left
value = 100
[]
[newtonp]
type = PorousFlowPiecewiseLinearSink
variable = pressure
boundary = right
pt_vals = '0 100000 200000 300000 400000 500000 600000 700000 800000 900000 1000000 1100000 1200000 1300000 1400000 1500000 1600000 1700000 1800000 1900000 2000000'
multipliers = '0. 5.6677197748570516e-6 0.000011931518841831313 0.00001885408740732065 0.000026504708864284114 0.000034959953203725676 0.000044304443352900224 0.00005463170211001232 0.00006604508815181467 0.00007865883048198513 0.00009259917167338928 0.00010800563134618119 0.00012503240252705603 0.00014384989486488752 0.00016464644014777016 0.00018763017719085535 0.0002130311349595711 0.00024110353477682344 0.00027212833465544285 0.00030641604122040985 0.00034430981736352295'
use_mobility = false
use_relperm = false
fluid_phase = 0
flux_function = 1
[]
[newton]
type = PorousFlowPiecewiseLinearSink
variable = temp
boundary = right
pt_vals = '0 100000 200000 300000 400000 500000 600000 700000 800000 900000 1000000 1100000 1200000 1300000 1400000 1500000 1600000 1700000 1800000 1900000 2000000'
multipliers = '0. 5.6677197748570516e-6 0.000011931518841831313 0.00001885408740732065 0.000026504708864284114 0.000034959953203725676 0.000044304443352900224 0.00005463170211001232 0.00006604508815181467 0.00007865883048198513 0.00009259917167338928 0.00010800563134618119 0.00012503240252705603 0.00014384989486488752 0.00016464644014777016 0.00018763017719085535 0.0002130311349595711 0.00024110353477682344 0.00027212833465544285 0.00030641604122040985 0.00034430981736352295'
use_mobility = false
use_relperm = false
use_internal_energy = true
fluid_phase = 0
flux_function = 1
[]
[]
[VectorPostprocessors]
[porepressure]
type = LineValueSampler
variable = pressure
start_point = '0 0.5 0'
end_point = '100 0.5 0'
sort_by = x
num_points = 11
execute_on = timestep_end
[]
[temperature]
type = LineValueSampler
variable = temp
start_point = '0 0.5 0'
end_point = '100 0.5 0'
sort_by = x
num_points = 11
execute_on = timestep_end
[]
[]
[Preconditioning]
[andy]
type = SMP
full = true
petsc_options = '-snes_converged_reason'
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol '
petsc_options_value = 'gmres asm lu 100 NONZERO 2 1E-8 1E-15'
[]
[]
[Executioner]
type = Steady
solve_type = Newton
[]
[Outputs]
file_base = nc06
execute_on = timestep_end
[along_line]
type = CSV
execute_vector_postprocessors_on = timestep_end
[]
[]
Hot ideal fluid in a bar
This test uses a similar setup to the previous section, except that here an ideal fluid is used. The use of an ideal gas simplifies the equations. Only the steady-state is studied in this section.
The governing equation for the fluid's porepressure is It is assumed that and are constant, and that holds (this is the ideal gas equation of state). In this formula is the gas molar mass, is the gas constant and is the temperature.
The equation governing the temperature is assumed to be just the fluid advection equation As in the previous section, heat conduction could be added, but it is actually irrelevant since the solution to the problem below is constant . The enthalpy, , for an ideal gas is
The boundary conditions at the left-hand end are Physically these correspond to fluid and heat being removed or added to the left-hand end by some external source in order to keep the porepressure and temperature fixed.
The porepressure boundary condition at the right-hand end of the bar is (2) Physically this corresponds to the mass-flow through the boundary being proportional to . Here is a fixed "environmental" porepressure, and this acts as a source or sink of fluid. is the "conductance" of the boundary. Notice the appearance of in the LHS of this equation means that this is truly a flux of fluid mass (measured in kg.m.s), and the appearance of on the RHS means that a PorousFlowPiecewiseLinearFlux may be used with use_mobility=true.
The temperature boundary condition at the right-hand end of the bar is Comparing this with Eq. (2), it is seen that this is exactly the heat loss (or gain) at the boundary corresponding to the loss (or gain) of the fluid. Notice the appearance of in the LHS of this equation means that this is truly a flux of fluid mass (measured in J.m.s), and the appearance of on the RHS means that a PorousFlowPiecewiseLinearFlux may be used with use_mobility=true and use_enthalpy=true.
There is a clear similarity between the fluid and heat equations. The heat equation does not actually depend on temperature, and is simply which is solved by The fluid equation then yields The constant may be determined from the either of the boundary conditions. For the special case of and , the solution is MOOSE produces this result exactly, as illustrated in Figure 3
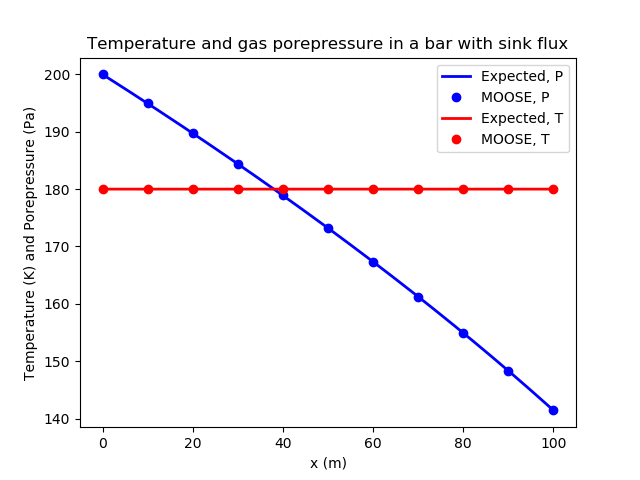
Figure 3: The steady-state porepressure and temperature distributions in the bar. MOOSE agrees well with theory illustrating that piecewise-linear fluid and heat sinks/sources as well as ideal fluids are correctly implemented in MOOSE.
# Newton cooling from a bar. 1-phase ideal fluid and heat, steady
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 1
xmin = 0
xmax = 100
ymin = 0
ymax = 1
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[dictator]
type = PorousFlowDictator
porous_flow_vars = 'pressure temp'
number_fluid_phases = 1
number_fluid_components = 1
[]
[pc]
type = PorousFlowCapillaryPressureVG
m = 0.8
alpha = 1e-5
[]
[]
[Variables]
[pressure]
[]
[temp]
[]
[]
[ICs]
# have to start these reasonably close to their steady-state values
[pressure]
type = FunctionIC
variable = pressure
function = '200-0.5*x'
[]
[temperature]
type = FunctionIC
variable = temp
function = 180+0.1*x
[]
[]
[Kernels]
[flux]
type = PorousFlowAdvectiveFlux
fluid_component = 0
gravity = '0 0 0'
variable = pressure
[]
[heat_advection]
type = PorousFlowHeatAdvection
gravity = '0 0 0'
variable = temp
[]
[]
[FluidProperties]
[idealgas]
type = IdealGasFluidProperties
molar_mass = 1.4
gamma = 1.2
mu = 1.2
[]
[]
[Materials]
[temperature]
type = PorousFlowTemperature
temperature = temp
[]
[ppss]
type = PorousFlow1PhaseP
porepressure = pressure
capillary_pressure = pc
[]
[massfrac]
type = PorousFlowMassFraction
[]
[dens0]
type = PorousFlowSingleComponentFluid
fp = idealgas
phase = 0
[]
[permeability]
type = PorousFlowPermeabilityConst
permeability = '1.1 0 0 0 1.1 0 0 0 1.1'
[]
[relperm]
type = PorousFlowRelativePermeabilityCorey # irrelevant in this fully-saturated situation
n = 2
phase = 0
[]
[]
[BCs]
[leftp]
type = DirichletBC
variable = pressure
boundary = left
value = 200
[]
[leftt]
type = DirichletBC
variable = temp
boundary = left
value = 180
[]
[newtonp]
type = PorousFlowPiecewiseLinearSink
variable = pressure
boundary = right
pt_vals = '-200 0 200'
multipliers = '-200 0 200'
use_mobility = true
use_relperm = true
fluid_phase = 0
flux_function = 0.005 # 1/2/L
[]
[newtont]
type = PorousFlowPiecewiseLinearSink
variable = temp
boundary = right
pt_vals = '-200 0 200'
multipliers = '-200 0 200'
use_mobility = true
use_relperm = true
use_enthalpy = true
fluid_phase = 0
flux_function = 0.005 # 1/2/L
[]
[]
[VectorPostprocessors]
[porepressure]
type = LineValueSampler
variable = pressure
start_point = '0 0.5 0'
end_point = '100 0.5 0'
sort_by = x
num_points = 11
execute_on = timestep_end
[]
[temperature]
type = LineValueSampler
variable = temp
start_point = '0 0.5 0'
end_point = '100 0.5 0'
sort_by = x
num_points = 11
execute_on = timestep_end
[]
[]
[Preconditioning]
[andy]
type = SMP
full = true
[]
[]
[Executioner]
type = Steady
solve_type = Newton
nl_rel_tol = 1E-10
nl_abs_tol = 1E-15
[]
[Outputs]
file_base = nc08
execute_on = timestep_end
[along_line]
type = CSV
execute_vector_postprocessors_on = timestep_end
[]
[]