Heat advection in a 1D bar

Consider the case of a single-phase fluid in 1 dimension, , with the porepressure fixed at the boundaries: With zero gravity, and high fluid bulk modulus, the Darcy equation implies that the solution is , with being the constant "Darcy velocity" from to . (The velocity of the individual fluid particles, this is divided by the porosity.). Here is the porous medium's permeability, and is the fluid dynamic viscosity.

Suppose that the fluid internal energy is given by , where is the specific heat capacity and is its temperature. Assuming that , then the fluid's enthalpy is also . In this case, the energy equation reads This is the wave equation with velocity Recall that the "Darcy velocity" is .

Let the initial condition for be . Apply the boundary conditions At this creates a front at . Choose the parameters , , , , , , (all in consistent units), so that is the front's velocity.

The input file used in this page is:

# 1phase, heat advecting with a moving fluid
# Using the PorousFlowFullySaturated Action with various stabilization options
# With stabilization=none, this should produce an identical result to heat_advection_1d_fully_saturated.i
# With stabilization=Full, this should produce an identical result to heat_advection_1d.i and heat_advection_1d_fullsat.i
# With stabilization=KT, this should produce an identical result to heat_advection_1D_KT.i
[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = 50
  xmin = 0
  xmax = 1
[]

[GlobalParams]
  PorousFlowDictator = dictator
  gravity = '0 0 0'
[]

[Variables]
  [temp]
    initial_condition = 200
  []
  [pp]
  []
[]

[ICs]
  [pp]
    type = FunctionIC
    variable = pp
    function = '1-x'
  []
[]

[BCs]
  [pp0]
    type = DirichletBC
    variable = pp
    boundary = left
    value = 1
  []
  [pp1]
    type = DirichletBC
    variable = pp
    boundary = right
    value = 0
  []
  [spit_heat]
    type = DirichletBC
    variable = temp
    boundary = left
    value = 300
  []
  [suck_heat]
    type = DirichletBC
    variable = temp
    boundary = right
    value = 200
  []
[]

[PorousFlowFullySaturated]
  porepressure = pp
  temperature = temp
  coupling_type = ThermoHydro
  fp = simple_fluid
  add_darcy_aux = false
  stabilization = none
  flux_limiter_type = superbee
[]

[FluidProperties]
  [simple_fluid]
    type = SimpleFluidProperties
    bulk_modulus = 100
    density0 = 1000
    viscosity = 4.4
    thermal_expansion = 0
    cv = 2
  []
[]

[Materials]
  [porosity]
    type = PorousFlowPorosityConst
    porosity = 0.2
  []
  [zero_thermal_conductivity]
    type = PorousFlowThermalConductivityIdeal
    dry_thermal_conductivity = '0 0 0  0 0 0  0 0 0'
  []
  [rock_heat]
    type = PorousFlowMatrixInternalEnergy
    specific_heat_capacity = 1.0
    density = 125
  []
  [permeability]
    type = PorousFlowPermeabilityConst
    permeability = '1.1 0 0 0 2 0 0 0 3'
  []
[]

[Preconditioning]
  [andy]
    type = SMP
    full = true
  []
[]

[Executioner]
  type = Transient
  solve_type = Newton
  dt = 0.01
  end_time = 0.6
[]

[VectorPostprocessors]
  [T]
    type = LineValueSampler
    start_point = '0 0 0'
    end_point = '1 0 0'
    num_points = 51
    sort_by = x
    variable = temp
  []
[]

[Outputs]
  file_base = heat_advection_1d_fully_saturation_action
  [csv]
    type = CSV
    sync_times = '0.1 0.6'
    sync_only = true
  []
[]
(modules/porous_flow/test/tests/heat_advection/heat_advection_1d_fully_saturated_action.i)

The sharp front is not maintained by MOOSE. This is due to numerical diffusion, whose magnitude depends on the stabilization scheme used. This is explained in great detail in the pages on numerical stabilization. Nevertheless, MOOSE advects the smooth front with the correct velocity, as shown in Figure 1.

Figure 1 shows three versions of the advection, which are activated by setting the stabilization parameter in the PorousFlowFullySaturated Action:

  • with no stabilization


  stabilization = none

  • with full upwinding


  stabilization = Full

  • with KT stabilization


  stabilization = KT

With no numerical stabilization, two additional points may also be noticed: (1) the lack of upwinding has produced a "bump" in the temperature profile near the hotter side; (2) the lack of upwinding means the temperature profile moves slightly slower than it should. These two affects reduce as the mesh density is increased, however.

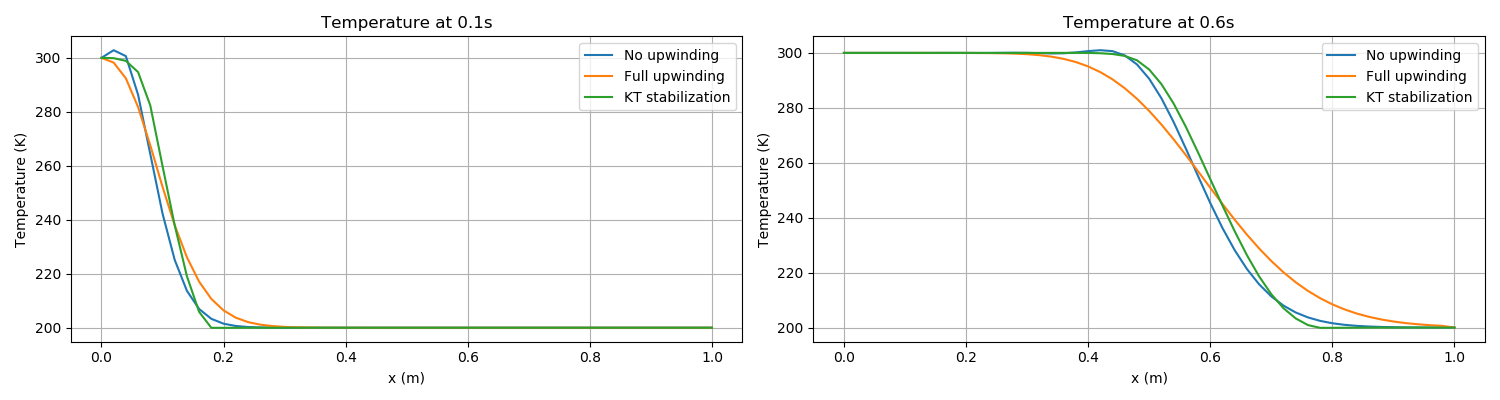
Figure 1: Results of heat advection via a fluid in 1D. The fluid flows with constant Darcy velocity of 0.25m/s to the right, and this advects a temperature front at velocity 1m/s to the right. The pictures above that the numerical implementation of PorousFlow (including upwinding) diffuses sharp fronts, but advects them at the correct velocity (notice the centre of the upwinded front is at the correct position in each picture). Less diffusion is experienced without upwinding or with KT stabilization. Left: temperature 0.1s. Right: temperature at 0.6s.