Electrostatic Contact Verification (Three Block Test)
This document describes the three block 1-D verification test for the ElectrostaticContactCondition object. Below is a summary of the test, along with a derivation of the analytic solution used for comparison and the relevant test input file for review.
Summary
A visual summary of the three block verification test domain, as well as relevant boundary and interface conditions is shown below (click to zoom):

Figure 1: Visual summary of the three block verification test with boundary and interface conditions.
It is important to note that in Figure 1:
is the electrical conductivity of material ,
is the electrical contact conductance at the interface, and
is the electrostatic potential of material .
See the ElectrostaticContactCondition documentation for more information about the particular definition of . As the ElectrostaticContactCondition object is intended for electrostatic field solves, the PDE being solved within each domain is Poisson's Equation for electrostatic potential. In this case, we are assuming a zero total charge density, which leads to
(1)Material properties being used in this case are constants in each block, and they are summarized below in Table 1. All material properties were evaluated at a temperature of ~300 K.
Table 1: Material properties for the three block electrostatic contact verification case.
| Property (unit) | Value | Source |
|---|---|---|
| Stainless Steel (304) Electrical Conductivity (S / m) | (Cincotti et al., 2007) | |
| Stainless Steel (304) Hardness (Pa) | (Cincotti et al., 2007) | |
| Graphite (AT 101) Electrical Conductivity (S / m) | (Cincotti et al., 2007) | |
| Graphite (AT 101) Hardness (Pa) | (Cincotti et al., 2007) |
The hardness values shown in Table 1 are used in the ElectrostaticContactCondition object as a harmonic mean of the two values. For reference, the harmonic mean calculation for two values, and , is given by
In the input file, the harmonic mean of hardness for stainless steel and graphite was calculated and set to be Pa.
Analytic Solution Derivation
In 1-D, Eq. (1) becomes
since is constant in all domains. This equation means a reasonable guess for a generic solution function for would be
where and are to-be-determined constant coefficients.
Apply boundary conditions
Using the boundary conditions in Figure 1, we can determine for both of the outer stainless steel regions:
Stainless Steel (left)
Stainless Steel (right)
Apply interface conditions
Now, the interface conditions can be applied from Figure 1. To begin, let's focus on the current density () equivalence condition on the left interface (at ):
Taking into account our initial guess for the solution function, this becomes
(2)Next, we can apply the conductance condition from Figure 1, which is
Taking into account our initial guess for the solution function and the constant coefficient solved for above, this becomes
Grouping terms, we have
(3)Next, let's focus on the current density () equivalence condition on the right interface (at ):
Taking into account our initial guess for the solution function, this becomes
(4)Next, we can apply the conductance condition from Figure 1, which is
Taking into account our initial guess for the solution function and the constant coefficient solved for above, this becomes
Grouping terms, we have
(5)Find the remaining coefficients
Using the Elimination Method and some algebra, we can combine Eq. (2), Eq. (3), Eq. (4), and Eq. (5) in order to solve for each remaining unknown coefficient. To begin, let's focus on Eq. (2) and Eq. (3). Multiplying Eq. (2) through by and Eq. (3) through by yields
and
(7)Combining Eq. (6) and Eq. (7) together via addition yields
which can then be solved for :
(8)
Next, we focus on Eq. (4) and Eq. (5). Multiplying Eq. (4) through by and Eq. (5) through by yields
(9)and
(10)Combining Eq. (9) and Eq. (10) together via addition yields
which can then be solved for :
(11)Note that Eq. (8) and Eq. (11) still depend on finding the coefficient . We can now solve for by using Eq. (2), which yields
and finally
(12)Returning to Eq. (11), we can now fully solve for :
Simplifying yields:
(13)Returning to Eq. (8), we can now fully solve for :
Simplifying yields:
(14)Returning to Eq. (4), we can now fully solve for :
(15)
Summarize
Now our determined coefficients can be combined to form the complete solutions for both stainless steel and graphite. To summarize, the derived analytical solutions for each domain given the boundary and interface conditions described in Figure 1 is:
For stainless steel from to :
For graphite from to :
For stainless steel from to :
This is implemented in source code as ElectricalContactTestFunc.C and is located within the test source code directory located at modules/electromagnetics/test/src.
Input File
# Regression test for ElectrostaticContactCondition with analytic solution with
# three blocks
#
# dim = 1D
# X = [0,3]
# Interfaces at X = 1 and X = 2
#
# stainless_steel graphite stainless_steel
# +------------------+------------------+------------------+
#
# Left BC: Potential = 1
# Right BC: Potential = 0
# Left Interface: ElectrostaticContactCondition (primary = stainless_steel)
# Right Interface: ElectrostaticContactCondition (primary = graphite)
#
[Mesh]
[line]
type = GeneratedMeshGenerator
dim = 1
nx = 6
xmax = 3
[]
[break_center]
type = SubdomainBoundingBoxGenerator
input = line
block_id = 1
block_name = 'graphite'
bottom_left = '1 0 0'
top_right = '2 0 0'
[]
[break_right]
type = SubdomainBoundingBoxGenerator
input = break_center
block_id = 2
bottom_left = '2 0 0'
top_right = '3 0 0'
[]
[ssg_interface]
type = SideSetsBetweenSubdomainsGenerator
input = break_right
primary_block = 0
paired_block = 1
new_boundary = 'ssg_interface'
[]
[gss_interface]
type = SideSetsBetweenSubdomainsGenerator
input = ssg_interface
primary_block = 1
paired_block = 2
new_boundary = 'gss_interface'
[]
[block_rename]
type = RenameBlockGenerator
input = gss_interface
old_block = '0 2'
new_block = 'stainless_steel_left stainless_steel_right'
[]
[]
[Variables]
[potential_graphite]
block = graphite
[]
[potential_stainless_steel_left]
block = stainless_steel_left
[]
[potential_stainless_steel_right]
block = stainless_steel_right
[]
[]
[AuxVariables]
[analytic_potential_stainless_steel_left]
block = stainless_steel_left
[]
[analytic_potential_stainless_steel_right]
block = stainless_steel_right
[]
[analytic_potential_graphite]
block = graphite
[]
[]
[Kernels]
[electric_graphite]
type = ADMatDiffusion
variable = potential_graphite
diffusivity = electrical_conductivity
block = graphite
[]
[electric_stainless_steel_left]
type = ADMatDiffusion
variable = potential_stainless_steel_left
diffusivity = electrical_conductivity
block = stainless_steel_left
[]
[electric_stainless_steel_right]
type = ADMatDiffusion
variable = potential_stainless_steel_right
diffusivity = electrical_conductivity
block = stainless_steel_right
[]
[]
[AuxKernels]
[analytic_function_aux_stainless_steel_left]
type = FunctionAux
function = potential_fxn_stainless_steel_left
variable = analytic_potential_stainless_steel_left
block = stainless_steel_left
[]
[analytic_function_aux_stainless_steel_right]
type = FunctionAux
function = potential_fxn_stainless_steel_right
variable = analytic_potential_stainless_steel_right
block = stainless_steel_right
[]
[analytic_function_aux_graphite]
type = FunctionAux
function = potential_fxn_graphite
variable = analytic_potential_graphite
block = graphite
[]
[]
[BCs]
[elec_left]
type = ADDirichletBC
variable = potential_stainless_steel_left
boundary = left
value = 1
[]
[elec_right]
type = ADDirichletBC
variable = potential_stainless_steel_right
boundary = right
value = 0
[]
[]
[InterfaceKernels]
[electric_contact_conductance_ssg]
type = ElectrostaticContactCondition
variable = potential_stainless_steel_left
neighbor_var = potential_graphite
boundary = ssg_interface
mean_hardness = mean_hardness
mechanical_pressure = 3000
[]
[electric_contact_conductance_gss]
type = ElectrostaticContactCondition
variable = potential_graphite
neighbor_var = potential_stainless_steel_right
boundary = gss_interface
mean_hardness = mean_hardness
mechanical_pressure = 3000
[]
[]
[Materials]
#graphite (at 300 K)
[sigma_graphite]
type = ADGenericConstantMaterial
prop_names = electrical_conductivity
prop_values = 73069.2
block = graphite
[]
#stainless_steel (at 300 K)
[sigma_stainless_steel_left]
type = ADGenericConstantMaterial
prop_names = electrical_conductivity
prop_values = 1.41867e6
block = stainless_steel_left
[]
[sigma_stainless_steel_right]
type = ADGenericConstantMaterial
prop_names = electrical_conductivity
prop_values = 1.41867e6
block = stainless_steel_right
[]
# harmonic mean of graphite and stainless steel hardness
[mean_hardness]
type = ADGenericConstantMaterial
prop_names = mean_hardness
prop_values = 2.4797e9
[]
[]
[Functions]
[potential_fxn_stainless_steel_left]
type = ElectricalContactTestFunc
domain = stainless_steel
three_block = true
three_block_side = left
[]
[potential_fxn_stainless_steel_right]
type = ElectricalContactTestFunc
domain = stainless_steel
three_block = true
three_block_side = right
[]
[potential_fxn_graphite]
type = ElectricalContactTestFunc
domain = graphite
three_block = true
[]
[]
[Postprocessors]
[error_stainless_steel_left]
type = ElementL2Error
variable = potential_stainless_steel_left
function = potential_fxn_stainless_steel_left
block = stainless_steel_left
[]
[error_graphite]
type = ElementL2Error
variable = potential_graphite
function = potential_fxn_graphite
block = graphite
[]
[error_stainless_steel_right]
type = ElementL2Error
variable = potential_stainless_steel_right
function = potential_fxn_stainless_steel_right
block = stainless_steel_right
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Steady
solve_type = NEWTON
automatic_scaling = true
[]
[Outputs]
csv = true
perf_graph = true
[]
Results
Results from the input file shown above (with Mesh/line/nx=60 and Outputs/exodus=true) compared to the analytic function are shown below in Figure 2. Note that the number of points shown in the plot has been down-sampled compared to the solved number of elements for readability.
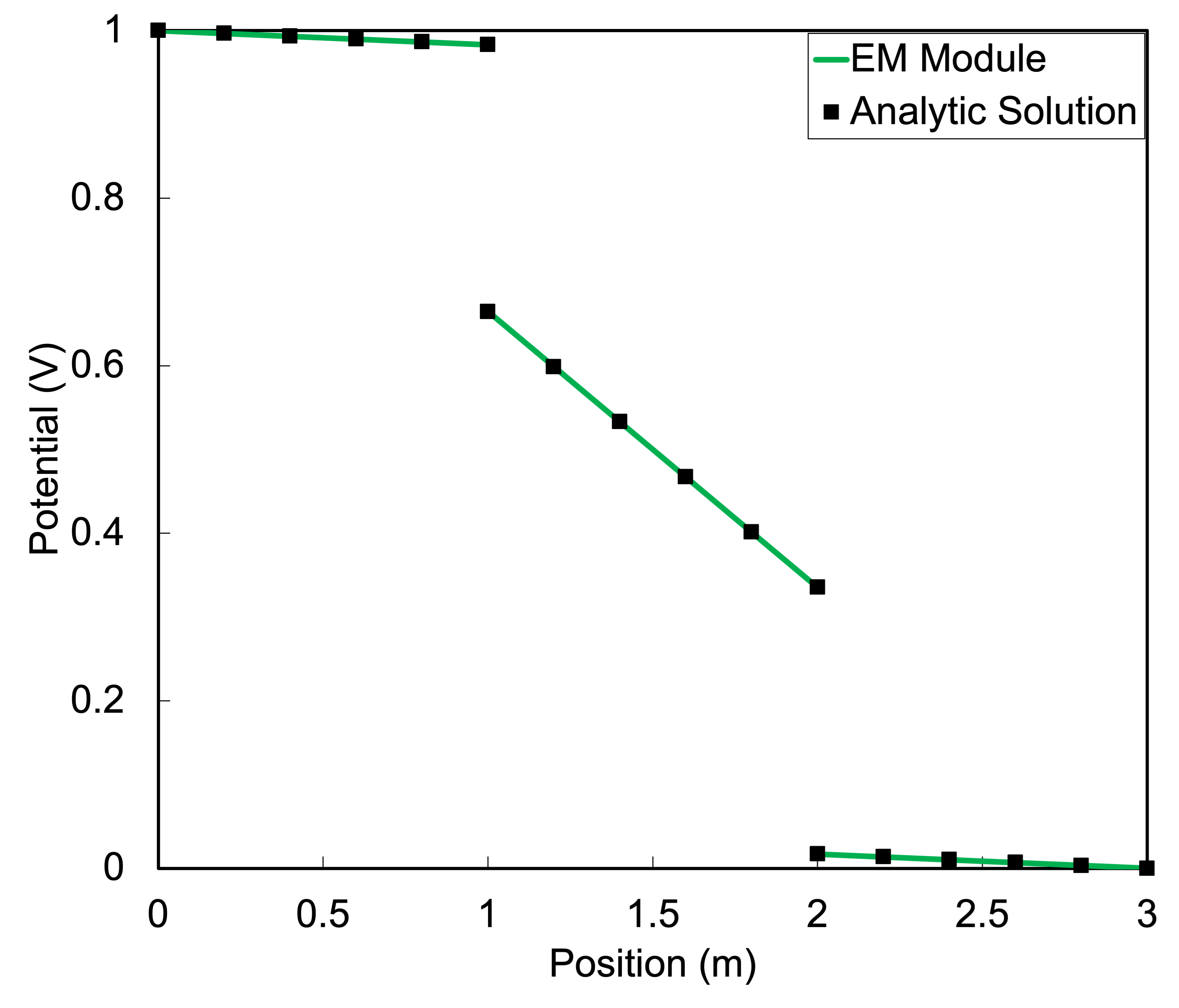
Figure 2: Results of electrostatic contact three block validation case.
References
- A. Cincotti, A. M. Locci, R. Orrù, and G. Cao.
Modeling of SPS apparatus: temperature, current and strain distribution with no powders.
AIChE Journal, 53(3):703–719, 2007.
doi:10.1002/aic.11102.[BibTeX]