MOOSE Workshop
September 2021
Idaho National Laboratory
www.inl.gov
Established in 2005, INL is the lead nuclear energy R&D laboratory for the Department of Energy
"Establish a world-class capability in the modeling and simulation of advanced energy systems..."
INL is the one of the largest employers in Idaho with 5,336 employees and 478 interns
In 2021 the INL budget was over $1 billion
INL is the site where 52 nuclear reactors were designed and constructed, including the first reactor to generate usable amounts of electricity: Experimental Breeder Reactor I (ERB-1)

Advanced Test Reactor (ATR)
World's most powerful test reactor
Constructed in 1967
Volume of 1.4 cubic meters, with 43 kg of uranium, and operates at 60C

Transient Reactor Test Facility (TREAT)
TREAT is test facility specifically designed to evaluate the response of fuels and materials to accident conditions
High-intensity (20 GW), short-duration (80 ms) neutron pulses for severe accident testing

MOOSE Introduction
Multi-physics Object Oriented Simulation Environment

History and Purpose
Development started in 2008
Open-sourced in 2014
Designed to solve computational engineering problems and reduce the expense and time required to develop new applications by:
being easily extended and maintained
working efficiently on a few and many processors
providing an object-oriented, extensible system for creating all aspects of a simulation tool
MOOSE Team


General Capabilities
continuous and Discontinuous Galerkin FEM
finite Volume
fully coupled, fully implicit (and explicit)
automatic differentiation (AD)
unstructured mesh with FEM shapes
higher order geometry
mesh adaptivity (refinement and coarsening)
massively parallel (MPI and threads)
user code agnostic of dimension, parallelism, shape functions, etc.
Object-oriented, pluggable system

Example Code

Software Quality
MOOSE follows an Nuclear Quality Assurance Level 1 (NQA-1) development process
all commits undergo review using GitHub Pull Requests and must pass a set of application regression tests before they are available to our users
MOOSE includes a test suite and documentation system to allow for agile development while maintaining a NQA-1 process
Utilizes the Continuous Integration Environment for Verification, Enhancement, and Testing (CIVET)
Development Process

Community
https://github.com/idaholab/moose/discussions



Creating a Multiphysics Code
Multiphysics is popular, but how is it achieved?
Scientists are adept at creating applications in their domain
What about collaborating across research groups and/or disciplines?
Head in the sand?
Development of "coupling" codes?
Is there something better?
Modularity is Key
Data should be accessed through strict interfaces with code having separation of responsibilities
Allows for "decoupling" of code
Leads to more reuse and less bugs
Challenging for FEM: Shape functions, DOFs, Elements, QPs, Material Properties, Analytic Functions, Global Integrals, Transferred Data and much more are needed in FEM assembly
The complexity makes computational science codes brittle and hard to reuse
A consistent set of "systems" are needed to carry out common actions, these systems should be separated by interfaces
MOOSE Pluggable Systems
Systems break apart responsibility
No direct communication between systems
Everything flows through MOOSE interfaces
Objects can be mixed and matched to achieve simulation goals
Incoming data can be changed dynamically
Outputs can be manipulated (e.g. multiplication by radius for cylindrical coordinates)
An object, by itself, can be lifted from one application and used by another
MOOSE Pluggable Systems
Actions
AuxKernels
Base
BCs
Constraints
Controls
Dampers
DGKernels
DiracKernels
Distributions
Executioners
Functions
Geomsearch
ICs
Indicators
InterfaceKernels
Kernels
LineSearches
Markers
Materials
Mesh
MeshGenerators
MeshModifiers
Multiapps
NodalKernels
Outputs
Parser
Partitioner
Postprocessors
Preconditioners
Predictors
Problems
RelationshipManagers
Samplers
Splits
TimeIntegrators
TimeSteppers
Transfers
UserObject
Utils
Variables
VectorPostprocessors
Finite-Element Reactor Fuel Simulation
MOOSE Physics Modules
Chemical Reactions
Contact
External PETSc Solver
Fluid Properties
Function Expansion Tools
Heat Conduction
Level Set
Navier Stokes
Phase Field
Porous Flow
rDG
Stochastic Tools
Tensor (solid) Mechanics
XFEM
Shallow Water (work in progress)
Ray Tracing (work in progress)

Problem Statement
Consider a system containing two pressure vessels at differing temperatures. The vessels are connected via a pipe that contains a filter consisting of close-packed steel spheres. Predict the velocity and temperature of the fluid inside the filter. The pipe is 0.304 m in length and 0.0514 m in diameter.

Pamuk and Ozdemir, "Friction factor, permeability, and inertial coefficient of oscillating flow through porous media of packed balls", Experimental Thermal and Fluid Science, v. 38, pp. 134-139, 2012.
Governing Equations
Conservation of Mass:
(1)Conservation of Energy:
(2)Darcy's Law:
(3)where is the fluid velocity, is porosity, is the permeability tensor, is fluid viscosity, is the pressure, is the density, is the gravity vector, and is the temperature.
Assuming that and imposing the divergence-free condition of Eq. (1) to Eq. (3) leads to the following system of two equations in the unknowns and :
The parameters , , and are the porosity-dependent density, heat capacity, and thermal conductivity of the combined fluid/solid medium, defined by:
where is the porosity, is the specific heat, and the subscripts and refer to fluid and solid, respectively.
Material Properties
| Property | Value | Units |
|---|---|---|
| Viscosity of water, | ||
| Density of water, | 995.7 | |
| Density of steel, | 8000 | |
| Thermal conductivity of water, | 0.6 | |
| Thermal conductivity of steel, | 18 | |
| Specific heat capacity of water, | 4181.3 | |
| Specific heat capacity of steel, | 466 |
Tutorial Steps
Step 1: Geometry and Diffusion
The first step is to solve a simple "Diffusion" problem, which requires no code. This step will introduce the basic system of MOOSE.
Step 2: Pressure Kernel
In order to implement the Darcy pressure equation, a Kernel object is needed to represent:
Step 3: Pressure Kernel with Material
Instead of passing constant parameters to the pressure diffusion Kernel object, the Material system can be used to supply the values. This allows for properties that vary in space and time as well as be coupled to variables in the simulation.
Step 4: Velocity Auxiliary Variable
The velocity is computed from the pressure based on Darcy's law as:
This velocity can be computed using the Auxiliary system.
Step 5: Heat Conduction
Solve the transient heat equation using the "heat conduction" module.
Step 6: Equation Coupling
Solve the pressure and temperature in a coupled system of equations by adding the advection term to the heat equation.
Step 7: Mesh Adaptivity
In the transient simulation, a "traveling wave" profile moves through the porous medium. Instead of using a uniform mesh to resolve the wave profile, we can dynamically adapt the mesh to the solution.
Step 8: Postprocessors
Postprocessor and VectorPostprocessor objects can be used to compute aggregate value(s) for a simulation, such as the average temperature on the boundary or the temperatures along a line within the solution domain.
Step 9: Mechanics
Thermal expansion of the porous media can be added to the coupled set of equations using the "tensor mechanics" module, without adding additional code.
Step 10: Multiscale Simulation
MOOSE is capable of running multiple applications together and transfer data between the various applications.
This problem replaces the thermal conductivity calculated by the Material with a value computed by another application that runs a phase-based micro-structure simulation.
Step 11: Custom Syntax
MOOSE includes a system to create custom input syntax for common tasks, in this step the syntax for the two equations and velocity auxiliary calculation are simplified for end-users.
Step 1: Geometry and Diffusion
First, consider the steady-state diffusion equation on the domain : find such that
where on the left, on the right and with on the remaining boundaries.
The weak form of this equation, in inner-product notation, is given by:
where are the test functions and is the finite element solution.
Input File(s)
All capabilities of MOOSE, modules, and your application are compiled into a single executable. An input file is used define which capabilities are used to perform a simulation.
MOOSE uses the "hierarchical input text" (hit) format.
[Kernels]
[diffusion]
type = ADDiffusion # Laplacian operator using automatic differentiation
variable = pressure # Operate on the "pressure" variable from above
[]
[]
A basic MOOSE input file requires six parts, each of which will be covered in greater detail later.
[Mesh]: Define the geometry of the domain[Variables]: Define the unknown(s) of the problem[Kernels]: Define the equation(s) to solve[BCs]: Define the boundary condition(s) of the problem[Executioner]: Define how the problem will solve[Outputs]: Define how the solution will be written
Step 1: Input File
[Mesh]
type = GeneratedMesh # Can generate simple lines, rectangles and rectangular prisms
dim = 2 # Dimension of the mesh
nx = 100 # Number of elements in the x direction
ny = 10 # Number of elements in the y direction
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
# Adds a Linear Lagrange variable by default
[]
[]
[Kernels]
[diffusion]
type = ADDiffusion # Laplacian operator using automatic differentiation
variable = pressure # Operate on the "pressure" variable from above
[]
[]
[BCs]
[inlet]
type = DirichletBC # Simple u=value BC
variable = pressure # Variable to be set
boundary = left # Name of a sideset in the mesh
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Problem]
type = FEProblem # This is the "normal" type of Finite Element Problem in MOOSE
coord_type = RZ # Axisymmetric RZ
rz_coord_axis = X # Which axis the symmetry is around
[]
[Executioner]
type = Steady # Steady state problem
solve_type = NEWTON # Perform a Newton solve, uses AD to compute Jacobian terms
petsc_options_iname = '-pc_type -pc_hypre_type' # PETSc option pairs with values below
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true # Output Exodus format
[]
Step 1: Run and Visualize with Peacock
cd ~/projects/moose/tutorials/darcy-thermo_mech/step01_diffusion
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step1.i
Step 1: Run via Command-line
cd ~/projects/moose/tutorials/darcy-thermo_mech/step01_diffusion
make -j 12 # use number of processors for you system
cd problems
../darcy_thermo_mech-opt -i step1.i
Step 1: Visualize Result
~/projects/moose/python/peacock/peacock -r step1_out.e

Finite Element Method (FEM)
Polynomial Fitting
To introduce the concept of FEM, consider a polynomial fitting exercise. When fitting a polynomial there is a known set of points as well as a set of coefficients that are unkown for a function that has the form:
where , and are scalar coefficients and , , are "basis functions". Thus, the problem is to find , , , etc. such that passes through the points given.
More generally,
where the are coefficients to be determined. is unique and interpolary if is the same as the number of points needed to fit. This defines a linear system that must be solved to find the coefficients.
Polynomial Example
Define a set of points:
Substitute data into the model:
This leads to the following linear system for , , and :
Solving for the coefficients results in:
These coefficients define the solution function:

The solution is the function, not the coefficients.
The coefficients are meaningless, they are just numbers used to define a function.
The solution is not the coefficients, but rather the function created when they are multiplied by their respective basis functions and summed.
The function does go through the points given, but it is also defined everywhere in between.
can be evaluated at the point , for example, by computing:
where the correspond to the coefficients in the solution vector, and the are the respective functions.
Simplified FEM
FEM is a method for numerically approximating the solution to partial differential equations (PDEs).
FEM finds a solution function that is made up of "shape functions" multiplied by coefficients and added together, just like in polynomial fitting, except the functions are not typically as simple (although they can be).
The Galerkin Finite Element method is different from finite difference and finite volume methods because it finds a piecewise continuous function which is an approximate solution to the governing PDEs.
Just as in polynomial fitting you can evaluate a finite element solution anywhere in the domain.
FEM is widely applicable for a large range of PDEs and domains.
It is supported by a rich mathematical theory with proofs about accuracy, stability, convergence and solution uniqueness.
Weak Form
Using FEM to find the solution to a PDE starts with forming a "weighted residual" or "variational statement" or "weak form", this processes if referred to here as generating a weak form.
The weak form provides flexibility, both mathematically and numerically and it is needed by MOOSE to solve a problem.
Generating a weak form generally involves these steps:
Write down strong form of PDE.
Rearrange terms so that zero is on the right of the equals sign.
Multiply the whole equation by a "test" function .
Integrate the whole equation over the domain .
Integrate by parts and use the divergence theorem to get the desired derivative order on your functions and simultaneously generate boundary integrals.
Integration by Parts and Divergence Theorem
Suppose is a scalar function, is a vector function, and both are continuously differentialable functions, then the product rule states:
The function can be integrated over the volume and rearranged as:
(4)The divergence theorem transforms a volume integral into a surface integral on surface :
(5)where is the outward normal vector for surface . Combining Eq. (4) and Eq. (5) yield:
(6)Example: Advection-Diffusion
(1) Write the strong form of the equation:
(2) Rearrange to get zero on the right-hand side:
(3) Multiply by the test function :
(4) Integrate over the domain :
(5) Integrate by parts and apply the divergence theorem, by using Eq. (6) on the left-most term of the PDE:
Write in inner product notation. Each term of the equation will inherit from an existing MOOSE type as shown below.
(7)Finite Element Shape Functions
Basis Functions
While the weak form is essentially what is needed for adding physics to MOOSE, in traditional finite element software more work is necessary.
The weak form must be discretized using a set of "basis functions" amenable for manipulation by a computer.

Images copyright Becker et al. (1981)

Shape Functions
The discretized expansion of takes on the following form:
where are the "basis functions", which form the basis for the the "trial function", . is the total number of functions for the discretized domain.
The gradient of can be expanded similarly:
In the Galerkin finite element method, the same basis functions are used for both the trial and test functions:
Substituting these expansions back into the example weak form (Eq. (7)) yields:
(8)The left-hand side of the equation above is referred to as the component of the "residual vector," .
Shape Functions are the functions that get multiplied by coefficients and summed to form the solution.
Individual shape functions are restrictions of the global basis functions to individual elements.
They are analogous to the functions from polynomial fitting (in fact, you can use those as shape functions).
Typical shape function families: Lagrange, Hermite, Hierarchic, Monomial, Clough-Toucher
Lagrange shape functions are the most common, which are interpolary at the nodes, i.e., the coefficients correspond to the values of the functions at the nodes.
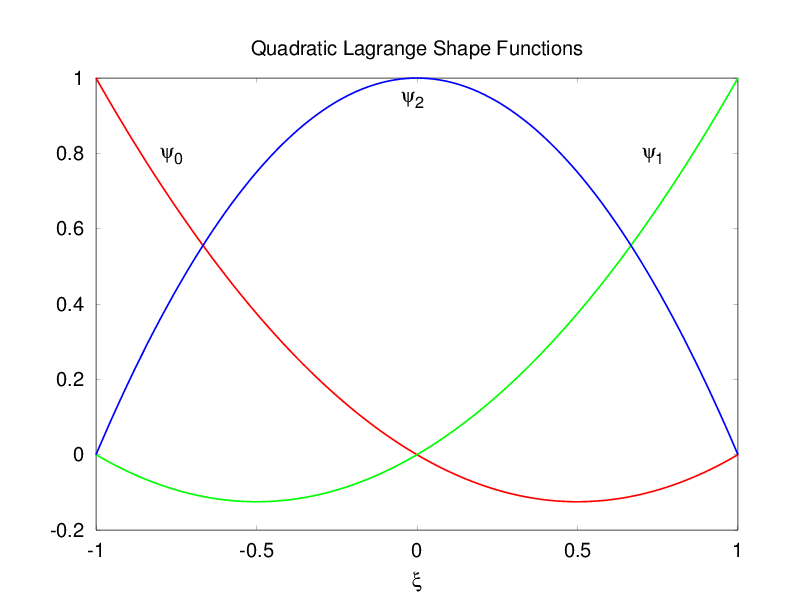
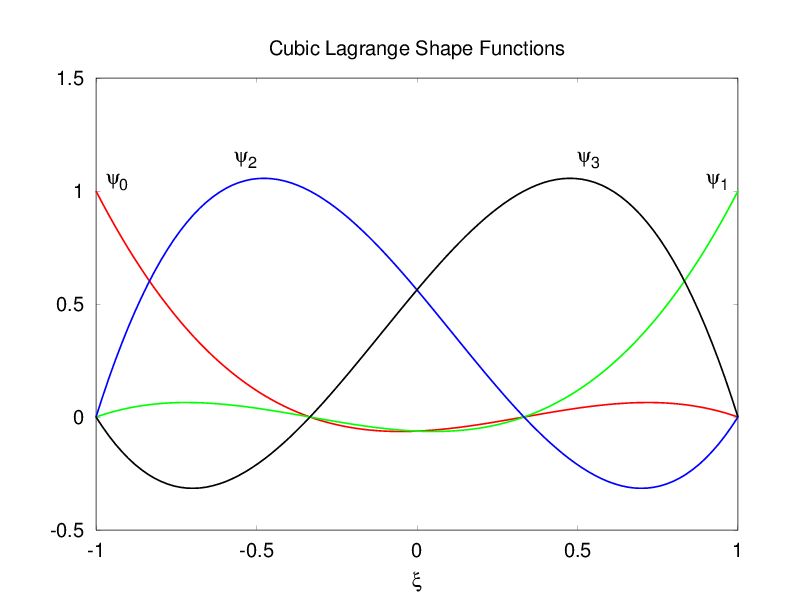
Example 1D Shape Functions


2D Lagrange Shape Functions
Example bi-quadratic basis functions defined on the Quad9 element:
is associated to a "corner" node, it is zero on the opposite edges.
is associated to a "mid-edge" node, it is zero on all other edges.
is associated to the "center" node, it is symmetric and on the element.



Numerical Implementation
Numerical Integration
The only remaining non-discretized parts of the weak form are the integrals. First, split the domain integral into a sum of integrals over elements:
(9)Through a change of variables, the element integrals are mapped to integrals over the "reference" elements .
where is the Jacobian of the map from the physical element to the reference element.
Reference Element (Quad9)

Quadrature
Quadrature, typically "Gaussian quadrature", is used to approximate the reference element integrals numerically.
where is the weight function at quadrature point .
Under certain common situations, the quadrature approximation is exact. For example, in 1 dimension, Gaussian Quadrature can exactly integrate polynomials of order with quadrature points.
Quadrature applied to Eq. (9) yields an equation that can be analyzed numerically:
where is the spatial location of the quadrature point and is its associated weight.
MOOSE handles multiplication by the Jacobian () and the weight () automatically, thus your Kernel object is only responsible for computing the part of the integrand.
Sampling at the quadrature points yields:
Thus, the weak form of Eq. (8) becomes:
(10)The second sum is over boundary faces, . MOOSE Kernel or BoundaryCondition objects provide each of the terms in square brackets (evaluated at or as necessary), respectively.
Newton's Method
Newton's method is a "root finding" method with good convergence properties, in "update form", for finding roots of a scalar equation it is defined as: , is given by
Newton's Method in MOOSE
The residual, , as defined by Eq. (10) is a nonlinear system of equations,
that is used to solve for the coefficients .
For this system of nonlinear equations Newton's method is defined as:
(11)where is the Jacobian matrix evaluated at the current iterate:
Jacobian Free Newton Krylov (JFNK)
is a linear system solved during each Newton step.
In MOOSE an iterative Krylov method is used to produce a sequence of iterates ,
and remain fixed during the iterative process.
The "linear residual" at step is defined as:
(12)MOOSE prints the norm of this vector, , at each linear iteration and the "nonlinear residual" printed by MOOSE is .
Krylov methods construct a subspace () for the iterate :
where and .
Different Krylov methods produce the iterates in different ways:
Conjugate Gradients: orthogonal to .
GMRES/MINRES: has minimum norm for in .
Biconjugate Gradients: is orthogonal to
The important part is that is never explicitly needed to construct the subspace, only the action of on a vector is required.
This action can be approximated by:
(13)This form has many advantages:
No need to do analytic derivatives to form
No time needed to compute (just residual computations)
No space needed to store
Preconditioned JFNK
Krylov methods need preconditioning to be efficient (or even effective!), see Knoll and Keyes (2004).
Reduces the total number of linear iterations
Krylov methods, in theory, converge in the number of linear iterations equal to the number of unknowns in the system
Even though the Jacobian is never formed, JFNK methods still require preconditioning.
When using right preconditioning:
symbolically represents the preconditioning matrix or process, and with GMRES only the action of on a vector is required.
When right-preconditioned, Eq. (12) becomes:
(14)and Eq. (13) becomes:
(15)MOOSE Solve Types
The solve type is specified in the [Executioner] block within the input file:
[Executioner]
solve_type = PJFNK
Available options include:
PJFNK: Preconditioned Jacobian Free Newton Krylov (default)
JFNK: Jacobian Free Newton Krylov
NEWTON: Performs solve using exact Jacobian for preconditioning
FD: PETSc computes terms using a finite difference method (debug)
JFNK
The Kernel method computeQpResidual is called to compute during the nonlinear step (Eq. (11)).
During each linear step of Eq. (12) the computeQpResidual method is called to compute using Eq. (13).
PJFNK
The Kernel method computeQpResidual is called to compute during the nonlinear step (Eq. (11)).
During each linear step of Eq. (14) the computeQpResidual method is called to compute using Eq. (15). The computeQpJacobian and computeQpOffDiagJacobian methods are used to compute values for the preconditioning matrix .
NEWTON
The Kernel method computeQpResidual is called to compute during the nonlinear step (Eq. (11)).
The computeQpJacobian and computeQpOffDiagJacobian methods are used to compute the preconditioning matrix . It is assumed that , thus the approximation in Eq. (15) is not needed allowing for the residual and Jacobian calculations to remain constant during the linear iterations in Eq. (14).
Summary
The Finite Element Method is a way of numerically approximating the solution of PDEs.
Just like polynomial fitting, FEM finds coefficients for basis functions.
The solution is the combination of the coefficients and the basis functions, and the solution can be sampled anywhere in the domain.
Integrals are computed numerically using quadrature.
Newton's method provides a mechanism for solving a system of nonlinear equations.
The Preconditioned Jacobian Free Newton Krylov (JFNK) method allows us to avoid explicitly forming the Jacobian matrix while still computing its action.
Automatic Jacobian Calculation
MOOSE uses forward mode automatic differentiation from the MetaPhysicL package.
Moving forward, the idea is for application developers to be able to develop entire apps without writing a single Jacobian statement. This has the potential to decrease application development time.
In terms of computing performance, presently AD Jacobians are slower to compute than hand-coded Jacobians, but they parallelize extremely well and can benefit from using a NEWTON solve, which often results in decreased solve time overall.
Manual Jacobian Calculation
The remainder of the tutorial will focus on using AD for computing Jacobian terms, but it is possible to compute them manually.
It is recommended that all new Kernel objects use AD.
FEM Derivative Identities
The following relationships are useful when computing Jacobian terms.
(16)(17)Newton for a Simple Equation
Again, consider the advection-diffusion equation with nonlinear , , and :
Thus, the component of the residual vector is:
Using the previously-defined rules in Eq. (16) and Eq. (17) for and , the entry of the Jacobian is then:
That even for this "simple" equation, the Jacobian entries are nontrivial: they depend on the partial derivatives of , , and , which may be difficult or time-consuming to compute analytically.
In a multiphysics setting with many coupled equations and complicated material properties, the Jacobian might be extremely difficult to determine.
C++
Fundamentals
C Preprocessor Commands
# Should be the first character on the line
#include <iostream>#include "myheader.h"#define SOMEWORD value#ifdef, #ifndef, #endif
#pragma once
#pragma clang diagnostic push
#pragma clang diagnostic ignored "-Wunused-parameter"
#pragma clang diagnostic pop
Intrinsic Data Types
| Basic Type | Variant(s) |
|---|---|
| |bool | | |
| |char | unsigned |
| int | unsigned, long, short |
| float | | |
| double | long |
| void | | |
Note, void is the "anti-datatype", used in functions returning nothing
Operators
| Purpose | Symbols |
|---|---|
| Math | + - * / % += -= /= %= ++ -- |
| Comparison | < > <= >= != == |
| Logical Comparison | && || ! |
| Memory | * & new delete sizeof |
| Assignment | = |
| Member Access | -> . |
| Name Resolution | :: |
Curly Braces { }
Used to group statements together
Creates new layer of scope (we will get to this)
Expressions
Composite mathematical expressions:
a = b * (c - 4) / d++;
Composite boolean expressions:
if (a && b && f()) { e = a; }
Note, Operators && and || use "short-circuiting," so "b" and "f()" in the example above may not get evaluated.
Scope resolution operator:
t = std::pow(r, 2);
b = std::sqrt(d);
Dot and Pointer Operator:
t = my_obj.someFunction();
b = my_ptr->someFunction();
Type Casting
float pi = 3.14;
int approx_pi = static_cast<int>(pi);
Limits to Type Casting
Does not work to change to fundamentally different types
float f = (float) "3.14"; // won't compile
Be careful with your assumptions
unsigned int huge_value = 4294967295; // ok
int i = static_cast<int>(huge_value); // won't work!
Control Statements
For, While, and Do-While Loops:
for (int i=0; i<10; ++i) { }
while (boolean-expression) { }
do { } while (boolean-expression);
If-Then-Else Tests:
if (boolean-expression) { }
else if (boolean-expression) { }
else { }
In the previous examples, boolean-expression is any valid C++ statement which results in true or false, such as:
if (0) // Always falsewhile (a > 5)
Switch Statement
switch (expression)
{
case constant1:
// commands to execute if
// expression==constant1 ...
break;
case constant2:
case constant3:
// commands to execute if
// expression==constant2 OR expression==constant3...
break;
default:
// commands to execute if no previous case matched
}
Declarations and Definitions
In C++ we split our code into multiple files
headers (*.h)
bodies (*.C)
Headers generally contain declarations
Statement of the types we will use
Gives names to types
Bodies generally contain definitions
Our descriptions of those types, including what they do or how they are built
Memory consumed
The operations functions perform
Declaration Examples
Free functions:
returnType functionName(type1 name1, type2 name2);
Object member functions (methods):
class ClassName
{
returnType methodName(type1 name1, type2 name2);
};
Definition Examples
Function definition:
returnType functionName(type1 name1, type2 name2)
{
// statesments
}
Class method definition:
returnType ClassName::methodName(type1 name1, type2 name2)
{
// statements
}
Function Example: Addition
#include <iostream>
int addition (int a, int b)
{
return a + b;
}
int main ()
{
int z = addition(5,3);
std::cout << "The result is " << z << "\n";
return 0;
}
Forward Declaration
#include <iostream>
int addition (int a, int b);
int main ()
{
int z = addition (5,3);
std::cout << "The result is " << z << "\n";
return 0;
}
int addition (int a, int b)
{
return a + b;
}
Make
A Makefile is a list of dependencies with rules to satisfy those dependencies All MOOSE-based applications are supplied with a complete Makefile To build a MOOSE-based application just type:
make
Compiling, Linking, Executing
Compile and Link
g++ -O3 -o myExample myExample.C
Compile only
g++ -O3 -o myExample.o -c myExample.C
Link only
g++ -O3 -o myExample myExample.o
Compiler/Linker Flags
Libraries (-L) and Include (-I) path Library Names (-l)
Remove the leading "lib" and trailing file extension when linking
libutils.so would link as -lutils
g++ -I/home/permcj/include -L/home/permcj/lib -lutils -Wall -o myExec myExec.o
Execution
Basic execution
./myExec
Finding shared libraries at runtime
Linux:
lddand$LD_LIBRARY_PATHMacOS:
otool
Addition Example (continued)
Header File (add.h)
#pragma once
int addition (int a, int b); // Function declaration
Headers typically contain declarations only
Source File (add.C)
#include "add.h"
int addition (int a, int b)
{
return a + b;
}
Driver Program (main.C)
#include "add.h"
#include <iostream>
int main ()
{
int z = addition(5,3);
std::cout << "The result is " << z;
return 0;
}
Compiling the Addition Example
g++ -g -c -o add.o add.Cg++ -g -c -o main.o main.Cg++ -g -o main main.o add.oThe -c flag means compile only, do not link
These commands can be stored in a Makefile and executed automatically with the make command
C++
Scope, Memory, and Overloading
Scope
A scope is the extent of the program where a variable can be seen and used.
local variables have scope from the point of declaration to the end of the enclosing block { }
global variables are not enclosed within any scope and are available within the entire file
Variables have a limited lifetime
When a variable goes out of scope, its destructor is called
Dynamically-allocated (via new) memory is not automatically freed at the end of scope
"Named" Scopes
class scope
class MyObject
{
public:
void myMethod();
};
namespace scope
namespace MyNamespace
{
float a;
void myMethod();
}
Scope Resolution Operator
"double colon" :: is used to refer to members inside of a named scope
// definition of the "myMethod" function of "MyObject"
void MyObject::myMethod()
{
std::cout << "Hello, World!\n";
}
MyNamespace::a = 2.718;
MyNamespace::myMethod();
Namespaces permit data organization, but do not have all the features needed for full encapsulation
Assignment
(Prequel to Pointers and Refs)
Recall that assignment in C++ uses the "single equals" operator:
a = b; // Assignment
Assignments are one of the most common operations in programming
Two operands are required
An assignable location on the left hand side (memory location)
An expression on the right hand side
Pointers
Native type just like an int or long
Hold the location of another variable or object in memory
Useful in avoiding expensive copies of large objects
Facilitate shared memory
Example: One object "owns" the memory associated with some data, and allows others objects access through a pointer
Pointer Syntax
Declare a pointer
int *p;
Use the address-of operator to initialize a pointer
int a;
p = &a;
Use the dereference operator to get or set values pointed-to by the pointer
*p = 5; // set value of "a" through "p"
std::cout << *p << "\n"; // prints 5
std::cout << a << "\n"; // prints 5
Pointer Syntax (continued)
int a = 5;
int *p; // declare a pointer
p = &a; // set 'p' equal to address of 'a'
*p = *p + 2; // get value pointed to by 'p', add 2,
// store result in same location
std::cout << a << "\n"; // prints 7
std::cout << *p << "\n"; // prints 7
std::cout << p << "\n"; // prints an address (0x7fff5fbfe95c)
Pointers are Powerful but Unsafe
On the previous slide we had this:
p = &a;
But we can do almost anything we want with p!
p = p + 1000;
Now what happens when we do this?
*p; // Access memory at &a + 1000
References to the Rescue
A reference is an alternative name for an object (Stroustrup), think of it as an alias for the original variable
int a = 5;
int &r = a; // define and initialize a ref
r = r + 2;
std::cout << a << "\n"; // prints 7
std::cout << r << "\n"; // prints 7
std::cout << &r << "\n"; // prints address of a
References are Safe
References cannot be modified
&r = &r + 1; // won't compile
References never start out un-initialized
int &r; // won't compile
Note, that class declarations may contain references
If so, initialization must occur in the constructor!
Summary: Pointers and References
A pointer is a variable that holds a memory address to another variable
int *iPtr; // Declaration
iPtr = &c;
int a = b + *iPtr;
A reference is an alternative name for an object (Stroustrup), so it must reference an existing object
int &iRef = c; // Must initialize
int a = b + iRef;
Calling Conventions
What happens when you make a function call?
result = someFunction(a, b, my_shape);
If the function changes the values inside of a, b or myshape, are those changes reflected in my code?
Is this call expensive? (Are arguments copied around?)
C++ by default is "Pass by Value" (copy) but you can pass arguments by reference (alias) with additional syntax
Swap Example (Pass by Value)
void swap(int a, int b)
{
int temp = a;
a = b;
b = temp;
}
int i = 1;
int j = 2;
swap (i, j); // i and j are arguments
std::cout << i << " " << j; // prints 1 2
// i and j are not swapped
Swap Example (Pass by Reference)
void swap(int &a, int &b)
{
int temp = a;
a = b;
b = temp;
}
int i = 1;
int j = 2;
swap (i, j); // i and j are arguments
std::cout << i << " " << j; // prints 2 1
// i and j are properly swapped
Dynamic Memory Allocation
Why do we need dynamic memory allocation?
Data size specified at run time (rather than compile time)
Persistence without global variables (scopes)
Efficient use of space
Flexibility
Dynamic Memory in C++
"new" allocates memory
"delete" frees memory
Recall that variables typically have limited lifetimes (within the nearest enclosing scope)
Dynamic memory allocations do not have limited lifetimes
No automatic memory cleanup!
Watch out for memory leaks
Should have a "delete" for every "new".
During normal usage, dynamic memory allocation is unnecessary.
Example: Dynamic Memory
int a;
int *b;
b = new int; // dynamic allocation, what is b's value?
a = 4;
*b = 5;
int c = a + *b;
std::cout << c; // prints 9
delete b;
Example: Dynamic Memory Using References
int a;
int *b = new int; // dynamic allocation
int &r = *b; // creating a reference to newly created variable
a = 4;
r = 5;
int c = a + r;
std::cout << c; // prints 9
delete b;
Const
The const keyword is used to mark a variable, parameter, method or other argument as constant
Typically used with references and pointers to share objects but guarantee that they will not be modified
{
std::string name("myObject");
print(name);
...
}
void print(const std::string & name)
{
// Attempting to modify name here will
// cause a compile time error
...
}
Function Overloading
In C++ you may reuse function names as long as they have different parameter lists or types. A difference only in the return type is not enough to differentiate overloaded signatures.
int foo(int value);
int foo(float value);
int foo(float value, bool is_initialized);
...
This is very useful when we get to object "constructors".
C++
Types, Templates, and
Standard Template Library (STL)
Static vs Dynamic Type Systems
C++ is a "statically-typed" language
This means that "type checking" is performed during compile-time as opposed to run-time
Python and MATLAB are examples of "dynamically-typed" languages
Static Typing Pros and Cons
Pros:
Safety: compilers can detect many errors
Optimization: compilers can optimize for size and speed
Documentation: flow of types and their uses in expression is self documenting
Cons:
More explicit code is needed to convert ("cast") between types
Abstracting or creating generic algorithms is more difficult
Templates
C++ implements the generic programming paradigm with "templates".
Many of the finer details of C++ template usage are beyond the scope of this short tutorial.
Fortunately, only a small amount of syntactic knowledge is required to make effective basic use of templates.
template <class T>
T getMax (T a, T b)
{
if (a > b)
return a;
else
return b;
}
Templates (continued)
template <class T>
T getMax (T a, T b)
{
return (a > b ? a : b); // "ternary" operator
}
int i = 5, j = 6, k;
float x = 3.142; y = 2.718, z;
k = getMax(i, j); // uses int version
z = getMax(x, y); // uses float version
k = getMax<int>(i, j); // explicitly calls int version
Template Specialization
template<class T>
void print(T value)
{
std::cout << value << std::endl;
}
template<>
void print<bool>(bool value)
{
if (value)
std::cout << "true\n";
else
std::cout << "false\n";
}
Template Specialization (continued)
int main()
{
int a = 5;
bool b = true;
print(a); // prints 5
print(b); // prints true
}
C++ Standard Template Library (STL)
Using the C++ Vector Container
#include <vector>
int main()
{
// start with 10 elements
std::vector<int> v(10);
for (unsigned int i=0; i<v.size(); ++i)
v[i] = i;
}
#include <vector>
int main()
{
// start with 0 elements
std::vector<int> v;
for (unsigned int i=0; i<10; ++i)
v.push_back(i);
}
#include <vector>
int main()
{
// start with 0 elements
std::vector<int> v;
v.resize(10); // creates 10 elements
for (unsigned int i=0; i<10; ++i)
v[i] = i;
}
C++
Classes and Object Oriented Programming
Object Oriented Definitions
A "class" is a new data type that contains data and methods for operating on that data
Think of it as a "blue print" for building an object
An "interface" is defined as a class's publicly available "methods" and "members"
An "instance" is a variable of one of these new data types.
Also known as an "object"
Analogy: You can use one "blue-print" to build many buildings. You can use one "class" to build many "objects".
Object Oriented Design
Instead of manipulating data, one manipulates objects that have defined interfaces
Data encapsulation is the idea that objects or new types should be black boxes. Implementation details are unimportant as long as an object works as advertised without side effects.
Inheritance gives us the ability to abstract or "factor out" common data and functions out of related types into a single location for consistency (avoids code duplication) and enables code re-use.
Polymorphism gives us the ability to write generic algorithms that automatically work with derived types.
Encapsulation (Point.h)
class Point
{
public:
Point(float x, float y); // Constructor
// Accessors
float getX();
float getY();
void setX(float x);
void setY(float y);
private:
float _x, _y;
};
Constructors
The method that is called explicitly or implicitly to build an object
Always has the same name as the class with no return type
May have many overloaded versions with different parameters
The constructor body uses a special syntax for initialization called an initialization list
Every member that can be initialized in the initialized list - should be
References have to be initialized here
Point Class Definitions (Point.C)
#include "Point.h"
Point::Point(float x, float y): _x(x), _y(y) { }
float Point::getX() { return _x; }
float Point::getY() { return _y; }
void Point::setX(float x) { _x = x; }
void Point::setY(float y) { _y = y; }
The data is safely encapsulated so we can change the implementation without affecting users of this type
Changing the Implementation (Point.h)
class Point
{
public:
Point(float x, float y);
float getX();
float getY();
void setX(float x);
void setY(float y);
private:
// Store a vector of values rather than separate scalars
std::vector<float> _coords;
};
New Point Class Body (Point.C)
#include "Point.h"
Point::Point(float x, float y)
{
_coords.push_back(x);
_coords.push_back(y);
}
float Point::getX() { return _coords[0]; }
float Point::getY() { return _coords[1]; }
void Point::setX(float x) { _coords[0] = x; }
void Point::setY(float y) { _coords[1] = y; }
Using the Point Class (main.C)
#include "Point.h"
int main()
{
Point p1(1, 2);
Point p2 = Point(3, 4);
Point p3; // compile error, no default constructor
std::cout << p1.getX() << "," << p1.getY() << "\n"
<< p2.getX() << "," << p2.getY() << "\n";
}
Operator Overloading
For some user-defined types (objects) it makes sense to use built-in operators to perform functions with those types
For example, without operator overloading, adding the coordinates of two points and assigning the result to a third object might be performed like this:
Point a(1,2), b(3,4), c(5,6);
// Assign c = a + b using accessors
c.setX(a.getX() + b.getX());
c.setY(a.getY() + b.getY());
However the ability to reuse existing operators on new types makes the following possible:
c = a + b;
Operator Overloading (continued)
Inside our Point class, we define new member functions with the special operator keyword:
Point Point::operator+(const Point & p)
{
return Point(_x + p._x, _y + p._y);
}
Point & Point::operator=(const Point & p)
{
_x = p._x;
_y = p._y;
return *this;
}
Using "Point" with Operators
#include "Point.h"
int main()
{
Point p1(0, 0), p2(1, 2), p3(3, 4);
p1 = p2 + p3;
std::cout << p1.getX() << "," << p1.getY() << "\n";
}
A More Advanced Example (Shape.h)
class Shape {
public:
Shape(int x=0, int y=0): _x(x), _y(y) {} // Constructor
virtual ~Shape() {} // Destructor
virtual float area()=0; // Pure Virtual Function
void printPosition(); // Body appears elsewhere
protected:
// Coordinates at the centroid of the shape
int _x;
int _y;
};
The Derived Class: Rectangle.h
#include "Shape.h"
class Rectangle: public Shape
{
public:
Rectangle(int width, int height, int x=0, int y=0) :
Shape(x,y),
_width(width),
_height(height)
{}
virtual ~Rectangle() {}
virtual float area() { return _width * _height; }
protected:
int _width;
int _height;
};
A Derived Class: Circle.h
#include "Shape.h"
class Circle: public Shape
{
public:
Circle(int radius, int x=0, int y=0) :
Shape(x,y),
_radius(radius)
{}
virtual ~Circle() {}
virtual float area() { return PI * _radius * _radius; }
protected:
int _radius;
const double PI = 3.14159265359;
};
Inheritance (Is a...)
When using inheritance, the derived class can be described in terms of the base class
A Rectangle "is a" Shape
Derived classes are "type" compatible with the base class (or any of its ancestors)
We can use a base class variable to point to or refer to an instance of a derived class
Rectangle rectangle(3, 4);
Shape & s_ref = rectangle;
Shape * s_ptr = &rectangle;
Deciphering Long Declarations
Read the declaration from right to left
// mesh is a pointer to a Mesh object
Mesh * mesh;
// params is a reference to an InputParameters object
InputParameters & params;
// the following are identical
// value is a reference to a constant Real object
const Real & value;
Real const & value;
Writing a Generic Algorithm
// create a couple of shapes
Rectangle r(3, 4);
Circle c(3, 10, 10);
printInformation(r); // pass a Rectangle into a Shape reference
printInformation(c); // pass a Circle into a Shape reference
...
void printInformation(const Shape & shape)
{
shape.printPosition();
std::cout << shape.area() << '\n';
}
// (0, 0)
// 12
// (10, 10)
// 28.274
Homework Ideas
Implement a new Shape called Square. Try deriving from Rectangle directly instead of Shape. What advantages/disadvantages do the two designs have?
Implement a Triangle shape. What interesting subclasses of Triangle can you imagine?
Add another constructor to the Rectangle class that accepts coordinates instead of height and width.
MOOSE C++ Standard
Clang Format
MOOSE uses "clang-format" to automatically format code:
git clang-format branch_name_here
Single spacing around all binary operators
No spacing around unary operators
No spacing on the inside of brackets or parenthesis in expressions
Avoid braces for single statement control statements (i.e for, if, while, etc.)
C++ constructor spacing is demonstrated in the bottom of the example below
File Layout
Header files should have a ".h" extension
Header files always go either into "include" or a sub-directory of "include"
C++ source files should have a ".C" extension
Source files go into "src" or a subdirectory of "src".
Files
Header and source file names must match the name of the class that the files define. Hence, each set of .h and .C files should contain code for a single class.
src/ClassName.C
include/ClassName.h
Naming
ClassNameClass names utilize camel case, note the .h and .C filenames must match the class name.methodName()Method and function names utilize camel case with the leading letter lower case._member_variableMember variables begin with underscore and are all lower case and use underscore between words.local_variableLocal variables are lowercase, begin with a letter, and use underscore between words
Example Code
Below is a sample that covers many (not all) of our code style conventions.
namespace moose // lower case namespace names
{
// don't add indentation level for namespaces
int // return type should go on separate line
junkFunction()
{
// indent two spaces!
if (name == "moose") // space after the control keyword "if"
{
// Spaces on both sides of '&' and '*'
SomeClass & a_ref;
SomeClass * a_pointer;
}
// Omit curly braces for single statements following an if the statement must be on its own line
if (name == "squirrel")
doStuff();
else
doOtherStuff();
// No curly braces for single statement branches and loops
for (unsigned int i = 0; i < some_number; ++i) // space after control keyword "for"
doSomething();
// space around assignment operator
Real foo = 5.0;
switch (stuff) // space after the control keyword "switch"
{
// Indent case statements
case 2:
junk = 4;
break;
case 3:
{ // Only use curly braces if you have a declaration in your case statement
int bar = 9;
junk = bar;
break;
}
default:
junk = 8;
}
while (--foo) // space after the control keyword "while"
std::cout << "Count down " << foo;
}
// (short) function definitions on a single line
SomeClass::SomeFunc() {}
// Constructor initialization lists can all be on the same line.
SomeClass::SomeClass() : member_a(2), member_b(3) { }
// Four-space indent and one item per line for long (i.e. won't fit on one line) initialization list.
SomeOtherClass::SomeOtherClass()
: member_a(2),
member_b(3),
member_c(4),
member_d(5),
member_e(6),
member_f(7),
member_g(8),
member_h(9)
{ // braces on separate lines since func def is already longer than 1 line
}
} // namespace moose
Using auto
Use auto for most new code unless it complicates readability. Make sure your variables have good names when using auto!
auto dof = elem->dof_number(0, 0, 0);
auto & obj = getSomeObject();
auto & elem_it = mesh.active_local_elements_begin();
auto & item_pair = map.find(some_item);
// Cannot use reference here
for (auto it = obj.begin(); it != obj.end(); ++it)
doSomething();
// Use reference here
for (auto & obj : container)
doSomething();
Do not use auto in any kind of function or method declaration
Lambdas
// List captured variables (by value or reference) in the capture list explicitly where possible.
std::for_each(container.begin(), container.end(), [= local_var](Foo & foo) {
foo.item = local_var;
foo.item2 = local_var2;
});
C++11
Use the
overridekeyword on overriddenvirtualmethodsUse
std::make_shared<T>()when allocating new memory for shared pointersUse
libmesh_make_unique<T>()when allocating new memory for unique pointersMake use of std::move() for efficiency when possible
Variable Initialization
When creating a new variable use these patterns:
unsigned int i = 4; // Built-in types
SomeObject junk(17); // Objects
SomeObject * stuff = new SomeObject(18); // Pointers
Trailing Whitespace and Tabs
MOOSE does not allow any trailing whitespace or tabs in the repository. Try running the following one-liner from the appropriate directory:
find . -name '*.[Chi]' -or -name '*.py' | xargs perl -pli -e 's/\s+$//'
Includes
Firstly, only include things that are absolutely necessary in header files. Please use forward declarations when you can:
// Forward declarations
class Something;
All non-system includes should use quotes and there is a space between include and the filename.
#include "LocalInclude.h"
#include "libmesh/libmesh_include.h"
#include <system_library>
In-Code Documentation
Try to document as much as possible, using Doxygen style comments
/**
* The Kernel class is responsible for calculating the residuals for various physics.
*/
class Kernel
{
public:
/**
* This constructor should be used most often. It initializes all internal
* references needed for residual computation.
*
* @param system The system this variable is in
* @param var_name The variable this Kernel is going to compute a residual for.
*/
Kernel(System * system, std::string var_name);
/**
* This function is used to get stuff based on junk.
*
* @param junk The index of the stuff you want to get
* @return The stuff associated with the junk you passed in
*/
int returnStuff(int junk);
protected:
/// This is the stuff this class holds on to.
std::vector<int> stuff;
};
Python
Where possible, follow the above rules for Python. The only modifications are:
Four spaces are used for indenting and
Member variables should be named as follows:
class MyClass:
def __init__(self):
self.public_member
self._protected_member
self.__private_member
Code Recommendations
Use references whenever possible
Methods should return pointers to objects if returned objects are stored as pointers and references if returned objects are stored as references
When creating a new class include dependent header files in the *.C file whenever possible
Avoid using a global variables
Every destructor must be virtual
All function definitions should be in *.C files, if possible
Step 2: Pressure Kernel
Kernel Object
To implement the Darcy pressure equation, a Kernel object is needed to add the coefficient to diffusion equation.
where is the permeability tensor and is the fluid viscosity.
A Kernel is C++ class, which inherits from MooseObject that is used by MOOSE for coding volume integrals of a partial differential equation (PDE).
MooseObject
All user-facing objects in MOOSE derive from MooseObject, this allows for a common structure for all applications and is the basis for the modular design of MOOSE.
Basic Header: CustomObject.h
#pragma once
#include "BaseObject.h"
class CustomObject : public BaseObject
{
public:
static InputParameters validParams();
CustomObject(const InputParameters & parameters);
protected:
virtual Real doSomething() override;
const Real & _scale;
};
Basic Source: CustomObject.C
#include "CustomObject.h"
registerMooseObject("CustomApp", CustomObject);
InputParameters
CustomObject::validParams()
{
InputParameters params = BaseObject::validParams();
params.addClassDescription("The CustomObject does something with a scale parameter.");
params.addParam<Real>("scale", 1, "A scale factor for use when doing something.");
return params;
}
CustomObject::CustomObject(const InputParameters & parameters) :
BaseObject(parameters),
_scale(getParam<Real>("scale"))
{
}
double
CustomObject::doSomething()
{
// Do some sort of import calculation here that needs a scale factor
return _scale;
}
Input Parameters
Every MooseObject includes a set of custom parameters within the InputParameters object that is used to construct the object.
The InputParameters object for each object is created using the static validParams method, which every class contains.
validParams Declaration
static InputParameters Convection::validParams();
validParams Definition
InputParameters
Convection::validParams()
{
InputParameters params = Kernel::validParams(); // Start with parent
params.addRequiredParam<RealVectorValue>("velocity", "Velocity Vector");
params.addParam<Real>("coefficient", "Diffusion coefficient");
return params;
}
InputParameters Object
Class Description
Class level documentation may be included within the source code using the addClassDescription method.
params.addClassDescription("Use this method to provide a summary of the class being created...");
Optional Parameter(s)
Adds an input file parameter, of type int, that includes a default value of 1980.
params.addParam<int>("year", 1980, "Provide the year you were born.");
[UserObjects]
[date_object]
type = Date
year = 1990
[]
[]
Required Parameter(s)
Adds an input file parameter, of type int, must be supplied in the input file.
params.addRequiredParam<int>("month", "Provide the month you were born.");
[UserObjects]
[date_object]
type = Date
month = 6
[]
[]
Coupled Variable
Various types of objects in MOOSE support variable coupling, this is done using the addCoupledVar method.
params.addCoupledVar("temperature", "The temperature (C) of interest.");
params.addCoupledVar("pressure", 101.325, "The pressure (kPa) of the atomsphere.");
[Variables]
[P][]
[T][]
[]
[UserObjects]
[temp_pressure_check]
type = CheckTemperatureAndPressue
temperature = T
pressure = P # if not provided a value of 101.325 would be used
[]
[]
Within the input file it is possible to used a variable name, a constant value, a function, or a postprocessor name as a the right-hand side.
pressure = P
pressure = 42
pressure = 3*x # more about this later
pressure = pp_name # more about this later
Range Checked Parameters
Input variables may be restricted to a range of values directly in the validParams function.
params.addRangeCheckedParam<Real>(
"growth_factor",
2,
"growth_factor>=1",
"Maximum ratio of new to previous timestep sizes following a step that required the time"
" step to be cut due to a failed solve.");
Documentation
Each application is capable of generating documentation from the validParams functions.
Option 1: All parameter documentation and class description is displayed in MOOSE GUI "peacock"
Option 2: Command line --dump
--dump [optional search string]the search string may contain wildcard characters
searches both block names and parameters
Option 3: Command line --show-input generates a tree based on your input file\\
Option 4: mooseframework.org/syntax
C++ Types
Built-in types and std::vector are supported via template methods:
addParam<Real>("year", 1980, "The year you were born.");`addParam<int>("count", 1, "doc");
addParam<unsigned int>("another_num", "doc");addParam<std::vector<int> >("vec", "doc");
Other supported parameter types include:
PointRealVectorValueRealTensorValueSubdomainIDBoundaryID
MOOSE uses a large number of string types to make Peacock more context-aware. All of these types can be treated just like strings, but will cause compile errors if mixed improperly in the template functions.
SubdomainName
BoundaryName
FileName
VariableName
FunctionName
UserObjectName
PostprocessorName
MeshFileName
OutFileName
NonlinearVariableName
AuxVariableName
A complete list, see the instantiations at the bottom of framework/include/utils/MooseTypes.h.
MooseEnum
MOOSE includes a "smart" enum utility to overcome many of the deficiencies in the standard C++ enum type. It works in both integer and string contexts and is self-checked for consistency.
#include "MooseEnum.h"
// The valid options are specified in a space separated list.
// You can optionally supply the default value as a second argument.
// MooseEnums are case preserving but case-insensitive.
MooseEnum option_enum("first=1 second fourth=4", "second");
// Use in a string context
if (option_enum == "first")
doSomething();
// Use in an integer context
switch (option_enum)
{
case 1: ... break;
case 2: ... break;
case 4: ... break;
default: ... ;
}
MooseEnum with InputParameters
Objects that have a specific set of named options should use a MooseEnum so that parsing and error checking code can be omitted.
InputParameters MyObject::validParams()
{
InputParameters params = ParentObject::validParams();
MooseEnum component("X Y Z"); // No default supplied
params.addRequiredParam<MooseEnum>("component", component,
"The X, Y, or Z component");
return params;
}
Peacock will create a drop box when using MooseEnum and if an invalid value is supplied, an error message is provided.
Multiple Value MooseEnums (MultiMooseEnum)
Operates the same way as MooseEnum but supports multiple ordered options.
InputParameters MyObject::validParams()
{
InputParameters params = ParentObject::validParams();
MultiMooseEnum transforms("scale rotate translate");
params.addRequiredParam<MultiMooseEnum>("transforms", transforms,
"The transforms to perform");
return params;
}
Kernel System
A system for computing the residual contribution from a volumetric term within a PDE using the Galerkin finite element method.
Kernel Object
A Kernel objects represents one or more terms in a PDE.
A Kernel object is required to compute a residual at a quadrature point, which is done by calling the computeQpResidual method.
Kernel Object Members
_u, _grad_u
Value and gradient of the variable this Kernel is operating on
_test, _grad_test
Value () and gradient () of the test functions at the quadrature points
_phi, _grad_phi
Value () and gradient () of the trial functions at the quadrature points
_q_point
Coordinates of the current quadrature point
_i, _j
Current index for test and trial functions, respectively
_qp
Current quadrature point index
Kernel Base Classes
| Base | Override | Use |
|---|---|---|
| Kernel ADKernel | computeQpResidual | Use when the term in the PDE is multiplied by both the test function and the gradient of the test function (_test and _grad_test must be applied) |
| KernelValue ADKernelValue | precomputeQpResidual | Use when the term computed in the PDE is only multiplied by the test function (do not use _test in the override, it is applied automatically) |
| KernelGrad ADKernelGrad | precomputeQpResidual | Use when the term computed in the PDE is only multiplied by the gradient of the test function (do not use _grad_test in the override, it is applied automatically) |
Diffusion
Recall the steady-state diffusion equation on the 3D domain :
The weak form of this equation includes a volume integral, which in inner-product notation, is given by:
where are the test functions and is the finite element solution.
ADDiffusion.h
#pragma once
#include "ADKernelGrad.h"
class ADDiffusion : public ADKernelGrad
{
public:
static InputParameters validParams();
ADDiffusion(const InputParameters & parameters);
protected:
virtual ADRealVectorValue precomputeQpResidual() override;
};
ADDiffusion.C
#include "ADDiffusion.h"
registerMooseObject("MooseApp", ADDiffusion);
InputParameters
ADDiffusion::validParams()
{
auto params = ADKernelGrad::validParams();
params.addClassDescription("Same as `Diffusion` in terms of physics/residual, but the Jacobian "
"is computed using forward automatic differentiation");
return params;
}
ADDiffusion::ADDiffusion(const InputParameters & parameters) : ADKernelGrad(parameters) {}
ADRealVectorValue
ADDiffusion::precomputeQpResidual()
{
return _grad_u[_qp];
}
Step 2: Pressure Kernel
(continued)
DarcyPressure Kernel
To implement the coefficient a new Kernel object must be created: DarcyPressure.
This object will inherit from ADDiffusion and will use input parameters for specifying the permeability and viscosity.
DarcyPressure.h
#pragma once
// Including the "ADKernel" Kernel here so we can extend it
#include "ADKernel.h"
/**
* Computes the residual contribution: K / mu * grad_u * grad_phi.
*/
class DarcyPressure : public ADKernel
{
public:
static InputParameters validParams();
DarcyPressure(const InputParameters & parameters);
protected:
/// ADKernel objects must override precomputeQpResidual
virtual ADReal computeQpResidual() override;
/// References to be set from input file
const Real & _permeability;
const Real & _viscosity;
};
DarcyPressure.C
#include "DarcyPressure.h"
registerMooseObject("DarcyThermoMechApp", DarcyPressure);
InputParameters
DarcyPressure::validParams()
{
InputParameters params = ADKernel::validParams();
params.addClassDescription("Compute the diffusion term for Darcy pressure ($p$) equation: "
"$-\\nabla \\cdot \\frac{\\mathbf{K}}{\\mu} \\nabla p = 0$");
// Add a required parameter. If this isn't provided in the input file MOOSE will error.
params.addRequiredParam<Real>("permeability", "The permeability ($\\mathrm{K}$) of the fluid.");
// Add a parameter with a default value; this value can be overridden in the input file.
params.addParam<Real>(
"viscosity",
7.98e-4,
"The viscosity ($\\mu$) of the fluid in Pa, the default is for water at 30 degrees C.");
return params;
}
DarcyPressure::DarcyPressure(const InputParameters & parameters)
: ADKernel(parameters),
// Get the parameters from the input file
_permeability(getParam<Real>("permeability")),
_viscosity(getParam<Real>("viscosity"))
{
}
ADReal
DarcyPressure::computeQpResidual()
{
return (_permeability / _viscosity) * _grad_test[_i][_qp] * _grad_u[_qp];
}
Step 2: Input File
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables/pressure]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
permeability = 0.8451e-9 # (m^2) 1mm spheres.
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
Step 2: Run and Visualize with Peacock
cd ~/projects/moose/tutorials/darcy-thermo_mech/step02_darcy_pressure
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step2.i
Step 2: Run via Command-line
cd ~/projects/moose/tutorials/darcy-thermo_mech/step02_darcy_pressure
make -j 12 # use number of processors for you system
cd problems
../darcy_thermo_mech-opt -i step2.i
Step 2: Visualize Result
~/projects/moose/python/peacock/peacock -r step2_out.e

Hands-on: Laplace Young
Problem Statement
Given a domain , find such that:
and
where
Laplace-Young Solution

Mesh System
A system for defining a finite element mesh.
Creating a Mesh
For complicated geometries, we generally use CUBIT from Sandia National Laboratories cubit.sandia.gov.
Other mesh generators can work as long as they output a file format that libMesh reads.
FileMesh
FileMesh is the default type:
[Mesh]
file = sample.msh
dim = 3
[]
MOOSE supports reading and writing a large number of formats and could be extended to read more.
| Extension | Description |
|---|---|
| .dat | Tecplot ASCII file |
| .e, .exd | Sandia's ExodusII format |
| .fro | ACDL's surface triangulation file |
| .gmv | LANL's GMV (General Mesh Viewer) format |
| .mat | Matlab triangular ASCII file (read only) |
| .msh | GMSH ASCII file |
| .n, .nem | Sandia's Nemesis format |
| .plt | Tecplot binary file (write only) |
| .node, .ele; .poly | TetGen ASCII file (read; write) |
| .inp | Abaqus .inp format (read only) |
| .ucd | AVS's ASCII UCD format |
| .unv | I-deas Universal format |
| .xda, .xdr | libMesh formats |
| .vtk, .pvtu | Visualization Toolkit |
GeneratedMesh
Built-in mesh generation is implemented for lines, rectangles, and rectangular prisms
[Mesh]
type = GeneratedMesh
dim = 2
xmin = -1
xmax = 1
ymin = -1
ymax = 1
nx = 2
ny = 2
elem_type = QUAD9
[]
The sides are named in a logical way and are numbered:
1D: left = 0, right = 1
2D: bottom = 0, right = 1, top = 2, left = 3
3D: back = 0, bottom = 1, right = 2, top = 3, left = 4, front = 5
Named Entity Support
Human-readable names can be assigned to blocks, sidesets, and nodesets that can be used throughout an input file.
A parameter that requires an ID will accept either numbers or "names".
Names can be assigned to IDs for existing meshes to ease input file maintenance.
[Mesh]
file = three_block.e
# These names will be applied on the fly to the
# mesh so that they can be used in the input file
# In addition they will show up in the output file
block_id = '1 2 3'
block_name = 'wood steel copper'
boundary_id = '1 2'
boundary_name = 'left right'
[]
[BCs]
active = 'left right'
[./left]
type = DirichletBC
variable = u
boundary = 'left'
value = 0
[../]
[./right]
type = DirichletBC
variable = u
boundary = 'right'
value = 1
[../]
[]
[Materials]
active = empty
[./empty]
type = MTMaterial
block = 'wood steel copper'
[../]
[]
Replicated Mesh
When running in parallel the default mode for operation is to use a replicated mesh, which creates a complete copy of the mesh for each processor.
parallel_type = replicated
Distributed Mesh
Changing the type to distributed when running in parallel operates such that only the portion of the mesh owned by a processor is stored on that processor.
parallel_type = distributed
If the mesh is too large to read in on a single processor, it can be split prior to the simulation.
Copy the mesh to a large memory machine
Use the
--split-meshoption to split the mesh into piecesRun the executable with
--use-split
Displaced Mesh
Calculations can take place in either the initial mesh configuration or, when requested, the "displaced" configuration.
To enable displacements, provide a vector of displacement variable names for each spatial dimension in the Mesh block.
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
displacements = 'disp_x disp_y'
[]
Objects can enforce the use of the displaced mesh within the validParams function.
params.set<bool>("use_displaced_mesh") = true;
Output System
A system for producing outputting simulation data to the screen or files.
The output system is designed to be just like any other system in MOOSE: modular and expandable.
It is possible to create multiple output objects for outputting:
at specific time or timestep intervals,
custom subsets of variables, and
to various file types.
There exists a short-cut syntax for common output types as well as common parameters.
Short-cut Syntax
The following two methods for creating an Output object are equivalent within the internals of MOOSE.
[Outputs]
exodus = true
[]
[Outputs]
[out]
type = Exodus
[]
[]
Common Parameters
[Outputs]
interval = 10
exodus = true
[all]
type = Exodus
interval = 1 # overrides interval from top-level
[]
[]
Output Names
The default naming scheme for output files utilizes the input file name (e.g., input.i) with a suffix that differs depending on how the output is defined: An "_out" suffix is used for Outputs created using the short-cut syntax. sub-blocks use the actual sub-block name as the suffix.
[Outputs]
exodus = true # creates input_out.e
[other] # creates input_other.e
type = Exodus
interval = 2
[]
[base]
type = Exodus
file_base = out # creates out.e
[]
[]
The use of 'file_base' anywhere in the [Outputs] block disables all default naming behavior.
| Short-cut | Sub-block ("type=") | Description |
|---|---|---|
| console | Console | Writes to the screen and optionally a file |
| exodus | Exodus | The most common,well supported, and controllable output type |
| vtk | VTK | Visualization Toolkit format, requires --enable-vtk when building libMesh |
| gmv | GMV | General Mesh Viewer format |
| nemesis | Nemesis | Parallel ExodusII format |
| tecplot | Tecplot | Requires --enable-tecplot when building libMesh |
| xda | XDA | libMesh internal format (ascii) |
| xdr | XDR | libMesh internal format (binary) |
| csv | CSV | Comma separated scalar values |
| gnuplot | GNUPlot | Only support scalar outputs |
| checkpoint | Checkpoint | MOOSE internal format used for restart and recovery |
Step 3: Pressure Kernel with Material
Instead of passing constant parameters to the DarcyPressure object use the Material system to supply the values.
where is the permeability tensor and is the fluid viscosity.
This system allows for properties that vary in space and time, that can be coupled to variables in the simulation.
Material System
A system for defining material properties to be used by multiple systems and allow for variable coupling.
The material system operates by creating a producer/consumer relationship among objects
Materialobjects produce properties.Other MOOSE objects (including materials) consume these properties.
Producing Properties
Each property to be produced must be declared to be available for use, the
declareProperty<TYPE>()method does this and returns a writable reference.Override
computeQpProperties()to compute all of the declared properties at one quadrature point. Within this method, the references obtained from declaring the property are updated.
Consuming Properties
To consume a material property, call the correct get method in an object and store the constant reference as a member variable.
getMaterialProperty<TYPE>()
Use within non-AD objects to retrieve non-AD material properties.
getADMaterialProperty<TYPE>()
Use within AD objects to retrieve AD material properties.
Material Property Evaluation
Quantities are recomputed at quadrature points, as needed.
Multiple Material objects may define the same "property" for different parts of the subdomain or boundaries.
Stateful Material Properties
The values are not stored between timesteps unless "stateful" properties are enabled, which is accomplished by calling getMaterialPropertyOld<TYPE>() or getMaterialPropertyOlder<TYPE>()
It can be useful to have "old" values of Material properties available in a simulation, such as in solid mechanics plasticity constitutive models.
Traditionally, this type of value is called a "state variable"; in MOOSE, they are called "stateful material properties".
Stateful Material properties require more memory.
Default Material Properties
Default values for material properties may be assigned within the validParams function.
addParam<MaterialPropertyName>("combination_property_name", 12345,
"The name of the property providing the luggage combination");
Only scalar (Real) values may have defaults.
When getMaterialProperty<Real>("combination_property_name") is called, the default will be returned if the value has not been computed via a delcareProperty call within a Material object.
Material Property Output
Output of Material properties is enabled by setting the "outputs" parameter.
The following example creates two additional variables called "mat1" and "mat2" that will show up in the output file.
[Materials]
[block_1]
type = OutputTestMaterial
block = 1
output_properties = 'real_property tensor_property'
outputs = exodus
variable = u
[]
[block_2]
type = OutputTestMaterial
block = 2
output_properties = 'vector_property tensor_property'
outputs = exodus
variable = u
[]
[]
[Outputs]
exodus = true
[]
Supported Property Types for Output
Material properties can be of arbitrary (C++) type, but not all types can be output.
| Type | AuxKernel | Variable Name(s) |
|---|---|---|
| Real | MaterialRealAux | prop |
| RealVectorValue | MaterialRealVectorValueAux | prop_1, prop_2, and prop_3 |
| RealTensorValue | MaterialRealTensorValueAux | prop_11, prop_12, prop_13, prop_21, etc. |
Function System
A system for defining analytic expressions based on the spatial location (, , ) and time, .
A Function object is created by inheriting from Function and overriding the virtual value() (and optionally other methods as well) functions.
Functions can be accessed in most MOOSE objects by calling getFunction("name"), where "name" matches a name from the input file.
Function Use
Many objects exist in MOOSE that utilize a function, such as:
FunctionDirichletBCFunctionNeumannBCFunctionICBodyForce
Each of these objects has a "function" parameter which is set in the input file, and controls which Function object is used.
Parsed Function
A ParsedFunction allow functions to be defined by strings directly in the input file, e.g.:
[Functions]
[sin_fn]
type = ParsedFunction
value = sin(x)
[]
[cos_fn]
type = ParsedFunction
value = cos(x)
[]
[fn]
type = ParsedFunction
value = 's/c'
vars = 's c'
vals = 'sin_fn cos_fn'
[]
[]
It is possible to include other functions, as shown above, as well as scalar variables and postprocessor values with the function definition.
Default Functions
Whenever a Function object is added via addParam(), a default can be provided.
Both constant values and parsed function strings can be used as the default.
// Adding a Function with a default constant
params.addParam<FunctionName>("pressure_grad", "0.5", "The gradient of ...");
// Adding a Function with a default parsed function
params.addParam<FunctionName>("power_history", "t+100*sin(y)", "The power history of ...");
A ParsedFunction or ConstantFunction object is automatically constructed based on the default value if a function name is not supplied in the input file.
Step 3: Pressure Kernel with Material
(continued)
PackedColumn Material
Two material properties must be produced for consumption by DarcyPressure object: permeability and viscosity.
Both shall be computed with a single Material object: PackedColumn.
As in the reference article, permeability varies with the size of the steel spheres, so linear interpolation will be used for defining this property.
PackedColumn.h
#pragma once
#include "Material.h"
// A helper class from MOOSE that linear interpolates x,y data
#include "LinearInterpolation.h"
/**
* Material objects inherit from Material and override computeQpProperties.
*
* Their job is to declare properties for use by other objects in the
* calculation such as Kernels and BoundaryConditions.
*/
class PackedColumn : public Material
{
public:
static InputParameters validParams();
PackedColumn(const InputParameters & parameters);
protected:
/// Necessary override. This is where the values of the properties are computed.
virtual void computeQpProperties() override;
/// The radius of the spheres in the column
const Function & _radius;
/// Value of viscosity from the input file
const Real & _input_viscosity;
/// Compute permeability based on the radius (mm)
LinearInterpolation _permeability_interpolation;
/// The permeability (K)
ADMaterialProperty<Real> & _permeability;
/// The viscosity of the fluid (mu)
ADMaterialProperty<Real> & _viscosity;
};
PackedColumn.C
#include "PackedColumn.h"
#include "Function.h"
registerMooseObject("DarcyThermoMechApp", PackedColumn);
InputParameters
PackedColumn::validParams()
{
InputParameters params = Material::validParams();
// Parameter for radius of the spheres used to interpolate permeability.
params.addParam<FunctionName>("radius",
"1.0",
"The radius of the steel spheres (mm) that are packed in the "
"column for computing permeability.");
params.addParam<Real>(
"viscosity",
7.98e-4,
"The viscosity ($\\mu$) of the fluid in Pa, the default is for water at 30 degrees C.");
return params;
}
PackedColumn::PackedColumn(const InputParameters & parameters)
: Material(parameters),
// Get the parameters from the input file
_radius(getFunction("radius")),
_input_viscosity(getParam<Real>("viscosity")),
// Declare two material properties by getting a reference from the MOOSE Material system
_permeability(declareADProperty<Real>("permeability")),
_viscosity(declareADProperty<Real>("viscosity"))
{
// From the paper: Table 1
std::vector<Real> sphere_sizes = {1, 3};
std::vector<Real> permeability = {0.8451e-9, 8.968e-9};
// Set the x,y data on the LinearInterpolation object.
_permeability_interpolation.setData(sphere_sizes, permeability);
}
void
PackedColumn::computeQpProperties()
{
Real value = _radius.value(_t, _q_point[_qp]);
mooseAssert(value >= 1 && value <= 3,
"The radius range must be in the range [1, 3], but " << value << " provided.");
_viscosity[_qp] = _input_viscosity;
_permeability[_qp] = _permeability_interpolation.sample(value);
}
DarcyPressure Kernel
The existing Kernel object uses input parameters for defining permeability and viscosity, it must be updated to consume the newly created material properties.
DarcyPressure.h
#pragma once
// Including the "ADKernel" Kernel here so we can extend it
#include "ADKernel.h"
/**
* Computes the residual contribution: K / mu * grad_u * grad_phi.
*/
class DarcyPressure : public ADKernel
{
public:
static InputParameters validParams();
DarcyPressure(const InputParameters & parameters);
protected:
/// ADKernel objects must override precomputeQpResidual
virtual ADReal computeQpResidual() override;
// References to be set from Material system
/// The permeability. Note that this is declared as a \p MaterialProperty. This means that if
/// calculation of this property in the producing \p Material depends on non-linear variables, the
/// derivative information will be lost here in the consumer and the non-linear solve will suffer
const ADMaterialProperty<Real> & _permeability;
/// The viscosity. This is declared as an \p ADMaterialProperty, meaning any derivative
/// information coming from the producing \p Material will be preserved and the integrity of the
/// non-linear solve will be likewise preserved
const ADMaterialProperty<Real> & _viscosity;
};
DarcyPressure.C
#include "DarcyPressure.h"
registerMooseObject("DarcyThermoMechApp", DarcyPressure);
InputParameters
DarcyPressure::validParams()
{
InputParameters params = ADKernel::validParams();
params.addClassDescription("Compute the diffusion term for Darcy pressure ($p$) equation: "
"$-\\nabla \\cdot \\frac{\\mathbf{K}}{\\mu} \\nabla p = 0$");
return params;
}
DarcyPressure::DarcyPressure(const InputParameters & parameters)
: ADKernel(parameters),
_permeability(getADMaterialProperty<Real>("permeability")),
_viscosity(getADMaterialProperty<Real>("viscosity"))
{
}
ADReal
DarcyPressure::computeQpResidual()
{
return (_permeability[_qp] / _viscosity[_qp]) * _grad_test[_i][_qp] * _grad_u[_qp];
}
Step 3: Input File
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables/pressure]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Materials]
[column]
type = PackedColumn
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
Step 3: Run and Visualize with Peacock
cd ~/projects/moose/tutorials/darcy-thermo_mech/step03_darcy_material
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step3.i
Step 3: Run via Command-line
cd ~/projects/moose/tutorials/darcy-thermo_mech/step03_darcy_material
make -j 12 # use number of processors for you system
cd problems
../darcy_thermo_mech-opt -i step3.i
Step 3: Visualize Result
~/projects/moose/python/peacock/peacock -r step3_out.e

Step 3b: Variable Spheres
Update the input file to vary the sphere size from 1 to 3 along the length of the pipe.
Step 3b: Input File
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables/pressure]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Materials]
[column]
type = PackedColumn
radius = '1 + 2/3.04*x'
outputs = exodus
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
Step 3b: Visualize Result

Test System
Overview
MOOSE includes an extendable test system (python) for executing code with different input files.
Each kernel (or logical set of kernels) should have test(s) for verification.
The test system is flexible, it performs many different operations such as testing for expected error conditions.
Additionally, custom "Tester" objects can be created.
Test Setup
Related tests should be grouped into an individual directory and have a consistent naming convention.
It is recommended to organize tests in a hierarchy similar to the application source (i.e., kernels, BCs, materials, etc).
Tests are found dynamically by matching patterns (highlighted below)
tests/
kernels/
my_kernel_test/
my_kernel_test.e [input mesh]
my_kernel_test.i [input file]
tests [test specification file]
gold/ [gold standard folder for validated solution]
out.e [solution]
Test Specification
Test specifications use the hit format, the same format as the standard MOOSE input file.
[Tests]
[my_kernel_test]
type = Exodiff
input = my_kernel_test.i
exodiff = my_kernel_test_out.e
[]
[kernel_check_exception]
type = RunException
input = my_kernel_exception.i
expect_err = 'Bad stuff happened with variable \w+'
[]
[]
Test Objects
RunApp: Runs a MOOSE-based application with specified options
Exodiff: Checks Exodus files for differences within specified tolerances
CSVDiff: Checks CSV files for differences within specified tolerances
VTKDiff: Checks VTK files for differences within specified tolerances
RunException: Tests for error conditions
CheckFiles: Checks for the existence of specific files after a completed run
ImageDiff: Compares images (e.g., *.png) for differences within specified tolerances
PythonUnitTest: Runs python "unittest" based tests
AnalyzeJacobian: Compares computed Jacobian with finite difference version
PetscJacobianTester: Compares computed Jacobian using PETSc
Running Tests
./run_tests -j 12
For more information view the help:
./run_tests -h
Test Object Options
./run_tests --dump
input: The name of the input file
exodiff: The list of output filenames to compare
abs_zero: Absolute zero tolerance for exodiff
rel_err: Relative error tolerance for exodiff
prereq: Name of the test that needs to complete before running this test
min_parallel: Minimum number of processors to use for a test (default: 1)
max_parallel: Maximum number of processors to use for a test
Notes on Tests
Individual tests should run relatively quickly (2 second rule)
Outputs or other generated files should not be checked into the repository
MOOSE developers rely on application tests when refactoring to verify correctness
poor test coverage = higher code failure rate
Step 4: Velocity Auxiliary Variable
The velocity is the primary variable of interest, it is computed base on the pressure as:
Auxiliary System
A system for direct calculation of field variables ("AuxVariables") that is designed for postprocessing, coupling, and proxy calculations.
The term "nonlinear variable" is defined, in MOOSE language, as a variable that is being solved for using a nonlinear system of PDEs using Kernel and BoundaryCondition objects.
The term "auxiliary variable" is defined, in MOOSE language, as a variable that is directly calculated using an AuxKernel object.
AuxVariables
Auxiliary variables are declared in the [AuxVariables] input file block
Auxiliary variables are field variables that are associated with finite element shape functions and can serve as a proxy for nonlinear variables
Auxiliary variables currently come in two flavors:
Element (constant or higher order monomials)
Nodal (linear Lagrange)
Auxiliary variables have "old" and "older" states just like nonlinear variables
Elemental Auxiliary Variables
Element auxiliary variables compute average values per element (constant)
AuxKernel objects computing elemental values can couple to nonlinear variables and both element and nodal auxiliary variables
[AuxVariables]
[aux]
order = CONSTANT
family = MONOMIAL
[]
[]
Nodal Auxiliary Variables
Element auxiliary variables are computed at each node and are stored as linear Lagrange variables
AuxKernel objects computing nodal values can only couple to nonlinear variables and other nodal auxiliary variables
[AuxVariables]
[aux]
order = LAGRANGE
family = FIRST
[]
[]
AuxKernel Objects
Directly compute AuxVariable values by overriding computeValue() and they can operate on both elemental and nodal auxiliary variable.
When operating on a nodal variable computeValue() operates on each node; when operating on a elemental variable it operates on each element.
AuxKernel Object Members
_u, _grad_u
Value and gradient of variable this AuxKernel is operating on
_q_point
Coordinates of the current q-point that is only valid for elemental AuxKernels, _current_node should be used for nodal variables
_qp
Current quadrature point, this is used for both nodal and elemental variables for consistency
_current_elem
Pointer to the current element that is being operated on (elemental only)
_current_node
Pointer to the current node that is being operated on (nodal only)
VectorAuxKernel Objects
Directly compute a vector AuxVariable values by overriding computeValue(), with the difference being the return value of a RealVectorValue instead of Real.
[AuxVariables]
[aux]
order = FIRST
family = LAGRANGE_VEC
[]
[]
Step 4: Velocity Auxiliary Variable
(continued)
DarcyVelocity AuxKernel
The primary unknown ("nonlinear variable") is the pressure
Once the pressure is computed, the AuxiliarySystem can compute and output the velocity field using the coupled pressure variable and the permeability and viscosity properties.
Auxiliary variables come in two flavors: Nodal and Elemental.
Nodal auxiliary variables cannot couple to gradients of nonlinear variables since gradients of continuous variables are not well-defined at the nodes.
Elemental auxiliary variables can couple to gradients of nonlinear variables since evaluation occurs in the element interiors.
DarcyVelocity.h
#pragma once
#include "AuxKernel.h"
/**
* Auxiliary kernel responsible for computing the Darcy velocity given
* several fluid properties and the pressure gradient.
*/
class DarcyVelocity : public VectorAuxKernel
{
public:
static InputParameters validParams();
DarcyVelocity(const InputParameters & parameters);
protected:
/**
* AuxKernels MUST override computeValue. computeValue() is called on
* every quadrature point. For Nodal Auxiliary variables those quadrature
* points coincide with the nodes.
*/
virtual RealVectorValue computeValue() override;
/// The gradient of a coupled variable
const VariableGradient & _pressure_gradient;
/// Holds the permeability and viscosity from the material system
const ADMaterialProperty<Real> & _permeability;
const ADMaterialProperty<Real> & _viscosity;
};
DarcyVelocity.C
#include "DarcyVelocity.h"
#include "metaphysicl/raw_type.h"
registerMooseObject("DarcyThermoMechApp", DarcyVelocity);
InputParameters
DarcyVelocity::validParams()
{
InputParameters params = VectorAuxKernel::validParams();
// Add a "coupling paramater" to get a variable from the input file.
params.addRequiredCoupledVar("pressure", "The pressure field.");
return params;
}
DarcyVelocity::DarcyVelocity(const InputParameters & parameters)
: VectorAuxKernel(parameters),
// Get the gradient of the variable
_pressure_gradient(coupledGradient("pressure")),
// Set reference to the permeability MaterialProperty.
// Only AuxKernels operating on Elemental Auxiliary Variables can do this
_permeability(getADMaterialProperty<Real>("permeability")),
// Set reference to the viscosity MaterialProperty.
// Only AuxKernels operating on Elemental Auxiliary Variables can do this
_viscosity(getADMaterialProperty<Real>("viscosity"))
{
}
RealVectorValue
DarcyVelocity::computeValue()
{
// Access the gradient of the pressure at this quadrature point, then pull out the "component" of
// it requested (x, y or z). Note, that getting a particular component of a gradient is done using
// the parenthesis operator.
return -MetaPhysicL::raw_value(_permeability[_qp] / _viscosity[_qp]) * _pressure_gradient[_qp];
}
Step 4: Input File
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables/pressure]
[]
[AuxVariables]
[velocity_x]
order = CONSTANT
family = MONOMIAL
[]
[velocity_y]
order = CONSTANT
family = MONOMIAL
[]
[velocity_z]
order = CONSTANT
family = MONOMIAL
[]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[velocity_x]
type = VectorVariableComponentAux
variable = velocity_x
component = x
execute_on = timestep_end
vector_variable = velocity
[]
[velocity_y]
type = VectorVariableComponentAux
variable = velocity_y
component = y
execute_on = timestep_end
vector_variable = velocity
[]
[velocity_z]
type = VectorVariableComponentAux
variable = velocity_z
component = z
execute_on = timestep_end
vector_variable = velocity
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = PJFNK
#nl_rel_tol = 1e-12
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
Step 4: Run and Visualize with Peacock
cd ~/projects/moose/tutorials/darcy-thermo_mech/step04_velocity_aux
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step4.i
Step 4: Run via Command-line
cd ~/projects/moose/tutorials/darcy-thermo_mech/step04_velocity_aux
make -j 12 # use number of processors for you system
cd problems
../darcy_thermo_mech-opt -i step3.i
Step 4: Visualize Result
~/projects/moose/python/peacock/peacock -r step4_out.e

Tighter Solve Tolerance
cd ~/projects/moose/tutorials/darcy-thermo_mech/step04_velocity_aux
make -j 12 # use number of processors for you system
cd problems
../darcy_thermo_mech-opt -i step4.i Executioner/nl_rel_tol=1e-12

Step 5: Heat Conduction
With the pressure equation handled, the heat conduction equation is next.
Initially, only the steady heat conduction equation is considered:
This is another diffusion-type term that depends on the thermal conductivity, . This term is implemented in the MOOSE heat conduction module as ADHeatConduction.
ADHeatConduction.h
#pragma once
#include "ADDiffusion.h"
class ADHeatConduction : public ADDiffusion
{
public:
static InputParameters validParams();
ADHeatConduction(const InputParameters & parameters);
protected:
virtual ADRealVectorValue precomputeQpResidual() override;
const ADMaterialProperty<Real> & _thermal_conductivity;
};
ADHeatConduction.C
#include "ADHeatConduction.h"
registerMooseObject("HeatConductionApp", ADHeatConduction);
InputParameters
ADHeatConduction::validParams()
{
InputParameters params = ADDiffusion::validParams();
params.addParam<MaterialPropertyName>("thermal_conductivity",
"thermal_conductivity",
"the name of the thermal conductivity material property");
params.set<bool>("use_displaced_mesh") = true;
return params;
}
ADHeatConduction::ADHeatConduction(const InputParameters & parameters)
: ADDiffusion(parameters),
_thermal_conductivity(getADMaterialProperty<Real>("thermal_conductivity"))
{
}
ADRealVectorValue
ADHeatConduction::precomputeQpResidual()
{
return _thermal_conductivity[_qp] * ADDiffusion::precomputeQpResidual();
}
The ADHeatCondution Kernel in conjunction with a GenericConstantMaterial is all that is needed to perform a steady state heat conduction solve (with at the inlet and at the outlet).
GenericConstantMaterial
GenericConstantMaterial is a simple way to define constant material properties.
Two input parameters are provided using "list" syntax common to MOOSE:
prop_names = 'conductivity density'
prop_values = '0.01 200'
Step 5a: Steady-State Input File
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[temperature]
[]
[]
[Kernels]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[]
[BCs]
[inlet_temperature]
type = DirichletBC
variable = temperature
boundary = left
value = 350 # (K)
[]
[outlet_temperature]
type = DirichletBC
variable = temperature
boundary = right
value = 300 # (K)
[]
[]
[Materials]
[steel]
type = ADGenericConstantMaterial
prop_names = thermal_conductivity
prop_values = 18 # K: (W/m*K) from wikipedia @296K
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Steady
solve_type = NEWTON
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
Step 5b: Running Input File
cd ~/projects/moose/tutorials/darcy-thermo_mech/step5_heat_conduction
make -j 12 # use number of processors for you system
cd problems
../darcy_thermo_mech-opt -i step5a_steady.i
Transient Heat Conduction (5b)
To create a time-dependent problem add in the time derivative:
The time term exists in the heat conduction module as ADHeatConductionTimeDerivative, thus only an update to the input file is required to run the transient case.
Executioner System
A system for dictating the simulation solving strategy.
Steady-state Executioner
Steady-state executioners generally solve the nonlinear system just once.
[Executioner]
type = Steady
[]
The Steady executioner can solve the nonlinear system multiple times while adaptively refining the mesh to improve the solution.
Transient Executioners
Transient executioners solve the nonlinear system at least once per time step.
| Option | Definition |
|---|---|
dt | Starting time step size |
num_steps | Number of time steps |
start_time | The start time of the simulation |
end_time | The end time of the simulation |
scheme | Time integration scheme (discussed next) |
[Executioner]
type = Transient
scheme = 'implicit-euler'
solve_type = 'PJFNK'
start_time = 0.0
num_steps = 5
dt = 0.1
[]
Steady-State Detection
| Option | Definition |
|---|---|
steady_state_detection | Whether to try and detect achievement of steady-state (Default = false) |
steady_state_tolerance | Used for determining a steady-state; Compared against the difference in solution vectors between current and old time steps (Default = 1e-8) |
Common Executioner Options
There are a number of options that appear in the executioner block and are used to control the solver. Here are a few common options:
| Option | Definition |
|---|---|
l_tol | Linear Tolerance (default: 1e-5) |
l_max_its | Max Linear Iterations (default: 10000) |
nl_rel_tol | Nonlinear Relative Tolerance (default: 1e-8) |
nl_abs_tol | Nonlinear Absolute Tolerance (default: 1e-50) |
nl_max_its | Max Nonlinear Iterations (default: 50) |
TimeKernel Object
The TimeKernel object adds two member variables to a Kernel object:
_u_dot
Time derivative of the associated nonlinear variable
_du_dot_du
The derivative of _u_dot with respect to _u
TimeKernel Base Classes
| Base | Override | Use |
|---|---|---|
| TimeKernel ADTimeKernel | computeQpResidual | Use when the time term in the PDE is multiplied by both the test function and the gradient of the test function (_test and _grad_test must be applied) |
| TimeKernelValue ADTimeKernelValue | precomputeQpResidual | Use when the time term computed in the PDE is only multiplied by the test function (do not use _test in the override, it is applied automatically) |
| TimeKernelGrad ADTimeKernelGrad | precomputeQpResidual | Use when the time term computed in the PDE is only multiplied by the gradient of the test function (do not use _grad_test in the override, it is applied automatically) |
Time Integrator System
A system for defining schemes for numerical integration in time.
The TimeIntegrator can be set using "scheme" parameter within the [Executioner] block, if the "type = Transient", the following options exist:
implicit-euler: Backward Euler (default)bdf2: Second order backward difference formulacrank-nicolson: Second order Crank-Nicolson methoddirk: Second order Diagonally-Implicit Runge-Kutta (DIRK)newmark-beta: Second order Newmark-beta method (structural dynamics)
TimeIntegrator Block
It is also possible to specify a time integrator as a separate sub-block within the input file. This allows for additional types and parameters to be defined, including custom TimeIntegrator objects.
[Executioner]
type = Transient
start_time = 0.0
num_steps = 6
dt = 0.1
[TimeIntegrator]
type = NewmarkBeta
beta = 0.4225
gamma = 0.8
[]
[]
Convergence Rates
Consider the test problem:
for , and , is chosen so the exact solution is given by and and are the initial and Dirichlet boundary conditions corresponding to this exact solution.

Time Stepper System
A system for suggesting time steps for transient executioners.
[Executioner]
type = Transient
solve_type = NEWTON
start_time = 0.0
end_time = 5.0
[TimeStepper]
type = IterationAdaptiveDT
dt = 1.0
optimal_iterations = 10
time_t = '0.0 5.0'
time_dt = '1.0 5.0'
[]
[]
Custom objects are created by inheriting from TimeStepper overriding computeDT().
Built-in TimeSteppers
MOOSE includes many built-in TimeStepper objects:
ConstantDTSolutionTimeAdaptiveDTIterationAdaptiveDTFunctionDTPostprocessorDTDT2TimeSequenceStepper
IterationAdaptiveDT
IterationAdaptiveDT grows or shrinks the time step based on the number of iterations taken to obtain a converged solution in the last converged step.
[Executioner]
type = Transient
solve_type = NEWTON
start_time = 0.0
dtmin = 1.0
end_time = 10.0
[TimeStepper]
type = IterationAdaptiveDT
optimal_iterations = 1
linear_iteration_ratio = 1
dt = 5.0
[]
[]
DT2 Adaptive TimeStepper
Take one time step of size to get from
Take two time steps of size to get from
Calculate local relative time discretization error estimate
Obtain global relative time discretization error estimate
Adaptivity is based on target error tolerance and a maximum acceptable error tolerance .
If , continue with a new time step size
where is the global convergence rate of the time stepping scheme.
If , or if the solver fails, shrink .
Parameters and can be specified in the input file as e_tol and e_max (in the Executioner block).
TimeSequenceStepper
Provide a vector of time points using parameter time_sequence, the object simply moves through these time points.
The and parameters are automatically added to the sequence.
Only time points satisfying are considered.
If a solve fails at step an additional time point is inserted and the step is resolved.
Step 5: Heat Conduction
(continued)
Transient Heat Conduction (5b)
To create a time-dependent problem add in the time derivative:
The time term exists in the heat conduction module as ADHeatConductionTimeDerivative, thus only an update to the input file is required to run the transient case.
ADHeatConductionTimeDerivative.h
#pragma once
#include "ADTimeDerivative.h"
class ADHeatConductionTimeDerivative : public ADTimeDerivative
{
public:
static InputParameters validParams();
ADHeatConductionTimeDerivative(const InputParameters & parameters);
protected:
virtual ADReal precomputeQpResidual() override;
/// Specific heat material property
const ADMaterialProperty<Real> & _specific_heat;
/// Density material property
const ADMaterialProperty<Real> & _density;
};
ADHeatConductionTimeDerivative.C
#include "ADHeatConductionTimeDerivative.h"
registerMooseObject("HeatConductionApp", ADHeatConductionTimeDerivative);
InputParameters
ADHeatConductionTimeDerivative::validParams()
{
InputParameters params = ADTimeDerivative::validParams();
params.addClassDescription(
"AD Time derivative term $\\rho c_p \\frac{\\partial T}{\\partial t}$ of "
"the heat equation for quasi-constant specific heat $c_p$ and the density $\\rho$.");
params.set<bool>("use_displaced_mesh") = true;
params.addParam<MaterialPropertyName>(
"specific_heat", "specific_heat", "Property name of the specific heat material property");
params.addParam<MaterialPropertyName>(
"density_name", "density", "Property name of the density material property");
return params;
}
ADHeatConductionTimeDerivative::ADHeatConductionTimeDerivative(const InputParameters & parameters)
: ADTimeDerivative(parameters),
_specific_heat(getADMaterialProperty<Real>("specific_heat")),
_density(getADMaterialProperty<Real>("density_name"))
{
}
ADReal
ADHeatConductionTimeDerivative::precomputeQpResidual()
{
return _specific_heat[_qp] * _density[_qp] * ADTimeDerivative::precomputeQpResidual();
}
Step 5b: Time-dependent Input File
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[Kernels]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[]
[BCs]
[inlet_temperature]
type = DirichletBC
variable = temperature
boundary = left
value = 350 # (K)
[]
[outlet_temperature]
type = DirichletBC
variable = temperature
boundary = right
value = 300 # (K)
[]
[]
[Materials]
[steel]
type = ADGenericConstantMaterial
prop_names = 'thermal_conductivity specific_heat density'
prop_values = '18 0.466 8000' # W/m*K, J/kg-K, kg/m^3 @ 296K
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
num_steps = 10
solve_type = NEWTON
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
Step 5b: Running Input File
cd ~/projects/moose/tutorials/darcy-thermo_mech/step5_heat_conduction
make -j 12 # use number of processors for you system
cd problems
../darcy_thermo_mech-opt -i step5b_transient.i
Outflow Boundary Condition (5c)
The flow is assumed to exit the pipe into a large tank, which is modeled with the "No BC" boundary condition of Griffiths (1997).
The boundary term, , is computed implicitly rather than being replaced with a known flux, as is done in a NeumannBC.
Boundary Condition System
System for computing residual contributions from boundary terms of a PDE.
A BoundaryCondition (BC) object computes a residual on a boundary (or internal side) of a domain.
There are two flavors of BC objects: Nodal and Integrated.
Integrated BC
Integrated BCs are integrated over a boundary or internal side and should inherit from ADIntegratedBC.
The structure is very similar to Kernels: objects must override computeQpResidual
ADIntegrtedBC Object Members
_u, _grad_u
Value and gradient of the variable this Kernel is operating on
_test, _grad_test
Value () and gradient () of the test functions at the quadrature points
_phi, _grad_phi
Value () and gradient () of the trial functions at the quadrature points
_i, _j, _qp
Current index for test function, trial functions, and quadrature point, respectively
_normals:
Outward normal vector for boundary element
_boundary_id
The boundary ID
_current_elem, _current_side
A pointer to the element and index to the current boundary side
Non-Integrated BC
Non-integrated BCs set values of the residual directly on a boundary or internal side and should inherit from ADNodalBC.
The structure is very similar to Kernels: objects must override computeQpResidual.
NodalBC Object Members
_u
Value of the variable this Kernel is operating on
_qp
Current index, used for interface consistency
_boundary_id
The boundary ID
_current_node
A pointer to the current node that is being operated on.
Dirichlet BCs
Set a condition on the value of a variable on a boundary:
becomes
DirichletBC.h
#pragma once
#include "DirichletBCBase.h"
class DirichletBC;
template <>
InputParameters validParams<DirichletBC>();
/**
* Boundary condition of a Dirichlet type
*
* Sets the value in the node
*/
class DirichletBC : public DirichletBCBase
{
public:
static InputParameters validParams();
DirichletBC(const InputParameters & parameters);
protected:
virtual Real computeQpValue() override;
/// The value for this BC
const Real & _value;
};
DirichletBC.C
#include "DirichletBC.h"
registerMooseObject("MooseApp", DirichletBC);
defineLegacyParams(DirichletBC);
InputParameters
DirichletBC::validParams()
{
InputParameters params = DirichletBCBase::validParams();
params.addRequiredParam<Real>("value", "Value of the BC");
params.declareControllable("value");
params.addClassDescription("Imposes the essential boundary condition $u=g$, where $g$ "
"is a constant, controllable value.");
return params;
}
DirichletBC::DirichletBC(const InputParameters & parameters)
: DirichletBCBase(parameters), _value(getParam<Real>("value"))
{
}
Real
DirichletBC::computeQpValue()
{
return _value;
}
Integrated BCs
Integrated BCs (including Neumann BCs) are actually integrated over the external face of an element.
becomes:
If , then the boundary integral is zero ("natural boundary condition").
NeumannBC.h
#pragma once
#include "GenericIntegratedBC.h"
/**
* Implements a simple constant Neumann BC where grad(u)=value on the boundary.
* Uses the term produced from integrating the diffusion operator by parts.
*/
template <bool is_ad>
class NeumannBCTempl : public GenericIntegratedBC<is_ad>
{
public:
static InputParameters validParams();
NeumannBCTempl(const InputParameters & parameters);
protected:
virtual GenericReal<is_ad> computeQpResidual() override;
/// Value of grad(u) on the boundary.
const Real & _value;
usingGenericIntegratedBCMembers;
};
typedef NeumannBCTempl<false> NeumannBC;
typedef NeumannBCTempl<true> ADNeumannBC;
NeumannBC.C
#include "NeumannBC.h"
registerMooseObject("MooseApp", NeumannBC);
registerMooseObject("MooseApp", ADNeumannBC);
template <bool is_ad>
InputParameters
NeumannBCTempl<is_ad>::validParams()
{
InputParameters params = GenericIntegratedBC<is_ad>::validParams();
params.addParam<Real>("value", 0.0, "The value of the gradient on the boundary.");
params.declareControllable("value");
params.addClassDescription("Imposes the integrated boundary condition "
"$\\frac{\\partial u}{\\partial n}=h$, "
"where $h$ is a constant, controllable value.");
return params;
}
template <bool is_ad>
NeumannBCTempl<is_ad>::NeumannBCTempl(const InputParameters & parameters)
: GenericIntegratedBC<is_ad>(parameters), _value(this->template getParam<Real>("value"))
{
}
template <bool is_ad>
GenericReal<is_ad>
NeumannBCTempl<is_ad>::computeQpResidual()
{
return -_test[_i][_qp] * _value;
}
template class NeumannBCTempl<false>;
template class NeumannBCTempl<true>;
Periodic BCs
Periodic boundary conditions are useful for modeling quasi-infinite domains and systems with conserved quantities.
1D, 2D, and 3D
With mesh adaptivity
Can be restricted to specific variables
Supports arbitrary translation vectors for defining periodicity
Step 5: Heat Conduction
(continued)
Outflow Boundary Condition (5c)
The flow is assumed to exit the pipe into a large tank, which is modeled with the "No BC" boundary condition of Griffiths (1997).
The boundary term, , is computed implicitly rather than being replaced with a known flux, as is done in a NeumannBC.
HeatConductionOutflow.h
#pragma once
// Include the base class so it can be extended
#include "ADIntegratedBC.h"
/**
* An IntegratedBC representing the "No BC" boundary condition for
* heat conduction.
*
* The residual is simply -test*k*grad_u*normal... the term you get
* from integration by parts. This is a standard technique for
* truncating longer domains when solving the convection/diffusion
* equation.
*
* See also: Griffiths, David F. "The 'no boundary condition' outflow
* boundary condition.", International Journal for Numerical Methods
* in Fluids, vol. 24, no. 4, 1997, pp. 393-411.
*/
class HeatConductionOutflow : public ADIntegratedBC
{
public:
static InputParameters validParams();
HeatConductionOutflow(const InputParameters & parameters);
protected:
/**
* This is called to integrate the residual across the boundary.
*/
virtual ADReal computeQpResidual() override;
/// Thermal conductivity of the material
const ADMaterialProperty<Real> & _thermal_conductivity;
};
HeatConductionOutflow.C
#include "HeatConductionOutflow.h"
registerMooseObject("DarcyThermoMechApp", HeatConductionOutflow);
InputParameters
HeatConductionOutflow::validParams()
{
InputParameters params = ADIntegratedBC::validParams();
params.addClassDescription("Compute the outflow boundary condition.");
return params;
}
HeatConductionOutflow::HeatConductionOutflow(const InputParameters & parameters)
: ADIntegratedBC(parameters),
_thermal_conductivity(getADMaterialProperty<Real>("thermal_conductivity"))
{
}
ADReal
HeatConductionOutflow::computeQpResidual()
{
return -_test[_i][_qp] * _thermal_conductivity[_qp] * _grad_u[_qp] * _normals[_qp];
}
Step5c: Outflow Input File
[Mesh]
type = GeneratedMesh
dim = 2
nx = 100
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[Kernels]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[]
[BCs]
[inlet_temperature]
type = DirichletBC
variable = temperature
boundary = left
value = 350 # (K)
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[steel]
type = ADGenericConstantMaterial
prop_names = 'thermal_conductivity specific_heat density'
prop_values = '18 466 8000' # W/m*K, J/kg-K, kg/m^3 @ 296K
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
num_steps = 10
solve_type = NEWTON
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
Step 5c: Run and Visualize with Peacock
cd ~/projects/moose/tutorials/darcy-thermo_mech/step05_heat_conduction
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step5b_transient.i
Step 5c: Results
Step 6: Equation Coupling
The pressure and heat equations have been developed independently up to this point, in this step, they are coupled together.
Objects have been created for everything except the term; a
Kernel,DarcyAdvection, will be developed for this term.A more sophisticated
Materialobject will be created that includes temperature dependence
DarcyAdvection.h
#pragma once
#include "ADKernelValue.h"
/**
* Kernel which implements the convective term in the transient heat
* conduction equation, and provides coupling with the Darcy pressure
* equation.
*/
class DarcyAdvection : public ADKernelValue
{
public:
static InputParameters validParams();
DarcyAdvection(const InputParameters & parameters);
protected:
/// ADKernelValue objects must override precomputeQpResidual
virtual ADReal precomputeQpResidual() override;
/// The gradient of pressure
const ADVariableGradient & _pressure_grad;
/// These references will be set by the initialization list so that
/// values can be pulled from the Material system.
const ADMaterialProperty<Real> & _permeability;
const ADMaterialProperty<Real> & _porosity;
const ADMaterialProperty<Real> & _viscosity;
const ADMaterialProperty<Real> & _density;
const ADMaterialProperty<Real> & _specific_heat;
};
DarcyAdvection.C
#include "DarcyAdvection.h"
registerMooseObject("DarcyThermoMechApp", DarcyAdvection);
InputParameters
DarcyAdvection::validParams()
{
InputParameters params = ADKernelValue::validParams();
params.addRequiredCoupledVar("pressure", "The variable representing the pressure.");
return params;
}
DarcyAdvection::DarcyAdvection(const InputParameters & parameters)
: ADKernelValue(parameters),
// Couple to the gradient of the pressure
_pressure_grad(adCoupledGradient("pressure")),
// Grab necessary material properties
_permeability(getADMaterialProperty<Real>("permeability")),
_porosity(getADMaterialProperty<Real>("porosity")),
_viscosity(getADMaterialProperty<Real>("viscosity")),
_density(getADMaterialProperty<Real>("density")),
_specific_heat(getADMaterialProperty<Real>("specific_heat"))
{
}
ADReal
DarcyAdvection::precomputeQpResidual()
{
// See also: E. Majchrzak and L. Turchan, "The Finite Difference
// Method For Transient Convection Diffusion", Scientific Research
// of the Institute of Mathematics and Computer Science, vol. 1,
// no. 11, 2012, pp. 63-72.
// http://srimcs.im.pcz.pl/2012_1/art_07.pdf
// http://en.wikipedia.org/wiki/Superficial_velocity
ADRealVectorValue superficial_velocity =
_porosity[_qp] * -(_permeability[_qp] / _viscosity[_qp]) * _pressure_grad[_qp];
return _density[_qp] * _specific_heat[_qp] * superficial_velocity * _grad_u[_qp];
}
PackedColumn.h
#pragma once
#include "ADMaterial.h"
// A helper class from MOOSE that linear interpolates x,y data
#include "LinearInterpolation.h"
/**
* Material-derived objects override the computeQpProperties()
* function. They must declare and compute material properties for
* use by other objects in the calculation such as Kernels and
* BoundaryConditions.
*/
class PackedColumn : public ADMaterial
{
public:
static InputParameters validParams();
PackedColumn(const InputParameters & parameters);
protected:
/**
* Necessary override. This is where the values of the properties
* are computed.
*/
virtual void computeQpProperties() override;
/**
* Helper function for reading CSV data for use in an interpolator object.
*/
bool initInputData(const std::string & param_name, ADLinearInterpolation & interp);
/// The radius of the spheres in the column
const Function & _input_radius;
/// The input porosity
const Function & _input_porosity;
/// Temperature
const ADVariableValue & _temperature;
/// Compute permeability based on the radius (mm)
LinearInterpolation _permeability_interpolation;
/// Fluid viscosity
bool _use_fluid_mu_interp;
const Real & _fluid_mu;
ADLinearInterpolation _fluid_mu_interpolation;
/// Fluid thermal conductivity
bool _use_fluid_k_interp = false;
const Real & _fluid_k;
ADLinearInterpolation _fluid_k_interpolation;
/// Fluid density
bool _use_fluid_rho_interp = false;
const Real & _fluid_rho;
ADLinearInterpolation _fluid_rho_interpolation;
/// Fluid specific heat
bool _use_fluid_cp_interp;
const Real & _fluid_cp;
ADLinearInterpolation _fluid_cp_interpolation;
/// Solid thermal conductivity
bool _use_solid_k_interp = false;
const Real & _solid_k;
ADLinearInterpolation _solid_k_interpolation;
/// Solid density
bool _use_solid_rho_interp = false;
const Real & _solid_rho;
ADLinearInterpolation _solid_rho_interpolation;
/// Fluid specific heat
bool _use_solid_cp_interp;
const Real & _solid_cp;
ADLinearInterpolation _solid_cp_interpolation;
/// The permeability (K)
ADMaterialProperty<Real> & _permeability;
/// The porosity (eps)
ADMaterialProperty<Real> & _porosity;
/// The viscosity of the fluid (mu)
ADMaterialProperty<Real> & _viscosity;
/// The bulk thermal conductivity
ADMaterialProperty<Real> & _thermal_conductivity;
/// The bulk heat capacity
ADMaterialProperty<Real> & _specific_heat;
/// The bulk density
ADMaterialProperty<Real> & _density;
};
PackedColumn.C
#include "PackedColumn.h"
#include "Function.h"
#include "DelimitedFileReader.h"
registerMooseObject("DarcyThermoMechApp", PackedColumn);
InputParameters
PackedColumn::validParams()
{
InputParameters params = ADMaterial::validParams();
params.addRequiredCoupledVar("temperature", "The temperature (C) of the fluid.");
// Add a parameter to get the radius of the spheres in the column
// (used later to interpolate permeability).
params.addParam<FunctionName>("radius",
"1.0",
"The radius of the steel spheres (mm) that are packed in the "
"column for computing permeability.");
// http://en.wikipedia.org/wiki/Close-packing_of_equal_spheres
params.addParam<FunctionName>(
"porosity", 0.25952, "Porosity of porous media, default is for closed packed spheres.");
// Fluid properties
params.addParam<Real>(
"fluid_viscosity", 1.002e-3, "Fluid viscosity (Pa s); default is for water at 20C).");
params.addParam<FileName>(
"fluid_viscosity_file",
"The name of a file containing the fluid viscosity (Pa-s) as a function of temperature "
"(C); if provided the constant value is ignored.");
params.addParam<Real>("fluid_thermal_conductivity",
0.59803,
"Fluid thermal conductivity (W/(mK); default is for water at 20C).");
params.addParam<FileName>(
"fluid_thermal_conductivity_file",
"The name of a file containing fluid thermal conductivity (W/(mK)) as a function of "
"temperature (C); if provided the constant value is ignored.");
params.addParam<Real>(
"fluid_density", 998.21, "Fluid density (kg/m^3); default is for water at 20C).");
params.addParam<FileName>("fluid_density_file",
"The name of a file containing fluid density (kg/m^3) as a function "
"of temperature (C); if provided the constant value is ignored.");
params.addParam<Real>(
"fluid_specific_heat", 4157.0, "Fluid specific heat (J/(kgK); default is for water at 20C).");
params.addParam<FileName>(
"fluid_specific_heat_file",
"The name of a file containing fluid specific heat (J/(kgK) as a function of temperature "
"(C); if provided the constant value is ignored.");
// Solid properties
// https://en.wikipedia.org/wiki/Stainless_steel#Properties
params.addParam<Real>("solid_thermal_conductivity",
15.0,
"Solid thermal conductivity (W/(mK); default is for AISI/ASTIM 304 "
"stainless steel at 20C).");
params.addParam<FileName>(
"solid_thermal_conductivity_file",
"The name of a file containing solid thermal conductivity (W/(mK)) as a function of "
"temperature (C); if provided the constant value is ignored.");
params.addParam<Real>(
"solid_density",
7900,
"Solid density (kg/m^3); default is for AISI/ASTIM 304 stainless steel at 20C).");
params.addParam<FileName>("solid_density_file",
"The name of a file containing solid density (kg/m^3) as a function "
"of temperature (C); if provided the constant value is ignored.");
params.addParam<Real>(
"solid_specific_heat",
500,
"Solid specific heat (J/(kgK); default is for AISI/ASTIM 304 stainless steel at 20C).");
params.addParam<FileName>(
"solid_specific_heat_file",
"The name of a file containing solid specific heat (J/(kgK) as a function of temperature "
"(C); if provided the constant value is ignored.");
return params;
}
PackedColumn::PackedColumn(const InputParameters & parameters)
: ADMaterial(parameters),
// Get the one parameter from the input file
_input_radius(getFunction("radius")),
_input_porosity(getFunction("porosity")),
_temperature(adCoupledValue("temperature")),
// Fluid
_fluid_mu(getParam<Real>("fluid_viscosity")),
_fluid_k(getParam<Real>("fluid_thermal_conductivity")),
_fluid_rho(getParam<Real>("fluid_density")),
_fluid_cp(getParam<Real>("fluid_specific_heat")),
// Solid
_solid_k(getParam<Real>("solid_thermal_conductivity")),
_solid_rho(getParam<Real>("solid_density")),
_solid_cp(getParam<Real>("solid_specific_heat")),
// Material Properties being produced by this object
_permeability(declareADProperty<Real>("permeability")),
_porosity(declareADProperty<Real>("porosity")),
_viscosity(declareADProperty<Real>("viscosity")),
_thermal_conductivity(declareADProperty<Real>("thermal_conductivity")),
_specific_heat(declareADProperty<Real>("specific_heat")),
_density(declareADProperty<Real>("density"))
{
// Set data for permeability interpolation
std::vector<Real> sphere_sizes = {1, 3};
std::vector<Real> permeability = {0.8451e-9, 8.968e-9};
_permeability_interpolation.setData(sphere_sizes, permeability);
// Fluid viscosity, thermal conductivity, density, and specific heat
_use_fluid_mu_interp = initInputData("fluid_viscosity_file", _fluid_mu_interpolation);
_use_fluid_k_interp = initInputData("fluid_thermal_conductivity_file", _fluid_k_interpolation);
_use_fluid_rho_interp = initInputData("fluid_density_file", _fluid_rho_interpolation);
_use_fluid_cp_interp = initInputData("fluid_specific_heat_file", _fluid_cp_interpolation);
// Solid thermal conductivity, density, and specific heat
_use_solid_k_interp = initInputData("solid_thermal_conductivity_file", _solid_k_interpolation);
_use_solid_rho_interp = initInputData("solid_density_file", _solid_rho_interpolation);
_use_solid_cp_interp = initInputData("solid_specific_heat_file", _solid_cp_interpolation);
}
void
PackedColumn::computeQpProperties()
{
// Current temperature
ADReal temp = _temperature[_qp] - 273.15;
// Permeability
Real radius_value = _input_radius.value(_t, _q_point[_qp]);
mooseAssert(radius_value >= 1 && radius_value <= 3,
"The radius range must be in the range [1, 3], but " << radius_value << " provided.");
_permeability[_qp] = _permeability_interpolation.sample(radius_value);
// Porosity
Real porosity_value = _input_porosity.value(_t, _q_point[_qp]);
mooseAssert(porosity_value > 0 && porosity_value <= 1,
"The porosity range must be in the range (0, 1], but " << porosity_value
<< " provided.");
_porosity[_qp] = porosity_value;
// Fluid properties
_viscosity[_qp] = _use_fluid_mu_interp ? _fluid_mu_interpolation.sample(temp) : _fluid_mu;
ADReal fluid_k = _use_fluid_k_interp ? _fluid_k_interpolation.sample(temp) : _fluid_k;
ADReal fluid_rho = _use_fluid_rho_interp ? _fluid_rho_interpolation.sample(temp) : _fluid_rho;
ADReal fluid_cp = _use_fluid_cp_interp ? _fluid_cp_interpolation.sample(temp) : _fluid_cp;
// Solid properties
ADReal solid_k = _use_solid_k_interp ? _solid_k_interpolation.sample(temp) : _solid_k;
ADReal solid_rho = _use_solid_rho_interp ? _solid_rho_interpolation.sample(temp) : _solid_rho;
ADReal solid_cp = _use_solid_cp_interp ? _solid_cp_interpolation.sample(temp) : _solid_cp;
// Compute the heat conduction material properties as a linear combination of
// the material properties for fluid and steel.
_thermal_conductivity[_qp] = _porosity[_qp] * fluid_k + (1.0 - _porosity[_qp]) * solid_k;
_density[_qp] = _porosity[_qp] * fluid_rho + (1.0 - _porosity[_qp]) * solid_rho;
_specific_heat[_qp] = _porosity[_qp] * fluid_cp + (1.0 - _porosity[_qp]) * solid_cp;
}
bool
PackedColumn::initInputData(const std::string & param_name, ADLinearInterpolation & interp)
{
if (isParamValid(param_name))
{
const std::string & filename = getParam<FileName>(param_name);
MooseUtils::DelimitedFileReader reader(filename, &_communicator);
reader.setComment("#");
reader.read();
interp.setData(reader.getData(0), reader.getData(1));
return true;
}
return false;
}
HeatConductionOutflow.h
#pragma once
// Include the base class so it can be extended
#include "ADIntegratedBC.h"
/**
* An IntegratedBC representing the "No BC" boundary condition for
* heat conduction.
*
* The residual is simply -test*k*grad_u*normal... the term you get
* from integration by parts. This is a standard technique for
* truncating longer domains when solving the convection/diffusion
* equation.
*
* See also: Griffiths, David F. "The 'no boundary condition' outflow
* boundary condition.", International Journal for Numerical Methods
* in Fluids, vol. 24, no. 4, 1997, pp. 393-411.
*/
class HeatConductionOutflow : public ADIntegratedBC
{
public:
static InputParameters validParams();
HeatConductionOutflow(const InputParameters & parameters);
protected:
/**
* This is called to integrate the residual across the boundary.
*/
virtual ADReal computeQpResidual() override;
/// Thermal conductivity of the material
const ADMaterialProperty<Real> & _thermal_conductivity;
};
HeatConductionOutflow.C
#include "HeatConductionOutflow.h"
registerMooseObject("DarcyThermoMechApp", HeatConductionOutflow);
InputParameters
HeatConductionOutflow::validParams()
{
InputParameters params = ADIntegratedBC::validParams();
params.addClassDescription("Compute the outflow boundary condition.");
return params;
}
HeatConductionOutflow::HeatConductionOutflow(const InputParameters & parameters)
: ADIntegratedBC(parameters),
_thermal_conductivity(getADMaterialProperty<Real>("thermal_conductivity"))
{
}
ADReal
HeatConductionOutflow::computeQpResidual()
{
return -_test[_i][_qp] * _thermal_conductivity[_qp] * _grad_u[_qp] * _normals[_qp];
}
Step 6a: Coupled Pressure and Heat Equations
[Mesh]
type = GeneratedMesh
dim = 2
nx = 200
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
temperature = temperature
radius = 1
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
exodus = true
[]
Auto Variable Scaling
To obtain an optimum numerical solution, the non-linear variables should be on the same scale.
MOOSE includes the ability to automatically scale non-linear variables
Condition Number without Scaling
The condition number can be used to determine if variable scaling is required.
cd ~/projects/moose/tutorials/darcy-thermo_mech/step06_coupled_darcy_heat_conduction
make -j 12
../darcy_thermo_mech-opt -i step6a_coupled.i Mesh/nx=50 Mesh/ny=3 Executioner/num_steps=1 Executioner/automatic_scaling=0 -pc_type svd -pc_svd_monitor -ksp_view_pmat
Time Step 1, time = 0.1, dt = 0.1
0 Nonlinear |R| = 8.000625e+03
SVD: condition number 2.835686200265e+15, 2 of 408 singular values are (nearly) zero
SVD: smallest singular values: 1.434461194336e-13 5.583840793234e-13 1.222432395761e-12 2.076808734751e-12 3.047037450013e-12
SVD: largest singular values : 4.006299266699e+02 4.029206639889e+02 4.047115548038e+02 4.059957077255e+02 4.067681813595e+02
0 Linear |R| = 8.000625e+03
1 Linear |R| = 8.101613e-09
Mat Object: () 1 MPI processes
type: seqaij
row 0: (0, 1.) (1, 0.) (2, 0.) (3, 0.) (4, 0.) (5, 0.) (6, 0.) (7, 0.)
row 1: (0, 0.) (1, 1.) (2, 0.) (3, 0.) (4, 0.) (5, 0.) (6, 0.) (7, 0.)
row 2: (0, 1.32667e-12) (1, 0.) (2, -1.07325e-11) (3, 0.) (4, 3.97056e-14) (5, 0.) (6, 4.01973e-12) (7, 0.) (8, 1.32667e-12) (9, 0.) (10, 4.01973e-12) (11, 0.)
row 3: (0, -2.81185e-20) (1, 3.41152) (2, -1.12474e-19) (3, 14.0732) (4, 1.12474e-19) (5, 13.7863) (6, 2.81185e-20) (7, 3.33981) (8, -2.81185e-20) (9, 3.41152) (10, 2.81185e-20) (11, 3.33981)
row 4: (0, 4.01973e-12) (1, 0.) (2, 3.97056e-14) (3, 0.) (4, -6.43156e-11) (5, 0.) (6, 1.59995e-11) (7, 0.) (8, 4.01973e-12) (9, 0.) (10, 1.59995e-11) (11, 0.) (204, 1.19117e-13) (205, 0.) (206, 1.20592e-11) (207, 0.) (208, 1.20592e-11) (209, 0.)
Condition Number with Scaling
cd ~/projects/moose/tutorials/darcy-thermo_mech/step06_coupled_darcy_heat_conduction
make -j 12
../darcy_thermo_mech-opt -i step6a_coupled.i Mesh/nx=50 Mesh/ny=3 Executioner/num_steps=1 -pc_type svd -pc_svd_monitor -ksp_view_pmat
Time Step 1, time = 0.1, dt = 0.1
0 Nonlinear |R| = 8.000625e+03
SVD: condition number 2.877175736279e+04, 0 of 408 singular values are (nearly) zero
SVD: smallest singular values: 1.413775933915e-02 5.524422458767e-02 1.194077235260e-01 2.001521770346e-01 2.889664356969e-01
SVD: largest singular values : 4.006299266699e+02 4.029206639889e+02 4.047115548038e+02 4.059957077255e+02 4.067681813595e+02
0 Linear |R| = 8.000625e+03
1 Linear |R| = 3.858046e-09
Mat Object: () 1 MPI processes
type: seqaij
row 0: (0, 1.) (1, 0.) (2, 0.) (3, 0.) (4, 0.) (5, 0.) (6, 0.) (7, 0.)
row 1: (0, 0.) (1, 1.) (2, 0.) (3, 0.) (4, 0.) (5, 0.) (6, 0.) (7, 0.)
row 2: (0, 0.132667) (1, 0.) (2, -1.07325) (3, 0.) (4, 0.00397056) (5, 0.) (6, 0.401973) (7, 0.) (8, 0.132667) (9, 0.) (10, 0.401973) (11, 0.)
row 3: (0, -2.81185e-20) (1, 3.41152) (2, -1.12474e-19) (3, 14.0732) (4, 1.12474e-19) (5, 13.7863) (6, 2.81185e-20) (7, 3.33981) (8, -2.81185e-20) (9, 3.41152) (10, 2.81185e-20) (11, 3.33981)
row 4: (0, 0.401973) (1, 0.) (2, 0.00397056) (3, 0.) (4, -6.43156) (5, 0.) (6, 1.59995) (7, 0.) (8, 0.401973) (9, 0.) (10, 1.59995) (11, 0.) (204, 0.0119117) (205, 0.) (206, 1.20592) (207, 0.) (208, 1.20592) (209, 0.)
Step 6a: Run and Visualize with Peacock
cd ~/projects/moose/tutorials/darcy-thermo_mech/step06_coupled_darcy_heat_conduction
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step6a_coupled.i
Step 6a: Results
Step 6b:
Oscillating Pressure and Temperature Dependence
Vary the inlet and output pressure:
Inlet (left):
Outlet (right):
Viscosity, density, thermal conductivity, and specific heat capacity of the fluid are setup to vary as a function of temperature.
Step 6b: Input File
[Mesh]
type = GeneratedMesh
dim = 2
nx = 200
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[Functions]
[inlet_function]
type = ParsedFunction
value = 2000*sin(0.466*pi*t) # Inlet signal from Fig. 3
[]
[outlet_function]
type = ParsedFunction
value = 2000*cos(0.466*pi*t) # Outlet signal from Fig. 3
[]
[]
[BCs]
[inlet]
type = FunctionDirichletBC
variable = pressure
boundary = left
function = inlet_function
[]
[outlet]
type = FunctionDirichletBC
variable = pressure
boundary = right
function = outlet_function
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
temperature = temperature
fluid_viscosity_file = data/water_viscosity.csv
fluid_density_file = data/water_density.csv
fluid_thermal_conductivity_file = data/water_thermal_conductivity.csv
fluid_specific_heat_file = data/water_specific_heat.csv
outputs = exodus
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,(2*pi/(0.466*pi))/16)' # dt to always hit the peaks of sine/cosine BC
[]
[]
[Outputs]
exodus = true
[]
Step 6b: Run and Visualize with Peacock
cd ~/projects/moose/tutorials/darcy-thermo_mech/step06_coupled_darcy_heat_conduction
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step6b_transient_inflow.i
Step 6b: Results
Decoupling Heat Equation
[Mesh]
type = GeneratedMesh
dim = 2
nx = 200
ny = 10
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[pressure]
[]
[]
[AuxKernels]
[pressure]
type = FunctionAux
variable = pressure
function = 't*x*x*y'
execute_on = timestep_end
[]
[]
[Kernels]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[BCs]
[inlet_temperature]
type = DirichletBC
variable = temperature
boundary = left
value = 350
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
temperature = 293.15 # 20C
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
num_steps = 300
dt = 0.1
solve_type = NEWTON
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Outputs]
exodus = true
[]
Step 7: Mesh Adaptivity
Adaptivity System
h-Adaptivity
-adaptivity is a method of automatically refining/coarsening the mesh in regions of high/low estimated solution error.
Concentrate degrees of freedom (DOFs) where the error is highest, while reducing DOFs where the solution is already well-captured.
Compute a measure of error using an
IndicatorobjectMark an element for refinement or coarsening based on the error using a
Markerobject
Mesh adaptivity can be employed in both Steady and Transient executioners.
Refinement Patterns
MOOSE employs "self-similar", isotropic refinement patterns: when refining an element is split into elements of the same type.
For example, when using Quad4 elements, four "child" elements are created when the element is refined.
Coarsening happens in reverse, children are deleted and the "parent" element is reactivated.
The original mesh starts at refinement level 0.

Indicator Objects
Indicators report an amount of "error" for each element, built-in Indicators include:
GradientJumpIndicator
Jump in the gradient of a variable across element edges. A good "curvature" indicator that works well over a wide range of problems.
FluxJumpIndicator
Similar to GradientJump, except that a scalar coefficient (e.g. thermal conductivity) can be provided to produce a physical "flux" quantity.
LaplacianJumpIndicator
Jump in the second derivative of a variable. Only useful for shape functions.
AnalyticIndicator
Computes the difference between the finite element solution and a user-supplied Function representing the analytic solution to the problem.
Marker Objects
After an Indicator has computed the error for each element, a decision to refine or coarsen elements must be made using a Marker object.
ErrorFractionMarker
Selects elements based on their contribution to the total error.
ErrorToleranceMaker
Refine if error is greater than a specified value and coarsen if it is less.
ValueThresholdMarker
Refine if variable value is greater than a specific value and coarsen if it is less.
UniformMarker
Refine or coarsen all elements.
BoxMarker
Refine or coarsen inside or outside a given box.
ComboMarker
Combine several of the above Markers.
Input Syntax
[Adaptivity]
initial_steps = 2
cycles_per_step = 2
marker = marker
initial_marker = marker
max_h_level = 2
[Indicators/indicator]
[Indicators/indicator]
[Indicators/indicator]
[Indicators/indicator]
type = GradientJumpIndicator
variable = u
[]
[]
[]
[]
[Markers/marker]
[Markers/marker]
[Markers/marker]
[Markers/marker]
type = ErrorFractionMarker
indicator = indicator
coarsen = 0.1
refine = 0.7
[]
[]
[]
[]
[]
Step 7: Mesh Adaptivity
(continued)
Step 7a: Coarse Solution
[Mesh]
type = GeneratedMesh
dim = 2
nx = 30
ny = 3
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
temperature = temperature
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
exodus = true
[]
Step 7a: Run and Visualize
cd ~/projects/moose/tutorials/darcy-thermo_mech/step07_adaptivity
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step7a_coarse.i
Step 7b: Fine Solution
[Mesh]
type = GeneratedMesh
dim = 2
nx = 30
ny = 3
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
uniform_refine = 3
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
temperature = temperature
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
exodus = true
[]
Step 7b: Run and Visualize
cd ~/projects/moose/tutorials/darcy-thermo_mech/step07_adaptivity
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step7b_fine.i
Step 7c: Adaptive Mesh Solution
[Mesh]
type = GeneratedMesh
dim = 2
nx = 30
ny = 3
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
uniform_refine = 3
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
temperature = temperature
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
exodus = true
[]
[Adaptivity]
marker = error_frac
max_h_level = 3
[Indicators]
[temperature_jump]
type = GradientJumpIndicator
variable = temperature
scale_by_flux_faces = true
[]
[]
[Markers]
[error_frac]
type = ErrorFractionMarker
coarsen = 0.15
indicator = temperature_jump
refine = 0.7
[]
[]
[]
Step 7c: Run and Visualize
cd ~/projects/moose/tutorials/darcy-thermo_mech/step07_adaptivity
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step7a_adapt.i
Step 7d: Multiple Subdomains
[Mesh]
uniform_refine = 3
[generate]
type = GeneratedMeshGenerator
dim = 2
nx = 40
ny = 4
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
[]
[bottom]
type = SubdomainBoundingBoxGenerator
input = generate
location = inside
bottom_left = '0 0 0'
top_right = '0.304 0.01285 0'
block_id = 1
[]
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
viscosity_file = data/water_viscosity.csv
density_file = data/water_density.csv
thermal_conductivity_file = data/water_thermal_conductivity.csv
specific_heat_file = data/water_specific_heat.csv
[column_bottom]
type = PackedColumn
block = 1
radius = 1.15
temperature = temperature
fluid_viscosity_file = ${viscosity_file}
fluid_density_file = ${density_file}
fluid_thermal_conductivity_file = ${thermal_conductivity_file}
fluid_specific_heat_file = ${specific_heat_file}
[]
[column_top]
type = PackedColumn
block = 0
radius = 1
temperature = temperature
porosity = '0.25952 + 0.7*x/0.304'
fluid_viscosity_file = ${viscosity_file}
fluid_density_file = ${density_file}
fluid_thermal_conductivity_file = ${thermal_conductivity_file}
fluid_specific_heat_file = ${specific_heat_file}
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Adaptivity]
marker = error_frac
max_h_level = 3
[Indicators]
[temperature_jump]
type = GradientJumpIndicator
variable = temperature
scale_by_flux_faces = true
[]
[]
[Markers]
[error_frac]
type = ErrorFractionMarker
coarsen = 0.025
indicator = temperature_jump
refine = 0.9
[]
[]
[]
[Outputs]
[out]
type = Exodus
output_material_properties = true
[]
[]
Step 8: Postprocessors
Aggregate values based on simulation data are useful for understanding the simulation as well as defining coupling values across coupled equations.
There are two main systems for aggregating data: Postprocessors and VectorPostprocessors.
UserObject System
A system for defining an arbitrary interface between MOOSE objects.
The UserObject system provides data and calculation results to other MOOSE objects.
Postprocessors are UserObjects that compute a single scalar value.
VectorPostprocessors are UserObjects that compute vectors of data.
UserObjects define their own interface, which other MOOSE objects can call to retrieve data.
Execution
UserObjects are computed at specified "times" by the execute_on option in the input file:
execute_on = 'initial timestep_end'execute_on = linearexecute_on = nonlinearexecute_on = 'timestep_begin final failed'\\
They can be restricted to specific blocks, sidesets, and nodesets
UserObject Types
There are various types of UserObjects:
ElementUserObject: execute on elements
NodalUserObject: execute on nodes
SideUserObject: execute on boundaries
InternalSideUserObject: execute on internal sides
InterfaceUserObject: execute on interfaces
GeneralUserObject: execute once
UserObject Anatomy
virtual void initialize();
Called once before beginning the UserObject calculation.
virtual void execute();
Called once on each geometric entity (element, node, etc.) or once per calculation for a GeneralUserObject.
virtual void threadJoin(const UserObject & uo);
During threaded execution this function is used to "join" together calculations generated on different threads.
Cast
uoto aconstreference of the specific UserObject type, then extract data and aggregate it to the data in "this" object.This is not required for a
GeneralUserObjectbecause it is not threaded.
virtual void finalize();
The last function called after all calculations have been completed.
Take data from all calculations performed in
execute()and perform an operation to get the final value(s)Perform parallel communication where necessary to ensure all processors compute the same value(s)
User Defined Interface
A UserObject defines its own interface by defining const functions.
For example, if a UserObject is computing the average value of a variable on every block in the mesh, it might provide a function like:
Real averageValue(SubdomainID block) const;
Another MooseObject needing this UserObject would then call averageValue() to get the result of the calculation.
Using a UserObject
Any MOOSE object can retrieve a UserObject in a manner similar to retrieving a Function.
Generally, it is a good idea to take the name of the UserObject to from the input file:
InputParameters
BlockAverageDiffusionMaterial::validParams()
{
InputParameters params = Material::validParams();
params.addRequiredParam<UserObjectName>("block_average_userobject", "Computes the ...");
return params;
}
A UserObject comes through as a const reference of the UserObject type. So, in your object:
const BlockAverageValue & _block_average_value;
The reference is set in the initialization list of your object by calling the templated getUserObject() method:
BlockAverageDiffusionMaterial::BlockAverageDiffusionMaterial(const InputParameters & parameters) :
Material(parameters),
_block_average_value(getUserObject<BlockAverageValue>("block_average_userobject"))
{}
Use the reference by calling some of the interface functions defined by the UserObject:
_diffusivity[_qp] = 0.5 * _block_average_value.averageValue(_current_elem->subdomain_id());
Postprocessor System
A system for computing a "reduction" or "aggregation" calculation based on the solution variables that results in a single scalar value.
Types of Postprocessors
ElementPostprocessor: operate on each element
NodalPostprocessor: operate on each node
SidePostprocessor: operate on boundaries
InternalSidePostprocessor: operate on internal element sides
InterfacePostprocessor: operator on subdomain interfaces
GeneralPostprocessor: operates once per execution
Postprocessor Anatomy
Postprocessor is a UserObject, so initialize, execute, threadJoin, and finalize methods are used for implementing the aggregation operation.
Real getValue()
This is called internally within MOOSE to retrieve the final scalar value, the value returned by this function is referenced by all other objects that are using the postprocessor.
Aggregation Routines
If the Postprocessor created has custom data it must be ensured that the value is communicated properly in (both MPI and thread-based) parallel simulations.
For MPI several utility methods exist to perform common aggregation operations:
gatherSum(scalar): sum across all processors.gatherMin(scalar): min from all processors.gatherMax(scalar): max from all processors.
Built-in Postprocessor Types
MOOSE includes a large number built-in Postprocessors: ElementAverageValue, SideAverageValue, ElementL2Error, ElementH1Error, and many more
By default, Postprocessors will output to a formatted table on the screen and optionally using the [Outputs] block be stored in CSV file.
[Output]
csv = true
[]
Using a Postprocessor
Postprocessor values are used within an object by creating a const reference to a PostprocessorValue and initializing the reference in the initialization list.
const PostprocessorValue & _pps_value;
_pps_value(getPostprocessorValue("postprocessor")),
Default Postprocessor Values
It is possible to set default values for Postprocessors to allow an object to operate without creating Postprocessor object.
params.addParam<PostprocessorName>("postprocessor", 1.2345, "Doc String");
Additionally, a value may be supplied in the input file in lieu of a Postprocessor name.
VectorPostprocessor System
A system for "reduction" or "aggregation" calculations based on the solution variables that results in one or many vectors of values.
Types of VectorPostprocessors
ElementVectorPostprocessor: operate on each element
NodalVectorPostprocessor: operate on each node
SideVectorPostprocessor: operate on boundaries
InternalSideVectorPostprocessor: operate on internal element sides
GeneralVectorPostprocessor: operates once per execution
VectorPostprocessor Anatomy
Postprocessor is a UserObject, so initialize, execute, threadJoin, and finalize methods are used for implementing the aggregation operation.
virtual VectorPostprocessorValue & getVector (const std::string &vector_name) This is called internally within MOOSE to retrieve the final vector value for the given name, the value returned by this function is referenced by all other objects that are using the vector postprocessor.
VectorPostprocessor objects operate a bit like Material objects, each vector is declared and then within the "initialize", "execute", "threadJoin", and "finalize" methods the vectors are updated with the desired data.
Create a member variable, as a reference, for the vector data
VectorPostprocessorValue & _pid;
Initialize the reference using the declareVector method with a name
_pid(declareVector("pid")),
Built-in VectorPostprocessor Types
MOOSE includes a large number built-in VectorPostprocessors: NodalValueSampler, LineValueSampler, PointValueSampler, and many more.
VectorPostprocessors output is optionally enabled using the [Outputs] block. A CSV file for each vector and timestep will be created.
[Output]
csv = true
[]
Using a VectorPostprocessor
Postprocessor values are used within an object by creating a const reference to a VectorPostprocessorValue and initializing the reference in the initialization list.
const VectorPostprocessorValue & _x_values;
_x_values(getVectorPostprocessorValue("vectorpostprocessor", _x_name)),
Step 8: Postprocessors
(continued)
Step 8: Input File
[Mesh]
type = GeneratedMesh
dim = 2
nx = 30
ny = 3
xmax = 0.304 # Length of test chamber
ymax = 0.0257 # Test chamber radius
uniform_refine = 2
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = left
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = right
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = left
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = right
[]
[]
[Materials]
[column]
type = PackedColumn
radius = 1
temperature = temperature
porosity = '0.25952 + 0.7*y/0.0257'
[]
[]
[Postprocessors]
[average_temperature]
type = ElementAverageValue
variable = temperature
[]
[outlet_heat_flux]
type = ADSideDiffusiveFluxIntegral
variable = temperature
boundary = right
diffusivity = thermal_conductivity
[]
[]
[VectorPostprocessors]
[temperature_sample]
type = LineValueSampler
num_points = 500
start_point = '0.1 0 0'
end_point = '0.1 0.0257 0'
variable = temperature
sort_by = y
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
rz_coord_axis = X
[]
[Executioner]
type = Transient
solve_type = NEWTON
automatic_scaling = true
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
end_time = 100
dt = 0.25
start_time = -1
steady_state_tolerance = 1e-5
steady_state_detection = true
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
exodus = true
csv = true
[]
Step 8: Run and Visualize
cd ~/projects/moose/tutorials/darcy-thermo_mech/step08_postprocessors
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step8.i
Step 9: Mechanics
Mechanics
Compute the elastic and thermal strain if the tube is only allowed to expand along the axial (y) direction.
where is the Cauchy stress tensor, is an additional source of stress (such as pore pressure), is the displacement vector, is the body force, is the unit normal to the boundary, is the prescribed displacement on the boundary and is the prescribed traction on the boundary.
Modules
Chemical Reactions
The chemical reactions module provides a set of tools for the calculation of multicomponent aqueous reactive transport in porous media, originally developed as the MOOSE application RAT (Guo et al., 2013).
Contact
The MOOSE contact module provides the necessary tools for modeling mechanical contact using algorithms to enforce constraints between surfaces in the mesh, to prevent penetration and develop contact forces.
External PETSc Solver
The External PETSc Solver module provides support for stand-alone native PETSc applications that to be coupled with moose-based applications.
Fluid Properties
The Fluid Properties module provides a consistent interface to fluid properties such as density, viscosity, enthalpy and many others, as well as derivatives with respect to the primary variables. The consistent interface allows different fluids to be used in an input file by simply swapping the name of the Fluid Properties UserObject in a plug-and-play manner.
Functional Expansion Tools
A MOOSE module for continuous, mesh-agnostic, high-fidelity, reduced-data MultiApp coupling
Functional expansions (FXs) are a methodology that represent information as moments of a functional series (Flusser et al., 2016). This is is related to a Fourier series representation of cyclic data. Moments are generated via numerical integration for each term in the functional series to represent the field of interest. These moments can then be used to reconstruct the field in a separate app (Wendt et al., 2018; Wendt and Kerby, 2017; Kerby et al., 2017).
Heat Conduction
Basic utilities for solving the transient heat conduction equation:
Level Set
The level set module provides basic functionality to solve the level set equation, which is simply the multi-dimensional advection equation:
Navier Stokes
The MOOSE Navier-Stokes module is a library for the implementation of simulation tools that solve the Navier-Stokes equations using the continuous Galerkin finite element (CGFE) method. The Navier-Stokes equations are usually solved using either the pressure-based, incompressible formulation (assuming a constant fluid density), or the density-based, compressible formulation.
Phase Field
The MOOSE phase field module is a library for simplifying the implementation of simulation tools that employ the phase field model.
Porous Flow
The PorousFlow module is a library of physics for fluid and heat flow in porous media. It is formulated in an extremely general manner, so is capable of solving problems with an arbitrary number of phases (gas, liquid, etc) and fluid components (species present in each fluid phase), using any set of primary variables.
Reconstructed Discontinuous Galerkin (rDG)
The MOOSE rDG module is a library for the implementation of simulation tools that solve convection-dominated problems using the class of so-called reconstructed discontinuous Galerkin (rDG) methods. The specific rDG method implemented in this module is rDG(P0P1), which is equivalent to the second-order cell-centered finite volume method (FVM).
Stochastic Tools
The stochastic tools module is a toolbox designed for performing stochastic analysis for MOOSE-based applications.
Tensor Mechanics
The Tensor Mechanics module is a library of simulation tools that solve continuum mechanics problems. The module can be used to simulation both linear and finite strain mechanics, including Elasticity and Cosserat elasticity, Plasticity and micromechanics plasticity, Creep, and Damage due to cracking and property degradation.
Extended Finite Element Method (XFEM)
A MOOSE-based implementation of the extended finite element method, which is a numerical method that is especially designed for treating discontinuities.
Step 9: Mechanics
(continued)
PackedColumn.h
#pragma once
#include "ADMaterial.h"
// A helper class from MOOSE that linear interpolates x,y data
#include "LinearInterpolation.h"
/**
* Material-derived objects override the computeQpProperties()
* function. They must declare and compute material properties for
* use by other objects in the calculation such as Kernels and
* BoundaryConditions.
*/
class PackedColumn : public ADMaterial
{
public:
static InputParameters validParams();
PackedColumn(const InputParameters & parameters);
protected:
/**
* Necessary override. This is where the values of the properties
* are computed.
*/
virtual void computeQpProperties() override;
/**
* Helper function for reading CSV data for use in an interpolator object.
*/
bool initInputData(const std::string & param_name, ADLinearInterpolation & interp);
/// The radius of the spheres in the column
const Function & _input_radius;
/// The input porosity
const Function & _input_porosity;
/// Temperature
const ADVariableValue & _temperature;
/// Compute permeability based on the radius (mm)
LinearInterpolation _permeability_interpolation;
/// Fluid viscosity
bool _use_fluid_mu_interp;
const Real & _fluid_mu;
ADLinearInterpolation _fluid_mu_interpolation;
/// Fluid thermal conductivity
bool _use_fluid_k_interp = false;
const Real & _fluid_k;
ADLinearInterpolation _fluid_k_interpolation;
/// Fluid density
bool _use_fluid_rho_interp = false;
const Real & _fluid_rho;
ADLinearInterpolation _fluid_rho_interpolation;
/// Fluid specific heat
bool _use_fluid_cp_interp;
const Real & _fluid_cp;
ADLinearInterpolation _fluid_cp_interpolation;
/// Fluid thermal expansion coefficient
bool _use_fluid_cte_interp;
const Real & _fluid_cte;
ADLinearInterpolation _fluid_cte_interpolation;
/// Solid thermal conductivity
bool _use_solid_k_interp = false;
const Real & _solid_k;
ADLinearInterpolation _solid_k_interpolation;
/// Solid density
bool _use_solid_rho_interp = false;
const Real & _solid_rho;
ADLinearInterpolation _solid_rho_interpolation;
/// Solid specific heat
bool _use_solid_cp_interp;
const Real & _solid_cp;
ADLinearInterpolation _solid_cp_interpolation;
/// Solid thermal expansion coefficient
bool _use_solid_cte_interp;
const Real & _solid_cte;
ADLinearInterpolation _solid_cte_interpolation;
/// The permeability (K)
ADMaterialProperty<Real> & _permeability;
/// The porosity (eps)
ADMaterialProperty<Real> & _porosity;
/// The viscosity of the fluid (mu)
ADMaterialProperty<Real> & _viscosity;
/// The bulk thermal conductivity
ADMaterialProperty<Real> & _thermal_conductivity;
/// The bulk heat capacity
ADMaterialProperty<Real> & _specific_heat;
/// The bulk density
ADMaterialProperty<Real> & _density;
/// The bulk thermal expansion coefficient
ADMaterialProperty<Real> & _thermal_expansion;
};
PackedColumn.C
#include "PackedColumn.h"
#include "Function.h"
#include "DelimitedFileReader.h"
registerMooseObject("DarcyThermoMechApp", PackedColumn);
InputParameters
PackedColumn::validParams()
{
InputParameters params = ADMaterial::validParams();
params.addRequiredCoupledVar("temperature", "The temperature (C) of the fluid.");
// Add a parameter to get the radius of the spheres in the column
// (used later to interpolate permeability).
params.addParam<FunctionName>("radius",
"1.0",
"The radius of the steel spheres (mm) that are packed in the "
"column for computing permeability.");
// http://en.wikipedia.org/wiki/Close-packing_of_equal_spheres
params.addParam<FunctionName>(
"porosity", 0.25952, "Porosity of porous media, default is for closed packed spheres.");
// Fluid properties
params.addParam<Real>(
"fluid_viscosity", 1.002e-3, "Fluid viscosity (Pa s); default is for water at 20C).");
params.addParam<FileName>(
"fluid_viscosity_file",
"The name of a file containing the fluid viscosity (Pa-s) as a function of temperature "
"(C); if provided the constant value is ignored.");
params.addParam<Real>("fluid_thermal_conductivity",
0.59803,
"Fluid thermal conductivity (W/(mK); default is for water at 20C).");
params.addParam<FileName>(
"fluid_thermal_conductivity_file",
"The name of a file containing fluid thermal conductivity (W/(mK)) as a function of "
"temperature (C); if provided the constant value is ignored.");
params.addParam<Real>(
"fluid_density", 998.21, "Fluid density (kg/m^3); default is for water at 20C).");
params.addParam<FileName>("fluid_density_file",
"The name of a file containing fluid density (kg/m^3) as a function "
"of temperature (C); if provided the constant value is ignored.");
params.addParam<Real>(
"fluid_specific_heat", 4157.0, "Fluid specific heat (J/(kgK); default is for water at 20C).");
params.addParam<FileName>(
"fluid_specific_heat_file",
"The name of a file containing fluid specific heat (J/(kgK) as a function of temperature "
"(C); if provided the constant value is ignored.");
params.addParam<Real>("fluid_thermal_expansion",
2.07e-4,
"Fluid thermal expansion coefficient (1/K); default is for water at 20C).");
params.addParam<FileName>("fluid_thermal_expansion_file",
"The name of a file containing fluid thermal expansion coefficient "
"(1/K) as a function of temperature "
"(C); if provided the constant value is ignored.");
// Solid properties
// https://en.wikipedia.org/wiki/Stainless_steel#Properties
params.addParam<Real>("solid_thermal_conductivity",
15.0,
"Solid thermal conductivity (W/(mK); default is for AISI/ASTIM 304 "
"stainless steel at 20C).");
params.addParam<FileName>(
"solid_thermal_conductivity_file",
"The name of a file containing solid thermal conductivity (W/(mK)) as a function of "
"temperature (C); if provided the constant value is ignored.");
params.addParam<Real>(
"solid_density",
7900,
"Solid density (kg/m^3); default is for AISI/ASTIM 304 stainless steel at 20C).");
params.addParam<FileName>("solid_density_file",
"The name of a file containing solid density (kg/m^3) as a function "
"of temperature (C); if provided the constant value is ignored.");
params.addParam<Real>(
"solid_specific_heat",
500,
"Solid specific heat (J/(kgK); default is for AISI/ASTIM 304 stainless steel at 20C).");
params.addParam<FileName>(
"solid_specific_heat_file",
"The name of a file containing solid specific heat (J/(kgK) as a function of temperature "
"(C); if provided the constant value is ignored.");
params.addParam<Real>("solid_thermal_expansion",
17.3e-6,
"Solid thermal expansion coefficient (1/K); default is for water at 20C).");
params.addParam<FileName>("solid_thermal_expansion_file",
"The name of a file containing solid thermal expansion coefficient "
"(1/K) as a function of temperature "
"(C); if provided the constant value is ignored.");
return params;
}
PackedColumn::PackedColumn(const InputParameters & parameters)
: ADMaterial(parameters),
// Get the one parameter from the input file
_input_radius(getFunction("radius")),
_input_porosity(getFunction("porosity")),
_temperature(adCoupledValue("temperature")),
// Fluid
_fluid_mu(getParam<Real>("fluid_viscosity")),
_fluid_k(getParam<Real>("fluid_thermal_conductivity")),
_fluid_rho(getParam<Real>("fluid_density")),
_fluid_cp(getParam<Real>("fluid_specific_heat")),
_fluid_cte(getParam<Real>("fluid_thermal_expansion")),
// Solid
_solid_k(getParam<Real>("solid_thermal_conductivity")),
_solid_rho(getParam<Real>("solid_density")),
_solid_cp(getParam<Real>("solid_specific_heat")),
_solid_cte(getParam<Real>("solid_thermal_expansion")),
// Material Properties being produced by this object
_permeability(declareADProperty<Real>("permeability")),
_porosity(declareADProperty<Real>("porosity")),
_viscosity(declareADProperty<Real>("viscosity")),
_thermal_conductivity(declareADProperty<Real>("thermal_conductivity")),
_specific_heat(declareADProperty<Real>("specific_heat")),
_density(declareADProperty<Real>("density")),
_thermal_expansion(declareADProperty<Real>("thermal_expansion"))
{
// Set data for permeability interpolation
std::vector<Real> sphere_sizes = {1, 3};
std::vector<Real> permeability = {0.8451e-9, 8.968e-9};
_permeability_interpolation.setData(sphere_sizes, permeability);
// Fluid viscosity, thermal conductivity, density, and specific heat
_use_fluid_mu_interp = initInputData("fluid_viscosity_file", _fluid_mu_interpolation);
_use_fluid_k_interp = initInputData("fluid_thermal_conductivity_file", _fluid_k_interpolation);
_use_fluid_rho_interp = initInputData("fluid_density_file", _fluid_rho_interpolation);
_use_fluid_cp_interp = initInputData("fluid_specific_heat_file", _fluid_cp_interpolation);
_use_fluid_cte_interp = initInputData("fluid_thermal_expansion_file", _fluid_cte_interpolation);
// Solid thermal conductivity, density, and specific heat
_use_solid_k_interp = initInputData("solid_thermal_conductivity_file", _solid_k_interpolation);
_use_solid_rho_interp = initInputData("solid_density_file", _solid_rho_interpolation);
_use_solid_cp_interp = initInputData("solid_specific_heat_file", _solid_cp_interpolation);
_use_solid_cte_interp = initInputData("solid_thermal_expansion_file", _solid_cte_interpolation);
}
void
PackedColumn::computeQpProperties()
{
// Current temperature
ADReal temp = _temperature[_qp] - 273.15;
// Permeability
Real radius_value = _input_radius.value(_t, _q_point[_qp]);
mooseAssert(radius_value >= 1 && radius_value <= 3,
"The radius range must be in the range [1, 3], but " << radius_value << " provided.");
_permeability[_qp] = _permeability_interpolation.sample(radius_value);
// Porosity
Real porosity_value = _input_porosity.value(_t, _q_point[_qp]);
mooseAssert(porosity_value > 0 && porosity_value <= 1,
"The porosity range must be in the range (0, 1], but " << porosity_value
<< " provided.");
_porosity[_qp] = porosity_value;
// Fluid properties
_viscosity[_qp] =
_use_fluid_mu_interp ? _fluid_mu_interpolation.sample(raw_value(temp)) : _fluid_mu;
ADReal fluid_k = _use_fluid_k_interp ? _fluid_k_interpolation.sample(raw_value(temp)) : _fluid_k;
ADReal fluid_rho =
_use_fluid_rho_interp ? _fluid_rho_interpolation.sample(raw_value(temp)) : _fluid_rho;
ADReal fluid_cp =
_use_fluid_cp_interp ? _fluid_cp_interpolation.sample(raw_value(temp)) : _fluid_cp;
ADReal fluid_cte =
_use_fluid_cte_interp ? _fluid_cte_interpolation.sample(raw_value(temp)) : _fluid_cte;
// Solid properties
ADReal solid_k = _use_solid_k_interp ? _solid_k_interpolation.sample(raw_value(temp)) : _solid_k;
ADReal solid_rho =
_use_solid_rho_interp ? _solid_rho_interpolation.sample(raw_value(temp)) : _solid_rho;
ADReal solid_cp =
_use_solid_cp_interp ? _solid_cp_interpolation.sample(raw_value(temp)) : _solid_cp;
ADReal solid_cte =
_use_solid_cte_interp ? _solid_cte_interpolation.sample(raw_value(temp)) : _solid_cte;
// Compute the heat conduction material properties as a linear combination of
// the material properties for fluid and steel.
_thermal_conductivity[_qp] = _porosity[_qp] * fluid_k + (1.0 - _porosity[_qp]) * solid_k;
_density[_qp] = _porosity[_qp] * fluid_rho + (1.0 - _porosity[_qp]) * solid_rho;
_specific_heat[_qp] = _porosity[_qp] * fluid_cp + (1.0 - _porosity[_qp]) * solid_cp;
_thermal_expansion[_qp] = _porosity[_qp] * fluid_cte + (1.0 - _porosity[_qp]) * solid_cte;
}
bool
PackedColumn::initInputData(const std::string & param_name, ADLinearInterpolation & interp)
{
if (isParamValid(param_name))
{
const std::string & filename = getParam<FileName>(param_name);
MooseUtils::DelimitedFileReader reader(filename, &_communicator);
reader.setComment("#");
reader.read();
interp.setData(reader.getData(0), reader.getData(1));
return true;
}
return false;
}
Step 9: Input File
[GlobalParams]
displacements = 'disp_r disp_z'
[]
[Mesh]
[generate]
type = GeneratedMeshGenerator
dim = 2
ny = 200
nx = 10
ymax = 0.304 # Length of test chamber
xmax = 0.0257 # Test chamber radius
[]
[bottom]
type = SubdomainBoundingBoxGenerator
input = generate
location = inside
bottom_left = '0 0 0'
top_right = '0.01285 0.304 0'
block_id = 1
[]
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Modules/TensorMechanics/Master]
[all]
# This block adds all of the proper Kernels, strain calculators, and Variables
# for TensorMechanics in the correct coordinate system (autodetected)
add_variables = true
strain = FINITE
eigenstrain_names = eigenstrain
use_automatic_differentiation = true
generate_output = 'vonmises_stress elastic_strain_xx elastic_strain_yy strain_xx strain_yy'
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = bottom
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = top
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = bottom
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = top
[]
[hold_inlet]
type = DirichletBC
variable = disp_z
boundary = bottom
value = 0
[]
[hold_center]
type = DirichletBC
variable = disp_r
boundary = left
value = 0
[]
[hold_outside]
type = DirichletBC
variable = disp_r
boundary = right
value = 0
[]
[]
[Materials]
viscosity_file = data/water_viscosity.csv
density_file = data/water_density.csv
thermal_conductivity_file = data/water_thermal_conductivity.csv
specific_heat_file = data/water_specific_heat.csv
thermal_expansion_file = data/water_thermal_expansion.csv
[column_top]
type = PackedColumn
block = 0
temperature = temperature
radius = 1.15
fluid_viscosity_file = ${viscosity_file}
fluid_density_file = ${density_file}
fluid_thermal_conductivity_file = ${thermal_conductivity_file}
fluid_specific_heat_file = ${specific_heat_file}
fluid_thermal_expansion_file = ${thermal_expansion_file}
[]
[column_bottom]
type = PackedColumn
block = 1
temperature = temperature
radius = 1
fluid_viscosity_file = ${viscosity_file}
fluid_density_file = ${density_file}
fluid_thermal_conductivity_file = ${thermal_conductivity_file}
fluid_specific_heat_file = ${specific_heat_file}
fluid_thermal_expansion_file = ${thermal_expansion_file}
[]
[elasticity_tensor]
type = ADComputeIsotropicElasticityTensor
youngs_modulus = 200e9 # (Pa) from wikipedia
poissons_ratio = .3 # from wikipedia
[]
[elastic_stress]
type = ADComputeFiniteStrainElasticStress
[]
[thermal_strain]
type = ADComputeThermalExpansionEigenstrain
stress_free_temperature = 300
eigenstrain_name = eigenstrain
temperature = temperature
thermal_expansion_coeff = 1e-5 # TM modules doesn't support material property, but it will
[]
[]
[Postprocessors]
[average_temperature]
type = ElementAverageValue
variable = temperature
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Executioner]
type = Transient
start_time = -1
end_time = 200
steady_state_tolerance = 1e-7
steady_state_detection = true
dt = 0.25
solve_type = PJFNK
automatic_scaling = true
compute_scaling_once = false
petsc_options_iname = '-pc_type'
petsc_options_value = 'lu'
#petsc_options_iname = '-pc_type -pc_hypre_type -ksp_gmres_restart'
#petsc_options_value = 'hypre boomeramg 500'
line_search = none
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
[out]
type = Exodus
elemental_as_nodal = true
[]
[]
Step 9: Run and Visualize
cd ~/projects/moose/tutorials/darcy-thermo_mech/step09_mechanics
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step9.i
Step 9: Results
Step 10: Multiscale Simulation
Run full simulation but compute thermal conductivity and porosity from micro-structure
MultiApp System
A system for performing multiple simulations within a main simulation.
MOOSE was originally created to solve fully-coupled systems of PDEs, but not all systems need to be/are fully coupled:
Multiscale systems are generally loosely coupled between scales
Systems with both fast and slow physics can be decoupled in time
Simulations involving input from external codes may be solved
The MultiApp system creates simulations of loosely-coupled systems of fully-coupled equations
MultiApp Hierarchy
Each "app" is considered to be a solve that is independent, and there is always a "main" that is driving the simulation
The "main" app can have any number of
MultiAppobjectsEach
MultiAppcan represent many sub-applications ("sub-apps")
Each sub-app can solve for different physics from the main application
A sub-app can be another MOOSE application or could be an external application
A sub-app can have MultiApps, thus create a multi-level solve

Input File Syntax
MultiApp objects are declared in the [MultiApps] block
app_type
The name of the MooseApp derived application to run (e.g., "AnimalApp")
positions
List of 3D coordinates describing the offset of the sub-application into the physical space of the main application
execute_on
Allows control when sub-applications are executed: INITIAL, LINEAR, NONLINEAR, TIMESTEP_BEGIN, TIMESTEP_END
input_files
One input file can be supplied for all the sub-apps or a file can be provided for each
[MultiApps]
[micro]
type = TransientMultiApp
app_type = DarcyThermoMechApp
positions = '0.01285 0.0 0
0.01285 0.0608 0
0.01285 0.1216 0
0.01285 0.1824 0
0.01285 0.2432 0
0.01285 0.304 0'
input_files = step10_micro.i
execute_on = 'timestep_end'
[]
[]
Parallel
The MultiApp system is designed for efficient parallel execution of hierarchical problems.
The main application utilizes all processors
The processors are split among each sub-apps within each MultiApp and are run simultaneously
Multiple MultiApps will be executed one after another
Transfer System
A system to move data to and from the "master" and "sub-applications" of a MultiApp.
Transferred data typically is handled by the Auxiliary and Postprocessor systems.
The data on the receiving application should couple to these values in the normal way and each sub-application should be able to solve on its own
Field Interpolation
An "interpolation"
Transfershould be used when the domains have some overlapping geometry.The source field is evaluated at the destination points (generally nodes or element centroids).
The evaluations are then put into the receiving
AuxVariablefield namedvariable.All
MultiAppTransferstake adirectionparameter to specify the flow of information. Options are:from_multiapporto_multiapp.
[Transfers]
[from_sub]
source_variable = sub_u
direction = from_multiapp
variable = transferred_u
type = MultiAppMeshFunctionTransfer
multi_app = sub
execute_on = 'initial timestep_end'
[]
[elemental_from_sub]
source_variable = sub_u
direction = from_multiapp
variable = elemental_transferred_u
type = MultiAppMeshFunctionTransfer
multi_app = sub
[]
[]
UserObject Interpolation
Many
UserObjectscompute spatially-varying data that is not associated directly with a meshAny
UserObjectcan overrideReal spatialValue(Point &)to provide a value given a point in spaceA
UserObjectTransfercan sample this spatially-varying data from one app and put the values into anAuxVariablein another
[Transfers]
[layered_transfer_to_sub_app]
type = MultiAppUserObjectTransfer
direction = to_multiapp
user_object = master_uo
variable = sub_app_var
multi_app = sub_app
displaced_target_mesh = true
[]
[layered_transfer_from_sub_app]
type = MultiAppUserObjectTransfer
direction = from_multiapp
user_object = sub_app_uo
variable = from_sub_app_var
multi_app = sub_app
displaced_source_mesh = true
[]
[]
Postprocessor Transfer
A Postprocessor transfer allows a transfer of scalar values between applications
When transferring to a
MultiApp, the value can either be put into aPostprocessorvalue or can be put into a constantAuxVariablefieldWhen transferring from a
MultiAppto the master, the value can be interpolated from all the sub-apps into an auxiliary field
[Transfers]
[pp_transfer]
type = MultiAppPostprocessorTransfer
direction = to_multiapp
multi_app = pp_sub
from_postprocessor = average
to_postprocessor = from_master
[]
[]
Step 10: Multiscale Simulation
(continued)
RandomCorrosion.h
#pragma once
// MOOSE includes
#include "AuxKernel.h"
#include "libmesh/bounding_box.h"
/**
* Creates artificial, temperature driven corrosion.
*
* Consider a multi-phase system represented by a field-variable varying
* from 0 to 1. This class randomly sets points within the field to have
* a value of 0. Additionally, there is a contrived relationship with the
* number of points where "corrosion" occurs, the greater the difference
* between the supplied postprocessor and the reference the more points
* that are used.
*/
class RandomCorrosion : public AuxKernel
{
public:
static InputParameters validParams();
/**
* Class constructor
* @param parameters The input parameters for the RandomCorrosion object.
*/
RandomCorrosion(const InputParameters & parameters);
/**
* At each timestep randomly create a vector of points to apply "corrosion".
*/
void timestepSetup() override;
protected:
/**
* Computes the "corrosion" for the supplied phase variable.
* @return The compute "phase" variable
*/
virtual Real computeValue() override;
/**
* A helper method for getting random points in the domiain.
* @return A random point within the bounding box of the domain
*/
Point getRandomPoint();
private:
/// The vector of random points to apply "corrosion"
std::vector<Point> _points;
/// The bounding box of the domain, used for generating "corrosion" points
BoundingBox _box;
/// Nodal tolerance for determining if "corrosion" should occur at the current node
const Real & _nodal_tol;
/// Minimum number of "corrosion" points to apply
const unsigned int & _num_points;
/// Reference temperature, used for creating a temperature dependence and corrosion
const Real & _ref_temperature;
/// System temperature, used for creating a temperature dependence and corrosion
const PostprocessorValue & _temperature;
};
RandomCorrosion.C
// MOOSE includes
#include "RandomCorrosion.h"
#include "MooseMesh.h"
#include "libmesh/mesh_tools.h"
registerMooseObject("DarcyThermoMechApp", RandomCorrosion);
InputParameters
RandomCorrosion::validParams()
{
InputParameters params = AuxKernel::validParams();
params.addParam<Real>("tolerance",
1e-3,
"When acting as a nodal AuxKernel determine if the "
"random point to apply corrosion is located at the "
"current node.");
params.addParam<unsigned int>("num_points",
10,
"The number of random points to apply artificial "
"corrosion. The number of points is increased by "
"a factor as the supplied temperatures diverge.");
params.addParam<Real>("reference_temperature",
273.15,
"Temperature at which corrosion begins, "
"the greater the 'temperature' drifts "
"from this the greater the amount of "
"corrosion locations that occurs.");
params.addParam<PostprocessorName>(
"temperature",
274.15,
"The temperature value to used for computing the temperature "
"multiplication factor for the number of corrosion locations.");
return params;
}
RandomCorrosion::RandomCorrosion(const InputParameters & parameters)
: AuxKernel(parameters),
_box(MeshTools::create_bounding_box(_mesh)),
_nodal_tol(getParam<Real>("tolerance")),
_num_points(getParam<unsigned int>("num_points")),
_ref_temperature(getParam<Real>("reference_temperature")),
_temperature(getPostprocessorValue("temperature"))
{
// This class only works with Nodal aux variables
if (!isNodal())
mooseError("RandomCorrosion only operates using nodal aux variables.");
// Setup the random number generation
setRandomResetFrequency(EXEC_TIMESTEP_BEGIN);
}
void
RandomCorrosion::timestepSetup()
{
// Increase the number of points as the temperature differs from the reference
Real factor = 1;
if (_temperature > _ref_temperature)
factor = 1 + (_temperature - _ref_temperature) * 0.1;
// Generater the random points to apply "corrosion"
_points.clear();
for (unsigned int i = 0; i < _num_points * factor; ++i)
_points.push_back(getRandomPoint());
}
Real
RandomCorrosion::computeValue()
{
// If the current node is at a "corrosion" point, set the phase variable to zero
for (const Point & pt : _points)
if (_current_node->absolute_fuzzy_equals(pt, _nodal_tol))
return 0.0;
// Do nothing to the phase variable if not at a "corrosion" point
return _u[_qp];
}
Point
RandomCorrosion::getRandomPoint()
{
// Generates a random point within the domain
const Point & min = _box.min();
const Point & max = _box.max();
Real x = getRandomReal() * (max(0) - min(0)) + min(0);
Real y = getRandomReal() * (max(1) - min(1)) + min(1);
Real z = getRandomReal() * (max(2) - min(2)) + min(2);
return Point(x, y, z);
}
Step 10: Micro-scale Input File
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 10
ymax = 0.1
xmax = 0.1
uniform_refine = 0
[]
[Adaptivity]
max_h_level = 4
initial_steps = 6
initial_marker = error_marker
cycles_per_step = 2
marker = error_marker
[Indicators]
[phi_jump]
type = GradientJumpIndicator
variable = phi
[]
[]
[Markers]
[error_marker]
type = ErrorFractionMarker
indicator = phi_jump
refine = 0.8
coarsen = 0.1
[]
[]
[]
[Variables]
[temperature]
initial_condition = 300
[]
[]
[AuxVariables]
[phi]
[]
[por_var]
family = MONOMIAL
order = CONSTANT
[]
[]
[AuxKernels]
[corrosion]
type = RandomCorrosion
variable = phi
reference_temperature = 300
temperature = temperature_in
execute_on = 'INITIAL TIMESTEP_END'
[]
[por_var]
type = ADMaterialRealAux
variable = por_var
property = porosity
execute_on = 'INITIAL TIMESTEP_END'
[]
[]
[Kernels]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[]
[BCs]
[left]
type = PostprocessorDirichletBC
variable = temperature
boundary = left
postprocessor = temperature_in
[]
[right]
type = NeumannBC
variable = temperature
boundary = right
value = 100 # prescribed flux
[]
[]
[Materials]
[column]
type = PackedColumn
temperature = temperature
radius = 1 # mm
phase = phi
[]
[]
[Postprocessors]
[temperature_in]
type = Receiver
default = 301
[]
[k_eff]
type = ThermalConductivity
variable = temperature
T_hot = temperature_in
flux = 100
dx = 0.1
boundary = right
length_scale = 1
k0 = 12.05
execute_on = 'INITIAL TIMESTEP_END'
[]
[por_var]
type = ElementAverageValue
variable = por_var
execute_on = 'INITIAL TIMESTEP_END'
[]
[t_right]
type = SideAverageValue
boundary = right
variable = temperature
execute_on = 'INITIAL TIMESTEP_END'
[]
[]
[Executioner]
type = Transient
end_time = 1000
dt = 1
steady_state_tolerance = 1e-9
steady_state_detection = true
solve_type = NEWTON
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
automatic_scaling = true
[]
[Outputs]
execute_on = 'initial timestep_end'
exodus = true
[]
[ICs]
[close_pack]
radius = 0.01 # meter
outvalue = 0 # water
variable = phi
invalue = 1 # steel
type = ClosePackIC
[]
[]
Step 10: Run and Visualize Micro-scale
cd ~/projects/moose/tutorials/darcy-thermo_mech/step10_multiapps
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step10_micro.i
Step 10: Micro-scale Results
PackedColumn.h
#pragma once
#include "ADMaterial.h"
// A helper class from MOOSE that linear interpolates x,y data
#include "LinearInterpolation.h"
/**
* Material-derived objects override the computeQpProperties()
* function. They must declare and compute material properties for
* use by other objects in the calculation such as Kernels and
* BoundaryConditions.
*/
class PackedColumn : public ADMaterial
{
public:
static InputParameters validParams();
PackedColumn(const InputParameters & parameters);
protected:
/**
* Necessary override. This is where the values of the properties
* are computed.
*/
virtual void computeQpProperties() override;
/**
* Helper function for reading CSV data for use in an interpolator object.
*/
bool initInputData(const std::string & param_name, ADLinearInterpolation & interp);
/// The radius of the spheres in the column
const Function & _input_radius;
/// The input porosity
const Function & _input_porosity;
/// Temperature
const ADVariableValue & _temperature;
/// Compute permeability based on the radius (mm)
LinearInterpolation _permeability_interpolation;
/// Fluid viscosity
bool _use_fluid_mu_interp;
const Real & _fluid_mu;
ADLinearInterpolation _fluid_mu_interpolation;
/// Fluid thermal conductivity
bool _use_fluid_k_interp = false;
const Real & _fluid_k;
ADLinearInterpolation _fluid_k_interpolation;
/// Fluid density
bool _use_fluid_rho_interp = false;
const Real & _fluid_rho;
ADLinearInterpolation _fluid_rho_interpolation;
/// Fluid specific heat
bool _use_fluid_cp_interp;
const Real & _fluid_cp;
ADLinearInterpolation _fluid_cp_interpolation;
/// Fluid thermal expansion coefficient
bool _use_fluid_cte_interp;
const Real & _fluid_cte;
ADLinearInterpolation _fluid_cte_interpolation;
/// Solid thermal conductivity
bool _use_solid_k_interp = false;
const Real & _solid_k;
ADLinearInterpolation _solid_k_interpolation;
/// Solid density
bool _use_solid_rho_interp = false;
const Real & _solid_rho;
ADLinearInterpolation _solid_rho_interpolation;
/// Fluid specific heat
bool _use_solid_cp_interp;
const Real & _solid_cp;
ADLinearInterpolation _solid_cp_interpolation;
/// Solid thermal expansion coefficient
bool _use_solid_cte_interp;
const Real & _solid_cte;
ADLinearInterpolation _solid_cte_interpolation;
/// The permeability (K)
ADMaterialProperty<Real> & _permeability;
/// The porosity (eps)
ADMaterialProperty<Real> & _porosity;
/// The viscosity of the fluid (mu)
ADMaterialProperty<Real> & _viscosity;
/// The bulk thermal conductivity
ADMaterialProperty<Real> & _thermal_conductivity;
/// The bulk heat capacity
ADMaterialProperty<Real> & _specific_heat;
/// The bulk density
ADMaterialProperty<Real> & _density;
/// The bulk thermal expansion coefficient
ADMaterialProperty<Real> & _thermal_expansion;
/// Flag for using the phase for porosity
bool _use_phase_variable;
/// The coupled phase variable
const VariableValue & _phase;
/// Flag for using a variable for thermal conductivity
bool _use_variable_conductivity;
/// The coupled thermal conductivity
const VariableValue & _conductivity_variable;
};
PackedColumn.C
#include "PackedColumn.h"
#include "Function.h"
#include "DelimitedFileReader.h"
registerMooseObject("DarcyThermoMechApp", PackedColumn);
InputParameters
PackedColumn::validParams()
{
InputParameters params = ADMaterial::validParams();
params.addRequiredCoupledVar("temperature", "The temperature (C) of the fluid.");
// Add a parameter to get the radius of the spheres in the column
// (used later to interpolate permeability).
params.addParam<FunctionName>("radius",
"1.0",
"The radius of the steel spheres (mm) that are packed in the "
"column for computing permeability.");
// http://en.wikipedia.org/wiki/Close-packing_of_equal_spheres
params.addParam<FunctionName>(
"porosity", 0.25952, "Porosity of porous media, default is for closed packed spheres.");
// Fluid properties
params.addParam<Real>(
"fluid_viscosity", 1.002e-3, "Fluid viscosity (Pa s); default is for water at 20C).");
params.addParam<FileName>(
"fluid_viscosity_file",
"The name of a file containing the fluid viscosity (Pa-s) as a function of temperature "
"(C); if provided the constant value is ignored.");
params.addParam<Real>("fluid_thermal_conductivity",
0.59803,
"Fluid thermal conductivity (W/(mK); default is for water at 20C).");
params.addParam<FileName>(
"fluid_thermal_conductivity_file",
"The name of a file containing fluid thermal conductivity (W/(mK)) as a function of "
"temperature (C); if provided the constant value is ignored.");
params.addParam<Real>(
"fluid_density", 998.21, "Fluid density (kg/m^3); default is for water at 20C).");
params.addParam<FileName>("fluid_density_file",
"The name of a file containing fluid density (kg/m^3) as a function "
"of temperature (C); if provided the constant value is ignored.");
params.addParam<Real>(
"fluid_specific_heat", 4157.0, "Fluid specific heat (J/(kgK); default is for water at 20C).");
params.addParam<FileName>(
"fluid_specific_heat_file",
"The name of a file containing fluid specific heat (J/(kgK) as a function of temperature "
"(C); if provided the constant value is ignored.");
params.addParam<Real>("fluid_thermal_expansion",
2.07e-4,
"Fluid thermal expansion coefficient (1/K); default is for water at 20C).");
params.addParam<FileName>("fluid_thermal_expansion_file",
"The name of a file containing fluid thermal expansion coefficient "
"(1/K) as a function of temperature "
"(C); if provided the constant value is ignored.");
// Solid properties
// https://en.wikipedia.org/wiki/Stainless_steel#Properties
params.addParam<Real>("solid_thermal_conductivity",
15.0,
"Solid thermal conductivity (W/(mK); default is for AISI/ASTIM 304 "
"stainless steel at 20C).");
params.addParam<FileName>(
"solid_thermal_conductivity_file",
"The name of a file containing solid thermal conductivity (W/(mK)) as a function of "
"temperature (C); if provided the constant value is ignored.");
params.addParam<Real>(
"solid_density",
7900,
"Solid density (kg/m^3); default is for AISI/ASTIM 304 stainless steel at 20C).");
params.addParam<FileName>("solid_density_file",
"The name of a file containing solid density (kg/m^3) as a function "
"of temperature (C); if provided the constant value is ignored.");
params.addParam<Real>(
"solid_specific_heat",
500,
"Solid specific heat (J/(kgK); default is for AISI/ASTIM 304 stainless steel at 20C).");
params.addParam<FileName>(
"solid_specific_heat_file",
"The name of a file containing solid specific heat (J/(kgK) as a function of temperature "
"(C); if provided the constant value is ignored.");
params.addParam<Real>("solid_thermal_expansion",
17.3e-6,
"Solid thermal expansion coefficient (1/K); default is for water at 20C).");
params.addParam<FileName>("solid_thermal_expansion_file",
"The name of a file containing solid thermal expansion coefficient "
"(1/K) as a function of temperature "
"(C); if provided the constant value is ignored.");
// Optional phase variable
params.addCoupledVar("phase",
"The variable indicating the phase (steel=1 or water=0). If "
"supplied this is used to compute the porosity instead of the "
"supplied value.");
// Optional thermal conductivity variable
params.addCoupledVar("thermal_conductivity",
"When supplied the variable be will be used for "
"thermal conductivity rather than being computed.");
return params;
}
PackedColumn::PackedColumn(const InputParameters & parameters)
: ADMaterial(parameters),
// Get the one parameter from the input file
_input_radius(getFunction("radius")),
_input_porosity(getFunction("porosity")),
_temperature(adCoupledValue("temperature")),
// Fluid
_fluid_mu(getParam<Real>("fluid_viscosity")),
_fluid_k(getParam<Real>("fluid_thermal_conductivity")),
_fluid_rho(getParam<Real>("fluid_density")),
_fluid_cp(getParam<Real>("fluid_specific_heat")),
_fluid_cte(getParam<Real>("fluid_thermal_expansion")),
// Solid
_solid_k(getParam<Real>("solid_thermal_conductivity")),
_solid_rho(getParam<Real>("solid_density")),
_solid_cp(getParam<Real>("solid_specific_heat")),
_solid_cte(getParam<Real>("solid_thermal_expansion")),
// Material Properties being produced by this object
_permeability(declareADProperty<Real>("permeability")),
_porosity(declareADProperty<Real>("porosity")),
_viscosity(declareADProperty<Real>("viscosity")),
_thermal_conductivity(declareADProperty<Real>("thermal_conductivity")),
_specific_heat(declareADProperty<Real>("specific_heat")),
_density(declareADProperty<Real>("density")),
_thermal_expansion(declareADProperty<Real>("thermal_expansion")),
// Optional phase variable
_use_phase_variable(isParamValid("phase")),
_phase(_use_phase_variable ? coupledValue("phase") : _zero),
// Optional thermal conductivity variable
_use_variable_conductivity(isParamValid("thermal_conductivity")),
_conductivity_variable(_use_variable_conductivity ? coupledValue("thermal_conductivity")
: _zero)
{
// Set data for permeability interpolation
std::vector<Real> sphere_sizes = {1, 3};
std::vector<Real> permeability = {0.8451e-9, 8.968e-9};
_permeability_interpolation.setData(sphere_sizes, permeability);
// Fluid viscosity, thermal conductivity, density, and specific heat
_use_fluid_mu_interp = initInputData("fluid_viscosity_file", _fluid_mu_interpolation);
_use_fluid_k_interp = initInputData("fluid_thermal_conductivity_file", _fluid_k_interpolation);
_use_fluid_rho_interp = initInputData("fluid_density_file", _fluid_rho_interpolation);
_use_fluid_cp_interp = initInputData("fluid_specific_heat_file", _fluid_cp_interpolation);
_use_fluid_cte_interp = initInputData("fluid_thermal_expansion_file", _fluid_cte_interpolation);
// Solid thermal conductivity, density, and specific heat
_use_solid_k_interp = initInputData("solid_thermal_conductivity_file", _solid_k_interpolation);
_use_solid_rho_interp = initInputData("solid_density_file", _solid_rho_interpolation);
_use_solid_cp_interp = initInputData("solid_specific_heat_file", _solid_cp_interpolation);
_use_solid_cte_interp = initInputData("solid_thermal_expansion_file", _solid_cte_interpolation);
}
void
PackedColumn::computeQpProperties()
{
// Current temperature
ADReal temp = _temperature[_qp] - 273.15;
// Permeability
Real radius_value = _input_radius.value(_t, _q_point[_qp]);
mooseAssert(radius_value >= 1 && radius_value <= 3,
"The radius range must be in the range [1, 3], but " << radius_value << " provided.");
_permeability[_qp] = _permeability_interpolation.sample(radius_value);
// Porosity
if (_use_phase_variable)
_porosity[_qp] = 1 - _phase[_qp];
else
{
Real porosity_value = _input_porosity.value(_t, _q_point[_qp]);
mooseAssert(porosity_value > 0 && porosity_value <= 1,
"The porosity range must be in the range (0, 1], but " << porosity_value
<< " provided.");
_porosity[_qp] = porosity_value;
}
// Fluid properties
_viscosity[_qp] = _use_fluid_mu_interp ? _fluid_mu_interpolation.sample(temp) : _fluid_mu;
ADReal fluid_rho = _use_fluid_rho_interp ? _fluid_rho_interpolation.sample(temp) : _fluid_rho;
ADReal fluid_cp = _use_fluid_cp_interp ? _fluid_cp_interpolation.sample(temp) : _fluid_cp;
ADReal fluid_cte = _use_fluid_cte_interp ? _fluid_cte_interpolation.sample(temp) : _fluid_cte;
// Solid properties
ADReal solid_rho = _use_solid_rho_interp ? _solid_rho_interpolation.sample(temp) : _solid_rho;
ADReal solid_cp = _use_solid_cp_interp ? _solid_cp_interpolation.sample(temp) : _solid_cp;
ADReal solid_cte = _use_solid_cte_interp ? _solid_cte_interpolation.sample(temp) : _solid_cte;
// Compute the heat conduction material properties as a linear combination of
// the material properties for fluid and steel.
if (_use_variable_conductivity)
_thermal_conductivity[_qp] = _conductivity_variable[_qp];
else
{
ADReal fluid_k = _use_fluid_k_interp ? _fluid_k_interpolation.sample(temp) : _fluid_k;
ADReal solid_k = _use_solid_k_interp ? _solid_k_interpolation.sample(temp) : _solid_k;
_thermal_conductivity[_qp] = _porosity[_qp] * fluid_k + (1.0 - _porosity[_qp]) * solid_k;
}
_density[_qp] = _porosity[_qp] * fluid_rho + (1.0 - _porosity[_qp]) * solid_rho;
_specific_heat[_qp] = _porosity[_qp] * fluid_cp + (1.0 - _porosity[_qp]) * solid_cp;
_thermal_expansion[_qp] = _porosity[_qp] * fluid_cte + (1.0 - _porosity[_qp]) * solid_cte;
}
bool
PackedColumn::initInputData(const std::string & param_name, ADLinearInterpolation & interp)
{
if (isParamValid(param_name))
{
const std::string & filename = getParam<FileName>(param_name);
MooseUtils::DelimitedFileReader reader(filename, &_communicator);
reader.setComment("#");
reader.read();
interp.setData(reader.getData(0), reader.getData(1));
return true;
}
return false;
}
Step 10: Multi-scale Input File
[GlobalParams]
displacements = 'disp_r disp_z'
[]
[Mesh]
type = GeneratedMesh
dim = 2
nx = 10
ny = 100
ymax = 0.304 # Length of test chamber
xmax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[AuxVariables]
[k_eff]
initial_condition = 15.0 # water at 20C
[]
[velocity]
order = CONSTANT
family = MONOMIAL_VEC
[]
[]
[Modules/TensorMechanics/Master]
[all]
# This block adds all of the proper Kernels, strain calculators, and Variables
# for TensorMechanics in the correct coordinate system (autodetected)
add_variables = true
strain = FINITE
eigenstrain_names = eigenstrain
use_automatic_differentiation = true
generate_output = 'vonmises_stress elastic_strain_xx elastic_strain_yy strain_xx strain_yy'
[]
[]
[Kernels]
[darcy_pressure]
type = DarcyPressure
variable = pressure
[]
[heat_conduction]
type = ADHeatConduction
variable = temperature
[]
[heat_conduction_time_derivative]
type = ADHeatConductionTimeDerivative
variable = temperature
[]
[heat_convection]
type = DarcyAdvection
variable = temperature
pressure = pressure
[]
[]
[AuxKernels]
[velocity]
type = DarcyVelocity
variable = velocity
execute_on = timestep_end
pressure = pressure
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = bottom
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = top
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = bottom
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = top
[]
[hold_inlet]
type = DirichletBC
variable = disp_z
boundary = bottom
value = 0
[]
[hold_center]
type = DirichletBC
variable = disp_r
boundary = left
value = 0
[]
[hold_outside]
type = DirichletBC
variable = disp_r
boundary = right
value = 0
[]
[]
[Materials]
viscosity_file = data/water_viscosity.csv
density_file = data/water_density.csv
specific_heat_file = data/water_specific_heat.csv
thermal_expansion_file = data/water_thermal_expansion.csv
[column]
type = PackedColumn
temperature = temperature
radius = 1
thermal_conductivity = k_eff # Use the AuxVariable instead of calculating
fluid_viscosity_file = ${viscosity_file}
fluid_density_file = ${density_file}
fluid_specific_heat_file = ${specific_heat_file}
fluid_thermal_expansion_file = ${thermal_expansion_file}
[]
[elasticity_tensor]
type = ADComputeIsotropicElasticityTensor
youngs_modulus = 200e9 # (Pa) from wikipedia
poissons_ratio = .3 # from wikipedia
[]
[elastic_stress]
type = ADComputeFiniteStrainElasticStress
[]
[thermal_strain]
type = ADComputeThermalExpansionEigenstrain
stress_free_temperature = 300
thermal_expansion_coeff = 1e-6
eigenstrain_name = eigenstrain
temperature = temperature
[]
[]
[Postprocessors]
[average_temperature]
type = ElementAverageValue
variable = temperature
[]
[]
[Executioner]
type = Transient
start_time = -1
end_time = 200
steady_state_tolerance = 1e-7
steady_state_detection = true
dt = 0.25
solve_type = PJFNK
automatic_scaling = true
compute_scaling_once = false
petsc_options_iname = '-pc_type -pc_hypre_type -ksp_gmres_restart'
petsc_options_value = 'hypre boomeramg 500'
line_search = none
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[MultiApps]
[micro]
type = TransientMultiApp
app_type = DarcyThermoMechApp
positions = '0.01285 0.0 0
0.01285 0.0608 0
0.01285 0.1216 0
0.01285 0.1824 0
0.01285 0.2432 0
0.01285 0.304 0'
input_files = step10_micro.i
execute_on = 'timestep_end'
[]
[]
[Transfers]
[keff_from_sub]
type = MultiAppPostprocessorInterpolationTransfer
direction = from_multiapp
multi_app = micro
variable = k_eff
power = 1
postprocessor = k_eff
execute_on = 'timestep_end'
[]
[temperature_to_sub]
type = MultiAppVariableValueSamplePostprocessorTransfer
direction = to_multiapp
multi_app = micro
source_variable = temperature
postprocessor = temperature_in
execute_on = 'timestep_end'
[]
[]
[Controls]
[multiapp]
type = TimePeriod
disable_objects = 'MultiApps::micro Transfers::keff_from_sub Transfers::temperature_to_sub'
start_time = '0'
execute_on = 'initial'
[]
[]
[Outputs]
[out]
type = Exodus
elemental_as_nodal = true
[]
[]
Step 10: Run and Visualize Multi-scale
cd ~/projects/moose/tutorials/darcy-thermo_mech/step10_multiapps
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step10.i
Step 10: Multi-scale Results
Step 11: Custom Syntax
Add custom syntax to build objects that are common to all Darcy thermal mecahnical problems:
Velocity auxiliary variables and kernels
Pressure kernel
Temperature kernels
Action System
A system for the programmatic creation of simulation objects and input file syntax.
Creating an Action
Inherit from Action or MooseObjectAction and override the act() method.
Notice, the constructor uses a copy of an InputParameters object. This is by design to allow the parameters to be manipulated and re-used during object creation.
Action Object
An action design to build specific objects, such as the case in Step 9: Mechanics for tensor mechanics.
[Modules/TensorMechanics/Master]
[Modules/TensorMechanics/Master]
[Modules/TensorMechanics/Master]
[all]
# This block adds all of the proper Kernels, strain calculators, and Variables
# for TensorMechanics in the correct coordinate system (autodetected)
add_variables = true
strain = FINITE
eigenstrain_names = eigenstrain
use_automatic_differentiation = true
generate_output = 'vonmises_stress elastic_strain_xx elastic_strain_yy strain_xx strain_yy'
[]
[]
[]
[]
Syntax and Tasks
The MOOSE action system operates on tasks, each task is connected to one or many actions.
For each task the act() method is called for each task, thus the act method can be used to create any number of objects.
In general, the following macros are called within an application registerAll method to create the necessary syntax and tasks to build the desired objects.
registerSyntax(action, action_syntax)
Creates input file syntax provided in "action_syntax" and associates with the "action" provided
registerSyntaxTask(action, action_syntax, task)
Same as above, but also creates a named task that will be executed.
registerTask(name, is_required)
Creates a named task that actions can be associated.
addTaskDependency(action, depends_on)
Create a dependency between two tasks to help control the order of operation of task execution
MooseObjectAction Object
An action designed to build one or many other MooseObjects, such as in the case of the [Dampers] block.
AddDamperAction.h
#pragma once
#include "MooseObjectAction.h"
class AddDamperAction;
template <>
InputParameters validParams<AddDamperAction>();
class AddDamperAction : public MooseObjectAction
{
public:
static InputParameters validParams();
AddDamperAction(InputParameters params);
virtual void act() override;
};
AddDamperAction.C
#include "AddDamperAction.h"
#include "FEProblem.h"
registerMooseAction("MooseApp", AddDamperAction, "add_damper");
defineLegacyParams(AddDamperAction);
InputParameters
AddDamperAction::validParams()
{
InputParameters params = MooseObjectAction::validParams();
params.addClassDescription("Add a Damper object to the simulation.");
return params;
}
AddDamperAction::AddDamperAction(InputParameters params) : MooseObjectAction(params) {}
void
AddDamperAction::act()
{
_problem->addDamper(_type, _name, _moose_object_pars);
}
Moose.C
registerSyntax("AddDamperAction", "Dampers/*");
Step 11: Custom Syntax
(continued)
SetupDarcySimulation.h
#pragma once
// MOOSE includes
#include "Action.h"
/**
* An action for creating the necessary objects to perform a thermal mechanics problem using
* Darcy's equation.
* */
class SetupDarcySimulation : public Action
{
public:
static InputParameters validParams();
SetupDarcySimulation(InputParameters params);
virtual void act() override;
protected:
const bool _compute_velocity;
const bool _compute_pressure;
const bool _compute_temperature;
};
SetupDarcySimulation.C
#include "SetupDarcySimulation.h"
// MOOSE includes
#include "FEProblem.h"
#include "AuxiliarySystem.h"
// libMesh includes
#include "libmesh/fe.h"
registerMooseAction("DarcyThermoMechApp", SetupDarcySimulation, "setup_darcy");
InputParameters
SetupDarcySimulation::validParams()
{
InputParameters params = Action::validParams();
params.addParam<VariableName>("pressure", "pressure", "The pressure variable.");
params.addParam<VariableName>("temperature", "temperature", "The temperature variable.");
params.addParam<bool>(
"compute_velocity", true, "Enable the auxiliary calculation of velocity from pressure.");
params.addParam<bool>("compute_pressure", true, "Enable the computation of pressure.");
params.addParam<bool>("compute_temperature", true, "Enable the computation of temperature.");
return params;
}
SetupDarcySimulation::SetupDarcySimulation(InputParameters parameters)
: Action(parameters),
_compute_velocity(getParam<bool>("compute_velocity")),
_compute_pressure(getParam<bool>("compute_pressure")),
_compute_temperature(getParam<bool>("compute_temperature"))
{
}
void
SetupDarcySimulation::act()
{
// Actual names of input variables
const std::string pressure = getParam<VariableName>("pressure");
const std::string temperature = getParam<VariableName>("temperature");
// Velocity AuxVariables
if (_compute_velocity && _current_task == "add_aux_variable")
{
InputParameters var_params = _factory.getValidParams("VectorMooseVariable");
var_params.set<MooseEnum>("family") = "MONOMIAL_VEC";
var_params.set<MooseEnum>("order") = "CONSTANT";
_problem->addAuxVariable("VectorMooseVariable", "velocity", var_params);
}
// Velocity AuxKernels
else if (_compute_velocity && _current_task == "add_aux_kernel")
{
InputParameters params = _factory.getValidParams("DarcyVelocity");
params.set<ExecFlagEnum>("execute_on") = EXEC_TIMESTEP_END;
params.set<std::vector<VariableName>>("pressure") = {pressure};
params.set<AuxVariableName>("variable") = "velocity";
_problem->addAuxKernel("DarcyVelocity", "velocity", params);
}
// Kernels
else if (_current_task == "add_kernel")
{
// Flags for aux variables
const bool is_pressure_aux = _problem->getAuxiliarySystem().hasVariable(pressure);
const bool is_temperature_aux = _problem->getAuxiliarySystem().hasVariable(temperature);
// Pressure
if (_compute_pressure && !is_pressure_aux)
{
InputParameters params = _factory.getValidParams("DarcyPressure");
params.set<NonlinearVariableName>("variable") = pressure;
_problem->addKernel("DarcyPressure", "darcy_pressure", params);
}
// Temperature
if (_compute_temperature && !is_temperature_aux)
{
{
InputParameters params = _factory.getValidParams("ADHeatConduction");
params.set<NonlinearVariableName>("variable") = temperature;
_problem->addKernel("ADHeatConduction", "heat_conduction", params);
}
{
InputParameters params = _factory.getValidParams("ADHeatConductionTimeDerivative");
params.set<NonlinearVariableName>("variable") = temperature;
_problem->addKernel("ADHeatConductionTimeDerivative", "heat_conduction_time", params);
}
{
InputParameters params = _factory.getValidParams("DarcyAdvection");
params.set<NonlinearVariableName>("variable") = temperature;
params.set<std::vector<VariableName>>("pressure") = {pressure};
_problem->addKernel("DarcyAdvection", "heat_advection", params);
}
}
}
}
DarcyThermoMechApp.h
#pragma once
#include "MooseApp.h"
class DarcyThermoMechApp : public MooseApp
{
public:
static InputParameters validParams();
DarcyThermoMechApp(InputParameters parameters);
static void registerApps();
static void registerAll(Factory & factory, ActionFactory & action_factory, Syntax & syntax);
};
DarcyThermoMechApp.C
// Tutorial Includes
#include "DarcyThermoMechApp.h"
// MOOSE Includes
#include "AppFactory.h"
#include "MooseSyntax.h"
#include "ModulesApp.h"
template <>
InputParameters
validParams<DarcyThermoMechApp>()
{
InputParameters params = validParams<MooseApp>();
params.set<bool>("automatic_automatic_scaling") = false;
return params;
}
DarcyThermoMechApp::DarcyThermoMechApp(InputParameters parameters) : MooseApp(parameters)
{
DarcyThermoMechApp::registerAll(_factory, _action_factory, _syntax);
}
void
DarcyThermoMechApp::registerApps()
{
registerApp(DarcyThermoMechApp);
}
void
DarcyThermoMechApp::registerAll(Factory & factory, ActionFactory & action_factory, Syntax & syntax)
{
Registry::registerObjectsTo(factory, {"DarcyThermoMechApp"});
Registry::registerActionsTo(action_factory, {"DarcyThermoMechApp"});
ModulesApp::registerAll(factory, action_factory, syntax);
registerSyntaxTask("SetupDarcySimulation", "DarcyThermoMech", "add_aux_variable");
registerSyntaxTask("SetupDarcySimulation", "DarcyThermoMech", "add_aux_kernel");
registerSyntaxTask("SetupDarcySimulation", "DarcyThermoMech", "add_kernel");
}
Step 11: Input File
[GlobalParams]
displacements = 'disp_r disp_z'
[]
[Mesh]
type = GeneratedMesh
dim = 2
ny = 200
nx = 10
ymax = 0.304 # Length of test chamber
xmax = 0.0257 # Test chamber radius
[]
[Variables]
[pressure]
[]
[temperature]
initial_condition = 300 # Start at room temperature
[]
[]
[DarcyThermoMech]
[]
[Modules/TensorMechanics/Master]
[all]
# This block adds all of the proper Kernels, strain calculators, and Variables
# for TensorMechanics in the correct coordinate system (autodetected)
add_variables = true
strain = FINITE
eigenstrain_names = eigenstrain
use_automatic_differentiation = true
generate_output = 'vonmises_stress elastic_strain_xx elastic_strain_yy strain_xx strain_yy'
[]
[]
[BCs]
[inlet]
type = DirichletBC
variable = pressure
boundary = bottom
value = 4000 # (Pa) From Figure 2 from paper. First data point for 1mm spheres.
[]
[outlet]
type = DirichletBC
variable = pressure
boundary = top
value = 0 # (Pa) Gives the correct pressure drop from Figure 2 for 1mm spheres
[]
[inlet_temperature]
type = FunctionDirichletBC
variable = temperature
boundary = bottom
function = 'if(t<0,350+50*t,350)'
[]
[outlet_temperature]
type = HeatConductionOutflow
variable = temperature
boundary = top
[]
[hold_inlet]
type = DirichletBC
variable = disp_z
boundary = bottom
value = 0
[]
[hold_center]
type = DirichletBC
variable = disp_r
boundary = left
value = 0
[]
[hold_outside]
type = DirichletBC
variable = disp_r
boundary = right
value = 0
[]
[]
[Materials]
viscosity_file = data/water_viscosity.csv
density_file = data/water_density.csv
thermal_conductivity_file = data/water_thermal_conductivity.csv
specific_heat_file = data/water_specific_heat.csv
thermal_expansion_file = data/water_thermal_expansion.csv
[column]
type = PackedColumn
block = 0
temperature = temperature
radius = 1.15
fluid_viscosity_file = ${viscosity_file}
fluid_density_file = ${density_file}
fluid_thermal_conductivity_file = ${thermal_conductivity_file}
fluid_specific_heat_file = ${specific_heat_file}
fluid_thermal_expansion_file = ${thermal_expansion_file}
[]
[elasticity_tensor]
type = ADComputeIsotropicElasticityTensor
youngs_modulus = 200e9 # (Pa) from wikipedia
poissons_ratio = .3 # from wikipedia
[]
[elastic_stress]
type = ADComputeFiniteStrainElasticStress
[]
[thermal_strain]
type = ADComputeThermalExpansionEigenstrain
stress_free_temperature = 300
eigenstrain_name = eigenstrain
temperature = temperature
thermal_expansion_coeff = 1e-5
[]
[]
[Postprocessors]
[average_temperature]
type = ElementAverageValue
variable = temperature
[]
[]
[Problem]
type = FEProblem
coord_type = RZ
[]
[Executioner]
type = Transient
start_time = -1
end_time = 200
steady_state_tolerance = 1e-7
steady_state_detection = true
dt = 0.25
solve_type = PJFNK
automatic_scaling = true
compute_scaling_once = false
petsc_options_iname = '-pc_type -pc_hypre_type -ksp_gmres_restart'
petsc_options_value = 'hypre boomeramg 500'
line_search = none
[TimeStepper]
type = FunctionDT
function = 'if(t<0,0.1,0.25)'
[]
[]
[Outputs]
[out]
type = Exodus
elemental_as_nodal = true
[]
[]
Step 11: Run and Visualize
cd ~/projects/moose/tutorials/darcy-thermo_mech/step11_action
make -j 12 # use number of processors for you system
cd problems
~/projects/moose/python/peacock/peacock -i step11.i
Step 11: Results
Method of Manufactured Solutions (MMS)
The Method of Manufactured Solutions (MMS) is a useful tool for code verification (making sure that a mathematical model is properly solved)
MMS works by assuming a solution, substituting it into the PDE, and obtaining a forcing term
The modified PDE (with forcing term added) is then solved numerically; the result can be compared to the assumed solution
By checking the norm of the error on successively finer grids you can verify your code obtains the theoretical convergence rates
Example 14: MMS
PDE:
Assumed solution:
Forcing function:
Need to solve:
Example 14: Input File
[Mesh]
type = GeneratedMesh
dim = 2
nx = 32
ny = 32
xmin = 0.0
xmax = 1.0
ymin = 0.0
ymax = 1.0
[]
[Variables]
[forced]
order = FIRST
family = LAGRANGE
[]
[]
[Functions]
# A ParsedFunction allows us to supply analytic expressions directly in the input file
[exact]
type = ParsedFunction
value = sin(alpha*pi*x)
vars = alpha
vals = 16
[]
# This function is an actual compiled function
[force]
type = ExampleFunction
alpha = 16
[]
[]
[Kernels]
[diff]
type = ADDiffusion
variable = forced
[]
# This Kernel can take a function name to use
[forcing]
type = ADBodyForce
variable = forced
function = force
[]
[]
[BCs]
# The BC can take a function name to use
[all]
type = FunctionDirichletBC
variable = forced
boundary = 'bottom right top left'
function = exact
[]
[]
[Executioner]
type = Steady
solve_type = NEWTON
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
[]
[Postprocessors]
[h]
type = AverageElementSize
[]
[error]
type = ElementL2Error
variable = forced
function = exact
[]
[]
[Outputs]
execute_on = 'timestep_end'
exodus = true
csv = true
[]
Example 14: Run via Command-line
cd ~/projects/moose/examples/ex14_pps
make -j 12 # use number of processors for you system
./ex14-opt -i ex14.i
MMS Python Package
export PYTHONPATH=$PYTHONPATH:~/projects/moose/python
Example 14: Exact Solution
mms_exact.py
#!/usr/bin/env python3
import mms
fs,ss = mms.evaluate('-div(grad(u))', 'sin(a*pi*x)', scalars=['a'])
mms.print_fparser(fs)
mms.print_hit(fs, 'force')
mms.print_hit(ss, 'exact')
cd ~/projects/moose/examples/ex14_pps
./mms_exact.py
pi^2*a^2*sin(x*pi*a)
[force]
type = ParsedFunction
value = 'pi^2*a^2*sin(x*pi*a)'
vars = 'a'
vals = '1.0'
[]
[exact]
type = ParsedFunction
value = 'sin(x*pi*a)'
vars = 'a'
vals = '1.0'
[]
Error Analysis
To compare two solutions (or a solution and an analytical solution) and , the following expressions are frequently used:
From finite element theory, the convergence rates are known for these quantities on successively refined grids. These two calculations are computed in MOOSE by utilizing the ElementL2Error or ElementH1SemiError postprocessor objects, respectively.
Example 14: Convergence Study
mms_spatial.py
#!/usr/bin/env python3
import mms
df1 = mms.run_spatial('ex14.i', 4, executable='./ex14-opt')
df2 = mms.run_spatial('ex14.i', 4, 'Mesh/second_order=true', 'Variables/forced/order=SECOND', executable='./ex14-opt')
fig = mms.ConvergencePlot(xlabel='Element Size ($h$)', ylabel='$L_2$ Error')
fig.plot(df1, label='1st Order', marker='o', markersize=8)
fig.plot(df2, label='2nd Order', marker='o', markersize=8)
fig.save('ex14_mms.png')
Example 14: Convergence Results
cd ~/projects/moose/examples/ex14_pps
./mms_spatial.py

Debugging
A debugger is often more effective than print statements in helping to find bugs
Many debuggers exist: LLDB, GDB, Totalview, ddd, Intel Debugger, etc.
Typically it is best to use a debugger that is associated with your compiler
Here LLDB/GDB are used, both are simple to use and are included in the MOOSE package
Segmentation Fault
A "Segmentation fault," "Segfault," or "Signal 11" error denotes a memory bug (often array access out of bounds).
Segmentation fault: 11
A segfault is a "good" error to have, because a debugger can easily pinpoint the problem.
Example 21: Input File
[Mesh]
file = reactor.e
#Let's assign human friendly names to the blocks on the fly
block_id = '1 2'
block_name = 'fuel deflector'
boundary_id = '4 5'
boundary_name = 'bottom top'
[]
[Variables]
#Use active lists to help debug problems. Switching on and off
#different Kernels or Variables is extremely useful!
active = 'diffused convected'
[diffused]
order = FIRST
family = LAGRANGE
initial_condition = 0.5
[]
[convected]
order = FIRST
family = LAGRANGE
initial_condition = 0.0
[]
[]
[Kernels]
#This Kernel consumes a real-gradient material property from the active material
active = 'convection diff_convected example_diff time_deriv_diffused time_deriv_convected'
[convection]
type = ExampleConvection
variable = convected
[]
[diff_convected]
type = Diffusion
variable = convected
[]
[example_diff]
type = ExampleDiffusion
variable = diffused
coupled_coef = convected
[]
[time_deriv_diffused]
type = TimeDerivative
variable = diffused
[]
[time_deriv_convected]
type = TimeDerivative
variable = convected
[]
[]
[BCs]
[bottom_diffused]
type = DirichletBC
variable = diffused
boundary = 'bottom'
value = 0
[]
[top_diffused]
type = DirichletBC
variable = diffused
boundary = 'top'
value = 5
[]
[bottom_convected]
type = DirichletBC
variable = convected
boundary = 'bottom'
value = 0
[]
[top_convected]
type = NeumannBC
variable = convected
boundary = 'top'
value = 1
[]
[]
[Materials]
[example]
type = ExampleMaterial
block = 'fuel'
diffusion_gradient = 'diffused'
#Approximate Parabolic Diffusivity
independent_vals = '0 0.25 0.5 0.75 1.0'
dependent_vals = '1e-2 5e-3 1e-3 5e-3 1e-2'
[]
[example1]
type = ExampleMaterial
block = 'deflector'
diffusion_gradient = 'diffused'
# Constant Diffusivity
independent_vals = '0 1.0'
dependent_vals = '1e-1 1e-1'
[]
[]
[Executioner]
type = Transient
solve_type = 'PJFNK'
petsc_options_iname = '-pc_type -pc_hypre_type'
petsc_options_value = 'hypre boomeramg'
dt = 0.1
num_steps = 10
[]
[Outputs]
execute_on = 'timestep_end'
exodus = true
[]
Example 21: Run Input File
cd ~/projects/moose/examples/ex21_debugging
make -j12
./ex21-opt -i ex21.i
Time Step 0, time = 0
dt = 0
Time Step 1, time = 0.1
dt = 0.1
Segmentation fault: 11
Debug Compile
To use a debugger with a MOOSE-based application, it must be compiled in something other than optimized mode (opt); debug (dbg) mode is recommended because it will produce full line number information in stack traces:
cd ~/projects/moose/examples/ex21_debugging
METHOD=dbg make -j12
This will create a "debug version" of and application: ex21-dbg
Running Debugger
The compiled debug application can be executed using either GDB (gcc) or LLDB (clang):
gdb --args ./ex21-dbg -i ex21.i
lldb -- ./ex21-dbg -i ex21.i
These commands will start debugger, load the executable, and open the debugger command prompt
Using GDB or LLDB
At any prompt in GDB or LLDB, you can type h and hit enter to get help
Set a "breakpoint" in
MPI_Abortso that the code pauses (maintaining the stack trace)(lldb) b MPI_Abort Breakpoint 1: where = libmpi.12.dylib`MPI_Abort, address = 0x000000010b18f460Run the application, type
rand hit enter, the application will hit the breakpoint.(lldb) r Process 77675 launched: './ex21-dbg' (x86_64)When the application stops, get the backtrace
(lldb) bt * thread #1, queue = 'com.apple.main-thread', stop reason = breakpoint 1.1 * frame #0: 0x000000010b18f460 libmpi.12.dylib`MPI_Abort frame #1: 0x00000001000e5f8c libex21-dbg.0.dylib`MooseArray<double>::operator[](this=0x0000000112919388, i=0) const at MooseArray.h:276 frame #2: 0x00000001000e580b libex21-dbg.0.dylib`ExampleDiffusion::computeQpResidual(this=0x0000000112918a18) at ExampleDiffusion.C:37 frame #3: 0x0000000100486b99 libmoose-dbg.0.dylib`Kernel::computeResidual(this=0x0000000112918a18) at Kernel.C:99
The backtrace shows that in ExampleDiffusion::computeQpResidual() an attempt was made to access entry 0 of a MooseArray with 0 entries.
return _coupled_coef[_qp] * Diffusion::computeQpResidual();
There is only one item being indexed on that line: _coupled_coef; therefore, consider how _coupled_coef was declared
Bug
In ExampleDiffusion.h, the member variable _coupled_coef is a VariableValue that should be declared as a reference:
const VariableValue _coupled_coef;
Not storing this as a reference will cause a copy of the VariableValue to be made during construction. This copy will never be resized, nor will it ever have values written to it.
ExampleDiffusion.h
#pragma once
#include "Diffusion.h"
// Forward Declarations
class ExampleDiffusion;
/**
* validParams returns the parameters that this Kernel accepts / needs
* The actual body of the function MUST be in the .C file.
*/
template <>
InputParameters validParams<ExampleDiffusion>();
class ExampleDiffusion : public Diffusion
{
public:
ExampleDiffusion(const InputParameters & parameters);
protected:
virtual Real computeQpResidual() override;
virtual Real computeQpJacobian() override;
/**
* THIS IS AN ERROR ON PURPOSE!
*
* The "&" is missing here!
*
* Do NOT copy this line of code!
*/
const VariableValue _coupled_coef;
};
ExampleDiffusion.C
#include "ExampleDiffusion.h"
/**
* This function defines the valid parameters for
* this Kernel and their default values
*/
registerMooseObject("ExampleApp", ExampleDiffusion);
template <>
InputParameters
validParams<ExampleDiffusion>()
{
InputParameters params = validParams<Diffusion>();
params.addRequiredCoupledVar(
"coupled_coef", "The value of this variable will be used as the diffusion coefficient.");
return params;
}
ExampleDiffusion::ExampleDiffusion(const InputParameters & parameters)
: Diffusion(parameters), _coupled_coef(coupledValue("coupled_coef"))
{
}
Real
ExampleDiffusion::computeQpResidual()
{
return _coupled_coef[_qp] * Diffusion::computeQpResidual();
}
Real
ExampleDiffusion::computeQpJacobian()
{
return _coupled_coef[_qp] * Diffusion::computeQpJacobian();
}
Restart and Recovery System
Definitions
Restart
Running a simulation that uses data from a previous simulation, using different input files
Recover
Resuming an existing simulation after a premature termination
Solution file
A mesh format containing field data in addition to the mesh (i.e. a normal output file)
Checkpoint
A snapshot of the simulation including all meshes, solutions, and stateful data
N to N
In a restart context, this means the number of processors for the previous and current simulations match
N to M
In a restart context, different numbers of processors may be used for the previous and current simulations
Variable Initialization
This method is best suited for restarting a simulation when the mesh in the previous simulation exactly matches the mesh in the current simulation and only initial conditions need to be set for one more variables.
This method requires only a valid solution file
MOOSE supports N to M restart when using this method
[Mesh]
# MOOSE supports reading field data from ExodusII, XDA/XDR, and mesh checkpoint files (.e, .xda, .xdr, .cp)
file = previous.e
# This method of restart is only supported on serial meshes
distribution = serial
[]
[Variables/nodal]
family = LAGRANGE
order = FIRST
initial_from_file_var = nodal
initial_from_file_timestep = 10
[]
[AuxVariables/elemental]
family = MONOMIAL
order = CONSTANT
initial_from_file_var = elemental
initial_from_file_timestep = 10
[]
Checkpoints
Advanced restart and recovery in MOOSE require checkpoint files
To enable automatic checkpoints using the default options (every time step, and keep last two) in a simulation simply add the following flag to your input file:
[Outputs]
checkpoint = true
[]
For more control over the checkpoint system, create a sub-block in the input file that will allow you to change the file format, suffix, frequency of output, the number of checkpoint files to keep, etc.
Set
num_filesto at least 2 to minimize the chance of ending up with a corrupt restart file
(test/tests/outputs/checkpoint/checkpoint_interval.i)[Outputs] exodus = true [out] type = Checkpoint interval = 3 num_files = 2 [] []
Advanced Restart
This method is best suited for situations when the mesh from the previous simulation and the current simulation match and the variables and stateful data should be loaded from the pervious simulation.
Support for modifying some variables is supported such as
dtandtime_step. By default, MOOSE will automatically use the last values found in the checkpoint filesOnly N to N restarts are supported using this method
[Mesh]
# Serial number should match corresponding Executioner parameter
file = out_cp/0010_mesh.cpr
# This method of restart is only supported on serial meshes
distribution = serial
[]
[Problem]
# Note that the suffix is left off in the parameter below.
restart_file_base = out_cp/LATEST # You may also use a specific number here
[]
Reloading Data
It is possible to load and project data onto a different mesh from a solution file usually as an initial condition in a new simulation.
MOOSE supports this through the use of a SolutionUserObject
Recover
A simulation that has terminated due to a fault can be recovered simply by using the --recover command-line flag, but it requires a checkpoint file.
./frog-opt -i input.i --recover
Multiapp Restart
When running a multiapp simulation you do not need to enable checkpoint output in each sub app input file. The master app stores the restart data for all sub apps in its file.
MOOSE Pluggable Systems
Action System
A system for the programmatic creation of simulation objects and input file syntax.
Auxiliary System
A system for direct calculation of field variables ("AuxVariables") that is designed for postprocessing, coupling, and proxy calculations.
Boundary Condition System
System for computing residual contributions from boundary terms of a PDE.
Constraint System
A system for imposing constraints within a simulation, such as limiting the heat flux across a gap or fixing solution variables across an interface using mortar methods.
Control System
A system for pragmatically modifying the input parameters of objects during a simulation.
Damper System
A system to limit the computed change to the solution during each non-linear iteration to prevent the solver from dramatically alteration of the solution from one step to the next. This may prevent, for example, the solver from attempting to evaluate non-physical values such as negative temperature.
DGKernel System
A system for computing residual contributions for volume terms for the discontinuous Galerkin finite element method.
DiracKernel System
A system for computing residual calculations from point sources.
Distribution System
A system for defining statistical distribution (e.g., uniform, normal, Weibull) functions for use with the stochastic tools module.
Executioner System
A system for dictating the simulation solving strategy.
Function System
A system for defining analytic expressions based on the spatial location (, , ) and time, .
Geometric Search System
A system for locating geometric elements within a simulation such as the nearest node across a gap.
Initial Condition System
A system for initialize field variables (non-linear and auxiliary) prior to execution of a simulation.
Indicator System
A system for computing an error estimation for use with automatic mesh refinement and coarsening.
InterfaceKernel System
A system to assist in coupling different physics across sub-domains, such as setting the flux of two species to be equivalent across a boundary between two domains.
Kernel System
A system for computing the residual contribution from a volumetric term within a PDE using the Galerkin finite element method.
Line Search System
This system is meant for creating custom line searches for use during the non-linear solve.
Marker System
A system for setting status of an element to refine, coarsen, or remain the same for automatic mesh adaptivity.
Material System
A system for defining material properties to be used by multiple systems and allow for variable coupling.
Mesh System
A system for defining a finite element mesh.
Mesh Generator System
A system for generating a finite element mesh using successive geometric construction routines such as building a 2D grid and then extruding into 3D space.
MeshModifer System
A system for altering a finite element mesh such as adding a sub-domain or boundary.
MultiApp System
A system for performing multiple simulations within a main simulation.
Nodal Kernel System
A system for computing a residual contribution of a PDE at nodes within the finite element mesh.
Output System
A system for producing outputting simulation data to the screen or files.
Parser System
A system for converting input data into MOOSE objects for creating a simulation.
Partitioner System
A system for partitioning a finite element mesh for parallel execution of a simulation.
Postprocessor System
A system for computing a "reduction" or "aggregation" calculation based on the solution variables that results in a single scalar value.
Preconditioner System
A system for defining the preconditioning matrix for use with the non-linear solver.
Predictor System
A system for predicting the next iteration of a simulation based on previous solution iterates.
Problem System
A system for defining the numerical systems that comprise a simulation.
Relationship Manager System
A system is defining geometric or algebraic information needed to perform a calculations in parallel.
Sampler System
A system for defining distribution sampling strategies for use with the stochastic tools module.
Split System
A system for splitting the preconditioning matrix to optimize the non-linear solving for multiphysics problems.
Time Integrator System
A system for defining schemes for numerical integration in time.
Time Stepper System
A system for suggesting time steps for transient executioners.
Transfer System
A system to move data to and from the "master" and "sub-applications" of a MultiApp.
UserObject System
A system for defining an arbitrary interface between MOOSE objects.
VectorPostprocessor System
A system for "reduction" or "aggregation" calculations based on the solution variables that results in one or many vectors of values.
References
- Eric B Becker, Graham F Carey, and John Tinsley Oden. Finite Elements, An Introduction: Volume I. Prentice Hall, 6 edition, 1981.
- Jan Flusser, Tomáš Suk, and Barbara Zitová. 2D & 3D image analysis by moments. John Wiley & Sons, Inc., 2016. ISBN 1119039355.
- David F. Griffiths. The 'no boundary condition' outflow boundary condition. International Journal for Numerical Methods in Fluids, 24(4):393–411, 1997. URL: https://onlinelibrary.wiley.com/doi/abs/10.1002/%28SICI%291097-0363%2819970228%2924%3A4%3C393%3A%3AAID-FLD505%3E3.0.CO%3B2-O, doi:10.1002/(SICI)1097-0363(19970228)24:4<393::AID-FLD505>3.0.CO;2-O.
- Luanjing Guo, Hai Huang, Derek R Gaston, Cody J Permann, David Andrs, George D Redden, Chuan Lu, Don T Fox, and Yoshiko Fujita. A parallel, fully coupled, fully implicit solution to reactive transport in porous media using the preconditioned Jacobian-Free Newton-Krylov Method. Advances in Water Resources, 53:101–108, 2013.
- Leslie Kerby, Aaron G Tumulak, Jaakko Leppänen, and Ville Valtavirta. Preliminary Serpent—MOOSE Coupling and Implementation of Functional Expansion Tallies in Serpent. In International Conference on Mathematics & Computational Methods Applied to Nuclear Science and Engineering (M&C 2017). 2017.
- Dana A. Knoll and David E. Keyes. Jacobian-free newton-krylov methods: a survey of approaches and applications. J. Comput. Phys, 193:357–397, 2004.
- Brycen Wendt and Leslie Kerby. Multiapp transfers in the moose framework based on functional expansions. Transactions of the American Nuclear Society, 117(1):735–738, October 2017.
- Brycen Wendt, April Novak, Leslie Kerby, and Paul Romano. Integration of functional expansion methodologies as a moose module. In PHYSOR 2018: Reactor Physics paving the way towards more efficient systems. April 2018.