Poroelasticity test descriptions

Introduction

The PorousFlow module includes the ability to couple fluid flow to solid mechanics, and thus includes poroelasticity, which is the theory of a fully-saturated single-phase fluid with constant bulk density and constant viscosity coupled to small-strain isotropic elasticity.

There is one important difference between the poroelasticity and most of PorousFlow, however. The time-derivative terms of poroelasticity are $(1)var element = document.getElementById("moose-equation-5730df77-eac3-4eac-a529-eed884c8dc05");katex.render("\\frac{1}{M}\\dot{P} + \\alpha\\dot{\\epsilon}_{ii} \\ , ", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ where $var element = document.getElementById("moose-equation-8ea4517d-3c19-4932-a9de-7265d9c85e4d");katex.render("M", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the Biot modulus: $(2)var element = document.getElementById("moose-equation-e64f487f-1c8c-4f5b-bf6d-29c36df546f0");katex.render("\\frac{1}{M} = \\frac{(1-\\alpha)(\\alpha - \\phi)}{K} + \\frac{\\phi}{K_{\\mathrm{f}}} \\ , ", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ $var element = document.getElementById("moose-equation-a2755d54-7c09-4651-be4b-495a9e73a89c");katex.render("P", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the fluid porepressure, $var element = document.getElementById("moose-equation-c61a483e-e9b6-44c2-8aef-55b168cb6a2c");katex.render("\\alpha", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the Biot coefficient, $var element = document.getElementById("moose-equation-12b87aa3-f5bb-4083-85e8-5a6aea2793ea");katex.render("\\epsilon_{ii}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the volumetric strain, $var element = document.getElementById("moose-equation-31ded2e8-4c06-4f00-b47d-9931ea6b0e6f");katex.render("\\phi", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the porosity, $var element = document.getElementById("moose-equation-862a6e81-89ea-4d91-8075-7170d11944cc");katex.render("K", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the solid (drained) bulk modulus, and $var element = document.getElementById("moose-equation-cee9e5f1-34cb-4f9d-baca-b790a29844a1");katex.render("K_{\\mathrm{f}}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the fluid bulk modulus. Evidently from Eq. (2), the Biot modulus, $var element = document.getElementById("moose-equation-38a40962-3fd5-42ea-97c3-b13bca7d2b52");katex.render("M", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , should evolve with time as the porosity evolves. Indeed, the terms in Eq. (1) are derived from the continuity equation $var element = document.getElementById("moose-equation-47302326-6d65-46b1-ab20-65c851419dc3");katex.render("\\partial (\\phi\\rho)/\\partial t + \\phi\\rho\\dot{\\epsilon}_{ii}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ using the evolution of $var element = document.getElementById("moose-equation-d4f65a54-c352-4a07-8560-c498e73fe422");katex.render("\\phi", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ (and $var element = document.getElementById("moose-equation-d3fffaa8-9857-4e01-b459-2a68ee8d0173");katex.render("\\rho = \\rho_{0}\\exp(P/K_{\\mathrm{f}})", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ ). This derivation is discussed further here. However, in the standard analytical solutions of poroelasticity theory, the Biot modulus, $var element = document.getElementById("moose-equation-2bb849cd-0309-4c96-8ab1-4c5bf506f6b2");katex.render("M", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is considered fixed.

The PorousFlow module allows porosity to vary with fluid porepressure and volumetric strain, so usually the Biot modulus would vary too, causing differences with the analytical solutions of poroelasticity. Therefore, PorousFlow offers a porosity relationship that evolves porosity in such a way as to keep $var element = document.getElementById("moose-equation-06f3b46b-ddd3-4224-967f-42ef99cabdb2");katex.render("M", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ fixed. This is called PorousFlowPorosityHMBiotModulus.

PorousFlow is also built with finite strains in mind, whereas poroelasticity is not. Therefore, in comparisons with solutions from poroelasticity theory, either the strain should be kept small, or the various finite-strain switches in PorousFlow should be turned off (they are all on by default).

Simple tests

Volumetric expansion due to increasing porepressure

The porepressure within a fully-saturated sample is increased: $var element = document.getElementById("moose-equation-a44e4d7a-83fe-45cd-84aa-aa7a24e4255b");katex.render("P_{\\mathrm{f}} = t \\ .", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ Zero mechanical pressure is applied to the sample's exterior, so that no Neumann BCs are needed on the sample. No fluid flow occurs since the porepressure is increased uniformly throughout the sample.

The input file:

# Apply an increasing porepressure, with zero mechanical forces,
# and observe the corresponding volumetric expansion
#
# P = t
# With the Biot coefficient being 0.3, the effective stresses should be
# stress_xx = stress_yy = stress_zz = 0.3t
# With bulk modulus = 1 then should have
# vol_strain = strain_xx + strain_yy + strain_zz = 0.3t.
# I use a single element lying 0<=x<=1, 0<=y<=1 and 0<=z<=1, and
# fix the left, bottom and back boundaries appropriately,
# so at the point x=y=z=1, the displacements should be
# disp_x = disp_y = disp_z = 0.3t/3 (small strain physics is used)
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
  type = GeneratedMesh
  dim = 3
  nx = 1
  ny = 1
  nz = 1
  xmin = 0
  xmax = 1
  ymin = 0
  ymax = 1
  zmin = 0
  zmax = 1
[]

[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
  displacements = 'disp_x disp_y disp_z'
  block = 0
  PorousFlowDictator = dictator
[]

[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [p]
  []
[]

[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
  [p]
    type = FunctionDirichletBC<<<{"description": "Imposes the essential boundary condition $u=g(t,\\vec{x})$, where $g$ is a (possibly) time and space-dependent MOOSE Function.", "href": "../../../../source/bcs/FunctionDirichletBC.html"}>>>
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'bottom top'
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = p
    function<<<{"description": "The forcing function."}>>> = t
  []
  [xmin]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    value<<<{"description": "Value of the BC"}>>> = 0
  []
  [ymin]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = bottom
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    value<<<{"description": "Value of the BC"}>>> = 0
  []
  [zmin]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = back
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    value<<<{"description": "Value of the BC"}>>> = 0
  []
[]

[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
  [p_does_not_really_diffuse]
    type = Diffusion<<<{"description": "The Laplacian operator ($-\\nabla \\cdot \\nabla u$), with the weak form of $(\\nabla \\phi_i, \\nabla u_h)$.", "href": "../../../../source/kernels/Diffusion.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = p
  []
  [TensorMechanics<<<{"href": "../../../../syntax/Kernels/TensorMechanics/index.html"}>>>]
    displacements<<<{"description": "The nonlinear displacement variables for the problem"}>>> = 'disp_x disp_y disp_z'
  []
  [poro_x]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.3
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 0
  []
  [poro_y]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.3
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 1
  []
  [poro_z]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.3
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 2
  []
[]

[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
  [stress_xx]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
  [stress_xy]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
  [stress_xz]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
  [stress_yy]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
  [stress_yz]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
  [stress_zz]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
[]

[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
  [stress_xx]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_xx
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 0
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 0
  []
  [stress_xy]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_xy
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 0
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 1
  []
  [stress_xz]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_xz
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 0
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 2
  []
  [stress_yy]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_yy
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 1
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 1
  []
  [stress_yz]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_yz
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 1
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 2
  []
  [stress_zz]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_zz
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 2
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 2
  []
[]

[Postprocessors<<<{"href": "../../../../syntax/Postprocessors/index.html"}>>>]
  [corner_x]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 1 1'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_x
  []
  [corner_y]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 1 1'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_y
  []
  [corner_z]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 1 1'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_z
  []
[]

[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
  [dictator]
    type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
    porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation.  Jacobian entries involving derivatives wrt these variables will be computed.  In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'p'
    number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
    number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
  []
  [pc]
    type = PorousFlowCapillaryPressureVG<<<{"description": "van Genuchten capillary pressure", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureVG.html"}>>>
    m<<<{"description": "van Genuchten exponent m. Must be between 0 and 1, and optimally should be set to >0.5"}>>> = 0.5
    alpha<<<{"description": "van Genuchten parameter alpha. Must be positive"}>>> = 1
  []
[]

[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
  [temperature]
    type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
  []
  [elasticity_tensor]
    type = ComputeElasticityTensor<<<{"description": "Compute an elasticity tensor.", "href": "../../../../source/materials/ComputeElasticityTensor.html"}>>>
    # bulk modulus = 1, poisson ratio = 0.2
    C_ijkl<<<{"description": "Stiffness tensor for material"}>>> = '0.5 0.75'
    fill_method<<<{"description": "The fill method"}>>> = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain<<<{"description": "Compute a small strain.", "href": "../../../../source/materials/ComputeSmallStrain.html"}>>>
    displacements<<<{"description": "The displacements appropriate for the simulation geometry and coordinate system"}>>> = 'disp_x disp_y disp_z'
  []
  [stress]
    type = ComputeLinearElasticStress<<<{"description": "Compute stress using elasticity for small strains", "href": "../../../../source/materials/ComputeLinearElasticStress.html"}>>>
  []
  [ppss]
    type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
    porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = p
    capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
  []
  [p_eff]
    type = PorousFlowEffectiveFluidPressure<<<{"description": "This Material calculates an effective fluid pressure: effective_stress = total_stress + biot_coeff*effective_fluid_pressure.  The effective_fluid_pressure = sum_{phases}(S_phase * P_phase)", "href": "../../../../source/materials/PorousFlowEffectiveFluidPressure.html"}>>>
  []
[]

[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
  [andy]
    type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
    full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
    petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it -ksp_atol -ksp_rtol'
    petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres bjacobi 1E-10 1E-10 10 1E-15 1E-10'
  []
[]

[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
  type = Transient
  solve_type = Newton
  start_time = 0
  dt = 0.1
  end_time = 1
[]

[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
  file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = vol_expansion
  exodus<<<{"description": "Output the results using the default settings for Exodus output."}>>> = true
[]

The effective stresses should then evolve as $var element = document.getElementById("moose-equation-c25637ba-799d-48d7-b6e4-39dbfe604157");katex.render("\\sigma_{ij}^{\\mathrm{eff}} = \\alpha t \\delta_{ij}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , and the volumetric strain $var element = document.getElementById("moose-equation-499d29d1-3290-4d92-9300-d8338c2502b5");katex.render("\\epsilon_{00}+\\epsilon_{11}+\\epsilon_{22} = \\alpha t/K", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ . MOOSE produces this result correctly.

Undrained oedometer test

A cubic single-element fully-saturated sample has roller BCs applied to its sides and bottom. All the sample's boundaries are impermeable. A downwards (normal) displacement, $var element = document.getElementById("moose-equation-393f0b50-6ce5-4815-9b82-9ed87d980323");katex.render("u_{z}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , is applied to its top, and the rise in porepressure and effective stress is observed. (Here $var element = document.getElementById("moose-equation-ba8ab9bc-1a4b-46bd-aaef-e8340a818538");katex.render("z", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ denotes the direction normal to the top face.) There is no fluid flow in the single element.

# An undrained oedometer test on a saturated poroelastic sample.
#
# The sample is a single unit element, with roller BCs on the sides
# and bottom.  A constant displacement is applied to the top: disp_z = -0.01*t.
# There is no fluid flow.
#
# Under these conditions
# porepressure = -(Fluid bulk modulus)*log(1 - 0.01t)
# stress_xx = (bulk - 2*shear/3)*disp_z/L (remember this is effective stress)
# stress_zz = (bulk + 4*shear/3)*disp_z/L (remember this is effective stress)
# where L is the height of the sample (L=1 in this test)
#
# Parameters:
# Bulk modulus = 2
# Shear modulus = 1.5
# fluid bulk modulus = 1
#
# Desired output:
# zdisp = -0.01*t
# p0 = 1*log(1-0.01t)
# stress_xx = stress_yy = -0.01*t
# stress_zz = -0.04*t
#
# Regarding the "log" - it just comes from conserving fluid mass

[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
  type = GeneratedMesh
  dim = 3
  nx = 1
  ny = 1
  nz = 1
  xmin = -0.5
  xmax = 0.5
  ymin = -0.5
  ymax = 0.5
  zmin = -0.5
  zmax = 0.5
[]

[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
  [confinex]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'left right'
  []
  [confiney]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'bottom top'
  []
  [basefixed]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = back
  []
  [top_velocity]
    type = FunctionDirichletBC<<<{"description": "Imposes the essential boundary condition $u=g(t,\\vec{x})$, where $g$ is a (possibly) time and space-dependent MOOSE Function.", "href": "../../../../source/bcs/FunctionDirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    function<<<{"description": "The forcing function."}>>> = -0.01*t
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = front
  []
[]

[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
  [grad_stress_x]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 0
  []
  [grad_stress_y]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 1
  []
  [grad_stress_z]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 2
  []
  [poro_vol_exp]
    type = PorousFlowMassVolumetricExpansion<<<{"description": "Component_mass*rate_of_solid_volumetric_expansion.  This Kernel lumps the component mass to the nodes.", "href": "../../../../source/kernels/PorousFlowMassVolumetricExpansion.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
  []
  [mass0]
    type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time.  Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
    fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
  []
[]

[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
  [stress_xx]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
  [stress_xy]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
  [stress_xz]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
  [stress_yy]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
  [stress_yz]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
  [stress_zz]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
[]

[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
  [stress_xx]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_xx
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 0
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 0
  []
  [stress_xy]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_xy
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 0
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 1
  []
  [stress_xz]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_xz
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 0
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 2
  []
  [stress_yy]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_yy
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 1
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 1
  []
  [stress_yz]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_yz
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 1
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 2
  []
  [stress_zz]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_zz
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 2
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 2
  []
[]

[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
  [simple_fluid]
    type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
    bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 1
    density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1
    thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
  []
[]

[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
  [temperature]
    type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
  []
  [elasticity_tensor]
    type = ComputeElasticityTensor<<<{"description": "Compute an elasticity tensor.", "href": "../../../../source/materials/ComputeElasticityTensor.html"}>>>
    C_ijkl<<<{"description": "Stiffness tensor for material"}>>> = '1 1.5'
    # bulk modulus is lambda + 2*mu/3 = 1 + 2*1.5/3 = 2
    fill_method<<<{"description": "The fill method"}>>> = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain<<<{"description": "Compute a small strain.", "href": "../../../../source/materials/ComputeSmallStrain.html"}>>>
  []
  [stress]
    type = ComputeLinearElasticStress<<<{"description": "Compute stress using elasticity for small strains", "href": "../../../../source/materials/ComputeLinearElasticStress.html"}>>>
  []
  [vol_strain]
    type = PorousFlowVolumetricStrain<<<{"description": "Compute volumetric strain and the volumetric_strain rate, for use in PorousFlow.", "href": "../../../../source/materials/PorousFlowVolumetricStrain.html"}>>>
  []
  [eff_fluid_pressure]
    type = PorousFlowEffectiveFluidPressure<<<{"description": "This Material calculates an effective fluid pressure: effective_stress = total_stress + biot_coeff*effective_fluid_pressure.  The effective_fluid_pressure = sum_{phases}(S_phase * P_phase)", "href": "../../../../source/materials/PorousFlowEffectiveFluidPressure.html"}>>>
  []
  [ppss]
    type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
    porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = porepressure
    capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
  []
  [massfrac]
    type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
  []
  [simple_fluid]
    type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
    fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
    phase<<<{"description": "The phase number"}>>> = 0
  []
  [porosity]
    type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>>
    porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material).  This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.1
  []
[]

[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
  [dictator]
    type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
    porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation.  Jacobian entries involving derivatives wrt these variables will be computed.  In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'porepressure disp_x disp_y disp_z'
    number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
    number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
  []
  [pc]
    type = PorousFlowCapillaryPressureVG<<<{"description": "van Genuchten capillary pressure", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureVG.html"}>>>
    m<<<{"description": "van Genuchten exponent m. Must be between 0 and 1, and optimally should be set to >0.5"}>>> = 0.8
    alpha<<<{"description": "van Genuchten parameter alpha. Must be positive"}>>> = 1
  []
[]

[Postprocessors<<<{"href": "../../../../syntax/Postprocessors/index.html"}>>>]
  [fluid_mass]
    type = PorousFlowFluidMass<<<{"description": "Calculates the mass of a fluid component in a region", "href": "../../../../source/postprocessors/PorousFlowFluidMass.html"}>>>
    fluid_component<<<{"description": "The index corresponding to the fluid component that this Postprocessor acts on"}>>> = 0
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'initial timestep_end'
  []
  [p0]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [zdisp]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0.5'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_z
  []
  [stress_xx]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = stress_xx
  []
  [stress_yy]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = stress_yy
  []
  [stress_zz]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = stress_zz
  []

[]

[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
  [andy]
    type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
    full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
    petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'bcgs bjacobi 1E-14 1E-8 10000'
  []
[]

[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 10
  dt = 1
[]

[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
  execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'timestep_end'
  file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = undrained_oedometer
  [csv]
    type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
  []
[]

Under these conditions, assuming constant porosity, and denoting the height ( $var element = document.getElementById("moose-equation-6b3365dc-c80c-4fc6-9822-9bca618ed389");katex.render("z", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ length) of the sample by $var element = document.getElementById("moose-equation-d3e84e88-8b7c-46cd-89a8-71814260fa06");katex.render("L", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ : $var element = document.getElementById("moose-equation-3b0f43b5-c5ed-4c32-9011-6947e08a8f96");katex.render("\\begin{array}{rcl} P_{\\mathrm{f}} & = & -K_{f}\\log(1 - u_{z}) \\ , \\\\ \\sigma_{xx}^{\\mathrm{eff}} & = & \\left(K - \\frac{2}{3}G\\right)u_{z}/L \\ , \\\\ \\sigma_{zz}^{\\mathrm{eff}} & = & \\left(K + \\frac{4}{3}G\\right)u_{z}/L \\ . \\end{array}", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ MOOSE produces these results correctly.

Porepressure generation of a confined sample

A single-element fully-saturated sample is constrained on all sides and its boundaries are impermeable. Fluid is pumped into the sample via a source $var element = document.getElementById("moose-equation-4d1a4786-e30c-4910-8a02-5658da547a19");katex.render("s", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ (kg.s $var element = document.getElementById("moose-equation-6dd6c4e8-98f9-4762-95b9-44dfb4928d2d");katex.render("^{-1}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ .m $var element = document.getElementById("moose-equation-5533920f-f27a-4230-8a0d-d934a082bcc3");katex.render("^{-3}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ ) and the rise in porepressure is observed.

The input file:

# Same as pp_generation.i, but using an Action
#
# A sample is constrained on all sides and its boundaries are
# also impermeable.  Fluid is pumped into the sample via a
# volumetric source (ie kg/second per cubic meter), and the
# rise in porepressure is observed.
#
# Source = s  (units = kg/m^3/second)
#
# Expect:
# fluid_mass = mass0 + s*t
# stress = 0 (remember this is effective stress)
# Porepressure = fluid_bulk*log(fluid_mass_density/density_P0), where fluid_mass_density = fluid_mass/porosity
# porosity = biot+(phi0-biot)*exp(pp(biot-1)/solid_bulk)
#
# Parameters:
# Biot coefficient = 0.3
# Phi0 = 0.1
# Solid Bulk modulus = 2
# fluid_bulk = 13
# density_P0 = 1

[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
  type = GeneratedMesh
  dim = 3
  nx = 1
  ny = 1
  nz = 1
  xmin = -0.5
  xmax = 0.5
  ymin = -0.5
  ymax = 0.5
  zmin = -0.5
  zmax = 0.5
[]

[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
  [the_simple_fluid]
    type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
    thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0.0
    bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 13.0
    viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1.0
    density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1.0
  []
[]

[PorousFlowFullySaturated<<<{"href": "../../../../syntax/PorousFlowFullySaturated/index.html"}>>>]
  coupling_type<<<{"description": "The type of simulation.  For simulations involving Mechanical deformations, you will need to supply the correct Biot coefficient.  For simulations involving Thermal flows, you will need an associated ConstantThermalExpansionCoefficient Material"}>>> = HydroMechanical
  displacements<<<{"description": "The name of the displacement variables (relevant only for mechanically-coupled simulations)"}>>> = 'disp_x disp_y disp_z'
  porepressure<<<{"description": "The name of the porepressure variable"}>>> = porepressure
  biot_coefficient<<<{"description": "The Biot coefficient (relevant only for mechanically-coupled simulations)"}>>> = 0.3
  gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
  fp<<<{"description": "The name of the user object for fluid properties. Only needed if fluid_properties_type = PorousFlowSingleComponentFluid"}>>> = the_simple_fluid
  stabilization<<<{"description": "Numerical stabilization used.  'Full' means full upwinding.  'KT' means FEM-TVD stabilization of Kuzmin-Turek"}>>> = none # not needed: there is no flow
  save_component_rate_in<<<{"description": "List of AuxVariables into which the rate-of-change of each fluid component at each node will be saved.  There must be exactly N of these to match the N fluid components.  The result will be measured in kg/s, where the kg is the mass of the fluid component at the node (or m^3/s if multiply_by_density=false).  Note that this saves the result from the MassTimeDerivative Kernels, but NOT from the MassVolumetricExpansion Kernels."}>>> = nodal_kg_per_s
[]

[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
  [confinex]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'left right'
  []
  [confiney]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'bottom top'
  []
  [confinez]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'back front'
  []
[]

[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
  [source]
    type = BodyForce<<<{"description": "Demonstrates the multiple ways that scalar values can be introduced into kernels, e.g. (controllable) constants, functions, and postprocessors. Implements the weak form $(\\psi_i, -f)$.", "href": "../../../../source/kernels/BodyForce.html"}>>>
    function<<<{"description": "A function that describes the body force"}>>> = 0.1
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
  []
[]

[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
  [nodal_kg_per_s]
  []
  [porosity]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
[]

[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
  [porosity]
    type = PorousFlowPropertyAux<<<{"description": "AuxKernel to provide access to properties evaluated at quadpoints. Note that elemental AuxVariables must be used, so that these properties are integrated over each element.", "href": "../../../../source/auxkernels/PorousFlowPropertyAux.html"}>>>
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = porosity
    property<<<{"description": "The fluid property that this auxillary kernel is to calculate"}>>> = porosity
  []
[]

[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
  [elasticity_tensor]
    type = ComputeElasticityTensor<<<{"description": "Compute an elasticity tensor.", "href": "../../../../source/materials/ComputeElasticityTensor.html"}>>>
    C_ijkl<<<{"description": "Stiffness tensor for material"}>>> = '1 1.5'
    # bulk modulus is lambda + 2*mu/3 = 1 + 2*1.5/3 = 2
    fill_method<<<{"description": "The fill method"}>>> = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain<<<{"description": "Compute a small strain.", "href": "../../../../source/materials/ComputeSmallStrain.html"}>>>
  []
  [stress]
    type = ComputeLinearElasticStress<<<{"description": "Compute stress using elasticity for small strains", "href": "../../../../source/materials/ComputeLinearElasticStress.html"}>>>
  []
  [porosity]
    type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../../../../source/materials/PorousFlowPorosity.html"}>>>
    fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
    mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
    porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry.  This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.1
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.3
    solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 2
  []
  [permeability]
    type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
    permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1 0 0   0 1 0   0 0 1' # unimportant
  []
[]

[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
  [porosity_analytic]
    type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../../../../source/functions/MooseParsedFunction.html"}>>>
    expression<<<{"description": "The user defined function."}>>> = 'biot+(phi0-biot)*exp(pp*(biot-1)/bulk)'
    symbol_names<<<{"description": "Symbols (excluding t,x,y,z) that are bound to the values provided by the corresponding items in the vals vector."}>>> = 'biot phi0 pp bulk'
    symbol_values<<<{"description": "Constant numeric values, postprocessor names, function names, and scalar variables corresponding to the symbols in symbol_names."}>>> = '0.3 0.1 p0 2'
  []
[]

[Postprocessors<<<{"href": "../../../../syntax/Postprocessors/index.html"}>>>]
  [nodal_kg_per_s]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = ' 0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = nodal_kg_per_s
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
  []
  [fluid_mass]
    type = PorousFlowFluidMass<<<{"description": "Calculates the mass of a fluid component in a region", "href": "../../../../source/postprocessors/PorousFlowFluidMass.html"}>>>
    fluid_component<<<{"description": "The index corresponding to the fluid component that this Postprocessor acts on"}>>> = 0
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'initial timestep_end'
  []
  [porosity]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = 'console csv'
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porosity
  []
  [p0]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [porosity_analytic]
    type = FunctionValuePostprocessor<<<{"description": "Computes the value of a supplied function at a single point (scalable)", "href": "../../../../source/postprocessors/FunctionValuePostprocessor.html"}>>>
    function<<<{"description": "The function which supplies the postprocessor value."}>>> = porosity_analytic
  []
  [zdisp]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0.5'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_z
  []
  [stress_xx]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = stress_xx
  []
  [stress_yy]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = stress_yy
  []
  [stress_zz]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = stress_zz
  []

[]

[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
  [andy]
    type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
    full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
    petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'bcgs bjacobi 1E-14 1E-10 10000'
  []
[]

[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 10
  dt = 1
[]

[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
  execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'timestep_end'
  file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = pp_generation_fullysat_action
  csv<<<{"description": "Output the scalar variable and postprocessors to a *.csv file using the default CSV output."}>>> = true
[]

Denoting the strength of the source by $var element = document.getElementById("moose-equation-05bd665c-c201-4e62-bfb3-f21e87df9705");katex.render("s", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ (units are s $var element = document.getElementById("moose-equation-a1ae6f35-b8a5-4c4a-bb81-4c325d9e0ff7");katex.render("^{-1}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ ), the expected result is $var element = document.getElementById("moose-equation-fdf66c68-c60e-4cd3-9187-eed334dd3108");katex.render("\\begin{array}{rcl} \\mathrm{fluid mass} & = & \\mathrm{fluid\\ mass}_{0} + st \\ , \\\\ \\sigma_{ij}^{\\mathrm{eff}} & = & 0 \\ , \\\\ P_{\\mathrm{f}} & = & K_{\\mathrm{f}}\\log(M/(\\phi\\rho_{0})) \\ , \\\\ \\rho & = & \\rho_{0}\\exp(P_{\\mathrm{f}}/K_{f}) \\ ,\\\\ \\phi & = & \\alpha + (\\phi_{0}-\\alpha)\\exp\\left( P_{\\mathrm{f}}(\\alpha - 1)/K\\right) \\ . \\\\ \\end{array}", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ Here $var element = document.getElementById("moose-equation-280fd414-bee5-4a3b-a4f1-433973c07135");katex.render("K", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the solid bulk modulus. MOOSE produces this result correctly.

Porepressure generation of an unconfined sample

A single-element fully-saturated sample is constrained on all sides, except its top. All its boundaries are impermeable. Fluid is pumped into the sample via a source $var element = document.getElementById("moose-equation-6ea42efe-b2f2-4b59-af3f-f96d1903b569");katex.render("s", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ (kg.s $var element = document.getElementById("moose-equation-cd7cba93-fbc4-40aa-996f-f52f073a40ff");katex.render("^{-1}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ .m $var element = document.getElementById("moose-equation-f7c1b0b9-2217-46d6-aa9f-05f3e10c9246");katex.render("^{-3}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ ) and the rise in the top surface, the porepressure, and the stress are observed.

The input file:

# Identical to pp_generation_unconfined_fullysat_volume.i but using an Action
#
# A sample is constrained on all sides, except its top
# and its boundaries are
# also impermeable.  Fluid is pumped into the sample via a
# volumetric source (ie m^3/second per cubic meter), and the
# rise in the top surface, porepressure, and stress are observed.
#
# In the standard poromechanics scenario, the Biot Modulus is held
# fixed and the source has units 1/s.  Then the expected result
# is
# strain_zz = disp_z = BiotCoefficient*BiotModulus*s*t/((bulk + 4*shear/3) + BiotCoefficient^2*BiotModulus)
# porepressure = BiotModulus*(s*t - BiotCoefficient*strain_zz)
# stress_xx = (bulk - 2*shear/3)*strain_zz   (remember this is effective stress)
# stress_zz = (bulk + 4*shear/3)*strain_zz   (remember this is effective stress)
#
# In standard porous_flow, everything is based on mass, eg the source has
# units kg/s/m^3.  This is discussed in the other pp_generation_unconfined
# models.  In this test, we use the FullySaturated Kernel and set
# multiply_by_density = false
# meaning the fluid Kernel has units of volume, and the source, s, has units 1/time
#
# The ratios are:
# stress_xx/strain_zz = (bulk - 2*shear/3) = 1 (for the parameters used here)
# stress_zz/strain_zz = (bulk + 4*shear/3) = 4 (for the parameters used here)
# porepressure/strain_zz = 13.3333333 (for the parameters used here)
#
# Expect
# disp_z = 0.3*10*s*t/((2 + 4*1.5/3) + 0.3^2*10) = 0.612245*s*t
# porepressure = 10*(s*t - 0.3*0.612245*s*t) = 8.163265*s*t
# stress_xx = (2 - 2*1.5/3)*0.612245*s*t = 0.612245*s*t
# stress_zz = (2 + 4*shear/3)*0.612245*s*t = 2.44898*s*t
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
  type = GeneratedMesh
  dim = 3
  nx = 1
  ny = 1
  nz = 1
  xmin = -0.5
  xmax = 0.5
  ymin = -0.5
  ymax = 0.5
  zmin = -0.5
  zmax = 0.5
[]

[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
  [confinex]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'left right'
  []
  [confiney]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'bottom top'
  []
  [confinez]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'back'
  []
[]

[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
  [source]
    type = BodyForce<<<{"description": "Demonstrates the multiple ways that scalar values can be introduced into kernels, e.g. (controllable) constants, functions, and postprocessors. Implements the weak form $(\\psi_i, -f)$.", "href": "../../../../source/kernels/BodyForce.html"}>>>
    function<<<{"description": "A function that describes the body force"}>>> = 0.1
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
  []
[]

[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
  [the_simple_fluid]
    type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
    thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0.0
    bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 3.3333333333
    viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1.0
    density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1.0
  []
[]

[PorousFlowBasicTHM<<<{"href": "../../../../syntax/PorousFlowBasicTHM/index.html"}>>>]
  coupling_type<<<{"description": "The type of simulation.  For simulations involving Mechanical deformations, you will need to supply the correct Biot coefficient.  For simulations involving Thermal flows, you will need an associated ConstantThermalExpansionCoefficient Material"}>>> = HydroMechanical
  displacements<<<{"description": "The name of the displacement variables (relevant only for mechanically-coupled simulations)"}>>> = 'disp_x disp_y disp_z'
  multiply_by_density<<<{"description": "If true, then the Kernels for fluid flow are multiplied by the fluid density.  If false, this multiplication is not performed, which means the problem linearises, but that care must be taken when using other PorousFlow objects."}>>> = false
  porepressure<<<{"description": "The name of the porepressure variable"}>>> = porepressure
  biot_coefficient<<<{"description": "The Biot coefficient (relevant only for mechanically-coupled simulations)"}>>> = 0.3
  gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
  fp<<<{"description": "The name of the user object for fluid properties. Only needed if fluid_properties_type = PorousFlowSingleComponentFluid"}>>> = the_simple_fluid
  save_component_rate_in<<<{"description": "List of AuxVariables into which the rate-of-change of each fluid component at each node will be saved.  There must be exactly N of these to match the N fluid components.  The result will be measured in kg/s, where the kg is the mass of the fluid component at the node (or m^3/s if multiply_by_density=false).  Note that this saves the result from the MassTimeDerivative Kernels, but NOT from the MassVolumetricExpansion Kernels."}>>> = nodal_m3_per_s
[]

[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
  [elasticity_tensor]
    type = ComputeElasticityTensor<<<{"description": "Compute an elasticity tensor.", "href": "../../../../source/materials/ComputeElasticityTensor.html"}>>>
    C_ijkl<<<{"description": "Stiffness tensor for material"}>>> = '1 1.5'
    # bulk modulus is lambda + 2*mu/3 = 1 + 2*1.5/3 = 2
    fill_method<<<{"description": "The fill method"}>>> = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain<<<{"description": "Compute a small strain.", "href": "../../../../source/materials/ComputeSmallStrain.html"}>>>
    displacements<<<{"description": "The displacements appropriate for the simulation geometry and coordinate system"}>>> = 'disp_x disp_y disp_z'
  []
  [stress]
    type = ComputeLinearElasticStress<<<{"description": "Compute stress using elasticity for small strains", "href": "../../../../source/materials/ComputeLinearElasticStress.html"}>>>
  []
  [porosity]
    type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>> # the "const" is irrelevant here: all that uses Porosity is the BiotModulus, which just uses the initial value of porosity
    porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material).  This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.1
    PorousFlowDictator<<<{"description": "The UserObject that holds the list of PorousFlow variable names"}>>> = dictator
  []
  [biot_modulus]
    type = PorousFlowConstantBiotModulus<<<{"description": "Computes the Biot Modulus, which is assumed to be constant for all time.  Sometimes 1 / BiotModulus is called storativity", "href": "../../../../source/materials/PorousFlowConstantBiotModulus.html"}>>>
    PorousFlowDictator<<<{"description": "The UserObject that holds the list of PorousFlow variable names"}>>> = dictator
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.3
    fluid_bulk_modulus<<<{"description": "Fluid bulk modulus"}>>> = 3.3333333333
    solid_bulk_compliance<<<{"description": "Reciprocal of the drained bulk modulus of the porous skeleton.  If strain = C * stress, then solid_bulk_compliance = de_ij de_kl C_ijkl.  If the grain bulk modulus is Kg then 1/Kg = (1 - biot_coefficient) * solid_bulk_compliance."}>>> = 0.5
  []
  [permeability_irrelevant]
    type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
    PorousFlowDictator<<<{"description": "The UserObject that holds the list of PorousFlow variable names"}>>> = dictator
    permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1.5 0 0   0 1.5 0   0 0 1.5'
  []
[]

[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
  [nodal_m3_per_s]
  []
[]

[Postprocessors<<<{"href": "../../../../syntax/Postprocessors/index.html"}>>>]
  [nodal_m3_per_s]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = nodal_m3_per_s
  []
  [p0]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [zdisp]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0.5'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_z
  []
  [stress_xx]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = stress_xx
  []
  [stress_yy]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = stress_yy
  []
  [stress_zz]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = stress_zz
  []
  [stress_xx_over_strain]
    type = FunctionValuePostprocessor<<<{"description": "Computes the value of a supplied function at a single point (scalable)", "href": "../../../../source/postprocessors/FunctionValuePostprocessor.html"}>>>
    function<<<{"description": "The function which supplies the postprocessor value."}>>> = stress_xx_over_strain_fcn
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
  []
  [stress_zz_over_strain]
    type = FunctionValuePostprocessor<<<{"description": "Computes the value of a supplied function at a single point (scalable)", "href": "../../../../source/postprocessors/FunctionValuePostprocessor.html"}>>>
    function<<<{"description": "The function which supplies the postprocessor value."}>>> = stress_zz_over_strain_fcn
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
  []
  [p_over_strain]
    type = FunctionValuePostprocessor<<<{"description": "Computes the value of a supplied function at a single point (scalable)", "href": "../../../../source/postprocessors/FunctionValuePostprocessor.html"}>>>
    function<<<{"description": "The function which supplies the postprocessor value."}>>> = p_over_strain_fcn
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
  []
[]

[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
  [stress_xx_over_strain_fcn]
    type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../../../../source/functions/MooseParsedFunction.html"}>>>
    expression<<<{"description": "The user defined function."}>>> = a/b
    symbol_names<<<{"description": "Symbols (excluding t,x,y,z) that are bound to the values provided by the corresponding items in the vals vector."}>>> = 'a b'
    symbol_values<<<{"description": "Constant numeric values, postprocessor names, function names, and scalar variables corresponding to the symbols in symbol_names."}>>> = 'stress_xx zdisp'
  []
  [stress_zz_over_strain_fcn]
    type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../../../../source/functions/MooseParsedFunction.html"}>>>
    expression<<<{"description": "The user defined function."}>>> = a/b
    symbol_names<<<{"description": "Symbols (excluding t,x,y,z) that are bound to the values provided by the corresponding items in the vals vector."}>>> = 'a b'
    symbol_values<<<{"description": "Constant numeric values, postprocessor names, function names, and scalar variables corresponding to the symbols in symbol_names."}>>> = 'stress_zz zdisp'
  []
  [p_over_strain_fcn]
    type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../../../../source/functions/MooseParsedFunction.html"}>>>
    expression<<<{"description": "The user defined function."}>>> = a/b
    symbol_names<<<{"description": "Symbols (excluding t,x,y,z) that are bound to the values provided by the corresponding items in the vals vector."}>>> = 'a b'
    symbol_values<<<{"description": "Constant numeric values, postprocessor names, function names, and scalar variables corresponding to the symbols in symbol_names."}>>> = 'p0 zdisp'
  []
[]

[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
  [andy]
    type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
    full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
    petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'bcgs bjacobi 1E-14 1E-10 10000'
  []
[]

[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 10
  dt = 1
[]

[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
  execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'timestep_end'
  file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = pp_generation_unconfined_basicthm
  [csv]
    type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
  []
[]

Regardless of the evolution of porosity, the following ratios result $var element = document.getElementById("moose-equation-4993048d-756d-48bd-a4fc-d76966a27739");katex.render("\\begin{array}{rcl} \\sigma_{xx}/\\epsilon_{zz} & = & K - 2G/3 \\ , \\\\ \\sigma_{zz}/\\epsilon_{zz} & = & K + 4G/3 \\ , \\\\ P/\\epsilon_{zz} & = & (K + 3G/3 + \\alpha^{2}M)/\\alpha - \\alpha M \\ . \\end{array}", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ where $var element = document.getElementById("moose-equation-daf78483-5253-4dd8-a173-f6bb948f0cf3");katex.render("K", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the undrained bulk modulus, $var element = document.getElementById("moose-equation-c0d64039-5d46-402d-90d5-a7ae3baaaf52");katex.render("G", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ the shear modulus, $var element = document.getElementById("moose-equation-ca21c042-26cb-4b21-9857-bc7138f64be8");katex.render("\\alpha", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ the Biot coefficient, and $var element = document.getElementById("moose-equation-79ecf3fa-4116-4b3e-8867-651f02f1ed91");katex.render("M", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the initial Biot modulus. MOOSE produces these results correctly.

However, if the Biot modulus, $var element = document.getElementById("moose-equation-9a37e732-867f-424b-a920-e4c06c1ed0eb");katex.render("M", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , is held fixed as the porosity evolves, and the source is $var element = document.getElementById("moose-equation-bf64a861-bfe8-4bba-b756-b9a30c78f321");katex.render("s = S \\rho_{0}\\exp(P/K_{\\mathrm{f}}) \\ ,", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ with $var element = document.getElementById("moose-equation-8cf309dc-4dbb-4cd1-a8a3-df5a299aeef8");katex.render("S", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ being a constant volumetric source (m $var element = document.getElementById("moose-equation-56a5b325-5ae2-4fd0-8450-48d56437251f");katex.render("^{3}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ .s $var element = document.getElementById("moose-equation-27e84de8-0867-425f-a611-dcb8434b662b");katex.render("^{-1}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ .m $var element = document.getElementById("moose-equation-37dc6361-9c1b-4e14-8f11-c2cc0a356455");katex.render("^{-3}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ ) then $var element = document.getElementById("moose-equation-ba54d7da-a42a-47b5-8cee-d55e999b3929");katex.render("\\begin{array}{rcl} \\epsilon_{zz} & = & \\frac{\\alpha M s t}{K + 4G/3 + \\alpha^{2}M} \\ , \\\\ P & = & M(st - \\alpha\\epsilon_{zz}) \\ , \\\\ \\sigma_{xx} & = & (K - 2G/3)\\epsilon_{zz} \\ , \\\\ \\sigma_{zz} & = & (K + 4G/3)\\epsilon_{zz} \\ . \\end{array}", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ The input file for this is:

# This file uses a PorousFlowFullySaturated Action.  The equivalent non-Action input file is pp_generation_unconfined_constM.i
#
# A sample is constrained on all sides, except its top
# and its boundaries are
# also impermeable.  Fluid is pumped into the sample via a
# volumetric source (ie kg/second per cubic meter), and the
# rise in the top surface, porepressure, and stress are observed.
#
# In the standard poromechanics scenario, the Biot Modulus is held
# fixed and the source, s, has units m^3/second/m^3.  Then the expected result
# is
# strain_zz = disp_z = BiotCoefficient*BiotModulus*s*t/((bulk + 4*shear/3) + BiotCoefficient^2*BiotModulus)
# porepressure = BiotModulus*(s*t - BiotCoefficient*strain_zz)
# stress_xx = (bulk - 2*shear/3)*strain_zz   (remember this is effective stress)
# stress_zz = (bulk + 4*shear/3)*strain_zz   (remember this is effective stress)
#
# In porous_flow, however, the source has units kg/second/m^3.  The ratios remain
# fixed:
# stress_xx/strain_zz = (bulk - 2*shear/3) = 1 (for the parameters used here)
# stress_zz/strain_zz = (bulk + 4*shear/3) = 4 (for the parameters used here)
# porepressure/strain_zz = 13.3333333 (for the parameters used here)
#
# Expect
# disp_z = 0.3*10*s*t/((2 + 4*1.5/3) + 0.3^2*10) = 0.612245*s*t
# porepressure = 10*(s*t - 0.3*0.612245*s*t) = 8.163265*s*t
# stress_xx = (2 - 2*1.5/3)*0.612245*s*t = 0.612245*s*t
# stress_zz = (2 + 4*shear/3)*0.612245*s*t = 2.44898*s*t
# The relationship between the constant poroelastic source
# s (m^3/second/m^3) and the PorousFlow source, S (kg/second/m^3) is
# S = fluid_density * s = s * exp(porepressure/fluid_bulk)

[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
  type = GeneratedMesh
  dim = 3
  nx = 1
  ny = 1
  nz = 1
  xmin = -0.5
  xmax = 0.5
  ymin = -0.5
  ymax = 0.5
  zmin = -0.5
  zmax = 0.5
[]

[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
  [confinex]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'left right'
  []
  [confiney]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'bottom top'
  []
  [confinez]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'back'
  []
[]

[PorousFlowFullySaturated<<<{"href": "../../../../syntax/PorousFlowFullySaturated/index.html"}>>>]
  porepressure<<<{"description": "The name of the porepressure variable"}>>> = porepressure
  biot_coefficient<<<{"description": "The Biot coefficient (relevant only for mechanically-coupled simulations)"}>>> = 0.3
  coupling_type<<<{"description": "The type of simulation.  For simulations involving Mechanical deformations, you will need to supply the correct Biot coefficient.  For simulations involving Thermal flows, you will need an associated ConstantThermalExpansionCoefficient Material"}>>> = HydroMechanical
  displacements<<<{"description": "The name of the displacement variables (relevant only for mechanically-coupled simulations)"}>>> = 'disp_x disp_y disp_z'
  gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
  fp<<<{"description": "The name of the user object for fluid properties. Only needed if fluid_properties_type = PorousFlowSingleComponentFluid"}>>> = simple_fluid
  stabilization<<<{"description": "Numerical stabilization used.  'Full' means full upwinding.  'KT' means FEM-TVD stabilization of Kuzmin-Turek"}>>> = Full
[]

[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
  [source]
    type = BodyForce<<<{"description": "Demonstrates the multiple ways that scalar values can be introduced into kernels, e.g. (controllable) constants, functions, and postprocessors. Implements the weak form $(\\psi_i, -f)$.", "href": "../../../../source/kernels/BodyForce.html"}>>>
    function<<<{"description": "A function that describes the body force"}>>> = '0.1*exp(8.163265306*0.1*t/3.3333333333)'
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
  []
[]

[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
  [simple_fluid]
    type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
    bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 3.3333333333
    density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1
    thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
    viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1
  []
[]

[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
  [elasticity_tensor]
    type = ComputeElasticityTensor<<<{"description": "Compute an elasticity tensor.", "href": "../../../../source/materials/ComputeElasticityTensor.html"}>>>
    C_ijkl<<<{"description": "Stiffness tensor for material"}>>> = '1 1.5'
    # bulk modulus is lambda + 2*mu/3 = 1 + 2*1.5/3 = 2
    fill_method<<<{"description": "The fill method"}>>> = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain<<<{"description": "Compute a small strain.", "href": "../../../../source/materials/ComputeSmallStrain.html"}>>>
    displacements<<<{"description": "The displacements appropriate for the simulation geometry and coordinate system"}>>> = 'disp_x disp_y disp_z'
  []
  [stress]
    type = ComputeLinearElasticStress<<<{"description": "Compute stress using elasticity for small strains", "href": "../../../../source/materials/ComputeLinearElasticStress.html"}>>>
  []
  [porosity]
    type = PorousFlowPorosityHMBiotModulus<<<{"description": "This Material calculates the porosity for hydro-mechanical simulations, assuming that the Biot modulus and the fluid bulk modulus are both constant.  This is useful for comparing with solutions from poroelasticity theory, but is less accurate than PorousFlowPorosity", "href": "../../../../source/materials/PorousFlowPorosityHMBiotModulus.html"}>>>
    porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry.  This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.1
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.3
    solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 2
    constant_fluid_bulk_modulus<<<{"description": "Fluid bulk modulus, which is constant for this Material"}>>> = 3.3333333333
    constant_biot_modulus<<<{"description": "Biot modulus, which is constant for this Material"}>>> = 10.0
  []
  [permeability]
    type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
    permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1 0 0   0 1 0   0 0 1' # unimportant
  []
[]

[Postprocessors<<<{"href": "../../../../syntax/Postprocessors/index.html"}>>>]
  [p0]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [zdisp]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0.5'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_z
  []
  [stress_xx]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = stress_xx
  []
  [stress_yy]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = stress_yy
  []
  [stress_zz]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = stress_zz
  []
[]

[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
  [stress_xx_over_strain_fcn]
    type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../../../../source/functions/MooseParsedFunction.html"}>>>
    expression<<<{"description": "The user defined function."}>>> = a/b
    symbol_names<<<{"description": "Symbols (excluding t,x,y,z) that are bound to the values provided by the corresponding items in the vals vector."}>>> = 'a b'
    symbol_values<<<{"description": "Constant numeric values, postprocessor names, function names, and scalar variables corresponding to the symbols in symbol_names."}>>> = 'stress_xx zdisp'
  []
  [stress_zz_over_strain_fcn]
    type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../../../../source/functions/MooseParsedFunction.html"}>>>
    expression<<<{"description": "The user defined function."}>>> = a/b
    symbol_names<<<{"description": "Symbols (excluding t,x,y,z) that are bound to the values provided by the corresponding items in the vals vector."}>>> = 'a b'
    symbol_values<<<{"description": "Constant numeric values, postprocessor names, function names, and scalar variables corresponding to the symbols in symbol_names."}>>> = 'stress_zz zdisp'
  []
  [p_over_strain_fcn]
    type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../../../../source/functions/MooseParsedFunction.html"}>>>
    expression<<<{"description": "The user defined function."}>>> = a/b
    symbol_names<<<{"description": "Symbols (excluding t,x,y,z) that are bound to the values provided by the corresponding items in the vals vector."}>>> = 'a b'
    symbol_values<<<{"description": "Constant numeric values, postprocessor names, function names, and scalar variables corresponding to the symbols in symbol_names."}>>> = 'p0 zdisp'
  []
[]

[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
  [andy]
    type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
    full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
    petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'bcgs bjacobi 1E-14 1E-10 10000'
  []
[]

[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 10
  dt = 1
[]

[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
  execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'timestep_end'
  file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = pp_generation_unconfined_constM_action
  [csv]
    type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
  []
[]

MOOSE produces these results correctly.

Terzaghi consolidation of a drained medium

A saturated sample sits in a bath of water. It is constrained on its sides and bottom. Its sides and bottom are also impermeable. Initially it is unstressed ( $var element = document.getElementById("moose-equation-3ef7d359-5531-41c4-9a51-9edeb66607b3");katex.render("\\sigma_{ij} = 0 = P_{\\mathrm{f}}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , at $var element = document.getElementById("moose-equation-67f746ba-9f3e-45f8-8ca7-ead429483928");katex.render("t=0", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ ). A normal stress, $var element = document.getElementById("moose-equation-3c87796a-5186-49e7-bb08-6beb926b01a0");katex.render("q", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , is applied to the sample's top. The sample compresses instantaneously due to the instantaneous application of $var element = document.getElementById("moose-equation-b2869ac8-e0e4-4489-9de8-3877b4efc1dc");katex.render("q", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , and then slowly compresses further as water is squeezed out from the sample's top surface.

This is a classic test. See, for example, Section 2.2 of the online manuscript: Arnold Verruijt "Theory and Problems of Poroelasticity" Delft University of Technology 2013. But note that the "sigma" in that paper is the negative of the stress in PorousFlow. Denote the sample's height ( $var element = document.getElementById("moose-equation-60e21428-1a6f-4b21-8342-a8eccf0f3d27");katex.render("z", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ -length) by $var element = document.getElementById("moose-equation-f94a98dd-acaf-4cbc-bb97-83d18289185d");katex.render("h", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ . Define $var element = document.getElementById("moose-equation-4013850e-bdd0-417e-b6b6-46175e5dcaff");katex.render("p_{0} = \\frac{\\alpha q M}{S(K + 4G/3) + \\alpha^{2}M} \\ .", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ This is the porepressure that results from the instantaneous application of $var element = document.getElementById("moose-equation-f3370ceb-e0ec-4ccf-9da1-3a6cf4679d53");katex.render("q", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ : MOOSE calculates this correctly. The solution for porepressure is $var element = document.getElementById("moose-equation-787f2b8e-5c0c-4eb5-8710-97b8a0e18c33");katex.render("P_{\\mathrm{f}} = \\frac{4p_{0}}{\\pi}\\sum_{n=1}^{\\infty} \\frac{(-1)^{n-1}}{2n-1} \\cos \\left( \\frac{(2n-1)\\pi z}{2h} \\right) \\exp \\left( -(2n-1)^{2} \\pi^{2} \\frac{ct}{4h^{2}} \\right) \\ .", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ In this equation, $var element = document.getElementById("moose-equation-5d3e13ba-0c02-4cb7-81b0-04b8266d95bf");katex.render("c", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the "consolidation coefficient": $var element = document.getElementById("moose-equation-36f89aa3-9487-4041-a092-b1069a67822b");katex.render("c = k (K + 4G/3) M/(K + 4G/3 + \\alpha^{2} M)", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , where the permeability tensor is $var element = document.getElementById("moose-equation-0d5552bc-a06b-4e0b-8ce6-1b46e3487da7");katex.render("k_{ij} = \\mathrm{diag}(k, k, k)", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ . The so-called degree-of-consolidation is defined by $var element = document.getElementById("moose-equation-b1b4ff52-a54e-418a-8176-a034f972b850");katex.render("U = \\frac{u_{z} - u_{z}^{0}}{u_{z}^{\\infty} - u_{z}^{0}} \\ ,", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ where $var element = document.getElementById("moose-equation-0f58a92f-3668-4c36-8749-818b298bcc32");katex.render("u_{z}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the vertical displacement of the top surface (downwards is positive), and $var element = document.getElementById("moose-equation-152283e1-3a69-4122-a413-6a73e53231fc");katex.render("u_{z}^{0}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the instantaneous displacement due to the instantaneous application of $var element = document.getElementById("moose-equation-0cb9243e-55d2-43e4-a7ca-7a5e5e701023");katex.render("q", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , and $var element = document.getElementById("moose-equation-ea645630-6fec-4dbb-a882-ecefbf3df70d");katex.render("u_{z}^{\\infty}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is the final displacement. This has solution $var element = document.getElementById("moose-equation-e3298f8d-9329-49ba-8a8d-462f3989e148");katex.render("U = 1 - \\frac{8}{\\pi^{2}}\\sum_{n=1}^{\\infty} \\frac{1}{(2n-1)^{2}} \\exp \\left(-(2n-1)^{2}\\pi^{2}\\frac{ct}{4h^{2}} \\right) \\ .", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$

There are a few different variants of this test in the test suite, that use the PorousFlow action system, constant Biot modulus, constant porosity, the fully-saturated version of PorousFlow, etc. You are encouraged to explore these to get a feeling for how the differences impact the output. The input file for that matches the theoretical setup exactly is:

# Terzaghi's problem of consolodation of a drained medium
#
# A saturated soil sample sits in a bath of water.
# It is constrained on its sides, and bottom.
# Its sides and bottom are also impermeable.
# Initially it is unstressed.
# A normal stress, q, is applied to the soil's top.
# The soil then slowly compresses as water is squeezed
# out from the sample from its top (the top BC for
# the porepressure is porepressure = 0).
#
# See, for example.  Section 2.2 of the online manuscript
# Arnold Verruijt "Theory and Problems of Poroelasticity" Delft University of Technology 2013
# but note that the "sigma" in that paper is the negative
# of the stress in TensorMechanics
#
# Here are the problem's parameters, and their values:
# Soil height.  h = 10
# Soil's Lame lambda.  la = 2
# Soil's Lame mu, which is also the Soil's shear modulus.  mu = 3
# Soil bulk modulus.  K = la + 2*mu/3 = 4
# Soil confined compressibility.  m = 1/(K + 4mu/3) = 0.125
# Soil bulk compliance.  1/K = 0.25
# Fluid bulk modulus.  Kf = 8
# Fluid bulk compliance.  1/Kf = 0.125
# Fluid mobility (soil permeability/fluid viscosity).  k = 1.5
# Soil initial porosity.  phi0 = 0.1
# Biot coefficient.  alpha = 0.6
# Soil initial storativity, which is the reciprocal of the initial Biot modulus.  S = phi0/Kf + (alpha - phi0)(1 - alpha)/K = 0.0625
# Consolidation coefficient.  c = k/(S + alpha^2 m) = 13.95348837
# Normal stress on top.  q = 1
# Initial porepressure, resulting from instantaneous application of q, assuming corresponding instantaneous increase of porepressure (Note that this is calculated by MOOSE: we only need it for the analytical solution).  p0 = alpha*m*q/(S + alpha^2 m) = 0.69767442
# Initial vertical displacement (down is positive), resulting from instantaneous application of q (Note this is calculated by MOOSE: we only need it for the analytical solution).  uz0 = q*m*h*S/(S + alpha^2 m)
# Final vertical displacement (down in positive) (Note this is calculated by MOOSE: we only need it for the analytical solution).  uzinf = q*m*h
#
# The solution for porepressure is
# P = 4*p0/\pi \sum_{k=1}^{\infty} \frac{(-1)^{k-1}}{2k-1} \cos ((2k-1)\pi z/(2h)) \exp(-(2k-1)^2 \pi^2 ct/(4 h^2))
# This series converges very slowly for ct/h^2 small, so in that domain
# P = p0 erf( (1-(z/h))/(2 \sqrt(ct/h^2)) )
#
# The degree of consolidation is defined as
# U = (uz - uz0)/(uzinf - uz0)
# where uz0 and uzinf are defined above, and
# uz = the vertical displacement of the top (down is positive)
# U = 1 - (8/\pi^2)\sum_{k=1}^{\infty} \frac{1}{(2k-1)^2} \exp(-(2k-1)^2 \pi^2 ct/(4 h^2))

[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
  type = GeneratedMesh
  dim = 3
  nx = 1
  ny = 1
  nz = 10
  xmin = -1
  xmax = 1
  ymin = -1
  ymax = 1
  zmin = 0
  zmax = 10
[]

[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
  [dictator]
    type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
    porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation.  Jacobian entries involving derivatives wrt these variables will be computed.  In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'porepressure disp_x disp_y disp_z'
    number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
    number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
  []
  [pc]
    type = PorousFlowCapillaryPressureVG<<<{"description": "van Genuchten capillary pressure", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureVG.html"}>>>
    m<<<{"description": "van Genuchten exponent m. Must be between 0 and 1, and optimally should be set to >0.5"}>>> = 0.8
    alpha<<<{"description": "van Genuchten parameter alpha. Must be positive"}>>> = 1
  []
[]

[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
  [confinex]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'left right'
  []
  [confiney]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'bottom top'
  []
  [basefixed]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = back
  []
  [topdrained]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = front
  []
  [topload]
    type = NeumannBC<<<{"description": "Imposes the integrated boundary condition $\\frac{\\partial u}{\\partial n}=h$, where $h$ is a constant, controllable value.", "href": "../../../../source/bcs/NeumannBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    value<<<{"description": "For a Laplacian problem, the value of the gradient dotted with the normals on the boundary."}>>> = -1
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = front
  []
[]

[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
  [grad_stress_x]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 0
  []
  [grad_stress_y]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 1
  []
  [grad_stress_z]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 2
  []
  [poro_x]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 0
  []
  [poro_y]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 1
  []
  [poro_z]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 2
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
  []
  [poro_vol_exp]
    type = PorousFlowMassVolumetricExpansion<<<{"description": "Component_mass*rate_of_solid_volumetric_expansion.  This Kernel lumps the component mass to the nodes.", "href": "../../../../source/kernels/PorousFlowMassVolumetricExpansion.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
  []
  [mass0]
    type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time.  Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
    fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
  []
  [flux]
    type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
    fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
  []
[]

[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
  [simple_fluid]
    type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
    bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 8
    density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1
    thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
    viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 0.96
  []
[]

[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
  [temperature]
    type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
  []
  [elasticity_tensor]
    type = ComputeElasticityTensor<<<{"description": "Compute an elasticity tensor.", "href": "../../../../source/materials/ComputeElasticityTensor.html"}>>>
    C_ijkl<<<{"description": "Stiffness tensor for material"}>>> = '2 3'
    # bulk modulus is lambda + 2*mu/3 = 2 + 2*3/3 = 4
    fill_method<<<{"description": "The fill method"}>>> = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain<<<{"description": "Compute a small strain.", "href": "../../../../source/materials/ComputeSmallStrain.html"}>>>
  []
  [stress]
    type = ComputeLinearElasticStress<<<{"description": "Compute stress using elasticity for small strains", "href": "../../../../source/materials/ComputeLinearElasticStress.html"}>>>
  []
  [eff_fluid_pressure]
    type = PorousFlowEffectiveFluidPressure<<<{"description": "This Material calculates an effective fluid pressure: effective_stress = total_stress + biot_coeff*effective_fluid_pressure.  The effective_fluid_pressure = sum_{phases}(S_phase * P_phase)", "href": "../../../../source/materials/PorousFlowEffectiveFluidPressure.html"}>>>
  []
  [vol_strain]
    type = PorousFlowVolumetricStrain<<<{"description": "Compute volumetric strain and the volumetric_strain rate, for use in PorousFlow.", "href": "../../../../source/materials/PorousFlowVolumetricStrain.html"}>>>
  []
  [ppss]
    type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
    porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = porepressure
    capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
  []
  [massfrac]
    type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
  []
  [simple_fluid]
    type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
    fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
    phase<<<{"description": "The phase number"}>>> = 0
  []
  [porosity]
    type = PorousFlowPorosityHMBiotModulus<<<{"description": "This Material calculates the porosity for hydro-mechanical simulations, assuming that the Biot modulus and the fluid bulk modulus are both constant.  This is useful for comparing with solutions from poroelasticity theory, but is less accurate than PorousFlowPorosity", "href": "../../../../source/materials/PorousFlowPorosityHMBiotModulus.html"}>>>
    porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry.  This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.1
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 4
    constant_fluid_bulk_modulus<<<{"description": "Fluid bulk modulus, which is constant for this Material"}>>> = 8
    constant_biot_modulus<<<{"description": "Biot modulus, which is constant for this Material"}>>> = 16
  []
  [permeability]
    type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
    permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1.5 0 0   0 1.5 0   0 0 1.5'
  []
  [relperm]
    type = PorousFlowRelativePermeabilityCorey<<<{"description": "This Material calculates relative permeability of the fluid phase, using the simple Corey model ((S-S_res)/(1-sum(S_res)))^n", "href": "../../../../source/materials/PorousFlowRelativePermeabilityCorey.html"}>>>
    n<<<{"description": "The Corey exponent of the phase."}>>> = 0 # unimportant in this fully-saturated situation
    phase<<<{"description": "The phase number"}>>> = 0
  []
[]

[Postprocessors<<<{"href": "../../../../syntax/Postprocessors/index.html"}>>>]
  [p0]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
    use_displaced_mesh<<<{"description": "Whether or not this object should use the displaced mesh for computation.  Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used."}>>> = false
  []
  [p1]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 1'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
    use_displaced_mesh<<<{"description": "Whether or not this object should use the displaced mesh for computation.  Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used."}>>> = false
  []
  [p2]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 2'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
    use_displaced_mesh<<<{"description": "Whether or not this object should use the displaced mesh for computation.  Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used."}>>> = false
  []
  [p3]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 3'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
    use_displaced_mesh<<<{"description": "Whether or not this object should use the displaced mesh for computation.  Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used."}>>> = false
  []
  [p4]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 4'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
    use_displaced_mesh<<<{"description": "Whether or not this object should use the displaced mesh for computation.  Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used."}>>> = false
  []
  [p5]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 5'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
    use_displaced_mesh<<<{"description": "Whether or not this object should use the displaced mesh for computation.  Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used."}>>> = false
  []
  [p6]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 6'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
    use_displaced_mesh<<<{"description": "Whether or not this object should use the displaced mesh for computation.  Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used."}>>> = false
  []
  [p7]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 7'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
    use_displaced_mesh<<<{"description": "Whether or not this object should use the displaced mesh for computation.  Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used."}>>> = false
  []
  [p8]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 8'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
    use_displaced_mesh<<<{"description": "Whether or not this object should use the displaced mesh for computation.  Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used."}>>> = false
  []
  [p9]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 9'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
    use_displaced_mesh<<<{"description": "Whether or not this object should use the displaced mesh for computation.  Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used."}>>> = false
  []
  [p99]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 10'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
    use_displaced_mesh<<<{"description": "Whether or not this object should use the displaced mesh for computation.  Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used."}>>> = false
  []
  [zdisp]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0 0 10'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_z
    use_displaced_mesh<<<{"description": "Whether or not this object should use the displaced mesh for computation.  Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used."}>>> = false
  []
  [dt]
    type = FunctionValuePostprocessor<<<{"description": "Computes the value of a supplied function at a single point (scalable)", "href": "../../../../source/postprocessors/FunctionValuePostprocessor.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = console
    function<<<{"description": "The function which supplies the postprocessor value."}>>> = if(0.5*t<0.1,0.5*t,0.1)
  []
[]

[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
  [andy]
    type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
    full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
  []
[]

[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 10
  [TimeStepper<<<{"href": "../../../../syntax/Executioner/TimeStepper/index.html"}>>>]
    type = PostprocessorDT
    postprocessor = dt
    dt = 0.0001
  []
[]

[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
  execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'timestep_end'
  file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = terzaghi_constM
  [csv]
    type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
  []
[]

MOOSE produces the expected results correctly, as may be seen from Figure 1 and Figure 2.

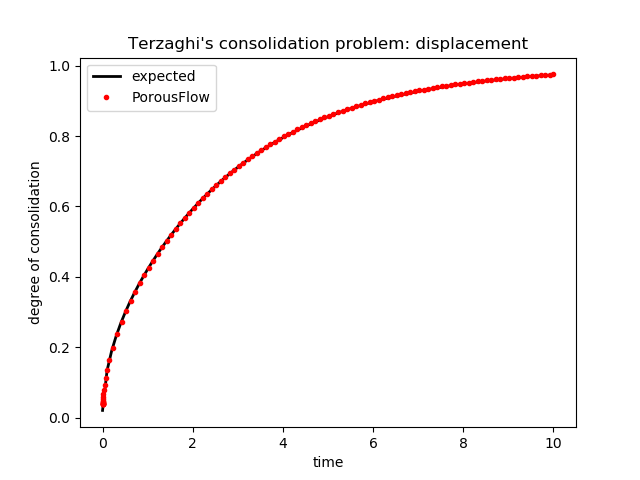
Figure 1: Degree of consolidation in the Terzaghi experiment.

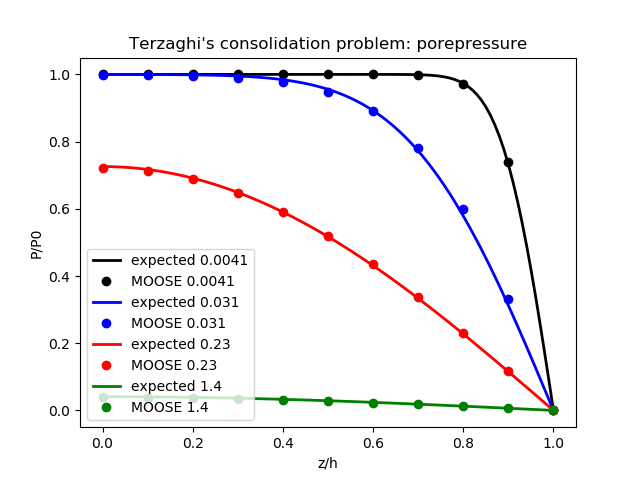
Figure 2: Porepressure at various times in the Terzaghi experiment.

Mandel's consolidation of a drained medium

A sample's dimensions are $var element = document.getElementById("moose-equation-e0292108-6693-46b6-a3d5-66912312f54d");katex.render("-a \\leq x \\leq a", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ and $var element = document.getElementById("moose-equation-68a4e4e7-93c4-42be-81ed-21c3a73954a7");katex.render("-b \\leq y \\leq b", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , and it is in plane strain (no $var element = document.getElementById("moose-equation-05a785dd-ba92-4c4a-8a4d-1176117d10b0");katex.render("z", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ displacement). It is squashed with constant normal force by impermeable, frictionless plattens on its top and bottom surfaces (at $var element = document.getElementById("moose-equation-f4e7da04-a1b7-4f74-8d5c-cc91d4a54ad1");katex.render("y = \\pm b", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ ). Fluid is allowed to leak out from its sides (at $var element = document.getElementById("moose-equation-988cbbfb-eac9-4084-a130-0f286654d9d7");katex.render("x = \\pm a", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ ), but all other surfaces are impermeable. This is called Mandel's problem and it is shown graphically in Figure 3

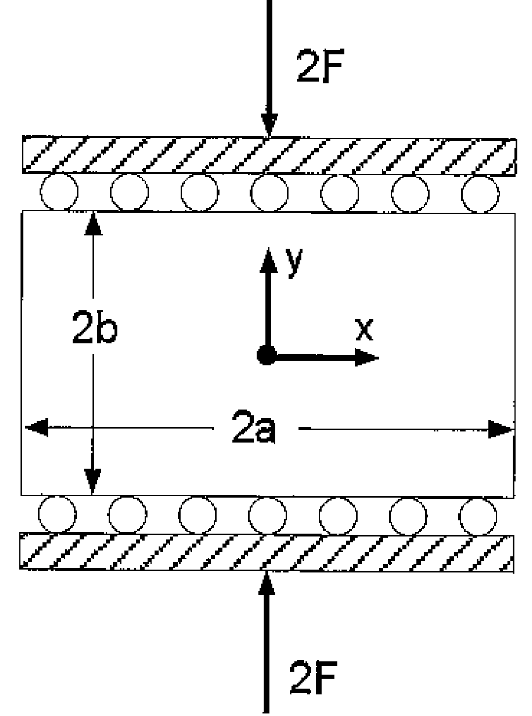
Figure 3: The setup of the Mandel experiment: a force squashes a porous material with impermeable plattens. This causes fluid to seep from the material.

The interesting feature of this problem (apart from that it can be solved analytically) is that the porepressure in the sample's center increases for a short time after application of the force. This is because the leakage of the fluid from the sample's sides causes an apparent softening of the material near those sides. This means stress concentrates towards the sample's center which causes an increase in porepressure. Of course, eventually the fluid totally drains from the sample, and the porepressure is zero. As the fluid drains from the sample's sides the plattens move slowly towards each other.

The solution for porepressure and displacements is given in Cheng and Detournay (1988). The solution involves rather lengthy infinite series, so I will not write it here.

As is common in the literature, this is simulated by considering the quarter-sample, $var element = document.getElementById("moose-equation-7013e265-aa2b-48fe-9438-fc02939ed45d");katex.render("0\\leq x \\leq a", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ and $var element = document.getElementById("moose-equation-d2c56de5-5d1c-4862-a06b-ef4d4c2f46a5");katex.render("0\\leq y\\leq b", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , with impermeable, roller BCs at $var element = document.getElementById("moose-equation-ecc6838c-42f4-4e36-99d8-83bf72eb9c04");katex.render("x=0", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ and $var element = document.getElementById("moose-equation-ce53fbd9-bb5b-4c47-a4df-d86d6a24ed2c");katex.render("y=0", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ and $var element = document.getElementById("moose-equation-e066a2f8-2295-47e2-9a7c-698779bc8038");katex.render("y=b", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ . Porepressure is fixed at zero on $var element = document.getElementById("moose-equation-e52c50de-20d7-4a0a-a9e5-06c772c57e9c");katex.render("x=a", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ . Porepressure and displacement are initialised to zero. Then the top ( $var element = document.getElementById("moose-equation-864a8e0a-b08c-4d92-a933-0c03d43c27d0");katex.render("y=b", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ ) is moved downwards with prescribed velocity, so that the total force that is induced by this downwards velocity is fixed. The velocity is worked out by solving Mandel's problem analytically, and the total force is monitored in the simulation to check that it indeed remains constant.

The simulations in the PorousFlow test suite use 10 elements in the $var element = document.getElementById("moose-equation-b5abb783-28c2-4602-b6a8-38e33ba38f06");katex.render("x", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ direction and 1 in the $var element = document.getElementById("moose-equation-189ebb7c-f876-4e7d-ae6a-bc4d49a1b353");katex.render("y", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ direction. Four types of simulation are run:

HM. This uses standard PorousFlow Materials and Kernels, in particular it uses the "HM" porosity relationship. This is not expected to agree perfectly with the analytical solutions because the solutions assume constant Biot modulus.

# Mandel's problem of consolodation of a drained medium
#
# A sample is in plane strain.
# -a <= x <= a
# -b <= y <= b
# It is squashed with constant force by impermeable, frictionless plattens on its top and bottom surfaces (at y=+/-b)
# Fluid is allowed to leak out from its sides (at x=+/-a)
# The porepressure within the sample is monitored.
#
# As is common in the literature, this is simulated by
# considering the quarter-sample, 0<=x<=a and 0<=y<=b, with
# impermeable, roller BCs at x=0 and y=0 and y=b.
# Porepressure is fixed at zero on x=a.
# Porepressure and displacement are initialised to zero.
# Then the top (y=b) is moved downwards with prescribed velocity,
# so that the total force that is inducing this downwards velocity
# is fixed.  The velocity is worked out by solving Mandel's problem
# analytically, and the total force is monitored in the simulation
# to check that it indeed remains constant.
#
# Here are the problem's parameters, and their values:
# Soil width.  a = 1
# Soil height.  b = 0.1
# Soil's Lame lambda.  la = 0.5
# Soil's Lame mu, which is also the Soil's shear modulus.  mu = G = 0.75
# Soil bulk modulus.  K = la + 2*mu/3 = 1
# Drained Poisson ratio.  nu = (3K - 2G)/(6K + 2G) = 0.2
# Soil bulk compliance.  1/K = 1
# Fluid bulk modulus.  Kf = 8
# Fluid bulk compliance.  1/Kf = 0.125
# Soil initial porosity.  phi0 = 0.1
# Biot coefficient.  alpha = 0.6
# Biot modulus.  M = 1/(phi0/Kf + (alpha - phi0)(1 - alpha)/K) = 4.705882
# Undrained bulk modulus. Ku = K + alpha^2*M = 2.694118
# Undrained Poisson ratio.  nuu = (3Ku - 2G)/(6Ku + 2G) = 0.372627
# Skempton coefficient.  B = alpha*M/Ku = 1.048035
# Fluid mobility (soil permeability/fluid viscosity).  k = 1.5
# Consolidation coefficient.  c = 2*k*B^2*G*(1-nu)*(1+nuu)^2/9/(1-nuu)/(nuu-nu) = 3.821656
# Normal stress on top.  F = 1
#
# The solution for porepressure and displacements is given in
# AHD Cheng and E Detournay "A direct boundary element method for plane strain poroelasticity" International Journal of Numerical and Analytical Methods in Geomechanics 12 (1988) 551-572.
# The solution involves complicated infinite series, so I shall not write it here
#
# FINAL NOTE: The above solution assumes constant Biot Modulus.
# In porous_flow this is not true.  Therefore the solution is
# a little different than in the paper.  This test was therefore
# validated against MOOSE's poromechanics, which can choose either
# a constant Biot Modulus (which has been shown to agree with
# the analytic solution), or a non-constant Biot Modulus (which
# gives the same results as porous_flow).

[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
  type = GeneratedMesh
  dim = 3
  nx = 10
  ny = 1
  nz = 1
  xmin = 0
  xmax = 1
  ymin = 0
  ymax = 0.1
  zmin = 0
  zmax = 1
[]

[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
  [dictator]
    type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
    porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation.  Jacobian entries involving derivatives wrt these variables will be computed.  In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'porepressure disp_x disp_y disp_z'
    number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
    number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
  []
  [pc]
    type = PorousFlowCapillaryPressureVG<<<{"description": "van Genuchten capillary pressure", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureVG.html"}>>>
    m<<<{"description": "van Genuchten exponent m. Must be between 0 and 1, and optimally should be set to >0.5"}>>> = 0.8
    alpha<<<{"description": "van Genuchten parameter alpha. Must be positive"}>>> = 1e-5
  []
[]

[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
  [roller_xmin]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'left'
  []
  [roller_ymin]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'bottom'
  []
  [plane_strain]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'back front'
  []
  [xmax_drained]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
  []
  [top_velocity]
    type = FunctionDirichletBC<<<{"description": "Imposes the essential boundary condition $u=g(t,\\vec{x})$, where $g$ is a (possibly) time and space-dependent MOOSE Function.", "href": "../../../../source/bcs/FunctionDirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    function<<<{"description": "The forcing function."}>>> = top_velocity
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = top
  []
[]

[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
  [top_velocity]
    type = PiecewiseLinear<<<{"description": "Linearly interpolates between pairs of x-y data", "href": "../../../../source/functions/PiecewiseLinear.html"}>>>
    x<<<{"description": "The abscissa values"}>>> = '0 0.002 0.006   0.014   0.03    0.046   0.062   0.078   0.094   0.11    0.126   0.142   0.158   0.174   0.19 0.206 0.222 0.238 0.254 0.27 0.286 0.302 0.318 0.334 0.35 0.366 0.382 0.398 0.414 0.43 0.446 0.462 0.478 0.494 0.51 0.526 0.542 0.558 0.574 0.59 0.606 0.622 0.638 0.654 0.67 0.686 0.702'
    y<<<{"description": "The ordinate values"}>>> = '-0.041824842    -0.042730269    -0.043412712    -0.04428867     -0.045509181    -0.04645965     -0.047268246 -0.047974749      -0.048597109     -0.0491467  -0.049632388     -0.050061697      -0.050441198     -0.050776675     -0.051073238      -0.0513354 -0.051567152      -0.051772022     -0.051953128 -0.052113227 -0.052254754 -0.052379865 -0.052490464 -0.052588233 -0.052674662 -0.052751065 -0.052818606 -0.052878312 -0.052931093 -0.052977751 -0.053018997 -0.053055459 -0.053087691 -0.053116185 -0.053141373 -0.05316364 -0.053183324 -0.053200724 -0.053216106 -0.053229704 -0.053241725 -0.053252351 -0.053261745 -0.053270049 -0.053277389 -0.053283879 -0.053289615'
  []
[]

[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
  [stress_yy]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
  [tot_force]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
[]

[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
  [stress_yy]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_yy
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 1
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 1
  []
  [tot_force]
    type = ParsedAux<<<{"description": "Sets a field variable value to the evaluation of a parsed expression.", "href": "../../../../source/auxkernels/ParsedAux.html"}>>>
    coupled_variables<<<{"description": "Vector of coupled variable names"}>>> = 'stress_yy porepressure'
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = tot_force
    expression<<<{"description": "Parsed function expression to compute"}>>> = '-stress_yy+0.6*porepressure'
  []
[]

[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
  [grad_stress_x]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 0
  []
  [grad_stress_y]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 1
  []
  [grad_stress_z]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 2
  []
  [poro_x]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 0
  []
  [poro_y]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 1
  []
  [poro_z]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 2
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
  []
  [poro_vol_exp]
    type = PorousFlowMassVolumetricExpansion<<<{"description": "Component_mass*rate_of_solid_volumetric_expansion.  This Kernel lumps the component mass to the nodes.", "href": "../../../../source/kernels/PorousFlowMassVolumetricExpansion.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
  []
  [mass0]
    type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time.  Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
    fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
  []
  [flux]
    type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
    fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
  []
[]

[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
  [simple_fluid]
    type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
    bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 8
    density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1
    thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
    viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1
  []
[]

[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
  [temperature]
    type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
  []
  [elasticity_tensor]
    type = ComputeElasticityTensor<<<{"description": "Compute an elasticity tensor.", "href": "../../../../source/materials/ComputeElasticityTensor.html"}>>>
    C_ijkl<<<{"description": "Stiffness tensor for material"}>>> = '0.5 0.75'
    # bulk modulus is lambda + 2*mu/3 = 0.5 + 2*0.75/3 = 1
    fill_method<<<{"description": "The fill method"}>>> = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain<<<{"description": "Compute a small strain.", "href": "../../../../source/materials/ComputeSmallStrain.html"}>>>
  []
  [stress]
    type = ComputeLinearElasticStress<<<{"description": "Compute stress using elasticity for small strains", "href": "../../../../source/materials/ComputeLinearElasticStress.html"}>>>
  []
  [eff_fluid_pressure]
    type = PorousFlowEffectiveFluidPressure<<<{"description": "This Material calculates an effective fluid pressure: effective_stress = total_stress + biot_coeff*effective_fluid_pressure.  The effective_fluid_pressure = sum_{phases}(S_phase * P_phase)", "href": "../../../../source/materials/PorousFlowEffectiveFluidPressure.html"}>>>
  []
  [vol_strain]
    type = PorousFlowVolumetricStrain<<<{"description": "Compute volumetric strain and the volumetric_strain rate, for use in PorousFlow.", "href": "../../../../source/materials/PorousFlowVolumetricStrain.html"}>>>
  []
  [ppss]
    type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
    porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = porepressure
    capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
  []
  [massfrac]
    type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
  []
  [simple_fluid]
    type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
    fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
    phase<<<{"description": "The phase number"}>>> = 0
  []
  [porosity]
    type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../../../../source/materials/PorousFlowPorosity.html"}>>>
    fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
    mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
    ensure_positive<<<{"description": "Modify the usual exponential relationships that governs porosity so that porosity is always positive"}>>> = false
    porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry.  This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.1
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1
  []
  [permeability]
    type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
    permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1.5 0 0   0 1.5 0   0 0 1.5'
  []
  [relperm]
    type = PorousFlowRelativePermeabilityCorey<<<{"description": "This Material calculates relative permeability of the fluid phase, using the simple Corey model ((S-S_res)/(1-sum(S_res)))^n", "href": "../../../../source/materials/PorousFlowRelativePermeabilityCorey.html"}>>>
    n<<<{"description": "The Corey exponent of the phase."}>>> = 0 # unimportant in this fully-saturated situation
    phase<<<{"description": "The phase number"}>>> = 0
  []
[]

[Postprocessors<<<{"href": "../../../../syntax/Postprocessors/index.html"}>>>]
  [p0]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p1]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.1 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p2]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.2 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p3]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.3 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p4]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.4 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p5]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.5 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p6]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.6 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p7]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.7 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p8]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.8 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p9]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.9 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p99]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [xdisp]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 0.1 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_x
  []
  [ydisp]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 0.1 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_y
  []
  [total_downwards_force]
     type = ElementAverageValue<<<{"description": "Computes the volumetric average of a variable", "href": "../../../../source/postprocessors/ElementAverageValue.html"}>>>
     outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
     variable<<<{"description": "The name of the variable that this object operates on"}>>> = tot_force
  []
  [dt]
    type = FunctionValuePostprocessor<<<{"description": "Computes the value of a supplied function at a single point (scalable)", "href": "../../../../source/postprocessors/FunctionValuePostprocessor.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = console
    function<<<{"description": "The function which supplies the postprocessor value."}>>> = if(0.15*t<0.01,0.15*t,0.01)
  []
[]

[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
  [andy]
    type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
    full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
    petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu 1E-14 1E-10 10000'
  []
[]

[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 0.7
  [TimeStepper<<<{"href": "../../../../syntax/Executioner/TimeStepper/index.html"}>>>]
    type = PostprocessorDT
    postprocessor = dt
    dt = 0.001
  []
[]

[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
  execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'timestep_end'
  file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = mandel
  [csv]
    time_step_interval<<<{"description": "The interval (number of time steps) at which output occurs. Unless explicitly set, the default value of this parameter is set to infinity if the wall_time_interval is explicitly set."}>>> = 3
    type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
  []
[]

constM. This is identical to the HM case, save that it uses a porosity evolution law that keeps the Biot modulus fixed. It is therefore expected to agree with the analytical solutions.

# Mandel's problem of consolodation of a drained medium
#
# A sample is in plane strain.
# -a <= x <= a
# -b <= y <= b
# It is squashed with constant force by impermeable, frictionless plattens on its top and bottom surfaces (at y=+/-b)
# Fluid is allowed to leak out from its sides (at x=+/-a)
# The porepressure within the sample is monitored.
#
# As is common in the literature, this is simulated by
# considering the quarter-sample, 0<=x<=a and 0<=y<=b, with
# impermeable, roller BCs at x=0 and y=0 and y=b.
# Porepressure is fixed at zero on x=a.
# Porepressure and displacement are initialised to zero.
# Then the top (y=b) is moved downwards with prescribed velocity,
# so that the total force that is inducing this downwards velocity
# is fixed.  The velocity is worked out by solving Mandel's problem
# analytically, and the total force is monitored in the simulation
# to check that it indeed remains constant.
#
# Here are the problem's parameters, and their values:
# Soil width.  a = 1
# Soil height.  b = 0.1
# Soil's Lame lambda.  la = 0.5
# Soil's Lame mu, which is also the Soil's shear modulus.  mu = G = 0.75
# Soil bulk modulus.  K = la + 2*mu/3 = 1
# Drained Poisson ratio.  nu = (3K - 2G)/(6K + 2G) = 0.2
# Soil bulk compliance.  1/K = 1
# Fluid bulk modulus.  Kf = 8
# Fluid bulk compliance.  1/Kf = 0.125
# Soil initial porosity.  phi0 = 0.1
# Biot coefficient.  alpha = 0.6
# Biot modulus.  M = 1/(phi0/Kf + (alpha - phi0)(1 - alpha)/K) = 4.705882
# Undrained bulk modulus. Ku = K + alpha^2*M = 2.694118
# Undrained Poisson ratio.  nuu = (3Ku - 2G)/(6Ku + 2G) = 0.372627
# Skempton coefficient.  B = alpha*M/Ku = 1.048035
# Fluid mobility (soil permeability/fluid viscosity).  k = 1.5
# Consolidation coefficient.  c = 2*k*B^2*G*(1-nu)*(1+nuu)^2/9/(1-nuu)/(nuu-nu) = 3.821656
# Normal stress on top.  F = 1
#
# The solution for porepressure and displacements is given in
# AHD Cheng and E Detournay "A direct boundary element method for plane strain poroelasticity" International Journal of Numerical and Analytical Methods in Geomechanics 12 (1988) 551-572.
# The solution involves complicated infinite series, so I shall not write it here

[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
  type = GeneratedMesh
  dim = 3
  nx = 10
  ny = 1
  nz = 1
  xmin = 0
  xmax = 1
  ymin = 0
  ymax = 0.1
  zmin = 0
  zmax = 1
[]

[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
  [dictator]
    type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
    porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation.  Jacobian entries involving derivatives wrt these variables will be computed.  In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'porepressure disp_x disp_y disp_z'
    number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
    number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
  []
  [pc]
    type = PorousFlowCapillaryPressureVG<<<{"description": "van Genuchten capillary pressure", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureVG.html"}>>>
    m<<<{"description": "van Genuchten exponent m. Must be between 0 and 1, and optimally should be set to >0.5"}>>> = 0.8
    alpha<<<{"description": "van Genuchten parameter alpha. Must be positive"}>>> = 1e-5
  []
[]

[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
  [roller_xmin]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'left'
  []
  [roller_ymin]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'bottom'
  []
  [plane_strain]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'back front'
  []
  [xmax_drained]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
  []
  [top_velocity]
    type = FunctionDirichletBC<<<{"description": "Imposes the essential boundary condition $u=g(t,\\vec{x})$, where $g$ is a (possibly) time and space-dependent MOOSE Function.", "href": "../../../../source/bcs/FunctionDirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    function<<<{"description": "The forcing function."}>>> = top_velocity
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = top
  []
[]

[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
  [top_velocity]
    type = PiecewiseLinear<<<{"description": "Linearly interpolates between pairs of x-y data", "href": "../../../../source/functions/PiecewiseLinear.html"}>>>
    x<<<{"description": "The abscissa values"}>>> = '0 0.002 0.006   0.014   0.03    0.046   0.062   0.078   0.094   0.11    0.126   0.142   0.158   0.174   0.19 0.206 0.222 0.238 0.254 0.27 0.286 0.302 0.318 0.334 0.35 0.366 0.382 0.398 0.414 0.43 0.446 0.462 0.478 0.494 0.51 0.526 0.542 0.558 0.574 0.59 0.606 0.622 0.638 0.654 0.67 0.686 0.702'
    y<<<{"description": "The ordinate values"}>>> = '-0.041824842    -0.042730269    -0.043412712    -0.04428867     -0.045509181    -0.04645965     -0.047268246 -0.047974749      -0.048597109     -0.0491467  -0.049632388     -0.050061697      -0.050441198     -0.050776675     -0.051073238      -0.0513354 -0.051567152      -0.051772022     -0.051953128 -0.052113227 -0.052254754 -0.052379865 -0.052490464 -0.052588233 -0.052674662 -0.052751065 -0.052818606 -0.052878312 -0.052931093 -0.052977751 -0.053018997 -0.053055459 -0.053087691 -0.053116185 -0.053141373 -0.05316364 -0.053183324 -0.053200724 -0.053216106 -0.053229704 -0.053241725 -0.053252351 -0.053261745 -0.053270049 -0.053277389 -0.053283879 -0.053289615'
  []
[]

[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
  [stress_yy]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
  [tot_force]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
[]

[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
  [stress_yy]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_yy
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 1
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 1
  []
  [tot_force]
    type = ParsedAux<<<{"description": "Sets a field variable value to the evaluation of a parsed expression.", "href": "../../../../source/auxkernels/ParsedAux.html"}>>>
    coupled_variables<<<{"description": "Vector of coupled variable names"}>>> = 'stress_yy porepressure'
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = tot_force
    expression<<<{"description": "Parsed function expression to compute"}>>> = '-stress_yy+0.6*porepressure'
  []
[]

[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
  [grad_stress_x]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 0
  []
  [grad_stress_y]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 1
  []
  [grad_stress_z]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 2
  []
  [poro_x]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 0
  []
  [poro_y]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 1
  []
  [poro_z]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 2
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
  []
  [poro_vol_exp]
    type = PorousFlowMassVolumetricExpansion<<<{"description": "Component_mass*rate_of_solid_volumetric_expansion.  This Kernel lumps the component mass to the nodes.", "href": "../../../../source/kernels/PorousFlowMassVolumetricExpansion.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
  []
  [mass0]
    type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time.  Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
    fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
  []
  [flux]
    type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
    fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
  []
[]

[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
  [simple_fluid]
    type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
    bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 8
    density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1
    thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
    viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1
  []
[]

[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
  [temperature]
    type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
  []
  [elasticity_tensor]
    type = ComputeElasticityTensor<<<{"description": "Compute an elasticity tensor.", "href": "../../../../source/materials/ComputeElasticityTensor.html"}>>>
    C_ijkl<<<{"description": "Stiffness tensor for material"}>>> = '0.5 0.75'
    # bulk modulus is lambda + 2*mu/3 = 0.5 + 2*0.75/3 = 1
    fill_method<<<{"description": "The fill method"}>>> = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain<<<{"description": "Compute a small strain.", "href": "../../../../source/materials/ComputeSmallStrain.html"}>>>
  []
  [stress]
    type = ComputeLinearElasticStress<<<{"description": "Compute stress using elasticity for small strains", "href": "../../../../source/materials/ComputeLinearElasticStress.html"}>>>
  []
  [eff_fluid_pressure]
    type = PorousFlowEffectiveFluidPressure<<<{"description": "This Material calculates an effective fluid pressure: effective_stress = total_stress + biot_coeff*effective_fluid_pressure.  The effective_fluid_pressure = sum_{phases}(S_phase * P_phase)", "href": "../../../../source/materials/PorousFlowEffectiveFluidPressure.html"}>>>
  []
  [vol_strain]
    type = PorousFlowVolumetricStrain<<<{"description": "Compute volumetric strain and the volumetric_strain rate, for use in PorousFlow.", "href": "../../../../source/materials/PorousFlowVolumetricStrain.html"}>>>
  []
  [ppss]
    type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
    porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = porepressure
    capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
  []
  [massfrac]
    type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
  []
  [simple_fluid]
    type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
    fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
    phase<<<{"description": "The phase number"}>>> = 0
  []
  [porosity]
    type = PorousFlowPorosityHMBiotModulus<<<{"description": "This Material calculates the porosity for hydro-mechanical simulations, assuming that the Biot modulus and the fluid bulk modulus are both constant.  This is useful for comparing with solutions from poroelasticity theory, but is less accurate than PorousFlowPorosity", "href": "../../../../source/materials/PorousFlowPorosityHMBiotModulus.html"}>>>
    porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry.  This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.1
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1
    constant_fluid_bulk_modulus<<<{"description": "Fluid bulk modulus, which is constant for this Material"}>>> = 8
    constant_biot_modulus<<<{"description": "Biot modulus, which is constant for this Material"}>>> = 4.7058823529
  []
  [permeability]
    type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
    permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1.5 0 0   0 1.5 0   0 0 1.5'
  []
  [relperm]
    type = PorousFlowRelativePermeabilityCorey<<<{"description": "This Material calculates relative permeability of the fluid phase, using the simple Corey model ((S-S_res)/(1-sum(S_res)))^n", "href": "../../../../source/materials/PorousFlowRelativePermeabilityCorey.html"}>>>
    n<<<{"description": "The Corey exponent of the phase."}>>> = 0 # unimportant in this fully-saturated situation
    phase<<<{"description": "The phase number"}>>> = 0
  []
[]

[Postprocessors<<<{"href": "../../../../syntax/Postprocessors/index.html"}>>>]
  [p0]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p1]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.1 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p2]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.2 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p3]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.3 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p4]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.4 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p5]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.5 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p6]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.6 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p7]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.7 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p8]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.8 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p9]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.9 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p99]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [xdisp]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 0.1 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_x
  []
  [ydisp]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 0.1 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_y
  []
  [total_downwards_force]
     type = ElementAverageValue<<<{"description": "Computes the volumetric average of a variable", "href": "../../../../source/postprocessors/ElementAverageValue.html"}>>>
     outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
     variable<<<{"description": "The name of the variable that this object operates on"}>>> = tot_force
  []
  [dt]
    type = FunctionValuePostprocessor<<<{"description": "Computes the value of a supplied function at a single point (scalable)", "href": "../../../../source/postprocessors/FunctionValuePostprocessor.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = console
    function<<<{"description": "The function which supplies the postprocessor value."}>>> = if(0.15*t<0.01,0.15*t,0.01)
  []
[]

[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
  [andy]
    type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
    full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
    petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu 1E-14 1E-10 10000'
  []
[]

[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 0.7
  [TimeStepper<<<{"href": "../../../../syntax/Executioner/TimeStepper/index.html"}>>>]
    type = PostprocessorDT
    postprocessor = dt
    dt = 0.001
  []
[]

[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
  execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'timestep_end'
  file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = mandel_constM
  [csv]
    time_step_interval<<<{"description": "The interval (number of time steps) at which output occurs. Unless explicitly set, the default value of this parameter is set to infinity if the wall_time_interval is explicitly set."}>>> = 3
    type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
  []
[]

FullSat. This uses the FullySaturated versions of the fluid mass time derivative and the fluid flux. In this case the Biot modulus is kept fixed, so it is expected to agree with the analytical solutions.

# Mandel's problem of consolodation of a drained medium
# Using the FullySaturatedDarcyBase and FullySaturatedMassTimeDerivative kernels
#
# A sample is in plane strain.
# -a <= x <= a
# -b <= y <= b
# It is squashed with constant force by impermeable, frictionless plattens on its top and bottom surfaces (at y=+/-b)
# Fluid is allowed to leak out from its sides (at x=+/-a)
# The porepressure within the sample is monitored.
#
# As is common in the literature, this is simulated by
# considering the quarter-sample, 0<=x<=a and 0<=y<=b, with
# impermeable, roller BCs at x=0 and y=0 and y=b.
# Porepressure is fixed at zero on x=a.
# Porepressure and displacement are initialised to zero.
# Then the top (y=b) is moved downwards with prescribed velocity,
# so that the total force that is inducing this downwards velocity
# is fixed.  The velocity is worked out by solving Mandel's problem
# analytically, and the total force is monitored in the simulation
# to check that it indeed remains constant.
#
# Here are the problem's parameters, and their values:
# Soil width.  a = 1
# Soil height.  b = 0.1
# Soil's Lame lambda.  la = 0.5
# Soil's Lame mu, which is also the Soil's shear modulus.  mu = G = 0.75
# Soil bulk modulus.  K = la + 2*mu/3 = 1
# Drained Poisson ratio.  nu = (3K - 2G)/(6K + 2G) = 0.2
# Soil bulk compliance.  1/K = 1
# Fluid bulk modulus.  Kf = 8
# Fluid bulk compliance.  1/Kf = 0.125
# Soil initial porosity.  phi0 = 0.1
# Biot coefficient.  alpha = 0.6
# Biot modulus.  M = 1/(phi0/Kf + (alpha - phi0)(1 - alpha)/K) = 4.705882
# Undrained bulk modulus. Ku = K + alpha^2*M = 2.694118
# Undrained Poisson ratio.  nuu = (3Ku - 2G)/(6Ku + 2G) = 0.372627
# Skempton coefficient.  B = alpha*M/Ku = 1.048035
# Fluid mobility (soil permeability/fluid viscosity).  k = 1.5
# Consolidation coefficient.  c = 2*k*B^2*G*(1-nu)*(1+nuu)^2/9/(1-nuu)/(nuu-nu) = 3.821656
# Normal stress on top.  F = 1
#
# The solution for porepressure and displacements is given in
# AHD Cheng and E Detournay "A direct boundary element method for plane strain poroelasticity" International Journal of Numerical and Analytical Methods in Geomechanics 12 (1988) 551-572.
# The solution involves complicated infinite series, so I shall not write it here

[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
  type = GeneratedMesh
  dim = 3
  nx = 10
  ny = 1
  nz = 1
  xmin = 0
  xmax = 1
  ymin = 0
  ymax = 0.1
  zmin = 0
  zmax = 1
[]

[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
  [dictator]
    type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
    porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation.  Jacobian entries involving derivatives wrt these variables will be computed.  In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'porepressure disp_x disp_y disp_z'
    number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
    number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
  []
[]

[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
  [roller_xmin]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'left'
  []
  [roller_ymin]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'bottom'
  []
  [plane_strain]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'back front'
  []
  [xmax_drained]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
  []
  [top_velocity]
    type = FunctionDirichletBC<<<{"description": "Imposes the essential boundary condition $u=g(t,\\vec{x})$, where $g$ is a (possibly) time and space-dependent MOOSE Function.", "href": "../../../../source/bcs/FunctionDirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    function<<<{"description": "The forcing function."}>>> = top_velocity
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = top
  []
[]

[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
  [top_velocity]
    type = PiecewiseLinear<<<{"description": "Linearly interpolates between pairs of x-y data", "href": "../../../../source/functions/PiecewiseLinear.html"}>>>
    x<<<{"description": "The abscissa values"}>>> = '0 0.002 0.006   0.014   0.03    0.046   0.062   0.078   0.094   0.11    0.126   0.142   0.158   0.174   0.19 0.206 0.222 0.238 0.254 0.27 0.286 0.302 0.318 0.334 0.35 0.366 0.382 0.398 0.414 0.43 0.446 0.462 0.478 0.494 0.51 0.526 0.542 0.558 0.574 0.59 0.606 0.622 0.638 0.654 0.67 0.686 0.702'
    y<<<{"description": "The ordinate values"}>>> = '-0.041824842    -0.042730269    -0.043412712    -0.04428867     -0.045509181    -0.04645965     -0.047268246 -0.047974749      -0.048597109     -0.0491467  -0.049632388     -0.050061697      -0.050441198     -0.050776675     -0.051073238      -0.0513354 -0.051567152      -0.051772022     -0.051953128 -0.052113227 -0.052254754 -0.052379865 -0.052490464 -0.052588233 -0.052674662 -0.052751065 -0.052818606 -0.052878312 -0.052931093 -0.052977751 -0.053018997 -0.053055459 -0.053087691 -0.053116185 -0.053141373 -0.05316364 -0.053183324 -0.053200724 -0.053216106 -0.053229704 -0.053241725 -0.053252351 -0.053261745 -0.053270049 -0.053277389 -0.053283879 -0.053289615'
  []
[]

[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
  [stress_yy]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
  [tot_force]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
[]

[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
  [stress_yy]
    type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../../../source/auxkernels/RankTwoAux.html"}>>>
    rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_yy
    index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 1
    index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 1
  []
  [tot_force]
    type = ParsedAux<<<{"description": "Sets a field variable value to the evaluation of a parsed expression.", "href": "../../../../source/auxkernels/ParsedAux.html"}>>>
    coupled_variables<<<{"description": "Vector of coupled variable names"}>>> = 'stress_yy porepressure'
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = tot_force
    expression<<<{"description": "Parsed function expression to compute"}>>> = '-stress_yy+0.6*porepressure'
  []
[]

[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
  [grad_stress_x]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 0
  []
  [grad_stress_y]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 1
  []
  [grad_stress_z]
    type = StressDivergenceTensors<<<{"description": "Stress divergence kernel for the Cartesian coordinate system", "href": "../../../../source/kernels/StressDivergenceTensors.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    component<<<{"description": "An integer corresponding to the direction the variable this kernel acts in. (0 for x, 1 for y, 2 for z)"}>>> = 2
  []
  [poro_x]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 0
  []
  [poro_y]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 1
  []
  [poro_z]
    type = PorousFlowEffectiveStressCoupling<<<{"description": "Implements the weak form of the expression biot_coefficient * grad(effective fluid pressure)", "href": "../../../../source/kernels/PorousFlowEffectiveStressCoupling.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    component<<<{"description": "The component (0 for x, 1 for y and 2 for z) of grad(P)"}>>> = 2
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
  []
  [mass0]
    type = PorousFlowFullySaturatedMassTimeDerivative<<<{"description": "Fully-saturated version of the single-component, single-phase fluid mass derivative wrt time", "href": "../../../../source/kernels/PorousFlowFullySaturatedMassTimeDerivative.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    coupling_type<<<{"description": "The type of simulation.  For simulations involving Mechanical deformations, you will need to supply the correct Biot coefficient.  For simulations involving Thermal flows, you will need an associated ConstantThermalExpansionCoefficient Material"}>>> = HydroMechanical
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
  []
  [flux]
    type = PorousFlowFullySaturatedDarcyBase<<<{"description": "Darcy flux suitable for models involving a fully-saturated, single phase, single component fluid.  No upwinding is used", "href": "../../../../source/kernels/PorousFlowFullySaturatedDarcyBase.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
  []
[]

[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
  [simple_fluid]
    type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
    bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 8
    density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1
    thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
    viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1
  []
[]

[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
  [temperature]
    type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
  []
  [elasticity_tensor]
    type = ComputeElasticityTensor<<<{"description": "Compute an elasticity tensor.", "href": "../../../../source/materials/ComputeElasticityTensor.html"}>>>
    C_ijkl<<<{"description": "Stiffness tensor for material"}>>> = '0.5 0.75'
    # bulk modulus is lambda + 2*mu/3 = 0.5 + 2*0.75/3 = 1
    fill_method<<<{"description": "The fill method"}>>> = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain<<<{"description": "Compute a small strain.", "href": "../../../../source/materials/ComputeSmallStrain.html"}>>>
  []
  [stress]
    type = ComputeLinearElasticStress<<<{"description": "Compute stress using elasticity for small strains", "href": "../../../../source/materials/ComputeLinearElasticStress.html"}>>>
  []
  [eff_fluid_pressure_qp]
    type = PorousFlowEffectiveFluidPressure<<<{"description": "This Material calculates an effective fluid pressure: effective_stress = total_stress + biot_coeff*effective_fluid_pressure.  The effective_fluid_pressure = sum_{phases}(S_phase * P_phase)", "href": "../../../../source/materials/PorousFlowEffectiveFluidPressure.html"}>>>
  []
  [vol_strain]
    type = PorousFlowVolumetricStrain<<<{"description": "Compute volumetric strain and the volumetric_strain rate, for use in PorousFlow.", "href": "../../../../source/materials/PorousFlowVolumetricStrain.html"}>>>
  []
  [ppss]
    type = PorousFlow1PhaseFullySaturated<<<{"description": "This Material is used for the fully saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseFullySaturated.html"}>>>
    porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = porepressure
  []
  [massfrac]
    type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
  []
  [simple_fluid_qp]
    type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
    fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
    phase<<<{"description": "The phase number"}>>> = 0
  []
  [porosity]
    type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>> # only the initial value of this is ever used
    porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material).  This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.1
  []
  [biot_modulus]
    type = PorousFlowConstantBiotModulus<<<{"description": "Computes the Biot Modulus, which is assumed to be constant for all time.  Sometimes 1 / BiotModulus is called storativity", "href": "../../../../source/materials/PorousFlowConstantBiotModulus.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    solid_bulk_compliance<<<{"description": "Reciprocal of the drained bulk modulus of the porous skeleton.  If strain = C * stress, then solid_bulk_compliance = de_ij de_kl C_ijkl.  If the grain bulk modulus is Kg then 1/Kg = (1 - biot_coefficient) * solid_bulk_compliance."}>>> = 1
    fluid_bulk_modulus<<<{"description": "Fluid bulk modulus"}>>> = 8
  []
  [permeability]
    type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
    permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1.5 0 0   0 1.5 0   0 0 1.5'
  []
[]

[Postprocessors<<<{"href": "../../../../syntax/Postprocessors/index.html"}>>>]
  [p0]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p1]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.1 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p2]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.2 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p3]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.3 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p4]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.4 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p5]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.5 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p6]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.6 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p7]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.7 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p8]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.8 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p9]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.9 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p99]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [xdisp]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 0.1 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_x
  []
  [ydisp]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 0.1 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_y
  []
  [total_downwards_force]
     type = ElementAverageValue<<<{"description": "Computes the volumetric average of a variable", "href": "../../../../source/postprocessors/ElementAverageValue.html"}>>>
     outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
     variable<<<{"description": "The name of the variable that this object operates on"}>>> = tot_force
  []
  [dt]
    type = FunctionValuePostprocessor<<<{"description": "Computes the value of a supplied function at a single point (scalable)", "href": "../../../../source/postprocessors/FunctionValuePostprocessor.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = console
    function<<<{"description": "The function which supplies the postprocessor value."}>>> = if(0.15*t<0.01,0.15*t,0.01)
  []
[]

[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
  [andy]
    type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
    full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
    petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu 1E-14 1E-10 10000'
  []
[]

[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 0.7
  [TimeStepper<<<{"href": "../../../../syntax/Executioner/TimeStepper/index.html"}>>>]
    type = PostprocessorDT
    postprocessor = dt
    dt = 0.001
  []
[]

[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
  execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'timestep_end'
  file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = mandel_fully_saturated
  [csv]
    time_step_interval<<<{"description": "The interval (number of time steps) at which output occurs. Unless explicitly set, the default value of this parameter is set to infinity if the wall_time_interval is explicitly set."}>>> = 3
    type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
  []
[]

FullSatVol. This uses the FullySaturated versions of the fluid mass time derivative and the fluid flux, and does not multiply by the fluid density. Therefore this version is identical to what is usually implemented in poro-elastic codes. It is linear and therefore converges in only one iteration. In this case the Biot modulus is kept fixed, so it is expected to agree with the analytical solutions.

# using a BasicTHM Action
#
# Mandel's problem of consolodation of a drained medium
# Using the FullySaturatedDarcyBase and FullySaturatedFullySaturatedMassTimeDerivative kernels
# with multiply_by_density = false, so that this problem becomes linear
#
# A sample is in plane strain.
# -a <= x <= a
# -b <= y <= b
# It is squashed with constant force by impermeable, frictionless plattens on its top and bottom surfaces (at y=+/-b)
# Fluid is allowed to leak out from its sides (at x=+/-a)
# The porepressure within the sample is monitored.
#
# As is common in the literature, this is simulated by
# considering the quarter-sample, 0<=x<=a and 0<=y<=b, with
# impermeable, roller BCs at x=0 and y=0 and y=b.
# Porepressure is fixed at zero on x=a.
# Porepressure and displacement are initialised to zero.
# Then the top (y=b) is moved downwards with prescribed velocity,
# so that the total force that is inducing this downwards velocity
# is fixed.  The velocity is worked out by solving Mandel's problem
# analytically, and the total force is monitored in the simulation
# to check that it indeed remains constant.
#
# Here are the problem's parameters, and their values:
# Soil width.  a = 1
# Soil height.  b = 0.1
# Soil's Lame lambda.  la = 0.5
# Soil's Lame mu, which is also the Soil's shear modulus.  mu = G = 0.75
# Soil bulk modulus.  K = la + 2*mu/3 = 1
# Drained Poisson ratio.  nu = (3K - 2G)/(6K + 2G) = 0.2
# Soil bulk compliance.  1/K = 1
# Fluid bulk modulus.  Kf = 8
# Fluid bulk compliance.  1/Kf = 0.125
# Soil initial porosity.  phi0 = 0.1
# Biot coefficient.  alpha = 0.6
# Biot modulus.  M = 1/(phi0/Kf + (alpha - phi0)(1 - alpha)/K) = 4.705882
# Undrained bulk modulus. Ku = K + alpha^2*M = 2.694118
# Undrained Poisson ratio.  nuu = (3Ku - 2G)/(6Ku + 2G) = 0.372627
# Skempton coefficient.  B = alpha*M/Ku = 1.048035
# Fluid mobility (soil permeability/fluid viscosity).  k = 1.5
# Consolidation coefficient.  c = 2*k*B^2*G*(1-nu)*(1+nuu)^2/9/(1-nuu)/(nuu-nu) = 3.821656
# Normal stress on top.  F = 1
#
# The solution for porepressure and displacements is given in
# AHD Cheng and E Detournay "A direct boundary element method for plane strain poroelasticity" International Journal of Numerical and Analytical Methods in Geomechanics 12 (1988) 551-572.
# The solution involves complicated infinite series, so I shall not write it here

[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
  type = GeneratedMesh
  dim = 3
  nx = 10
  ny = 1
  nz = 1
  xmin = 0
  xmax = 1
  ymin = 0
  ymax = 0.1
  zmin = 0
  zmax = 1
[]

[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
  [roller_xmin]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'left'
  []
  [roller_ymin]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'bottom'
  []
  [plane_strain]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'back front'
  []
  [xmax_drained]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
    value<<<{"description": "Value of the BC"}>>> = 0
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
  []
  [top_velocity]
    type = FunctionDirichletBC<<<{"description": "Imposes the essential boundary condition $u=g(t,\\vec{x})$, where $g$ is a (possibly) time and space-dependent MOOSE Function.", "href": "../../../../source/bcs/FunctionDirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
    function<<<{"description": "The forcing function."}>>> = top_velocity
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = top
  []
[]

[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
  [top_velocity]
    type = PiecewiseLinear<<<{"description": "Linearly interpolates between pairs of x-y data", "href": "../../../../source/functions/PiecewiseLinear.html"}>>>
    x<<<{"description": "The abscissa values"}>>> = '0 0.002 0.006   0.014   0.03    0.046   0.062   0.078   0.094   0.11    0.126   0.142   0.158   0.174   0.19 0.206 0.222 0.238 0.254 0.27 0.286 0.302 0.318 0.334 0.35 0.366 0.382 0.398 0.414 0.43 0.446 0.462 0.478 0.494 0.51 0.526 0.542 0.558 0.574 0.59 0.606 0.622 0.638 0.654 0.67 0.686 0.702'
    y<<<{"description": "The ordinate values"}>>> = '-0.041824842    -0.042730269    -0.043412712    -0.04428867     -0.045509181    -0.04645965     -0.047268246 -0.047974749      -0.048597109     -0.0491467  -0.049632388     -0.050061697      -0.050441198     -0.050776675     -0.051073238      -0.0513354 -0.051567152      -0.051772022     -0.051953128 -0.052113227 -0.052254754 -0.052379865 -0.052490464 -0.052588233 -0.052674662 -0.052751065 -0.052818606 -0.052878312 -0.052931093 -0.052977751 -0.053018997 -0.053055459 -0.053087691 -0.053116185 -0.053141373 -0.05316364 -0.053183324 -0.053200724 -0.053216106 -0.053229704 -0.053241725 -0.053252351 -0.053261745 -0.053270049 -0.053277389 -0.053283879 -0.053289615'
  []
[]

[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
  [tot_force]
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
  []
[]

[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
  [tot_force]
    type = ParsedAux<<<{"description": "Sets a field variable value to the evaluation of a parsed expression.", "href": "../../../../source/auxkernels/ParsedAux.html"}>>>
    coupled_variables<<<{"description": "Vector of coupled variable names"}>>> = 'stress_yy porepressure'
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = tot_force
    expression<<<{"description": "Parsed function expression to compute"}>>> = '-stress_yy+0.6*porepressure'
  []
[]

[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
  [the_simple_fluid]
    type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
    thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0.0
    bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 8.0
    viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1.0
    density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1.0
  []
[]

[PorousFlowBasicTHM<<<{"href": "../../../../syntax/PorousFlowBasicTHM/index.html"}>>>]
  coupling_type<<<{"description": "The type of simulation.  For simulations involving Mechanical deformations, you will need to supply the correct Biot coefficient.  For simulations involving Thermal flows, you will need an associated ConstantThermalExpansionCoefficient Material"}>>> = HydroMechanical
  displacements<<<{"description": "The name of the displacement variables (relevant only for mechanically-coupled simulations)"}>>> = 'disp_x disp_y disp_z'
  multiply_by_density<<<{"description": "If true, then the Kernels for fluid flow are multiplied by the fluid density.  If false, this multiplication is not performed, which means the problem linearises, but that care must be taken when using other PorousFlow objects."}>>> = false
  porepressure<<<{"description": "The name of the porepressure variable"}>>> = porepressure
  biot_coefficient<<<{"description": "The Biot coefficient (relevant only for mechanically-coupled simulations)"}>>> = 0.6
  gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
  fp<<<{"description": "The name of the user object for fluid properties. Only needed if fluid_properties_type = PorousFlowSingleComponentFluid"}>>> = the_simple_fluid
[]

[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
  [elasticity_tensor]
    type = ComputeElasticityTensor<<<{"description": "Compute an elasticity tensor.", "href": "../../../../source/materials/ComputeElasticityTensor.html"}>>>
    C_ijkl<<<{"description": "Stiffness tensor for material"}>>> = '0.5 0.75'
    # bulk modulus is lambda + 2*mu/3 = 0.5 + 2*0.75/3 = 1
    fill_method<<<{"description": "The fill method"}>>> = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain<<<{"description": "Compute a small strain.", "href": "../../../../source/materials/ComputeSmallStrain.html"}>>>
  []
  [stress]
    type = ComputeLinearElasticStress<<<{"description": "Compute stress using elasticity for small strains", "href": "../../../../source/materials/ComputeLinearElasticStress.html"}>>>
  []
  [porosity]
    type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>> # only the initial value of this is ever used
    porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material).  This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.1
  []
  [biot_modulus]
    type = PorousFlowConstantBiotModulus<<<{"description": "Computes the Biot Modulus, which is assumed to be constant for all time.  Sometimes 1 / BiotModulus is called storativity", "href": "../../../../source/materials/PorousFlowConstantBiotModulus.html"}>>>
    biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.6
    solid_bulk_compliance<<<{"description": "Reciprocal of the drained bulk modulus of the porous skeleton.  If strain = C * stress, then solid_bulk_compliance = de_ij de_kl C_ijkl.  If the grain bulk modulus is Kg then 1/Kg = (1 - biot_coefficient) * solid_bulk_compliance."}>>> = 1
    fluid_bulk_modulus<<<{"description": "Fluid bulk modulus"}>>> = 8
  []
  [permeability]
    type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
    permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1.5 0 0   0 1.5 0   0 0 1.5'
  []
[]

[Postprocessors<<<{"href": "../../../../syntax/Postprocessors/index.html"}>>>]
  [p0]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.0 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p1]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.1 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p2]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.2 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p3]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.3 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p4]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.4 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p5]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.5 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p6]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.6 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p7]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.7 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p8]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.8 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p9]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '0.9 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [p99]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 0 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = porepressure
  []
  [xdisp]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 0.1 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_x
  []
  [ydisp]
    type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../../../source/postprocessors/PointValue.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
    point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '1 0.1 0'
    variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = disp_y
  []
  [total_downwards_force]
     type = ElementAverageValue<<<{"description": "Computes the volumetric average of a variable", "href": "../../../../source/postprocessors/ElementAverageValue.html"}>>>
     outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = csv
     variable<<<{"description": "The name of the variable that this object operates on"}>>> = tot_force
  []
  [dt]
    type = FunctionValuePostprocessor<<<{"description": "Computes the value of a supplied function at a single point (scalable)", "href": "../../../../source/postprocessors/FunctionValuePostprocessor.html"}>>>
    outputs<<<{"description": "Vector of output names where you would like to restrict the output of variables(s) associated with this object"}>>> = console
    function<<<{"description": "The function which supplies the postprocessor value."}>>> = if(0.15*t<0.01,0.15*t,0.01)
  []
[]

[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
  [andy]
    type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
    full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
    petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu 1E-14 1E-10 10000'
  []
[]

[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 0.7
  [TimeStepper<<<{"href": "../../../../syntax/Executioner/TimeStepper/index.html"}>>>]
    type = PostprocessorDT
    postprocessor = dt
    dt = 0.001
  []
[]

[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
  execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'timestep_end'
  file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = mandel_basicthm
  [csv]
    time_step_interval<<<{"description": "The interval (number of time steps) at which output occurs. Unless explicitly set, the default value of this parameter is set to infinity if the wall_time_interval is explicitly set."}>>> = 3
    type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
  []
[]

Of course there are minor discrepancies between the last three and the analytical solution that are brought about through spatial and temporal discretisation errors. The figures below present the results.

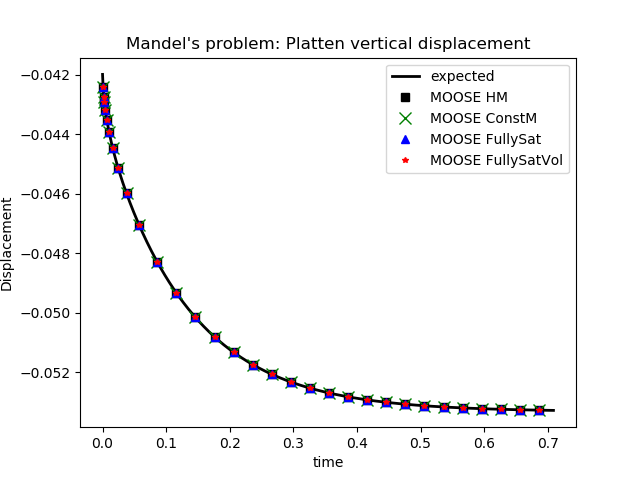
Figure 4: The vertical displacement of the platten as a function of time.

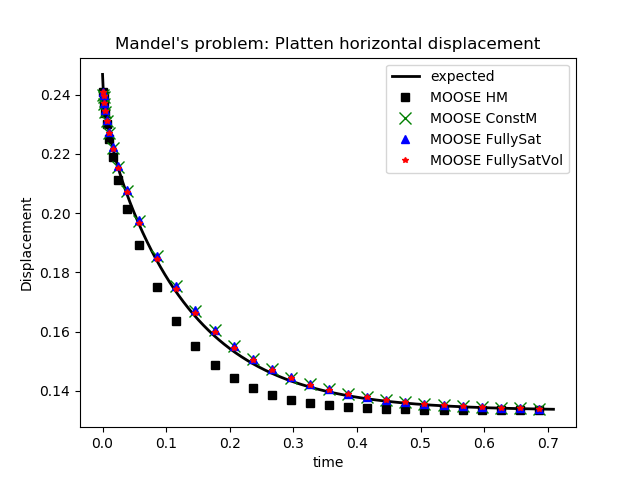
Figure 5: The horizontal displacement of the platten's top-right corner.

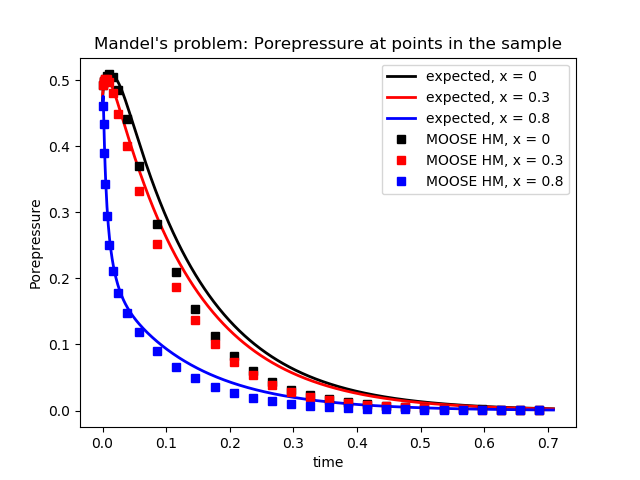
Figure 6: The porepressure at various points in the sample in the HM model ("a" is equal to unity).

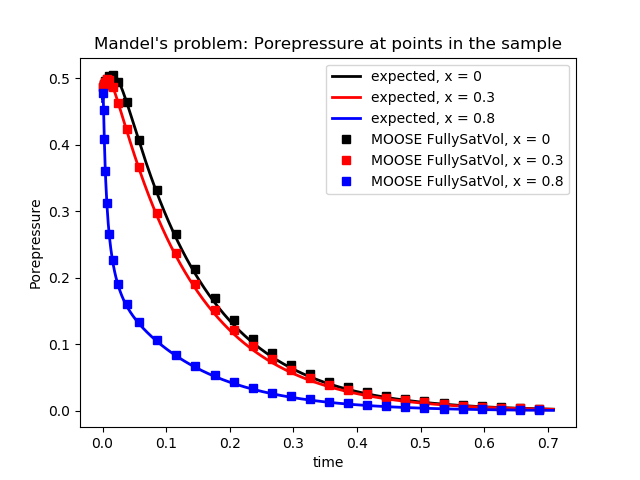
Figure 7: The porepressure at various points in the sample in the FullSatVol model ("a" is equal to unity).

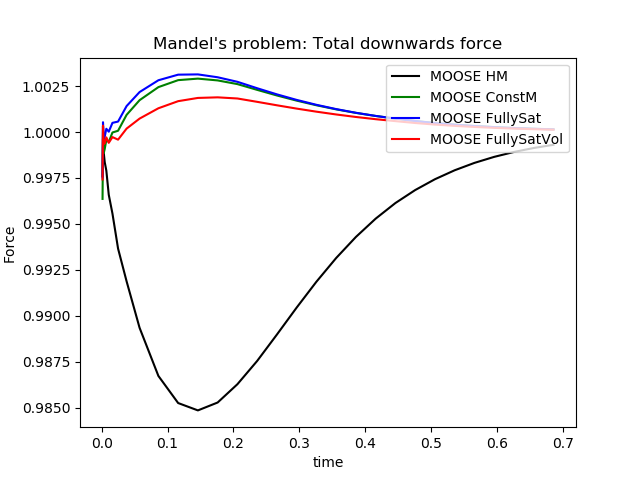
Figure 8: The total downwards force on the platten as a function of time. This should be unity.

References

Alexander H.-D. Cheng and Emmanuel Detournay. A direct boundary element method for plane strain poroelasticity. International Journal for Numerical and Analytical Methods in Geomechanics, 12(5):551–572, 1988. URL: https://onlinelibrary.wiley.com/doi/abs/10.1002/nag.1610120508, arXiv:https://onlinelibrary.wiley.com/doi/pdf/10.1002/nag.1610120508, doi:10.1002/nag.1610120508.

@article{doi:10.1002/nag.1610120508,
    author = "Cheng, Alexander H.-D. and Detournay, Emmanuel",
    title = "A direct boundary element method for plane strain poroelasticity",
    journal = "International Journal for Numerical and Analytical Methods in Geomechanics",
    volume = "12",
    number = "5",
    pages = "551-572",
    doi = "10.1002/nag.1610120508",
    url = "https://onlinelibrary.wiley.com/doi/abs/10.1002/nag.1610120508",
    eprint = "https://onlinelibrary.wiley.com/doi/pdf/10.1002/nag.1610120508",
    year = "1988"
}

(modules/porous_flow/test/tests/poro_elasticity/vol_expansion.i)

# Apply an increasing porepressure, with zero mechanical forces,
# and observe the corresponding volumetric expansion
#
# P = t
# With the Biot coefficient being 0.3, the effective stresses should be
# stress_xx = stress_yy = stress_zz = 0.3t
# With bulk modulus = 1 then should have
# vol_strain = strain_xx + strain_yy + strain_zz = 0.3t.
# I use a single element lying 0<=x<=1, 0<=y<=1 and 0<=z<=1, and
# fix the left, bottom and back boundaries appropriately,
# so at the point x=y=z=1, the displacements should be
# disp_x = disp_y = disp_z = 0.3t/3 (small strain physics is used)
[Mesh]
  type = GeneratedMesh
  dim = 3
  nx = 1
  ny = 1
  nz = 1
  xmin = 0
  xmax = 1
  ymin = 0
  ymax = 1
  zmin = 0
  zmax = 1
[]

[GlobalParams]
  displacements = 'disp_x disp_y disp_z'
  block = 0
  PorousFlowDictator = dictator
[]

[Variables]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [p]
  []
[]

[BCs]
  [p]
    type = FunctionDirichletBC
    boundary = 'bottom top'
    variable = p
    function = t
  []
  [xmin]
    type = DirichletBC
    boundary = left
    variable = disp_x
    value = 0
  []
  [ymin]
    type = DirichletBC
    boundary = bottom
    variable = disp_y
    value = 0
  []
  [zmin]
    type = DirichletBC
    boundary = back
    variable = disp_z
    value = 0
  []
[]

[Kernels]
  [p_does_not_really_diffuse]
    type = Diffusion
    variable = p
  []
  [TensorMechanics]
    displacements = 'disp_x disp_y disp_z'
  []
  [poro_x]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.3
    variable = disp_x
    component = 0
  []
  [poro_y]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.3
    variable = disp_y
    component = 1
  []
  [poro_z]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.3
    variable = disp_z
    component = 2
  []
[]

[AuxVariables]
  [stress_xx]
    order = CONSTANT
    family = MONOMIAL
  []
  [stress_xy]
    order = CONSTANT
    family = MONOMIAL
  []
  [stress_xz]
    order = CONSTANT
    family = MONOMIAL
  []
  [stress_yy]
    order = CONSTANT
    family = MONOMIAL
  []
  [stress_yz]
    order = CONSTANT
    family = MONOMIAL
  []
  [stress_zz]
    order = CONSTANT
    family = MONOMIAL
  []
[]

[AuxKernels]
  [stress_xx]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_xx
    index_i = 0
    index_j = 0
  []
  [stress_xy]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_xy
    index_i = 0
    index_j = 1
  []
  [stress_xz]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_xz
    index_i = 0
    index_j = 2
  []
  [stress_yy]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_yy
    index_i = 1
    index_j = 1
  []
  [stress_yz]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_yz
    index_i = 1
    index_j = 2
  []
  [stress_zz]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_zz
    index_i = 2
    index_j = 2
  []
[]

[Postprocessors]
  [corner_x]
    type = PointValue
    point = '1 1 1'
    variable = disp_x
  []
  [corner_y]
    type = PointValue
    point = '1 1 1'
    variable = disp_y
  []
  [corner_z]
    type = PointValue
    point = '1 1 1'
    variable = disp_z
  []
[]

[UserObjects]
  [dictator]
    type = PorousFlowDictator
    porous_flow_vars = 'p'
    number_fluid_phases = 1
    number_fluid_components = 1
  []
  [pc]
    type = PorousFlowCapillaryPressureVG
    m = 0.5
    alpha = 1
  []
[]

[Materials]
  [temperature]
    type = PorousFlowTemperature
  []
  [elasticity_tensor]
    type = ComputeElasticityTensor
    # bulk modulus = 1, poisson ratio = 0.2
    C_ijkl = '0.5 0.75'
    fill_method = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain
    displacements = 'disp_x disp_y disp_z'
  []
  [stress]
    type = ComputeLinearElasticStress
  []
  [ppss]
    type = PorousFlow1PhaseP
    porepressure = p
    capillary_pressure = pc
  []
  [p_eff]
    type = PorousFlowEffectiveFluidPressure
  []
[]

[Preconditioning]
  [andy]
    type = SMP
    full = true
    petsc_options_iname = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it -ksp_atol -ksp_rtol'
    petsc_options_value = 'gmres bjacobi 1E-10 1E-10 10 1E-15 1E-10'
  []
[]

[Executioner]
  type = Transient
  solve_type = Newton
  start_time = 0
  dt = 0.1
  end_time = 1
[]

[Outputs]
  file_base = vol_expansion
  exodus = true
[]

(modules/porous_flow/test/tests/poro_elasticity/undrained_oedometer.i)

# An undrained oedometer test on a saturated poroelastic sample.
#
# The sample is a single unit element, with roller BCs on the sides
# and bottom.  A constant displacement is applied to the top: disp_z = -0.01*t.
# There is no fluid flow.
#
# Under these conditions
# porepressure = -(Fluid bulk modulus)*log(1 - 0.01t)
# stress_xx = (bulk - 2*shear/3)*disp_z/L (remember this is effective stress)
# stress_zz = (bulk + 4*shear/3)*disp_z/L (remember this is effective stress)
# where L is the height of the sample (L=1 in this test)
#
# Parameters:
# Bulk modulus = 2
# Shear modulus = 1.5
# fluid bulk modulus = 1
#
# Desired output:
# zdisp = -0.01*t
# p0 = 1*log(1-0.01t)
# stress_xx = stress_yy = -0.01*t
# stress_zz = -0.04*t
#
# Regarding the "log" - it just comes from conserving fluid mass

[Mesh]
  type = GeneratedMesh
  dim = 3
  nx = 1
  ny = 1
  nz = 1
  xmin = -0.5
  xmax = 0.5
  ymin = -0.5
  ymax = 0.5
  zmin = -0.5
  zmax = 0.5
[]

[GlobalParams]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[Variables]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs]
  [confinex]
    type = DirichletBC
    variable = disp_x
    value = 0
    boundary = 'left right'
  []
  [confiney]
    type = DirichletBC
    variable = disp_y
    value = 0
    boundary = 'bottom top'
  []
  [basefixed]
    type = DirichletBC
    variable = disp_z
    value = 0
    boundary = back
  []
  [top_velocity]
    type = FunctionDirichletBC
    variable = disp_z
    function = -0.01*t
    boundary = front
  []
[]

[Kernels]
  [grad_stress_x]
    type = StressDivergenceTensors
    variable = disp_x
    component = 0
  []
  [grad_stress_y]
    type = StressDivergenceTensors
    variable = disp_y
    component = 1
  []
  [grad_stress_z]
    type = StressDivergenceTensors
    variable = disp_z
    component = 2
  []
  [poro_vol_exp]
    type = PorousFlowMassVolumetricExpansion
    variable = porepressure
    fluid_component = 0
  []
  [mass0]
    type = PorousFlowMassTimeDerivative
    fluid_component = 0
    variable = porepressure
  []
[]

[AuxVariables]
  [stress_xx]
    order = CONSTANT
    family = MONOMIAL
  []
  [stress_xy]
    order = CONSTANT
    family = MONOMIAL
  []
  [stress_xz]
    order = CONSTANT
    family = MONOMIAL
  []
  [stress_yy]
    order = CONSTANT
    family = MONOMIAL
  []
  [stress_yz]
    order = CONSTANT
    family = MONOMIAL
  []
  [stress_zz]
    order = CONSTANT
    family = MONOMIAL
  []
[]

[AuxKernels]
  [stress_xx]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_xx
    index_i = 0
    index_j = 0
  []
  [stress_xy]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_xy
    index_i = 0
    index_j = 1
  []
  [stress_xz]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_xz
    index_i = 0
    index_j = 2
  []
  [stress_yy]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_yy
    index_i = 1
    index_j = 1
  []
  [stress_yz]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_yz
    index_i = 1
    index_j = 2
  []
  [stress_zz]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_zz
    index_i = 2
    index_j = 2
  []
[]

[FluidProperties]
  [simple_fluid]
    type = SimpleFluidProperties
    bulk_modulus = 1
    density0 = 1
    thermal_expansion = 0
  []
[]

[Materials]
  [temperature]
    type = PorousFlowTemperature
  []
  [elasticity_tensor]
    type = ComputeElasticityTensor
    C_ijkl = '1 1.5'
    # bulk modulus is lambda + 2*mu/3 = 1 + 2*1.5/3 = 2
    fill_method = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain
  []
  [stress]
    type = ComputeLinearElasticStress
  []
  [vol_strain]
    type = PorousFlowVolumetricStrain
  []
  [eff_fluid_pressure]
    type = PorousFlowEffectiveFluidPressure
  []
  [ppss]
    type = PorousFlow1PhaseP
    porepressure = porepressure
    capillary_pressure = pc
  []
  [massfrac]
    type = PorousFlowMassFraction
  []
  [simple_fluid]
    type = PorousFlowSingleComponentFluid
    fp = simple_fluid
    phase = 0
  []
  [porosity]
    type = PorousFlowPorosityConst
    porosity = 0.1
  []
[]

[UserObjects]
  [dictator]
    type = PorousFlowDictator
    porous_flow_vars = 'porepressure disp_x disp_y disp_z'
    number_fluid_phases = 1
    number_fluid_components = 1
  []
  [pc]
    type = PorousFlowCapillaryPressureVG
    m = 0.8
    alpha = 1
  []
[]

[Postprocessors]
  [fluid_mass]
    type = PorousFlowFluidMass
    fluid_component = 0
    execute_on = 'initial timestep_end'
  []
  [p0]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = porepressure
  []
  [zdisp]
    type = PointValue
    outputs = csv
    point = '0 0 0.5'
    variable = disp_z
  []
  [stress_xx]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = stress_xx
  []
  [stress_yy]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = stress_yy
  []
  [stress_zz]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = stress_zz
  []

[]

[Preconditioning]
  [andy]
    type = SMP
    full = true
    petsc_options_iname = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value = 'bcgs bjacobi 1E-14 1E-8 10000'
  []
[]

[Executioner]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 10
  dt = 1
[]

[Outputs]
  execute_on = 'timestep_end'
  file_base = undrained_oedometer
  [csv]
    type = CSV
  []
[]

(modules/porous_flow/test/tests/poro_elasticity/pp_generation_fullysat_action.i)

# Same as pp_generation.i, but using an Action
#
# A sample is constrained on all sides and its boundaries are
# also impermeable.  Fluid is pumped into the sample via a
# volumetric source (ie kg/second per cubic meter), and the
# rise in porepressure is observed.
#
# Source = s  (units = kg/m^3/second)
#
# Expect:
# fluid_mass = mass0 + s*t
# stress = 0 (remember this is effective stress)
# Porepressure = fluid_bulk*log(fluid_mass_density/density_P0), where fluid_mass_density = fluid_mass/porosity
# porosity = biot+(phi0-biot)*exp(pp(biot-1)/solid_bulk)
#
# Parameters:
# Biot coefficient = 0.3
# Phi0 = 0.1
# Solid Bulk modulus = 2
# fluid_bulk = 13
# density_P0 = 1

[Mesh]
  type = GeneratedMesh
  dim = 3
  nx = 1
  ny = 1
  nz = 1
  xmin = -0.5
  xmax = 0.5
  ymin = -0.5
  ymax = 0.5
  zmin = -0.5
  zmax = 0.5
[]

[GlobalParams]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[Variables]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[FluidProperties]
  [the_simple_fluid]
    type = SimpleFluidProperties
    thermal_expansion = 0.0
    bulk_modulus = 13.0
    viscosity = 1.0
    density0 = 1.0
  []
[]

[PorousFlowFullySaturated]
  coupling_type = HydroMechanical
  displacements = 'disp_x disp_y disp_z'
  porepressure = porepressure
  biot_coefficient = 0.3
  gravity = '0 0 0'
  fp = the_simple_fluid
  stabilization = none # not needed: there is no flow
  save_component_rate_in = nodal_kg_per_s
[]

[BCs]
  [confinex]
    type = DirichletBC
    variable = disp_x
    value = 0
    boundary = 'left right'
  []
  [confiney]
    type = DirichletBC
    variable = disp_y
    value = 0
    boundary = 'bottom top'
  []
  [confinez]
    type = DirichletBC
    variable = disp_z
    value = 0
    boundary = 'back front'
  []
[]


[Kernels]
  [source]
    type = BodyForce
    function = 0.1
    variable = porepressure
  []
[]

[AuxVariables]
  [nodal_kg_per_s]
  []
  [porosity]
    order = CONSTANT
    family = MONOMIAL
  []
[]

[AuxKernels]
  [porosity]
    type = PorousFlowPropertyAux
    variable = porosity
    property = porosity
  []
[]

[Materials]
  [elasticity_tensor]
    type = ComputeElasticityTensor
    C_ijkl = '1 1.5'
    # bulk modulus is lambda + 2*mu/3 = 1 + 2*1.5/3 = 2
    fill_method = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain
  []
  [stress]
    type = ComputeLinearElasticStress
  []
  [porosity]
    type = PorousFlowPorosity
    fluid = true
    mechanical = true
    porosity_zero = 0.1
    biot_coefficient = 0.3
    solid_bulk = 2
  []
  [permeability]
    type = PorousFlowPermeabilityConst
    permeability = '1 0 0   0 1 0   0 0 1' # unimportant
  []
[]

[Functions]
  [porosity_analytic]
    type = ParsedFunction
    expression = 'biot+(phi0-biot)*exp(pp*(biot-1)/bulk)'
    symbol_names = 'biot phi0 pp bulk'
    symbol_values = '0.3 0.1 p0 2'
  []
[]

[Postprocessors]
  [nodal_kg_per_s]
    type = PointValue
    point = ' 0 0 0'
    variable = nodal_kg_per_s
    outputs = csv
  []
  [fluid_mass]
    type = PorousFlowFluidMass
    fluid_component = 0
    execute_on = 'initial timestep_end'
  []
  [porosity]
    type = PointValue
    outputs = 'console csv'
    point = '0 0 0'
    variable = porosity
  []
  [p0]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = porepressure
  []
  [porosity_analytic]
    type = FunctionValuePostprocessor
    function = porosity_analytic
  []
  [zdisp]
    type = PointValue
    outputs = csv
    point = '0 0 0.5'
    variable = disp_z
  []
  [stress_xx]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = stress_xx
  []
  [stress_yy]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = stress_yy
  []
  [stress_zz]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = stress_zz
  []

[]


[Preconditioning]
  [andy]
    type = SMP
    full = true
    petsc_options_iname = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value = 'bcgs bjacobi 1E-14 1E-10 10000'
  []
[]

[Executioner]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 10
  dt = 1
[]

[Outputs]
  execute_on = 'timestep_end'
  file_base = pp_generation_fullysat_action
  csv = true
[]

(modules/porous_flow/test/tests/poro_elasticity/pp_generation_unconfined_basicthm.i)

# Identical to pp_generation_unconfined_fullysat_volume.i but using an Action
#
# A sample is constrained on all sides, except its top
# and its boundaries are
# also impermeable.  Fluid is pumped into the sample via a
# volumetric source (ie m^3/second per cubic meter), and the
# rise in the top surface, porepressure, and stress are observed.
#
# In the standard poromechanics scenario, the Biot Modulus is held
# fixed and the source has units 1/s.  Then the expected result
# is
# strain_zz = disp_z = BiotCoefficient*BiotModulus*s*t/((bulk + 4*shear/3) + BiotCoefficient^2*BiotModulus)
# porepressure = BiotModulus*(s*t - BiotCoefficient*strain_zz)
# stress_xx = (bulk - 2*shear/3)*strain_zz   (remember this is effective stress)
# stress_zz = (bulk + 4*shear/3)*strain_zz   (remember this is effective stress)
#
# In standard porous_flow, everything is based on mass, eg the source has
# units kg/s/m^3.  This is discussed in the other pp_generation_unconfined
# models.  In this test, we use the FullySaturated Kernel and set
# multiply_by_density = false
# meaning the fluid Kernel has units of volume, and the source, s, has units 1/time
#
# The ratios are:
# stress_xx/strain_zz = (bulk - 2*shear/3) = 1 (for the parameters used here)
# stress_zz/strain_zz = (bulk + 4*shear/3) = 4 (for the parameters used here)
# porepressure/strain_zz = 13.3333333 (for the parameters used here)
#
# Expect
# disp_z = 0.3*10*s*t/((2 + 4*1.5/3) + 0.3^2*10) = 0.612245*s*t
# porepressure = 10*(s*t - 0.3*0.612245*s*t) = 8.163265*s*t
# stress_xx = (2 - 2*1.5/3)*0.612245*s*t = 0.612245*s*t
# stress_zz = (2 + 4*shear/3)*0.612245*s*t = 2.44898*s*t
[Mesh]
  type = GeneratedMesh
  dim = 3
  nx = 1
  ny = 1
  nz = 1
  xmin = -0.5
  xmax = 0.5
  ymin = -0.5
  ymax = 0.5
  zmin = -0.5
  zmax = 0.5
[]

[Variables]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs]
  [confinex]
    type = DirichletBC
    variable = disp_x
    value = 0
    boundary = 'left right'
  []
  [confiney]
    type = DirichletBC
    variable = disp_y
    value = 0
    boundary = 'bottom top'
  []
  [confinez]
    type = DirichletBC
    variable = disp_z
    value = 0
    boundary = 'back'
  []
[]


[Kernels]
  [source]
    type = BodyForce
    function = 0.1
    variable = porepressure
  []
[]

[FluidProperties]
  [the_simple_fluid]
    type = SimpleFluidProperties
    thermal_expansion = 0.0
    bulk_modulus = 3.3333333333
    viscosity = 1.0
    density0 = 1.0
  []
[]

[PorousFlowBasicTHM]
  coupling_type = HydroMechanical
  displacements = 'disp_x disp_y disp_z'
  multiply_by_density = false
  porepressure = porepressure
  biot_coefficient = 0.3
  gravity = '0 0 0'
  fp = the_simple_fluid
  save_component_rate_in = nodal_m3_per_s
[]


[Materials]
  [elasticity_tensor]
    type = ComputeElasticityTensor
    C_ijkl = '1 1.5'
    # bulk modulus is lambda + 2*mu/3 = 1 + 2*1.5/3 = 2
    fill_method = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain
    displacements = 'disp_x disp_y disp_z'
  []
  [stress]
    type = ComputeLinearElasticStress
  []
  [porosity]
    type = PorousFlowPorosityConst # the "const" is irrelevant here: all that uses Porosity is the BiotModulus, which just uses the initial value of porosity
    porosity = 0.1
    PorousFlowDictator = dictator
  []
  [biot_modulus]
    type = PorousFlowConstantBiotModulus
    PorousFlowDictator = dictator
    biot_coefficient = 0.3
    fluid_bulk_modulus = 3.3333333333
    solid_bulk_compliance = 0.5
  []
  [permeability_irrelevant]
    type = PorousFlowPermeabilityConst
    PorousFlowDictator = dictator
    permeability = '1.5 0 0   0 1.5 0   0 0 1.5'
  []
[]

[AuxVariables]
  [nodal_m3_per_s]
  []
[]

[Postprocessors]
  [nodal_m3_per_s]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = nodal_m3_per_s
  []
  [p0]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = porepressure
  []
  [zdisp]
    type = PointValue
    outputs = csv
    point = '0 0 0.5'
    variable = disp_z
  []
  [stress_xx]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = stress_xx
  []
  [stress_yy]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = stress_yy
  []
  [stress_zz]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = stress_zz
  []
  [stress_xx_over_strain]
    type = FunctionValuePostprocessor
    function = stress_xx_over_strain_fcn
    outputs = csv
  []
  [stress_zz_over_strain]
    type = FunctionValuePostprocessor
    function = stress_zz_over_strain_fcn
    outputs = csv
  []
  [p_over_strain]
    type = FunctionValuePostprocessor
    function = p_over_strain_fcn
    outputs = csv
  []
[]

[Functions]
  [stress_xx_over_strain_fcn]
    type = ParsedFunction
    expression = a/b
    symbol_names = 'a b'
    symbol_values = 'stress_xx zdisp'
  []
  [stress_zz_over_strain_fcn]
    type = ParsedFunction
    expression = a/b
    symbol_names = 'a b'
    symbol_values = 'stress_zz zdisp'
  []
  [p_over_strain_fcn]
    type = ParsedFunction
    expression = a/b
    symbol_names = 'a b'
    symbol_values = 'p0 zdisp'
  []
[]


[Preconditioning]
  [andy]
    type = SMP
    full = true
    petsc_options_iname = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value = 'bcgs bjacobi 1E-14 1E-10 10000'
  []
[]

[Executioner]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 10
  dt = 1
[]

[Outputs]
  execute_on = 'timestep_end'
  file_base = pp_generation_unconfined_basicthm
  [csv]
    type = CSV
  []
[]

(modules/porous_flow/test/tests/poro_elasticity/pp_generation_unconfined_constM_action.i)

# This file uses a PorousFlowFullySaturated Action.  The equivalent non-Action input file is pp_generation_unconfined_constM.i
#
# A sample is constrained on all sides, except its top
# and its boundaries are
# also impermeable.  Fluid is pumped into the sample via a
# volumetric source (ie kg/second per cubic meter), and the
# rise in the top surface, porepressure, and stress are observed.
#
# In the standard poromechanics scenario, the Biot Modulus is held
# fixed and the source, s, has units m^3/second/m^3.  Then the expected result
# is
# strain_zz = disp_z = BiotCoefficient*BiotModulus*s*t/((bulk + 4*shear/3) + BiotCoefficient^2*BiotModulus)
# porepressure = BiotModulus*(s*t - BiotCoefficient*strain_zz)
# stress_xx = (bulk - 2*shear/3)*strain_zz   (remember this is effective stress)
# stress_zz = (bulk + 4*shear/3)*strain_zz   (remember this is effective stress)
#
# In porous_flow, however, the source has units kg/second/m^3.  The ratios remain
# fixed:
# stress_xx/strain_zz = (bulk - 2*shear/3) = 1 (for the parameters used here)
# stress_zz/strain_zz = (bulk + 4*shear/3) = 4 (for the parameters used here)
# porepressure/strain_zz = 13.3333333 (for the parameters used here)
#
# Expect
# disp_z = 0.3*10*s*t/((2 + 4*1.5/3) + 0.3^2*10) = 0.612245*s*t
# porepressure = 10*(s*t - 0.3*0.612245*s*t) = 8.163265*s*t
# stress_xx = (2 - 2*1.5/3)*0.612245*s*t = 0.612245*s*t
# stress_zz = (2 + 4*shear/3)*0.612245*s*t = 2.44898*s*t
# The relationship between the constant poroelastic source
# s (m^3/second/m^3) and the PorousFlow source, S (kg/second/m^3) is
# S = fluid_density * s = s * exp(porepressure/fluid_bulk)

[Mesh]
  type = GeneratedMesh
  dim = 3
  nx = 1
  ny = 1
  nz = 1
  xmin = -0.5
  xmax = 0.5
  ymin = -0.5
  ymax = 0.5
  zmin = -0.5
  zmax = 0.5
[]

[GlobalParams]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[Variables]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs]
  [confinex]
    type = DirichletBC
    variable = disp_x
    value = 0
    boundary = 'left right'
  []
  [confiney]
    type = DirichletBC
    variable = disp_y
    value = 0
    boundary = 'bottom top'
  []
  [confinez]
    type = DirichletBC
    variable = disp_z
    value = 0
    boundary = 'back'
  []
[]

[PorousFlowFullySaturated]
  porepressure = porepressure
  biot_coefficient = 0.3
  coupling_type = HydroMechanical
  displacements = 'disp_x disp_y disp_z'
  gravity = '0 0 0'
  fp = simple_fluid
  stabilization = Full
[]

[Kernels]
  [source]
    type = BodyForce
    function = '0.1*exp(8.163265306*0.1*t/3.3333333333)'
    variable = porepressure
  []
[]

[FluidProperties]
  [simple_fluid]
    type = SimpleFluidProperties
    bulk_modulus = 3.3333333333
    density0 = 1
    thermal_expansion = 0
    viscosity = 1
  []
[]

[Materials]
  [elasticity_tensor]
    type = ComputeElasticityTensor
    C_ijkl = '1 1.5'
    # bulk modulus is lambda + 2*mu/3 = 1 + 2*1.5/3 = 2
    fill_method = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain
    displacements = 'disp_x disp_y disp_z'
  []
  [stress]
    type = ComputeLinearElasticStress
  []
  [porosity]
    type = PorousFlowPorosityHMBiotModulus
    porosity_zero = 0.1
    biot_coefficient = 0.3
    solid_bulk = 2
    constant_fluid_bulk_modulus = 3.3333333333
    constant_biot_modulus = 10.0
  []
  [permeability]
    type = PorousFlowPermeabilityConst
    permeability = '1 0 0   0 1 0   0 0 1' # unimportant
  []
[]

[Postprocessors]
  [p0]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = porepressure
  []
  [zdisp]
    type = PointValue
    outputs = csv
    point = '0 0 0.5'
    variable = disp_z
  []
  [stress_xx]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = stress_xx
  []
  [stress_yy]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = stress_yy
  []
  [stress_zz]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = stress_zz
  []
[]

[Functions]
  [stress_xx_over_strain_fcn]
    type = ParsedFunction
    expression = a/b
    symbol_names = 'a b'
    symbol_values = 'stress_xx zdisp'
  []
  [stress_zz_over_strain_fcn]
    type = ParsedFunction
    expression = a/b
    symbol_names = 'a b'
    symbol_values = 'stress_zz zdisp'
  []
  [p_over_strain_fcn]
    type = ParsedFunction
    expression = a/b
    symbol_names = 'a b'
    symbol_values = 'p0 zdisp'
  []
[]

[Preconditioning]
  [andy]
    type = SMP
    full = true
    petsc_options_iname = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value = 'bcgs bjacobi 1E-14 1E-10 10000'
  []
[]

[Executioner]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 10
  dt = 1
[]

[Outputs]
  execute_on = 'timestep_end'
  file_base = pp_generation_unconfined_constM_action
  [csv]
    type = CSV
  []
[]

(modules/porous_flow/test/tests/poro_elasticity/terzaghi_constM.i)

# Terzaghi's problem of consolodation of a drained medium
#
# A saturated soil sample sits in a bath of water.
# It is constrained on its sides, and bottom.
# Its sides and bottom are also impermeable.
# Initially it is unstressed.
# A normal stress, q, is applied to the soil's top.
# The soil then slowly compresses as water is squeezed
# out from the sample from its top (the top BC for
# the porepressure is porepressure = 0).
#
# See, for example.  Section 2.2 of the online manuscript
# Arnold Verruijt "Theory and Problems of Poroelasticity" Delft University of Technology 2013
# but note that the "sigma" in that paper is the negative
# of the stress in TensorMechanics
#
# Here are the problem's parameters, and their values:
# Soil height.  h = 10
# Soil's Lame lambda.  la = 2
# Soil's Lame mu, which is also the Soil's shear modulus.  mu = 3
# Soil bulk modulus.  K = la + 2*mu/3 = 4
# Soil confined compressibility.  m = 1/(K + 4mu/3) = 0.125
# Soil bulk compliance.  1/K = 0.25
# Fluid bulk modulus.  Kf = 8
# Fluid bulk compliance.  1/Kf = 0.125
# Fluid mobility (soil permeability/fluid viscosity).  k = 1.5
# Soil initial porosity.  phi0 = 0.1
# Biot coefficient.  alpha = 0.6
# Soil initial storativity, which is the reciprocal of the initial Biot modulus.  S = phi0/Kf + (alpha - phi0)(1 - alpha)/K = 0.0625
# Consolidation coefficient.  c = k/(S + alpha^2 m) = 13.95348837
# Normal stress on top.  q = 1
# Initial porepressure, resulting from instantaneous application of q, assuming corresponding instantaneous increase of porepressure (Note that this is calculated by MOOSE: we only need it for the analytical solution).  p0 = alpha*m*q/(S + alpha^2 m) = 0.69767442
# Initial vertical displacement (down is positive), resulting from instantaneous application of q (Note this is calculated by MOOSE: we only need it for the analytical solution).  uz0 = q*m*h*S/(S + alpha^2 m)
# Final vertical displacement (down in positive) (Note this is calculated by MOOSE: we only need it for the analytical solution).  uzinf = q*m*h
#
# The solution for porepressure is
# P = 4*p0/\pi \sum_{k=1}^{\infty} \frac{(-1)^{k-1}}{2k-1} \cos ((2k-1)\pi z/(2h)) \exp(-(2k-1)^2 \pi^2 ct/(4 h^2))
# This series converges very slowly for ct/h^2 small, so in that domain
# P = p0 erf( (1-(z/h))/(2 \sqrt(ct/h^2)) )
#
# The degree of consolidation is defined as
# U = (uz - uz0)/(uzinf - uz0)
# where uz0 and uzinf are defined above, and
# uz = the vertical displacement of the top (down is positive)
# U = 1 - (8/\pi^2)\sum_{k=1}^{\infty} \frac{1}{(2k-1)^2} \exp(-(2k-1)^2 \pi^2 ct/(4 h^2))

[Mesh]
  type = GeneratedMesh
  dim = 3
  nx = 1
  ny = 1
  nz = 10
  xmin = -1
  xmax = 1
  ymin = -1
  ymax = 1
  zmin = 0
  zmax = 10
[]

[GlobalParams]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[UserObjects]
  [dictator]
    type = PorousFlowDictator
    porous_flow_vars = 'porepressure disp_x disp_y disp_z'
    number_fluid_phases = 1
    number_fluid_components = 1
  []
  [pc]
    type = PorousFlowCapillaryPressureVG
    m = 0.8
    alpha = 1
  []
[]

[Variables]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs]
  [confinex]
    type = DirichletBC
    variable = disp_x
    value = 0
    boundary = 'left right'
  []
  [confiney]
    type = DirichletBC
    variable = disp_y
    value = 0
    boundary = 'bottom top'
  []
  [basefixed]
    type = DirichletBC
    variable = disp_z
    value = 0
    boundary = back
  []
  [topdrained]
    type = DirichletBC
    variable = porepressure
    value = 0
    boundary = front
  []
  [topload]
    type = NeumannBC
    variable = disp_z
    value = -1
    boundary = front
  []
[]

[Kernels]
  [grad_stress_x]
    type = StressDivergenceTensors
    variable = disp_x
    component = 0
  []
  [grad_stress_y]
    type = StressDivergenceTensors
    variable = disp_y
    component = 1
  []
  [grad_stress_z]
    type = StressDivergenceTensors
    variable = disp_z
    component = 2
  []
  [poro_x]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.6
    variable = disp_x
    component = 0
  []
  [poro_y]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.6
    variable = disp_y
    component = 1
  []
  [poro_z]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.6
    component = 2
    variable = disp_z
  []
  [poro_vol_exp]
    type = PorousFlowMassVolumetricExpansion
    variable = porepressure
    fluid_component = 0
  []
  [mass0]
    type = PorousFlowMassTimeDerivative
    fluid_component = 0
    variable = porepressure
  []
  [flux]
    type = PorousFlowAdvectiveFlux
    variable = porepressure
    gravity = '0 0 0'
    fluid_component = 0
  []
[]

[FluidProperties]
  [simple_fluid]
    type = SimpleFluidProperties
    bulk_modulus = 8
    density0 = 1
    thermal_expansion = 0
    viscosity = 0.96
  []
[]

[Materials]
  [temperature]
    type = PorousFlowTemperature
  []
  [elasticity_tensor]
    type = ComputeElasticityTensor
    C_ijkl = '2 3'
    # bulk modulus is lambda + 2*mu/3 = 2 + 2*3/3 = 4
    fill_method = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain
  []
  [stress]
    type = ComputeLinearElasticStress
  []
  [eff_fluid_pressure]
    type = PorousFlowEffectiveFluidPressure
  []
  [vol_strain]
    type = PorousFlowVolumetricStrain
  []
  [ppss]
    type = PorousFlow1PhaseP
    porepressure = porepressure
    capillary_pressure = pc
  []
  [massfrac]
    type = PorousFlowMassFraction
  []
  [simple_fluid]
    type = PorousFlowSingleComponentFluid
    fp = simple_fluid
    phase = 0
  []
  [porosity]
    type = PorousFlowPorosityHMBiotModulus
    porosity_zero = 0.1
    biot_coefficient = 0.6
    solid_bulk = 4
    constant_fluid_bulk_modulus = 8
    constant_biot_modulus = 16
  []
  [permeability]
    type = PorousFlowPermeabilityConst
    permeability = '1.5 0 0   0 1.5 0   0 0 1.5'
  []
  [relperm]
    type = PorousFlowRelativePermeabilityCorey
    n = 0 # unimportant in this fully-saturated situation
    phase = 0
  []
[]

[Postprocessors]
  [p0]
    type = PointValue
    outputs = csv
    point = '0 0 0'
    variable = porepressure
    use_displaced_mesh = false
  []
  [p1]
    type = PointValue
    outputs = csv
    point = '0 0 1'
    variable = porepressure
    use_displaced_mesh = false
  []
  [p2]
    type = PointValue
    outputs = csv
    point = '0 0 2'
    variable = porepressure
    use_displaced_mesh = false
  []
  [p3]
    type = PointValue
    outputs = csv
    point = '0 0 3'
    variable = porepressure
    use_displaced_mesh = false
  []
  [p4]
    type = PointValue
    outputs = csv
    point = '0 0 4'
    variable = porepressure
    use_displaced_mesh = false
  []
  [p5]
    type = PointValue
    outputs = csv
    point = '0 0 5'
    variable = porepressure
    use_displaced_mesh = false
  []
  [p6]
    type = PointValue
    outputs = csv
    point = '0 0 6'
    variable = porepressure
    use_displaced_mesh = false
  []
  [p7]
    type = PointValue
    outputs = csv
    point = '0 0 7'
    variable = porepressure
    use_displaced_mesh = false
  []
  [p8]
    type = PointValue
    outputs = csv
    point = '0 0 8'
    variable = porepressure
    use_displaced_mesh = false
  []
  [p9]
    type = PointValue
    outputs = csv
    point = '0 0 9'
    variable = porepressure
    use_displaced_mesh = false
  []
  [p99]
    type = PointValue
    outputs = csv
    point = '0 0 10'
    variable = porepressure
    use_displaced_mesh = false
  []
  [zdisp]
    type = PointValue
    outputs = csv
    point = '0 0 10'
    variable = disp_z
    use_displaced_mesh = false
  []
  [dt]
    type = FunctionValuePostprocessor
    outputs = console
    function = if(0.5*t<0.1,0.5*t,0.1)
  []
[]

[Preconditioning]
  [andy]
    type = SMP
    full = true
  []
[]

[Executioner]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 10
  [TimeStepper]
    type = PostprocessorDT
    postprocessor = dt
    dt = 0.0001
  []
[]

[Outputs]
  execute_on = 'timestep_end'
  file_base = terzaghi_constM
  [csv]
    type = CSV
  []
[]

(modules/porous_flow/test/tests/poro_elasticity/mandel.i)

# Mandel's problem of consolodation of a drained medium
#
# A sample is in plane strain.
# -a <= x <= a
# -b <= y <= b
# It is squashed with constant force by impermeable, frictionless plattens on its top and bottom surfaces (at y=+/-b)
# Fluid is allowed to leak out from its sides (at x=+/-a)
# The porepressure within the sample is monitored.
#
# As is common in the literature, this is simulated by
# considering the quarter-sample, 0<=x<=a and 0<=y<=b, with
# impermeable, roller BCs at x=0 and y=0 and y=b.
# Porepressure is fixed at zero on x=a.
# Porepressure and displacement are initialised to zero.
# Then the top (y=b) is moved downwards with prescribed velocity,
# so that the total force that is inducing this downwards velocity
# is fixed.  The velocity is worked out by solving Mandel's problem
# analytically, and the total force is monitored in the simulation
# to check that it indeed remains constant.
#
# Here are the problem's parameters, and their values:
# Soil width.  a = 1
# Soil height.  b = 0.1
# Soil's Lame lambda.  la = 0.5
# Soil's Lame mu, which is also the Soil's shear modulus.  mu = G = 0.75
# Soil bulk modulus.  K = la + 2*mu/3 = 1
# Drained Poisson ratio.  nu = (3K - 2G)/(6K + 2G) = 0.2
# Soil bulk compliance.  1/K = 1
# Fluid bulk modulus.  Kf = 8
# Fluid bulk compliance.  1/Kf = 0.125
# Soil initial porosity.  phi0 = 0.1
# Biot coefficient.  alpha = 0.6
# Biot modulus.  M = 1/(phi0/Kf + (alpha - phi0)(1 - alpha)/K) = 4.705882
# Undrained bulk modulus. Ku = K + alpha^2*M = 2.694118
# Undrained Poisson ratio.  nuu = (3Ku - 2G)/(6Ku + 2G) = 0.372627
# Skempton coefficient.  B = alpha*M/Ku = 1.048035
# Fluid mobility (soil permeability/fluid viscosity).  k = 1.5
# Consolidation coefficient.  c = 2*k*B^2*G*(1-nu)*(1+nuu)^2/9/(1-nuu)/(nuu-nu) = 3.821656
# Normal stress on top.  F = 1
#
# The solution for porepressure and displacements is given in
# AHD Cheng and E Detournay "A direct boundary element method for plane strain poroelasticity" International Journal of Numerical and Analytical Methods in Geomechanics 12 (1988) 551-572.
# The solution involves complicated infinite series, so I shall not write it here
#
# FINAL NOTE: The above solution assumes constant Biot Modulus.
# In porous_flow this is not true.  Therefore the solution is
# a little different than in the paper.  This test was therefore
# validated against MOOSE's poromechanics, which can choose either
# a constant Biot Modulus (which has been shown to agree with
# the analytic solution), or a non-constant Biot Modulus (which
# gives the same results as porous_flow).

[Mesh]
  type = GeneratedMesh
  dim = 3
  nx = 10
  ny = 1
  nz = 1
  xmin = 0
  xmax = 1
  ymin = 0
  ymax = 0.1
  zmin = 0
  zmax = 1
[]

[GlobalParams]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[UserObjects]
  [dictator]
    type = PorousFlowDictator
    porous_flow_vars = 'porepressure disp_x disp_y disp_z'
    number_fluid_phases = 1
    number_fluid_components = 1
  []
  [pc]
    type = PorousFlowCapillaryPressureVG
    m = 0.8
    alpha = 1e-5
  []
[]

[Variables]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs]
  [roller_xmin]
    type = DirichletBC
    variable = disp_x
    value = 0
    boundary = 'left'
  []
  [roller_ymin]
    type = DirichletBC
    variable = disp_y
    value = 0
    boundary = 'bottom'
  []
  [plane_strain]
    type = DirichletBC
    variable = disp_z
    value = 0
    boundary = 'back front'
  []
  [xmax_drained]
    type = DirichletBC
    variable = porepressure
    value = 0
    boundary = right
  []
  [top_velocity]
    type = FunctionDirichletBC
    variable = disp_y
    function = top_velocity
    boundary = top
  []
[]

[Functions]
  [top_velocity]
    type = PiecewiseLinear
    x = '0 0.002 0.006   0.014   0.03    0.046   0.062   0.078   0.094   0.11    0.126   0.142   0.158   0.174   0.19 0.206 0.222 0.238 0.254 0.27 0.286 0.302 0.318 0.334 0.35 0.366 0.382 0.398 0.414 0.43 0.446 0.462 0.478 0.494 0.51 0.526 0.542 0.558 0.574 0.59 0.606 0.622 0.638 0.654 0.67 0.686 0.702'
    y = '-0.041824842    -0.042730269    -0.043412712    -0.04428867     -0.045509181    -0.04645965     -0.047268246 -0.047974749      -0.048597109     -0.0491467  -0.049632388     -0.050061697      -0.050441198     -0.050776675     -0.051073238      -0.0513354 -0.051567152      -0.051772022     -0.051953128 -0.052113227 -0.052254754 -0.052379865 -0.052490464 -0.052588233 -0.052674662 -0.052751065 -0.052818606 -0.052878312 -0.052931093 -0.052977751 -0.053018997 -0.053055459 -0.053087691 -0.053116185 -0.053141373 -0.05316364 -0.053183324 -0.053200724 -0.053216106 -0.053229704 -0.053241725 -0.053252351 -0.053261745 -0.053270049 -0.053277389 -0.053283879 -0.053289615'
  []
[]

[AuxVariables]
  [stress_yy]
    order = CONSTANT
    family = MONOMIAL
  []
  [tot_force]
    order = CONSTANT
    family = MONOMIAL
  []
[]

[AuxKernels]
  [stress_yy]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_yy
    index_i = 1
    index_j = 1
  []
  [tot_force]
    type = ParsedAux
    coupled_variables = 'stress_yy porepressure'
    execute_on = timestep_end
    variable = tot_force
    expression = '-stress_yy+0.6*porepressure'
  []
[]

[Kernels]
  [grad_stress_x]
    type = StressDivergenceTensors
    variable = disp_x
    component = 0
  []
  [grad_stress_y]
    type = StressDivergenceTensors
    variable = disp_y
    component = 1
  []
  [grad_stress_z]
    type = StressDivergenceTensors
    variable = disp_z
    component = 2
  []
  [poro_x]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.6
    variable = disp_x
    component = 0
  []
  [poro_y]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.6
    variable = disp_y
    component = 1
  []
  [poro_z]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.6
    component = 2
    variable = disp_z
  []
  [poro_vol_exp]
    type = PorousFlowMassVolumetricExpansion
    variable = porepressure
    fluid_component = 0
  []
  [mass0]
    type = PorousFlowMassTimeDerivative
    fluid_component = 0
    variable = porepressure
  []
  [flux]
    type = PorousFlowAdvectiveFlux
    variable = porepressure
    gravity = '0 0 0'
    fluid_component = 0
  []
[]

[FluidProperties]
  [simple_fluid]
    type = SimpleFluidProperties
    bulk_modulus = 8
    density0 = 1
    thermal_expansion = 0
    viscosity = 1
  []
[]

[Materials]
  [temperature]
    type = PorousFlowTemperature
  []
  [elasticity_tensor]
    type = ComputeElasticityTensor
    C_ijkl = '0.5 0.75'
    # bulk modulus is lambda + 2*mu/3 = 0.5 + 2*0.75/3 = 1
    fill_method = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain
  []
  [stress]
    type = ComputeLinearElasticStress
  []
  [eff_fluid_pressure]
    type = PorousFlowEffectiveFluidPressure
  []
  [vol_strain]
    type = PorousFlowVolumetricStrain
  []
  [ppss]
    type = PorousFlow1PhaseP
    porepressure = porepressure
    capillary_pressure = pc
  []
  [massfrac]
    type = PorousFlowMassFraction
  []
  [simple_fluid]
    type = PorousFlowSingleComponentFluid
    fp = simple_fluid
    phase = 0
  []
  [porosity]
    type = PorousFlowPorosity
    fluid = true
    mechanical = true
    ensure_positive = false
    porosity_zero = 0.1
    biot_coefficient = 0.6
    solid_bulk = 1
  []
  [permeability]
    type = PorousFlowPermeabilityConst
    permeability = '1.5 0 0   0 1.5 0   0 0 1.5'
  []
  [relperm]
    type = PorousFlowRelativePermeabilityCorey
    n = 0 # unimportant in this fully-saturated situation
    phase = 0
  []
[]

[Postprocessors]
  [p0]
    type = PointValue
    outputs = csv
    point = '0.0 0 0'
    variable = porepressure
  []
  [p1]
    type = PointValue
    outputs = csv
    point = '0.1 0 0'
    variable = porepressure
  []
  [p2]
    type = PointValue
    outputs = csv
    point = '0.2 0 0'
    variable = porepressure
  []
  [p3]
    type = PointValue
    outputs = csv
    point = '0.3 0 0'
    variable = porepressure
  []
  [p4]
    type = PointValue
    outputs = csv
    point = '0.4 0 0'
    variable = porepressure
  []
  [p5]
    type = PointValue
    outputs = csv
    point = '0.5 0 0'
    variable = porepressure
  []
  [p6]
    type = PointValue
    outputs = csv
    point = '0.6 0 0'
    variable = porepressure
  []
  [p7]
    type = PointValue
    outputs = csv
    point = '0.7 0 0'
    variable = porepressure
  []
  [p8]
    type = PointValue
    outputs = csv
    point = '0.8 0 0'
    variable = porepressure
  []
  [p9]
    type = PointValue
    outputs = csv
    point = '0.9 0 0'
    variable = porepressure
  []
  [p99]
    type = PointValue
    outputs = csv
    point = '1 0 0'
    variable = porepressure
  []
  [xdisp]
    type = PointValue
    outputs = csv
    point = '1 0.1 0'
    variable = disp_x
  []
  [ydisp]
    type = PointValue
    outputs = csv
    point = '1 0.1 0'
    variable = disp_y
  []
  [total_downwards_force]
     type = ElementAverageValue
     outputs = csv
     variable = tot_force
  []
  [dt]
    type = FunctionValuePostprocessor
    outputs = console
    function = if(0.15*t<0.01,0.15*t,0.01)
  []
[]


[Preconditioning]
  [andy]
    type = SMP
    full = true
    petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value = 'gmres asm lu 1E-14 1E-10 10000'
  []
[]

[Executioner]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 0.7
  [TimeStepper]
    type = PostprocessorDT
    postprocessor = dt
    dt = 0.001
  []
[]

[Outputs]
  execute_on = 'timestep_end'
  file_base = mandel
  [csv]
    time_step_interval = 3
    type = CSV
  []
[]

(modules/porous_flow/test/tests/poro_elasticity/mandel_constM.i)

# Mandel's problem of consolodation of a drained medium
#
# A sample is in plane strain.
# -a <= x <= a
# -b <= y <= b
# It is squashed with constant force by impermeable, frictionless plattens on its top and bottom surfaces (at y=+/-b)
# Fluid is allowed to leak out from its sides (at x=+/-a)
# The porepressure within the sample is monitored.
#
# As is common in the literature, this is simulated by
# considering the quarter-sample, 0<=x<=a and 0<=y<=b, with
# impermeable, roller BCs at x=0 and y=0 and y=b.
# Porepressure is fixed at zero on x=a.
# Porepressure and displacement are initialised to zero.
# Then the top (y=b) is moved downwards with prescribed velocity,
# so that the total force that is inducing this downwards velocity
# is fixed.  The velocity is worked out by solving Mandel's problem
# analytically, and the total force is monitored in the simulation
# to check that it indeed remains constant.
#
# Here are the problem's parameters, and their values:
# Soil width.  a = 1
# Soil height.  b = 0.1
# Soil's Lame lambda.  la = 0.5
# Soil's Lame mu, which is also the Soil's shear modulus.  mu = G = 0.75
# Soil bulk modulus.  K = la + 2*mu/3 = 1
# Drained Poisson ratio.  nu = (3K - 2G)/(6K + 2G) = 0.2
# Soil bulk compliance.  1/K = 1
# Fluid bulk modulus.  Kf = 8
# Fluid bulk compliance.  1/Kf = 0.125
# Soil initial porosity.  phi0 = 0.1
# Biot coefficient.  alpha = 0.6
# Biot modulus.  M = 1/(phi0/Kf + (alpha - phi0)(1 - alpha)/K) = 4.705882
# Undrained bulk modulus. Ku = K + alpha^2*M = 2.694118
# Undrained Poisson ratio.  nuu = (3Ku - 2G)/(6Ku + 2G) = 0.372627
# Skempton coefficient.  B = alpha*M/Ku = 1.048035
# Fluid mobility (soil permeability/fluid viscosity).  k = 1.5
# Consolidation coefficient.  c = 2*k*B^2*G*(1-nu)*(1+nuu)^2/9/(1-nuu)/(nuu-nu) = 3.821656
# Normal stress on top.  F = 1
#
# The solution for porepressure and displacements is given in
# AHD Cheng and E Detournay "A direct boundary element method for plane strain poroelasticity" International Journal of Numerical and Analytical Methods in Geomechanics 12 (1988) 551-572.
# The solution involves complicated infinite series, so I shall not write it here

[Mesh]
  type = GeneratedMesh
  dim = 3
  nx = 10
  ny = 1
  nz = 1
  xmin = 0
  xmax = 1
  ymin = 0
  ymax = 0.1
  zmin = 0
  zmax = 1
[]

[GlobalParams]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[UserObjects]
  [dictator]
    type = PorousFlowDictator
    porous_flow_vars = 'porepressure disp_x disp_y disp_z'
    number_fluid_phases = 1
    number_fluid_components = 1
  []
  [pc]
    type = PorousFlowCapillaryPressureVG
    m = 0.8
    alpha = 1e-5
  []
[]

[Variables]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs]
  [roller_xmin]
    type = DirichletBC
    variable = disp_x
    value = 0
    boundary = 'left'
  []
  [roller_ymin]
    type = DirichletBC
    variable = disp_y
    value = 0
    boundary = 'bottom'
  []
  [plane_strain]
    type = DirichletBC
    variable = disp_z
    value = 0
    boundary = 'back front'
  []
  [xmax_drained]
    type = DirichletBC
    variable = porepressure
    value = 0
    boundary = right
  []
  [top_velocity]
    type = FunctionDirichletBC
    variable = disp_y
    function = top_velocity
    boundary = top
  []
[]

[Functions]
  [top_velocity]
    type = PiecewiseLinear
    x = '0 0.002 0.006   0.014   0.03    0.046   0.062   0.078   0.094   0.11    0.126   0.142   0.158   0.174   0.19 0.206 0.222 0.238 0.254 0.27 0.286 0.302 0.318 0.334 0.35 0.366 0.382 0.398 0.414 0.43 0.446 0.462 0.478 0.494 0.51 0.526 0.542 0.558 0.574 0.59 0.606 0.622 0.638 0.654 0.67 0.686 0.702'
    y = '-0.041824842    -0.042730269    -0.043412712    -0.04428867     -0.045509181    -0.04645965     -0.047268246 -0.047974749      -0.048597109     -0.0491467  -0.049632388     -0.050061697      -0.050441198     -0.050776675     -0.051073238      -0.0513354 -0.051567152      -0.051772022     -0.051953128 -0.052113227 -0.052254754 -0.052379865 -0.052490464 -0.052588233 -0.052674662 -0.052751065 -0.052818606 -0.052878312 -0.052931093 -0.052977751 -0.053018997 -0.053055459 -0.053087691 -0.053116185 -0.053141373 -0.05316364 -0.053183324 -0.053200724 -0.053216106 -0.053229704 -0.053241725 -0.053252351 -0.053261745 -0.053270049 -0.053277389 -0.053283879 -0.053289615'
  []
[]

[AuxVariables]
  [stress_yy]
    order = CONSTANT
    family = MONOMIAL
  []
  [tot_force]
    order = CONSTANT
    family = MONOMIAL
  []
[]

[AuxKernels]
  [stress_yy]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_yy
    index_i = 1
    index_j = 1
  []
  [tot_force]
    type = ParsedAux
    coupled_variables = 'stress_yy porepressure'
    execute_on = timestep_end
    variable = tot_force
    expression = '-stress_yy+0.6*porepressure'
  []
[]

[Kernels]
  [grad_stress_x]
    type = StressDivergenceTensors
    variable = disp_x
    component = 0
  []
  [grad_stress_y]
    type = StressDivergenceTensors
    variable = disp_y
    component = 1
  []
  [grad_stress_z]
    type = StressDivergenceTensors
    variable = disp_z
    component = 2
  []
  [poro_x]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.6
    variable = disp_x
    component = 0
  []
  [poro_y]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.6
    variable = disp_y
    component = 1
  []
  [poro_z]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.6
    component = 2
    variable = disp_z
  []
  [poro_vol_exp]
    type = PorousFlowMassVolumetricExpansion
    variable = porepressure
    fluid_component = 0
  []
  [mass0]
    type = PorousFlowMassTimeDerivative
    fluid_component = 0
    variable = porepressure
  []
  [flux]
    type = PorousFlowAdvectiveFlux
    variable = porepressure
    gravity = '0 0 0'
    fluid_component = 0
  []
[]

[FluidProperties]
  [simple_fluid]
    type = SimpleFluidProperties
    bulk_modulus = 8
    density0 = 1
    thermal_expansion = 0
    viscosity = 1
  []
[]

[Materials]
  [temperature]
    type = PorousFlowTemperature
  []
  [elasticity_tensor]
    type = ComputeElasticityTensor
    C_ijkl = '0.5 0.75'
    # bulk modulus is lambda + 2*mu/3 = 0.5 + 2*0.75/3 = 1
    fill_method = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain
  []
  [stress]
    type = ComputeLinearElasticStress
  []
  [eff_fluid_pressure]
    type = PorousFlowEffectiveFluidPressure
  []
  [vol_strain]
    type = PorousFlowVolumetricStrain
  []
  [ppss]
    type = PorousFlow1PhaseP
    porepressure = porepressure
    capillary_pressure = pc
  []
  [massfrac]
    type = PorousFlowMassFraction
  []
  [simple_fluid]
    type = PorousFlowSingleComponentFluid
    fp = simple_fluid
    phase = 0
  []
  [porosity]
    type = PorousFlowPorosityHMBiotModulus
    porosity_zero = 0.1
    biot_coefficient = 0.6
    solid_bulk = 1
    constant_fluid_bulk_modulus = 8
    constant_biot_modulus = 4.7058823529
  []
  [permeability]
    type = PorousFlowPermeabilityConst
    permeability = '1.5 0 0   0 1.5 0   0 0 1.5'
  []
  [relperm]
    type = PorousFlowRelativePermeabilityCorey
    n = 0 # unimportant in this fully-saturated situation
    phase = 0
  []
[]

[Postprocessors]
  [p0]
    type = PointValue
    outputs = csv
    point = '0.0 0 0'
    variable = porepressure
  []
  [p1]
    type = PointValue
    outputs = csv
    point = '0.1 0 0'
    variable = porepressure
  []
  [p2]
    type = PointValue
    outputs = csv
    point = '0.2 0 0'
    variable = porepressure
  []
  [p3]
    type = PointValue
    outputs = csv
    point = '0.3 0 0'
    variable = porepressure
  []
  [p4]
    type = PointValue
    outputs = csv
    point = '0.4 0 0'
    variable = porepressure
  []
  [p5]
    type = PointValue
    outputs = csv
    point = '0.5 0 0'
    variable = porepressure
  []
  [p6]
    type = PointValue
    outputs = csv
    point = '0.6 0 0'
    variable = porepressure
  []
  [p7]
    type = PointValue
    outputs = csv
    point = '0.7 0 0'
    variable = porepressure
  []
  [p8]
    type = PointValue
    outputs = csv
    point = '0.8 0 0'
    variable = porepressure
  []
  [p9]
    type = PointValue
    outputs = csv
    point = '0.9 0 0'
    variable = porepressure
  []
  [p99]
    type = PointValue
    outputs = csv
    point = '1 0 0'
    variable = porepressure
  []
  [xdisp]
    type = PointValue
    outputs = csv
    point = '1 0.1 0'
    variable = disp_x
  []
  [ydisp]
    type = PointValue
    outputs = csv
    point = '1 0.1 0'
    variable = disp_y
  []
  [total_downwards_force]
     type = ElementAverageValue
     outputs = csv
     variable = tot_force
  []
  [dt]
    type = FunctionValuePostprocessor
    outputs = console
    function = if(0.15*t<0.01,0.15*t,0.01)
  []
[]

[Preconditioning]
  [andy]
    type = SMP
    full = true
    petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value = 'gmres asm lu 1E-14 1E-10 10000'
  []
[]

[Executioner]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 0.7
  [TimeStepper]
    type = PostprocessorDT
    postprocessor = dt
    dt = 0.001
  []
[]

[Outputs]
  execute_on = 'timestep_end'
  file_base = mandel_constM
  [csv]
    time_step_interval = 3
    type = CSV
  []
[]

(modules/porous_flow/test/tests/poro_elasticity/mandel_fully_saturated.i)

# Mandel's problem of consolodation of a drained medium
# Using the FullySaturatedDarcyBase and FullySaturatedMassTimeDerivative kernels
#
# A sample is in plane strain.
# -a <= x <= a
# -b <= y <= b
# It is squashed with constant force by impermeable, frictionless plattens on its top and bottom surfaces (at y=+/-b)
# Fluid is allowed to leak out from its sides (at x=+/-a)
# The porepressure within the sample is monitored.
#
# As is common in the literature, this is simulated by
# considering the quarter-sample, 0<=x<=a and 0<=y<=b, with
# impermeable, roller BCs at x=0 and y=0 and y=b.
# Porepressure is fixed at zero on x=a.
# Porepressure and displacement are initialised to zero.
# Then the top (y=b) is moved downwards with prescribed velocity,
# so that the total force that is inducing this downwards velocity
# is fixed.  The velocity is worked out by solving Mandel's problem
# analytically, and the total force is monitored in the simulation
# to check that it indeed remains constant.
#
# Here are the problem's parameters, and their values:
# Soil width.  a = 1
# Soil height.  b = 0.1
# Soil's Lame lambda.  la = 0.5
# Soil's Lame mu, which is also the Soil's shear modulus.  mu = G = 0.75
# Soil bulk modulus.  K = la + 2*mu/3 = 1
# Drained Poisson ratio.  nu = (3K - 2G)/(6K + 2G) = 0.2
# Soil bulk compliance.  1/K = 1
# Fluid bulk modulus.  Kf = 8
# Fluid bulk compliance.  1/Kf = 0.125
# Soil initial porosity.  phi0 = 0.1
# Biot coefficient.  alpha = 0.6
# Biot modulus.  M = 1/(phi0/Kf + (alpha - phi0)(1 - alpha)/K) = 4.705882
# Undrained bulk modulus. Ku = K + alpha^2*M = 2.694118
# Undrained Poisson ratio.  nuu = (3Ku - 2G)/(6Ku + 2G) = 0.372627
# Skempton coefficient.  B = alpha*M/Ku = 1.048035
# Fluid mobility (soil permeability/fluid viscosity).  k = 1.5
# Consolidation coefficient.  c = 2*k*B^2*G*(1-nu)*(1+nuu)^2/9/(1-nuu)/(nuu-nu) = 3.821656
# Normal stress on top.  F = 1
#
# The solution for porepressure and displacements is given in
# AHD Cheng and E Detournay "A direct boundary element method for plane strain poroelasticity" International Journal of Numerical and Analytical Methods in Geomechanics 12 (1988) 551-572.
# The solution involves complicated infinite series, so I shall not write it here

[Mesh]
  type = GeneratedMesh
  dim = 3
  nx = 10
  ny = 1
  nz = 1
  xmin = 0
  xmax = 1
  ymin = 0
  ymax = 0.1
  zmin = 0
  zmax = 1
[]

[GlobalParams]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[UserObjects]
  [dictator]
    type = PorousFlowDictator
    porous_flow_vars = 'porepressure disp_x disp_y disp_z'
    number_fluid_phases = 1
    number_fluid_components = 1
  []
[]

[Variables]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs]
  [roller_xmin]
    type = DirichletBC
    variable = disp_x
    value = 0
    boundary = 'left'
  []
  [roller_ymin]
    type = DirichletBC
    variable = disp_y
    value = 0
    boundary = 'bottom'
  []
  [plane_strain]
    type = DirichletBC
    variable = disp_z
    value = 0
    boundary = 'back front'
  []
  [xmax_drained]
    type = DirichletBC
    variable = porepressure
    value = 0
    boundary = right
  []
  [top_velocity]
    type = FunctionDirichletBC
    variable = disp_y
    function = top_velocity
    boundary = top
  []
[]

[Functions]
  [top_velocity]
    type = PiecewiseLinear
    x = '0 0.002 0.006   0.014   0.03    0.046   0.062   0.078   0.094   0.11    0.126   0.142   0.158   0.174   0.19 0.206 0.222 0.238 0.254 0.27 0.286 0.302 0.318 0.334 0.35 0.366 0.382 0.398 0.414 0.43 0.446 0.462 0.478 0.494 0.51 0.526 0.542 0.558 0.574 0.59 0.606 0.622 0.638 0.654 0.67 0.686 0.702'
    y = '-0.041824842    -0.042730269    -0.043412712    -0.04428867     -0.045509181    -0.04645965     -0.047268246 -0.047974749      -0.048597109     -0.0491467  -0.049632388     -0.050061697      -0.050441198     -0.050776675     -0.051073238      -0.0513354 -0.051567152      -0.051772022     -0.051953128 -0.052113227 -0.052254754 -0.052379865 -0.052490464 -0.052588233 -0.052674662 -0.052751065 -0.052818606 -0.052878312 -0.052931093 -0.052977751 -0.053018997 -0.053055459 -0.053087691 -0.053116185 -0.053141373 -0.05316364 -0.053183324 -0.053200724 -0.053216106 -0.053229704 -0.053241725 -0.053252351 -0.053261745 -0.053270049 -0.053277389 -0.053283879 -0.053289615'
  []
[]

[AuxVariables]
  [stress_yy]
    order = CONSTANT
    family = MONOMIAL
  []
  [tot_force]
    order = CONSTANT
    family = MONOMIAL
  []
[]

[AuxKernels]
  [stress_yy]
    type = RankTwoAux
    rank_two_tensor = stress
    variable = stress_yy
    index_i = 1
    index_j = 1
  []
  [tot_force]
    type = ParsedAux
    coupled_variables = 'stress_yy porepressure'
    execute_on = timestep_end
    variable = tot_force
    expression = '-stress_yy+0.6*porepressure'
  []
[]

[Kernels]
  [grad_stress_x]
    type = StressDivergenceTensors
    variable = disp_x
    component = 0
  []
  [grad_stress_y]
    type = StressDivergenceTensors
    variable = disp_y
    component = 1
  []
  [grad_stress_z]
    type = StressDivergenceTensors
    variable = disp_z
    component = 2
  []
  [poro_x]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.6
    variable = disp_x
    component = 0
  []
  [poro_y]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.6
    variable = disp_y
    component = 1
  []
  [poro_z]
    type = PorousFlowEffectiveStressCoupling
    biot_coefficient = 0.6
    component = 2
    variable = disp_z
  []
  [mass0]
    type = PorousFlowFullySaturatedMassTimeDerivative
    biot_coefficient = 0.6
    coupling_type = HydroMechanical
    variable = porepressure
  []
  [flux]
    type = PorousFlowFullySaturatedDarcyBase
    variable = porepressure
    gravity = '0 0 0'
  []
[]

[FluidProperties]
  [simple_fluid]
    type = SimpleFluidProperties
    bulk_modulus = 8
    density0 = 1
    thermal_expansion = 0
    viscosity = 1
  []
[]

[Materials]
  [temperature]
    type = PorousFlowTemperature
  []
  [elasticity_tensor]
    type = ComputeElasticityTensor
    C_ijkl = '0.5 0.75'
    # bulk modulus is lambda + 2*mu/3 = 0.5 + 2*0.75/3 = 1
    fill_method = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain
  []
  [stress]
    type = ComputeLinearElasticStress
  []
  [eff_fluid_pressure_qp]
    type = PorousFlowEffectiveFluidPressure
  []
  [vol_strain]
    type = PorousFlowVolumetricStrain
  []
  [ppss]
    type = PorousFlow1PhaseFullySaturated
    porepressure = porepressure
  []
  [massfrac]
    type = PorousFlowMassFraction
  []
  [simple_fluid_qp]
    type = PorousFlowSingleComponentFluid
    fp = simple_fluid
    phase = 0
  []
  [porosity]
    type = PorousFlowPorosityConst # only the initial value of this is ever used
    porosity = 0.1
  []
  [biot_modulus]
    type = PorousFlowConstantBiotModulus
    biot_coefficient = 0.6
    solid_bulk_compliance = 1
    fluid_bulk_modulus = 8
  []
  [permeability]
    type = PorousFlowPermeabilityConst
    permeability = '1.5 0 0   0 1.5 0   0 0 1.5'
  []
[]

[Postprocessors]
  [p0]
    type = PointValue
    outputs = csv
    point = '0.0 0 0'
    variable = porepressure
  []
  [p1]
    type = PointValue
    outputs = csv
    point = '0.1 0 0'
    variable = porepressure
  []
  [p2]
    type = PointValue
    outputs = csv
    point = '0.2 0 0'
    variable = porepressure
  []
  [p3]
    type = PointValue
    outputs = csv
    point = '0.3 0 0'
    variable = porepressure
  []
  [p4]
    type = PointValue
    outputs = csv
    point = '0.4 0 0'
    variable = porepressure
  []
  [p5]
    type = PointValue
    outputs = csv
    point = '0.5 0 0'
    variable = porepressure
  []
  [p6]
    type = PointValue
    outputs = csv
    point = '0.6 0 0'
    variable = porepressure
  []
  [p7]
    type = PointValue
    outputs = csv
    point = '0.7 0 0'
    variable = porepressure
  []
  [p8]
    type = PointValue
    outputs = csv
    point = '0.8 0 0'
    variable = porepressure
  []
  [p9]
    type = PointValue
    outputs = csv
    point = '0.9 0 0'
    variable = porepressure
  []
  [p99]
    type = PointValue
    outputs = csv
    point = '1 0 0'
    variable = porepressure
  []
  [xdisp]
    type = PointValue
    outputs = csv
    point = '1 0.1 0'
    variable = disp_x
  []
  [ydisp]
    type = PointValue
    outputs = csv
    point = '1 0.1 0'
    variable = disp_y
  []
  [total_downwards_force]
     type = ElementAverageValue
     outputs = csv
     variable = tot_force
  []
  [dt]
    type = FunctionValuePostprocessor
    outputs = console
    function = if(0.15*t<0.01,0.15*t,0.01)
  []
[]

[Preconditioning]
  [andy]
    type = SMP
    full = true
    petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value = 'gmres asm lu 1E-14 1E-10 10000'
  []
[]

[Executioner]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 0.7
  [TimeStepper]
    type = PostprocessorDT
    postprocessor = dt
    dt = 0.001
  []
[]

[Outputs]
  execute_on = 'timestep_end'
  file_base = mandel_fully_saturated
  [csv]
    time_step_interval = 3
    type = CSV
  []
[]

(modules/porous_flow/test/tests/poro_elasticity/mandel_basicthm.i)

# using a BasicTHM Action
#
# Mandel's problem of consolodation of a drained medium
# Using the FullySaturatedDarcyBase and FullySaturatedFullySaturatedMassTimeDerivative kernels
# with multiply_by_density = false, so that this problem becomes linear
#
# A sample is in plane strain.
# -a <= x <= a
# -b <= y <= b
# It is squashed with constant force by impermeable, frictionless plattens on its top and bottom surfaces (at y=+/-b)
# Fluid is allowed to leak out from its sides (at x=+/-a)
# The porepressure within the sample is monitored.
#
# As is common in the literature, this is simulated by
# considering the quarter-sample, 0<=x<=a and 0<=y<=b, with
# impermeable, roller BCs at x=0 and y=0 and y=b.
# Porepressure is fixed at zero on x=a.
# Porepressure and displacement are initialised to zero.
# Then the top (y=b) is moved downwards with prescribed velocity,
# so that the total force that is inducing this downwards velocity
# is fixed.  The velocity is worked out by solving Mandel's problem
# analytically, and the total force is monitored in the simulation
# to check that it indeed remains constant.
#
# Here are the problem's parameters, and their values:
# Soil width.  a = 1
# Soil height.  b = 0.1
# Soil's Lame lambda.  la = 0.5
# Soil's Lame mu, which is also the Soil's shear modulus.  mu = G = 0.75
# Soil bulk modulus.  K = la + 2*mu/3 = 1
# Drained Poisson ratio.  nu = (3K - 2G)/(6K + 2G) = 0.2
# Soil bulk compliance.  1/K = 1
# Fluid bulk modulus.  Kf = 8
# Fluid bulk compliance.  1/Kf = 0.125
# Soil initial porosity.  phi0 = 0.1
# Biot coefficient.  alpha = 0.6
# Biot modulus.  M = 1/(phi0/Kf + (alpha - phi0)(1 - alpha)/K) = 4.705882
# Undrained bulk modulus. Ku = K + alpha^2*M = 2.694118
# Undrained Poisson ratio.  nuu = (3Ku - 2G)/(6Ku + 2G) = 0.372627
# Skempton coefficient.  B = alpha*M/Ku = 1.048035
# Fluid mobility (soil permeability/fluid viscosity).  k = 1.5
# Consolidation coefficient.  c = 2*k*B^2*G*(1-nu)*(1+nuu)^2/9/(1-nuu)/(nuu-nu) = 3.821656
# Normal stress on top.  F = 1
#
# The solution for porepressure and displacements is given in
# AHD Cheng and E Detournay "A direct boundary element method for plane strain poroelasticity" International Journal of Numerical and Analytical Methods in Geomechanics 12 (1988) 551-572.
# The solution involves complicated infinite series, so I shall not write it here

[Mesh]
  type = GeneratedMesh
  dim = 3
  nx = 10
  ny = 1
  nz = 1
  xmin = 0
  xmax = 1
  ymin = 0
  ymax = 0.1
  zmin = 0
  zmax = 1
[]

[GlobalParams]
  displacements = 'disp_x disp_y disp_z'
  PorousFlowDictator = dictator
  block = 0
[]

[Variables]
  [disp_x]
  []
  [disp_y]
  []
  [disp_z]
  []
  [porepressure]
  []
[]

[BCs]
  [roller_xmin]
    type = DirichletBC
    variable = disp_x
    value = 0
    boundary = 'left'
  []
  [roller_ymin]
    type = DirichletBC
    variable = disp_y
    value = 0
    boundary = 'bottom'
  []
  [plane_strain]
    type = DirichletBC
    variable = disp_z
    value = 0
    boundary = 'back front'
  []
  [xmax_drained]
    type = DirichletBC
    variable = porepressure
    value = 0
    boundary = right
  []
  [top_velocity]
    type = FunctionDirichletBC
    variable = disp_y
    function = top_velocity
    boundary = top
  []
[]

[Functions]
  [top_velocity]
    type = PiecewiseLinear
    x = '0 0.002 0.006   0.014   0.03    0.046   0.062   0.078   0.094   0.11    0.126   0.142   0.158   0.174   0.19 0.206 0.222 0.238 0.254 0.27 0.286 0.302 0.318 0.334 0.35 0.366 0.382 0.398 0.414 0.43 0.446 0.462 0.478 0.494 0.51 0.526 0.542 0.558 0.574 0.59 0.606 0.622 0.638 0.654 0.67 0.686 0.702'
    y = '-0.041824842    -0.042730269    -0.043412712    -0.04428867     -0.045509181    -0.04645965     -0.047268246 -0.047974749      -0.048597109     -0.0491467  -0.049632388     -0.050061697      -0.050441198     -0.050776675     -0.051073238      -0.0513354 -0.051567152      -0.051772022     -0.051953128 -0.052113227 -0.052254754 -0.052379865 -0.052490464 -0.052588233 -0.052674662 -0.052751065 -0.052818606 -0.052878312 -0.052931093 -0.052977751 -0.053018997 -0.053055459 -0.053087691 -0.053116185 -0.053141373 -0.05316364 -0.053183324 -0.053200724 -0.053216106 -0.053229704 -0.053241725 -0.053252351 -0.053261745 -0.053270049 -0.053277389 -0.053283879 -0.053289615'
  []
[]

[AuxVariables]
  [tot_force]
    order = CONSTANT
    family = MONOMIAL
  []
[]

[AuxKernels]
  [tot_force]
    type = ParsedAux
    coupled_variables = 'stress_yy porepressure'
    execute_on = timestep_end
    variable = tot_force
    expression = '-stress_yy+0.6*porepressure'
  []
[]

[FluidProperties]
  [the_simple_fluid]
    type = SimpleFluidProperties
    thermal_expansion = 0.0
    bulk_modulus = 8.0
    viscosity = 1.0
    density0 = 1.0
  []
[]

[PorousFlowBasicTHM]
  coupling_type = HydroMechanical
  displacements = 'disp_x disp_y disp_z'
  multiply_by_density = false
  porepressure = porepressure
  biot_coefficient = 0.6
  gravity = '0 0 0'
  fp = the_simple_fluid
[]

[Materials]
  [elasticity_tensor]
    type = ComputeElasticityTensor
    C_ijkl = '0.5 0.75'
    # bulk modulus is lambda + 2*mu/3 = 0.5 + 2*0.75/3 = 1
    fill_method = symmetric_isotropic
  []
  [strain]
    type = ComputeSmallStrain
  []
  [stress]
    type = ComputeLinearElasticStress
  []
  [porosity]
    type = PorousFlowPorosityConst # only the initial value of this is ever used
    porosity = 0.1
  []
  [biot_modulus]
    type = PorousFlowConstantBiotModulus
    biot_coefficient = 0.6
    solid_bulk_compliance = 1
    fluid_bulk_modulus = 8
  []
  [permeability]
    type = PorousFlowPermeabilityConst
    permeability = '1.5 0 0   0 1.5 0   0 0 1.5'
  []
[]

[Postprocessors]
  [p0]
    type = PointValue
    outputs = csv
    point = '0.0 0 0'
    variable = porepressure
  []
  [p1]
    type = PointValue
    outputs = csv
    point = '0.1 0 0'
    variable = porepressure
  []
  [p2]
    type = PointValue
    outputs = csv
    point = '0.2 0 0'
    variable = porepressure
  []
  [p3]
    type = PointValue
    outputs = csv
    point = '0.3 0 0'
    variable = porepressure
  []
  [p4]
    type = PointValue
    outputs = csv
    point = '0.4 0 0'
    variable = porepressure
  []
  [p5]
    type = PointValue
    outputs = csv
    point = '0.5 0 0'
    variable = porepressure
  []
  [p6]
    type = PointValue
    outputs = csv
    point = '0.6 0 0'
    variable = porepressure
  []
  [p7]
    type = PointValue
    outputs = csv
    point = '0.7 0 0'
    variable = porepressure
  []
  [p8]
    type = PointValue
    outputs = csv
    point = '0.8 0 0'
    variable = porepressure
  []
  [p9]
    type = PointValue
    outputs = csv
    point = '0.9 0 0'
    variable = porepressure
  []
  [p99]
    type = PointValue
    outputs = csv
    point = '1 0 0'
    variable = porepressure
  []
  [xdisp]
    type = PointValue
    outputs = csv
    point = '1 0.1 0'
    variable = disp_x
  []
  [ydisp]
    type = PointValue
    outputs = csv
    point = '1 0.1 0'
    variable = disp_y
  []
  [total_downwards_force]
     type = ElementAverageValue
     outputs = csv
     variable = tot_force
  []
  [dt]
    type = FunctionValuePostprocessor
    outputs = console
    function = if(0.15*t<0.01,0.15*t,0.01)
  []
[]


[Preconditioning]
  [andy]
    type = SMP
    full = true
    petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value = 'gmres asm lu 1E-14 1E-10 10000'
  []
[]

[Executioner]
  type = Transient
  solve_type = Newton
  start_time = 0
  end_time = 0.7
  [TimeStepper]
    type = PostprocessorDT
    postprocessor = dt
    dt = 0.001
  []
[]

[Outputs]
  execute_on = 'timestep_end'
  file_base = mandel_basicthm
  [csv]
    time_step_interval = 3
    type = CSV
  []
[]

Introduction
Simple tests
Terzaghi consolidation of a drained medium
Mandel ' s consolidation of a drained medium
References