Infiltration and drainage test descriptions
The 2-phase analytic infiltration solution
The physical setup studied in this section is a 1D column that is initially unsaturated, and which is subject to a constant injection of fluid from its top. This is of physical importance because it is a model of constant rainfall recharge to an initially dry groundwater system. The top surface becomes saturated, and this saturated zone moves downwards into the column, diffusing as it goes. The problem is of computational interest because under certain conditions an analytic solution is available for the saturation profile as a function of depth and time.
The Richards' equation for an incompressible fluid in one spatial dimension () reads where and Here which is the capillary pressure, and recall that .
The analytic solution of this nonlinear diffusion-advection relevant to constant infiltration to groundwater has been derived by Broadbridge and White (Broadbridge and White, 1988) for certain functions and . Broadbridge and White assume the hydraulic conductivity is (1) where and the parameters obey , , and . The diffusivity is of the form . This leads to very complicated relationships between the capillary pressure, , and the saturation, except in the case where is small, when they are related through with being the final parameter introduced by Broadbridge and White.
Broadbridge and White derive time-dependent solutions for constant recharge to one end of a semi-infinite line. Their solutions are quite lengthy, will not be written here. To compare with MOOSE, the following parameters are used — the hydraulic parameters are those used in Figure 3 of Broadbridge and White:
Table 1: Parameter values used in the 2-phase tests
| Parameter | Value |
|---|---|
| Bar length | 20m |
| Bar porosity | 0.25 |
| Bar permeability | 1 |
| Gravity | 0.1m.s |
| Fluid density | 10kg.m |
| Fluid viscosity | 4Pa.s |
| 0m.s | |
| 1m.s | |
| 0m.s | |
| 1m.s | |
| 1.5 | |
| 2Pa | |
| Recharge rate | 0.5 |
Broadbridge and white consider the case where the initial condition is , but this yields , which is impossible to use in a MOOSE model. Therefore the initial condition Pa is used which avoids any underflow problems. The recharge rate of corresponds in the MOOSE model to a recharge rate of kg.m.s. Note that m.s, so that the and may be encoded as and in the relative permeability function Eq. (1) in a straightforward way.
Figure 1 shows good agreement between the analytic solution of Broadbridge and White and the MOOSE implementation. There are minor discrepancies for small values of saturation: these get smaller as the temporal and spatial resolution is increased, but never totally disappear due to the initial condition of Pa.
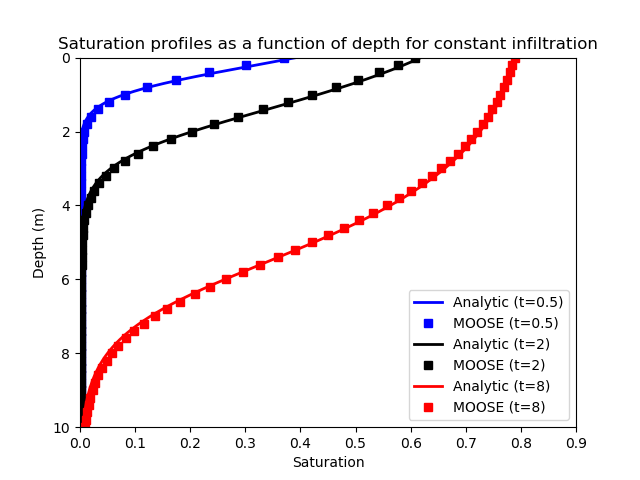
Figure 1: Comparison of the Broadbridge and White analytical solution with the MOOSE solution for 3 times. This figure is shown in the standard format used in the Broadbridge-White paper: the constant recharge is applied to the top (where depth is zero) and gravity acts downwards in this figure.
Two tests are part of the automatic test suite (one is marked "heavy" because it is a high-resolution version).
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
type = GeneratedMesh
dim = 2
nx = 400
ny = 1
xmin = -10
xmax = 10
ymin = 0
ymax = 0.05
[]
[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
PorousFlowDictator = dictator
[]
[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
[dts]
type = PiecewiseLinear<<<{"description": "Linearly interpolates between pairs of x-y data", "href": "../../../../source/functions/PiecewiseLinear.html"}>>>
y<<<{"description": "The ordinate values"}>>> = '1E-5 1E-2 1E-2 1E-1'
x<<<{"description": "The abscissa values"}>>> = '0 1E-5 1 10'
[]
[]
[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
[dictator]
type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation. Jacobian entries involving derivatives wrt these variables will be computed. In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = pressure
number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
[]
[pc]
type = PorousFlowCapillaryPressureBW<<<{"description": "Broadbridge and White capillary pressure for negligable Kn", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureBW.html"}>>>
Sn<<<{"description": "Low saturation. This must be < Ss, and non-negative. This is BW's initial effective saturation, below which effective saturation never goes in their simulations/models. If Kn=0 then Sn is the immobile saturation. This form of effective saturation is only correct for Kn small."}>>> = 0.0
Ss<<<{"description": "High saturation. This must be > Sn and <= 1. Effective saturation where porepressure = 0. Effective saturation never exceeds this value in BW's simulations/models."}>>> = 1.0
C<<<{"description": "BW's C parameter. Must be > 1. Typical value would be 1.05."}>>> = 1.5
las<<<{"description": "BW's lambda_s parameter multiplied by (fluid_density * gravity). Must be > 0. Typical value would be 1E5"}>>> = 2
[]
[]
[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
[simple_fluid]
type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 2e9
viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 4
density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 10
thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
[]
[]
[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
[massfrac]
type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
[]
[temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
[]
[simple_fluid]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
phase<<<{"description": "The phase number"}>>> = 0
[]
[ppss]
type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = pressure
capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
[]
[relperm]
type = PorousFlowRelativePermeabilityBW<<<{"description": "Broadbridge-White form of relative permeability", "href": "../../../../source/materials/PorousFlowRelativePermeabilityBW.html"}>>>
Sn<<<{"description": "Low saturation. This must be < Ss, and non-negative. This is BW's initial effective saturation, below which effective saturation never goes in their simulations/models. If Kn=0 then Sn is the immobile saturation. This form of effective saturation is only correct for Kn small."}>>> = 0.0
Ss<<<{"description": "High saturation. This must be > Sn and <= 1. Effective saturation where porepressure = 0. Effective saturation never exceeds this value in BW's simulations/models."}>>> = 1.0
Kn<<<{"description": "Low relative permeability. This must be < Ks, and non-negative."}>>> = 0
Ks<<<{"description": "High relative permeability. This must be > Kn and less than unity"}>>> = 1
C<<<{"description": "BW's C parameter. Must be > 1. Typical value would be 1.05."}>>> = 1.5
phase<<<{"description": "The phase number"}>>> = 0
[]
[porosity]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>>
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.25
[]
[permeability]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1 0 0 0 1 0 0 0 1'
[]
[]
[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
[pressure]
initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = -9E2
[]
[]
[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
[mass0]
type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time. Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[flux0]
type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '-0.1 0 0'
[]
[]
[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
[SWater]
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
[]
[]
[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
[SWater]
type = MaterialStdVectorAux<<<{"description": "Extracts a component of a material type std::vector<Real> to an aux variable. If the std::vector is not of sufficient size then zero is returned", "href": "../../../../source/auxkernels/MaterialStdVectorAux.html"}>>>
property<<<{"description": "The material property name."}>>> = PorousFlow_saturation_qp
index<<<{"description": "The index to consider for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this object applies to"}>>> = SWater
[]
[]
[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
[recharge]
type = PorousFlowSink<<<{"description": "Applies a flux sink to a boundary.", "href": "../../../../source/bcs/PorousFlowSink.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
flux_function<<<{"description": "The flux. The flux is OUT of the medium: hence positive values of this function means this BC will act as a SINK, while negative values indicate this flux will be a SOURCE. The functional form is useful for spatially or temporally varying sinks. Without any use_*, this function is measured in kg.m^-2.s^-1 (or J.m^-2.s^-1 for the case with only heat and no fluids)"}>>> = -1.25 # corresponds to Rstar being 0.5 because i have to multiply by density*porosity
[]
[]
[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
[andy]
type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
petsc_options<<<{"description": "Singleton PETSc options"}>>> = '-snes_converged_reason -ksp_diagonal_scale -ksp_diagonal_scale_fix -ksp_gmres_modifiedgramschmidt -snes_linesearch_monitor'
petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol -snes_max_it'
petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu NONZERO 2 1E-10 1E-10 10000'
[]
[]
[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
[swater]
type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
warn_discontinuous_face_values<<<{"description": "Whether to return a warning if a discontinuous variable is sampled on a face"}>>> = false
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = SWater
start_point<<<{"description": "The beginning of the line"}>>> = '-10 0 0'
end_point<<<{"description": "The ending of the line"}>>> = '10 0 0'
sort_by<<<{"description": "What to sort the samples by"}>>> = x
num_points<<<{"description": "The number of points to sample along the line"}>>> = 101
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[]
[]
[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
type = Transient
solve_type = Newton
petsc_options = '-snes_converged_reason'
end_time = 8
[TimeStepper<<<{"href": "../../../../syntax/Executioner/TimeStepper/index.html"}>>>]
type = FunctionDT
function = dts
[]
[]
[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = bw01
sync_times<<<{"description": "Times at which the output and solution is forced to occur"}>>> = '0.5 2 8'
[exodus]
type = Exodus<<<{"description": "Object for output data in the Exodus format", "href": "../../../../source/outputs/Exodus.html"}>>>
sync_only<<<{"description": "Only export results at sync times"}>>> = true
[]
[along_line]
type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
sync_only<<<{"description": "Only export results at sync times"}>>> = true
[]
[]The two-phase analytic drainage solution
Warrick, Lomen and Islas (Warrick et al., 1990) extended the analysis of Broadbridge and White to include the case of drainage from a medium.
The setup is an initially-saturated semi-infinite column of material that drains freely from its lower end. This is simulated by placing a boundary condition of at the lower end. To obtain their analytical solutions, Warrick, Lomen and Islas make the same assumptions as Broadbridge and White concerning the diffusivity and conductivity of the medium. Their solutions are quite lengthy, so are not written here
A MOOSE model with the parameters almost identical to those listed in Table 1 is compared with the analytical solutions. The only differences are that the "bar" length is m (to avoid any interference from the lower Dirichlet boundary condition), and since there is no recharge. The initial condition is Pa: the choice leads to poor convergence since by construction the Broadbridge-White capillary function is only designed to simulate the unsaturated zone and a sensible extension to is discontinuous at .
Figure 2 shows good agreement between the analytic solution and the MOOSE implementation. Any minor discrepancies get smaller as the temporal and spatial resolution increase.
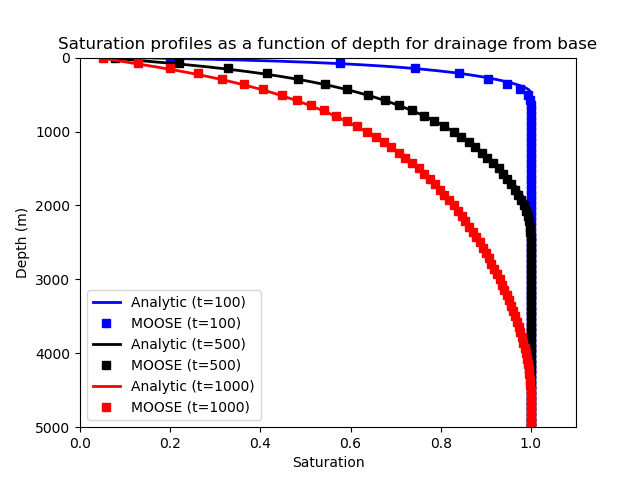
Figure 2: Comparison of the Warrick, Lomen and Islas analytical solution with the MOOSE solution for 3 times. This figure is shown in the standard format used in the literature: the top of the model is at the top of the figure, and gravity acts downwards in this figure, with fluid draining from the infinitely deep point.
Two tests are part of the automatic test suite (one is marked "heavy" because it is a high-resolution version).
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
type = GeneratedMesh
dim = 2
nx = 1000
ny = 1
xmin = -10000
xmax = 0
ymin = 0
ymax = 0.05
[]
[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
PorousFlowDictator = dictator
[]
[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
[dictator]
type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation. Jacobian entries involving derivatives wrt these variables will be computed. In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = pressure
number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
[]
[pc]
type = PorousFlowCapillaryPressureBW<<<{"description": "Broadbridge and White capillary pressure for negligable Kn", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureBW.html"}>>>
Sn<<<{"description": "Low saturation. This must be < Ss, and non-negative. This is BW's initial effective saturation, below which effective saturation never goes in their simulations/models. If Kn=0 then Sn is the immobile saturation. This form of effective saturation is only correct for Kn small."}>>> = 0.0
Ss<<<{"description": "High saturation. This must be > Sn and <= 1. Effective saturation where porepressure = 0. Effective saturation never exceeds this value in BW's simulations/models."}>>> = 1.0
C<<<{"description": "BW's C parameter. Must be > 1. Typical value would be 1.05."}>>> = 1.5
las<<<{"description": "BW's lambda_s parameter multiplied by (fluid_density * gravity). Must be > 0. Typical value would be 1E5"}>>> = 2
[]
[]
[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
[simple_fluid]
type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 2e9
viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 4
density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 10
thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
[]
[]
[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
[massfrac]
type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
[]
[temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
[]
[simple_fluid]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
phase<<<{"description": "The phase number"}>>> = 0
[]
[ppss]
type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = pressure
capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
[]
[relperm]
type = PorousFlowRelativePermeabilityBW<<<{"description": "Broadbridge-White form of relative permeability", "href": "../../../../source/materials/PorousFlowRelativePermeabilityBW.html"}>>>
Sn<<<{"description": "Low saturation. This must be < Ss, and non-negative. This is BW's initial effective saturation, below which effective saturation never goes in their simulations/models. If Kn=0 then Sn is the immobile saturation. This form of effective saturation is only correct for Kn small."}>>> = 0.0
Ss<<<{"description": "High saturation. This must be > Sn and <= 1. Effective saturation where porepressure = 0. Effective saturation never exceeds this value in BW's simulations/models."}>>> = 1.0
Kn<<<{"description": "Low relative permeability. This must be < Ks, and non-negative."}>>> = 0
Ks<<<{"description": "High relative permeability. This must be > Kn and less than unity"}>>> = 1
C<<<{"description": "BW's C parameter. Must be > 1. Typical value would be 1.05."}>>> = 1.5
phase<<<{"description": "The phase number"}>>> = 0
[]
[porosity]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>>
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.25
[]
[permeability]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1 0 0 0 1 0 0 0 1'
[]
[]
[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
[pressure]
initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = -1E-4
[]
[]
[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
[mass0]
type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time. Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[flux0]
type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '-0.1 0 0'
[]
[]
[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
[SWater]
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
[]
[]
[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
[SWater]
type = MaterialStdVectorAux<<<{"description": "Extracts a component of a material type std::vector<Real> to an aux variable. If the std::vector is not of sufficient size then zero is returned", "href": "../../../../source/auxkernels/MaterialStdVectorAux.html"}>>>
property<<<{"description": "The material property name."}>>> = PorousFlow_saturation_qp
index<<<{"description": "The index to consider for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this object applies to"}>>> = SWater
[]
[]
[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
[base]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'left'
value<<<{"description": "Value of the BC"}>>> = -1E-4
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[]
[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
[andy]
type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
petsc_options<<<{"description": "Singleton PETSc options"}>>> = '-snes_converged_reason -ksp_diagonal_scale -ksp_diagonal_scale_fix -ksp_gmres_modifiedgramschmidt -snes_linesearch_monitor'
petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol -snes_max_it'
petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu NONZERO 2 1E-10 1E-10 10000'
[]
[]
[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
[swater]
type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
warn_discontinuous_face_values<<<{"description": "Whether to return a warning if a discontinuous variable is sampled on a face"}>>> = false
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = SWater
start_point<<<{"description": "The beginning of the line"}>>> = '-5000 0 0'
end_point<<<{"description": "The ending of the line"}>>> = '0 0 0'
sort_by<<<{"description": "What to sort the samples by"}>>> = x
num_points<<<{"description": "The number of points to sample along the line"}>>> = 71
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[]
[]
[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
type = Transient
solve_type = Newton
petsc_options = '-snes_converged_reason'
end_time = 1000
dt = 1
[]
[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = wli01
sync_times<<<{"description": "Times at which the output and solution is forced to occur"}>>> = '100 500 1000'
[exodus]
type = Exodus<<<{"description": "Object for output data in the Exodus format", "href": "../../../../source/outputs/Exodus.html"}>>>
sync_only<<<{"description": "Only export results at sync times"}>>> = true
[]
[along_line]
type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
sync_only<<<{"description": "Only export results at sync times"}>>> = true
[]
[]Single-phase infiltration and drainage
Forsyth, Wu and Pruess (Forsyth et al., 1995) describe a HYDRUS simulation of an experiment involving infiltration (experiment 1) and subsequent drainage (experiment 2) in a large caisson. The simulation is effectively one dimensional, and is shown in Figure 3.
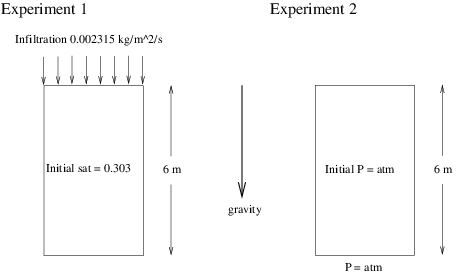
Figure 3: Two experimental setups from Forsyth, Wu and Pruess. Experiment 1 involves infiltration of water into an initially unsaturated caisson. Experiment 2 involves drainage of water from an initially saturated caisson.
The properties common to each experiment are listed in Table 2
Table 2: Parameter values used in the single-phase infiltration and drainage tests
| Parameter | Value |
|---|---|
| Caisson porosity | 0.33 |
| Caisson permeability | m |
| Gravity | 10m.s |
| Water density at STP | 1000kg.m |
| Water viscosity | 0.00101Pa.s |
| Water bulk modulus | 20MPa |
| Water residual saturation | 0.0 |
| Air residual saturation | 0.0 |
| Air pressure | 0.0 |
| van Genuchten | Pa |
| van Genuchten | 0.336 |
| van Genuchten turnover | 0.99 |
In each experiment 120 finite elements are used along the length of the Caisson. The modified van Genuchten relative permeability curve with a "turnover" (set at ) is employed in order to improve convergence significantly. Hydrus also uses a modified van Genuchten curve, although I couldn't find any details on the modification.
In experiment 1, the caisson is initially at saturation 0.303 (Pa), and water is pumped into the top with a rate 0.002315kg.m.s. This causes a front of water to advance down the caisson. Figure 4 shows the agreement between MOOSE and the published result (this result was obtained by extracting data by hand from online graphics).
In experiment 2, the caisson is initially fully saturated at , and the bottom is held at to cause water to drain via the action of gravity. Figure 4 and Figure 5 show the agreement between MOOSE and the published result.
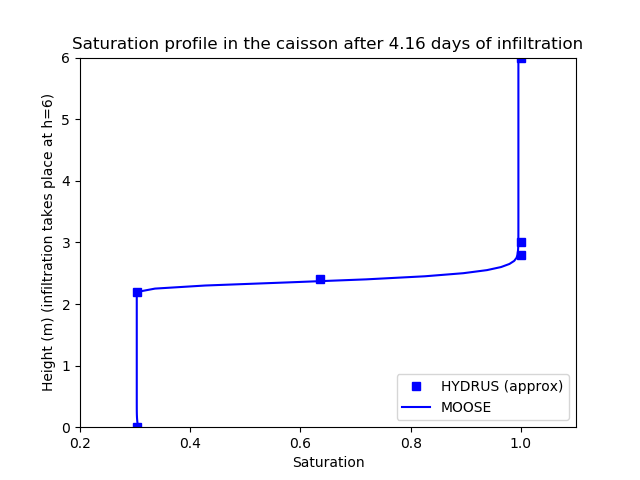
Figure 4: Saturation profile in the caisson after 4.16 days of infiltration. Note that the HYDRUS results are only approximate they were extracted by hand from online graphics.
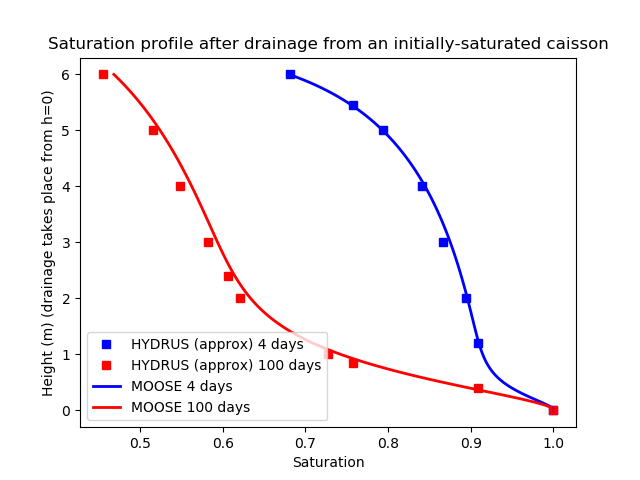
Figure 5: Saturation profiles in the caisson after drainage from an initially-saturated simulation (4 days and 100 days profiles). Note that the HYDRUS results are only approximate they were extracted by hand from online graphics.
Experiment 1 and the first 4 simulation days of experiment 2 are marked as "heavy" in the PorousFlow test suite since the simulations take around 3 seconds to complete.
The input file for Experiment 1:
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
type = GeneratedMesh
dim = 2
nx = 120
ny = 1
xmin = 0
xmax = 6
ymin = 0
ymax = 0.05
[]
[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
PorousFlowDictator = dictator
[]
[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
[dts]
type = PiecewiseLinear<<<{"description": "Linearly interpolates between pairs of x-y data", "href": "../../../../source/functions/PiecewiseLinear.html"}>>>
y<<<{"description": "The ordinate values"}>>> = '1E-2 1 10 500 5000 5000'
x<<<{"description": "The abscissa values"}>>> = '0 10 100 1000 10000 100000'
[]
[]
[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
[dictator]
type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation. Jacobian entries involving derivatives wrt these variables will be computed. In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = pressure
number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
[]
[pc]
type = PorousFlowCapillaryPressureVG<<<{"description": "van Genuchten capillary pressure", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureVG.html"}>>>
m<<<{"description": "van Genuchten exponent m. Must be between 0 and 1, and optimally should be set to >0.5"}>>> = 0.336
alpha<<<{"description": "van Genuchten parameter alpha. Must be positive"}>>> = 1.43e-4
[]
[]
[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
[simple_fluid]
type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 2e7
viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1.01e-3
density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1000
thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
[]
[]
[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
[massfrac]
type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
[]
[temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
[]
[simple_fluid]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
phase<<<{"description": "The phase number"}>>> = 0
[]
[ppss]
type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = pressure
capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
[]
[relperm]
type = PorousFlowRelativePermeabilityVG<<<{"description": "This Material calculates relative permeability of a phase using the van Genuchten model", "href": "../../../../source/materials/PorousFlowRelativePermeabilityVG.html"}>>>
m<<<{"description": "The van Genuchten exponent of the phase"}>>> = 0.336
seff_turnover<<<{"description": "The relative permeability will be a cubic for seff > seff_turnover. The cubic is chosen so that its derivative and value matche the VG function at seff=seff_turnover"}>>> = 0.99
phase<<<{"description": "The phase number"}>>> = 0
[]
[porosity]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>>
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.33
[]
[permeability]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '0.295E-12 0 0 0 0.295E-12 0 0 0 0.295E-12'
[]
[]
[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
[pressure]
initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = -72620.4
[]
[]
[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
[mass0]
type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time. Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[flux0]
type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '-10 0 0'
[]
[]
[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
[SWater]
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
[]
[]
[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
[SWater]
type = MaterialStdVectorAux<<<{"description": "Extracts a component of a material type std::vector<Real> to an aux variable. If the std::vector is not of sufficient size then zero is returned", "href": "../../../../source/auxkernels/MaterialStdVectorAux.html"}>>>
property<<<{"description": "The material property name."}>>> = PorousFlow_saturation_qp
index<<<{"description": "The index to consider for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this object applies to"}>>> = SWater
[]
[]
[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
[base]
type = PorousFlowSink<<<{"description": "Applies a flux sink to a boundary.", "href": "../../../../source/bcs/PorousFlowSink.html"}>>>
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
flux_function<<<{"description": "The flux. The flux is OUT of the medium: hence positive values of this function means this BC will act as a SINK, while negative values indicate this flux will be a SOURCE. The functional form is useful for spatially or temporally varying sinks. Without any use_*, this function is measured in kg.m^-2.s^-1 (or J.m^-2.s^-1 for the case with only heat and no fluids)"}>>> = -2.315E-3
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[]
[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
[andy]
type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
petsc_options<<<{"description": "Singleton PETSc options"}>>> = '-snes_converged_reason -ksp_diagonal_scale -ksp_diagonal_scale_fix -ksp_gmres_modifiedgramschmidt -snes_linesearch_monitor'
petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol -snes_max_it'
petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu NONZERO 2 1E-10 1E-10 10'
[]
[]
[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
[swater]
type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
warn_discontinuous_face_values<<<{"description": "Whether to return a warning if a discontinuous variable is sampled on a face"}>>> = false
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = SWater
start_point<<<{"description": "The beginning of the line"}>>> = '0 0 0'
end_point<<<{"description": "The ending of the line"}>>> = '6 0 0'
sort_by<<<{"description": "What to sort the samples by"}>>> = x
num_points<<<{"description": "The number of points to sample along the line"}>>> = 121
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[]
[]
[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
type = Transient
solve_type = Newton
petsc_options = '-snes_converged_reason'
end_time = 359424
[TimeStepper<<<{"href": "../../../../syntax/Executioner/TimeStepper/index.html"}>>>]
type = FunctionDT
function = dts
[]
[]
[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = rd01
[exodus]
type = Exodus<<<{"description": "Object for output data in the Exodus format", "href": "../../../../source/outputs/Exodus.html"}>>>
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'initial final'
[]
[along_line]
type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = final
[]
[]The input file for the first 4 simulation days of Experiment 2:
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
type = GeneratedMesh
dim = 2
nx = 120
ny = 1
xmin = 0
xmax = 6
ymin = 0
ymax = 0.05
[]
[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
PorousFlowDictator = dictator
[]
[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
[dts]
type = PiecewiseLinear<<<{"description": "Linearly interpolates between pairs of x-y data", "href": "../../../../source/functions/PiecewiseLinear.html"}>>>
y<<<{"description": "The ordinate values"}>>> = '1E-2 1 10 500 5000 50000'
x<<<{"description": "The abscissa values"}>>> = '0 10 100 1000 10000 500000'
[]
[]
[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
[dictator]
type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation. Jacobian entries involving derivatives wrt these variables will be computed. In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = pressure
number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
[]
[pc]
type = PorousFlowCapillaryPressureVG<<<{"description": "van Genuchten capillary pressure", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureVG.html"}>>>
m<<<{"description": "van Genuchten exponent m. Must be between 0 and 1, and optimally should be set to >0.5"}>>> = 0.336
alpha<<<{"description": "van Genuchten parameter alpha. Must be positive"}>>> = 1.43e-4
[]
[]
[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
[simple_fluid]
type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 2e7
viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1.01e-3
density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1000
thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
[]
[]
[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
[massfrac]
type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
[]
[temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
[]
[simple_fluid]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
phase<<<{"description": "The phase number"}>>> = 0
[]
[ppss]
type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = pressure
capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
[]
[relperm]
type = PorousFlowRelativePermeabilityVG<<<{"description": "This Material calculates relative permeability of a phase using the van Genuchten model", "href": "../../../../source/materials/PorousFlowRelativePermeabilityVG.html"}>>>
m<<<{"description": "The van Genuchten exponent of the phase"}>>> = 0.336
seff_turnover<<<{"description": "The relative permeability will be a cubic for seff > seff_turnover. The cubic is chosen so that its derivative and value matche the VG function at seff=seff_turnover"}>>> = 0.99
phase<<<{"description": "The phase number"}>>> = 0
[]
[porosity]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>>
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.33
[]
[permeability]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '0.295E-12 0 0 0 0.295E-12 0 0 0 0.295E-12'
[]
[]
[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
[pressure]
initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 0.0
[]
[]
[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
[mass0]
type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time. Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[flux0]
type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '-10 0 0'
[]
[]
[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
[SWater]
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
[]
[]
[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
[SWater]
type = MaterialStdVectorAux<<<{"description": "Extracts a component of a material type std::vector<Real> to an aux variable. If the std::vector is not of sufficient size then zero is returned", "href": "../../../../source/auxkernels/MaterialStdVectorAux.html"}>>>
property<<<{"description": "The material property name."}>>> = PorousFlow_saturation_qp
index<<<{"description": "The index to consider for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this object applies to"}>>> = SWater
[]
[]
[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
[base]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
value<<<{"description": "Value of the BC"}>>> = 0.0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[]
[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
[andy]
type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
petsc_options<<<{"description": "Singleton PETSc options"}>>> = '-snes_converged_reason -ksp_diagonal_scale -ksp_diagonal_scale_fix -ksp_gmres_modifiedgramschmidt -snes_linesearch_monitor'
petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol -snes_max_it'
petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu NONZERO 2 1E-10 1E-10 10'
[]
[]
[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
[swater]
type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
warn_discontinuous_face_values<<<{"description": "Whether to return a warning if a discontinuous variable is sampled on a face"}>>> = false
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = SWater
start_point<<<{"description": "The beginning of the line"}>>> = '0 0 0'
end_point<<<{"description": "The ending of the line"}>>> = '6 0 0'
sort_by<<<{"description": "What to sort the samples by"}>>> = x
num_points<<<{"description": "The number of points to sample along the line"}>>> = 121
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[]
[]
[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
type = Transient
solve_type = Newton
petsc_options = '-snes_converged_reason'
end_time = 345600
[TimeStepper<<<{"href": "../../../../syntax/Executioner/TimeStepper/index.html"}>>>]
type = FunctionDT
function = dts
[]
[]
[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = rd02
[exodus]
type = Exodus<<<{"description": "Object for output data in the Exodus format", "href": "../../../../source/outputs/Exodus.html"}>>>
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'initial final'
[]
[along_line]
type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = final
[]
[]The input file for the latter 96 days of Experiment 2:
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
file = gold/rd02.e
[]
[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
PorousFlowDictator = dictator
[]
[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
[dts]
type = PiecewiseLinear<<<{"description": "Linearly interpolates between pairs of x-y data", "href": "../../../../source/functions/PiecewiseLinear.html"}>>>
y<<<{"description": "The ordinate values"}>>> = '2E4 1E6'
x<<<{"description": "The abscissa values"}>>> = '0 1E6'
[]
[]
[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
[dictator]
type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation. Jacobian entries involving derivatives wrt these variables will be computed. In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = pressure
number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
[]
[pc]
type = PorousFlowCapillaryPressureVG<<<{"description": "van Genuchten capillary pressure", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureVG.html"}>>>
m<<<{"description": "van Genuchten exponent m. Must be between 0 and 1, and optimally should be set to >0.5"}>>> = 0.336
alpha<<<{"description": "van Genuchten parameter alpha. Must be positive"}>>> = 1.43e-4
[]
[]
[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
[simple_fluid]
type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 2e7
viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1.01e-3
density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1000
thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
[]
[]
[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
[massfrac]
type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
[]
[temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
[]
[simple_fluid]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
phase<<<{"description": "The phase number"}>>> = 0
[]
[ppss]
type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = pressure
capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
[]
[relperm]
type = PorousFlowRelativePermeabilityVG<<<{"description": "This Material calculates relative permeability of a phase using the van Genuchten model", "href": "../../../../source/materials/PorousFlowRelativePermeabilityVG.html"}>>>
m<<<{"description": "The van Genuchten exponent of the phase"}>>> = 0.336
seff_turnover<<<{"description": "The relative permeability will be a cubic for seff > seff_turnover. The cubic is chosen so that its derivative and value matche the VG function at seff=seff_turnover"}>>> = 0.99
phase<<<{"description": "The phase number"}>>> = 0
[]
[porosity]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>>
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.33
[]
[permeability]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '0.295E-12 0 0 0 0.295E-12 0 0 0 0.295E-12'
[]
[]
[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
[pressure]
initial_from_file_timestep<<<{"description": "Gives the timestep (or \"LATEST\") for which to read a solution from a file for a given variable. (Default: LATEST)"}>>> = LATEST
initial_from_file_var<<<{"description": "Gives the name of a variable for which to read an initial condition from a mesh file"}>>> = pressure
[]
[]
[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
[mass0]
type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time. Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[flux0]
type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '-10 0 0'
[]
[]
[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
[SWater]
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
[]
[]
[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
[SWater]
type = MaterialStdVectorAux<<<{"description": "Extracts a component of a material type std::vector<Real> to an aux variable. If the std::vector is not of sufficient size then zero is returned", "href": "../../../../source/auxkernels/MaterialStdVectorAux.html"}>>>
property<<<{"description": "The material property name."}>>> = PorousFlow_saturation_qp
index<<<{"description": "The index to consider for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this object applies to"}>>> = SWater
[]
[]
[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
[base]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
value<<<{"description": "Value of the BC"}>>> = 0.0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pressure
[]
[]
[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
[andy]
type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
petsc_options<<<{"description": "Singleton PETSc options"}>>> = '-snes_converged_reason -ksp_diagonal_scale -ksp_diagonal_scale_fix -ksp_gmres_modifiedgramschmidt -snes_linesearch_monitor'
petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol -snes_max_it'
petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu NONZERO 2 1E-10 1E-10 10'
[]
[]
[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
[swater]
type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
warn_discontinuous_face_values<<<{"description": "Whether to return a warning if a discontinuous variable is sampled on a face"}>>> = false
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = SWater
start_point<<<{"description": "The beginning of the line"}>>> = '0 0 0'
end_point<<<{"description": "The ending of the line"}>>> = '6 0 0'
sort_by<<<{"description": "What to sort the samples by"}>>> = x
num_points<<<{"description": "The number of points to sample along the line"}>>> = 121
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[]
[]
[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
type = Transient
solve_type = Newton
petsc_options = '-snes_converged_reason'
end_time = 8.2944E6
[TimeStepper<<<{"href": "../../../../syntax/Executioner/TimeStepper/index.html"}>>>]
type = FunctionDT
function = dts
[]
[]
[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = rd03
[exodus]
type = Exodus<<<{"description": "Object for output data in the Exodus format", "href": "../../../../source/outputs/Exodus.html"}>>>
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'initial final'
[]
[along_line]
type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = final
[]
[]Water infiltration into a two-phase (oil-water) system
An analytic solution of the two-phase Richards' equations with gravity on a semi-infinite line , with a constant water infiltration flux at has been derived by (Rogers et al., 1983) (Unfortunately there must be a typo in the RSC paper as for nonzero gravity their results are clearly incorrect.). The authors assume incompressible fluids; linear relative permeability relationships; the "oil" (or "gas") viscosity is larger than the water viscosity; and, a certain functional form for the capillary pressure. When the oil viscosity is exactly twice the water viscosity, their effective saturation reads (2) where is the capillary pressure, and and are arbitrary parameters to be defined by the user in the PorousFlow implementation. For other oil/water viscosity ratios is more complicated, and note that their formulation allows , but only the particular form Eq. (2) need be used to validate the MOOSE implementation.
RSC's solutions are quite lengthy, so I will not write them here. To compare with MOOSE, the following parameters are used:
Table 3: Parameter values used in the Rogers-Stallybrass-Clements infiltration tests
| Parameter | Value |
|---|---|
| Bar length | 10 m |
| Bar porosity | 0.25 |
| Bar permeability | m |
| Gravity | 0 m.s |
| Water density | 10 kg.m |
| Water viscosity | Pa.s |
| Oil density | 20 kg.m |
| Oil viscosity | Pa.s |
| Capillary | 10 Pa |
| Capillary | 1 Pa |
| Initial water pressure | 0 Pa |
| Initial oil pressure | 15 Pa |
| Initial water saturation | 0.08181 |
| Initial oil saturation | 0.91819 |
| Water injection rate | 1 kg.s.m |
The input file:
# RSC test with high-res time and spatial resolution
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
type = GeneratedMesh
dim = 2
nx = 600
ny = 1
xmin = 0
xmax = 10 # x is the depth variable, called zeta in RSC
ymin = 0
ymax = 0.05
[]
[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
[dts]
type = PiecewiseLinear<<<{"description": "Linearly interpolates between pairs of x-y data", "href": "../../../../source/functions/PiecewiseLinear.html"}>>>
y<<<{"description": "The ordinate values"}>>> = '3E-3 3E-2 0.05'
x<<<{"description": "The abscissa values"}>>> = '0 1 5'
[]
[]
[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
[dictator]
type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation. Jacobian entries involving derivatives wrt these variables will be computed. In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'pwater poil'
number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 2
number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 2
[]
[pc]
type = PorousFlowCapillaryPressureRSC<<<{"description": "Rogers-Stallybrass-Clements version of effective saturation for the water phase, valid for residual saturations = 0, and viscosityOil = 2 * viscosityWater. seff_water = 1 / sqrt(1 + exp((Pc - shift) / scale)), where scale = 0.25 * scale_ratio * oil_viscosity.", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureRSC.html"}>>>
oil_viscosity<<<{"description": "Viscosity of oil (gas) phase. It is assumed this is double the water-phase viscosity. (Note that this effective saturation is mostly useful for 2-phase, not single-phase.)"}>>> = 2E-3
scale_ratio<<<{"description": "This is porosity / permeability / beta^2, where beta may be chosen by the user. It has dimensions [time]"}>>> = 2E3
shift<<<{"description": "effective saturation is a function of (Pc - shift)"}>>> = 10
[]
[]
[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
[water]
type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 2e9
density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 10
thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1e-3
[]
[oil]
type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 2e9
density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 20
thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 2e-3
[]
[]
[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
[temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
[]
[ppss]
type = PorousFlow2PhasePP<<<{"description": "This Material calculates the 2 porepressures and the 2 saturations in a 2-phase situation, and derivatives of these with respect to the PorousFlowVariables", "href": "../../../../source/materials/PorousFlow2PhasePP.html"}>>>
phase0_porepressure<<<{"description": "Variable that is the porepressure of phase 0 (eg, the water phase). It will be <= phase1_porepressure."}>>> = pwater
phase1_porepressure<<<{"description": "Variable that is the porepressure of phase 1 (eg, the gas phase)"}>>> = poil
capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
[]
[massfrac]
type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
mass_fraction_vars<<<{"description": "List of variables that represent the mass fractions. Format is 'f_ph0^c0 f_ph0^c1 f_ph0^c2 ... f_ph0^c(N-2) f_ph1^c0 f_ph1^c1 fph1^c2 ... fph1^c(N-2) ... fphP^c0 f_phP^c1 fphP^c2 ... fphP^c(N-2)' where N=num_components and P=num_phases, and it is assumed that f_ph^c(N-1)=1-sum(f_ph^c,{c,0,N-2}) so that f_ph^c(N-1) need not be given. If no variables are provided then num_phases=1=num_components."}>>> = 'massfrac_ph0_sp0 massfrac_ph1_sp0'
[]
[water]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = water
phase<<<{"description": "The phase number"}>>> = 0
compute_enthalpy<<<{"description": "Compute the fluid enthalpy"}>>> = false
compute_internal_energy<<<{"description": "Compute the fluid internal energy"}>>> = false
[]
[oil]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = oil
phase<<<{"description": "The phase number"}>>> = 1
compute_enthalpy<<<{"description": "Compute the fluid enthalpy"}>>> = false
compute_internal_energy<<<{"description": "Compute the fluid internal energy"}>>> = false
[]
[relperm_water]
type = PorousFlowRelativePermeabilityCorey<<<{"description": "This Material calculates relative permeability of the fluid phase, using the simple Corey model ((S-S_res)/(1-sum(S_res)))^n", "href": "../../../../source/materials/PorousFlowRelativePermeabilityCorey.html"}>>>
n<<<{"description": "The Corey exponent of the phase."}>>> = 1
phase<<<{"description": "The phase number"}>>> = 0
[]
[relperm_oil]
type = PorousFlowRelativePermeabilityCorey<<<{"description": "This Material calculates relative permeability of the fluid phase, using the simple Corey model ((S-S_res)/(1-sum(S_res)))^n", "href": "../../../../source/materials/PorousFlowRelativePermeabilityCorey.html"}>>>
n<<<{"description": "The Corey exponent of the phase."}>>> = 1
phase<<<{"description": "The phase number"}>>> = 1
[]
[porosity]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>>
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.25
[]
[permeability]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1E-5 0 0 0 1E-5 0 0 0 1E-5'
[]
[]
[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
[pwater]
[]
[poil]
[]
[]
[ICs<<<{"href": "../../../../syntax/ICs/index.html"}>>>]
[water_init]
type = ConstantIC<<<{"description": "Sets a constant field value.", "href": "../../../../source/ics/ConstantIC.html"}>>>
variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = pwater
value<<<{"description": "The value to be set in IC"}>>> = 0
[]
[oil_init]
type = ConstantIC<<<{"description": "Sets a constant field value.", "href": "../../../../source/ics/ConstantIC.html"}>>>
variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = poil
value<<<{"description": "The value to be set in IC"}>>> = 15
[]
[]
[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
[mass0]
type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time. Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pwater
[]
[flux0]
type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pwater
[]
[mass1]
type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time. Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 1
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = poil
[]
[flux1]
type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 1
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = poil
[]
[]
[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
[SWater]
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
[]
[SOil]
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
[]
[massfrac_ph0_sp0]
initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 1
[]
[massfrac_ph1_sp0]
initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 0
[]
[]
[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
[SWater]
type = MaterialStdVectorAux<<<{"description": "Extracts a component of a material type std::vector<Real> to an aux variable. If the std::vector is not of sufficient size then zero is returned", "href": "../../../../source/auxkernels/MaterialStdVectorAux.html"}>>>
property<<<{"description": "The material property name."}>>> = PorousFlow_saturation_qp
index<<<{"description": "The index to consider for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this object applies to"}>>> = SWater
[]
[SOil]
type = MaterialStdVectorAux<<<{"description": "Extracts a component of a material type std::vector<Real> to an aux variable. If the std::vector is not of sufficient size then zero is returned", "href": "../../../../source/auxkernels/MaterialStdVectorAux.html"}>>>
property<<<{"description": "The material property name."}>>> = PorousFlow_saturation_qp
index<<<{"description": "The index to consider for this kernel"}>>> = 1
variable<<<{"description": "The name of the variable that this object applies to"}>>> = SOil
[]
[]
[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
# we are pumping water into a system that has virtually incompressible fluids, hence the pressures rise enormously. this adversely affects convergence because of almost-overflows and precision-loss problems. The fixed things help keep pressures low and so prevent these awful behaviours. the movement of the saturation front is the same regardless of the fixed things.
active<<<{"description": "If specified only the blocks named will be visited and made active"}>>> = 'recharge fixedoil fixedwater'
[recharge]
type = PorousFlowSink<<<{"description": "Applies a flux sink to a boundary.", "href": "../../../../source/bcs/PorousFlowSink.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pwater
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'left'
flux_function<<<{"description": "The flux. The flux is OUT of the medium: hence positive values of this function means this BC will act as a SINK, while negative values indicate this flux will be a SOURCE. The functional form is useful for spatially or temporally varying sinks. Without any use_*, this function is measured in kg.m^-2.s^-1 (or J.m^-2.s^-1 for the case with only heat and no fluids)"}>>> = -1.0
[]
[fixedwater]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pwater
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'right'
value<<<{"description": "Value of the BC"}>>> = 0
[]
[fixedoil]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = poil
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'right'
value<<<{"description": "Value of the BC"}>>> = 15
[]
[]
[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
[andy]
type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
petsc_options<<<{"description": "Singleton PETSc options"}>>> = '-snes_converged_reason -ksp_diagonal_scale -ksp_diagonal_scale_fix -ksp_gmres_modifiedgramschmidt -snes_linesearch_monitor'
petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap -snes_atol -snes_rtol -snes_max_it'
petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu NONZERO 2 1E-10 1E-10 10000'
[]
[]
[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
[swater]
type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
warn_discontinuous_face_values<<<{"description": "Whether to return a warning if a discontinuous variable is sampled on a face"}>>> = false
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = SWater
start_point<<<{"description": "The beginning of the line"}>>> = '0 0 0'
end_point<<<{"description": "The ending of the line"}>>> = '7 0 0'
sort_by<<<{"description": "What to sort the samples by"}>>> = x
num_points<<<{"description": "The number of points to sample along the line"}>>> = 21
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[]
[]
[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
type = Transient
solve_type = Newton
petsc_options = '-snes_converged_reason'
end_time = 5
[TimeStepper<<<{"href": "../../../../syntax/Executioner/TimeStepper/index.html"}>>>]
type = FunctionDT
function = dts
[]
[]
[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = rsc01
[along_line]
type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
execute_vector_postprocessors_on<<<{"description": "Enable/disable the output of VectorPostprocessors"}>>> = final
[]
[exodus]
type = Exodus<<<{"description": "Object for output data in the Exodus format", "href": "../../../../source/outputs/Exodus.html"}>>>
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'initial final'
[]
[]In the RSC theory water is injected into a semi-infinite domain, whereas of course the MOOSE implementation has finite extent ( is chosen). Because of the near incompressibility of the fluids (I choose the bulk modulus to be 2 GPa) this causes the porepressures to rise enormously, and the problem can suffer from precision-loss problems. Therefore, the porepressures are fixed at . This does not affect the progress of the water saturation front.
Figure 6 shows good agreement between the analytic solution and the MOOSE implementation. Any minor discrepancies get smaller as the temporal and spatial resolution increase, as is suggested by the two comparisons in that figure.
The "low-resolution" test has 200 elements in and uses 15 time steps is part the automatic test suite that is run every time the code is updated. The "high-resolution" test has 600 elements and uses 190 time steps, and is marked as "heavy".
Figure 6: Water saturation profile after 5 seconds of injection in the Rogers-Stallybrass-Clements test. The initial water saturation is 0.08181, and water is injected at the top of this figure at a constant rate. This forms a water front which displaces the oil. Black line: RSC's analytic solution. Red squares: high-resolution MOOSE simulation. Green triangles: lower resolution MOOSE simulation.
References
- P. Broadbridge and I. White.
Constant rate rainfall infiltration: a versatile nonlinear model, 1. analytical solution.
Water Resources Research, 24:145–154, 1988.[BibTeX]
- P. A. Forsyth, Y. S. Wu, and K. Pruess.
Robust numerical methods for saturated-unsaturated flow with dry initial conditions in heterogeneous media.
Water Resources Research, 18:25–38, 1995.[BibTeX]
- C. Rogers, M. P. Stallybrass, and D. L. Clements.
On two phase filtration under gravity and with boundary infiltration: application of a Backlund transformation.
Nonlinear Analysis, Theory, Methods and Applications, 7:785–799, 1983.[BibTeX]
- A. W. Warrick, D. O. Lomen, and A. Islas.
An analytical solution to Richards' Equation for a Draining Soil Profile.
Water Resources Research, 26:253–258, 1990.[BibTeX]