Diffusion and hydrodynamic dispersion Tests
Diffusion
The results of PorousFlow are compared with the classical diffusion profile for a simple 1D model with mass diffusion. In this example, the left end of a 1D mesh is held at a constant mass fraction of 1, while the right hand end is prescribed a zero mass fraction boundary condition. No advection takes place, so mass transfer is by diffusion only. The input file:
# Test diffusive part of PorousFlowDispersiveFlux kernel by setting dispersion
# coefficients to zero. Pressure is held constant over the mesh, and gravity is
# set to zero so that no advective transport of mass takes place.
# Mass fraction is set to 1 on the left hand side and 0 on the right hand side.
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
type = GeneratedMesh
dim = 1
nx = 20
xmax = 10
bias_x = 1.1
[]
[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
PorousFlowDictator = andy_heheheh
[]
[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
[pp]
[]
[massfrac0]
[]
[]
[ICs<<<{"href": "../../../../syntax/ICs/index.html"}>>>]
[pp]
type = ConstantIC<<<{"description": "Sets a constant field value.", "href": "../../../../source/ics/ConstantIC.html"}>>>
variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = pp
value<<<{"description": "The value to be set in IC"}>>> = 1e5
[]
[massfrac0]
type = ConstantIC<<<{"description": "Sets a constant field value.", "href": "../../../../source/ics/ConstantIC.html"}>>>
variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = massfrac0
value<<<{"description": "The value to be set in IC"}>>> = 0
[]
[]
[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
[left]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
value<<<{"description": "Value of the BC"}>>> = 1
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = massfrac0
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
[]
[right]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
value<<<{"description": "Value of the BC"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = massfrac0
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
[]
[pright]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pp
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
value<<<{"description": "Value of the BC"}>>> = 1e5
[]
[pleft]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pp
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
value<<<{"description": "Value of the BC"}>>> = 1e5
[]
[]
[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
[diff0]
type = PorousFlowDispersiveFlux<<<{"description": "Dispersive and diffusive flux of the component given by fluid_component in all phases", "href": "../../../../source/kernels/PorousFlowDispersiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = massfrac0
disp_trans<<<{"description": "Vector of transverse dispersion coefficients for each phase"}>>> = 0
disp_long<<<{"description": "Vector of longitudinal dispersion coefficients for each phase"}>>> = 0
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
[]
[diff1]
type = PorousFlowDispersiveFlux<<<{"description": "Dispersive and diffusive flux of the component given by fluid_component in all phases", "href": "../../../../source/kernels/PorousFlowDispersiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 1
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pp
disp_trans<<<{"description": "Vector of transverse dispersion coefficients for each phase"}>>> = 0
disp_long<<<{"description": "Vector of longitudinal dispersion coefficients for each phase"}>>> = 0
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
[]
[]
[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
[the_simple_fluid]
type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0.0
bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 1E7
viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 0.001
density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1000.0
[]
[]
[PorousFlowUnsaturated<<<{"href": "../../../../syntax/PorousFlowUnsaturated/index.html"}>>>]
porepressure<<<{"description": "The name of the porepressure variable"}>>> = pp
gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
fp<<<{"description": "The name of the user object for fluid properties. Only needed if fluid_properties_type = PorousFlowSingleComponentFluid"}>>> = the_simple_fluid
dictator_name<<<{"description": "The name of the dictator user object that is created by this Action"}>>> = andy_heheheh
relative_permeability_type<<<{"description": "Type of relative-permeability function. FLAC relperm = (1+m)S^m - mS^(1+m). Corey relperm = S^m. m is the exponent. Here S = (saturation - residual)/(1 - residual)"}>>> = Corey
relative_permeability_exponent<<<{"description": "Relative permeability exponent"}>>> = 0.0
mass_fraction_vars<<<{"description": "List of variables that represent the mass fractions. With only one fluid component, this may be left empty. With N fluid components, the format is 'f_0 f_1 f_2 ... f_(N-1)'. That is, the N^th component need not be specified because f_N = 1 - (f_0 + f_1 + ... + f_(N-1)). It is best numerically to choose the N-1 mass fraction variables so that they represent the fluid components with small concentrations. This Action will associated the i^th mass fraction variable to the equation for the i^th fluid component, and the pressure variable to the N^th fluid component."}>>> = massfrac0
[]
[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
[poro]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>>
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.3
[]
[diff]
type = PorousFlowDiffusivityConst<<<{"description": "This Material provides constant tortuosity and diffusion coefficients", "href": "../../../../source/materials/PorousFlowDiffusivityConst.html"}>>>
diffusion_coeff<<<{"description": "List of diffusion coefficients. Order is i) component 0 in phase 0; ii) component 1 in phase 0 ...; component 0 in phase 1; ... component k in phase n (m^2/s"}>>> = '1 1'
tortuosity<<<{"description": "List of tortuosities. Order is i) phase 0; ii) phase 1; etc"}>>> = 0.1
[]
[permeability]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1e-9 0 0 0 1e-9 0 0 0 1e-9'
[]
[]
[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
[smp]
type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu NONZERO 2 '
[]
[]
[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
type = Transient
solve_type = NEWTON
dt = 1
end_time = 20
[]
[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
[xmass]
type = NodalValueSampler<<<{"description": "Samples values of nodal variable(s).", "href": "../../../../source/vectorpostprocessors/NodalValueSampler.html"}>>>
sort_by<<<{"description": "What to sort the samples by"}>>> = id
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = massfrac0
[]
[]
[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
[out]
type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = final
[]
[]This concentration profile has a well-known similarity solution given by where is the complementary error function, and is the similarity solution, is distance, is time, and is the diffusion coefficient.
The comparison between PorousFlow and this analytical solution is presented in Figure 1, where we observe a very good agreement between the two solutions.
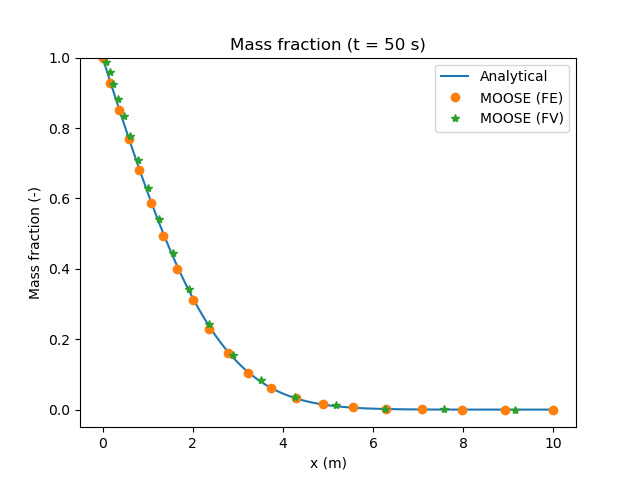
Figure 1: Mass fraction profile from diffusion only.
Hydrodynamic dispersion
The PorousFlow results are compared to known analytical solutions for simple problems in order to verify that the MOOSE implementation is working properly. For a simple 1D model with no diffusion and constant velocity , an analytical solution for the mass fraction profile is given by (Javandel et al., 1984) where all parameters have been previously defined.
The input file:
# Test dispersive part of PorousFlowDispersiveFlux kernel by setting diffusion
# coefficients to zero. A pressure gradient is applied over the mesh to give a
# uniform velocity. Gravity is set to zero.
# Mass fraction is set to 1 on the left hand side and 0 on the right hand side.
[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
type = GeneratedMesh
dim = 1
nx = 200
xmax = 10
[]
[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
PorousFlowDictator = dictator
gravity = '0 0 0'
compute_enthalpy = false
compute_internal_energy = false
[]
[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
[pp]
[]
[massfrac0]
[]
[]
[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
[velocity]
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = FIRST
[]
[]
[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
[velocity]
type = PorousFlowDarcyVelocityComponent<<<{"description": "Darcy velocity (in m^3.s^-1.m^-2, or m.s^-1) -(k_ij * krel /mu (nabla_j P - w_j)), where k_ij is the permeability tensor, krel is the relative permeability, mu is the fluid viscosity, P is the fluid pressure, and w_j is the fluid weight.", "href": "../../../../source/auxkernels/PorousFlowDarcyVelocityComponent.html"}>>>
variable<<<{"description": "The name of the variable that this object applies to"}>>> = velocity
component<<<{"description": "The spatial component of the Darcy flux to return"}>>> = x
[]
[]
[ICs<<<{"href": "../../../../syntax/ICs/index.html"}>>>]
[pp]
type = FunctionIC<<<{"description": "An initial condition that uses a normal function of x, y, z to produce values (and optionally gradients) for a field variable.", "href": "../../../../source/ics/FunctionIC.html"}>>>
variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = pp
function<<<{"description": "The initial condition function."}>>> = pic
[]
[massfrac0]
type = ConstantIC<<<{"description": "Sets a constant field value.", "href": "../../../../source/ics/ConstantIC.html"}>>>
variable<<<{"description": "The variable this initial condition is supposed to provide values for."}>>> = massfrac0
value<<<{"description": "The value to be set in IC"}>>> = 0
[]
[]
[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
[pic]
type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../../../../source/functions/MooseParsedFunction.html"}>>>
expression<<<{"description": "The user defined function."}>>> = 1.1e5-x*1e3
[]
[]
[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
[xleft]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
value<<<{"description": "Value of the BC"}>>> = 1
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = massfrac0
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
[]
[xright]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
value<<<{"description": "Value of the BC"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = massfrac0
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
[]
[pright]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pp
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
value<<<{"description": "Value of the BC"}>>> = 1e5
[]
[pleft]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pp
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
value<<<{"description": "Value of the BC"}>>> = 1.1e5
[]
[]
[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
[mass0]
type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time. Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pp
[]
[adv0]
type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pp
[]
[diff0]
type = PorousFlowDispersiveFlux<<<{"description": "Dispersive and diffusive flux of the component given by fluid_component in all phases", "href": "../../../../source/kernels/PorousFlowDispersiveFlux.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pp
disp_trans<<<{"description": "Vector of transverse dispersion coefficients for each phase"}>>> = 0
disp_long<<<{"description": "Vector of longitudinal dispersion coefficients for each phase"}>>> = 0.2
[]
[mass1]
type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time. Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 1
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = massfrac0
[]
[adv1]
type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 1
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = massfrac0
[]
[diff1]
type = PorousFlowDispersiveFlux<<<{"description": "Dispersive and diffusive flux of the component given by fluid_component in all phases", "href": "../../../../source/kernels/PorousFlowDispersiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 1
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = massfrac0
disp_trans<<<{"description": "Vector of transverse dispersion coefficients for each phase"}>>> = 0
disp_long<<<{"description": "Vector of longitudinal dispersion coefficients for each phase"}>>> = 0.2
[]
[]
[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
[dictator]
type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation. Jacobian entries involving derivatives wrt these variables will be computed. In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'pp massfrac0'
number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 2
[]
[]
[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
[simple_fluid]
type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 1e9
density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1000
viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 0.001
thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
[]
[]
[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
[temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
[]
[ppss]
type = PorousFlow1PhaseFullySaturated<<<{"description": "This Material is used for the fully saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseFullySaturated.html"}>>>
porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = pp
[]
[massfrac]
type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
mass_fraction_vars<<<{"description": "List of variables that represent the mass fractions. Format is 'f_ph0^c0 f_ph0^c1 f_ph0^c2 ... f_ph0^c(N-2) f_ph1^c0 f_ph1^c1 fph1^c2 ... fph1^c(N-2) ... fphP^c0 f_phP^c1 fphP^c2 ... fphP^c(N-2)' where N=num_components and P=num_phases, and it is assumed that f_ph^c(N-1)=1-sum(f_ph^c,{c,0,N-2}) so that f_ph^c(N-1) need not be given. If no variables are provided then num_phases=1=num_components."}>>> = massfrac0
[]
[simple_fluid]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
phase<<<{"description": "The phase number"}>>> = 0
[]
[poro]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>>
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.3
[]
[diff]
type = PorousFlowDiffusivityConst<<<{"description": "This Material provides constant tortuosity and diffusion coefficients", "href": "../../../../source/materials/PorousFlowDiffusivityConst.html"}>>>
diffusion_coeff<<<{"description": "List of diffusion coefficients. Order is i) component 0 in phase 0; ii) component 1 in phase 0 ...; component 0 in phase 1; ... component k in phase n (m^2/s"}>>> = '0 0'
tortuosity<<<{"description": "List of tortuosities. Order is i) phase 0; ii) phase 1; etc"}>>> = 0.1
[]
[relp]
type = PorousFlowRelativePermeabilityConst<<<{"description": "This class sets the relative permeability to a constant value (default = 1)", "href": "../../../../source/materials/PorousFlowRelativePermeabilityConst.html"}>>>
phase<<<{"description": "The phase number"}>>> = 0
[]
[permeability]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1e-9 0 0 0 1e-9 0 0 0 1e-9'
[]
[]
[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
[smp]
type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres asm lu NONZERO 2 '
[]
[]
[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
type = Transient
solve_type = NEWTON
end_time = 1e3
dtmax = 10
[TimeStepper<<<{"href": "../../../../syntax/Executioner/TimeStepper/index.html"}>>>]
type = IterationAdaptiveDT
growth_factor = 1.5
cutback_factor = 0.5
dt = 1
[]
[]
[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
[xmass]
type = NodalValueSampler<<<{"description": "Samples values of nodal variable(s).", "href": "../../../../source/vectorpostprocessors/NodalValueSampler.html"}>>>
sort_by<<<{"description": "What to sort the samples by"}>>> = id
variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = massfrac0
[]
[]
[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
[out]
type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = final
[]
[]The comparison between the PorousFlow and the analytical formula is presented in Figure 2. For the non-heavy case, the MOOSE results do not coincide with the analytical solution near the top and bottom of the concentration front due to numerical dispersion. If the number of elements in the mesh is increased and the time step size is reduced (the "heavy" case), numerical dispersion is reduced and a much closer fit to the analytical solution is obtained.
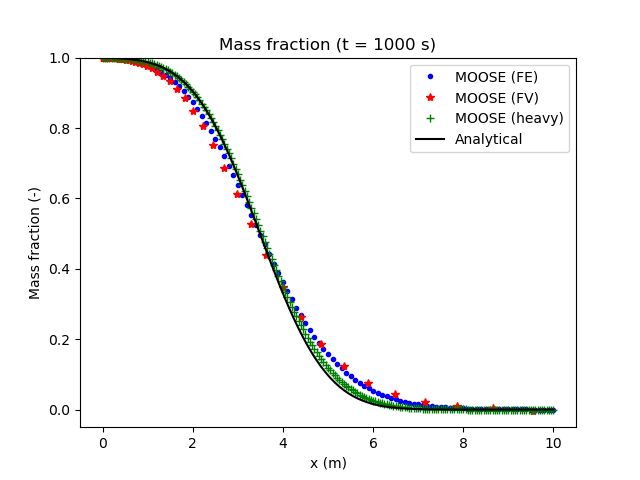
Figure 2: Mass fraction profile from hydrodynamic dispersion only.
References
- I. Javandel, C. Doughty, and C. F. Tsang.
Groundwater Transport, Handbook of Mathematical Models.
AGU, 1984.[BibTeX]