Injection ala Buckley and Leverett

PorousFlow is compared with a simple single-phase one-dimensional Buckley-Leverett problem (Buckley and Leverett, 1942). The single-phase fluid moves in a region $var element = document.getElementById("moose-equation-5f2200b2-d086-407d-9ce4-538afe56f99a");katex.render("0\\leq x\\leq 15\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ m. A fully-saturated front initially sits at position $var element = document.getElementById("moose-equation-a5a122dc-96b4-4d3c-aad5-de417af23e81");katex.render("x=5", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , while the region $var element = document.getElementById("moose-equation-16da968a-b0ed-4fe2-a56f-92e4edf43f82");katex.render("x>5", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ is initially unsaturated. With zero suction function $var element = document.getElementById("moose-equation-b998c4d9-5ab5-436c-921c-dd42dbf427e8");katex.render("P_{c} = 0", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , there is no diffusion of the sharp front, and it progresses towards the right (increasing $var element = document.getElementById("moose-equation-b362ad36-23f0-4f19-a39b-ab619612d148");katex.render("x", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ ).

# Buckley-Leverett 1-phase.
# The front starts at (around) x=5, and at t=50 it should
# have moved to x=9.6.  The version below has a nonzero
# suction function, and at t=50, the front sits between
# (about) x=9.6 and x=9.9.  Changing the van-Genuchten
# al parameter to 1E-4 softens the front so it sits between
# (about) x=9.7 and x=10.4, and the simulation runs much faster.
# With al=1E-2 and nx=600, the front sits between x=9.6 and x=9.8,
# but takes about 100 times longer to run.

[Mesh<<<{"href": "../../../../syntax/Mesh/index.html"}>>>]
  type = GeneratedMesh
  dim = 1
  nx = 150
  xmin = 0
  xmax = 15
[]

[GlobalParams<<<{"href": "../../../../syntax/GlobalParams/index.html"}>>>]
  PorousFlowDictator = dictator
  compute_enthalpy = false
  compute_internal_energy = false
[]

[Variables<<<{"href": "../../../../syntax/Variables/index.html"}>>>]
  [pp]
    [InitialCondition]
      type = FunctionIC
      function = 'max((1000000-x/5*1000000)-20000,-20000)'
    []
  []
[]

[Kernels<<<{"href": "../../../../syntax/Kernels/index.html"}>>>]
  [mass0]
    type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time.  Mass lumping to the nodes is used.", "href": "../../../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
    fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pp
  []
  [flux0]
    type = PorousFlowAdvectiveFlux<<<{"description": "Fully-upwinded advective flux of the component given by fluid_component", "href": "../../../../source/kernels/PorousFlowAdvectiveFlux.html"}>>>
    fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pp
    gravity<<<{"description": "Gravitational acceleration vector downwards (m/s^2)"}>>> = '0 0 0'
  []
[]

[BCs<<<{"href": "../../../../syntax/BCs/index.html"}>>>]
  [left]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../../../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = pp
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
    value<<<{"description": "Value of the BC"}>>> = 980000
  []
[]

[AuxVariables<<<{"href": "../../../../syntax/AuxVariables/index.html"}>>>]
  [sat]
    family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
    order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
  []
[]

[AuxKernels<<<{"href": "../../../../syntax/AuxKernels/index.html"}>>>]
  [sat]
    type = MaterialStdVectorAux<<<{"description": "Extracts a component of a material type std::vector<Real> to an aux variable.  If the std::vector is not of sufficient size then zero is returned", "href": "../../../../source/auxkernels/MaterialStdVectorAux.html"}>>>
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = sat
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
    index<<<{"description": "The index to consider for this kernel"}>>> = 0
    property<<<{"description": "The material property name."}>>> = PorousFlow_saturation_qp
  []
[]

[UserObjects<<<{"href": "../../../../syntax/UserObjects/index.html"}>>>]
  [dictator]
    type = PorousFlowDictator<<<{"description": "Holds information on the PorousFlow variable names", "href": "../../../../source/userobjects/PorousFlowDictator.html"}>>>
    porous_flow_vars<<<{"description": "List of primary variables that are used in the PorousFlow simulation.  Jacobian entries involving derivatives wrt these variables will be computed.  In single-phase models you will just have one (eg 'pressure'), in two-phase models you will have two (eg 'p_water p_gas', or 'p_water s_water'), etc."}>>> = 'pp'
    number_fluid_phases<<<{"description": "The number of fluid phases in the simulation"}>>> = 1
    number_fluid_components<<<{"description": "The number of fluid components in the simulation"}>>> = 1
  []
  [pc]
    type = PorousFlowCapillaryPressureVG<<<{"description": "van Genuchten capillary pressure", "href": "../../../../source/userobjects/PorousFlowCapillaryPressureVG.html"}>>>
    m<<<{"description": "van Genuchten exponent m. Must be between 0 and 1, and optimally should be set to >0.5"}>>> = 0.8
    alpha<<<{"description": "van Genuchten parameter alpha. Must be positive"}>>> = 1e-3
  []
[]

[FluidProperties<<<{"href": "../../../../syntax/FluidProperties/index.html"}>>>]
  [simple_fluid]
    type = SimpleFluidProperties<<<{"description": "Fluid properties for a simple fluid with a constant bulk density", "href": "../../../../source/fluidproperties/SimpleFluidProperties.html"}>>>
    bulk_modulus<<<{"description": "Constant bulk modulus (Pa)"}>>> = 2e6
    viscosity<<<{"description": "Constant dynamic viscosity (Pa.s)"}>>> = 1e-3
    density0<<<{"description": "Density at zero pressure and zero temperature"}>>> = 1000
    thermal_expansion<<<{"description": "Constant coefficient of thermal expansion (1/K)"}>>> = 0
  []
[]

[Materials<<<{"href": "../../../../syntax/Materials/index.html"}>>>]
  [temperature]
    type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../../../source/materials/PorousFlowTemperature.html"}>>>
  []
  [ppss]
    type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../../../../source/materials/PorousFlow1PhaseP.html"}>>>
    porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = pp
    capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
  []
  [massfrac]
    type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../../../source/materials/PorousFlowMassFraction.html"}>>>
  []
  [simple_fluid]
    type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
    fp<<<{"description": "The name of the user object for fluid properties"}>>> = simple_fluid
    phase<<<{"description": "The phase number"}>>> = 0
  []
  [permeability]
    type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../../../source/materials/PorousFlowPermeabilityConst.html"}>>>
    permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1E-10 0 0  0 1E-10 0  0 0 1E-10'
  []
  [relperm]
    type = PorousFlowRelativePermeabilityCorey<<<{"description": "This Material calculates relative permeability of the fluid phase, using the simple Corey model ((S-S_res)/(1-sum(S_res)))^n", "href": "../../../../source/materials/PorousFlowRelativePermeabilityCorey.html"}>>>
    n<<<{"description": "The Corey exponent of the phase."}>>> = 2
    phase<<<{"description": "The phase number"}>>> = 0
  []
  [porosity]
    type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../../../source/materials/PorousFlowPorosityConst.html"}>>>
    porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material).  This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.15
  []
[]

[Preconditioning<<<{"href": "../../../../syntax/Preconditioning/index.html"}>>>]
  active<<<{"description": "If specified only the blocks named will be visited and made active"}>>> = andy
  [andy]
    type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../../../../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
    full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
    petsc_options_iname<<<{"description": "Names of PETSc name/value pairs"}>>> = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value<<<{"description": "Values of PETSc name/value pairs (must correspond with \"petsc_options_iname\""}>>> = 'gmres bjacobi 1E-10 1E-10 20'
  []
[]

[Functions<<<{"href": "../../../../syntax/Functions/index.html"}>>>]
  [timestepper]
    type = PiecewiseLinear<<<{"description": "Linearly interpolates between pairs of x-y data", "href": "../../../../source/functions/PiecewiseLinear.html"}>>>
    x<<<{"description": "The abscissa values"}>>> = '0    0.01 0.1 1   1.5 2   20  30  40  50'
    y<<<{"description": "The ordinate values"}>>> = '0.01 0.1  0.2 0.3 0.1 0.3 0.3 0.4 0.4 0.5'
  []
[]

[Executioner<<<{"href": "../../../../syntax/Executioner/index.html"}>>>]
  type = Transient
  solve_type = Newton
  end_time = 50
  [TimeStepper<<<{"href": "../../../../syntax/Executioner/TimeStepper/index.html"}>>>]
    type = FunctionDT
    function = timestepper
  []
[]

[VectorPostprocessors<<<{"href": "../../../../syntax/VectorPostprocessors/index.html"}>>>]
  [pp]
    type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
    start_point<<<{"description": "The beginning of the line"}>>> = '0 0 0'
    end_point<<<{"description": "The ending of the line"}>>> = '15 0 0'
    num_points<<<{"description": "The number of points to sample along the line"}>>> = 150
    sort_by<<<{"description": "What to sort the samples by"}>>> = x
    variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = pp
  []
  [sat]
    type = LineValueSampler<<<{"description": "Samples variable(s) along a specified line", "href": "../../../../source/vectorpostprocessors/LineValueSampler.html"}>>>
    warn_discontinuous_face_values<<<{"description": "Whether to return a warning if a discontinuous variable is sampled on a face"}>>> = false
    start_point<<<{"description": "The beginning of the line"}>>> = '0 0 0'
    end_point<<<{"description": "The ending of the line"}>>> = '15 0 0'
    num_points<<<{"description": "The number of points to sample along the line"}>>> = 150
    sort_by<<<{"description": "What to sort the samples by"}>>> = x
    variable<<<{"description": "The names of the variables that this VectorPostprocessor operates on"}>>> = sat
  []
[]

[Outputs<<<{"href": "../../../../syntax/Outputs/index.html"}>>>]
  file_base<<<{"description": "Common file base name to be utilized with all output objects"}>>> = bl01
  [csv]
    type = CSV<<<{"description": "Output for postprocessors, vector postprocessors, and scalar variables using comma seperated values (CSV).", "href": "../../../../source/outputs/CSV.html"}>>>
    sync_only<<<{"description": "Only export results at sync times"}>>> = true
    sync_times<<<{"description": "Times at which the output and solution is forced to occur"}>>> = '0.01 50'
  []
  [exodus]
    type = Exodus<<<{"description": "Object for output data in the Exodus format", "href": "../../../../source/outputs/Exodus.html"}>>>
    execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = 'initial final'
  []
[]

This is a difficult problem to simulate numerically as maintaining the sharp front is hard. The front's speed is independent of the relative permeability, since the fluid is flowing from a fully-saturated region (where $var element = document.getElementById("moose-equation-75efb331-5b0e-4ac9-a489-85100b296691");katex.render("\\kappa_{\\mathrm{rel}}=1", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ ). This problem is therefore a good test of the full upwinding.

In the simulation listed above, the pressure at the left boundary is kept fixed at $var element = document.getElementById("moose-equation-b6f438e1-5654-44e1-9f78-a2f315a2eb79");katex.render("P_{0}=0.98\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ MPa, while the right boundary is kept fixed at $var element = document.getElementById("moose-equation-917e6b80-3d55-40da-9d20-2583493a1c40");katex.render("P_{15}=-20000\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ Pa, so the difference is $var element = document.getElementById("moose-equation-319befaf-23a2-4355-a67d-be1e25bc8030");katex.render("1\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ MPa. The medium's permeability is set to $var element = document.getElementById("moose-equation-463e0356-afdf-4a30-aa2c-d3b9e3382ecb");katex.render("\\kappa = 10^{-10}\\,\\mathrm{m}^{2}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ and its porosity is $var element = document.getElementById("moose-equation-1d2e2236-6571-4ad3-918c-1bf34e11577a");katex.render("\\phi = 0.15", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ . It is not possible to use a zero suction function in the MOOSE implementation, but using the van Genuchten parameters $var element = document.getElementById("moose-equation-007d91a0-b6b4-4c02-815c-7b1702abf8c2");katex.render("\\alpha = 10^{-3}\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ Pa $var element = document.getElementById("moose-equation-32ff8223-c574-4c65-a35b-b0c4e5fcb631");katex.render("^{-1}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ and $var element = document.getElementById("moose-equation-63c4198a-5741-4bae-a649-ba7d84fa447c");katex.render("m=0.8", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ approximates it. The fluid viscosity is $var element = document.getElementById("moose-equation-2fc8b1ad-c12e-4fd5-a910-f07ffbc76763");katex.render("\\mu = 10^{-3}\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ Pa.s.

The initial condition is $var element = document.getElementById("moose-equation-8e4408a6-07f2-4d57-924d-f79334c4d89d");katex.render("P(t=0) = \\left\\{ \\begin{array}{ll} P_{0} - (P_{0}-P_{15})x/5 & \\ \\ \\ \\mathrm{for }\\ \\ x<5 \\\\ P_{15} & \\ \\ \\ \\mathrm{for }\\ \\ x\\geq 5 \\end{array} \\right. \\ ,", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ which is shown in Figure 1. With the suction function defined above this gives $var element = document.getElementById("moose-equation-1f8d024f-97e6-4e5d-ae57-44007c2cea9c");katex.render("S(t=0) = \\left\\{ \\begin{array}{ll} 1 & \\ \\ \\ \\mathrm{for }\\ \\ x\\leq 4.9 \\\\ 6\\times 10^{-6} & \\ \\ \\ \\mathrm{for} \\ \\ x \\geq 5 \\end{array} \\right.", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$

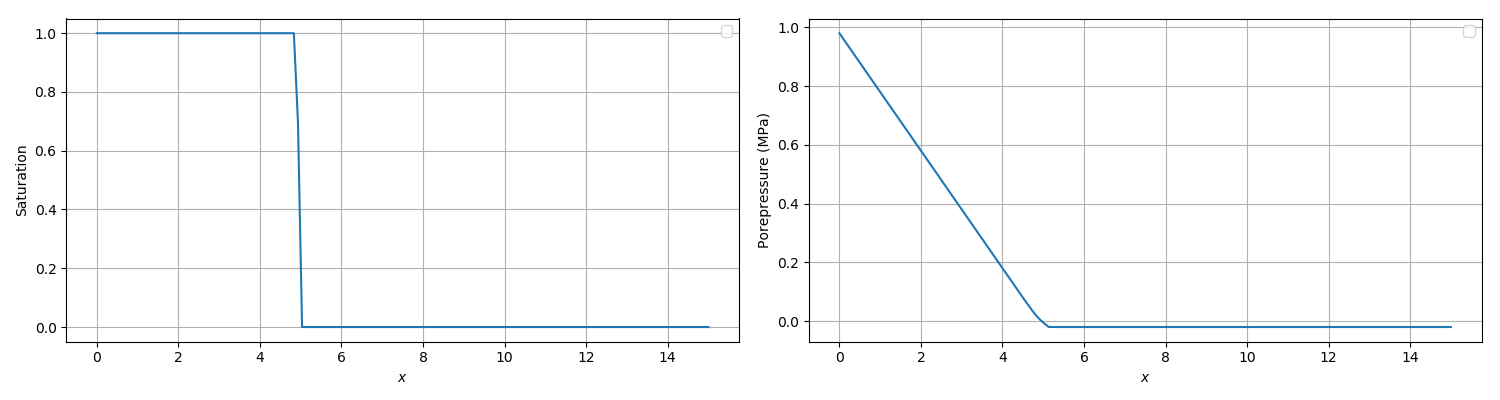
Figure 1: Initial setup of the Buckley-Leverett problem where porepressure is a piecewise linear function. The region on the left is fully saturated, while the region on the right has saturation 0.000006. During simulation the value of porepressure on the left boundary is held fixed.

Good approximations for the pressure $var element = document.getElementById("moose-equation-b8f7221f-f243-498a-a66c-059f08d45049");katex.render("P(x,t)", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ and the front position $var element = document.getElementById("moose-equation-5f3c2173-1254-4c2e-80e2-13d452e3f863");katex.render("f(t)", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ may be determined from $(1)var element = document.getElementById("moose-equation-a4524281-f1e2-4320-973f-944f85a26541");katex.render("\\begin{array}{rcl} \\frac{{\\mathrm d} f}{{\\mathrm d} t} & = & -\\frac{\\kappa}{\\phi\\mu} \\left.\\frac{\\partial P}{\\partial x}\\right|_{x = f} \\ , \\\\ P(x,t) & = & \\left\\{ \\begin{array}{ll} P_{0} - (P_{0}-P_{15})x/f & \\ \\ \\mathrm{ for }\\ \\ x\\leq f \\\\ P_{15} &\\ \\ \\mathrm{ for }\\ \\ x>f \\end{array} \\right. \\ , \\end{array}", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ which has solution $var element = document.getElementById("moose-equation-39bc5a91-49a4-479a-8186-cdc55ee8df7d");katex.render("f(t) = \\sqrt{f(0)^{2} + \\frac{2\\kappa}{\\phi\\mu}(P_{0}-P_{15})t} \\ .", element, {displayMode:true,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ For the parameters listed above, the front will be at position $var element = document.getElementById("moose-equation-6d879cbe-6dd3-45b6-8023-98faeaf3a6f7");katex.render("f=9.6\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ m at $var element = document.getElementById("moose-equation-ab799612-0e3a-4f0d-9406-3a1364aa04cb");katex.render("t=50\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ s. This solution is only valid for zero capillary suction. A nonzero suction function will tend to diffuse the sharp front.

With coarse meshes it is impossible to simulate a sharp front, of course, since the front is spread over at least one element.

Figure 2 shows the results from a MOOSE simulation with a uniform mesh of size $var element = document.getElementById("moose-equation-f09d380e-0759-4326-8985-ea1d0df397aa");katex.render("0.1\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ m. At $var element = document.getElementById("moose-equation-e6e1e62e-c0e4-4599-ad82-85d670ab7c22");katex.render("t=50\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ s the front in this simulation sits at $var element = document.getElementById("moose-equation-48865da3-8f48-42d9-9462-9bdfd8264839");katex.render("x=9.6\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ m as desired. However, the simulation takes $var element = document.getElementById("moose-equation-cc24c404-6271-4c5a-bdf9-de510a6d1463");katex.render("10\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ seconds to complete due to the very low values of saturation obtained for van Genuchten $var element = document.getElementById("moose-equation-0588cbd3-61f5-4f9b-839e-9adcf7b24603");katex.render("\\alpha=10^{-3}\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ Pa $var element = document.getElementById("moose-equation-1969f8d0-4b7f-448c-99ce-c3d2a2a26460");katex.render("^{-1}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ . Other simulations give similar results but run much faster. For instance, the test suite listed above uses the van Genuchten parameter $var element = document.getElementById("moose-equation-36fe4c3b-ba76-4d53-9136-b9302142073b");katex.render("\\alpha=10^{-4}\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ Pa $var element = document.getElementById("moose-equation-b1f42e39-ce61-4386-a603-fe8a3c6ef995");katex.render("^{-1}", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ , but the front diffuses a little into the unsaturated region (the front sits between $var element = document.getElementById("moose-equation-b5232d8b-1f42-4739-92ad-ff602891a497");katex.render("x=9.7\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ m and $var element = document.getElementById("moose-equation-3b3cb32f-ad4b-4d7f-94ef-7ce6658213d3");katex.render("x=10.4\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ m at $var element = document.getElementById("moose-equation-a3dd0cc7-0167-4693-8f7d-6c9e1af587ad");katex.render("t=50\\,", element, {displayMode:false,throwOnError:false,macros:{"\\eqc":"\\,,","\\eqp":"\\,.","\\pd":"\\frac{\\partial #1}{\\partial #2}","\\pr":"\\left(#1\\right)","\\ddt":"\\frac{d #1}{d t}"}});$ s).

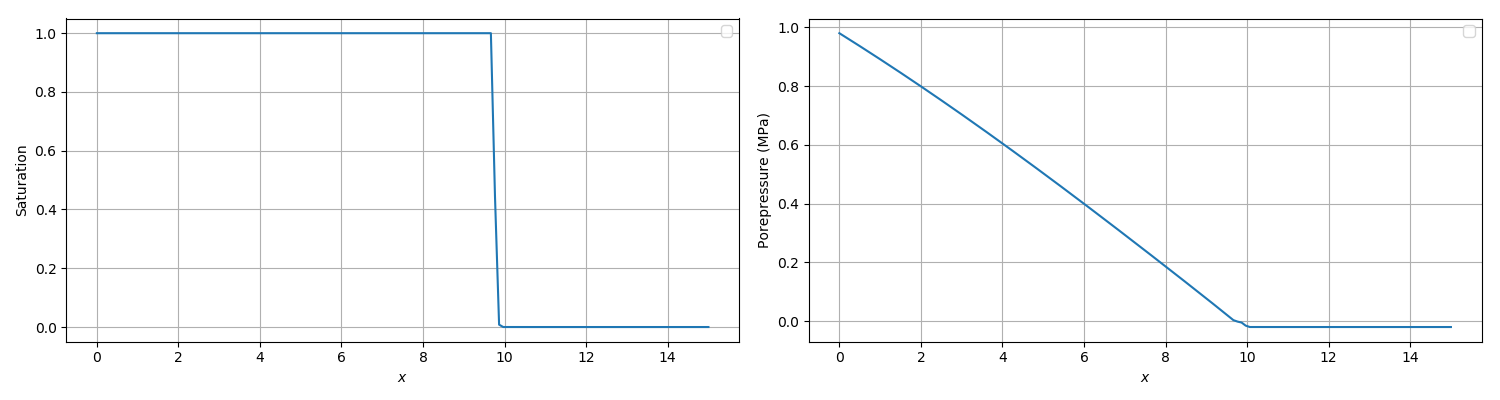
Figure 2: The MOOSE solution of the Buckley-Leverett problem at time 50s. Left: saturation. Right: porepressure. The front sits at x 9.6m as expected from the analytical solution.

References

E. Buckley and M. Leverett. Mechanism of fluid displacement in sands. Transactions of the AIME, 146:107–116, 04 1942. doi:10.2118/942107-G.

@article{buckley_leverett,
    author = "Buckley, E. and Leverett, M.",
    year = "1942",
    month = "04",
    pages = "107--116",
    title = "Mechanism of Fluid Displacement in Sands",
    volume = "146",
    journal = "Transactions of the AIME",
    doi = "10.2118/942107-G"
}

(modules/porous_flow/test/tests/buckley_leverett/bl01.i)

# Buckley-Leverett 1-phase.
# The front starts at (around) x=5, and at t=50 it should
# have moved to x=9.6.  The version below has a nonzero
# suction function, and at t=50, the front sits between
# (about) x=9.6 and x=9.9.  Changing the van-Genuchten
# al parameter to 1E-4 softens the front so it sits between
# (about) x=9.7 and x=10.4, and the simulation runs much faster.
# With al=1E-2 and nx=600, the front sits between x=9.6 and x=9.8,
# but takes about 100 times longer to run.

[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = 150
  xmin = 0
  xmax = 15
[]

[GlobalParams]
  PorousFlowDictator = dictator
  compute_enthalpy = false
  compute_internal_energy = false
[]

[Variables]
  [pp]
    [InitialCondition]
      type = FunctionIC
      function = 'max((1000000-x/5*1000000)-20000,-20000)'
    []
  []
[]

[Kernels]
  [mass0]
    type = PorousFlowMassTimeDerivative
    fluid_component = 0
    variable = pp
  []
  [flux0]
    type = PorousFlowAdvectiveFlux
    fluid_component = 0
    variable = pp
    gravity = '0 0 0'
  []
[]

[BCs]
  [left]
    type = DirichletBC
    variable = pp
    boundary = left
    value = 980000
  []
[]

[AuxVariables]
  [sat]
    family = MONOMIAL
    order = CONSTANT
  []
[]

[AuxKernels]
  [sat]
    type = MaterialStdVectorAux
    variable = sat
    execute_on = timestep_end
    index = 0
    property = PorousFlow_saturation_qp
  []
[]

[UserObjects]
  [dictator]
    type = PorousFlowDictator
    porous_flow_vars = 'pp'
    number_fluid_phases = 1
    number_fluid_components = 1
  []
  [pc]
    type = PorousFlowCapillaryPressureVG
    m = 0.8
    alpha = 1e-3
  []
[]

[FluidProperties]
  [simple_fluid]
    type = SimpleFluidProperties
    bulk_modulus = 2e6
    viscosity = 1e-3
    density0 = 1000
    thermal_expansion = 0
  []
[]

[Materials]
  [temperature]
    type = PorousFlowTemperature
  []
  [ppss]
    type = PorousFlow1PhaseP
    porepressure = pp
    capillary_pressure = pc
  []
  [massfrac]
    type = PorousFlowMassFraction
  []
  [simple_fluid]
    type = PorousFlowSingleComponentFluid
    fp = simple_fluid
    phase = 0
  []
  [permeability]
    type = PorousFlowPermeabilityConst
    permeability = '1E-10 0 0  0 1E-10 0  0 0 1E-10'
  []
  [relperm]
    type = PorousFlowRelativePermeabilityCorey
    n = 2
    phase = 0
  []
  [porosity]
    type = PorousFlowPorosityConst
    porosity = 0.15
  []
[]

[Preconditioning]
  active = andy
  [andy]
    type = SMP
    full = true
    petsc_options_iname = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
    petsc_options_value = 'gmres bjacobi 1E-10 1E-10 20'
  []
[]

[Functions]
  [timestepper]
    type = PiecewiseLinear
    x = '0    0.01 0.1 1   1.5 2   20  30  40  50'
    y = '0.01 0.1  0.2 0.3 0.1 0.3 0.3 0.4 0.4 0.5'
  []
[]

[Executioner]
  type = Transient
  solve_type = Newton
  end_time = 50
  [TimeStepper]
    type = FunctionDT
    function = timestepper
  []
[]

[VectorPostprocessors]
  [pp]
    type = LineValueSampler
    start_point = '0 0 0'
    end_point = '15 0 0'
    num_points = 150
    sort_by = x
    variable = pp
  []
  [sat]
    type = LineValueSampler
    warn_discontinuous_face_values = false
    start_point = '0 0 0'
    end_point = '15 0 0'
    num_points = 150
    sort_by = x
    variable = sat
  []
[]


[Outputs]
  file_base = bl01
  [csv]
    type = CSV
    sync_only = true
    sync_times = '0.01 50'
  []
  [exodus]
    type = Exodus
    execute_on = 'initial final'
  []
[]

References