Deformation Gradients

Deformation gradient in Continuum Mechanics

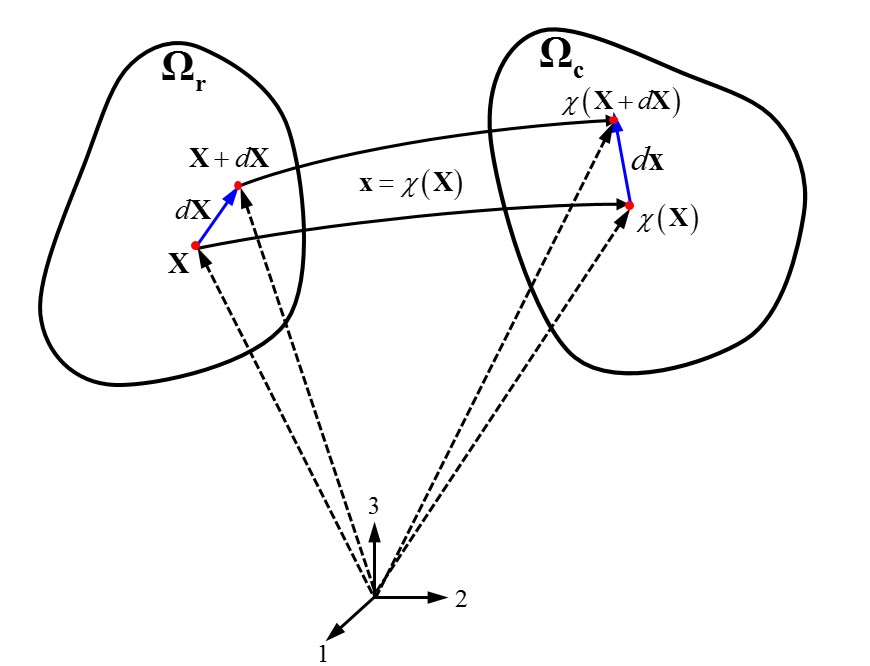
Line segment mapping under deformation

Consider a line segment $d\mathbf{X}$ emanating from position $\mathbf{X}$ in the reference configuration $\Omega_r$ which deforms to $d\mathbf{x}$ in the current configuration $\Omega_c$. Thus, the line segment in the deformed configuration $\Omega_c$ is given by

$$d\mathbf{x} = \chi(\mathbf{X} + d\mathbf{X}) - \chi(\mathbf{X})$$

A Taylor expansion of $\chi(\mathbf{X} + d\mathbf{X})$ gives

$$\chi(\mathbf{X} + d\mathbf{X}) = \chi(\mathbf{X}) + \frac{\partial \chi}{\partial \mathbf{X}}(\mathbf{X}) \cdot d\mathbf{X} + O(d\mathbf{X})$$ where $O(d\mathbf{X})$ indicates higher-order terms of $d\mathbf{X}$.

Substituting above Taylor expansion into previous equation and assuming that $|d\mathbf{X}|$ is infinitesimally small gives

$$d\mathbf{x} \approx \frac{\partial \chi}{\partial \mathbf{X}}(\mathbf{X}) \cdot d\mathbf{X} \equiv \mathbf{F}(\mathbf{X}) \cdot d\mathbf{X}$$

The expression tends to the exact solution as the differential $d\mathbf{X}$ goes to zero.

The deformation gradient thus characterizes the deformation in the neighborhood of material point $\mathbf{X}$, mapping infinitesimal line segment $d\mathbf{X}$ emanating from $\mathbf{X}$ in the reference configuration to the infinitesimal line segment $d\mathbf{x}$ emanating from $\mathbf{x}$ in the deformed configuration.

Peridynamic material point deformation gradient

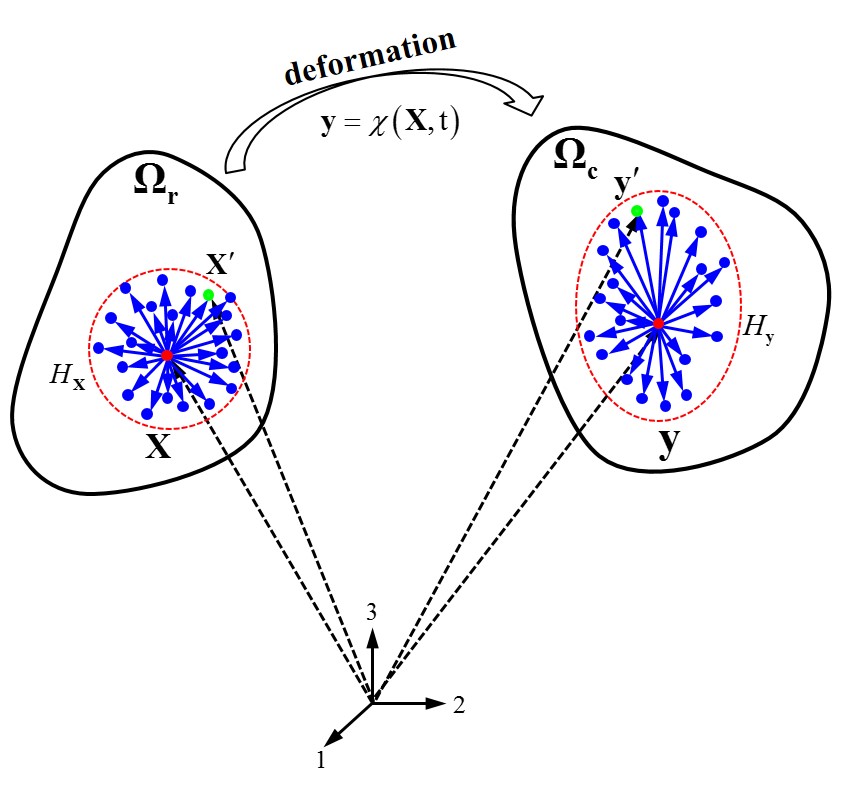
Configuration for conventional peridynamic deformation gradient approximation

For a bond $\boldsymbol{\xi}$, there exists a unique mapping that transfers the relative position vector state $\underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle$ in the reference configuration to the relative position vector state $\underline{\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle$ in the current configuration:

$$\underline{\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle = \mathbf{F}_{\boldsymbol{\xi}} \cdot \underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle$$ where $\mathbf{F}_{\boldsymbol{\xi}}$ is the value of the deformation gradient for bond $\boldsymbol{\xi}$ connecting material point $\mathbf{X}$ and its neighboring material point $\mathbf{X}^{\prime}$.

Above equation defines the operation of a peridynamic deformation gradient in a manner analogous to the continuum deformation gradient in that it maps a vector state in the reference configuration to a vector state in the current configuration. $\mathbf{F}_{\boldsymbol{\xi}}$ becomes the deformation gradient at material point $\mathbf{X}$ when bond $\boldsymbol{\xi}$ tends to an infinitesimal length.

Apply above formulation for material point $\mathbf{X}$ and each of the bonds connecting it with its neighbors leads to a system of over-constrained linear equations that cannot generally satisfied by a single mapping $\mathbf{F}_{\boldsymbol{\xi}}$. For this reason, a technique to compute an optimal deformation gradient $\mathbf{F}$ is sought.

The mapping error between material point $\mathbf{X}$ and a single neighbor $\mathbf{X}^{\prime}$ as the ${\ell}^2$ norm of the difference between the $\underline{\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle$ and $\underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle$ :

$$\ell_{\mathbf{X}^{\prime}} = \left(\underline{\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle - \mathbf{F} \cdot \underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle \right)^{T} \left(\underline{\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle - \mathbf{F} \cdot \underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle \right)$$

Thus, the weighted least squares error among the neighbors of $\mathbf{X}$ can be given by

$$\ell = \int_{\mathcal{H}_{\mathbf{X}}}{\omega\left\langle \boldsymbol{\xi} \right\rangle \left(\underline{\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle - \mathbf{F} \cdot \underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle \right)^{T} \left(\underline{\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle - \mathbf{F} \cdot \underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle \right)}dV_{\mathbf{X}^{\prime}}$$ where $\omega\left\langle \boldsymbol{\xi} \right\rangle$ is a non-negative weight (influence) factor for bond $\boldsymbol{\xi}$.

In above formulation of weighted least square error, the volume integral has been used, which is consistent with the volume integral in the governing equation for peridynamic correspondence material model.

The optimal local deformation gradient $\mathbf{F}$, in a weighted least squares sense, is obtained by minimizing $\ell$ with respect to its components as

$$\frac{\partial \ell}{\partial \mathbf{F}} = \int_{\mathcal{H}_{\mathbf{X}}}{\omega\left\langle \boldsymbol{\xi} \right\rangle \left(-2\underline{\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle \otimes \underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle + \mathbf{F} \cdot \underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle \otimes \underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle \right)}dV_{\mathbf{X}^{\prime}}$$

Setting above equation to zero yields the local deformation gradient in the weighted least squares sense as

$$\mathbf{F} = \mathbf{K}_{c} \cdot \mathbf{K}_{r}^{-1}$$ where $$\mathbf{K}_{r} = \int_{\mathcal{H}_{\mathbf{X}}}{\omega\left\langle \boldsymbol{\xi} \right\rangle \underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle \otimes \underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle}dV_{\mathbf{X}^{\prime}}$$

is called $\textit{shape tensor}$ and

$$\mathbf{K}_{c} = \int_{\mathcal{H}_{\mathbf{X}}}{\omega\left\langle \boldsymbol{\xi} \right\rangle \underline{\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle \otimes \underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle}dV_{\mathbf{X}^{\prime}}$$

For above derived nonlocal deformation gradient to be valid, a few necessary conditions must be satisfied in cases of three dimensional analysis. First, for $\mathbf{K}_{r}$ to be invertible, a material point's neighbors should be $\textbf{non-coplanar}$. Second, since the deformation gradient has nine independent components, a material point must have at least $\textbf{three}$ neighbors. And similar constraints apply to two-dimensional cases. Given all these conditions, the derived deformation gradient can be proven to be symmetric positive-definite.

It should be noted that the above derived deformation gradient for peridynamics is different from its continuum mechanics counterpart in that it doesn't require smooth motion of a continuous region in space and it is not a continuous function of spatial position, but instead is defined only at material point locations. The compatibility condition, i.e., that the curl of the deformation gradient is zero, is usually not satisfied by the deformation gradient in peridynamics. For the case of homogeneously applied deformation $\mathbf{F}_{0}$ , the peridynamic deformation gradient is exact for regular discretization as is its continuum mechanics counterpart.

$\textbf{NOTE}$: Definitions of different peridynamic states used in above derivation can be found at the Horizon and States page.

Peridynamic bond-associated deformation gradient

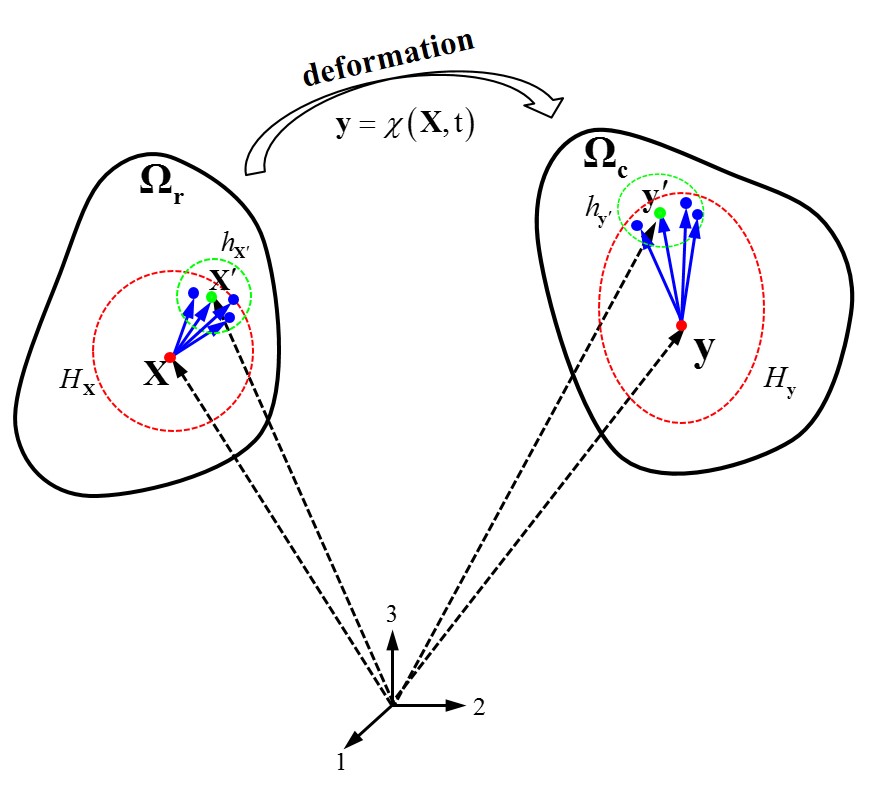
Configuration for peridynamic bond-associated deformation gradient approximation

Based on how the peridynamic nodal deformation gradient is constructed in above section, it's obvious that an optimal peridynamic deformation gradient at a material point cannot accurately reflect the deformation of every bond associated with that material point. As a consequence, the force state calculated from this deformation gradient differs from the actual force state of that bond. This can sometimes lead to severe unphysical issues in peridynamic modeling, such as sub-horizon material collapse and material penetration. The use of a bond-associated deformation gradient, defined below, can be used to remedy these unphysical issues inherent in the peridynamic correspondence model.

As discussed previously, the deformation gradient $\mathbf{F}_{\boldsymbol{\xi}}$ can accurately capture the deformation of bond $\boldsymbol{\xi}$. However, forming this full deformation gradient is problematic because it has more components than there are constraints in a bond. In the case of three dimensions, there are nine independent components for the deformation gradient $\mathbf{F}_{\boldsymbol{\xi}}$, and only three independent constraints are available based on the reference and current configurations of bond $\boldsymbol{\xi}$. One possible way to introduce more constraints but not change the solution such that mapped deformation of bond $\boldsymbol{\xi}$ differs significantly from the actual solution is to also use the deformation state of neighboring bonds. It is proposed that this be done using an additional local bond-associated horizon $\mathbf{h}_{\mathbf{X}^{\prime}}$ defined at material point $\mathbf{X}^{\prime}$. The set of material points within this horizon that are neighbors of material point $\mathbf{X}$ is used to approximate a bond-associated deformation gradient for bond $\boldsymbol{\xi}$ at material point $\mathbf{X}$. The same methodology can be applied while calculating the bond-associated deformation gradient for bond $-\boldsymbol{\xi}$ at material point $\mathbf{X}^{\prime}$. This approximated bond-associated deformation gradient is more optimal for bond deformation mapping compared to the nodal deformation gradient, since only the deformation state adjacent to this bond is used in the approximation process and the force state calculation. The same necessary conditions discussed previously for the approximation of the nodal deformation gradient and shape tensor apply to the bond-associated deformation gradient and shape tensor.

Following the same definition for nodal deformation gradient but using a different domain $\mathcal{H}_{\mathbf{X}} \cap \mathcal{h}_{\mathbf{X}^{\prime}}$ rather than $\mathcal{H}_{\mathbf{X}}$ for its weighted least squares approximation, the bond-associated deformation gradient for bond $\boldsymbol{\xi}$ at material point $\mathbf{X}$ can be readily obtained as

$$\mathbf{F}_{\boldsymbol{\xi}} = \left( \int_{\mathcal{H}_{\mathbf{X}} \cap \mathcal{h}_{\mathbf{X}^{\prime}}}{\omega\left\langle \boldsymbol{\zeta} \right\rangle \underline{\mathbf{Y}}\left\langle \boldsymbol{\zeta} \right\rangle \otimes \underline{\mathbf{X}}\left\langle \boldsymbol{\zeta} \right\rangle}dV_{\mathbf{X}^{\prime}} \right) \cdot \mathbf{K}_{\boldsymbol{\xi}}^{-1}$$ with the bond-associated shape tensor as $$\mathbf{K}_{\boldsymbol{\xi}} = \int_{\mathcal{H}_{\mathbf{X}} \cap \mathcal{h}_{\mathbf{X}^{\prime}}}{\omega\left\langle \boldsymbol{\zeta} \right\rangle \underline{\mathbf{X}}\left\langle \boldsymbol{\zeta} \right\rangle \otimes \underline{\mathbf{X}}\left\langle \boldsymbol{\zeta} \right\rangle}dV_{\mathbf{X}^{\prime}}$$

Given bond-associated deformation gradients, a nodal deformation gradient can be calculated as a weighted average of these bond-associated deformation gradients as

$$\mathbf{F} = \frac{\displaystyle\sum_{n=1}^{NP}w\left\langle \boldsymbol{\xi}_n \right\rangle \mathbf{F}_{\boldsymbol{\xi}_n}}{\displaystyle\sum_{n=1}^{NP}w\left\langle \boldsymbol{\xi}_n \right\rangle} = \frac{\displaystyle\sum_{n=1}^{NP}w\left\langle \boldsymbol{\xi}_n \right\rangle \left( \int_{\mathcal{H}_{\mathbf{X}} \cap \mathcal{h}_{\mathbf{X}^{\prime}}}{\omega\left\langle \boldsymbol{\xi} \right\rangle \underline{\mathbf{Y}}\left\langle \boldsymbol{\xi} \right\rangle \otimes \underline{\mathbf{X}}\left\langle \boldsymbol{\xi} \right\rangle}dV_{\mathbf{X}^{\prime}} \right) \cdot \mathbf{K}_{\boldsymbol{\xi}_n}^{-1}}{\displaystyle\sum_{n=1}^{NP}w\left\langle \boldsymbol{\xi}_n \right\rangle}$$ where $NP$ is the number of neighbors for material point $\mathbf{X}$, the weight function $w\left\langle \boldsymbol{\xi}_n \right\rangle$ determines the contribution of each individual bond-associated deformation gradient to the deformation gradient at a material point.

A bond-associated deformation gradient can better capture the deformation state for each bond, i.e., the deformation between two material points. Compared to nodal deformation gradient, a bond-associated deformation gradient uses deformation state of material points within its vicinity, rather than the whole family. When the family size is infinitesimal, both the nodal deformation gradient and bond-associated deformation gradient recover their counterpart in classical continuum mechanics. More information can be found in (Chen, 2018) and (Chen and Spencer, 2019).

References