Phase 2: Time-dependent Multiphysics Coupling
Description
This phase is composed of a sole task which aims to verify the multiphysics coupled transient calculations. The heat transfer coefficient is represented by a sinusoidal function of the following form (1) where is the reference volumetric heat transfer coefficient, and f is the frequency which results in a sinusoidal behavior of the reactor power. In the simulation, varying values of frequency used are 0.0125, 0.025, 0.05, 0.1, 0.2, 0.4, 0.8. The power gain in the reactor with the varying power can be calculated as a function of frequency according to the following equation
There are two coupled inputs for this stage. The first performs the neutronics calculations and the second performs the Navier-Stocks solution. The sinusoidal power behavior modeling is defined in the neutronics input as a function within the Functions
[Functions]
[alpha_val]
type = ParsedFunction
expression = '1.0e+6*(1.0 + 0.1*sin(2.0*pi*${frequency}*t))' # 'alpha_0*(1.0 + a*sin(fq*t))'
[]
[]
(msr/cnrs/s21/cnrs_s21_ns_flow.i)For each frequency, 10 cycles are ran to obtain the asymptotic power wave. The last three cycles are used to obtain the power gain and phase shift. The problem is set to transient and the time step size is set inversely proportional to the frequency. This is requested in the Executioner
[Executioner]
type = Transient
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
start_time = 0.0
dt = '${fparse max(0.005, 0.05*0.0125/frequency)}'
end_time = '${fparse 10/frequency}'
#[TimeStepper]
# type = IterationAdaptiveDT
# dt = 0.1
# growth_factor = 2
#[]
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-6
nl_abs_tol = 1e-8
# MultiApp iteration parameters
fixed_point_min_its = 2
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-6
fixed_point_abs_tol = 1e-6
[]
(msr/cnrs/s21/cnrs_s21_griffin_neutronics.i)The rest of the transport solve input has a structure similar to that of the transport input in Step 1.3. The difference is in assigning a transienteigenvaluetypeExecutionerTransient
On the Navier-Stokes solve side, the problem is still executed as a transient solver. However, instead of running the problem for a long time to achieve steady state, the problem is defined as follows
[Executioner]
type = Transient
start_time = 0.0
dt = '${fparse max(0.005, 0.05*0.0125/frequency)}'
end_time = '${fparse 10/frequency}'
#[TimeStepper]
# type = IterationAdaptiveDT
# dt = 0.1
# growth_factor = 2
#[]
solve_type = 'NEWTON'
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
line_search = l2 #'none'
nl_rel_tol = 1e-6
nl_abs_tol = 2e-8
nl_max_its = 200
l_max_its = 200
automatic_scaling = true
[]
(msr/cnrs/s21/cnrs_s21_ns_flow.i)Results
The results for this exercise report the power gain and the phase shift as a function of the frequency as defined above. The power gain decreases with increases the frequency, and the phase shift approaches 90 degrees with increasing the frequency. These results are displayed in Figure 1
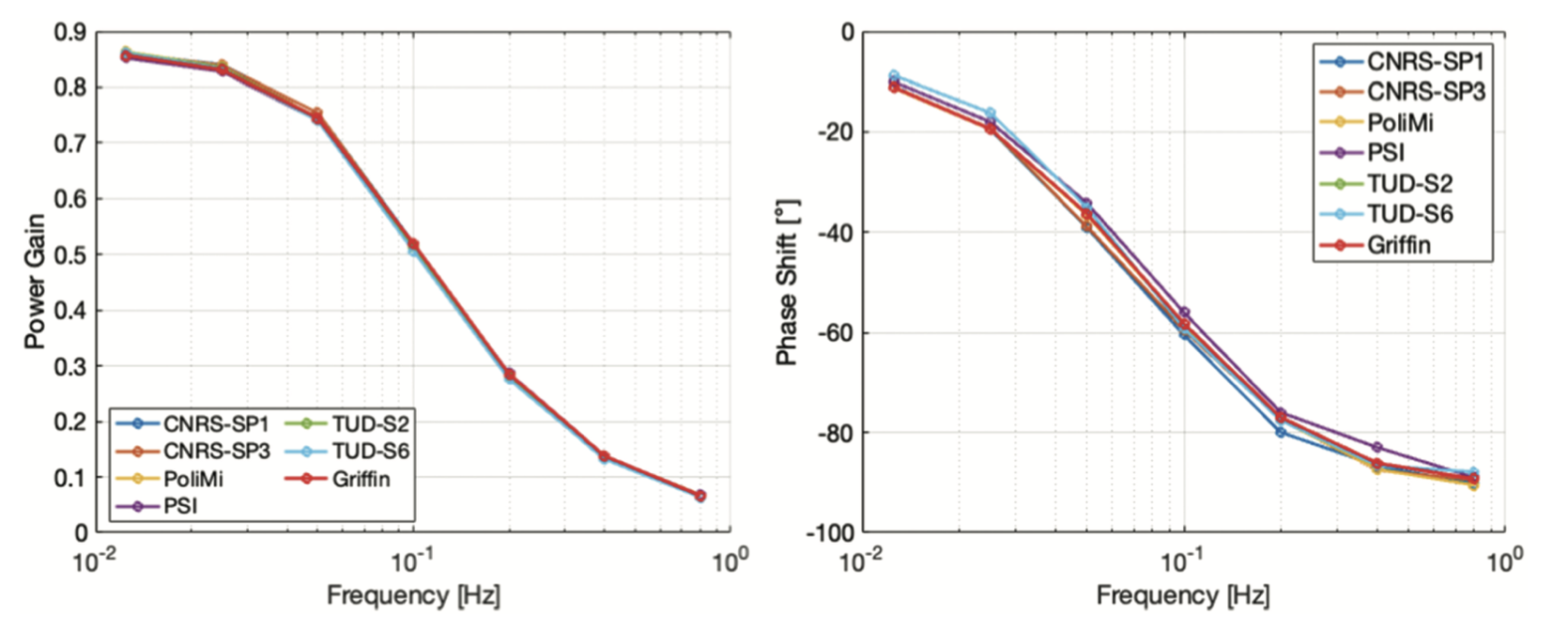
Figure 1:
(msr/cnrs/s21/cnrs_s21_ns_flow.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 2.1: Time dependent coupling
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
alpha = 2.0e-4
rho = 2.0e+3
cp = 3.075e+3
k = 1.0e-3
mu = 5.0e+1
# Sc_t = 2.0e8
Ulid = 0.5
lambda0 = 1.24667E-02
lambda1 = 2.82917E-02
lambda2 = 4.25244E-02
lambda3 = 1.33042E-01
lambda4 = 2.92467E-01
lambda5 = 6.66488E-01
lambda6 = 1.63478E+00
lambda7 = 3.55460E+00
beta0 = 2.33102e-4
beta1 = 1.03262e-3
beta2 = 6.81878e-4
beta3 = 1.37726e-3
beta4 = 2.14493e-3
beta5 = 6.40917e-4
beta6 = 6.05805e-4
beta7 = 1.66016e-4
frequency = 0.125
[Mesh]
[fmg]
type = FileMeshGenerator
file = '../s14/cnrs_s14_griffin_neutronics_out_ns_flow0.e'
use_for_exodus_restart = true
[]
[]
[Physics]
[NavierStokes]
[Flow]
[all]
compressibility = 'incompressible'
density = ${rho}
dynamic_viscosity = 'mu'
# Restart parameters
initialize_variables_from_mesh_file = true
# Boussinesq parameters
boussinesq_approximation = true
gravity = '0 -9.81 0'
thermal_expansion = ${alpha}
ref_temperature = 900
# Initial conditions
initial_velocity = '${Ulid} 0 0'
initial_pressure = 1e5
# Boundary conditions
# Note: we could do a no-slip with a wall velocity, same
inlet_boundaries = 'top'
momentum_inlet_types = 'fixed-velocity'
momentum_inlet_functors = '${Ulid} 0'
wall_boundaries = 'left right bottom'
momentum_wall_types = 'noslip noslip noslip'
# Pressure pin
pin_pressure = true
pinned_pressure_type = average
pinned_pressure_value = 1e5
# Numerical Scheme
momentum_advection_interpolation = 'upwind'
mass_advection_interpolation = 'upwind'
[]
[]
[FluidHeatTransfer]
[all]
initial_temperature = 900
# Restart parameters
initialize_variables_from_mesh_file = true
# Material properties
thermal_conductivity = 'k'
specific_heat = 'cp'
# Boundary conditions
energy_inlet_types = 'fixed-temperature'
energy_inlet_functors = 900
energy_wall_types = 'heatflux heatflux heatflux'
energy_wall_functors = '0 0 0'
# Heat source
external_heat_source = power_density
ambient_convection_alpha = 1.0e+6
ambient_temperature = 900.0
# Numerical Scheme
energy_advection_interpolation = 'upwind'
energy_two_term_bc_expansion = true
energy_scaling = 1e-3
[]
[]
[ScalarTransport]
[scalars]
# Restart parameters
initialize_variables_from_mesh_file = true
passive_scalar_names = 'dnp0 dnp1 dnp2 dnp3
dnp4 dnp5 dnp6 dnp7'
passive_scalar_coupled_source = 'fission_source dnp0; fission_source dnp1;
fission_source dnp2; fission_source dnp3;
fission_source dnp4; fission_source dnp5;
fission_source dnp6; fission_source dnp7'
passive_scalar_coupled_source_coeff = '${beta0} ${fparse -lambda0}; ${beta1} ${fparse -lambda1};
${beta2} ${fparse -lambda2}; ${beta3} ${fparse -lambda3};
${beta4} ${fparse -lambda4}; ${beta5} ${fparse -lambda5};
${beta6} ${fparse -lambda6}; ${beta7} ${fparse -lambda7}'
passive_scalar_inlet_types = 'fixed-value fixed-value fixed-value fixed-value
fixed-value fixed-value fixed-value fixed-value'
passive_scalar_inlet_functors = '1.0; 1.0; 1.0; 1.0;
1.0; 1.0; 1.0; 1.0'
# Numerical parameters
system_names= 's1 s2 s3 s4 s5 s6 s7 s8'
passive_scalar_advection_interpolation = 'upwind'
[]
[]
[]
[]
[Problem]
nl_sys_names = 'nl0 s1 s2 s3 s4 s5 s6 s7 s8'
[]
[AuxVariables]
[power_density]
type = MooseVariableFVReal
initial_from_file_var = power_density
initial_from_file_timestep = LATEST
[]
[fission_source]
type = MooseVariableFVReal
initial_from_file_var = fission_source
initial_from_file_timestep = LATEST
[]
[]
[Functions]
[alpha_val]
type = ParsedFunction
expression = '1.0e+6*(1.0 + 0.1*sin(2.0*pi*${frequency}*t))' # 'alpha_0*(1.0 + a*sin(fq*t))'
[]
[]
[FunctorMaterials]
[functor_constants]
type = ADGenericFunctorMaterial
prop_names = 'k rho mu'
prop_values = '${k} ${rho} ${mu}'
[]
[cp]
type = ADGenericFunctorMaterial
prop_names = 'cp'
prop_values = '${cp}'
[]
[alpha_t]
type = ADGenericFunctorMaterial
prop_names = 'alpha_t'
prop_values = alpha_val
block = '1'
[]
[]
[Debug]
show_var_residual_norms = False
[]
[Postprocessors]
[dt]
type = TimestepSize
[]
[Tfuel_avg]
type = ElementAverageValue
variable = T_fluid
[]
[]
[Executioner]
type = Transient
start_time = 0.0
dt = ${fparse max(0.005, 0.05*0.0125/frequency)}
end_time = ${fparse 10/frequency}
#[TimeStepper]
# type = IterationAdaptiveDT
# dt = 0.1
# growth_factor = 2
#[]
solve_type = 'NEWTON'
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
line_search = l2#'none'
nl_rel_tol = 1e-6
nl_abs_tol = 2e-8
nl_max_its = 200
l_max_its = 200
automatic_scaling = true
[]
[Outputs]
exodus = false
csv = true
print_linear_converged_reason = false
print_linear_residuals = false
print_nonlinear_converged_reason = false
[]
(msr/cnrs/s21/cnrs_s21_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 2.1: Time dependent coupling
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
frequency = 0.0125
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = transient
G = 6
VacuumBoundary = 'left bottom right top'
# Only for exodus restart, not SolutionFile restart
# restart_transport_system = true
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin timestep_end'
[]
[]
[UserObjects]
[transport_solution]
type = TransportSolutionVectorFile
transport_system = diff
writing = false
execute_on = 'INITIAL'
scale_with_keff = false
folder = '../s14'
[]
[TH_solution]
type = SolutionVectorFile
var = 'tfuel densityf dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
loading_var = 'tfuel densityf dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
writing = false
execute_on = 'INITIAL'
folder = '../s14'
[]
[]
[Materials]
[nm]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Transient
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
start_time = 0.0
dt = ${fparse max(0.005, 0.05*0.0125/frequency)}
end_time = ${fparse 10/frequency}
#[TimeStepper]
# type = IterationAdaptiveDT
# dt = 0.1
# growth_factor = 2
#[]
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-6
nl_abs_tol = 1e-8
# MultiApp iteration parameters
fixed_point_min_its = 2
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-6
fixed_point_abs_tol = 1e-6
[]
[MultiApps]
[ns_flow]
type = TransientMultiApp
input_files = cnrs_s21_ns_flow.i
execute_on = 'timestep_end'
keep_solution_during_restore = true
catch_up = true
cli_args = 'frequency=${frequency}'
[]
[]
[Transfers]
# Multiphysics coupling
# Send production terms
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'timestep_end'
[]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
# get quantities computed by the fluid flow caculation
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'timestep_end'
[]
[Tfuel_avg]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = ns_flow
postprocessor = Tfuel_avg
source_variable = 'tfuel_avg'
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'initial timestep_end'
[]
[]
[Outputs]
exodus = true
csv = true
print_linear_converged_reason = false
print_linear_residuals = false
print_nonlinear_converged_reason = false
[]
(msr/cnrs/s21/cnrs_s21_ns_flow.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 2.1: Time dependent coupling
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
alpha = 2.0e-4
rho = 2.0e+3
cp = 3.075e+3
k = 1.0e-3
mu = 5.0e+1
# Sc_t = 2.0e8
Ulid = 0.5
lambda0 = 1.24667E-02
lambda1 = 2.82917E-02
lambda2 = 4.25244E-02
lambda3 = 1.33042E-01
lambda4 = 2.92467E-01
lambda5 = 6.66488E-01
lambda6 = 1.63478E+00
lambda7 = 3.55460E+00
beta0 = 2.33102e-4
beta1 = 1.03262e-3
beta2 = 6.81878e-4
beta3 = 1.37726e-3
beta4 = 2.14493e-3
beta5 = 6.40917e-4
beta6 = 6.05805e-4
beta7 = 1.66016e-4
frequency = 0.125
[Mesh]
[fmg]
type = FileMeshGenerator
file = '../s14/cnrs_s14_griffin_neutronics_out_ns_flow0.e'
use_for_exodus_restart = true
[]
[]
[Physics]
[NavierStokes]
[Flow]
[all]
compressibility = 'incompressible'
density = ${rho}
dynamic_viscosity = 'mu'
# Restart parameters
initialize_variables_from_mesh_file = true
# Boussinesq parameters
boussinesq_approximation = true
gravity = '0 -9.81 0'
thermal_expansion = ${alpha}
ref_temperature = 900
# Initial conditions
initial_velocity = '${Ulid} 0 0'
initial_pressure = 1e5
# Boundary conditions
# Note: we could do a no-slip with a wall velocity, same
inlet_boundaries = 'top'
momentum_inlet_types = 'fixed-velocity'
momentum_inlet_functors = '${Ulid} 0'
wall_boundaries = 'left right bottom'
momentum_wall_types = 'noslip noslip noslip'
# Pressure pin
pin_pressure = true
pinned_pressure_type = average
pinned_pressure_value = 1e5
# Numerical Scheme
momentum_advection_interpolation = 'upwind'
mass_advection_interpolation = 'upwind'
[]
[]
[FluidHeatTransfer]
[all]
initial_temperature = 900
# Restart parameters
initialize_variables_from_mesh_file = true
# Material properties
thermal_conductivity = 'k'
specific_heat = 'cp'
# Boundary conditions
energy_inlet_types = 'fixed-temperature'
energy_inlet_functors = 900
energy_wall_types = 'heatflux heatflux heatflux'
energy_wall_functors = '0 0 0'
# Heat source
external_heat_source = power_density
ambient_convection_alpha = 1.0e+6
ambient_temperature = 900.0
# Numerical Scheme
energy_advection_interpolation = 'upwind'
energy_two_term_bc_expansion = true
energy_scaling = 1e-3
[]
[]
[ScalarTransport]
[scalars]
# Restart parameters
initialize_variables_from_mesh_file = true
passive_scalar_names = 'dnp0 dnp1 dnp2 dnp3
dnp4 dnp5 dnp6 dnp7'
passive_scalar_coupled_source = 'fission_source dnp0; fission_source dnp1;
fission_source dnp2; fission_source dnp3;
fission_source dnp4; fission_source dnp5;
fission_source dnp6; fission_source dnp7'
passive_scalar_coupled_source_coeff = '${beta0} ${fparse -lambda0}; ${beta1} ${fparse -lambda1};
${beta2} ${fparse -lambda2}; ${beta3} ${fparse -lambda3};
${beta4} ${fparse -lambda4}; ${beta5} ${fparse -lambda5};
${beta6} ${fparse -lambda6}; ${beta7} ${fparse -lambda7}'
passive_scalar_inlet_types = 'fixed-value fixed-value fixed-value fixed-value
fixed-value fixed-value fixed-value fixed-value'
passive_scalar_inlet_functors = '1.0; 1.0; 1.0; 1.0;
1.0; 1.0; 1.0; 1.0'
# Numerical parameters
system_names= 's1 s2 s3 s4 s5 s6 s7 s8'
passive_scalar_advection_interpolation = 'upwind'
[]
[]
[]
[]
[Problem]
nl_sys_names = 'nl0 s1 s2 s3 s4 s5 s6 s7 s8'
[]
[AuxVariables]
[power_density]
type = MooseVariableFVReal
initial_from_file_var = power_density
initial_from_file_timestep = LATEST
[]
[fission_source]
type = MooseVariableFVReal
initial_from_file_var = fission_source
initial_from_file_timestep = LATEST
[]
[]
[Functions]
[alpha_val]
type = ParsedFunction
expression = '1.0e+6*(1.0 + 0.1*sin(2.0*pi*${frequency}*t))' # 'alpha_0*(1.0 + a*sin(fq*t))'
[]
[]
[FunctorMaterials]
[functor_constants]
type = ADGenericFunctorMaterial
prop_names = 'k rho mu'
prop_values = '${k} ${rho} ${mu}'
[]
[cp]
type = ADGenericFunctorMaterial
prop_names = 'cp'
prop_values = '${cp}'
[]
[alpha_t]
type = ADGenericFunctorMaterial
prop_names = 'alpha_t'
prop_values = alpha_val
block = '1'
[]
[]
[Debug]
show_var_residual_norms = False
[]
[Postprocessors]
[dt]
type = TimestepSize
[]
[Tfuel_avg]
type = ElementAverageValue
variable = T_fluid
[]
[]
[Executioner]
type = Transient
start_time = 0.0
dt = ${fparse max(0.005, 0.05*0.0125/frequency)}
end_time = ${fparse 10/frequency}
#[TimeStepper]
# type = IterationAdaptiveDT
# dt = 0.1
# growth_factor = 2
#[]
solve_type = 'NEWTON'
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
line_search = l2#'none'
nl_rel_tol = 1e-6
nl_abs_tol = 2e-8
nl_max_its = 200
l_max_its = 200
automatic_scaling = true
[]
[Outputs]
exodus = false
csv = true
print_linear_converged_reason = false
print_linear_residuals = false
print_nonlinear_converged_reason = false
[]
