Phase 1 Model: Steady State MultiPhysics Coupling
This phase of the benchmark is concerned with the steady state multiphysics solution. It is comprised of four steps and following is a description of the four steps and their inputs.
Step 1.1
In this step, the influence of the delayed neutron precursor drift on the reactivity and delayed neutron source distribution is explored. This step comprises a neutronic and Navier-Stokes solves. The neutronics solve is performed as a diffusion problem as defined in step 0.2. The main input file contains instructions to perform a neutronic solution. The characteristics of the transport solve are defined TransportSystems block as follows
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]The power of the problem from which the power density will be normalized can be defined in the PowerDensity block as follows
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]auxiliary variables for the problem are defined in the AuxVariables block as follows
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]where pronghorn will be used to obtain the temperature distributions and the delayed neutron precursor distributions. Operations to act on the auxiliary variables are defined in the AuxKernels block
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]The characteristics of executing the calculations are provided in the Executioner block as follows
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]To obtain the temperature and delayed neutron precursor distribution, pronghorn is used to performed these thermo-fluid calculations. A MultiApps block is used to call the pronghorn solver as in the following block of code
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s11_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]where ''cnrs_s01_ns_flow.i'' is the pronghorn input. The transfer of variables between Griffin and pronghorn is instructed through the Transfers block, where the fission source is obtained using Griffin and sent to pronghorn. Then pronghorn is used to calculate the distribution of the precursor
[Transfers]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
[]The pronghorn input to obtain the delayed neutron precursor distribution and fuel temperature is similar in structure to the input developed in step 0.1. Some differences in the input file for the Navier-Stokes solve include modifying the input to include introducing the fission_source as an auxiliary variable that pronghorn will expect to receive from the Griffin Solve.
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]Step 1.1 Results
The delayed neutron source distribution along AA` and BB` are collected from the results of the Griffin run. These are as follows
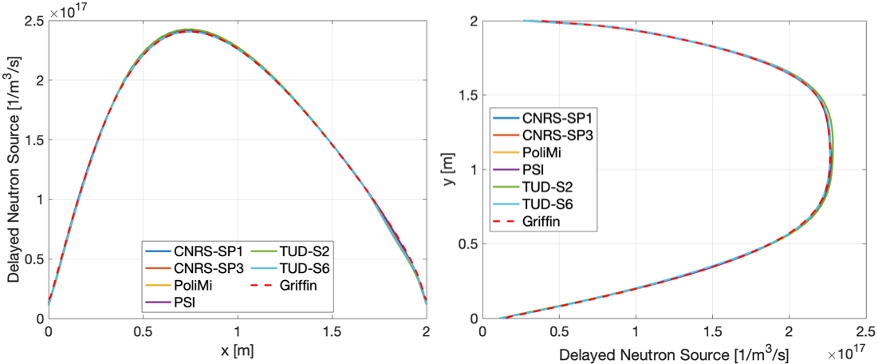
Step 1.2
This step resembles step 1.1 with the difference being in introducing the temperature feedback. The problem is treated as a transport solve coupled with two Navier-Stokes solves as will be described later. The transport solve is specified in the TransportSystems block as follows
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]The power density in the fuel salt normalization given a reactor power is instructed in the PowerDensity as follows
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]A set of auxiliary variables which will be obtained using other applications (i.e. pronghorn) are defined as follows. These variables include the temperature distributions in the fuel, flow field, and delayed neutron precursor distribution which are obtained using Navier-Stokes solves as will be demonstrated later.
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[FRD]
order = FIRST
family = L2_LAGRANGE
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]Compared to the previous step (i.e. Step 1.1), there will be two pronghorn Navier-Stokes solutions to apply the temperature feedback. These are called in a MultiApps fashion as
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s12_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]The first solve (i.e. ns_flow) will be used to solve for the flow field (i.e. velocity field) and the delayed neutron precursor distribution. The input for the first solve will be the fission_source obtained by the Griffin transport solve. The second solve (i.e. ns_temp) is used to solve for the temperature distribution given the fission source solution obtained by the transport solve. The inputs for the second solve are velocity field obtained by the ns_flow solve, and the power density obtained by the Griffin transport solve. The instructions of data transfer between the transport solve and the two Navier-Stokes solves are provided in the Transfers block as follows
[Transfers]
# MultiPhysics coupling
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'TIMESTEP_BEGIN'
[]
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'TIMESTEP_END'
[]
# Computed in the flow simulation
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'TIMESTEP_END'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'TIMESTEP_END'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'TIMESTEP_END'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'TIMESTEP_END'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'TIMESTEP_END'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'TIMESTEP_END'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'TIMESTEP_END'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'TIMESTEP_END'
[]
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'TIMESTEP_END'
[]
[]Te sequence of TransportSystems solve, ns_flow solve, and ns_temp solve is performed till the convergence criteria is met. These are specified in the main input file (i.e. Griffin solve), within the Executioner block as follows
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]Step 1.2 Results
The fuel salt temperature distribution along AA` and BB` is collected and plotted as follows
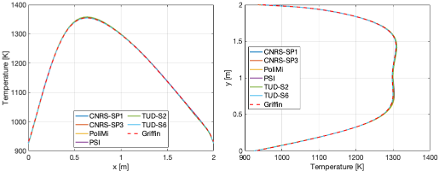
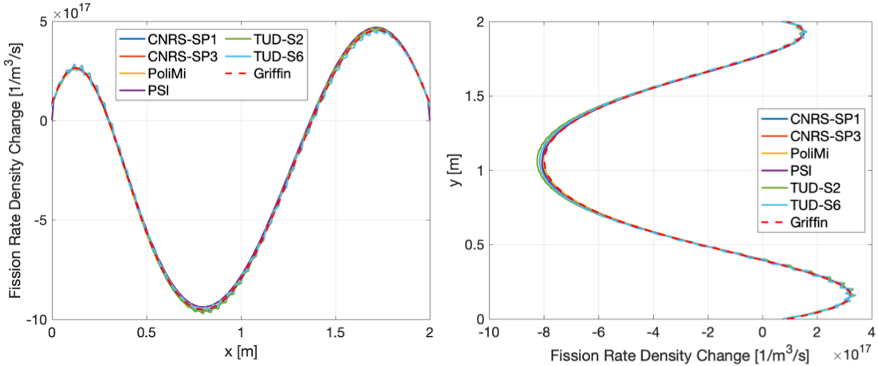
The fission rate density is also reported along AA` and BB` in this exercise
Step 1.3:
In this step, the coupled multiphysics modeling is performed with zero fuel salt lid velocity. This means the flow is only driven by natural circulation and without forced convection.
The modeling of this problem takes two solvers. The first is a transport solve specified through the TransportSystems block
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]Power density instructions are provided in the PowerDensity block
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]The set of auxiliary variables that will be obtained using the Navier-Stokes solves are defined as follows
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]The transport solve characteristics and the tolerances to converge the problem are specified as follows
[Executioner]
type = Eigenvalue
solve_type = PJFNKMO
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
l_max_its = 200
l_tol = 1e-3
# Nonlinear solve
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
line_search = none #l2
# MultiApps fixed point iterations
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]The Navier-Stokes solve input is specified through the MultiApps block as
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s13_ns_flow.i
execute_on = 'timestep_end'
[]
[]Then the data transfer between the transport solve and the Navier-Stokes solve are managed through the Transfers block
[Transfers]
# Multiphysics coupling
# Send production terms
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'timestep_end'
[]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
# get quantities computed by the fluid flow caculation
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
# For postprocessing purposes
[Tfuel_avg]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = ns_flow
source_variable = 'tfuel_avg'
postprocessor = Tfuel_avg
execute_on = 'timestep_end'
[]
[vel_x_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_x'
variable = 'vel_x'
execute_on = 'TIMESTEP_END'
[]
[vel_y_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_y'
variable = 'vel_y'
execute_on = 'TIMESTEP_END'
[]
[]Step 1.3 Results
The horizontal velocity component distribution along AA` is reported in Figure 1.
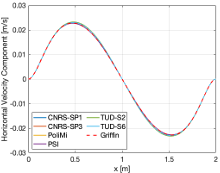
Figure 1:
The vertical velocity component distribution along AA` and BB` is also reported in Figure 2.
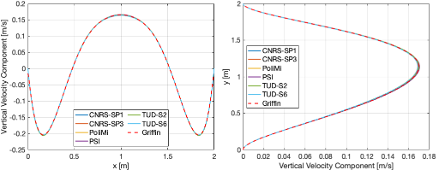
Figure 2:
The fuel salt temperature distribution along AA` and BB` in this exercise is reported in Figure 3.
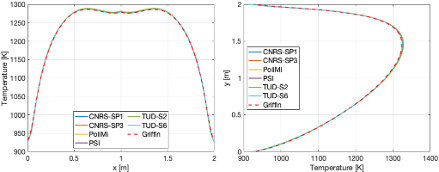
Figure 3:
Finally, the delayed neutron source distribution along AA` and BB` is reported in Figure 4.
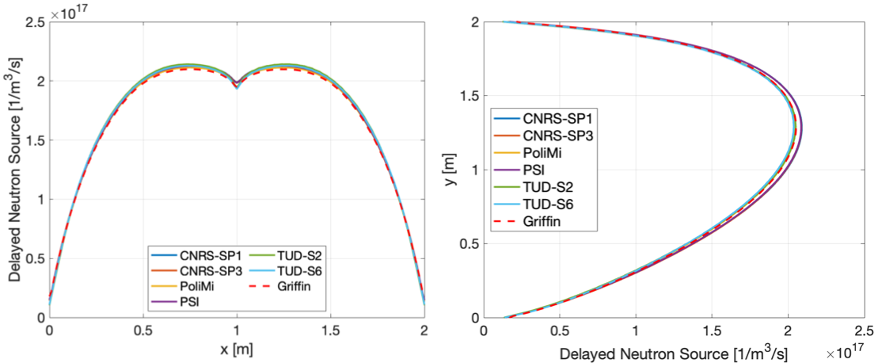
Figure 4:
Step 1.4:
This phase performs a similar task to that of Step 1.3 for a combination of reactor power and lid velocities. The set of reactor powers and lid velocities are presented in the following table
| Lid Velocity | Reactor Power |
|---|---|
| 0.0 | 1.0E9 |
| 0.1 | 0.2E9 |
| 0.1 | 0.4E9 |
| 0.1 | 0.6E9 |
| 0.1 | 0.8E9 |
| 0.1 | 1.0E9 |
| 0.2 | 0.2E9 |
| 0.2 | 0.4E9 |
| 0.2 | 0.6E9 |
| 0.2 | 0.8E9 |
| 0.2 | 1.0E9 |
| 0.3 | 0.2E9 |
| 0.3 | 0.4E9 |
| 0.3 | 0.6E9 |
| 0.3 | 0.8E9 |
| 0.3 | 1.0E9 |
| 0.4 | 0.2E9 |
| 0.4 | 0.4E9 |
| 0.4 | 0.6E9 |
| 0.4 | 0.8E9 |
| 0.4 | 1.0E9 |
| 0.5 | 0.2E9 |
| 0.5 | 0.4E9 |
| 0.5 | 0.6E9 |
| 0.5 | 0.8E9 |
| 0.5 | 1.0E9 |
A shell script is used to run all these cases.
Step 1.4 Results
In this exercise, the reported results are the delayed neutron precursor density distribution depending on the lid velocity
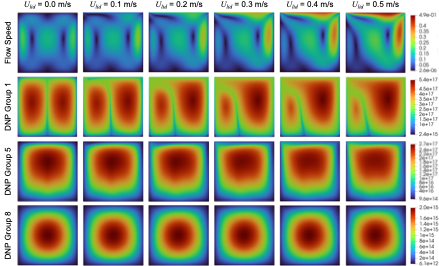
(msr/cnrs/s11/cnrs_s11_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.1: Circulating fuel
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s11_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s11/cnrs_s11_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.1: Circulating fuel
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s11_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s11/cnrs_s11_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.1: Circulating fuel
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s11_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s11/cnrs_s11_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.1: Circulating fuel
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s11_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s11/cnrs_s11_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.1: Circulating fuel
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s11_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s11/cnrs_s11_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.1: Circulating fuel
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s11_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s11/cnrs_s11_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.1: Circulating fuel
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s11_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s11/cnrs_s11_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.1: Circulating fuel
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s11_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s12/cnrs_s12_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.2: Power coupling
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[FRD]
order = FIRST
family = L2_LAGRANGE
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[fission_rate_density]
type = VectorReactionRate
scalar_flux = 'sflux_g0 sflux_g1 sflux_g2 sflux_g3 sflux_g4 sflux_g5'
cross_section = sigma_fission
variable = FRD
scale_factor = Normalization
block = 'cavity'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s12_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
# MultiPhysics coupling
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'TIMESTEP_BEGIN'
[]
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'TIMESTEP_END'
[]
# Computed in the flow simulation
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'TIMESTEP_END'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'TIMESTEP_END'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'TIMESTEP_END'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'TIMESTEP_END'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'TIMESTEP_END'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'TIMESTEP_END'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'TIMESTEP_END'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'TIMESTEP_END'
[]
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'TIMESTEP_END'
[]
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s12/cnrs_s12_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.2: Power coupling
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[FRD]
order = FIRST
family = L2_LAGRANGE
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[fission_rate_density]
type = VectorReactionRate
scalar_flux = 'sflux_g0 sflux_g1 sflux_g2 sflux_g3 sflux_g4 sflux_g5'
cross_section = sigma_fission
variable = FRD
scale_factor = Normalization
block = 'cavity'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s12_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
# MultiPhysics coupling
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'TIMESTEP_BEGIN'
[]
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'TIMESTEP_END'
[]
# Computed in the flow simulation
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'TIMESTEP_END'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'TIMESTEP_END'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'TIMESTEP_END'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'TIMESTEP_END'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'TIMESTEP_END'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'TIMESTEP_END'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'TIMESTEP_END'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'TIMESTEP_END'
[]
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'TIMESTEP_END'
[]
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s12/cnrs_s12_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.2: Power coupling
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[FRD]
order = FIRST
family = L2_LAGRANGE
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[fission_rate_density]
type = VectorReactionRate
scalar_flux = 'sflux_g0 sflux_g1 sflux_g2 sflux_g3 sflux_g4 sflux_g5'
cross_section = sigma_fission
variable = FRD
scale_factor = Normalization
block = 'cavity'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s12_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
# MultiPhysics coupling
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'TIMESTEP_BEGIN'
[]
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'TIMESTEP_END'
[]
# Computed in the flow simulation
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'TIMESTEP_END'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'TIMESTEP_END'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'TIMESTEP_END'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'TIMESTEP_END'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'TIMESTEP_END'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'TIMESTEP_END'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'TIMESTEP_END'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'TIMESTEP_END'
[]
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'TIMESTEP_END'
[]
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s12/cnrs_s12_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.2: Power coupling
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[FRD]
order = FIRST
family = L2_LAGRANGE
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[fission_rate_density]
type = VectorReactionRate
scalar_flux = 'sflux_g0 sflux_g1 sflux_g2 sflux_g3 sflux_g4 sflux_g5'
cross_section = sigma_fission
variable = FRD
scale_factor = Normalization
block = 'cavity'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s12_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
# MultiPhysics coupling
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'TIMESTEP_BEGIN'
[]
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'TIMESTEP_END'
[]
# Computed in the flow simulation
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'TIMESTEP_END'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'TIMESTEP_END'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'TIMESTEP_END'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'TIMESTEP_END'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'TIMESTEP_END'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'TIMESTEP_END'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'TIMESTEP_END'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'TIMESTEP_END'
[]
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'TIMESTEP_END'
[]
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s12/cnrs_s12_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.2: Power coupling
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[FRD]
order = FIRST
family = L2_LAGRANGE
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[fission_rate_density]
type = VectorReactionRate
scalar_flux = 'sflux_g0 sflux_g1 sflux_g2 sflux_g3 sflux_g4 sflux_g5'
cross_section = sigma_fission
variable = FRD
scale_factor = Normalization
block = 'cavity'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s12_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
# MultiPhysics coupling
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'TIMESTEP_BEGIN'
[]
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'TIMESTEP_END'
[]
# Computed in the flow simulation
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'TIMESTEP_END'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'TIMESTEP_END'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'TIMESTEP_END'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'TIMESTEP_END'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'TIMESTEP_END'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'TIMESTEP_END'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'TIMESTEP_END'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'TIMESTEP_END'
[]
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'TIMESTEP_END'
[]
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s12/cnrs_s12_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.2: Power coupling
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[FRD]
order = FIRST
family = L2_LAGRANGE
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[fission_rate_density]
type = VectorReactionRate
scalar_flux = 'sflux_g0 sflux_g1 sflux_g2 sflux_g3 sflux_g4 sflux_g5'
cross_section = sigma_fission
variable = FRD
scale_factor = Normalization
block = 'cavity'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNK
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
line_search = none #l2
l_max_its = 200
l_tol = 1e-3
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s12_ns_flow.i
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
# MultiPhysics coupling
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'TIMESTEP_BEGIN'
[]
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'TIMESTEP_END'
[]
# Computed in the flow simulation
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'TIMESTEP_END'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'TIMESTEP_END'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'TIMESTEP_END'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'TIMESTEP_END'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'TIMESTEP_END'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'TIMESTEP_END'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'TIMESTEP_END'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'TIMESTEP_END'
[]
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'TIMESTEP_END'
[]
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'FRD tfuel'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s13/cnrs_s13_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.3: Buoyancy
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNKMO
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
l_max_its = 200
l_tol = 1e-3
# Nonlinear solve
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
line_search = none #l2
# MultiApps fixed point iterations
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s13_ns_flow.i
execute_on = 'timestep_end'
[]
[]
[Transfers]
# Multiphysics coupling
# Send production terms
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'timestep_end'
[]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
# get quantities computed by the fluid flow caculation
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
# For postprocessing purposes
[Tfuel_avg]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = ns_flow
source_variable = 'tfuel_avg'
postprocessor = Tfuel_avg
execute_on = 'timestep_end'
[]
[vel_x_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_x'
variable = 'vel_x'
execute_on = 'TIMESTEP_END'
[]
[vel_y_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_y'
variable = 'vel_y'
execute_on = 'TIMESTEP_END'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s13/cnrs_s13_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.3: Buoyancy
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNKMO
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
l_max_its = 200
l_tol = 1e-3
# Nonlinear solve
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
line_search = none #l2
# MultiApps fixed point iterations
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s13_ns_flow.i
execute_on = 'timestep_end'
[]
[]
[Transfers]
# Multiphysics coupling
# Send production terms
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'timestep_end'
[]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
# get quantities computed by the fluid flow caculation
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
# For postprocessing purposes
[Tfuel_avg]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = ns_flow
source_variable = 'tfuel_avg'
postprocessor = Tfuel_avg
execute_on = 'timestep_end'
[]
[vel_x_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_x'
variable = 'vel_x'
execute_on = 'TIMESTEP_END'
[]
[vel_y_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_y'
variable = 'vel_y'
execute_on = 'TIMESTEP_END'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s13/cnrs_s13_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.3: Buoyancy
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNKMO
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
l_max_its = 200
l_tol = 1e-3
# Nonlinear solve
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
line_search = none #l2
# MultiApps fixed point iterations
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s13_ns_flow.i
execute_on = 'timestep_end'
[]
[]
[Transfers]
# Multiphysics coupling
# Send production terms
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'timestep_end'
[]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
# get quantities computed by the fluid flow caculation
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
# For postprocessing purposes
[Tfuel_avg]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = ns_flow
source_variable = 'tfuel_avg'
postprocessor = Tfuel_avg
execute_on = 'timestep_end'
[]
[vel_x_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_x'
variable = 'vel_x'
execute_on = 'TIMESTEP_END'
[]
[vel_y_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_y'
variable = 'vel_y'
execute_on = 'TIMESTEP_END'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s13/cnrs_s13_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.3: Buoyancy
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNKMO
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
l_max_its = 200
l_tol = 1e-3
# Nonlinear solve
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
line_search = none #l2
# MultiApps fixed point iterations
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s13_ns_flow.i
execute_on = 'timestep_end'
[]
[]
[Transfers]
# Multiphysics coupling
# Send production terms
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'timestep_end'
[]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
# get quantities computed by the fluid flow caculation
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
# For postprocessing purposes
[Tfuel_avg]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = ns_flow
source_variable = 'tfuel_avg'
postprocessor = Tfuel_avg
execute_on = 'timestep_end'
[]
[vel_x_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_x'
variable = 'vel_x'
execute_on = 'TIMESTEP_END'
[]
[vel_y_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_y'
variable = 'vel_y'
execute_on = 'TIMESTEP_END'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s13/cnrs_s13_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.3: Buoyancy
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNKMO
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
l_max_its = 200
l_tol = 1e-3
# Nonlinear solve
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
line_search = none #l2
# MultiApps fixed point iterations
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s13_ns_flow.i
execute_on = 'timestep_end'
[]
[]
[Transfers]
# Multiphysics coupling
# Send production terms
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'timestep_end'
[]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
# get quantities computed by the fluid flow caculation
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
# For postprocessing purposes
[Tfuel_avg]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = ns_flow
source_variable = 'tfuel_avg'
postprocessor = Tfuel_avg
execute_on = 'timestep_end'
[]
[vel_x_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_x'
variable = 'vel_x'
execute_on = 'TIMESTEP_END'
[]
[vel_y_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_y'
variable = 'vel_y'
execute_on = 'TIMESTEP_END'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]
(msr/cnrs/s13/cnrs_s13_griffin_neutronics.i)
# ==============================================================================
# Model description
# ------------------------------------------------------------------------------
# CNRS Benchmark model Created & modifed by Dr. Mustafa Jaradat and Dr. Namjae Choi
# November 22, 2022
# Step 1.3: Buoyancy
# ==============================================================================
# Tiberga, et al., 2020. Results from a multi-physics numerical benchmark for codes
# dedicated to molten salt fast reactors. Ann. Nucl. Energy 142(2020)107428.
# URL:http://www.sciencedirect.com/science/article/pii/S0306454920301262
# ==============================================================================
[GlobalParams]
isotopes = 'pseudo'
densities = 'densityf'
library_file = '../xs/msr_cavity_xslib.xml'
library_name = 'CNRS-Benchmark'
grid_names = 'Tfuel'
grid_variables = 'tfuel'
is_meter = true
plus = 1
[]
[Mesh]
type = MeshGeneratorMesh
block_id = '1'
block_name = 'cavity'
[cartesian_mesh]
type = CartesianMeshGenerator
dim = 2
dx = '1.0 1.0'
ix = '100 100'
dy = '1.0 1.0'
iy = '100 100'
subdomain_id = ' 1 1
1 1'
[]
[assign_material_id]
type = SubdomainExtraElementIDGenerator
input = cartesian_mesh
extra_element_id_names = 'material_id'
subdomains = '1'
extra_element_ids = '1'
[]
[]
[TransportSystems]
particle = neutron
equation_type = eigenvalue
G = 6
VacuumBoundary = 'left bottom right top'
[diff]
scheme = CFEM-Diffusion
n_delay_groups = 8
family = LAGRANGE
order = FIRST
external_dnp_variable = 'dnp'
fission_source_aux = true
assemble_scattering_jacobian = true
assemble_fission_jacobian = true
[]
[]
[PowerDensity]
power = 1.0e9
power_density_variable = power_density
integrated_power_postprocessor = total_power
power_scaling_postprocessor = Normalization
family = LAGRANGE
order = FIRST
[]
[AuxVariables]
[tfuel]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[tfuel_avg]
order = CONSTANT
family = MONOMIAL
initial_condition = 900
[]
[vel_x]
order = CONSTANT
family = MONOMIAL
[]
[vel_y]
order = CONSTANT
family = MONOMIAL
[]
[densityf]
order = CONSTANT
family = MONOMIAL
initial_condition = 1.0
[]
[dnp_src]
order = CONSTANT
family = MONOMIAL
[]
[dnp]
order = CONSTANT
family = MONOMIAL
components = 8
[]
[dnp0]
order = CONSTANT
family = MONOMIAL
[]
[dnp1]
order = CONSTANT
family = MONOMIAL
[]
[dnp2]
order = CONSTANT
family = MONOMIAL
[]
[dnp3]
order = CONSTANT
family = MONOMIAL
[]
[dnp4]
order = CONSTANT
family = MONOMIAL
[]
[dnp5]
order = CONSTANT
family = MONOMIAL
[]
[dnp6]
order = CONSTANT
family = MONOMIAL
[]
[dnp7]
order = CONSTANT
family = MONOMIAL
[]
[]
[AuxKernels]
[density_fuel]
type = ParsedAux
block = 'cavity'
variable = densityf
coupled_variables = 'tfuel'
expression = '(1.0-0.0002*(tfuel-900.0))'
execute_on = 'INITIAL timestep_end'
[]
[build_dnp]
type = BuildArrayVariableAux
variable = dnp
component_variables = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
execute_on = 'initial timestep_begin final'
[]
[delayed_neutron_source]
type = VectorReactionRate
scalar_flux = 'dnp0 dnp1 dnp2 dnp3 dnp4 dnp5 dnp6 dnp7'
cross_section = lambda_vec
variable = dnp_src
scale_factor = Normalization
block = '1'
[]
[]
[Materials]
[fuel_salt]
type = CoupledFeedbackMatIDNeutronicsMaterial
block = 'cavity'
[]
[]
[Preconditioning]
[SMP]
type = SMP
full = true
[]
[]
[Executioner]
type = Eigenvalue
solve_type = PJFNKMO
petsc_options_iname = '-pc_type -pc_factor_shift_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu NONZERO superlu_dist'
free_power_iterations = 2
l_max_its = 200
l_tol = 1e-3
# Nonlinear solve
nl_max_its = 200
nl_rel_tol = 1e-5
nl_abs_tol = 1e-6
line_search = none #l2
# MultiApps fixed point iterations
fixed_point_min_its = 3
fixed_point_max_its = 50
fixed_point_rel_tol = 1e-5
fixed_point_abs_tol = 1e-6
[]
[VectorPostprocessors]
[AA_line_values_left]
type = LineValueSampler
start_point = '0 0.995 0'
end_point = '2 0.995 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[AA_line_values_right]
type = LineValueSampler
start_point = '0 1.005 0'
end_point = '2 1.005 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = x
[]
[BB_line_values_left]
type = LineValueSampler
start_point = '0.995 0 0'
end_point = '0.995 2 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[BB_line_values_right]
type = LineValueSampler
start_point = '1.005 0 0'
end_point = '1.005 2 0'
variable = 'dnp_src tfuel vel_x vel_y'
num_points = 201
execute_on = 'FINAL'
sort_by = y
[]
[]
[MultiApps]
[ns_flow]
type = FullSolveMultiApp
input_files = cnrs_s13_ns_flow.i
execute_on = 'timestep_end'
[]
[]
[Transfers]
# Multiphysics coupling
# Send production terms
[power_dens]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = 'power_density'
variable = 'power_density'
execute_on = 'timestep_end'
[]
[fission_source]
type = MultiAppProjectionTransfer
to_multi_app = ns_flow
source_variable = fission_source
variable = fission_source
execute_on = 'timestep_end'
[]
# get quantities computed by the fluid flow caculation
[fuel_temp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'T_fluid'
variable = 'tfuel'
execute_on = 'timestep_end'
[]
[c1]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp0'
variable = 'dnp0'
execute_on = 'timestep_end'
[]
[c2]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp1'
variable = 'dnp1'
execute_on = 'timestep_end'
[]
[c3]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp2'
variable = 'dnp2'
execute_on = 'timestep_end'
[]
[c4]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp3'
variable = 'dnp3'
execute_on = 'timestep_end'
[]
[c5]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp4'
variable = 'dnp4'
execute_on = 'timestep_end'
[]
[c6]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp5'
variable = 'dnp5'
execute_on = 'timestep_end'
[]
[c7]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp6'
variable = 'dnp6'
execute_on = 'timestep_end'
[]
[c8]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'dnp7'
variable = 'dnp7'
execute_on = 'timestep_end'
[]
# For postprocessing purposes
[Tfuel_avg]
type = MultiAppVariableValueSamplePostprocessorTransfer
from_multi_app = ns_flow
source_variable = 'tfuel_avg'
postprocessor = Tfuel_avg
execute_on = 'timestep_end'
[]
[vel_x_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_x'
variable = 'vel_x'
execute_on = 'TIMESTEP_END'
[]
[vel_y_comp]
type = MultiAppCopyTransfer
from_multi_app = ns_flow
source_variable = 'vel_y'
variable = 'vel_y'
execute_on = 'TIMESTEP_END'
[]
[]
[Postprocessors]
[Tfuel_avg2]
type = ElementAverageValue
variable = tfuel
execute_on = 'timestep_end'
[]
[]
[Outputs]
exodus = true
[csv]
type = CSV
execute_on = 'FINAL'
[]
[]