Results

There are three types of output files:

1. csv files that write the user-specified scalar and vector variables to a comma-separated-values file. The data can be imported to Excel for further processing or in Python using the csv module, Pandas, or other methods.

2. Checkpoint folders where snapshots of the simulation data including all meshes, solutions are saved. Users can restart the run from where it ended using the file in the checkpoint folder.

3. ExodusII file that has all mesh and solution data. Users can use Paraview to open this .e file to visualize, plot, and analyze the data.

Steady-state

The steady-state simulation results are presented in this section. The power density profile imposed on the multi-D model is shown Figure 1. The power density profile is obtained from the Pronghorn/Griffin model by (Jaradat et al., 2023). Radially, the core has a bi-modal profile with a peak at the inner region of the core and the outer region near the side reflector. The peak at the outer region is because a considerable amount of neutrons that escape the bed are thermalized and scattered back into the pebble bed. Axially, the power density peaks at the top half of the reflector slightly above the centerline.

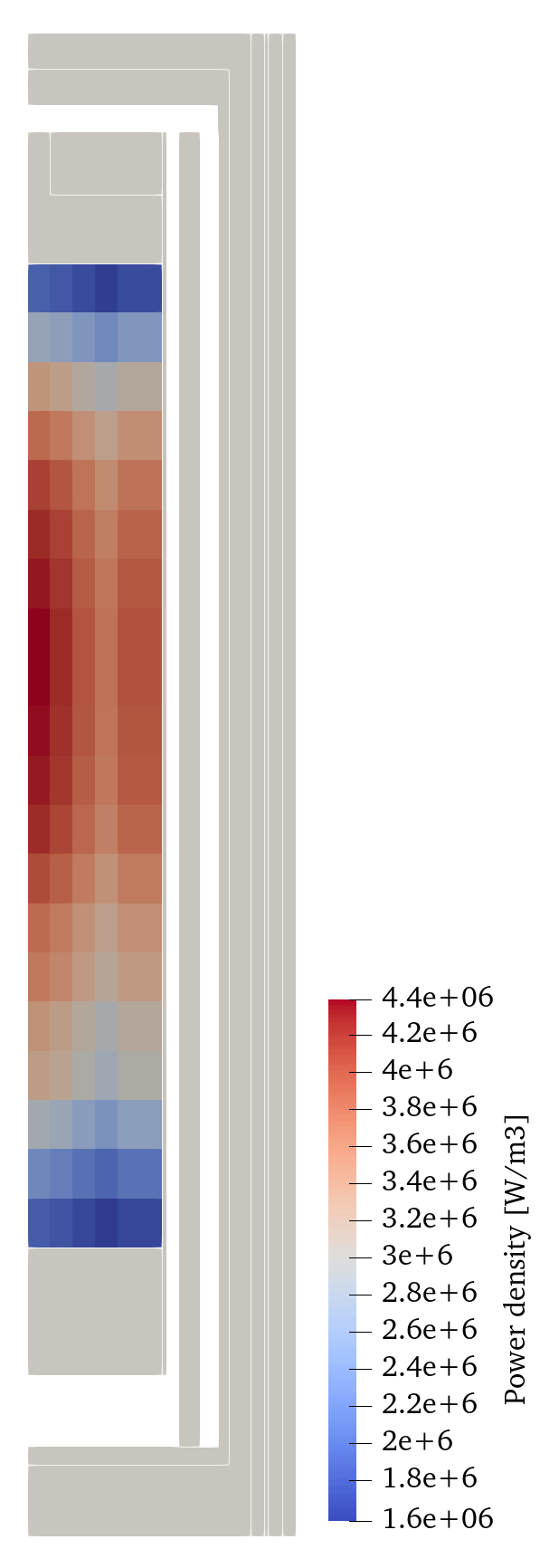
Figure 1: Power density distribution of the SAM HTR-PM model during steady-state normal operating condition.

The fluid and solid temperature profiles are shown in Figure 2 and Figure 3, respectively. The overall solid and fluid temperature profiles are similar. Temperature in the pebble bed increases from the top to the bottom following the flow direction. The inner region of the pebble bed is also hotter due to higher power density as shown in Figure 1. The temperature of the solid blocks outside of the pebble is significantly lower than the temperature in the pebble bed. This shows that majority of the heat generated by the pebble bed during steady-state normal operating condition is removed by forced convection while only a small amount of heat escapes to the side reflectors. Furthermore, the helium flows in the riser and bypass channels further act as another layer of barrier that restricts the radial conduction of heat.

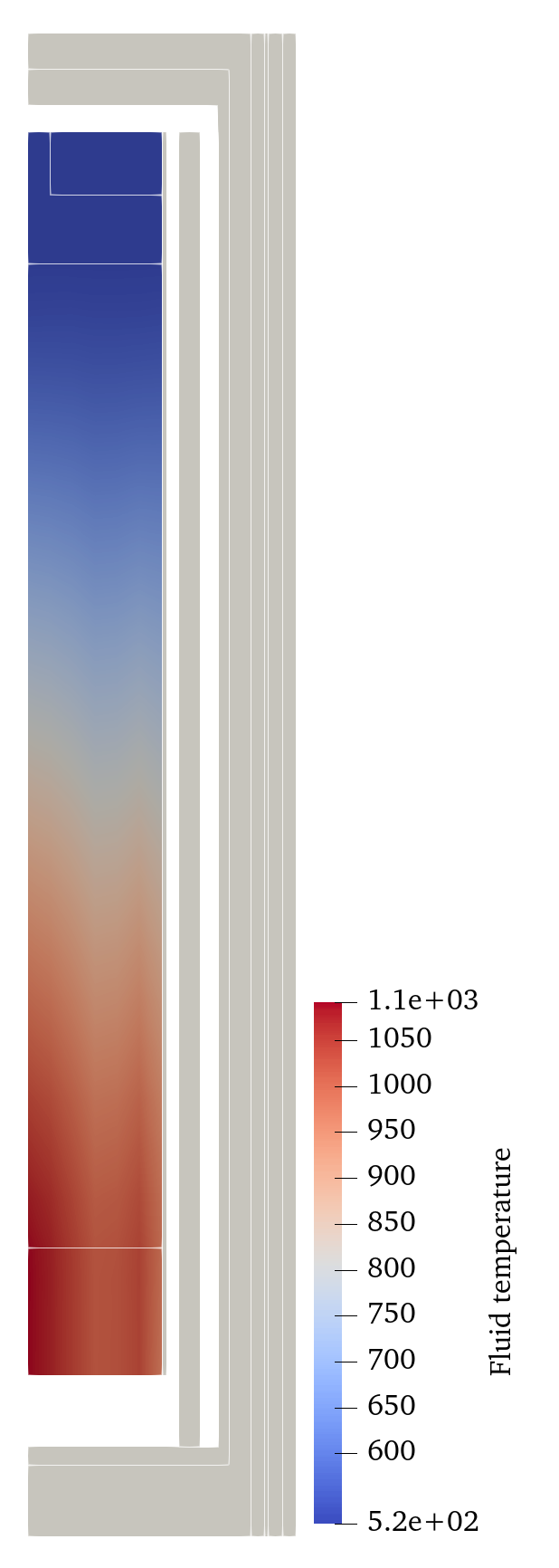
Figure 2: Fluid temperature distribution of the SAM HTR-PM model during steady-state normal operating condition.

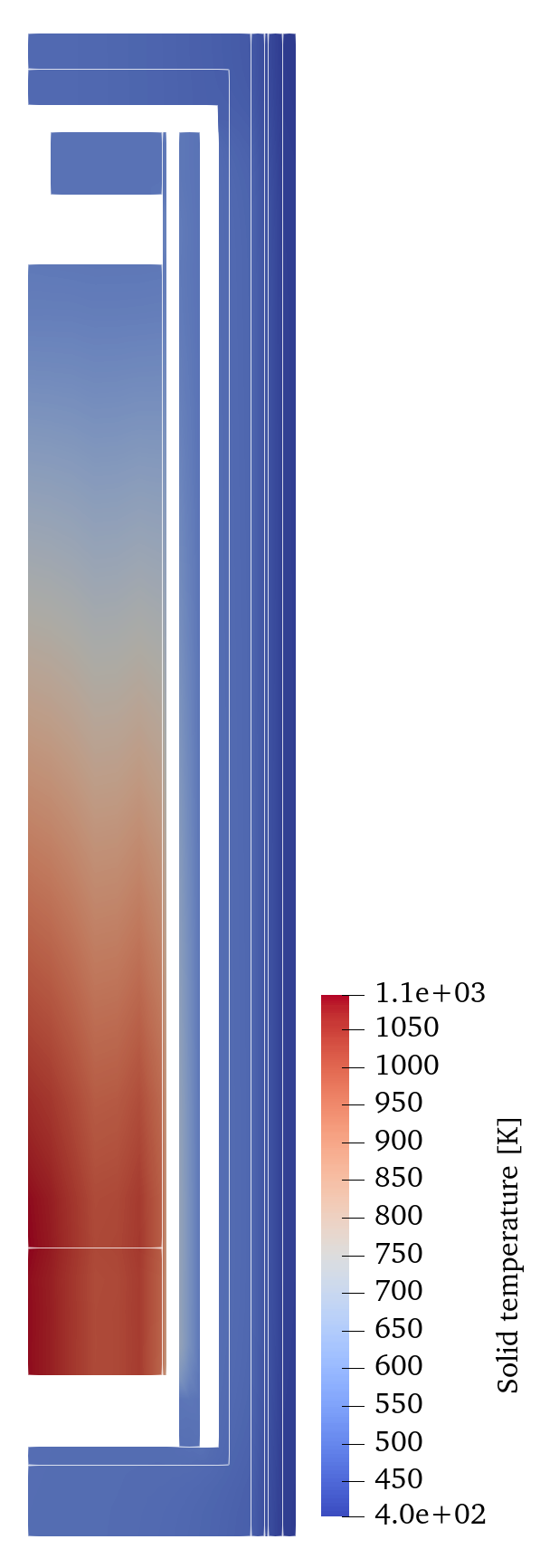
Figure 3: Solid temperature distribution of the SAM HTR-PM model during steady-state normal operating condition.

The axial fluid and solid temperature profiles are shown in Figure 4 and Figure 5, respectively. The temperature profiles are obtained at =0.125, 0.375, 0.625, 0.875, 1.125, 1.375 m. Overall, the solid and fluid temperature profiles are similar where the temperatures increase from the top to the bottom of the pebble bed. The axial velocity profiles are shown in Figure 6. Helium accelerates as it flows through the core due to increasing temperature that leads to decreasing density. Some fluctuations are observed at the top of the pebble bed at the inner core region due to the flow acceleration as caused by helium flowing into the top cavity through the small opening.

Figure 4: Fluid temperature axial profile of the SAM HTR-PM model during steady-state normal operating condition.

Figure 5: Solid temperature axial profile of the SAM HTR-PM model during steady-state normal operating condition.

Figure 6: Axial velocity profile of the SAM HTR-PM model during steady-state normal operating condition.

Some key parameters during steady-state normal operating condition are summarized in Figure 7. The pebble bed has a maximum temperature of 1090.5 K and a core-wide mean temperature of 799.8 K. Helium enter the riser at 523.9 K and exits the core at 1013.4 K, which is slightly lower than the theoretical value of 1020 K. The discrepancy is due to the loss of heat from the pebble bed to the side reflectors and eventually to the RCCS. The total helium mass flow rate is 96.3 kg/s, with 95.2 kg/s going into the pebble bed while the remaining 1.1 kg/s going through the bypass channel.

Figure 7: Summary of the SAM HTR-PM model during steady-state normal operating condition.

Pressurized Loss of Forced Cooling Transient

THe pressurized loss of forced cooling (PLOFC) transient is simulated and presented in this section. The sequence of events of the simulated PLOFC is shown in Figure 8. The model is first simulated until steady-state is achieved. At the start of the transient, the reactor is SCRAM and a decay heat curve is used to determine the reactor power level throughout the accident. At the same time, the helium flow rate is reduced linearly from the nominal value to zero over 13 seconds. During the accident, the pressure boundary is assumed to be intact where the system pressure is able to maintain at 7 MPa.

Figure 8: Sequence of events during PLOFC.

The evolution of the maximum pebble surface temperature is shown in Figure 9. At the beginning of transient, the maximum temperature rises sharply due to the loss of forced convection. As natural circulation is established in the core, the maximum temperature drops slightly before increasing again due to decay heat in the pebble bed. As heat is transferred radially through thermal conduction across the solid layers and eventually to the RCCS through thermal radiation, the maximum fuel temperature eventually starts to come down at roughly 90 hours from the beginning of the transient. The pebble surface temperature peaks at about 1350 K, which is far lower than the theoretical safety limit of TRISO fuel of about 1900 K.

The volume-averaged pebble surface temperature is shown in Figure 10. The average temperature increases rapidly within the first few hours of the transient due to loss of forced cooling. However, the rate of increase gradually slows down as natural circulation is established and heat is removed via radial conduction to the surrounding side reflectors. The average temperature peaks at about 1160 K about 90 hours into the transient before it starts to decrease.

It should be emphasized that the heat removal rate, and thus the temperature profile during PLOFC, is dependent on the design of the RCCS. Hence, the quantitative results presented here may not accurately reflect the progression of the transient. Nevertheless, the qualitative results and the trends of major parameters may still be relevant.

Figure 9: Maximum pebble surface temperature during the PLOFC transient.

Figure 10: Mean pebble surface temperature during the PLOFC transient.

The volume-averaged temperatures of side reflectors, carbon bricks, core barrel, and RPV are shown in Figure 11. Solid structures that are closer to the pebble bed show higher average temperatures. Furthermore, the rate of temperature increase of the structures is also dependent on their proximity to the pebble bed. For instance, the average temperature of the side reflector increases more rapidly in the first 25 hours of the transient compared to the RPV as heat takes longer to travel from the pebble bed to the RPV.

Figure 11: Mean solid structure temperatures during the PLOFC transient.

The temperature increase of the water in the RCCS across the riser is shown in Figure 12. The temperature profile largely follows the temperature profiles of the solid structures shown in Figure 11. As more heat is transferred to the RCCS, the temperature increase rises accordingly until a peak increase of roughly 8 K is reached. The RCCS mass flow rate is shown in Figure 13. As the mass flow rate is driven by the thermal driving head, the profile of the mass flow rate closely follows that of the temperature increase. At its peak, the RCCS has a flow rate of roughly 30 kg/s. The heat removal rate and the decay heat of the reactor are plotted in Figure 14. The heat removal rate exceeds the decay heat at about 75 hours in to the transient, after which the temperatures of the reactor start to come down.

Figure 12: RCCS temperature increase during the PLOFC transient.

Figure 13: RCCS mass flow rate during the PLOFC transient.

Figure 14: RCCS heat removal rate and decay heat during the PLOFC transient.

Acknowledgements

This report was prepared as an account of work sponsored by an agency of the U.S. Government. Neither the U.S. Government nor any agency thereof, nor any of their employees, makes any warranty, expressed or implied, or assumes any legal liability or responsibility for any third party’s use, or the results of such use, of any information, apparatus, product, or process disclosed in this report, or represents that its use by such third party would not infringe privately owned rights. The views expressed in this paper are not necessarily those of the U.S. Nuclear Regulatory Commission. This work is supported by the U.S. Nuclear Regulatory Commission, under Task Order Agreement No. 31310021F0005. The authors would like to acknowledge the support and assistance from Dr. Mustafa Jaradat, Dr. Sebastian Schunert, and Dr. Javier Ortensi of Idaho National Laboratory in the completion of this work.