Step 7

In Step 7, we add the bypass flow through the control rod. The flow splits at the upper plenum into the portion that flows through the bed and a small bypass flow portion (a few percent) that flows through the control rod. This increases pebble bed temperatures slightly, but ensures that the control rod is cooled during reactor operations.

Modifying the Geometry

A portion of the side reflector between the riser and pebble bed is replaced by the control_rods block (block 8). The modification that needs to be made in the cartesian_mesh object is simple. Some of the numbers that represents the side reflector are replaced by block number 8. We assume that the control rods are not inserted in this model so the porous medium contains only flow volume and graphite. The geometry is depicted in Figure 1.

Note, the control_rods block defines both flow variables and T_solid and the corresponding block definitions must be updated.

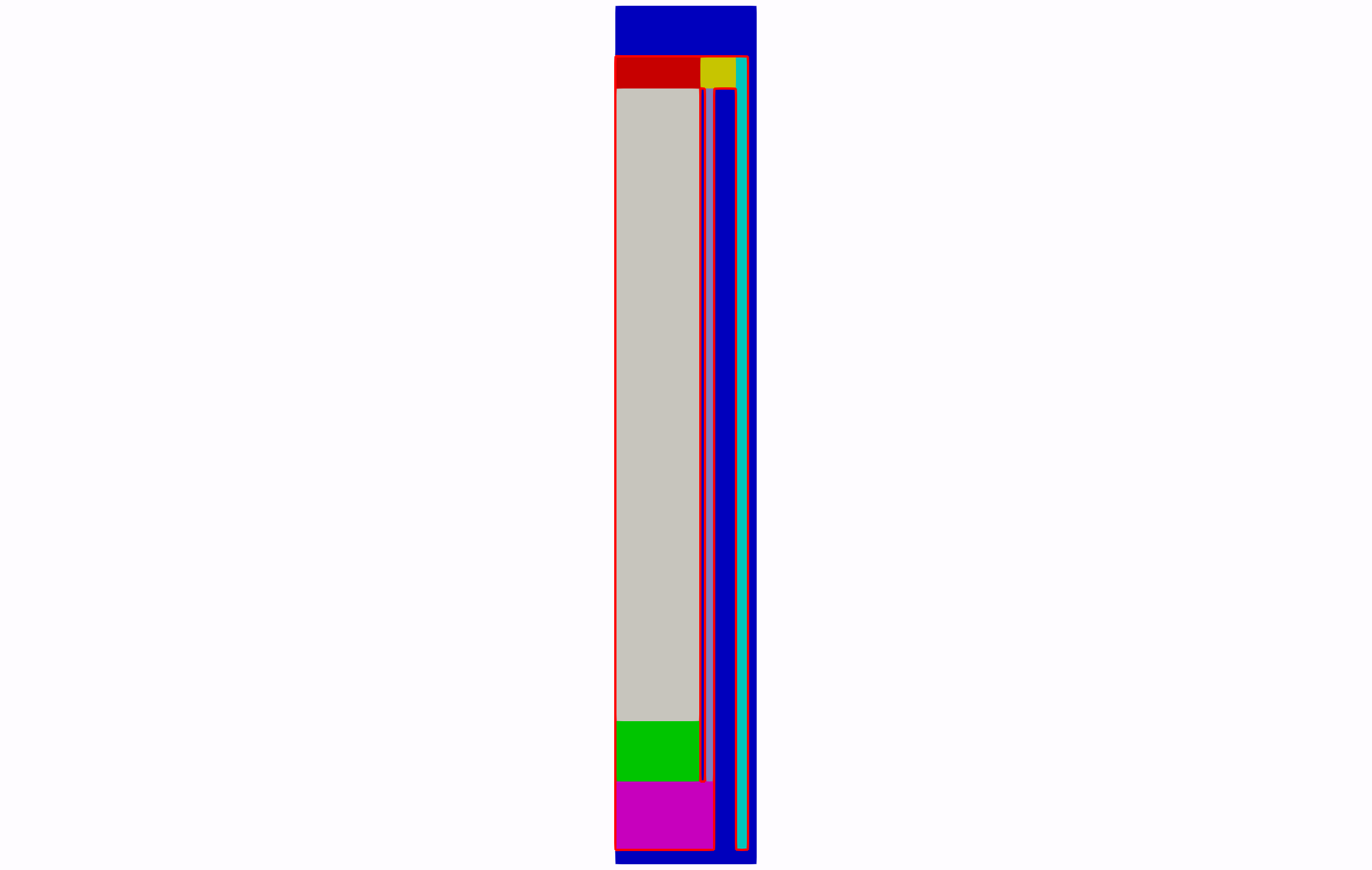
Figure 1: Geometry for Step 7 with the fluid domain framed in red.

Updated Parameters

The thermal_mass_scaling is reduced to obtain faster convergence to steady-state during the pseudo-transient. The hydraulic diameter of the control rods is set to control_rod_Dh = 0.1 because we assume that the control is an empty channel with a diameter of m.

outlet_pressure = 5.84e+6
T_inlet = 533.25
inlet_density = 5.3305
pebble_diameter = 0.06
thermal_mass_scaling = 0.01

mass_flow_rate = 64.3
riser_inner_radius = 1.701
riser_outer_radius = 1.871
flow_area = '${fparse pi * (riser_outer_radius * riser_outer_radius - riser_inner_radius * riser_inner_radius)}'
flow_vel = '${fparse mass_flow_rate / flow_area / inlet_density}'

# scales the heat source to integrate to 200 MW
power_fn_scaling = 0.9792628

# drag coefficient in open flow spaces, set to allow convergence
c_drag_old = 10

# moves the heat source around axially to have the peak in the right spot
offset = -1.45819

# the y-coordinate of the top of the core
top_core = 10.9515

# hydraulic diameters (excluding bed where it's pebble diameter)
bottom_reflector_Dh = 0.1
riser_Dh = 0.17
control_rod_Dh = 0.1

Materials

The control rod block has a porosity of . The porosity is computed as the ratio of control rod channel area (number of control rods times area of a circle of diameter m) and the area of the porous flow region perpendicular to the vertical axis that represent the control rod in this model. The porosity is added here:

[FunctorMaterials]
  [porosity_material]
    type = ADPiecewiseByBlockFunctorMaterial
    prop_name = porosity
    subdomain_to_prop_value = 'pebble_bed       0.39
                               cavity           1
                               bottom_reflector 0.3
                               side_reflector   0
                               riser            0.32
                               upper_plenum     0.2
                               bottom_plenum    0.2
                               control_rods     0.32'
  []
[]

and the hydraulic diameter is added here:

[FunctorMaterials]
  [characteristic_length]
    type = PiecewiseByBlockFunctorMaterial
    prop_name = characteristic_length
    subdomain_to_prop_value = 'pebble_bed       ${pebble_diameter}
                               bottom_reflector ${bottom_reflector_Dh}
                               riser            ${riser_Dh}
                               control_rods     ${control_rod_Dh}'
  []
[]

The solid properties (rho_s, cp_s, kappa_s) are set just like for the other non-pebble-bed regions using a ADGenericFunctorMaterial:

[FunctorMaterials]
  [graphite_rho_and_cp_riser_control_rods]
    type = ADGenericFunctorMaterial
    prop_names = 'rho_s  cp_s kappa_s'
    prop_values = '1780.0 1697 ${fparse 0.68 * 26}'
    block = 'riser control_rods'
  []
[]

The drag coefficient in the control_rods is used to adjust the bypass flow to between and % of the nominal mass flow rate. The Darcy coefficient is set to and the Forchheimer coefficient is set by a LinearFrictionFactorFunctorMaterial object.

  [Darcy_control_rods]
    type = ADGenericVectorFunctorMaterial
    prop_names = 'Darcy_coefficient'
    prop_values = '0 0 0'
    block = 'control_rods'
  []

  [quad_drag_new_convention]
    type = ADParsedFunctorMaterial
    # This performs the conversion from the old convention of specifying W for a (W rho u) friction term
    # to the current one of specifying the coefficient for friction computed as: Forchheimer_coef * rho * v / 2
    expression = '1000 * 2 / porosity / speed'
    property_name = new_g
    functor_symbols = 'porosity speed'
    functor_names = 'porosity speed'
  []
  [Forchheimer_control_rods]
    type = LinearFrictionFactorFunctorMaterial
    porosity = porosity
    functor_name = Forchheimer_coefficient
    superficial_vel_x = superficial_vel_x
    superficial_vel_y = superficial_vel_y
    f = 0
    g = new_g
    B = '1 1 1'
    block = 'control_rods'
  []

In Forchheimer_control_rods, g=1000 is the Forchheimer coefficient and B can be used to make the Forchheimer coefficient anisotropic. In this case, we just make it isotropic. f must be provided but it corresponds to a linear contribution to the pressure drop which we choose to not use in this example.

Postprocessors

The mass flow rate through the bypass flow channel is measured using this postprocessor:

[Postprocessors]
  [cr_mfr]
    type = VolumetricFlowRate
    advected_quantity = rho
    vel_x = 'superficial_vel_x'
    vel_y = 'superficial_vel_y'
    boundary = 'control_rod_outlet'
    rhie_chow_user_object = pins_rhie_chow_interpolator
    outputs = none
  []
[]

Note, the postprocessor is not outputted anywhere because of the outputs = none line. The fraction of mass flow going through the control rod channel is computed by cr_mfr_fraction:

[Postprocessors]
  [cr_mfr_fraction]
    type = ParsedPostprocessor
    pp_names = 'cr_mfr inlet_mfr'
    expression = 'abs(cr_mfr / inlet_mfr * 100)'
  []
[]

Executioner

MOOSE allows the user to run a pseudo-transient until it achieves steady-state. This is accomplished by adding:

  steady_state_detection = true
  steady_state_tolerance = 1e-10
  steady_state_start_time = 1000

to the Executioner block. This switches on steady-state detection starting at t=1000s and stops the simulation once the steady-state relative differential norm has dropped below .

Execution

./pronghorn-opt -i step7.i