Step 4

In this step, a heat source representing fission is added in the pebble-bed region. Neutrons cause fission in the fuel kernels dispersed in the pebbles. The pebbles conduct the heat to the outside of the pebble where it is transferred to the helium coolant via convection. Note that in this step, many parameters (such as mass flow rate and inlet temperature) and material property values (such as heat transfer coefficients) are not set to realistic values and therefore the obtained results are quite different from prototypical gas cooled reactors.

Added Inputs

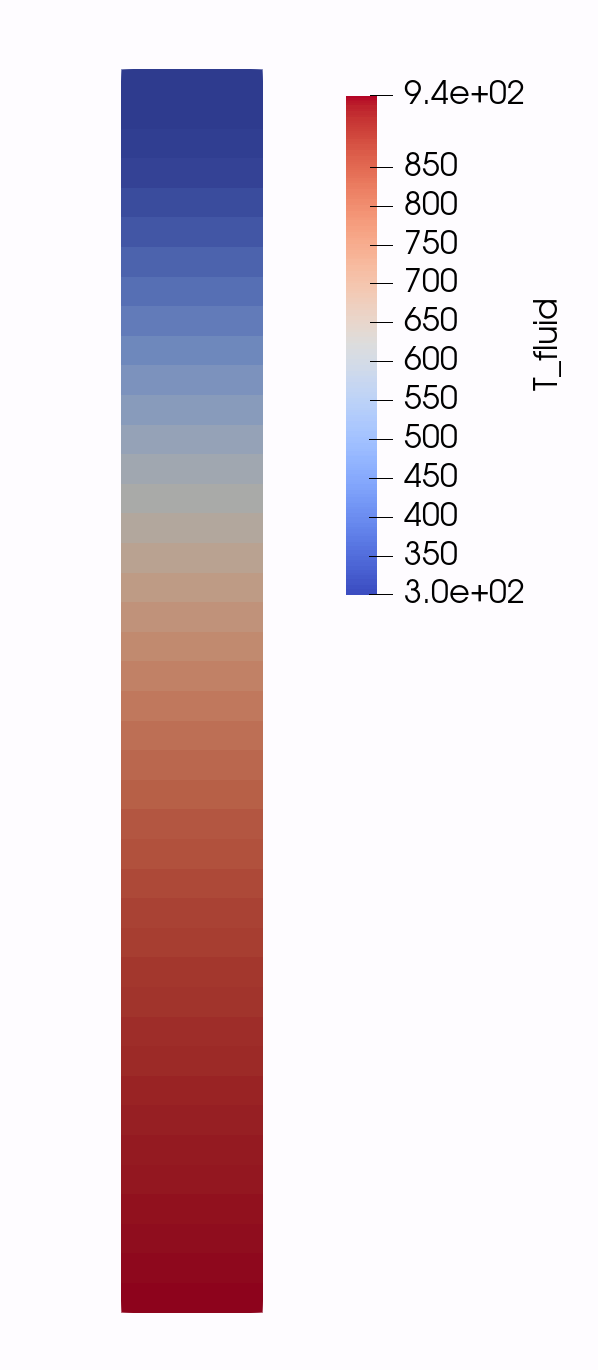
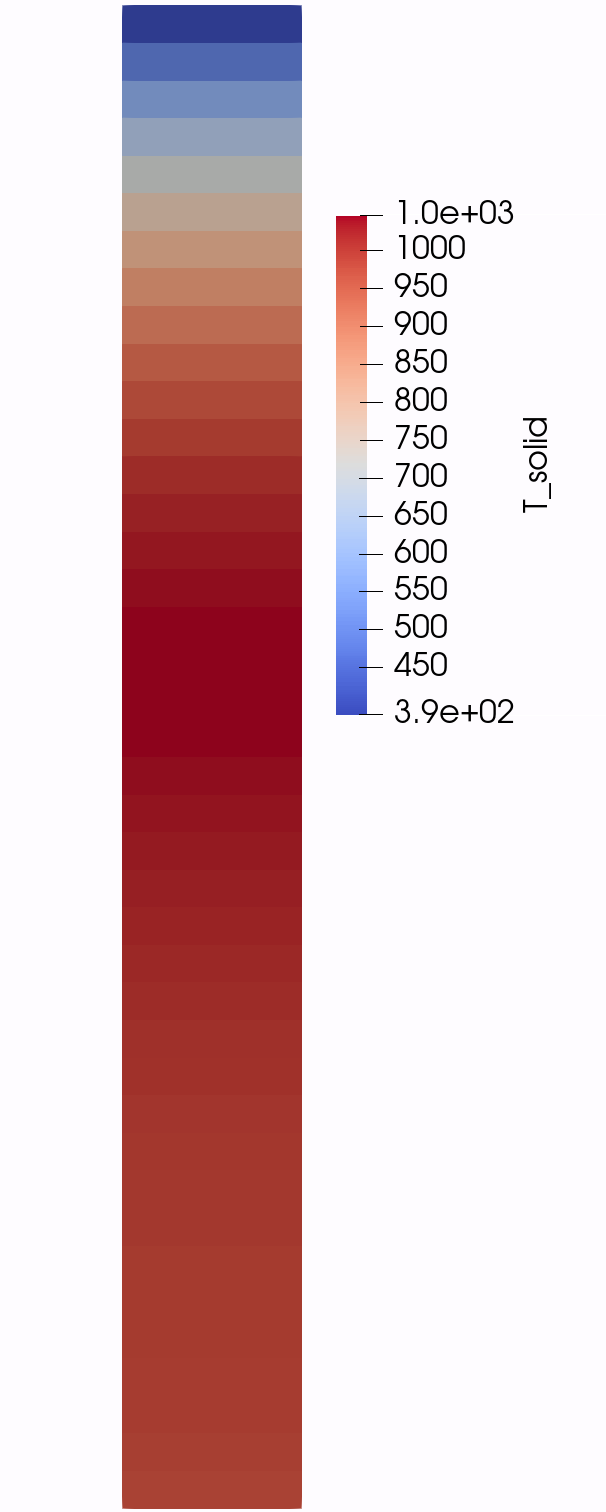
In this step, a heat equation for the solid temperature is added. This is done by first adding solid temperature variable that is block-restricted to the pebble-bed:

[Variables]
  [T_solid]
    type = INSFVEnergyVariable
    initial_condition = ${T_inlet}
    block = 'pebble_bed'
  []
[]

The initial temperature is set to the inlet temperature ${T_inlet} which is K. The solid heat conduction equation contains four terms: time derivative, heat conduction, source, and convective cooling by the helium. These terms are added using the FVKernels block:

[FVKernels]
  [energy_storage]
    type = PINSFVEnergyTimeDerivative
    variable = T_solid
    rho = rho_s
    cp = cp_s
    is_solid = true
    scaling = ${thermal_mass_scaling}
    porosity = porosity
  []

  [solid_energy_diffusion]
    type = FVAnisotropicDiffusion
    variable = T_solid
    coeff = 'effective_thermal_conductivity'
  []

  [source]
    type = FVBodyForce
    variable = T_solid
    function = heat_source_fn
    block = 'pebble_bed'
  []

  [convection_pebble_bed_fluid]
    type = PINSFVEnergyAmbientConvection
    variable = T_solid
    T_fluid = T_fluid
    T_solid = T_solid
    is_solid = true
    h_solid_fluid = 'alpha'
  []
[]

energy_storage is the time derivative term that uses two material properties, namely the solid density rho and the solid specific heat cp. solid_energy_diffusion represents heat conduction and uses the thermal conductivity property provided to the coeff parameter. source provides the heat source and is discussed later. convection_pebble_bed_fluid models convective heat transfer between the solid pebbles and the helium coolant. It uses the volumetric heat transfer coefficient h_solid_fluid as property.

In solid_energy_diffusion the coeff parameter should be provided with an effective thermal conductivity that takes into account porosity and heat transfer mechanisms other than conduction. This will be accomplished in Step 5.

For energy_storage, the values of density, specific heat, and porosity do not matter for the steady-state solution of this problem because the time derivative term vanishes at steady-state. These properties affect the progression of the pseudo transient and can in principle be chosen to get to the steady-state result in fewer time steps. However, for true transient problems the values of porosity, density, and specific heat matter and need to represent physical reality. Their dual use in pseudo-transient and transient scenarios may lead to user error because transient inputs are often created by modifying steady-state/pseudo-transient inputs. Therefore, the PINSFVEnergyTimeDerivative provides the scaling parameter to adjust the thermal capacity to accelerate the pseudo-transient.

The shape of the heat source is represented as a ParsedFunction in the input file.

[Functions]
  [heat_source_fn]
    type = ParsedFunction
    expression = '${power_fn_scaling} * (-1.0612e4 * pow(y+${offset}, 4) + 1.5963e5 * pow(y+${offset}, 3)
                   -6.2993e5 * pow(y+${offset}, 2) + 1.4199e6 * (y+${offset}) + 5.5402e4)'
  []
[]

The expression declares the heat source as a function of the y-coordinate that is aligned with the up/down direction in this model. Note, that we omitted the dependence of the heat source on the radial dimension. The prefactor of power_fn_scaling= rescales the function to yield a power of 200 MW.

heat_source_fn is used in two places in the Step 4 input file. First, it is used as a source term in the solid conduction equation which has been shown above and second a postprocessor is used to integrate the heat source over the pebble-bed block.

[Postprocessors]
  [heat_source_integral]
    type = ElementIntegralFunctorPostprocessor
    functor = heat_source_fn
    block = 'pebble_bed'
  []
[]

The heat source is block restricted to just the pebble bed block due to heat being generate only in that block. The postprocessor named heat_source_integral should return .

Properties used by the kernels are provided in the Materials block as functors. In addition to the functors defined in Step 3, we add the effective bed conductivity, the solid/fluid volumetric heat transfer coefficient, and the density and specific heat in the bed. Step 5 will go into a lot more detail about setting up realistic material properties.

We add postprocessors to compute the inlet enthalpy, outlet enthalpy, and enthalpy difference as well as the total heat source.

  [enthalpy_inlet]
    type = VolumetricFlowRate
    boundary = top
    vel_x = superficial_vel_x
    vel_y = superficial_vel_y
    rhie_chow_user_object = 'pins_rhie_chow_interpolator'
    advected_quantity = 'rho_cp_temp'
    advected_interp_method = 'upwind'
    outputs = none
  []

  [enthalpy_outlet]
    type = VolumetricFlowRate
    boundary = bottom
    vel_x = superficial_vel_x
    vel_y = superficial_vel_y
    rhie_chow_user_object = 'pins_rhie_chow_interpolator'
    advected_quantity = 'rho_cp_temp'
    advected_interp_method = 'upwind'
    outputs = none
  []

  [enthalpy_balance]
    type = ParsedPostprocessor
    pp_names = 'enthalpy_inlet enthalpy_outlet'
    expression = 'enthalpy_inlet + enthalpy_outlet'
  []

  [heat_source_integral]
    type = ElementIntegralFunctorPostprocessor
    functor = heat_source_fn
    block = 'pebble_bed'
  []
[]

Note that the outputs = none suppresses postprocessors from being printed, but they are nonetheless computed by the system and can be used in other objects.

Execution

./pronghorn-opt -i step4.i

Results

From the screen output we find that at steady-state, the enthalpy_balance matches the heat_source_integral indicating that Pronghorn conserves energy.

The geometry/mesh, fluid temperature, solid temperature, and superficial velocity mangitude are shown in Figure 1 to Figure 4. A few remarks are in order:

• Fluid temperature increases monotonically from top to bottom. The temperature increases by about K which is K more than a typical pebble-bed high-temperature gas-cooled reactor.

• The difference between solid and fluid temperature is much larger than in reality because the heat transfer coefficient is much smaller than in reality.

• The solid temperature peaks roughly at core mid-height because of the peak in power density and the large difference between fluid and solid temperature.

• Velocity increases towards the outlet because the fluid density decreases.

Figure 1: Block and mesh definition for Step 4.

Figure 2: Tempurature of the fluid for Step 4.

Figure 3: Tempurature of the solid for Step 4. Note that the cavity is not shown in this figure.

Figure 4: Velocity of the system for Step 4.