General Case Description

This verification case is an extension ofver-1ja, which tests radioactive decay capabilities of TMAP8 on their own. In ver-1jb, tritium decay is coupled with trapping, which itself was verified in several TMAP8 verification cases including ver-1d. Similarly to ver-1ja, the model assumes pre-charging of an m long slab (with an assumed width and thickness of 1 m) with tritium. Further complexity is added to the problem by introducing mobile tritium and trapping sites whose locations follow a normal distribution centered at the mid-plane of the slab with a standard deviation of . The peak atomic fraction of traps is , and the trap energy is eV. The material density used to calculate the number of traps is based on tungsten, and is defined as 6.34 atoms/m. The traps are initially filled with trapped tritium to 50% of trap concentration.

The evolution of the mobile tritium, trapped tritium, and helium concentrations, i.e., , , and , respectively, is governed by

(1) (2) and where is the time in s, concentrations are in atoms/m, is the tritium diffusivity in m/s, is a factor converting the magnitude of to be closer to for better numerical convergence, is the decay rate constant in 1/s, years is the half life of tritium decay to He, is the concentration of empty trapping sites, is the host density, and are the trapping and release rate coefficients, and is the fraction of host sites that can contribute to trapping.

The tritium diffusivity is defined as where is the ideal gas constant in J/K/mol from Physical Constants and K is the temperature of the domain. The trapping frequency is defined as and the release frequency is equal to where is the Boltzmann constant in eV/K from Physical Constants.

We define two different initial conditions for the mobile tritium concentration :

• atoms/m, which is much lower than the initial trapped tritium concentration. This case corresponds to the TMAP7 case in (Ambrosek and Longhurst, 2008).

• atoms/m, which makes it equivalent to the initial trapped tritium concentration. This new case demonstrates TMAP8's improved ability (over TMAP7) to model the decay, trapping, detrapping, and diffusion of tritium when the concentration of mobile tritium is non-negligible.

To limit the computational challenges related to the orders-of-magnitude difference in trapped and mobile tritium in the first case, we make the concentration dimensionless by dividing them by atoms/m and setting (-). In the second case, when the concentrations are equivalent, (-).

Analytical Solution

The total inventory of T in atoms, where and are the mobile and trapped tritium inventories, respectively, is given at any given time by

where atoms/m is the initial total inventory of tritium ( and are the initial mobile and trapped tritium inventories, respectively). Applying a mass balance over the system, the inventory of helium in atoms, , is given by

Results

With a small concentration of mobile tritium compared to trapped tritium

Figure 1 shows the TMAP8 predictions and how they compare to the analytical solution for the decay of tritium and associated growth of He in a distributed trap. TMAP8 matches the analytical solution, with a root mean square percentage error (RMSPE) of 0.82% and 0.20% for the and concentration curves, respectively, and can also provide the trapped and mobile tritium concentrations.

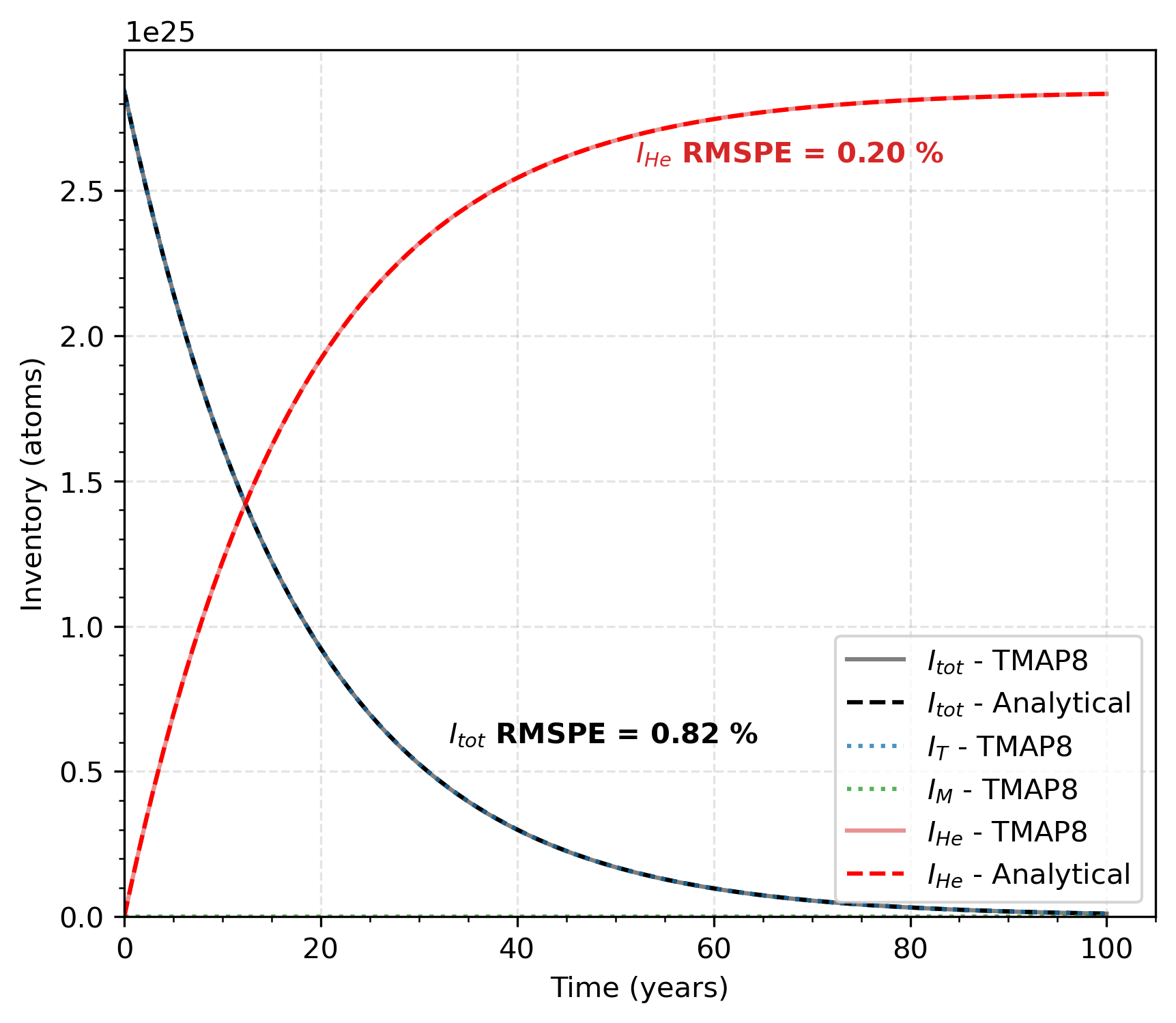
Figure 1: Comparison of TMAP8 predictions against the analytical solution for the decay of tritium and associated growth of He in a distributed trap with a small concentration of mobile tritium compared to trapped tritium.

Figure 2 shows the depth profile of the initial trapped atoms of tritium, the concentration of trapped atoms of tritium after 45 years, and the distribution of He at the end of that time period across the distributed trapping sites as predicted by TMAP8. The concentration of mobile tritium remains very low.

Note that because He is given a null diffusivity in this verification problem, the shape of the He concentration does not broaden. This could be easily implemented with existing TMAP8 diffusive capabilities, as was shown in many other TMAP8 cases, including ver-1d.

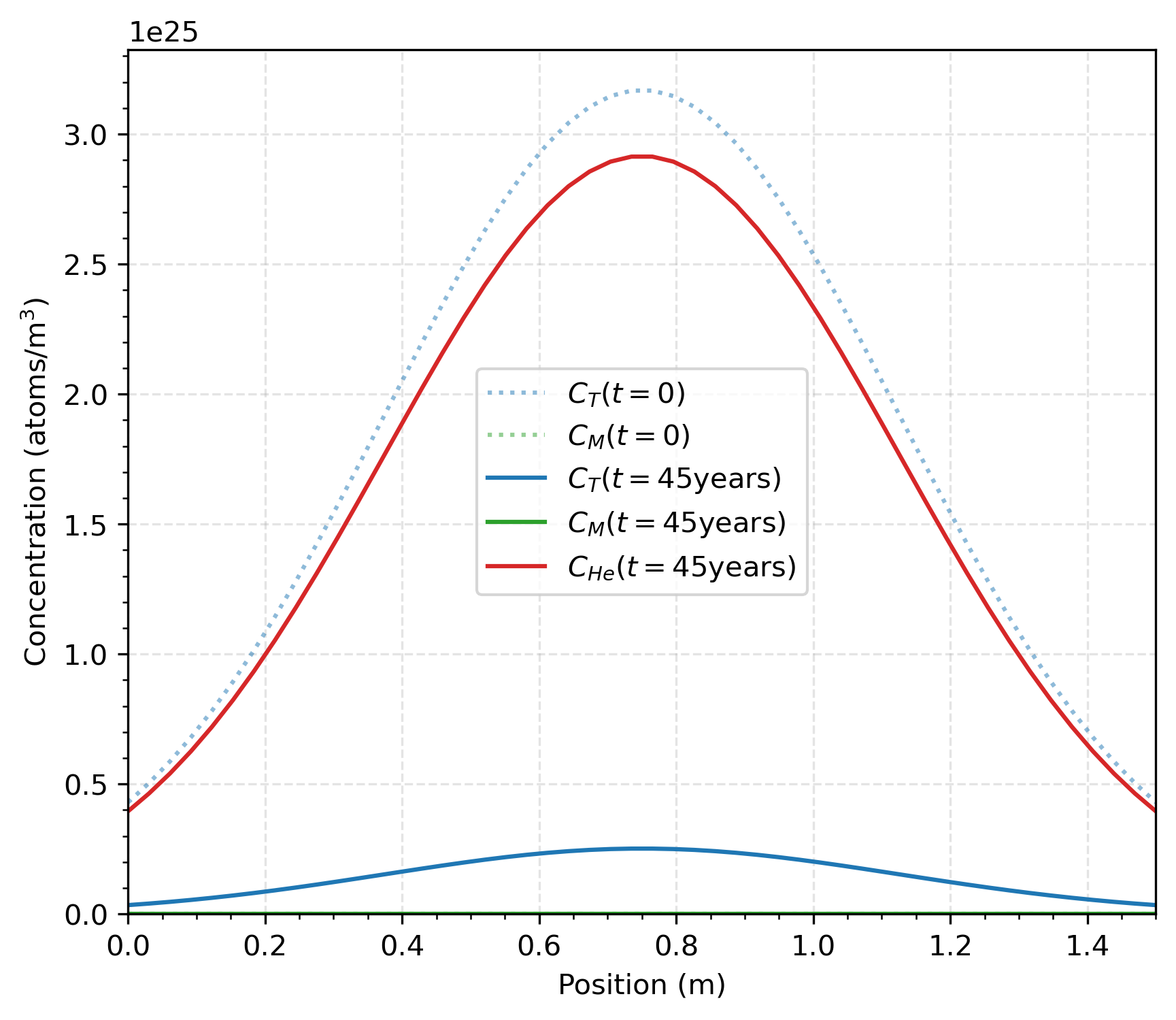
Figure 2: Concentration profiles of initially trapped tritium that decayed to He over 45 years with a small concentration of mobile tritium compared to trapped tritium.

With equivalent mobile and trapped tritium initial concentrations

Figure 3 and Figure 4 show the results of the simulations when the initial concentrations of mobile and trapped tritium are equivalent. Figure 3 shows TMAP8's time predictions of the inventories and how they compare to the analytical solution. The RMSPE values are as low as in the previous case.

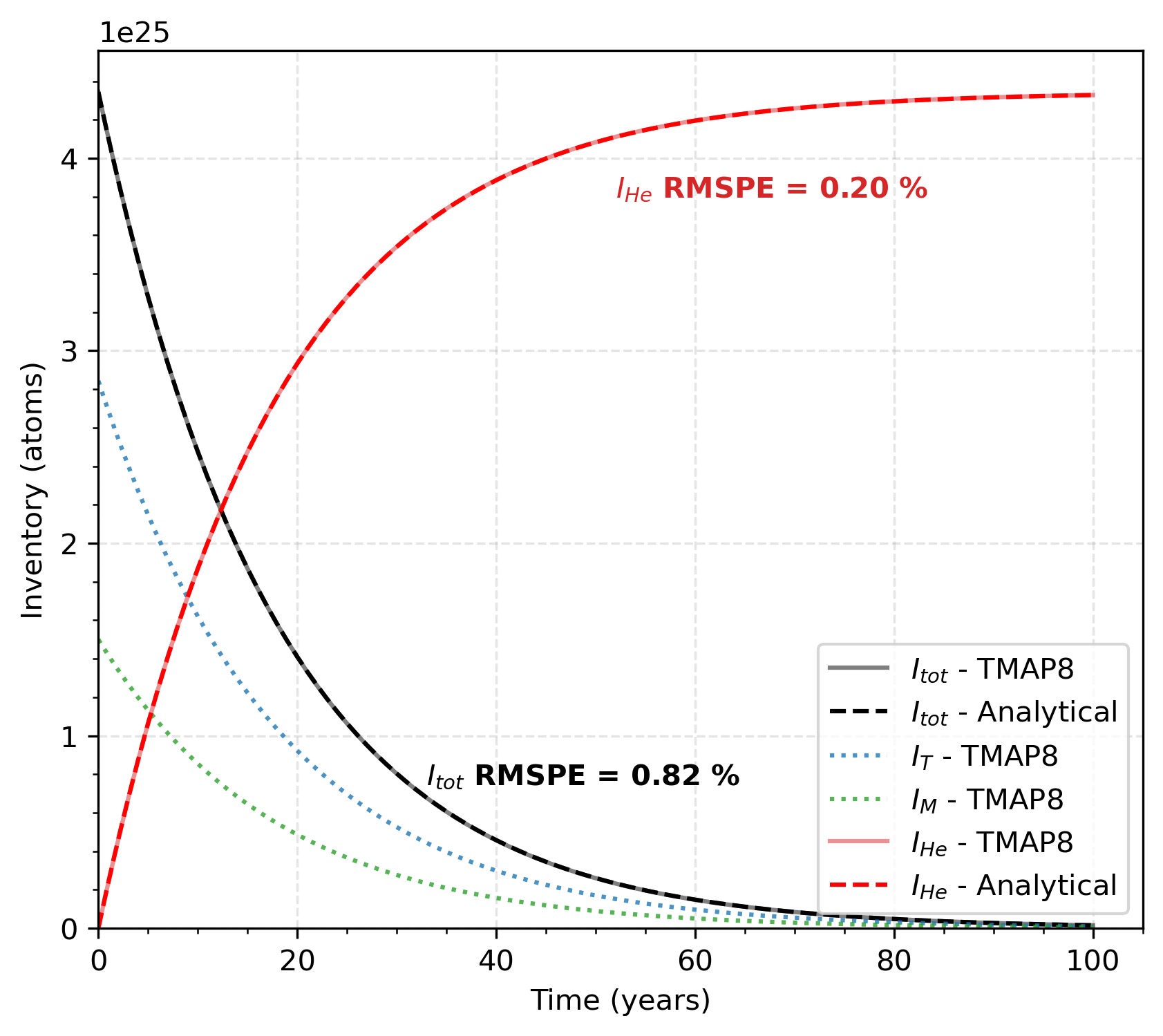
Figure 3: Comparison of TMAP8 predictions against the analytical solution for the decay of tritium and associated growth of He in a distributed trap with equivalent initial concentrations of mobile and trapped tritium.

Figure 4 shows the depth profile of the initial trapped atoms of tritium, the concentration of mobile and trapped atoms of tritium after 45 years, and the distribution of He at the end of that time period across the distributed trapping sites as predicted by TMAP8.

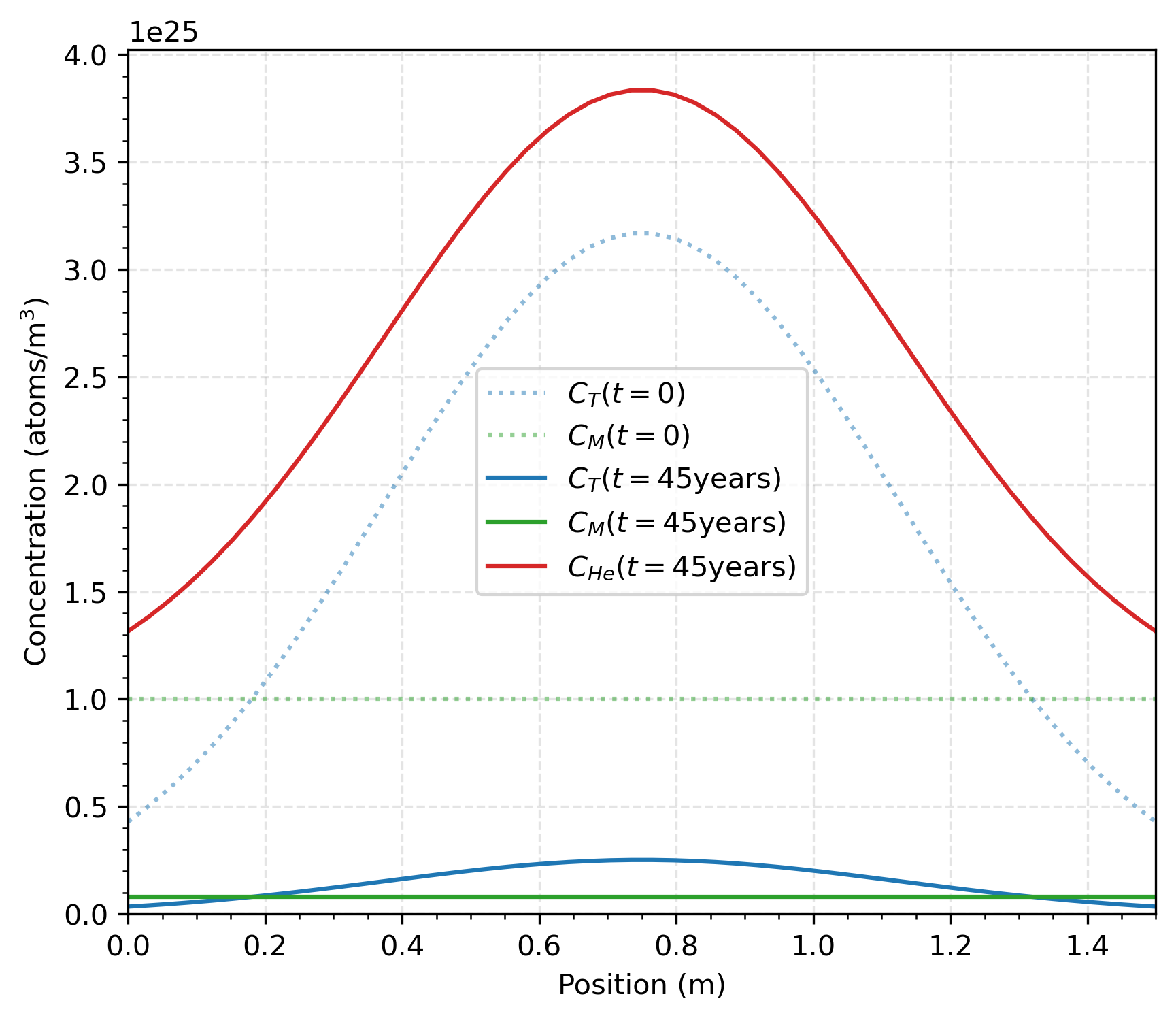
Figure 4: Concentration profiles of initially trapped tritium that decayed to He over 45 years with equivalent initial concentrations of mobile and trapped tritium.

References