Sinks test descriptions
Introduction
As described in the page on boundary conditions, a number of different sink boundary conditions have been implemented in PorousFlow. This page describes some of the tests of the various forms of sink/source boundary conditions.
To make these into sources instead of sinks, the strength of the flux just needs to be made negative. All the sinks are implemented using full upwinding. This is to prevent the sink from attempting to remove fluid from a node that actually contains no fluid.
The basic sink uses a Function to specify the flux on the boundary, and also has the option of multiplying by any combination of: the fluid mobility, the relative permeability, or a mass fraction. These latter multiplying factors are all useful in the case of sinks to prevent an unlimited amount of fluid being withdrawn from the porous medium, which can lead to extremely poor nonlinear convergence even if only one node in the entire mesh is "running dry".
Derived from the basic one, is another boundary condition that allows the flux to be modified by a piecewise-linear function of porepressure, which is useful for the case where transfer coefficients are defined across the boundary, or more complicated situations.
Also derived from the basic one are two others, in which the flux is governed by a half Gaussian or half cubic function of porepressure, which are useful for modelling evapotranspiration through a boundary.
Basic PorousFlow Sink
Test 1
A sink flux of strength 6kg.m.s is applied to the left edge () of a 3D mesh. A single-phase, single-component fluid is used, and the porepressure is initialised to (for ). No fluid flow within the element is used, so the masses of fluid at the finite-element nodes behave independently. The fluid is assumed to have density kg.m. The porosity is 0.1.
The input file:
# apply a sink flux and observe the correct behavior
[Mesh]
type = GeneratedMesh
dim = 3
nx = 1
ny = 1
nz = 1
xmin = 0
xmax = 1
ymin = 0
ymax = 1
zmin = 0
zmax = 2
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pp'
number_fluid_phases = 1
number_fluid_components = 1
[../]
[./pc]
type = PorousFlowCapillaryPressureVG
m = 0.5
alpha = 1
[../]
[]
[Variables]
[./pp]
[../]
[]
[ICs]
[./pp]
type = FunctionIC
variable = pp
function = y+1
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pp
[../]
[]
[Modules]
[./FluidProperties]
[./simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 1.3
density0 = 1.1
thermal_expansion = 0
viscosity = 1.1
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./ppss]
type = PorousFlow1PhaseP
porepressure = pp
capillary_pressure = pc
[../]
[./massfrac]
type = PorousFlowMassFraction
[../]
[./simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.1
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-5 0 0 0 1E-5 0 0 0 1E-5'
[../]
[./relperm]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
[../]
[]
[AuxVariables]
[./flux_out]
[../]
[./xval]
[../]
[./yval]
[../]
[]
[ICs]
[./xval]
type = FunctionIC
variable = xval
function = x
[../]
[./yval]
type = FunctionIC
variable = yval
function = y
[../]
[]
[Functions]
[./mass00]
type = ParsedFunction
value = 'vol*por*dens0*exp(pp/bulk)'
vars = 'vol por dens0 pp bulk'
vals = '0.25 0.1 1.1 p00 1.3'
[../]
[./mass01]
type = ParsedFunction
value = 'vol*por*dens0*exp(pp/bulk)'
vars = 'vol por dens0 pp bulk'
vals = '0.25 0.1 1.1 p01 1.3'
[../]
[./expected_mass_change00]
type = ParsedFunction
value = 'fcn*perm*dens0*exp(pp/bulk)/visc*area*dt'
vars = 'fcn perm dens0 pp bulk visc area dt'
vals = '6 1 1 0 1.3 1 0.5 1E-3'
[../]
[]
[Postprocessors]
[./p00]
type = PointValue
point = '0 0 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m00]
type = FunctionValuePostprocessor
function = mass00
execute_on = 'initial timestep_end'
[../]
[./del_m00]
type = FunctionValuePostprocessor
function = expected_mass_change00
execute_on = 'timestep_end'
[../]
[./p10]
type = PointValue
point = '1 0 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./p01]
type = PointValue
point = '0 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m01]
type = FunctionValuePostprocessor
function = mass01
execute_on = 'initial timestep_end'
[../]
[./p11]
type = PointValue
point = '1 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[]
[BCs]
[./flux]
type = PorousFlowSink
boundary = 'left'
variable = pp
use_mobility = false
use_relperm = true
fluid_phase = 0
flux_function = 6
save_in = flux_out
[../]
[]
[Preconditioning]
[./andy]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = 'gmres asm lu 10000 NONZERO 2'
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
dt = 1E-3
end_time = 1E-2
nl_rel_tol = 1E-12
nl_abs_tol = 1E-12
[]
[Outputs]
file_base = s01
[./console]
type = Console
execute_on = 'nonlinear linear'
[../]
[./csv]
type = CSV
execute_on = 'initial timestep_end'
[../]
[]
Under these conditions, assuming so that the porous medium is fully saturated with fluid, the fluid mass at a node should obey where is the volume occupied by the node, and is its area exposed to the flux. MOOSE correctly produces this result, as illustrated in Figure 1.
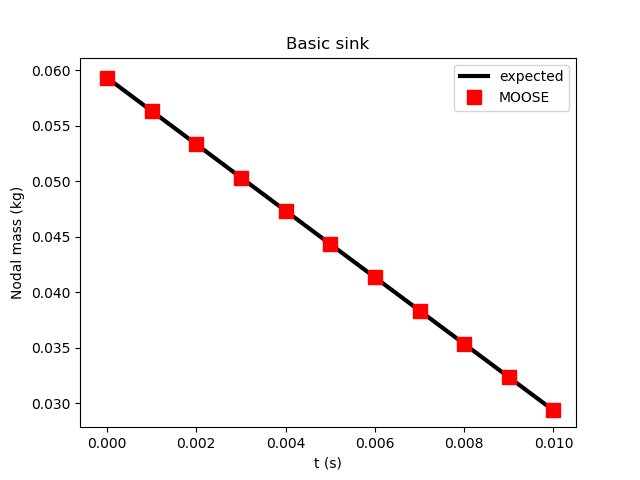
Figure 1: Results of Test 1, illustrating that MOOSE correctly applies a constant sink flux to boundary nodes.
Test 2
An identical setup to Test 1 is used here, but with the sink flux strength being multiplied by the mobility: where is the permeability tensor projected onto the normal direction to the boundary , and the fluid density and viscosity are and , respectively. In this example Pa.s and m. The other parameters are the same as Test 1, except now the strength of the flux is 6Pa.s.
The input file:
# apply a sink flux with use_mobility=true and observe the correct behavior
[Mesh]
type = GeneratedMesh
dim = 3
nx = 1
ny = 1
nz = 1
xmin = 0
xmax = 1
ymin = 0
ymax = 1
zmin = 0
zmax = 2
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pp'
number_fluid_phases = 1
number_fluid_components = 1
[../]
[./pc]
type = PorousFlowCapillaryPressureVG
m = 0.5
alpha = 1
[../]
[]
[Variables]
[./pp]
[../]
[]
[ICs]
[./pp]
type = FunctionIC
variable = pp
function = y+1
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pp
[../]
[]
[Modules]
[./FluidProperties]
[./simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 1.3
density0 = 1.1
thermal_expansion = 0
viscosity = 1.1
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./ppss]
type = PorousFlow1PhaseP
porepressure = pp
capillary_pressure = pc
[../]
[./massfrac]
type = PorousFlowMassFraction
[../]
[./simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.1
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '0.2 0 0 0 0.1 0 0 0 0.1'
[../]
[./relperm]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
[../]
[]
[AuxVariables]
[./flux_out]
[../]
[./xval]
[../]
[./yval]
[../]
[]
[ICs]
[./xval]
type = FunctionIC
variable = xval
function = x
[../]
[./yval]
type = FunctionIC
variable = yval
function = y
[../]
[]
[Functions]
[./mass00]
type = ParsedFunction
value = 'vol*por*dens0*exp(pp/bulk)'
vars = 'vol por dens0 pp bulk'
vals = '0.25 0.1 1.1 p00 1.3'
[../]
[./mass01]
type = ParsedFunction
value = 'vol*por*dens0*exp(pp/bulk)'
vars = 'vol por dens0 pp bulk'
vals = '0.25 0.1 1.1 p01 1.3'
[../]
[./expected_mass_change00]
type = ParsedFunction
value = 'fcn*perm*dens0*exp(pp/bulk)/visc*area*dt'
vars = 'fcn perm dens0 pp bulk visc area dt'
vals = '6 0.2 1.1 p00 1.3 1.1 0.5 1E-3'
[../]
[./expected_mass_change01]
type = ParsedFunction
value = 'fcn*perm*dens0*exp(pp/bulk)/visc*area*dt'
vars = 'fcn perm dens0 pp bulk visc area dt'
vals = '6 0.2 1.1 p01 1.3 1.1 0.5 1E-3'
[../]
[./mass00_expect]
type = ParsedFunction
value = 'mass_prev-mass_change'
vars = 'mass_prev mass_change'
vals = 'm00_prev del_m00'
[../]
[./mass01_expect]
type = ParsedFunction
value = 'mass_prev-mass_change'
vars = 'mass_prev mass_change'
vals = 'm01_prev del_m01'
[../]
[]
[Postprocessors]
[./p00]
type = PointValue
point = '0 0 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m00]
type = FunctionValuePostprocessor
function = mass00
execute_on = 'initial timestep_end'
[../]
[./m00_prev]
type = FunctionValuePostprocessor
function = mass00
execute_on = 'timestep_begin'
outputs = 'console'
[../]
[./del_m00]
type = FunctionValuePostprocessor
function = expected_mass_change00
execute_on = 'timestep_end'
outputs = 'console'
[../]
[./m00_expect]
type = FunctionValuePostprocessor
function = mass00_expect
execute_on = 'timestep_end'
[../]
[./p10]
type = PointValue
point = '1 0 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./p01]
type = PointValue
point = '0 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m01]
type = FunctionValuePostprocessor
function = mass01
execute_on = 'initial timestep_end'
[../]
[./m01_prev]
type = FunctionValuePostprocessor
function = mass01
execute_on = 'timestep_begin'
outputs = 'console'
[../]
[./del_m01]
type = FunctionValuePostprocessor
function = expected_mass_change01
execute_on = 'timestep_end'
outputs = 'console'
[../]
[./m01_expect]
type = FunctionValuePostprocessor
function = mass01_expect
execute_on = 'timestep_end'
[../]
[./p11]
type = PointValue
point = '1 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[]
[BCs]
[./flux]
type = PorousFlowSink
boundary = 'left'
variable = pp
use_mobility = true
use_relperm = true
fluid_phase = 0
flux_function = 6
save_in = flux_out
[../]
[]
[Preconditioning]
[./andy]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = 'gmres asm lu 10000 NONZERO 2'
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
dt = 1E-3
end_time = 0.03
nl_rel_tol = 1E-12
nl_abs_tol = 1E-12
[]
[Outputs]
file_base = s02
[./console]
type = Console
execute_on = 'nonlinear linear'
interval = 30
[../]
[./csv]
type = CSV
execute_on = 'timestep_end'
interval = 3
[../]
[]
In this case, the expected result is (for ) MOOSE correctly produces this result, as illustrated in Figure 2.
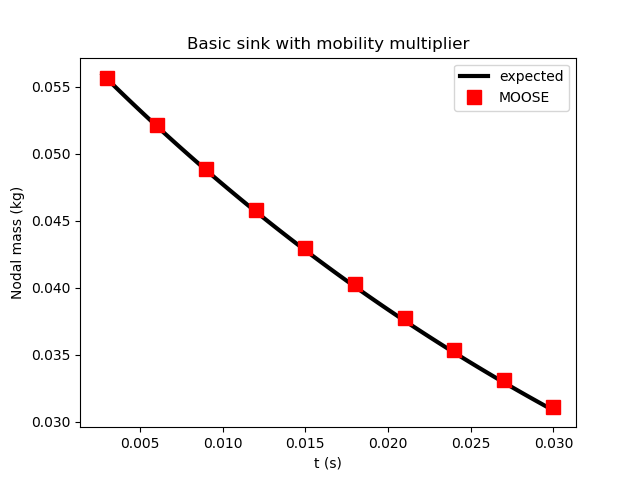
Figure 2: Results of Test 2, illustrating that MOOSE correctly applies a constant sink flux modified by the fluid mobility. (A slight drift away from the expected result is due to MOOSE taking large time steps.)
Test 3
An identical setup to Test 1 is used here, but with the sink flux strength being multiplied by the relative permeability, which is chosen to be: with being the fluid saturation. A van-Genuchten capillary relationship is used: with Pa, and . The porepressure is initialised to be . The other parameters are identical to Test 1.
The input file:
# apply a sink flux with use_mobility=true and observe the correct behavior
[Mesh]
type = GeneratedMesh
dim = 3
nx = 1
ny = 1
nz = 1
xmin = 0
xmax = 1
ymin = 0
ymax = 1
zmin = 0
zmax = 2
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pp'
number_fluid_phases = 1
number_fluid_components = 1
[../]
[./pc]
type = PorousFlowCapillaryPressureVG
m = 0.5
alpha = 1
[../]
[]
[Variables]
[./pp]
[../]
[]
[ICs]
[./pp]
type = FunctionIC
variable = pp
function = y+1
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pp
[../]
[]
[Modules]
[./FluidProperties]
[./simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 1.3
density0 = 1.1
thermal_expansion = 0
viscosity = 1.1
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./ppss]
type = PorousFlow1PhaseP
porepressure = pp
capillary_pressure = pc
[../]
[./massfrac]
type = PorousFlowMassFraction
[../]
[./simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.1
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '0.2 0 0 0 0.1 0 0 0 0.1'
[../]
[./relperm]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
[../]
[]
[AuxVariables]
[./flux_out]
[../]
[./xval]
[../]
[./yval]
[../]
[]
[ICs]
[./xval]
type = FunctionIC
variable = xval
function = x
[../]
[./yval]
type = FunctionIC
variable = yval
function = y
[../]
[]
[Functions]
[./mass00]
type = ParsedFunction
value = 'vol*por*dens0*exp(pp/bulk)'
vars = 'vol por dens0 pp bulk'
vals = '0.25 0.1 1.1 p00 1.3'
[../]
[./mass01]
type = ParsedFunction
value = 'vol*por*dens0*exp(pp/bulk)'
vars = 'vol por dens0 pp bulk'
vals = '0.25 0.1 1.1 p01 1.3'
[../]
[./expected_mass_change00]
type = ParsedFunction
value = 'fcn*perm*dens0*exp(pp/bulk)/visc*area*dt'
vars = 'fcn perm dens0 pp bulk visc area dt'
vals = '6 0.2 1.1 p00 1.3 1.1 0.5 1E-3'
[../]
[./expected_mass_change01]
type = ParsedFunction
value = 'fcn*perm*dens0*exp(pp/bulk)/visc*area*dt'
vars = 'fcn perm dens0 pp bulk visc area dt'
vals = '6 0.2 1.1 p01 1.3 1.1 0.5 1E-3'
[../]
[./mass00_expect]
type = ParsedFunction
value = 'mass_prev-mass_change'
vars = 'mass_prev mass_change'
vals = 'm00_prev del_m00'
[../]
[./mass01_expect]
type = ParsedFunction
value = 'mass_prev-mass_change'
vars = 'mass_prev mass_change'
vals = 'm01_prev del_m01'
[../]
[]
[Postprocessors]
[./p00]
type = PointValue
point = '0 0 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m00]
type = FunctionValuePostprocessor
function = mass00
execute_on = 'initial timestep_end'
[../]
[./m00_prev]
type = FunctionValuePostprocessor
function = mass00
execute_on = 'timestep_begin'
outputs = 'console'
[../]
[./del_m00]
type = FunctionValuePostprocessor
function = expected_mass_change00
execute_on = 'timestep_end'
outputs = 'console'
[../]
[./m00_expect]
type = FunctionValuePostprocessor
function = mass00_expect
execute_on = 'timestep_end'
[../]
[./p10]
type = PointValue
point = '1 0 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./p01]
type = PointValue
point = '0 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m01]
type = FunctionValuePostprocessor
function = mass01
execute_on = 'initial timestep_end'
[../]
[./m01_prev]
type = FunctionValuePostprocessor
function = mass01
execute_on = 'timestep_begin'
outputs = 'console'
[../]
[./del_m01]
type = FunctionValuePostprocessor
function = expected_mass_change01
execute_on = 'timestep_end'
outputs = 'console'
[../]
[./m01_expect]
type = FunctionValuePostprocessor
function = mass01_expect
execute_on = 'timestep_end'
[../]
[./p11]
type = PointValue
point = '1 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[]
[BCs]
[./flux]
type = PorousFlowSink
boundary = 'left'
variable = pp
use_mobility = true
use_relperm = true
fluid_phase = 0
flux_function = 6
save_in = flux_out
[../]
[]
[Preconditioning]
[./andy]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = 'gmres asm lu 10000 NONZERO 2'
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
dt = 1E-3
end_time = 0.03
nl_rel_tol = 1E-12
nl_abs_tol = 1E-12
[]
[Outputs]
file_base = s02
[./console]
type = Console
execute_on = 'nonlinear linear'
interval = 30
[../]
[./csv]
type = CSV
execute_on = 'timestep_end'
interval = 3
[../]
[]
In this case, the expected result is MOOSE correctly produces this result, as illustrated in Figure 3.
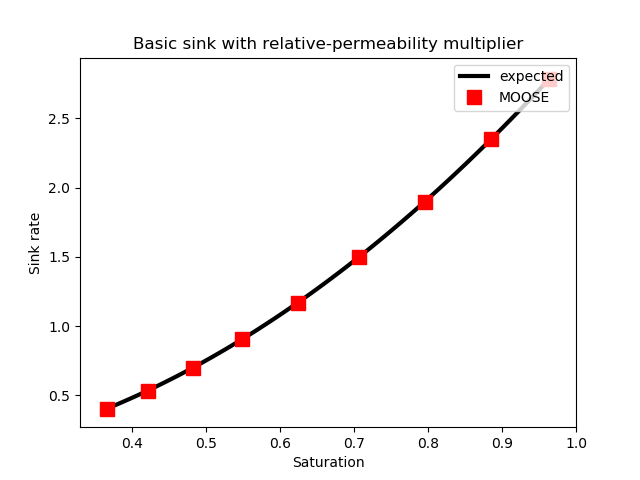
Figure 3: Results of Test 3, illustrating that MOOSE correctly applies a constant sink flux modified by the fluid relative permeability.
Test 4
A similar setup to Test 1 is used here, but with a 3-component, single-phase fluid, with the sink flux only extracting the second component, with a rate proportional to the mass fraction of that component.
The input file:
# apply a sink flux on just one component of a 3-component system and observe the correct behavior
[Mesh]
type = GeneratedMesh
dim = 3
nx = 1
ny = 1
nz = 1
xmin = 0
xmax = 1
ymin = 0
ymax = 1
zmin = 0
zmax = 2
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pp frac0 frac1'
number_fluid_phases = 1
number_fluid_components = 3
[../]
[./pc]
type = PorousFlowCapillaryPressureVG
m = 0.5
alpha = 1.1
[../]
[]
[Variables]
[./pp]
[../]
[./frac0]
initial_condition = 0.1
[../]
[./frac1]
initial_condition = 0.6
[../]
[]
[ICs]
[./pp]
type = FunctionIC
variable = pp
function = y
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = frac0
[../]
[./mass1]
type = PorousFlowMassTimeDerivative
fluid_component = 1
variable = frac1
[../]
[./mass2]
type = PorousFlowMassTimeDerivative
fluid_component = 2
variable = pp
[../]
[]
[Modules]
[./FluidProperties]
[./simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 1.3
density0 = 1.1
thermal_expansion = 0
viscosity = 1.1
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./ppss]
type = PorousFlow1PhaseP
porepressure = pp
capillary_pressure = pc
[../]
[./massfrac]
type = PorousFlowMassFraction
mass_fraction_vars = 'frac0 frac1'
[../]
[./simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.1
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '0.2 0 0 0 0.1 0 0 0 0.1'
[../]
[./relperm]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
[../]
[]
[AuxVariables]
[./flux_out]
[../]
[]
[Functions]
[./mass1_00]
type = ParsedFunction
value = 'frac*vol*por*dens0*exp(pp/bulk)*pow(1+pow(-al*pp,1.0/(1-m)),-m)'
vars = 'frac vol por dens0 pp bulk al m'
vals = 'f1_00 0.25 0.1 1.1 p00 1.3 1.1 0.5'
[../]
[./expected_mass_change1_00]
type = ParsedFunction
value = 'frac*fcn*area*dt'
vars = 'frac fcn area dt'
vals = 'f1_00 6 0.5 1E-3'
[../]
[./mass1_00_expect]
type = ParsedFunction
value = 'mass_prev-mass_change'
vars = 'mass_prev mass_change'
vals = 'm1_00_prev del_m1_00'
[../]
[./mass1_01]
type = ParsedFunction
value = 'frac*vol*por*dens0*exp(pp/bulk)*pow(1+pow(-al*pp,1.0/(1-m)),-m)'
vars = 'frac vol por dens0 pp bulk al m'
vals = 'f1_01 0.25 0.1 1.1 p01 1.3 1.1 0.5'
[../]
[./expected_mass_change1_01]
type = ParsedFunction
value = 'frac*fcn*area*dt'
vars = 'frac fcn area dt'
vals = 'f1_01 6 0.5 1E-3'
[../]
[./mass1_01_expect]
type = ParsedFunction
value = 'mass_prev-mass_change'
vars = 'mass_prev mass_change'
vals = 'm1_01_prev del_m1_01'
[../]
[]
[Postprocessors]
[./f1_00]
type = PointValue
point = '0 0 0'
variable = frac1
execute_on = 'initial timestep_end'
[../]
[./flux_00]
type = PointValue
point = '0 0 0'
variable = flux_out
execute_on = 'initial timestep_end'
[../]
[./p00]
type = PointValue
point = '0 0 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m1_00]
type = FunctionValuePostprocessor
function = mass1_00
execute_on = 'initial timestep_end'
[../]
[./m1_00_prev]
type = FunctionValuePostprocessor
function = mass1_00
execute_on = 'timestep_begin'
outputs = 'console'
[../]
[./del_m1_00]
type = FunctionValuePostprocessor
function = expected_mass_change1_00
execute_on = 'timestep_end'
outputs = 'console'
[../]
[./m1_00_expect]
type = FunctionValuePostprocessor
function = mass1_00_expect
execute_on = 'timestep_end'
[../]
[./f1_01]
type = PointValue
point = '0 1 0'
variable = frac1
execute_on = 'initial timestep_end'
[../]
[./flux_01]
type = PointValue
point = '0 1 0'
variable = flux_out
execute_on = 'initial timestep_end'
[../]
[./p01]
type = PointValue
point = '0 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m1_01]
type = FunctionValuePostprocessor
function = mass1_01
execute_on = 'initial timestep_end'
[../]
[./m1_01_prev]
type = FunctionValuePostprocessor
function = mass1_01
execute_on = 'timestep_begin'
outputs = 'console'
[../]
[./del_m1_01]
type = FunctionValuePostprocessor
function = expected_mass_change1_01
execute_on = 'timestep_end'
outputs = 'console'
[../]
[./m1_01_expect]
type = FunctionValuePostprocessor
function = mass1_01_expect
execute_on = 'timestep_end'
[../]
[./f1_11]
type = PointValue
point = '1 1 0'
variable = frac1
execute_on = 'initial timestep_end'
[../]
[./flux_11]
type = PointValue
point = '1 1 0'
variable = flux_out
execute_on = 'initial timestep_end'
[../]
[./p11]
type = PointValue
point = '1 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[]
[BCs]
[./flux]
type = PorousFlowSink
boundary = 'left'
variable = frac1
use_mobility = false
use_relperm = false
mass_fraction_component = 1
fluid_phase = 0
flux_function = 6
save_in = flux_out
[../]
[]
[Preconditioning]
[./andy]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = 'gmres asm lu 10 NONZERO 2'
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
dt = 1E-3
end_time = 0.01
nl_rel_tol = 1E-12
nl_abs_tol = 1E-12
[]
[Outputs]
file_base = s07
[./console]
type = Console
execute_on = 'nonlinear linear'
[../]
[./csv]
type = CSV
execute_on = 'timestep_end'
[../]
[]
This test checks that the flux is correctly implemented (see Figure 4) and that the correct fluid component is being withdrawn from the correct nodes. MOOSE produces the expected result.
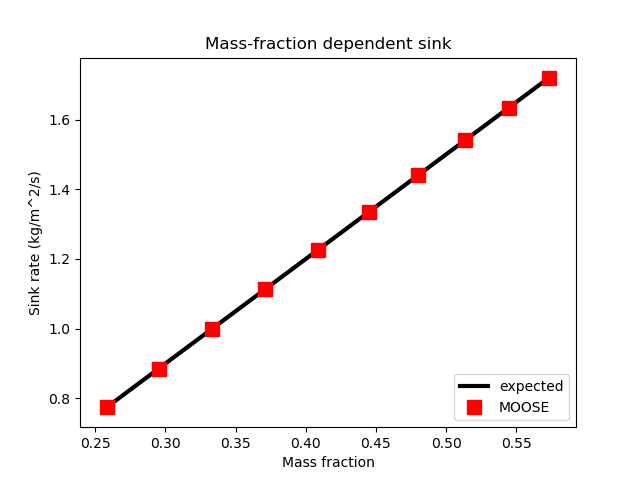
Figure 4: Results of Test 4, illustrating that MOOSE correctly applies a sink flux of a particular fluid component proportional to the component's mass fraction.
Test 5
A sink is applied to the left edge () of a 3D mesh. A 3-component, 2-phase fluid is used. Call the two phases "water" and "gas". The porepressures are initialised to and . The mass fractions are initialised to in the water phase, and in the gas phase. The water phase is assumed to have density , and the gas phase . A van-Genuchten capillary relationship is used: with Pa, and . The water relative permeaility is assumed to be Corey type with exponent , and the gas phase has exponent (that is , with ).
The sink flux acts only on the second component. It is multiplied by the relative permeability of the gas phase, and the mass fraction of the second component in the gas phase. This is possibly meaningless physically, but acts as a good test of the PorousFlowSink. In this test the mass fractions remain fixed: there is nothing to induce a change of a component from the water phase to the gas phase since the only Kernels used are mass-conservation Kernels that simply demand mass conservation of each fluid component (summed over each phase).
The input file:
# apply a sink flux on just one component of a 3-component, 2-phase system and observe the correct behavior
[Mesh]
type = GeneratedMesh
dim = 3
nx = 1
ny = 1
nz = 1
xmin = 0
xmax = 1
ymin = 0
ymax = 1
zmin = 0
zmax = 2
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pwater frac_ph0_c0 pgas'
number_fluid_phases = 2
number_fluid_components = 3
[../]
[./pc]
type = PorousFlowCapillaryPressureVG
m = 0.5
alpha = 1.1
[../]
[]
[Variables]
[./pwater]
[../]
[./frac_ph0_c0]
initial_condition = 0.3
[../]
[./pgas]
[../]
[]
[ICs]
[./pwater]
type = FunctionIC
variable = pwater
function = y
[../]
[./pgas]
type = FunctionIC
variable = pgas
function = y+3
[../]
[]
[Kernels]
[./mass_c0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = frac_ph0_c0
[../]
[./mass_c1]
type = PorousFlowMassTimeDerivative
fluid_component = 1
variable = pwater
[../]
[./mass_c2]
type = PorousFlowMassTimeDerivative
fluid_component = 2
variable = pgas
[../]
[]
[Modules]
[./FluidProperties]
[./simple_fluid0]
type = SimpleFluidProperties
bulk_modulus = 2.3
density0 = 1.5
thermal_expansion = 0
viscosity = 2.1
[../]
[./simple_fluid1]
type = SimpleFluidProperties
bulk_modulus = 1.3
density0 = 1.1
thermal_expansion = 0
viscosity = 1.1
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./ppss]
type = PorousFlow2PhasePP
phase0_porepressure = pwater
phase1_porepressure = pgas
capillary_pressure = pc
[../]
[./massfrac]
type = PorousFlowMassFraction
mass_fraction_vars = 'frac_ph0_c0 frac_ph0_c1 frac_ph1_c0 frac_ph1_c1'
[../]
[./simple_fluid0]
type = PorousFlowSingleComponentFluid
fp = simple_fluid0
phase = 0
[../]
[./simple_fluid1]
type = PorousFlowSingleComponentFluid
fp = simple_fluid1
phase = 1
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.1
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '0.2 0 0 0 0.1 0 0 0 0.1'
[../]
[./relperm0]
type = PorousFlowRelativePermeabilityCorey
n = 1
phase = 0
[../]
[./relperm1]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 1
[../]
[]
[AuxVariables]
[./flux_out]
[../]
[./frac_ph0_c1]
initial_condition = 0.35
[../]
[./frac_ph1_c0]
initial_condition = 0.1
[../]
[./frac_ph1_c1]
initial_condition = 0.8
[../]
[]
[Functions]
[./mass1_00]
type = ParsedFunction
value = 'fgas*vol*por*dens0gas*exp(pgas/bulkgas)*(1-pow(1+pow(al*(pgas-pwater),1.0/(1-m)),-m))+fwater*vol*por*dens0water*exp(pwater/bulkwater)*(pow(1+pow(al*(pgas-pwater),1.0/(1-m)),-m))'
vars = 'vol por dens0gas pgas pwater bulkgas al m dens0water bulkwater fgas fwater'
vals = '0.25 0.1 1.1 pgas_00 pwater_00 1.3 1.1 0.5 1.5 2.3 frac_ph1_c1_00 frac_ph0_c1_00'
[../]
[./expected_mass_change1_00]
type = ParsedFunction
value = 'frac*fcn*area*dt*pow(1-pow(1+pow(al*(pgas-pwater),1.0/(1-m)),-m), 2)'
vars = 'frac fcn area dt pgas pwater al m'
vals = 'frac_ph1_c1_00 100 0.5 1E-3 pgas_00 pwater_00 1.1 0.5'
[../]
[./mass1_00_expect]
type = ParsedFunction
value = 'mass_prev-mass_change'
vars = 'mass_prev mass_change'
vals = 'm1_00_prev del_m1_00'
[../]
[]
[Postprocessors]
[./total_mass_comp0]
type = PorousFlowFluidMass
fluid_component = 0
[../]
[./total_mass_comp1]
type = PorousFlowFluidMass
fluid_component = 1
[../]
[./total_mass_comp2]
type = PorousFlowFluidMass
fluid_component = 2
[../]
[./frac_ph1_c1_00]
type = PointValue
point = '0 0 0'
variable = frac_ph1_c1
execute_on = 'initial timestep_end'
[../]
[./frac_ph0_c1_00]
type = PointValue
point = '0 0 0'
variable = frac_ph0_c1
execute_on = 'initial timestep_end'
[../]
[./flux_00]
type = PointValue
point = '0 0 0'
variable = flux_out
execute_on = 'initial timestep_end'
[../]
[./pgas_00]
type = PointValue
point = '0 0 0'
variable = pgas
execute_on = 'initial timestep_end'
[../]
[./pwater_00]
type = PointValue
point = '0 0 0'
variable = pwater
execute_on = 'initial timestep_end'
[../]
[./m1_00]
type = FunctionValuePostprocessor
function = mass1_00
execute_on = 'initial timestep_end'
[../]
[./m1_00_prev]
type = FunctionValuePostprocessor
function = mass1_00
execute_on = 'timestep_begin'
outputs = 'console'
[../]
[./del_m1_00]
type = FunctionValuePostprocessor
function = expected_mass_change1_00
execute_on = 'timestep_end'
outputs = 'console'
[../]
[./m1_00_expect]
type = FunctionValuePostprocessor
function = mass1_00_expect
execute_on = 'timestep_end'
[../]
[]
[BCs]
[./flux_ph1_c1]
type = PorousFlowSink
boundary = 'left'
variable = pwater # sink applied to the mass_c1 Kernel
use_mobility = false
use_relperm = true
mass_fraction_component = 1
fluid_phase = 1
flux_function = 100
save_in = flux_out
[../]
[]
[Preconditioning]
[./andy]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = 'gmres asm lu 100 NONZERO 2'
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
dt = 1E-3
end_time = 0.01
nl_rel_tol = 1E-12
nl_abs_tol = 1E-12
[]
[Outputs]
file_base = s08
exodus = true
[./console]
type = Console
execute_on = 'nonlinear linear'
[../]
[./csv]
type = CSV
execute_on = 'timestep_end'
[../]
[]
The test checks whether MOOSE is correctly applying the sink flux, and that the fluid-component masses at the nodes respond correctly to the flux. Figure 5 demonstrates that MOOSE produces the expected result.
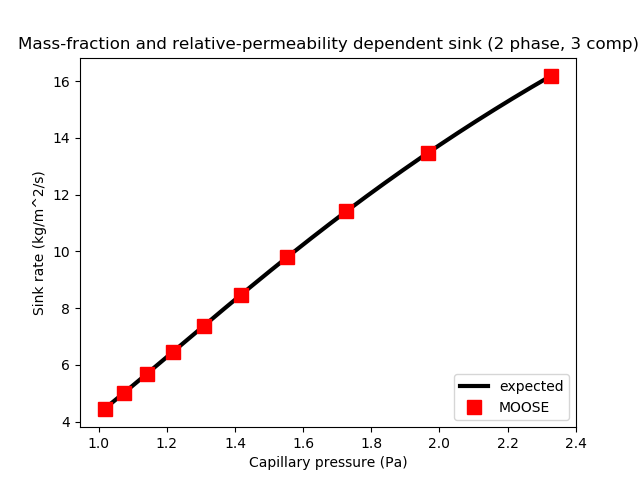
Figure 5: Results of Test 5, illustrating that in a 2-phase system MOOSE correctly applies a sink flux of a particular fluid component proportional to the component's mass fraction and the relative permeaility of the gas phase.
Piecewise-linear sink
A sink flux of strength (measured in kg.m.s) is applied to the right side () of a 3D mesh. A single-phase, single-component fluid is used, and the porepressure is initialised to (for ). No fluid flow within the element is used, so the masses of fluid at the finite-element nodes behave independently. The fluid is assumed to have density kg.m. The porosity is 0.1.
The input file:
# apply a piecewise-linear sink flux and observe the correct behavior
[Mesh]
type = GeneratedMesh
dim = 3
nx = 1
ny = 1
nz = 1
xmin = 0
xmax = 1
ymin = 0
ymax = 1
zmin = 0
zmax = 2
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pp'
number_fluid_phases = 1
number_fluid_components = 1
[../]
[./pc]
type = PorousFlowCapillaryPressureVG
m = 0.5
alpha = 1
[../]
[]
[Variables]
[./pp]
[../]
[]
[ICs]
[./pp]
type = FunctionIC
variable = pp
function = y+1
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pp
[../]
[]
[Modules]
[./FluidProperties]
[./simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 1.3
density0 = 1.1
thermal_expansion = 0
viscosity = 1.1
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./ppss]
type = PorousFlow1PhaseP
porepressure = pp
capillary_pressure = pc
[../]
[./massfrac]
type = PorousFlowMassFraction
[../]
[./simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.1
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-5 0 0 0 1E-5 0 0 0 1E-5'
[../]
[./relperm]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
[../]
[]
[AuxVariables]
[./flux_out]
[../]
[./xval]
[../]
[./yval]
[../]
[./pt_shift]
initial_condition = 0.3
[../]
[]
[ICs]
[./xval]
type = FunctionIC
variable = xval
function = x
[../]
[./yval]
type = FunctionIC
variable = yval
function = y
[../]
[]
[Functions]
[./mass10]
type = ParsedFunction
value = 'vol*por*dens0*exp(pp/bulk)'
vars = 'vol por dens0 pp bulk'
vals = '0.25 0.1 1.1 p10 1.3'
[../]
[./rate10]
type = ParsedFunction
value = 'fcn*if(pp>0.8,1,if(pp<0.3,0.5,0.2+pp))'
vars = 'fcn pp'
vals = '8 p10'
[../]
[./mass10_expect]
type = ParsedFunction
value = 'mass_prev-rate*area*dt'
vars = 'mass_prev rate area dt'
vals = 'm10_prev m10_rate 0.5 1E-3'
[../]
[./mass11]
type = ParsedFunction
value = 'vol*por*dens0*exp(pp/bulk)'
vars = 'vol por dens0 pp bulk'
vals = '0.25 0.1 1.1 p11 1.3'
[../]
[./rate11]
type = ParsedFunction
value = 'fcn*if(pp>0.8,1,if(pp<0.3,0.5,0.2+pp))'
vars = 'fcn pp'
vals = '8 p11'
[../]
[./mass11_expect]
type = ParsedFunction
value = 'mass_prev-rate*area*dt'
vars = 'mass_prev rate area dt'
vals = 'm11_prev m11_rate 0.5 1E-3'
[../]
[]
[Postprocessors]
[./p00]
type = PointValue
point = '0 0 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./p10]
type = PointValue
point = '1 0 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m10]
type = FunctionValuePostprocessor
function = mass10
execute_on = 'initial timestep_end'
[../]
[./m10_prev]
type = FunctionValuePostprocessor
function = mass10
execute_on = 'timestep_begin'
outputs = 'console'
[../]
[./m10_rate]
type = FunctionValuePostprocessor
function = rate10
execute_on = 'timestep_end'
[../]
[./m10_expect]
type = FunctionValuePostprocessor
function = mass10_expect
execute_on = 'timestep_end'
[../]
[./p01]
type = PointValue
point = '0 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./p11]
type = PointValue
point = '1 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m11]
type = FunctionValuePostprocessor
function = mass11
execute_on = 'initial timestep_end'
[../]
[./m11_prev]
type = FunctionValuePostprocessor
function = mass11
execute_on = 'timestep_begin'
outputs = 'console'
[../]
[./m11_rate]
type = FunctionValuePostprocessor
function = rate11
execute_on = 'timestep_end'
[../]
[./m11_expect]
type = FunctionValuePostprocessor
function = mass11_expect
execute_on = 'timestep_end'
[../]
[]
[BCs]
[./flux]
type = PorousFlowPiecewiseLinearSink
boundary = 'right'
PT_shift = pt_shift
pt_vals = '0.0 0.5'
multipliers = '0.5 1'
variable = pp
use_mobility = false
use_relperm = false
fluid_phase = 0
flux_function = 8
save_in = flux_out
[../]
[]
[Preconditioning]
[./andy]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = 'gmres asm lu 10000 NONZERO 2'
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
dt = 1E-3
end_time = 1E-2
nl_rel_tol = 1E-12
nl_abs_tol = 1E-12
[]
[Outputs]
file_base = s04
[./console]
type = Console
execute_on = 'nonlinear linear'
[../]
[./csv]
type = CSV
execute_on = 'timestep_end'
[../]
[]
Under these conditions, the expected result for the fluid mass at a node on the right side of the mesh is The notation is the same as in previous sections.
The test checks that the mass evolves according to this equation, and that the flux is applied correctly. Figure 6 demonstrates agreement with the expected flux and the MOOSE implementation.
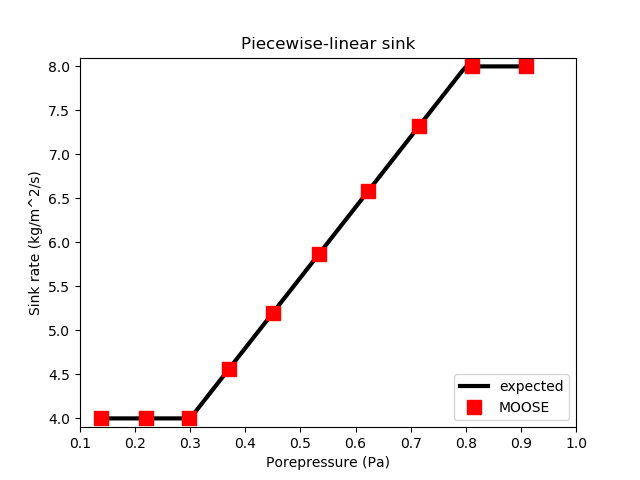
Figure 6: A piecewise-linear sink flux is correctly modelled by MOOSE.
Half-Gaussian sink
A sink flux of strength (measured in kg.m.s) is applied to the right side () of a 3D mesh. This is a half-Gaussian sink with center 0.9Pa, standard deviation 0.5Pa and maximum 6. A single-phase, single-component fluid is used, and the porepressure is initialised to (for ). No fluid flow within the element is used, so the masses of fluid at the finite-element nodes behave independently. The fluid is assumed to have density kg.m. The porosity is 0.1. A van-Genuchten capillary relationship is used: with \,Pa, and .
The input file:
# apply a half-gaussian sink flux and observe the correct behavior
[Mesh]
type = GeneratedMesh
dim = 3
nx = 1
ny = 1
nz = 1
xmin = 0
xmax = 1
ymin = 0
ymax = 1
zmin = 0
zmax = 2
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pp'
number_fluid_phases = 1
number_fluid_components = 1
[../]
[./pc]
type = PorousFlowCapillaryPressureVG
m = 0.5
alpha = 1.1
[../]
[]
[Variables]
[./pp]
[../]
[]
[ICs]
[./pp]
type = FunctionIC
variable = pp
function = y+1.4
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pp
[../]
[]
[Modules]
[./FluidProperties]
[./simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 1.3
density0 = 1.1
thermal_expansion = 0
viscosity = 1.1
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./ppss]
type = PorousFlow1PhaseP
porepressure = pp
capillary_pressure = pc
[../]
[./massfrac]
type = PorousFlowMassFraction
[../]
[./simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.1
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-5 0 0 0 1E-5 0 0 0 1E-5'
[../]
[./relperm]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
[../]
[]
[AuxVariables]
[./flux_out]
[../]
[]
[Functions]
[./mass10]
type = ParsedFunction
value = 'vol*por*dens0*exp(pp/bulk)*if(pp>=0,1,pow(1+pow(-al*pp,1.0/(1-m)),-m))'
vars = 'vol por dens0 pp bulk al m'
vals = '0.25 0.1 1.1 p10 1.3 1.1 0.5'
[../]
[./rate10]
type = ParsedFunction
value = 'if(pp>center,fcn,fcn*exp(-0.5*(pp-center)*(pp-center)/sd/sd))'
vars = 'fcn pp center sd'
vals = '6 p10 0.9 0.5'
[../]
[./mass10_expect]
type = ParsedFunction
value = 'mass_prev-rate*area*dt'
vars = 'mass_prev rate area dt'
vals = 'm10_prev m10_rate 0.5 2E-3'
[../]
[./mass11]
type = ParsedFunction
value = 'vol*por*dens0*exp(pp/bulk)*if(pp>=0,1,pow(1+pow(-al*pp,1.0/(1-m)),-m))'
vars = 'vol por dens0 pp bulk al m'
vals = '0.25 0.1 1.1 p11 1.3 1.1 0.5'
[../]
[./rate11]
type = ParsedFunction
value = 'if(pp>center,fcn,fcn*exp(-0.5*(pp-center)*(pp-center)/sd/sd))'
vars = 'fcn pp center sd'
vals = '6 p11 0.9 0.5'
[../]
[./mass11_expect]
type = ParsedFunction
value = 'mass_prev-rate*area*dt'
vars = 'mass_prev rate area dt'
vals = 'm11_prev m11_rate 0.5 2E-3'
[../]
[]
[Postprocessors]
[./flux10]
type = PointValue
variable = flux_out
point = '1 0 0'
[../]
[./p00]
type = PointValue
point = '0 0 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./p10]
type = PointValue
point = '1 0 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m10]
type = FunctionValuePostprocessor
function = mass10
execute_on = 'initial timestep_end'
[../]
[./m10_prev]
type = FunctionValuePostprocessor
function = mass10
execute_on = 'timestep_begin'
outputs = 'console'
[../]
[./m10_rate]
type = FunctionValuePostprocessor
function = rate10
execute_on = 'timestep_end'
[../]
[./m10_expect]
type = FunctionValuePostprocessor
function = mass10_expect
execute_on = 'timestep_end'
[../]
[./p01]
type = PointValue
point = '0 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./p11]
type = PointValue
point = '1 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m11]
type = FunctionValuePostprocessor
function = mass11
execute_on = 'initial timestep_end'
[../]
[./m11_prev]
type = FunctionValuePostprocessor
function = mass11
execute_on = 'timestep_begin'
outputs = 'console'
[../]
[./m11_rate]
type = FunctionValuePostprocessor
function = rate11
execute_on = 'timestep_end'
[../]
[./m11_expect]
type = FunctionValuePostprocessor
function = mass11_expect
execute_on = 'timestep_end'
[../]
[]
[BCs]
[./flux]
type = PorousFlowHalfGaussianSink
boundary = 'right'
max = 6
sd = 0.5
center = 0.9
variable = pp
use_mobility = false
use_relperm = false
fluid_phase = 0
flux_function = 1
save_in = flux_out
[../]
[]
[Preconditioning]
[./andy]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = 'gmres asm lu 10000 NONZERO 2'
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
dt = 2E-3
end_time = 6E-2
nl_rel_tol = 1E-12
nl_abs_tol = 1E-12
[]
[Outputs]
file_base = s05
[./console]
type = Console
execute_on = 'nonlinear linear'
interval = 5
[../]
[./csv]
type = CSV
execute_on = 'timestep_end'
interval = 3
[../]
[]
Under these conditions, the expected result for the fluid mass at a node on the right side of the mesh is The notation is the same as in previous sections.
The test checks that the mass evolves according to this equation, and that the flux is applied correctly. Figure 7 demonstrates agreement with the expected flux and the MOOSE implementation.
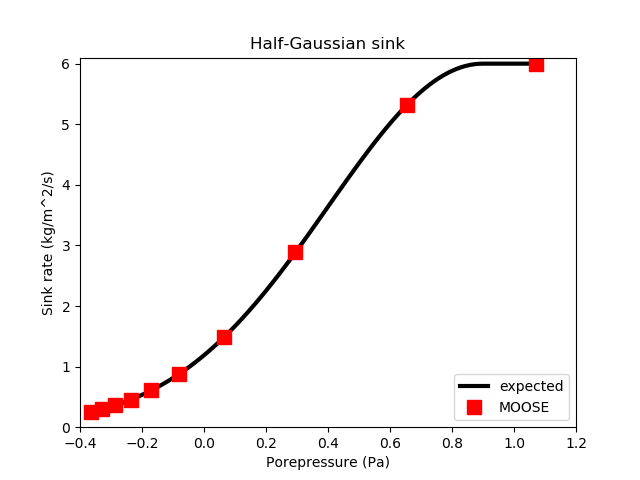
Figure 7: A half-Gaussian sink flux with center 0.9Pa and standard deviation 0.5Pa is correctly modelled by MOOSE.
Half-cubic sink
A sink flux of strength (measured in kg.m.s) is applied to the right side () of a 3D mesh. This is a half-cubic sink with center 0.9Pa, cutoff Pa, and maximum 3kg.m.s. A single-phase, single-component fluid is used, and the porepressure is initialised to (for and ). No fluid flow within the element is used, so the masses of fluid at the finite-element nodes behave independently. The fluid is assumed to have density kg.m. The porosity is 0.1.
The input file:
# apply a half-cubic sink flux and observe the correct behavior
[Mesh]
type = GeneratedMesh
dim = 3
nx = 1
ny = 1
nz = 1
xmin = 0
xmax = 1
ymin = 0
ymax = 1
zmin = 0
zmax = 2
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pp'
number_fluid_phases = 1
number_fluid_components = 1
[../]
[./pc]
type = PorousFlowCapillaryPressureVG
m = 0.5
alpha = 1.1
[../]
[]
[Variables]
[./pp]
[../]
[]
[ICs]
[./pp]
type = FunctionIC
variable = pp
function = x*(y+1)
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pp
[../]
[]
[Modules]
[./FluidProperties]
[./simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 1.3
density0 = 1.1
thermal_expansion = 0
viscosity = 1.1
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./ppss]
type = PorousFlow1PhaseP
porepressure = pp
capillary_pressure = pc
[../]
[./massfrac]
type = PorousFlowMassFraction
[../]
[./simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.1
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1E-5 0 0 0 1E-5 0 0 0 1E-5'
[../]
[./relperm]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
[../]
[]
[AuxVariables]
[./flux_out]
[../]
[]
[Functions]
[./mass10]
type = ParsedFunction
value = 'vol*por*dens0*exp(pp/bulk)*if(pp>=0,1,pow(1+pow(-al*pp,1.0/(1-m)),-m))'
vars = 'vol por dens0 pp bulk al m'
vals = '0.25 0.1 1.1 p10 1.3 1.1 0.5'
[../]
[./rate10]
type = ParsedFunction
value = 'fcn*if(pp>center,m,if(pp<themin,0,m/c/c/c*(2*(pp-center)+c)*((pp-center)-c)*((pp-center)-c)))'
vars = 'm fcn pp center sd themin c'
vals = '2 3 p10 0.9 0.5 0.1 -0.8'
[../]
[./mass10_expect]
type = ParsedFunction
value = 'mass_prev-rate*area*dt'
vars = 'mass_prev rate area dt'
vals = 'm10_prev m10_rate 0.5 2E-3'
[../]
[./mass11]
type = ParsedFunction
value = 'vol*por*dens0*exp(pp/bulk)*if(pp>=0,1,pow(1+pow(-al*pp,1.0/(1-m)),-m))'
vars = 'vol por dens0 pp bulk al m'
vals = '0.25 0.1 1.1 p11 1.3 1.1 0.5'
[../]
[./rate11]
type = ParsedFunction
value = 'fcn*if(pp>center,m,if(pp<themin,0,m/c/c/c*(2*(pp-center)+c)*((pp-center)-c)*((pp-center)-c)))'
vars = 'm fcn pp center sd themin c'
vals = '2 3 p11 0.9 0.5 0.1 -0.8'
[../]
[./mass11_expect]
type = ParsedFunction
value = 'mass_prev-rate*area*dt'
vars = 'mass_prev rate area dt'
vals = 'm11_prev m11_rate 0.5 2E-3'
[../]
[]
[Postprocessors]
[./flux00]
type = PointValue
variable = flux_out
point = '0 0 0'
[../]
[./flux01]
type = PointValue
variable = flux_out
point = '0 1 0'
[../]
[./flux10]
type = PointValue
variable = flux_out
point = '1 0 0'
[../]
[./flux11]
type = PointValue
variable = flux_out
point = '1 1 0'
[../]
[./p00]
type = PointValue
point = '0 0 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./p10]
type = PointValue
point = '1 0 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m10]
type = FunctionValuePostprocessor
function = mass10
execute_on = 'initial timestep_end'
[../]
[./m10_prev]
type = FunctionValuePostprocessor
function = mass10
execute_on = 'timestep_begin'
outputs = 'console'
[../]
[./m10_rate]
type = FunctionValuePostprocessor
function = rate10
execute_on = 'timestep_end'
[../]
[./m10_expect]
type = FunctionValuePostprocessor
function = mass10_expect
execute_on = 'timestep_end'
[../]
[./p01]
type = PointValue
point = '0 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./p11]
type = PointValue
point = '1 1 0'
variable = pp
execute_on = 'initial timestep_end'
[../]
[./m11]
type = FunctionValuePostprocessor
function = mass11
execute_on = 'initial timestep_end'
[../]
[./m11_prev]
type = FunctionValuePostprocessor
function = mass11
execute_on = 'timestep_begin'
outputs = 'console'
[../]
[./m11_rate]
type = FunctionValuePostprocessor
function = rate11
execute_on = 'timestep_end'
[../]
[./m11_expect]
type = FunctionValuePostprocessor
function = mass11_expect
execute_on = 'timestep_end'
[../]
[]
[BCs]
[./flux]
type = PorousFlowHalfCubicSink
boundary = 'left right'
max = 2
cutoff = -0.8
center = 0.9
variable = pp
use_mobility = false
use_relperm = false
fluid_phase = 0
flux_function = 3
save_in = flux_out
[../]
[]
[Preconditioning]
[./andy]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = 'gmres asm lu 10000 NONZERO 2'
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
dt = 2E-3
end_time = 6E-2
nl_rel_tol = 1E-12
nl_abs_tol = 1E-12
[]
[Outputs]
file_base = s06
[./console]
type = Console
execute_on = 'nonlinear linear'
interval = 5
[../]
[./csv]
type = CSV
execute_on = 'timestep_end'
interval = 3
[../]
[]
Under these conditions, the expected result for the fluid mass at a node on the right side of the mesh is The notation is the same as in previous sections.
The test checks that the mass evolves according to this equation, and that the flux is applied correctly. Figure 8 demonstrates agreement with the expected flux and the MOOSE implementation.
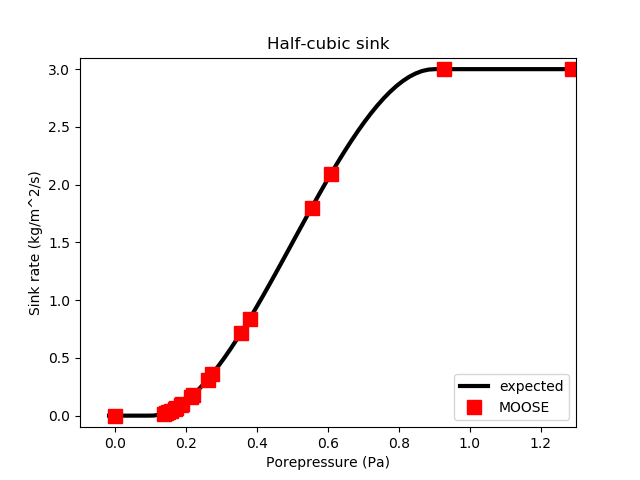
Figure 8: A half-cubic sink with center 0.9Pa, cutoff -0.8Pa, and maximum 3kg/m2/s is correctly modelled by MOOSE.
Piecewise linear sink, and advection of a fluid component
The porepressure at a boundary may be maintained at a fixed value by applying a sufficiently strong piecewise-linear sink: (measured in kg.m.s) for large conductance . Note that if is too large then it will dominate the numerics and MOOSE will not converge.
Similarly, for the multi-component case, the flux of of fluid component should be made proportional to the component mass fraction, : (1) This is a "natural" boundary condition, in that fluid exits or enters the porous material at a rate dictated by the mass-fraction within the porous material. This means, for instance, that if fluid is exiting ( in this case) then only components that exist at the boundary system will exit, and MOOSE will not attempt to extract fluid components that have zero mass-fraction.
This example concerns a 1D porous material occupying the space . It contains a single phase fluid with two fluid components. The porous material initially only contains fluid component , and there is a pressure gradient: For , fluid component is introduced on the material's left side (), by applying the fixed boundary conditions: The right-hand side, at , is subjected to the flux of Eq. (1). The fluid-component flows from the left side to the right side via the pressure gradient. To simplify the following analysis, the fluid bulk modulus is taken to be very large.
The input file:
# Apply a piecewise-linear sink flux to the right-hand side and watch fluid flow to it
#
# This test has a single phase with two components. The test initialises with
# the porous material fully filled with component=1. The left-hand side is fixed
# at porepressure=1 and mass-fraction of the zeroth component being unity.
# The right-hand side has a very strong piecewise-linear flux that keeps the
# porepressure~0 at that side. Fluid mass is extracted by this flux in proportion
# to the fluid component mass fraction.
#
# Therefore, the zeroth fluid component will flow from left to right (down the
# pressure gradient).
#
# The important DE is
# porosity * dc/dt = (perm / visc) * grad(P) * grad(c)
# which is true for c = mass-fraction, and very large bulk modulus of the fluid.
# For grad(P) constant in time and space (as in this example) this is just the
# advection equation for c, with velocity = perm / visc / porosity. The parameters
# are chosen to velocity = 1 m/s.
# In the numerical world, and especially with full upwinding, the advection equation
# suffers from diffusion. In this example, the diffusion is obvious when plotting
# the mass-fraction along the line, but the average velocity of the front is still
# correct at 1 m/s.
[Mesh]
type = GeneratedMesh
dim = 1
nx = 100
xmin = 0
xmax = 1
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pp frac'
number_fluid_phases = 1
number_fluid_components = 2
[../]
[./pc]
type = PorousFlowCapillaryPressureVG
m = 0.5
alpha = 1
[../]
[]
[Variables]
[./pp]
[../]
[./frac]
[../]
[]
[ICs]
[./pp]
type = FunctionIC
variable = pp
function = 1-x
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = frac
[../]
[./mass1]
type = PorousFlowMassTimeDerivative
fluid_component = 1
variable = pp
[../]
[./flux0]
type = PorousFlowAdvectiveFlux
fluid_component = 0
gravity = '0 0 0'
variable = frac
[../]
[./flux1]
type = PorousFlowAdvectiveFlux
fluid_component = 1
gravity = '0 0 0'
variable = pp
[../]
[]
[Modules]
[./FluidProperties]
[./simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 1e10 # need large in order for constant-velocity advection
density0 = 1 # almost irrelevant, except that the ability of the right BC to keep P fixed at zero is related to density_P0
thermal_expansion = 0
viscosity = 11
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./ppss]
type = PorousFlow1PhaseP
porepressure = pp
capillary_pressure = pc
[../]
[./massfrac]
type = PorousFlowMassFraction
mass_fraction_vars = frac
[../]
[./simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.1
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1.1 0 0 0 1.1 0 0 0 1.1'
[../]
[./relperm]
type = PorousFlowRelativePermeabilityCorey
n = 2 # irrelevant in this fully-saturated situation
phase = 0
[../]
[]
[BCs]
[./lhs_fixed_a]
type = DirichletBC
boundary = 'left'
variable = frac
value = 1
[../]
[./lhs_fixed_b]
type = DirichletBC
boundary = 'left'
variable = pp
value = 1
[../]
[./flux0]
type = PorousFlowPiecewiseLinearSink
boundary = 'right'
pt_vals = '-100 100'
multipliers = '-1 1'
variable = frac # the zeroth comonent
mass_fraction_component = 0
use_mobility = false
use_relperm = false
fluid_phase = 0
flux_function = 1E4
[../]
[./flux1]
type = PorousFlowPiecewiseLinearSink
boundary = 'right'
pt_vals = '-100 100'
multipliers = '-1 1'
variable = pp # comonent 1
mass_fraction_component = 1
use_mobility = false
use_relperm = false
fluid_phase = 0
flux_function = 1E4
[../]
[]
[Preconditioning]
[./andy]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = 'gmres asm lu 10000 NONZERO 2'
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
dt = 1E-2
end_time = 1
nl_rel_tol = 1E-12
nl_abs_tol = 1E-12
[]
[VectorPostprocessors]
[./mf]
type = LineValueSampler
start_point = '0 0 0'
end_point = '1 0 0'
num_points = 100
sort_by = x
variable = frac
[../]
[]
[Outputs]
file_base = s09
[./console]
type = Console
execute_on = 'nonlinear linear'
[../]
[./csv]
type = CSV
sync_times = '0.1 0.5 1'
sync_only = true
[../]
interval = 10
[]
Because the fluid bulk modulus is very large, is a solution for all time. This means that the governing equation reduces to In this equation is the porosity, is the permeability tensor, and is the fluid viscosity. This is just the advection equation for the mass fraction , with velocity In this test, the parameters are chosen such that velocitym.s.
The sharp front (described by the advection equation with the initial and boundary conditions) is not maintained by MOOSE. This is due to numerical diffusion, which is particularly strong in the upwinding scheme used in this test. For many more details, see the stabilization page. Nevertheless, MOOSE advects the smooth front with the correct velocity, as shown in Figure 9.
The sharp front is not maintained by MOOSE even when no upwinding is used. In the case at hand, which uses a fully-saturated single-phase fluid, the FullySaturated versions of the Kernels may be used in order to compare with the standard fully-upwinded Kernels. These Kernels do not employ any upwinding whatsoever, so less numerical diffusion is expected. This is demonstrated in Figure 9. Two additional points may also be nocied: (1) the lack of upwinding has produced a "bump" in the mass-fraction profile near the concentrated side; (2) the lack of upwinding means the temperature profile moves slightly slower than it should. These two affects reduce as the mesh density is increased, however.
The input file using the fully-saturated Kernels:
# Apply a piecewise-linear sink flux to the right-hand side and watch fluid flow to it
#
# This test has a single phase with two components. The test initialises with
# the porous material fully filled with component=1. The left-hand side is fixed
# at porepressure=1 and mass-fraction of the zeroth component being unity.
# The right-hand side has a very strong piecewise-linear flux that keeps the
# porepressure~0 at that side. Fluid mass is extracted by this flux in proportion
# to the fluid component mass fraction.
#
# Therefore, the zeroth fluid component will flow from left to right (down the
# pressure gradient).
#
# The important DE is
# porosity * dc/dt = (perm / visc) * grad(P) * grad(c)
# which is true for c = mass-fraction, and very large bulk modulus of the fluid.
# For grad(P) constant in time and space (as in this example) this is just the
# advection equation for c, with velocity = perm / visc / porosity. The parameters
# are chosen to velocity = 1 m/s.
# In the numerical world, and especially with full upwinding, the advection equation
# suffers from diffusion. In this example, the diffusion is obvious when plotting
# the mass-fraction along the line, but the average velocity of the front is still
# correct at 1 m/s.
# This test uses the FullySaturated version of the flow Kernel. This does not
# suffer from as much numerical diffusion as the standard PorousFlow Kernel since
# it does not employ any upwinding.
[Mesh]
type = GeneratedMesh
dim = 1
nx = 100
xmin = 0
xmax = 1
[]
[GlobalParams]
PorousFlowDictator = dictator
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'pp frac'
number_fluid_phases = 1
number_fluid_components = 2
[../]
[./pc]
type = PorousFlowCapillaryPressureVG
m = 0.5
alpha = 1
[../]
[]
[Variables]
[./pp]
[../]
[./frac]
[../]
[]
[ICs]
[./pp]
type = FunctionIC
variable = pp
function = 1-x
[../]
[]
[Kernels]
[./mass0]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = frac
[../]
[./mass1]
type = PorousFlowMassTimeDerivative
fluid_component = 1
variable = pp
[../]
[./flux0]
type = PorousFlowFullySaturatedDarcyFlow
fluid_component = 0
gravity = '0 0 0'
variable = frac
[../]
[./flux1]
type = PorousFlowFullySaturatedDarcyFlow
fluid_component = 1
gravity = '0 0 0'
variable = pp
[../]
[]
[Modules]
[./FluidProperties]
[./simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 1e10 # need large in order for constant-velocity advection
density0 = 1 # almost irrelevant, except that the ability of the right BC to keep P fixed at zero is related to density_P0
thermal_expansion = 0
viscosity = 11
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
[../]
[./ppss]
type = PorousFlow1PhaseP
porepressure = pp
capillary_pressure = pc
[../]
[./massfrac]
type = PorousFlowMassFraction
mass_fraction_vars = frac
[../]
[./simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.1
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1.1 0 0 0 1.1 0 0 0 1.1'
[../]
[./relperm]
type = PorousFlowRelativePermeabilityCorey
n = 2 # irrelevant in this fully-saturated situation
phase = 0
[../]
[]
[BCs]
[./lhs_fixed_a]
type = DirichletBC
boundary = 'left'
variable = frac
value = 1
[../]
[./lhs_fixed_b]
type = DirichletBC
boundary = 'left'
variable = pp
value = 1
[../]
[./flux0]
type = PorousFlowPiecewiseLinearSink
boundary = 'right'
pt_vals = '-100 100'
multipliers = '-1 1'
variable = frac # the zeroth comonent
mass_fraction_component = 0
use_mobility = false
use_relperm = false
fluid_phase = 0
flux_function = 1E4
[../]
[./flux1]
type = PorousFlowPiecewiseLinearSink
boundary = 'right'
pt_vals = '-100 100'
multipliers = '-1 1'
variable = pp # comonent 1
mass_fraction_component = 1
use_mobility = false
use_relperm = false
fluid_phase = 0
flux_function = 1E4
[../]
[]
[Preconditioning]
[./andy]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -snes_max_it -sub_pc_factor_shift_type -pc_asm_overlap'
petsc_options_value = 'gmres asm lu 10000 NONZERO 2'
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
dt = 1E-2
end_time = 1
nl_rel_tol = 1E-11
nl_abs_tol = 1E-11
[]
[VectorPostprocessors]
[./mf]
type = LineValueSampler
start_point = '0 0 0'
end_point = '1 0 0'
num_points = 100
sort_by = x
variable = frac
[../]
[]
[Outputs]
file_base = s09_fully_saturated
[./console]
type = Console
execute_on = 'nonlinear linear'
[../]
[./csv]
type = CSV
sync_times = '0.1 0.5 1'
sync_only = true
[../]
interval = 10
[]
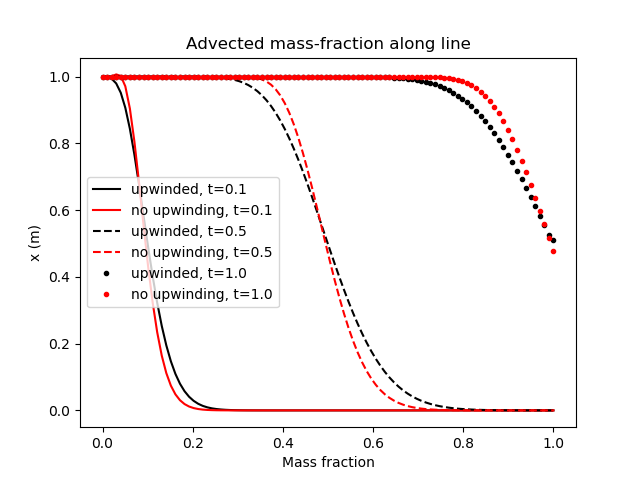
Figure 9: Results of the advection of a fluid component test, illustrating that the numerical implementation of porous flow within MOOSE diffuses sharp fronts, but advects them at the correct velocity (which is 1m/s in this case). Notice the centre of the front is at the correct position in each picture. Less diffusion is experienced when upwinding is not used, but notice the slight "bump" in the non-upwinded version at early times.