Heat advection in a 1D bar
Consider the case of a single-phase fluid in 1 dimension, , with the porepressure fixed at the boundaries: With zero gravity, and high fluid bulk modulus, the Darcy equation implies that the solution is , with being the constant "Darcy velocity" from to . (The velocity of the individual fluid particles, this is divided by the porosity.). Here is the porous medium's permeability, and is the fluid dynamic viscosity.
Suppose that the fluid internal energy is given by , where is the specific heat capacity and is its temperature. Assuming that , then the fluid's enthalpy is also . In this case, the energy equation reads This is the wave equation with velocity Recall that the "Darcy velocity" is .
Let the initial condition for be . Apply the boundary conditions At this creates a front at . Choose the parameters , , , , , , (all in consistent units), so that is the front's velocity.
The input file:
# 1phase, heat advecting with a moving fluid
[Mesh]
type = GeneratedMesh
dim = 1
nx = 50
xmin = 0
xmax = 1
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[./temp]
initial_condition = 200
[../]
[./pp]
[../]
[]
[ICs]
[./pp]
type = FunctionIC
variable = pp
function = '1-x'
[../]
[]
[BCs]
[./pp0]
type = DirichletBC
variable = pp
boundary = left
value = 1
[../]
[./pp1]
type = DirichletBC
variable = pp
boundary = right
value = 0
[../]
[./spit_heat]
type = DirichletBC
variable = temp
boundary = left
value = 300
[../]
[./suck_heat]
type = DirichletBC
variable = temp
boundary = right
value = 200
[../]
[]
[Kernels]
[./mass_dot]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pp
[../]
[./advection]
type = PorousFlowAdvectiveFlux
fluid_component = 0
variable = pp
[../]
[./energy_dot]
type = PorousFlowEnergyTimeDerivative
variable = temp
[../]
[./heat_advection]
type = PorousFlowHeatAdvection
variable = temp
[../]
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'temp pp'
number_fluid_phases = 1
number_fluid_components = 1
[../]
[./pc]
type = PorousFlowCapillaryPressureVG
m = 0.6
alpha = 1.3
[../]
[]
[Modules]
[./FluidProperties]
[./simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 100
density0 = 1000
viscosity = 4.4
thermal_expansion = 0
cv = 2
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
temperature = temp
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.2
[../]
[./rock_heat]
type = PorousFlowMatrixInternalEnergy
specific_heat_capacity = 1.0
density = 125
[../]
[./simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1.1 0 0 0 2 0 0 0 3'
[../]
[./relperm]
type = PorousFlowRelativePermeabilityCorey
n = 2
phase = 0
[../]
[./massfrac]
type = PorousFlowMassFraction
[../]
[./PS]
type = PorousFlow1PhaseP
porepressure = pp
capillary_pressure = pc
[../]
[]
[Preconditioning]
[./andy]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
petsc_options_value = 'gmres bjacobi 1E-15 1E-10 10000'
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
dt = 0.01
end_time = 0.6
[]
[VectorPostprocessors]
[./T]
type = LineValueSampler
start_point = '0 0 0'
end_point = '1 0 0'
num_points = 51
sort_by = x
variable = temp
[../]
[]
[Outputs]
[./csv]
type = CSV
sync_times = '0.1 0.6'
sync_only = true
[../]
[]
The sharp front is not maintained by MOOSE. This is due to numerical diffusion, which is particularly strong when full upwinding is used. This is explained in great detail in the pages on numerical stabilization. Nevertheless, MOOSE advects the smooth front with the correct velocity, as shown in Figure 1.
The sharp front is not maintained by MOOSE even when no upwinding is used. In the case at hand, which uses a fully-saturated single-phase fluid, the FullySaturatedHeatAdvection Kernel may be used in order to compare with the standard fully-upwinded Kernels. The input file using the fully-saturated approach:
# 1phase, heat advecting with a moving fluid
# Using the FullySaturated Kernel
[Mesh]
type = GeneratedMesh
dim = 1
nx = 50
xmin = 0
xmax = 1
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[./temp]
initial_condition = 200
[../]
[./pp]
[../]
[]
[ICs]
[./pp]
type = FunctionIC
variable = pp
function = '1-x'
[../]
[]
[BCs]
[./pp0]
type = DirichletBC
variable = pp
boundary = left
value = 1
[../]
[./pp1]
type = DirichletBC
variable = pp
boundary = right
value = 0
[../]
[./spit_heat]
type = DirichletBC
variable = temp
boundary = left
value = 300
[../]
[./suck_heat]
type = DirichletBC
variable = temp
boundary = right
value = 200
[../]
[]
[Kernels]
[./mass_dot]
type = PorousFlowMassTimeDerivative
fluid_component = 0
variable = pp
[../]
[./advection]
type = PorousFlowFullySaturatedDarcyBase
variable = pp
[../]
[./energy_dot]
type = PorousFlowEnergyTimeDerivative
variable = temp
[../]
[./convection]
type = PorousFlowFullySaturatedHeatAdvection
variable = temp
[../]
[]
[UserObjects]
[./dictator]
type = PorousFlowDictator
porous_flow_vars = 'temp pp'
number_fluid_phases = 1
number_fluid_components = 1
[../]
[]
[Modules]
[./FluidProperties]
[./simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 100
density0 = 1000
viscosity = 4.4
thermal_expansion = 0
cv = 2
[../]
[../]
[]
[Materials]
[./temperature]
type = PorousFlowTemperature
temperature = temp
[../]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.2
[../]
[./rock_heat]
type = PorousFlowMatrixInternalEnergy
specific_heat_capacity = 1.0
density = 125
[../]
[./simple_fluid]
type = PorousFlowSingleComponentFluid
fp = simple_fluid
phase = 0
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1.1 0 0 0 2 0 0 0 3'
[../]
[./massfrac]
type = PorousFlowMassFraction
[../]
[./PS]
type = PorousFlow1PhaseFullySaturated
porepressure = pp
[../]
[]
[Preconditioning]
[./andy]
type = SMP
full = true
petsc_options_iname = '-ksp_type -pc_type -snes_atol -snes_rtol -snes_max_it'
petsc_options_value = 'gmres bjacobi 1E-15 1E-10 10000'
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
dt = 0.01
end_time = 0.6
[]
[VectorPostprocessors]
[./T]
type = LineValueSampler
start_point = '0 0 0'
end_point = '1 0 0'
num_points = 51
sort_by = x
variable = temp
[../]
[]
[Outputs]
file_base = heat_advection_1d_fully_saturated
[./csv]
type = CSV
sync_times = '0.1 0.6'
sync_only = true
[../]
[]
The FullySaturated Kernels do not employ any upwinding whatsoever, so less numerical diffusion is expected. This is demonstrated in Figure 1. Two additional points may also be nocied: (1) the lack of upwinding has produced a "bump" in the temperature profile near the hotter side; (2) the lack of upwinding means the temperature profile moves slightly slower than it should. These two affects reduce as the mesh density is increased, however.
Finally, the same simulation may be run using Kuzmin-Turek stabilization, with input file (that employs the PorousFlowFullySaturated Action):
# 1phase, heat advecting with a moving fluid
# Using the PorousFlowFullySaturated Action with KT stabilization
# This should produce an identical result to heat_advection_1D_KT
[Mesh]
type = GeneratedMesh
dim = 1
nx = 50
xmin = 0
xmax = 1
[]
[GlobalParams]
PorousFlowDictator = dictator
gravity = '0 0 0'
[]
[Variables]
[./temp]
initial_condition = 200
[../]
[./pp]
[../]
[]
[ICs]
[./pp]
type = FunctionIC
variable = pp
function = '1-x'
[../]
[]
[BCs]
[./pp0]
type = DirichletBC
variable = pp
boundary = left
value = 1
[../]
[./pp1]
type = DirichletBC
variable = pp
boundary = right
value = 0
[../]
[./spit_heat]
type = DirichletBC
variable = temp
boundary = left
value = 300
[../]
[./suck_heat]
type = DirichletBC
variable = temp
boundary = right
value = 200
[../]
[]
[PorousFlowFullySaturated]
porepressure = pp
temperature = temp
coupling_type = ThermoHydro
fp = simple_fluid
add_darcy_aux = false
stabilization = KT
flux_limiter_type = superbee
[]
[Modules]
[./FluidProperties]
[./simple_fluid]
type = SimpleFluidProperties
bulk_modulus = 100
density0 = 1000
viscosity = 4.4
thermal_expansion = 0
cv = 2
[../]
[../]
[]
[Materials]
[./porosity]
type = PorousFlowPorosityConst
porosity = 0.2
[../]
[./zero_thermal_conductivity]
type = PorousFlowThermalConductivityIdeal
dry_thermal_conductivity = '0 0 0 0 0 0 0 0 0'
[../]
[./rock_heat]
type = PorousFlowMatrixInternalEnergy
specific_heat_capacity = 1.0
density = 125
[../]
[./permeability]
type = PorousFlowPermeabilityConst
permeability = '1.1 0 0 0 2 0 0 0 3'
[../]
[]
[Preconditioning]
[./andy]
type = SMP
full = true
[../]
[]
[Executioner]
type = Transient
solve_type = Newton
dt = 0.01
end_time = 0.6
[]
[VectorPostprocessors]
[./T]
type = LineValueSampler
start_point = '0 0 0'
end_point = '1 0 0'
num_points = 51
sort_by = x
variable = temp
[../]
[]
[Outputs]
file_base = heat_advection_1d_fully_saturation_action
[./csv]
type = CSV
sync_times = '0.1 0.6'
sync_only = true
[../]
[]
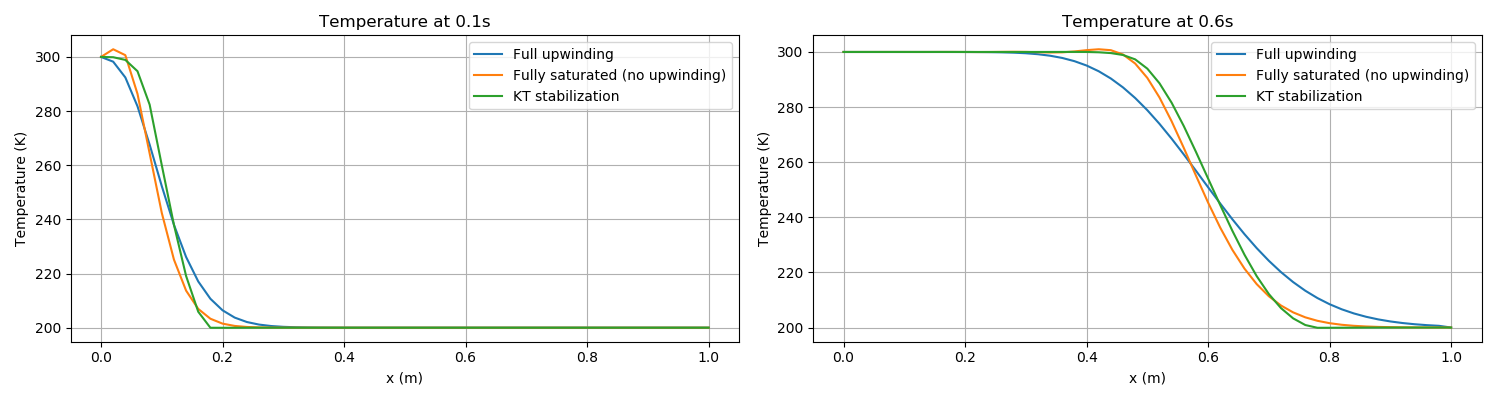
Figure 1: Results of heat advection via a fluid in 1D. The fluid flows with constant Darcy velocity of 0.25m/s to the right, and this advects a temperature front at velocity 1m/s to the right. The pictures above that the numerical implementation of PorousFlow (including upwinding) diffuses sharp fronts, but advects them at the correct velocity (notice the centre of the upwinded front is at the correct position in each picture). Less diffusion is experienced without upwinding or with KT stabilization. Left: temperature 0.1s. Right: temperature at 0.6s.