Peridynamic Mechanics Models
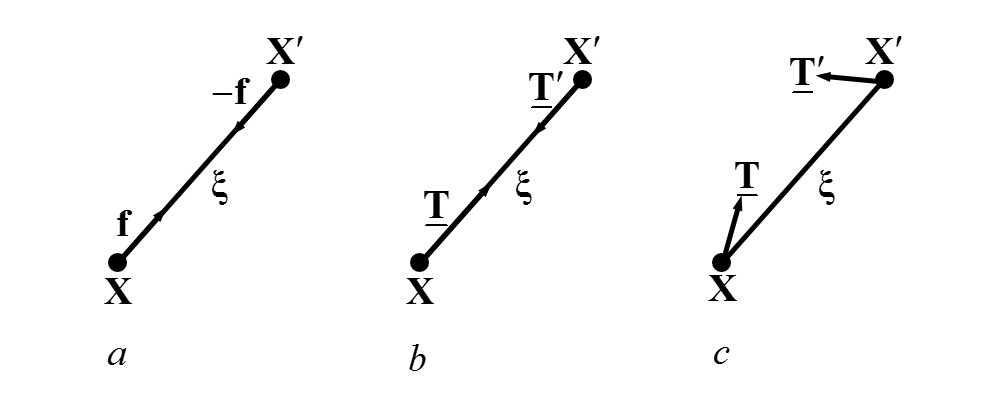
Schematics of bond-based (a), ordinary (b) and non-ordinary (c) state based peridynamic material response
The first peridynamic model, termed the bond-based peridynamic model (BPD), was proposed by Silling in the year of 2000 citep:. In BPD, material points interact in a pair-wise fashion with neighboring material points that fall within their horizon. The interaction between two material points depends only on their own deformations.
Later, Silling et al. citep: generalized BPD model in what is termed state-based peridynamic models (SPD) by introducing the concept of states. In SPD, the force state between two material points depends not only on their own deformation states, but also on the deformation states of other material points within their horizons. Depending on the direction of force state between a material point pair, SPD models can be classified into ordinary state-based peridynamic (OSPD) and non-ordinary state-based peridynamic (NOSPD) models.
SPD models overcome several issues within BPD model, such as only permitting a fixed Poisson's ratio of 0.25, inconsistency in modeling plastic deformation for metals, and requiring a complete recast of standard continuum material models in terms of pairwise force function to permit their use within peridynamics. A review of BPD and SPD and their applications can be found in (Bobaru et al., 2016).
In peridynamics theory, the Equation of Motion (EOM) for a material point in the reference configuration at time is given by
where is the mass density, is the force density function, and is external force density vector.
Depending on different peridynamics models, the force density function has different formulation. Various formulations for force density functions are outlined below.
Bond-based models
with has values of
for spatial discretization
for spatial discretization
with where is the bulk modulus and is the two-dimensional bulk modulus, is the Young's modulus, is the plane thickness and is the cross-sectional area. where is the Poisson's Ratio.
being the and defined as the change in bond length divided by initial bond length
being the unit vector in the direction of the deformed bond from to
Ordinary state-based models
with force density vector as
where is the bond stretch, is the dilatation at a material point which can be calculated as
and
for spatial discretization
for spatial discretization
with is the shear modulus.
Reference for case of regular uniform spatial discretization can be found at citep: and citep:. For case of irregular non-uniform spatial discretization can be found at citep:.
Non-ordinary state-based models
The general expression for force density function can be written as: where , in short , is the force density state exerted on material point from , while , in short , is the force density state exerted on material point from .
Conventional correspondence material model
where is the first Piola-Kirchhoff stress tensor and is the shape tensor. Definition of shape tensor can be found on Deformation Gradients page.
Bond-associated correspondence material model
It should be noted that the First Piola-Kirchhoff stress tensor and shape tensor are all bond-associated quatities.
Peridynamic Heat Conduction Models
The peridynamic heat conduction equation is
where is the specific heat capacity, is the response function, and is specific heat source or sink.
Bond-based models
with has values of
for spatial discretization
for spatial discretization
where is the material thermal conductivity, is the volume coefficient which has the same expression as in bond-based mechanics model.
Coupled Peridynamic Thermo-Mechanical Models
For coupled peridynamic thermo-mechanical modeling, the temperature from heat conduction model will contribute to the mechanical stretch and strain calculation in the mechanics model. And the kinematics can be written as
For bond stretch in bond-based and ordinary state-based mechanics models,
and the dilatation in ordinary state-based mechanics models
Besides, the force density vector needs to be updated considering the thermal effect as
where for three-dimensional analysis and for two-dimensional analysis.
For non-ordinary state-based mechanics models, the mechanical strain tensor is the subtraction of thermal eigen-strain from the total strain.
In return, the bond status determined from the mechanics models will affect the response between material points in peridynamic heat conduction models.
- Florin Bobaru, John T. Foster, Philippe H. Geubelle, and Stewart A. Silling.
Handbook of Peridynamic Modeling.
Chapman and Hall/CRC, 2016.[BibTeX]