Diffusion and hydrodynamic dispersion Tests

Diffusion

The results of PorousFlow are compared with the classical diffusion profile for a simple 1D model with mass diffusion. In this example, the left end of a 1D mesh is held at a constant mass fraction of 1, while the right hand end is prescribed a zero mass fraction boundary condition. No advection takes place, so mass transfer is by diffusion only. The input file:

# Test diffusive part of PorousFlowDispersiveFlux kernel by setting dispersion
# coefficients to zero. Pressure is held constant over the mesh, and gravity is
# set to zero so that no advective transport of mass takes place.
# Mass fraction is set to 1 on the left hand side and 0 on the right hand side.

[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = 20
  xmax = 10
  bias_x = 1.1
[]

[GlobalParams]
  PorousFlowDictator = andy_heheheh
[]

[Variables]
  [pp]
  []
  [massfrac0]
  []
[]

[ICs]
  [pp]
    type = ConstantIC
    variable = pp
    value = 1e5
  []
  [massfrac0]
    type = ConstantIC
    variable = massfrac0
    value = 0
  []
[]

[BCs]
  [left]
    type = DirichletBC
    value = 1
    variable = massfrac0
    boundary = left
  []
  [right]
    type = DirichletBC
    value = 0
    variable = massfrac0
    boundary = right
  []
  [pright]
    type = DirichletBC
    variable = pp
    boundary = right
    value = 1e5
  []
  [pleft]
    type = DirichletBC
    variable = pp
    boundary = left
    value = 1e5
  []
[]

[Kernels]
  [diff0]
    type = PorousFlowDispersiveFlux
    fluid_component = 0
    variable = massfrac0
    disp_trans = 0
    disp_long = 0
    gravity = '0 0 0'
  []
  [diff1]
    type = PorousFlowDispersiveFlux
    fluid_component = 1
    variable = pp
    disp_trans = 0
    disp_long = 0
    gravity = '0 0 0'
  []
[]

[Modules]
  [FluidProperties]
    [the_simple_fluid]
      type = SimpleFluidProperties
      thermal_expansion = 0.0
      bulk_modulus = 1E7
      viscosity = 0.001
      density0 = 1000.0
    []
  []
[]

[PorousFlowUnsaturated]
  porepressure = pp
  gravity = '0 0 0'
  fp = the_simple_fluid
  dictator_name = andy_heheheh
  relative_permeability_type = Corey
  relative_permeability_exponent = 0.0
  mass_fraction_vars = massfrac0
[]

[Materials]
  [poro]
    type = PorousFlowPorosityConst
    porosity = 0.3
  []
  [diff]
    type = PorousFlowDiffusivityConst
    diffusion_coeff = '1 1'
    tortuosity = 0.1
  []
  [permeability]
    type = PorousFlowPermeabilityConst
    permeability = '1e-9 0 0 0 1e-9 0 0 0 1e-9'
  []
[]

[Preconditioning]
  [smp]
    type = SMP
    full = true
    petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
    petsc_options_value = 'gmres      asm      lu           NONZERO                   2             '
  []
[]

[Executioner]
  type = Transient
  solve_type = NEWTON
  dt = 1
  end_time = 20
[]

[VectorPostprocessors]
  [xmass]
    type = NodalValueSampler
    sort_by = id
    variable = massfrac0
  []
[]

[Outputs]
  [out]
    type = CSV
    execute_on = final
  []
[]

This concentration profile has a well-known similarity solution given by where is the complentary error function, and is the similarity solution, is distance, is time, and is the diffusion coefficient.

The comparison between PorousFlow and this analytical solution is presented in Figure 1, where we observe a very good agreement between the two solutions.

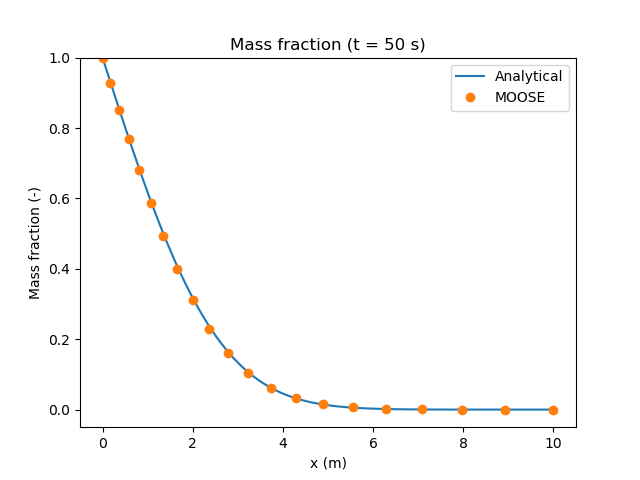
Figure 1: Mass fraction profile from diffusion only.

Hydrodynamic dispersion

The PorousFlow results are compared to known analytical solutions for simple problems in order to verify that the MOOSE implementation is working properly. For a simple 1D model with no diffusion and constant velocity , an analytical solution for the mass fraction profile is given by (Javandel et al., 1984) where all parameters have been previously defined.

The input file:

# Test dispersive part of PorousFlowDispersiveFlux kernel by setting diffusion
# coefficients to zero. A pressure gradient is applied over the mesh to give a
# uniform velocity. Gravity is set to zero.
# Mass fraction is set to 1 on the left hand side and 0 on the right hand side.

[Mesh]
  type = GeneratedMesh
  dim = 1
  nx = 200
  xmax = 10
[]

[GlobalParams]
  PorousFlowDictator = dictator
  gravity = '0 0 0'
  compute_enthalpy = false
  compute_internal_energy = false
[]

[Variables]
  [pp]
  []
  [massfrac0]
  []
[]

[AuxVariables]
  [velocity]
    family = MONOMIAL
    order = FIRST
  []
[]

[AuxKernels]
  [velocity]
    type = PorousFlowDarcyVelocityComponent
    variable = velocity
    component = x
  []
[]

[ICs]
  [pp]
    type = FunctionIC
    variable = pp
    function = pic
  []
  [massfrac0]
    type = ConstantIC
    variable = massfrac0
    value = 0
  []
[]

[Functions]
  [pic]
    type = ParsedFunction
    value = 1.1e5-x*1e3
  []
[]

[BCs]
  [xleft]
    type = DirichletBC
    value = 1
    variable = massfrac0
    boundary = left
  []
  [xright]
    type = DirichletBC
    value = 0
    variable = massfrac0
    boundary = right
  []
  [pright]
    type = DirichletBC
    variable = pp
    boundary = right
    value = 1e5
  []
  [pleft]
    type = DirichletBC
    variable = pp
    boundary = left
    value = 1.1e5
  []
[]

[Kernels]
  [mass0]
    type = PorousFlowMassTimeDerivative
    fluid_component = 0
    variable = pp
  []
  [adv0]
    type = PorousFlowAdvectiveFlux
    fluid_component = 0
    variable = pp
  []
  [diff0]
    type = PorousFlowDispersiveFlux
    variable = pp
    disp_trans = 0
    disp_long = 0.2
  []
  [mass1]
    type = PorousFlowMassTimeDerivative
    fluid_component = 1
    variable = massfrac0
  []
  [adv1]
    type = PorousFlowAdvectiveFlux
    fluid_component = 1
    variable = massfrac0
  []
  [diff1]
    type = PorousFlowDispersiveFlux
    fluid_component = 1
    variable = massfrac0
    disp_trans = 0
    disp_long = 0.2
  []
[]

[UserObjects]
  [dictator]
    type = PorousFlowDictator
    porous_flow_vars = 'pp massfrac0'
    number_fluid_phases = 1
    number_fluid_components = 2
  []
[]

[Modules]
  [FluidProperties]
    [simple_fluid]
      type = SimpleFluidProperties
      bulk_modulus = 1e9
      density0 = 1000
      viscosity = 0.001
      thermal_expansion = 0
    []
  []
[]

[Materials]
  [temperature]
    type = PorousFlowTemperature
  []
  [ppss]
    type = PorousFlow1PhaseFullySaturated
    porepressure = pp
  []
  [massfrac]
    type = PorousFlowMassFraction
    mass_fraction_vars = massfrac0
  []
  [simple_fluid]
    type = PorousFlowSingleComponentFluid
    fp = simple_fluid
    phase = 0
  []
  [poro]
    type = PorousFlowPorosityConst
    porosity = 0.3
  []
  [diff]
    type = PorousFlowDiffusivityConst
    diffusion_coeff = '0 0'
    tortuosity = 0.1
  []
  [relp]
    type = PorousFlowRelativePermeabilityConst
    phase = 0
  []
  [permeability]
    type = PorousFlowPermeabilityConst
    permeability = '1e-9 0 0 0 1e-9 0 0 0 1e-9'
  []
[]

[Preconditioning]
  [smp]
    type = SMP
    full = true
    petsc_options_iname = '-ksp_type -pc_type -sub_pc_type -sub_pc_factor_shift_type -pc_asm_overlap'
    petsc_options_value = 'gmres      asm      lu           NONZERO                   2             '
  []
[]

[Executioner]
  type = Transient
  solve_type = NEWTON
  end_time = 1e3
  dtmax = 10
  [TimeStepper]
    type = IterationAdaptiveDT
    growth_factor = 1.5
    cutback_factor = 0.5
    dt = 1
  []
[]

[VectorPostprocessors]
  [xmass]
    type = NodalValueSampler
    sort_by = id
    variable = massfrac0
  []
[]

[Outputs]
  [out]
    type = CSV
    execute_on = final
  []
[]

The comparison between the PorousFlow and the analytical formula is presented in Figure 2. For the non-heavy case, the MOOSE results do not coincide with the analytical solution near the top and bottom of the concentration front due to numerical dispersion. If the number of elements in the mesh is increased and the time step size is reduced (the "heavy" case), numerical dispersion is reduced and a much closer fit to the analytical solution is obtained.

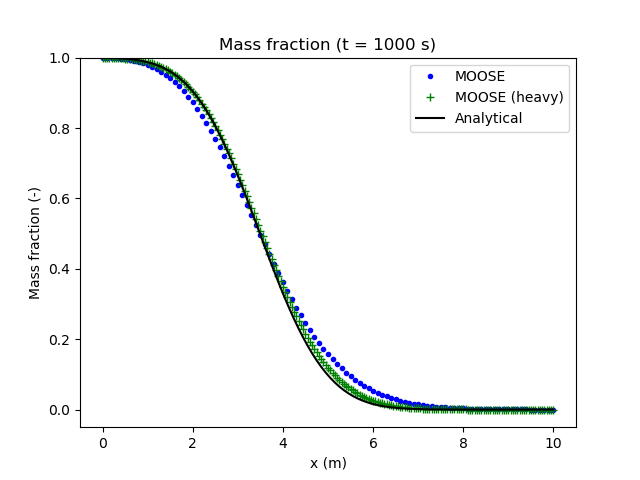
Figure 2: Mass fraction profile from hydrodynamic dispersion only.

References