Two-dimensional spherical indenter (mortar)
A two-dimensional problem with RZ symmetry is used to model the penetration of a spherical indenter into an inelastic base material.
Background
Indentation tests are often used to characterize the behavior of materials at small scales. In this example, we use a spherical indenter driven by a prescribed displacement as a boundary condition. Frictionless contact with a lower-dimensional enforcement (mortar) formulation is employed to drive base material deformation. As a result, a load displacement curve can be obtained.
Creating contact input
Mechanical contact can be enforced on lower-dimensional domains in a weak sense. This type of approach is usually referred to as mortar. To employ this approach, the user can manually build the lower-dimensional subdomains. primary and secondary subdomains are created from mesh sidesets.
[Mesh]
patch_update_strategy = auto
patch_size = 2
partitioner = centroid
centroid_partitioner_direction = y
[simple_mesh]
type = FileMeshGenerator
file = indenter_rz_fine_bigsideset.e
[]
[secondary]
type = LowerDBlockFromSidesetGenerator
sidesets = '4'
new_block_id = '10001'
new_block_name = 'secondary_lower'
input = simple_mesh
[]
[primary]
type = LowerDBlockFromSidesetGenerator
sidesets = '6'
new_block_id = '10000'
new_block_name = 'primary_lower'
input = secondary
[]
# For NodalVariableValue to work with distributed mesh
allow_renumbering = false
Mortar-based mechanical contact can be defined through the contact action. Here, a more manual, user-driven definition is used.
Fig. 1: Spherical indenter.
For frictionless contact in two dimensions, three blocks need to be defined. First, the NormalNodalLMMechanicalContact constraint is used to enforce the Karush-Kuhn-Tucker contact conditions. Then, NormalMortarMechanicalContact enforces contact constaints in an integral or weak sense in both problem dimensions.
[Constraints]
# All constraints below for mechanical contact (Mortar)
[lm]
type = NormalNodalLMMechanicalContact
secondary = '4'
primary = 6
variable = frictionless_normal_lm
primary_variable = disp_x
disp_y = disp_y
use_displaced_mesh = true
tangential_tolerance = 0.01
[]
[x]
type = NormalMortarMechanicalContact
primary_boundary = '6'
secondary_boundary = '4'
primary_subdomain = '10000'
secondary_subdomain = '10001'
variable = frictionless_normal_lm
secondary_variable = disp_x
component = x
use_displaced_mesh = true
compute_lm_residuals = true
[]
[y]
type = NormalMortarMechanicalContact
primary_boundary = '6'
secondary_boundary = '4'
primary_subdomain = '10000'
secondary_subdomain = '10001'
variable = frictionless_normal_lm
secondary_variable = disp_y
component = y
use_displaced_mesh = true
compute_lm_residuals = true
[]
Note that the subdomain blocks had been created in the mesh input using LowerDBlockFromSidesetGenerator.
Mortar enforcement is only available for two-dimensional contact.
Other input
The problem is axisymmetric Compute Axisymmetric RZ Finite Strain and symmetric boundary conditions are used.
Numerical results
The resulting force exerted as material resistance on the indenter may be plotted against the vertical displacement. In this problem, the base material is a monocrystal with body-centered cubic (bcc) unit cell with arbitrary parameters. Platic deformation causes the piling up of the base material's contact surface, as shown in the animation in Fig. 1.
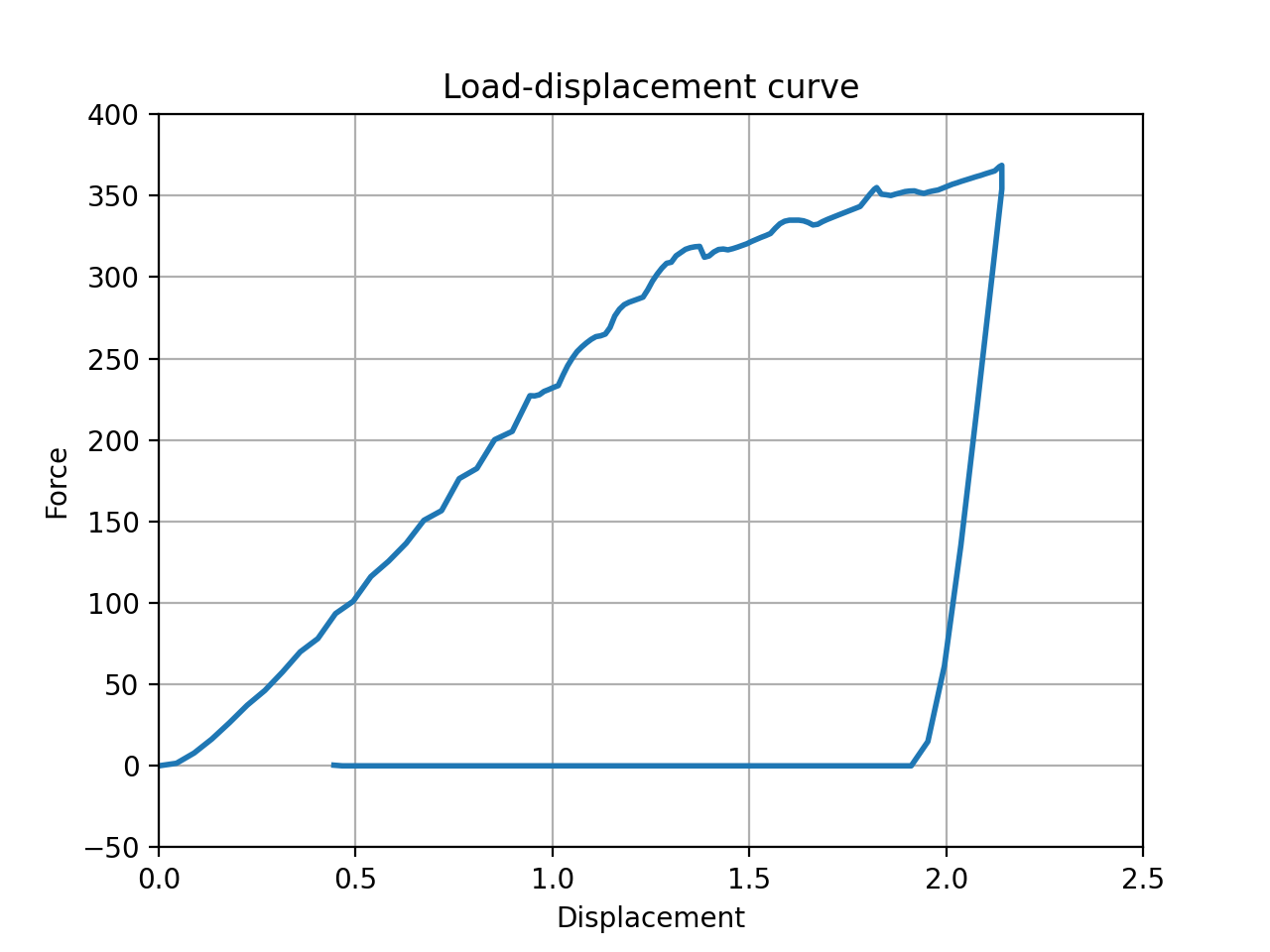
Fig. 2: Load-displacement curve.
Crystal plasticity parameters can be calibrated to match a given experimental nano-indentation test. For this example, the load-displacement curve is shown in Fig. 2.
Notes:
Friction may alter results
Indenter geometry does not reproduce that of a real problem's. Its geometry can be modified in the journal file.
Element distortions may become large