Cold CO2_{2} injection into a reactive, elastic reservoir - a multi-phase THMC problem

Another example describes cold CO2_{2} injection into a warmer, elastic reservoir, and the MOOSE results were benchmarked against analytical solutions. This page extends that example by assuming the reservoir is chemically reactive to demonstrate how to solve thermal-hydraulic-mechanical-chemical (THMC) problems. There are two possibilities for including geochemical reactions in such a model:

  1. use the simple chemical-reactions functionality built into the PorousFlow module, as described in this page;

  2. couple with the Geochemistry module for more sophisticated geochemical modelling functionality

The geochemistry included here is only meant to illustrate how the functionality of the PorousFlow module could be used, and is not intended to represent reactions in any realistic reservoir.

The chemical reaction

Consider a hypothetical, kinetically-controlled, dissolution reaction of the form ∑iνimi⇄M .\sum_{i}\nu_{i}m_{i} \rightleftarrows M \ . In this equation

  • νi\nu_{i} [dimensionless] is the stoichiometric coefficient for basis chemical species ii

  • mim_{i} [mol] is the mole number of the basis chemical species ii

  • MM [mol] is the mol number of mineral that is being dissolved

The general form of the reaction rate for such an equation in PorousFlow is I=SϕrAVexp⁡(ER(1T−1Tref))∣1−(∏iaiνiK)θ∣ηI = S\phi r AV \exp\left(\frac{E}{R}\left(\frac{1}{T} - \frac{1}{T_{\mathrm{ref}}}\right) \right) \left| 1 - \left(\frac{\prod_{i} a_{i}^{\nu_{i}}}{K}\right)^{\theta} \right|^{\eta} where

  • II [L(mineral)/L(solution)/s] is the reaction rate

  • SS [dimensionless] is the saturation of the phase involved in the chemical reaction

  • ϕ\phi [dimensionless] is the porosity

  • rr [mol.m−2^{-2}.s−1^{-1}] is the intrinsic reaction rate

  • AA [m2^{2}/L(solution)] is the specific reactive surface area

  • VV [L(mineral).mol−1^{-1}] is the molar volume of the mineral

  • EE [J.mol−1^{-1}] is the activation energy

  • RR [J.mol−1^{-1}.K−1^{-1}] is the gas constant

  • TT [K] is the temperature

  • TrefT_{\mathrm{ref}} [K] is the reference temperature

  • aia_{i} is the activity of the primary species ii

  • KK is the equilibrium constant for the reaction

  • η\eta and θ\theta are dimensionless exponents

This reaction rate without the SϕS \phi term is computed using a PorousFlowAqueousPreDisChemistry Material. The time-dependent volume-fraction of mineral is computed using a PorousFlowAqueousPreDisMineral Material.

In the case at hand, it is assumed that the hypothetical reaction only occurs when the gas phase is present. It is also assumed that the activities of all the primary chemical species are fixed. Physically, this could be due to the CO2_{2}(g) causing changes in the equilibrium aqueous geochemistry, perhaps by altering the pH, which in turn causes mineral dissolution. To model this, SS can be taken to be the gas saturation and ∏iai=1\prod_{i}a_{i} = 1. It is also assumed the Arrhenius prefactor is irrelevant.

These idealised, hypothetical assumptions lead to a particularly simple reaction rate. In the presence of gas, the reaction rate is controlled by the temperature-dependence of the equilibrium constant, and reads I=SϕrAV∣1−K−1∣ ,I = S\phi r AV \left| 1 - K^{-1} \right| \ , with η=1=θ\eta = 1 = \theta. Assuming that K≠1K\neq 1 and there is some gas present, this reaction will continue until all the mineral has dissolved.

Using rAV=10−6 rAV = 10^{-6}\,s−1^{-1}, the Materials that compute the reaction rate and the resulting Mineral concentration (m3^{3}(mineral)/m3^{3}(porous-material)) are

[predis]
  type = PorousFlowAqueousPreDisChemistry
  num_reactions = 1
  primary_concentrations = 1.0 # fixed activity
  equilibrium_constants_as_log10 = true
  equilibrium_constants = eqm_const
  primary_activity_coefficients = 1.0 # fixed activity
  reactions = 1
  kinetic_rate_constant = 1E-6
  molar_volume = 1.0
  specific_reactive_surface_area = 1.0
  activation_energy = 0.0 # no Arrhenius
[]
[mineral_conc]
  type = PorousFlowAqueousPreDisMineral
  initial_concentrations = 0.1
[]
(modules/porous_flow/examples/thm_example/2D_c.i)

The PorousFlowDictator must be enhanced to include the number of reactions and a specification of the phase number of the phase involved in these reactions.

[dictator]
  type = PorousFlowDictator
  porous_flow_vars = 'temp pwater sgas disp_r'
  number_fluid_phases = 2
  number_fluid_components = 2
  number_aqueous_kinetic = 1
  aqueous_phase_number = 1
[]
(modules/porous_flow/examples/thm_example/2D_c.i)

The phase involved in the reactions is usually the aqueous phase, hence the aqueous in the keywords, but in this case setting aqueous_phase_number = 1 means the SS in the above equation is actually the gas saturation.

The equilibrium constant is assumed to be temperature dependent: log⁡10K=358−T358−294 .\log_{10}K = \frac{358 - T}{358 - 294} \ .

[eqm_const_auxk]
  type = ParsedAux
  variable = eqm_const
  coupled_variables = temp
  expression = '(358 - temp) / (358 - 294)'
[]
(modules/porous_flow/examples/thm_example/2D_c.i)

Impact of dissolution on porosity

In PorousFlow, the porosity can depend on mineral concentration as well as the effective porepressure, strain and temperature. In this case, assume that the porosity only depends on the degree of mineralisation: ϕ=ϕ0−M+Mref .\phi = \phi_{0} - M + M_{\mathrm{ref}} \ . Here:

  • ϕ\phi [dimensionless] is the porosity

  • ϕ0\phi_{0} [dimensionless] is the reference porosity when M=MrefM=M_{\mathrm{ref}}

  • MM [m3^{3}(mineral)/m3^{3}(porous-material)] is the "concentration" of the mineral that is dissolving

  • MrefM_{\mathrm{ref}} [m3^{3}(mineral)/m3^{3}(porous-material)] is the reference concentration

For this example, assume ϕ0=0.2\phi_{0} = 0.2 and Mref=0.1M_{\mathrm{ref}} = 0.1. The relevant Material is:

[porosity_reservoir]
  type = PorousFlowPorosity
  porosity_zero = 0.2
  chemical = true
  reference_chemistry = 0.1
  initial_mineral_concentrations = 0.1
[]
(modules/porous_flow/examples/thm_example/2D_c.i)

Results

Figure 1 shows the results. The porosity changes due to reservoir dissolution are kinetically controlled and temperature-dependent, so do not occur as soon as the gas front reaches any given point. Nevertheless, after gas has occupied a region for some time and cooled it, the mineral will completely dissolve, resulting in a porosity of ϕ=0.3\phi = 0.3.

Comparing with the case that has no chemistry active (Figure 2 from here), it is seen that the CO2_{2} front appears at a similar position, but the gas saturation profile is influenced by the porosity changes.

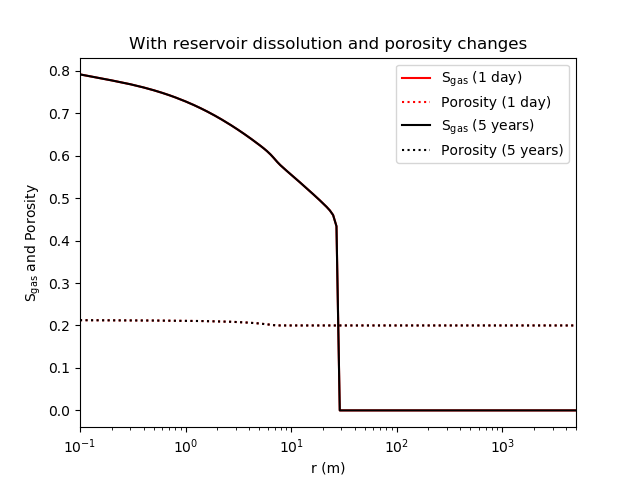
Figure 1: Gas saturation and porosity are impacted through reservoir-rock dissolution.

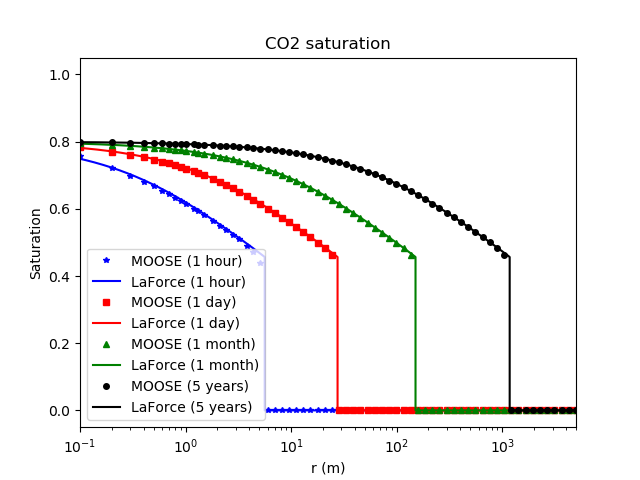
Figure 2: Gas saturation when there is no chemistry active.

References

No citations exist within this document.