Horizon
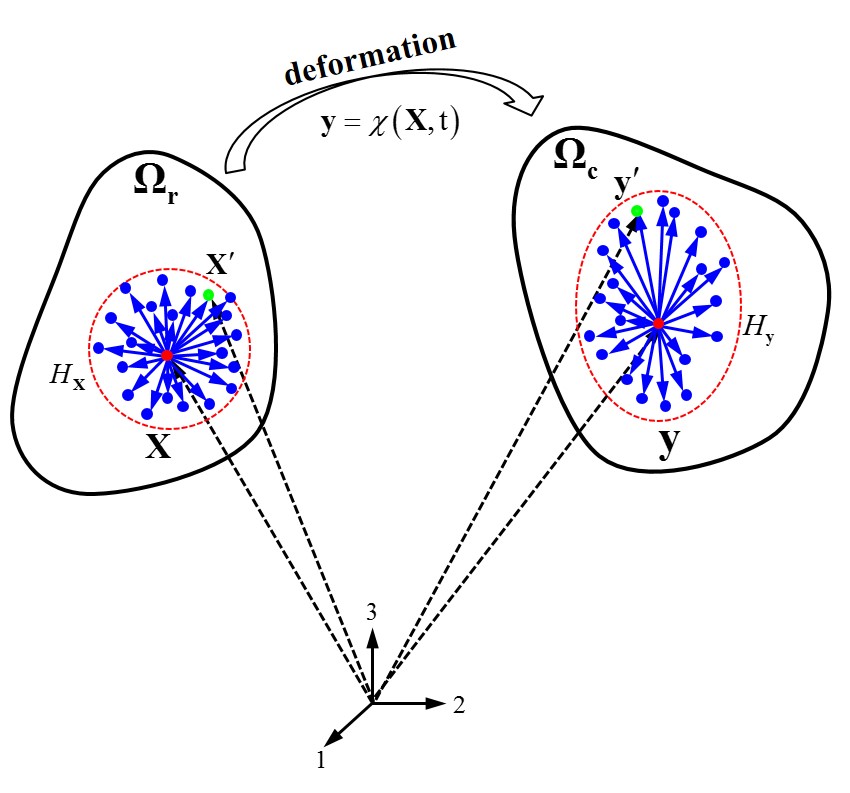
Configuration of a discrete material point in peridynamic theory
In peridynamics theory, material points separated by a finite distance interact directly with each other. This nonlocal interaction region for a material point within the bulk is called the , in short, . Most commonly, the region is taken to be of spherical/circular shape and the radius of the horizon region is referred to as , or simply the horizon.
Horizon is usually denoted using the symbol of , and its size as . Material points can have different horizon size, horizon for material point is denoted as .
More discussion about can be found in (Bobaru and Hu, 2012).
States
Let denote the set of all tensors of order (thus ).
A is a function
Thus, the image of a vector under the state is a tensor of order , written . the set of all states of order is denoted as . Angle brackets are used to indicate the vector on which a state operates.
A state of order 1 is called a . The set of all vector states is denoted as , thus, . Vector states and other higher order states are usually written in uppercase bold font with an underscore, e.g., .
A state of order 0 is called a . The set of all scalar states is denoted as , thus . Scalar states are usually written as lower case, non-bold font with an underscore, e.g., .
More information about can be found in (Silling et al., 2007).
The of two material points in reference configuration is
where and are the position vectors in reference configuration.
The of two material points is
where and are the displacement vectors. The square bracket notation has the similar meaning to standard parentheses, indicating dependence on quantities, but is used for peridynamic states.
The or of two material points in the current configuration is
with
where and are the position vectors in the current configuration.
References
- Florin Bobaru and Wenke Hu.
The meaning, selection, and use of the peridynamic horizon and its relation to crack branching in brittle materials.
International Journal of Fracture, 176(2):215–222, Aug 2012.
URL: https://doi.org/10.1007/s10704-012-9725-z, doi:10.1007/s10704-012-9725-z.[BibTeX]
- S. A. Silling, M. Epton, O. Weckner, J. Xu, and E. Askari.
Peridynamic states and constitutive modeling.
Journal of Elasticity, 88(2):151–184, Aug 2007.
URL: https://doi.org/10.1007/s10659-007-9125-1, doi:10.1007/s10659-007-9125-1.[BibTeX]