Thermal Contact Condition Verification Case

This document describes the two block 1-D verification test for the ThermalContactCondition object. Below is a summary of the test, along with a derivation of the analytic solution used for comparison and the relevant test input file for review.

Summary

A visual summary of the two block verification test domain, as well as relevant boundary and interface conditions is shown below (click to zoom):

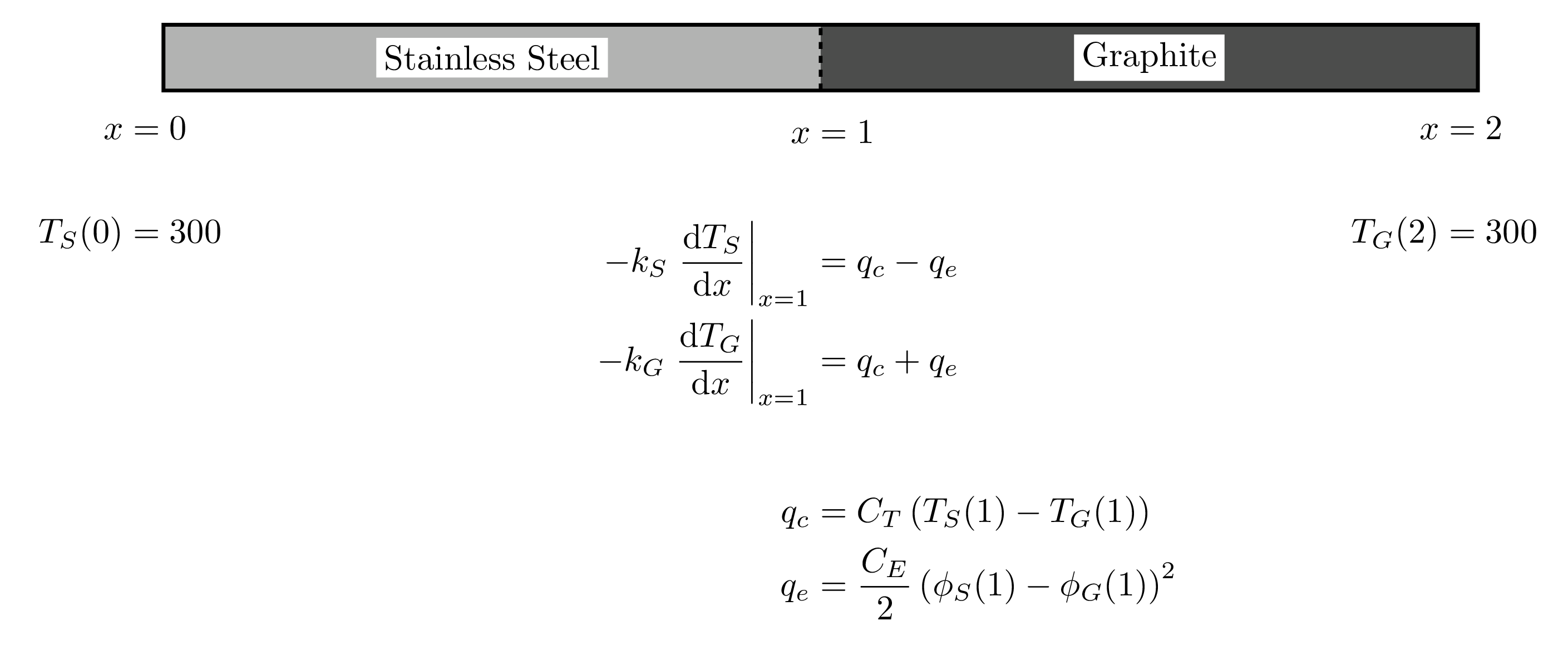
Figure 1: Visual summary of the two block verification test with boundary and interface conditions.

It is important to note that in Figure 1:

$var element = document.getElementById("moose-equation-0e7f661d-9208-4e4c-95cb-a3fd0bf35748");katex.render("k_{i}", element, {displayMode:false,throwOnError:false});$ is the thermal conductivity of material $var element = document.getElementById("moose-equation-50f3bb2e-a841-4e6c-b1e7-6aef8ef6a95b");katex.render("i", element, {displayMode:false,throwOnError:false});$ ,
$var element = document.getElementById("moose-equation-42cca211-94f2-4908-9c69-be6db37a8b33");katex.render("C_E", element, {displayMode:false,throwOnError:false});$ is the electrical contact conductance at the interface,
$var element = document.getElementById("moose-equation-a4d550b9-4e44-40ad-90c2-956ed5b1d49a");katex.render("C_T", element, {displayMode:false,throwOnError:false});$ is the thermal contact conductance at the interface,
$var element = document.getElementById("moose-equation-561e5aeb-aea2-4016-8d41-b7c5ff2b2e92");katex.render("\\phi_i", element, {displayMode:false,throwOnError:false});$ is the electrostatic potential of material $var element = document.getElementById("moose-equation-24bc98fb-0316-49af-9419-3b07baf1410c");katex.render("i", element, {displayMode:false,throwOnError:false});$ , and
$var element = document.getElementById("moose-equation-21d1c303-edcf-4ee5-91ee-3b77becef686");katex.render("T_i", element, {displayMode:false,throwOnError:false});$ is the temperature of material $var element = document.getElementById("moose-equation-2a5394b4-48d3-496f-925f-77e5a4a137e0");katex.render("i", element, {displayMode:false,throwOnError:false});$ .

See the ThermalContactCondition documentation for more information about the particular definition of $var element = document.getElementById("moose-equation-723c644e-58a1-44d7-8467-2de43e5ae5ac");katex.render("C_T", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-7511c4bc-c520-4a9d-b91e-e9e5dbe3b781");katex.render("C_E", element, {displayMode:false,throwOnError:false});$ . In order to simplify for the analytic solution derivation, the scenario was assumed to be steady state in order to remove the time derivative term of the heat conduction equation. The heating source term is electrothermal (or Joule) heating. This leads to

(1)var element = document.getElementById("moose-equation-ba610474-a2fb-4c42-a9ad-f13ac275e229");katex.render("-\\nabla(k_i \\nabla T_i) = \\sigma_{el, i} \\left( \\nabla \\phi_i \\right)^2", element, {displayMode:true,throwOnError:false});

where $var element = document.getElementById("moose-equation-5efdaf46-cc21-4b0d-a1fd-3a30207a5cfd");katex.render("\\sigma_{el, i}", element, {displayMode:false,throwOnError:false});$ is the electrical conductivity of material $var element = document.getElementById("moose-equation-1944634c-4872-4ea5-8a25-ce5274ce82ab");katex.render("i", element, {displayMode:false,throwOnError:false});$ . Material properties being used in this case are constants within each block, and they are summarized below in Table 1. All material properties were evaluated at a temperature of ~300 K.

Table 1: Material properties for the two block thermal contact verification case.

Property (unit)	Value	Source
Stainless Steel (304) Electrical Conductivity (S / m)	$var element = document.getElementById("moose-equation-1ad9d371-a9d9-4c46-b6d6-3ce24fcbf2db");katex.render("1.41867 \\times 10^6", element, {displayMode:false,throwOnError:false});$	(Cincotti et al., 2007)
Stainless Steel (304) Thermal Conductivity (W / (m K))	$var element = document.getElementById("moose-equation-c3ed6de9-48b3-401d-af05-26e15888158a");katex.render("15", element, {displayMode:false,throwOnError:false});$	(Cincotti et al., 2007)
Stainless Steel (304) Hardness (Pa)	$var element = document.getElementById("moose-equation-93735c82-ee8e-48c2-a0ef-70babd5a65a2");katex.render("1.92 \\times 10^9", element, {displayMode:false,throwOnError:false});$	(Cincotti et al., 2007)
Graphite (AT 101) Electrical Conductivity (S / m)	$var element = document.getElementById("moose-equation-421a4335-ef36-40dc-a061-46c3963e745b");katex.render("73069.2", element, {displayMode:false,throwOnError:false});$	(Cincotti et al., 2007)
Graphite (AT 101) Thermal Conductivity (W / (m K))	$var element = document.getElementById("moose-equation-2a13bb31-d592-41eb-8af4-c25e9a3f9e9f");katex.render("100", element, {displayMode:false,throwOnError:false});$	(Cincotti et al., 2007)
Graphite (AT 101) Hardness (Pa)	$var element = document.getElementById("moose-equation-c2aab362-d50a-4432-8232-23d042f434a7");katex.render("3.5 \\times 10^9", element, {displayMode:false,throwOnError:false});$	(Cincotti et al., 2007)

The hardness values shown in Table 1 are used in the ThermalContactCondition object as a harmonic mean of the two values. For reference, the harmonic mean calculation for two values, $var element = document.getElementById("moose-equation-0f574b45-5128-4d84-b68b-2e252ccd778f");katex.render("V_a", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-02a2c262-c0b5-4962-83f4-94c02f24dc70");katex.render("V_b", element, {displayMode:false,throwOnError:false});$ , is given by

var element = document.getElementById("moose-equation-a8027cfb-5ef7-4715-8dc9-9744d21c9dcf");katex.render("V_{Harm} = \\frac{2 V_a V_b}{V_a + V_b}", element, {displayMode:true,throwOnError:false});

The harmonic mean of hardness for stainless steel and graphite was calculated and set to be $var element = document.getElementById("moose-equation-472a3c0e-c731-4387-a030-b6e686dca3a3");katex.render("2.4797 \\times 10^9", element, {displayMode:false,throwOnError:false});$ Pa. Harmonic mean values for the conductivities of stainless steel and graphite were also calculated in this way. Applied mechanical pressure was set to be $var element = document.getElementById("moose-equation-b7de4a2d-58d9-4b78-bd3a-032b1c19ed71");katex.render("3000", element, {displayMode:false,throwOnError:false});$ $var element = document.getElementById("moose-equation-5c31e874-96fd-4e8f-8a34-03bda27088f9");katex.render("kN/m^2", element, {displayMode:false,throwOnError:false});$ . The mean hardness, mean conductivities, and applied mechanical pressure are all used to determine $var element = document.getElementById("moose-equation-7fda26a5-4752-487d-9bb5-9c31061c279f");katex.render("C_E", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-2987c33b-7138-4c15-b827-97ca86ed2d0d");katex.render("C_T", element, {displayMode:false,throwOnError:false});$ (see the ThermalContactCondition documentation, (Cincotti et al., 2007), and (Madhusudana, 1996) for more information). The resulting calculated contact conductances were hard-coded in the input file shown near the bottom of this page, and are summarized below in Table 2.

Table 2: Thermal and electrical conductance values used in the thermal contact verification input file.

Conductance (units)	Value
$var element = document.getElementById("moose-equation-357400d5-d6a0-4f38-9977-625519c78e60");katex.render("C_E", element, {displayMode:false,throwOnError:false});$ ( $var element = document.getElementById("moose-equation-7fabf60a-4c98-4186-8a73-7c092e036e15");katex.render("\\Omega^{-1} m^{-2}", element, {displayMode:false,throwOnError:false});$ )	75524.0
$var element = document.getElementById("moose-equation-8b88fbce-4c7c-4c5c-9537-319a4749d6aa");katex.render("C_T", element, {displayMode:false,throwOnError:false});$ ( $var element = document.getElementById("moose-equation-77dd51fb-675e-4b13-87c4-721cd4f83811");katex.render("W m^{-2} K^{-1}", element, {displayMode:false,throwOnError:false});$ )	0.242

Potential Function

The electrostatic potential function used in this test was determined based on the following scenario

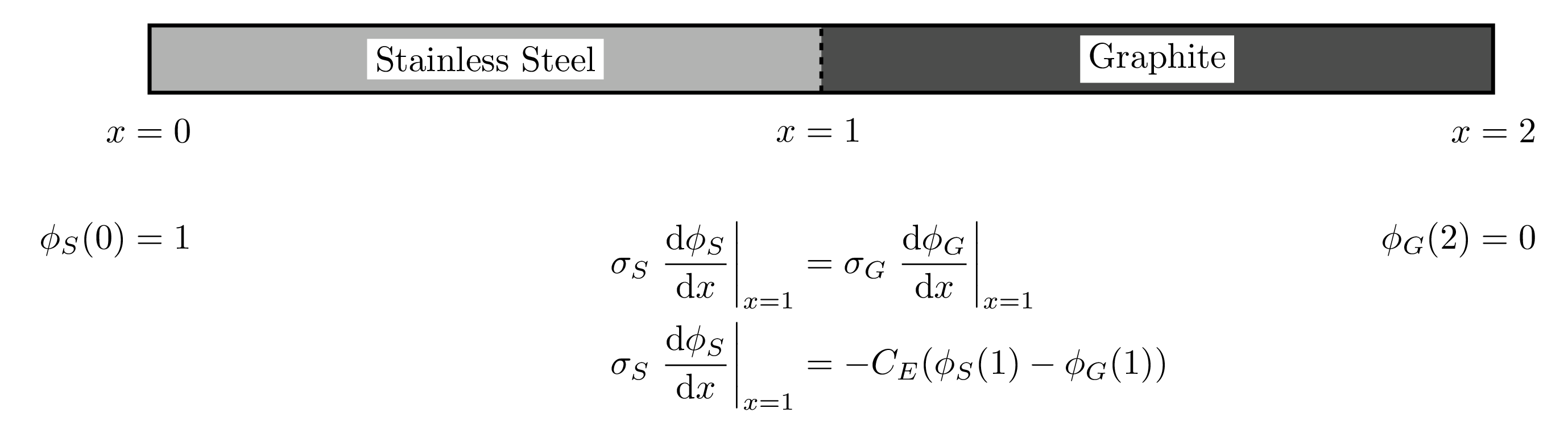
Figure 2: Visual summary of the two block electrostatic verification test with boundary and interface conditions.

where the interface condition above is the ElectrostaticContactCondition. Solving for $var element = document.getElementById("moose-equation-b1795e52-c7df-46a8-be20-c4907c6fe2bd");katex.render("\\phi_i", element, {displayMode:false,throwOnError:false});$ in each domain (using the same material properties and parameters outlined for this verification test) results in

$var element = document.getElementById("moose-equation-a5046c6f-cbab-4797-a460-6b87a16fd97c");katex.render("\\begin{aligned} \\phi_S (x) &= \\frac{-C_E \\sigma_G}{\\sigma_G \\sigma_S + C_E \\sigma_G + C_E \\sigma_S} x + 1 \\\\ \\phi_G (x) &= \\frac{-C_E \\sigma_S}{\\sigma_G \\sigma_S + C_E \\sigma_G + C_E \\sigma_S} (x - 2) \\end{aligned}", element, {displayMode:true,throwOnError:false});$

This result was implemented in source code in both ThermalContactTemperatureTestFunc (for use in the final analytic result presented below) and in ThermalContactPotentialTestFunc (for use in the input file as the value of an auxiliary coupled variable). Both of these can be found in malamute/test/src.

Analytic Solution Derivation

In 1-D, Eq. (1) becomes

(2)var element = document.getElementById("moose-equation-a55ff23b-b89d-41d7-9835-443cc6b3619f");katex.render("-k_i \\frac{\\text{d}^2 T_i}{\\text{d} x^2} = \\sigma_{el, i} \\left( \\frac{\\text{d} \\phi_i}{\\text{d} x} \\right)^2", element, {displayMode:true,throwOnError:false});

since $var element = document.getElementById("moose-equation-9d2acd97-064b-4de6-8b51-1abb9f060764");katex.render("k_i", element, {displayMode:false,throwOnError:false});$ is constant in both domains. Given that the gradient of the potential function used in this example is a linear one (so the right-hand-side is constant), this equation suggests a reasonable guess for a generic solution function for $var element = document.getElementById("moose-equation-543d2b13-88e5-48b1-937e-9db3bde9e213");katex.render("T_i", element, {displayMode:false,throwOnError:false});$ would be

(3)var element = document.getElementById("moose-equation-01e514fc-c093-48d6-8477-6fd7b58f5838");katex.render("T_i (x) = A_i x^2 + B_i x + D_i", element, {displayMode:true,throwOnError:false});

where $var element = document.getElementById("moose-equation-fba08635-a2fc-49ec-92f4-1301887f866f");katex.render("A_i", element, {displayMode:false,throwOnError:false});$ , $var element = document.getElementById("moose-equation-23fe5cb1-211d-4c41-8ac4-f984c18e7920");katex.render("B_i", element, {displayMode:false,throwOnError:false});$ , and $var element = document.getElementById("moose-equation-568538ce-51f3-4cb5-88ef-31d6b9b55172");katex.render("D_i", element, {displayMode:false,throwOnError:false});$ are to-be-determined constant coefficients.

Apply differential equation

Using Eq. (2) and Eq. (3), we can determine $var element = document.getElementById("moose-equation-461773ba-31e2-4d9c-a9fe-ea5e5f56aaee");katex.render("A", element, {displayMode:false,throwOnError:false});$ for both the stainless steel and graphite domains:

Stainless Steel

$var element = document.getElementById("moose-equation-23e7a1d2-a532-475e-a53c-2ed5e50ed685");katex.render("\\begin{aligned} \\frac{\\text{d}^2 T_S}{\\text{d} x^2} &= 2 A_S \\\\ -k_S \\frac{\\text{d}^2 T_S}{\\text{d} x^2} &= -2 k_S A_S \\\\ -2 k_S A_S &= \\sigma_{el, S} \\left( \\frac{\\text{d} \\phi_S}{\\text{d} x} \\right)^2 \\\\ A_S &= -\\frac{\\sigma_{el, S}}{2 k_S} \\left( \\frac{\\text{d} \\phi_S}{\\text{d} x} \\right)^2 \\end{aligned}", element, {displayMode:true,throwOnError:false});$

Graphite

$var element = document.getElementById("moose-equation-34e451b9-6237-45c0-8b4d-4d8684c51938");katex.render("\\begin{aligned} \\frac{\\text{d}^2 T_G}{\\text{d} x^2} &= 2 A_G \\\\ -k_G \\frac{\\text{d}^2 T_G}{\\text{d} x^2} &= -2 k_G A_G \\\\ -2 k_G A_G &= \\sigma_{el, G} \\left( \\frac{\\text{d} \\phi_G}{\\text{d} x} \\right)^2 \\\\ A_G &= -\\frac{\\sigma_{el, G}}{2 k_G} \\left( \\frac{\\text{d} \\phi_G}{\\text{d} x} \\right)^2 \\end{aligned}", element, {displayMode:true,throwOnError:false});$

Apply boundary conditions

Applying the boundary conditions, we can determine $var element = document.getElementById("moose-equation-cf34f816-6851-427f-a806-32a945c4f700");katex.render("D", element, {displayMode:false,throwOnError:false});$ for both the stainless steel and graphite domains (with the caveat that we still need to do a bit more work for $var element = document.getElementById("moose-equation-ce56a5d0-f71c-47cc-87dd-d6ee5125279f");katex.render("D_G", element, {displayMode:false,throwOnError:false});$ ):

Stainless Steel

$var element = document.getElementById("moose-equation-320f1013-33a6-4468-ba99-fbc651907163");katex.render("\\begin{aligned} T_S (0) &= A_S (0)^2 + B_S (0) + D_S \\\\ T_S (0) &= D_S \\\\ D_S &= 300 \\end{aligned}", element, {displayMode:true,throwOnError:false});$

Graphite

$var element = document.getElementById("moose-equation-e3778e0f-ac1e-4888-b20a-9cdee6f38021");katex.render("\\begin{aligned} T_G (2) &= A_G (2)^2 + B_G (2) + D_G \\\\ T_G (2) &= 4 A_G + 2 B_G + D_G \\\\ D_G &= T_G (2) - 4 A_G - 2 B_G \\\\ D_G &= 300 - 4 A_G - 2 B_G \\end{aligned}", element, {displayMode:true,throwOnError:false});$

Apply interface conditions

Now, the interface conditions can be applied from Figure 1. To begin, let's focus on the heat flux condition on the stainless steel side of the interface at $var element = document.getElementById("moose-equation-8c919613-f414-461c-ae9b-f41aa0cc492d");katex.render("x = 1", element, {displayMode:false,throwOnError:false});$ .

var element = document.getElementById("moose-equation-f429be1b-e8f2-4a52-8c00-647cde671587");katex.render("-k_S \\left. \\frac{\\text{d} T_S}{\\text{d} x} \\right|_{x = 1} = q_c - q_e", element, {displayMode:true,throwOnError:false});

Given that $var element = document.getElementById("moose-equation-ef550d8a-8cd8-4d3c-983a-354693803ee0");katex.render("q_c = C_T \\left( T_S (1) - T_G (1) \\right)", element, {displayMode:false,throwOnError:false});$ and $var element = document.getElementById("moose-equation-e85737f7-001b-4dad-9320-a8d2184eaa65");katex.render("T_i", element, {displayMode:false,throwOnError:false});$ has the form in Eq. (3), we have

$var element = document.getElementById("moose-equation-36d52a07-55f8-4cfe-8649-cb45cef8783b");katex.render("\\begin{aligned} -k_S \\left. \\frac{\\text{d} T_S}{\\text{d} x} \\right|_{x = 1} &= C_T \\left( T_S (1) - T_G (1) \\right) - q_e \\\\ &= C_T \\left( A_S (1)^2 + B_S (1) + 300 - \\left[ A_G (1)^2 + B_G (1) + 300 - 4 A_G - 2 B_G \\right] \\right) - q_e \\\\ -k_S \\left( 2 A_S (1) + B_S \\right) &= C_T \\left( A_S + B_S + 300 - A_G - B_G - 300 + 4 A_G + 2 B_G \\right) - q_e \\\\ -2 k_S A_S - k_S B_S &= C_T \\left( A_S + B_S + 3 A_G + B_G \\right) - q_e \\\\ -2 k_S A_S - k_S B_S &= C_T A_S + C_T B_S + 3 C_T A_G + C_T B_G - q_e \\\\ -(k_S + C_T) B_S - C_T B_G &= 2 k_S A_S + C_T A_S + 3 C_T A_G - q_e \\end{aligned}", element, {displayMode:true,throwOnError:false});$

If we let $var element = document.getElementById("moose-equation-d19412a1-4825-4a34-bc5e-827596fed799");katex.render("J_S = 2 k_S A_S + C_T A_S + 3 C_T A_G - q_e", element, {displayMode:false,throwOnError:false});$ , then we have

(4)var element = document.getElementById("moose-equation-4b4d1ab5-a2be-4e54-ad32-11e919fb629d");katex.render("-(k_S + C_T) B_S - C_T B_G = J_S", element, {displayMode:true,throwOnError:false});

Next, we can apply the heat flux condition on the graphite side of the interface at $var element = document.getElementById("moose-equation-394877e7-84e5-4d42-9b76-e6263bee0cd5");katex.render("x = 1", element, {displayMode:false,throwOnError:false});$ .

var element = document.getElementById("moose-equation-dfe914a7-3ff3-4d59-a929-874d6fca65ea");katex.render("-k_G \\left. \\frac{\\text{d} T_G}{\\text{d} x} \\right|_{x = 1} = q_c + q_e", element, {displayMode:true,throwOnError:false});

Again, given $var element = document.getElementById("moose-equation-af4cc4d7-e3a4-4bf7-9a1d-064daacfcec4");katex.render("q_c", element, {displayMode:false,throwOnError:false});$ and Eq. (3), we have

$var element = document.getElementById("moose-equation-844de1f6-8eca-4e67-9304-d8d4cdd283c4");katex.render("\\begin{aligned} -k_G \\left. \\frac{\\text{d} T_G}{\\text{d} x} \\right|_{x = 1} &= C_T \\left( T_S (1) - T_G (1) \\right) + q_e \\\\ &= C_T \\left( A_S (1)^2 + B_S (1) + 300 - \\left[ A_G (1)^2 + B_G (1) + 300 - 4 A_G - 2 B_G \\right] \\right) + q_e \\\\ -k_G \\left( 2 A_G (1) + B_G \\right) &= C_T \\left( A_S + B_S + 300 - A_G - B_G - 300 + 4 A_G + 2 B_G \\right) + q_e \\\\ -2 k_G A_G - k_G B_G &= C_T \\left( A_S + B_S + 3 A_G + B_G \\right) + q_e \\\\ -2 k_G A_G - k_G B_G &= C_T A_S + C_T B_S + 3 C_T A_G + C_T B_G + q_e \\\\ -C_T B_S - (k_G + C_T) B_G &= 2 k_G A_G + C_T A_S + 3 C_T A_G + q_e \\end{aligned}", element, {displayMode:true,throwOnError:false});$

If we let $var element = document.getElementById("moose-equation-2a7c4f91-bf31-47ac-ad6f-fa398215ff49");katex.render("J_G = 2 k_G A_G + C_T A_S + 3 C_T A_G + q_e", element, {displayMode:false,throwOnError:false});$ , then we have

(5)var element = document.getElementById("moose-equation-e5ad2c3d-6783-4ab7-9a18-4727df76dbf8");katex.render("-C_T B_S - (k_G + C_T) B_G = J_G", element, {displayMode:true,throwOnError:false});

Find the remaining coefficients

Using the Elimination Method, we can combine Eq. (4) and Eq. (5) in order to solve for each remaining unknown coefficient. If Eq. (4) is multiplied through on both sides by $var element = document.getElementById("moose-equation-26485e1e-5bd2-4a0a-a7fb-370bbf3b83a1");katex.render("C_T", element, {displayMode:false,throwOnError:false});$ and Eq. (5) is multiplied through on both sides by $var element = document.getElementById("moose-equation-d93f4534-6602-4144-aa78-7e0c644f796e");katex.render("-(k_S + C_T)", element, {displayMode:false,throwOnError:false});$ , we have

(6)var element = document.getElementById("moose-equation-a429ba4d-7c99-4ba0-853b-ba1a0c70423a");katex.render("-C_T (k_S + C_T) B_S - C_T^2 B_G = C_T J_S", element, {displayMode:true,throwOnError:false});

and

(7)var element = document.getElementById("moose-equation-929d2de9-42d8-4f1d-a03a-086f72d306ac");katex.render("C_T (k_S + C_T) B_S + (k_S + C_T) (k_G + C_T) B_G = -(k_S + C_T) J_G", element, {displayMode:true,throwOnError:false});

Combining Eq. (6) and Eq. (7) together via addition yields

$var element = document.getElementById("moose-equation-22e633c2-1d88-49f5-b729-0455fd502019");katex.render("\\begin{aligned} C_T (k_S + C_T) B_S + (k_S + C_T) (k_G + C_T) B_G - C_T (k_S + C_T) B_S - C_T^2 B_G &= C_T J_S - (k_S + C_T) J_G \\\\ (k_S + C_T) (k_G + C_T) B_G - C_T^2 B_G &= C_T J_S - (k_S + C_T) J_G \\\\ ((k_S + C_T) (k_G + C_T) - C_T^2) B_G &= C_T J_S - (k_S + C_T) J_G \\\\ \\end{aligned}", element, {displayMode:true,throwOnError:false});$

which can then be solved for $var element = document.getElementById("moose-equation-89e6810b-bf1c-4fad-bcea-01840a5c1cc4");katex.render("B_G", element, {displayMode:false,throwOnError:false});$

var element = document.getElementById("moose-equation-b686ae01-2a0c-4765-a17a-d6c075ebf90f");katex.render("B_G = \\frac{C_T J_S - (k_S + C_T) J_G}{(k_S + C_T) (k_G + C_T) - C_T^2}", element, {displayMode:true,throwOnError:false});

Using Eq. (5) and $var element = document.getElementById("moose-equation-28aad15f-5246-4d11-9836-941befab1647");katex.render("B_G", element, {displayMode:false,throwOnError:false});$ , we can now solve for $var element = document.getElementById("moose-equation-cdd0d2dc-0597-4ebd-9230-9fe0bb0b3bc2");katex.render("B_S", element, {displayMode:false,throwOnError:false});$ :

$var element = document.getElementById("moose-equation-8cd4043b-a1c1-4229-98a7-f6a118897511");katex.render("\\begin{aligned} -C_T B_S - (k_G + C_T) \\frac{C_T J_S - (k_S + C_T) J_G}{(k_S + C_T) (k_G + C_T) - C_T^2} &= J_G \\\\ -C_T B_S &= J_G + (k_G + C_T) \\frac{C_T J_S - (k_S + C_T) J_G}{(k_S + C_T) (k_G + C_T) - C_T^2} \\\\ -C_T B_S &= \\frac{(k_S + C_T) (k_G + C_T) J_G - C_T^2 J_G}{(k_S + C_T) (k_G + C_T) - C_T^2} + \\frac{C_T (k_G + C_T) J_S - (k_S + C_T) (k_G + C_T) J_G}{(k_S + C_T) (k_G + C_T) - C_T^2} \\\\ -C_T B_S &= \\frac{(k_S + C_T) (k_G + C_T) J_G - C_T^2 J_G + C_T (k_G + C_T) J_S - (k_S + C_T) (k_G + C_T) J_G}{(k_S + C_T) (k_G + C_T) - C_T^2} \\\\ -C_T B_S &= \\frac{-C_T^2 J_G + C_T (k_G + C_T) J_S}{(k_S + C_T) (k_G + C_T) - C_T^2} \\\\ B_S &= \\frac{C_T J_G - (k_G + C_T) J_S}{(k_S + C_T) (k_G + C_T) - C_T^2} \\\\ \\end{aligned}", element, {displayMode:true,throwOnError:false});$

Summarize

Now our determined coefficients can be combined to form the complete solutions for both stainless steel and graphite. To summarize, the derived analytical solutions for each domain given the boundary and interface conditions described in Figure 1 is

$var element = document.getElementById("moose-equation-56972342-5149-40d5-9f08-ab166d9be0f2");katex.render("\\begin{aligned} T_S (x) &= -\\frac{\\sigma_{el, S}}{2 k_S} \\left( \\frac{\\text{d} \\phi_S}{\\text{d} x} \\right)^2 x^2 + \\frac{C_T J_G - (k_G + C_T) J_S}{(k_S + C_T) (k_G + C_T) - C_T^2} x + 300 \\\\ T_G (x) &= -\\frac{\\sigma_{el, G}}{2 k_G} \\left( \\frac{\\text{d} \\phi_G}{\\text{d} x} \\right)^2 (x^2 - 4) + \\frac{C_T J_S - (k_S + C_T) J_G}{(k_S + C_T) (k_G + C_T) - C_T^2} (x - 2) + 300 \\end{aligned}", element, {displayMode:true,throwOnError:false});$

where

$var element = document.getElementById("moose-equation-f8749a95-bf9b-4038-9a16-b754bfcef62c");katex.render("\\begin{aligned} J_S &= -(2 k_S + C_T) \\frac{\\sigma_{el, S}}{2 k_S} \\left( \\frac{\\text{d} \\phi_S}{\\text{d} x} \\right)^2 - 3 C_T \\frac{\\sigma_{el, G}}{2 k_G} \\left( \\frac{\\text{d} \\phi_G}{\\text{d} x} \\right)^2 - q_e \\\\ J_G &= -(2 k_G + 3 C_T) \\frac{\\sigma_{el, G}}{2 k_G} \\left( \\frac{\\text{d} \\phi_G}{\\text{d} x} \\right)^2 - C_T \\frac{\\sigma_{el, S}}{2 k_S} \\left( \\frac{\\text{d} \\phi_S}{\\text{d} x} \\right)^2 + q_e \\\\ q_e &= \\frac{C_E}{2} \\left( \\phi_S (1) - \\phi_G(1) \\right)^2 \\end{aligned}", element, {displayMode:true,throwOnError:false});$

This is implemented in source code as ThermalContactTemperatureTestFunc. It can be found in the test source code directory located at malamute/test/src.

Input File

[Mesh<<<{"href": "../syntax/Mesh/index.html"}>>>]
  [line]
    type = GeneratedMeshGenerator<<<{"description": "Create a line, square, or cube mesh with uniformly spaced or biased elements.", "href": "../source/meshgenerators/GeneratedMeshGenerator.html"}>>>
    xmax<<<{"description": "Upper X Coordinate of the generated mesh"}>>> = 2
    dim<<<{"description": "The dimension of the mesh to be generated"}>>> = 1
    nx<<<{"description": "Number of elements in the X direction"}>>> = 400
  []
  [split]
    type = SubdomainBoundingBoxGenerator<<<{"description": "Changes the subdomain ID of elements either (XOR) inside or outside the specified box to the specified ID.", "href": "../source/meshgenerators/SubdomainBoundingBoxGenerator.html"}>>>
    bottom_left<<<{"description": "The bottom left point (in x,y,z with spaces in-between)."}>>> = '0 0 0'
    top_right<<<{"description": "The bottom left point (in x,y,z with spaces in-between)."}>>> = '1 0 0'
    block_id<<<{"description": "Subdomain id to set for inside/outside the bounding box"}>>> = 1
    block_name<<<{"description": "Subdomain name to set for inside/outside the bounding box (optional)"}>>> = 'stainless_steel'
    input<<<{"description": "The mesh we want to modify"}>>> = line
  []
  [rename_right]
    type = RenameBlockGenerator<<<{"description": "Changes the block IDs and/or block names for a given set of blocks defined by either block ID or block name. The changes are independent of ordering. The merging of blocks is supported.", "href": "../source/meshgenerators/RenameBlockGenerator.html"}>>>
    old_block<<<{"description": "Elements with these block ID(s)/name(s) will be given the new block information specified in 'new_block'"}>>> = 0
    new_block<<<{"description": "The new block ID(s)/name(s) to be given by the elements defined in 'old_block'."}>>> = 'graphite'
    input<<<{"description": "The mesh we want to modify"}>>> = split
  []
  [interface]
    type = SideSetsBetweenSubdomainsGenerator<<<{"description": "MeshGenerator that creates a sideset composed of the nodes located between two or more subdomains.", "href": "../source/meshgenerators/SideSetsBetweenSubdomainsGenerator.html"}>>>
    input<<<{"description": "The mesh we want to modify"}>>> = rename_right
    primary_block<<<{"description": "The primary set of blocks for which to draw a sideset between"}>>> = 'stainless_steel'
    paired_block<<<{"description": "The paired set of blocks for which to draw a sideset between"}>>> = 'graphite'
    new_boundary<<<{"description": "The list of boundary names to create on the supplied subdomain"}>>> = 'ssg_interface'
  []
[]

[Variables<<<{"href": "../syntax/Variables/index.html"}>>>]
  [temperature_graphite]
    initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 300.0
    block = graphite
  []
  [temperature_stainless_steel]
    initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 300.0
    block = stainless_steel
  []
[]

[AuxVariables<<<{"href": "../syntax/AuxVariables/index.html"}>>>]
  [analytic_potential_graphite]
    block = graphite
  []
  [analytic_potential_stainless_steel]
    block = stainless_steel
  []
  [analytic_temperature_graphite]
    block = graphite
  []
  [analytic_temperature_stainless_steel]
    block = stainless_steel
  []
[]

[Kernels<<<{"href": "../syntax/Kernels/index.html"}>>>]
  [HeatDiff_graphite]
    type = ADHeatConduction<<<{"description": "Same as `Diffusion` in terms of physics/residual, but the Jacobian is computed using forward automatic differentiation", "href": "../source/kernels/ADHeatConduction.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temperature_graphite
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = graphite
  []
  [HeatSource_graphite]
    type = ADJouleHeatingSource<<<{"description": "Calculates the heat source term corresponding to electrostatic or electromagnetic Joule heating, with Jacobian contributions calculated using the automatic differentiation system.", "href": "../source/kernels/ADJouleHeatingSource.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temperature_graphite
    elec<<<{"description": "Electrostatic potential for joule heating."}>>> = analytic_potential_graphite
    electrical_conductivity<<<{"description": "Material property providing electrical conductivity of the material."}>>> = electrical_conductivity
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = graphite
  []

  [HeatDiff_stainless_steel]
    type = ADHeatConduction<<<{"description": "Same as `Diffusion` in terms of physics/residual, but the Jacobian is computed using forward automatic differentiation", "href": "../source/kernels/ADHeatConduction.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temperature_stainless_steel
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = stainless_steel
  []
  [HeatSource_stainless_steel]
    type = ADJouleHeatingSource<<<{"description": "Calculates the heat source term corresponding to electrostatic or electromagnetic Joule heating, with Jacobian contributions calculated using the automatic differentiation system.", "href": "../source/kernels/ADJouleHeatingSource.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temperature_stainless_steel
    elec<<<{"description": "Electrostatic potential for joule heating."}>>> = analytic_potential_stainless_steel
    electrical_conductivity<<<{"description": "Material property providing electrical conductivity of the material."}>>> = electrical_conductivity
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = stainless_steel
  []
[]

[AuxKernels<<<{"href": "../syntax/AuxKernels/index.html"}>>>]
  [analytic_potential_function_aux_stainless_steel]
    type = FunctionAux<<<{"description": "Auxiliary Kernel that creates and updates a field variable by sampling a function through space and time.", "href": "../source/auxkernels/FunctionAux.html"}>>>
    function<<<{"description": "The function to use as the value"}>>> = potential_fxn_stainless_steel
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = analytic_potential_stainless_steel
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = stainless_steel
  []
  [analytic_potential_function_aux_graphite]
    type = FunctionAux<<<{"description": "Auxiliary Kernel that creates and updates a field variable by sampling a function through space and time.", "href": "../source/auxkernels/FunctionAux.html"}>>>
    function<<<{"description": "The function to use as the value"}>>> = potential_fxn_graphite
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = analytic_potential_graphite
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = graphite
  []
  [analytic_temperature_function_aux_stainless_steel]
    type = FunctionAux<<<{"description": "Auxiliary Kernel that creates and updates a field variable by sampling a function through space and time.", "href": "../source/auxkernels/FunctionAux.html"}>>>
    function<<<{"description": "The function to use as the value"}>>> = temperature_fxn_stainless_steel
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = analytic_temperature_stainless_steel
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = stainless_steel
  []
  [analytic_temperature_function_aux_graphite]
    type = FunctionAux<<<{"description": "Auxiliary Kernel that creates and updates a field variable by sampling a function through space and time.", "href": "../source/auxkernels/FunctionAux.html"}>>>
    function<<<{"description": "The function to use as the value"}>>> = temperature_fxn_graphite
    variable<<<{"description": "The name of the variable that this object applies to"}>>> = analytic_temperature_graphite
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = graphite
  []
[]

[BCs<<<{"href": "../syntax/BCs/index.html"}>>>]
  [thermal_left]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temperature_stainless_steel
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
    value<<<{"description": "Value of the BC"}>>> = 300
  []
  [thermal_right]
    type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../source/bcs/DirichletBC.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temperature_graphite
    boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
    value<<<{"description": "Value of the BC"}>>> = 300
  []
[]

[InterfaceKernels<<<{"href": "../syntax/InterfaceKernels/index.html"}>>>]
  [thermal_contact_conductance]
    type = ThermalContactCondition<<<{"description": "Interface condition that describes the thermal contact resistance across a boundary formed between two dissimilar materials (resulting in a temperature discontinuity) under the influence of an electrostatic potential, as described in Cincotti, et al (DOI: 10.1002/aic.11102). Thermal conductivity on each side of the boundary is defined via the material properties system.", "href": "../source/interfacekernels/ThermalContactCondition.html"}>>>
    variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = temperature_stainless_steel
    neighbor_var<<<{"description": "The variable on the other side of the interface."}>>> = temperature_graphite
    primary_potential<<<{"description": "Electrostatic potential on the primary block."}>>> = analytic_potential_stainless_steel
    secondary_potential<<<{"description": "Electrostatic potential on the secondary block."}>>> = analytic_potential_graphite
    primary_thermal_conductivity<<<{"description": "Thermal conductivity on the primary block."}>>> = thermal_conductivity
    secondary_thermal_conductivity<<<{"description": "Thermal conductivity on the secondary block."}>>> = thermal_conductivity
    primary_electrical_conductivity<<<{"description": "Electrical conductivity on the primary block."}>>> = electrical_conductivity
    secondary_electrical_conductivity<<<{"description": "Electrical conductivity on the secondary block."}>>> = electrical_conductivity
    user_electrical_contact_conductance<<<{"description": "User-provided electrical contact conductance coefficient."}>>> = 75524 # at 300K with 3 kN/m^2 applied pressure
    user_thermal_contact_conductance<<<{"description": "User-provided thermal contact conductance coefficient."}>>> = 0.242 # also from Cincotti et al
    boundary<<<{"description": "The list of boundaries (ids or names) from the mesh where this object applies"}>>> = ssg_interface
  []
[]

[Materials<<<{"href": "../syntax/Materials/index.html"}>>>]
  #graphite
  [heat_conductor_graphite]
    type = ADGenericConstantMaterial<<<{"description": "Declares material properties based on names and values prescribed by input parameters.", "href": "../source/materials/GenericConstantMaterial.html"}>>>
    prop_names<<<{"description": "The names of the properties this material will have"}>>> = thermal_conductivity
    prop_values<<<{"description": "The values associated with the named properties"}>>> = 100
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = graphite
  []
  [sigma_graphite]
    type = ADGenericConstantMaterial<<<{"description": "Declares material properties based on names and values prescribed by input parameters.", "href": "../source/materials/GenericConstantMaterial.html"}>>>
    prop_names<<<{"description": "The names of the properties this material will have"}>>> = electrical_conductivity
    prop_values<<<{"description": "The values associated with the named properties"}>>> = 73069.2
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = graphite
  []

  #stainless_steel
  [heat_conductor_stainless_steel]
    type = ADGenericConstantMaterial<<<{"description": "Declares material properties based on names and values prescribed by input parameters.", "href": "../source/materials/GenericConstantMaterial.html"}>>>
    prop_names<<<{"description": "The names of the properties this material will have"}>>> = thermal_conductivity
    prop_values<<<{"description": "The values associated with the named properties"}>>> = 15
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = stainless_steel
  []
  [sigma_stainless_steel]
    type = ADGenericConstantMaterial<<<{"description": "Declares material properties based on names and values prescribed by input parameters.", "href": "../source/materials/GenericConstantMaterial.html"}>>>
    prop_names<<<{"description": "The names of the properties this material will have"}>>> = electrical_conductivity
    prop_values<<<{"description": "The values associated with the named properties"}>>> = 1.41867e6
    block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = stainless_steel
  []
[]

[Functions<<<{"href": "../syntax/Functions/index.html"}>>>]
  [potential_fxn_stainless_steel]
    type = ThermalContactPotentialTestFunc
    domain = stainless_steel
  []
  [potential_fxn_graphite]
    type = ThermalContactPotentialTestFunc
    domain = graphite
  []
  [temperature_fxn_stainless_steel]
    type = ThermalContactTemperatureTestFunc
    domain = stainless_steel
  []
  [temperature_fxn_graphite]
    type = ThermalContactTemperatureTestFunc
    domain = graphite
  []
[]

[Preconditioning<<<{"href": "../syntax/Preconditioning/index.html"}>>>]
  [SMP]
    type = SMP<<<{"description": "Single matrix preconditioner (SMP) builds a preconditioner using user defined off-diagonal parts of the Jacobian.", "href": "../source/preconditioners/SingleMatrixPreconditioner.html"}>>>
    full<<<{"description": "Set to true if you want the full set of couplings between variables simply for convenience so you don't have to set every off_diag_row and off_diag_column combination."}>>> = true
  []
[]

[Executioner<<<{"href": "../syntax/Executioner/index.html"}>>>]
  type = Steady
  solve_type = NEWTON
  petsc_options_iname = '-pc_type'
  petsc_options_value = 'lu'
[]

[Outputs<<<{"href": "../syntax/Outputs/index.html"}>>>]
  exodus<<<{"description": "Output the results using the default settings for Exodus output."}>>> = true
  perf_graph<<<{"description": "Enable printing of the performance graph to the screen (Console)"}>>> = true
[]

Results

Results from the input file shown above compared to the analytic function are shown below in Figure 3. Note that the number of points shown in the plot has been down-sampled compared to the solved number of elements for readability.

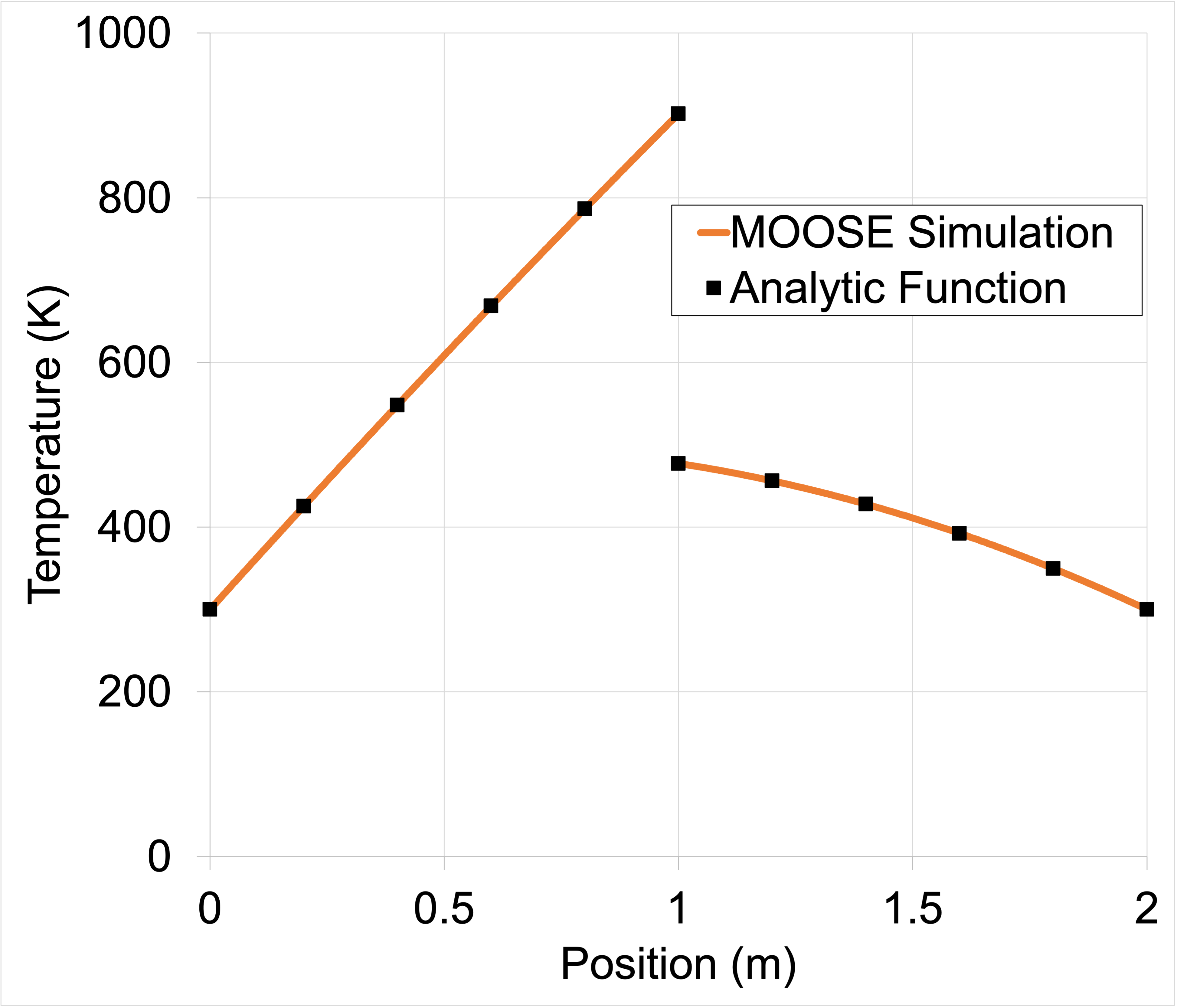
Figure 3: Results of electrothermal contact two block validation case.

References

A. Cincotti, A. M. Locci, R. Orrù, and G. Cao. Modeling of SPS apparatus: temperature, current and strain distribution with no powders. AIChE Journal, 53(3):703–719, 2007. doi:10.1002/aic.11102.

@article{cincotti2007sps,
    author = "Cincotti, A. and Locci, A. M. and Orrù, R. and Cao, G.",
    title = "Modeling of {SPS} apparatus: Temperature, current and strain distribution with no powders",
    journal = "AIChE Journal",
    volume = "53",
    number = "3",
    pages = "703-719",
    doi = "10.1002/aic.11102",
    year = "2007"
}

Chakravarti V. Madhusudana. Thermal Contact Conductance. Springer-Verlag, 1996.

(test/tests/interfacekernels/thermal_conductance/thermal_interface_analytic_solution_two_block.i)

[Mesh]
  [line]
    type = GeneratedMeshGenerator
    xmax = 2
    dim = 1
    nx = 400
  []
  [split]
    type = SubdomainBoundingBoxGenerator
    bottom_left = '0 0 0'
    top_right = '1 0 0'
    block_id = 1
    block_name = 'stainless_steel'
    input = line
  []
  [rename_right]
    type = RenameBlockGenerator
    old_block = 0
    new_block = 'graphite'
    input = split
  []
  [interface]
    type = SideSetsBetweenSubdomainsGenerator
    input = rename_right
    primary_block = 'stainless_steel'
    paired_block = 'graphite'
    new_boundary = 'ssg_interface'
  []
[]

[Variables]
  [temperature_graphite]
    initial_condition = 300.0
    block = graphite
  []
  [temperature_stainless_steel]
    initial_condition = 300.0
    block = stainless_steel
  []
[]

[AuxVariables]
  [analytic_potential_graphite]
    block = graphite
  []
  [analytic_potential_stainless_steel]
    block = stainless_steel
  []
  [analytic_temperature_graphite]
    block = graphite
  []
  [analytic_temperature_stainless_steel]
    block = stainless_steel
  []
[]

[Kernels]
  [HeatDiff_graphite]
    type = ADHeatConduction
    variable = temperature_graphite
    block = graphite
  []
  [HeatSource_graphite]
    type = ADJouleHeatingSource
    variable = temperature_graphite
    elec = analytic_potential_graphite
    electrical_conductivity = electrical_conductivity
    block = graphite
  []

  [HeatDiff_stainless_steel]
    type = ADHeatConduction
    variable = temperature_stainless_steel
    block = stainless_steel
  []
  [HeatSource_stainless_steel]
    type = ADJouleHeatingSource
    variable = temperature_stainless_steel
    elec = analytic_potential_stainless_steel
    electrical_conductivity = electrical_conductivity
    block = stainless_steel
  []
[]

[AuxKernels]
  [analytic_potential_function_aux_stainless_steel]
    type = FunctionAux
    function = potential_fxn_stainless_steel
    variable = analytic_potential_stainless_steel
    block = stainless_steel
  []
  [analytic_potential_function_aux_graphite]
    type = FunctionAux
    function = potential_fxn_graphite
    variable = analytic_potential_graphite
    block = graphite
  []
  [analytic_temperature_function_aux_stainless_steel]
    type = FunctionAux
    function = temperature_fxn_stainless_steel
    variable = analytic_temperature_stainless_steel
    block = stainless_steel
  []
  [analytic_temperature_function_aux_graphite]
    type = FunctionAux
    function = temperature_fxn_graphite
    variable = analytic_temperature_graphite
    block = graphite
  []
[]

[BCs]
  [thermal_left]
    type = DirichletBC
    variable = temperature_stainless_steel
    boundary = left
    value = 300
  []
  [thermal_right]
    type = DirichletBC
    variable = temperature_graphite
    boundary = right
    value = 300
  []
[]

[InterfaceKernels]
  [thermal_contact_conductance]
    type = ThermalContactCondition
    variable = temperature_stainless_steel
    neighbor_var = temperature_graphite
    primary_potential = analytic_potential_stainless_steel
    secondary_potential = analytic_potential_graphite
    primary_thermal_conductivity = thermal_conductivity
    secondary_thermal_conductivity = thermal_conductivity
    primary_electrical_conductivity = electrical_conductivity
    secondary_electrical_conductivity = electrical_conductivity
    user_electrical_contact_conductance = 75524 # at 300K with 3 kN/m^2 applied pressure
    user_thermal_contact_conductance = 0.242 # also from Cincotti et al
    boundary = ssg_interface
  []
[]

[Materials]
  #graphite
  [heat_conductor_graphite]
    type = ADGenericConstantMaterial
    prop_names = thermal_conductivity
    prop_values = 100
    block = graphite
  []
  [sigma_graphite]
    type = ADGenericConstantMaterial
    prop_names = electrical_conductivity
    prop_values = 73069.2
    block = graphite
  []

  #stainless_steel
  [heat_conductor_stainless_steel]
    type = ADGenericConstantMaterial
    prop_names = thermal_conductivity
    prop_values = 15
    block = stainless_steel
  []
  [sigma_stainless_steel]
    type = ADGenericConstantMaterial
    prop_names = electrical_conductivity
    prop_values = 1.41867e6
    block = stainless_steel
  []
[]

[Functions]
  [potential_fxn_stainless_steel]
    type = ThermalContactPotentialTestFunc
    domain = stainless_steel
  []
  [potential_fxn_graphite]
    type = ThermalContactPotentialTestFunc
    domain = graphite
  []
  [temperature_fxn_stainless_steel]
    type = ThermalContactTemperatureTestFunc
    domain = stainless_steel
  []
  [temperature_fxn_graphite]
    type = ThermalContactTemperatureTestFunc
    domain = graphite
  []
[]

[Preconditioning]
  [SMP]
    type = SMP
    full = true
  []
[]

[Executioner]
  type = Steady
  solve_type = NEWTON
  petsc_options_iname = '-pc_type'
  petsc_options_value = 'lu'
[]

[Outputs]
  exodus = true
  perf_graph = true
[]

Summary
Analytic Solution Derivation
Input File
Results
References