Biogeochemistry with an arsenate reducer

This follows the example in Section 33.1 of Bethke (2007). Suppose that an arsenate-reducing microbe acts in the presence of lactate to catalyse the reaction (1) Bethke provides some background information. In this situation, thermodynamic factors are the main control of the reaction rate: as the reaction proceeds and products accumulate, the energy liberated by the reaction reduces to the energy needed to synthesize cellular ATP, and the thermodynamic drive reduces to zero.

The standard MOOSE geochemical database contains the information:

    "arsenate_reducer": {
      "species": {
        "Lactate-": -1.0,
        "HAsO4--": -2.0,
        "H2O": -2.0,
        "CO3--": 1.0,
        "CH3COO-": 1.0,
        "As(OH)4-": 2.0
      },
      "charge": 0.0,
      "radius": -1.5,
      "molecular weight": 1,
	"logk": [6.742, 26.75, 49.93, 71.18, 92.42, 109.5, 123.8, 136.1]
    },

This appears in the redox couples section, but it could equally appear in the mineral species section. The main biogeochemistry page discusses this further. If this entry did not appear in the database, it could be manually entered, but the equilibrium constants would have to be derived from those already in the database (or from experimental measurements). This is easily done by using the GeochemicalModelInterrogator:

[GeochemicalModelInterrogator<<<{"href": "../../../syntax/GeochemicalModelInterrogator/index.html"}>>>]
  model_definition<<<{"description": "The name of the GeochemicalModelDefinition user object"}>>> = definition
  swap_into_basis<<<{"description": "Species that should be removed from the model_definition's equilibrium species list and added to the basis"}>>> = 'CO3-- HAsO4-- CH3COO-'
  swap_out_of_basis<<<{"description": "Species that should be removed from the model_definition's basis and be replaced with the swap_into_basis species.  There must be the same number of species in swap_out_of_basis and swap_into_basis.  If this list contains more than one species, the swapping is performed one-by-one, starting with the first pair (swap_out_of_basis[0] and swap_into_basis[0]), then the next pair, etc"}>>> = 'HCO3- H+ O2(aq)'
  temperature<<<{"description": "Equilibrium constants will be computed at this temperature [degC].  This is ignored if interrogation=eqm_temperature."}>>> = 25.0
[]

and the appropriate model definition:

[UserObjects<<<{"href": "../../../syntax/UserObjects/index.html"}>>>]
  [definition]
    type = GeochemicalModelDefinition<<<{"description": "User object that parses a geochemical database file, and only retains information relevant to the current geochemical model", "href": "../../../source/userobjects/GeochemicalModelDefinition.html"}>>>
    database_file<<<{"description": "The name of the geochemical database file"}>>> = "../../../database/moose_geochemdb.json"
    basis_species<<<{"description": "A list of basis components relevant to the aqueous-equilibrium problem. H2O must appear first in this list.  These components must be chosen from the 'basis species' in the database, the sorbing sites (if any) and the decoupled redox states that are in disequilibrium (if any)."}>>> = "H2O Na+ HCO3- O2(aq) H+ As(OH)4-"
    piecewise_linear_interpolation<<<{"description": "If true then use a piecewise-linear interpolation of logK and Debye-Huckel parameters, regardless of the interpolation type specified in the database file.  This can be useful for comparing with results using other geochemistry software"}>>> = true
  []
[]

In this example, the microbe is treated as a kinetic species, and all other species (lactate, etc) are at equilibrium. The main biogeochemistry page discusses this further. Hence, the GeochemicalModelDefinition is:

[UserObjects<<<{"href": "../../../syntax/UserObjects/index.html"}>>>]
  [definition]
    type = GeochemicalModelDefinition<<<{"description": "User object that parses a geochemical database file, and only retains information relevant to the current geochemical model", "href": "../../../source/userobjects/GeochemicalModelDefinition.html"}>>>
    database_file<<<{"description": "The name of the geochemical database file"}>>> = "../../../database/moose_geochemdb.json"
    basis_species<<<{"description": "A list of basis components relevant to the aqueous-equilibrium problem. H2O must appear first in this list.  These components must be chosen from the 'basis species' in the database, the sorbing sites (if any) and the decoupled redox states that are in disequilibrium (if any)."}>>> = "H2O Na+ Cl- HCO3- H+ As(OH)4- Lactate- CH3COO- AsO4---"
    kinetic_redox<<<{"description": "A list alternative oxidation states (eg Fe+++) whose dynamics are governed by a rate law.  These are not in equilibrium with the aqueous solution.  All members of this list must be in the 'redox couples' section of the database file."}>>> = "arsenate_reducer"
    kinetic_rate_descriptions<<<{"description": "A list of GeochemistryKineticRate UserObject names that define the kinetic rates.  If a kinetic species has no rate prescribed to it, its reaction rate will be zero"}>>> = "rate_arsenate_reducer"
  []
[]

The rate of Eq. (1) is assumed to be of the form (2) (this is simpler than Bethke's form, although the results are almost the same) where

• (units: kg) is the mass of solvent water;

• mol.mg.smol.g.day is the intrinsic rate constant, where the mass (grams) in the denominator is the mass of microbe, and the direction is forward (dissolution of acetate only, not the reverse);

• (units: g.kg) is the microbe concentration, where the mass (kg) in the denominator is the mass of solvent water;

• (units: mol.kg) is the molality of HAsO (this is the free concentration, not the bulk composition);

• mol.kg is the half-saturation constant of the acetate;

• is the activity product of Eq. (1);

• is the equilibrium constant of Eq. (1);

• J.mol is an estimate of the energy captured by the microbe for each mole turnover of Eq. (1);

• J.K.mol is the gas constant;

• (units: K) is the temperature.

In this example, microbe mortality is unimportant. For each mole turnover of this reaction, Bethke estimates the microbe mass increases by g.

The arsenate_reducer species has a molar mass of g.mol in the database file. It is unimportant that this is definitely incorrect: it is only important to remember this value when entering numerical values for the kinetic rate, below.

Eq. (2) is implemented using the following GeochemistryKineticRate UserObject:

[UserObjects<<<{"href": "../../../syntax/UserObjects/index.html"}>>>]
  [rate_arsenate_reducer]
    type = GeochemistryKineticRate<<<{"description": "User object that defines a kinetic rate.  Note that more than one rate can be prescribed to a single kinetic_species: the sum the individual rates defines the overall rate.  GeochemistryKineticRate simply specifies the algebraic form for a kinetic rate: to actually use it in a calculation, you must use it in the GeochemicalModelDefinition.  The rate is intrinsic_rate_constant * area_quantity * (optionally, mass of kinetic_species in grams) * kinetic_molality^kinetic_molal_index / (kinetic_molality^kinetic_molal_index + kinetic_half_saturation^kinetic_molal_index)^kinetic_monod_index * (product_over_promoting_species m^promoting_index / (m^promoting_index + promoting_half_saturation^promiting_index)^promoting_monod_index) * |1 - (Q/K)^theta|^eta * exp(activation_energy / R * (1/T0 - 1/T)) * Direction(1 - (Q/K)).  Please see the markdown documentation for examples", "href": "../../../source/userobjects/GeochemistryKineticRate.html"}>>>
    kinetic_species_name<<<{"description": "The name of the kinetic species that will be controlled by this rate"}>>> = "arsenate_reducer"
    intrinsic_rate_constant<<<{"description": "The intrinsic rate constant for the reaction"}>>> = 0.6048 # 7E-9 mol/mg/s = 0.6048 mol/g/day
    promoting_species_names<<<{"description": "Names of any promoting species"}>>> = 'HAsO4--'
    promoting_indices<<<{"description": "Indices of the promoting species"}>>> = '1'
    promoting_monod_indices<<<{"description": "Indices of the monod denominators of the promoting species.  If not given, then the default is 0 for each promoting species, meaning that there is no monod form"}>>> = '1'
    promoting_half_saturation<<<{"description": "Half-saturation constants for the monod expression.  If not given, then the default is 0 for each promoting species"}>>> = 10E-6
    multiply_by_mass<<<{"description": "Whether the rate should be multiplied by the kinetic_species mass (in grams)"}>>> = true
    direction<<<{"description": "Direction of reaction.  Let Q = the activity product of the kinetic reaction, and K = the equilibrium constant of the reaction.  Then direction means the following.  both = dissolution and precipitation are allowed.  (Specifically, if Q < K then dissolution will occur, that is, the kinetic species mass will decrease with time.  If Q > K then precipitation will occur, that is, the kinetic species mass will increase with time.)  dissolution = if Q < K then dissolution will occur, and when Q > K then the rate will be set to zero so that precipitation will be prevented.  precipitation = if Q > K then precipitation will occur, and when Q < K then the rate will be set to zero so that dissolution will be prevented.  raw = the rate will not depend on sgn(1 - (Q/K)), which means dissolution will occur if intrinsic_rate_constant > 0, and precipitation will occur when intrinsic_rate_constant < 0.  death = the rate will not depend on sgn(1 - (Q/K)), which means dissolution will occur if intrinsic_rate_constant > 0, and precipitation will occur when intrinsic_rate_constant < 0, and, in addition, no reactants will be produced or consumed by this kinetic reaction (only the kinetic species mass will change)."}>>> = dissolution
    kinetic_biological_efficiency<<<{"description": "This is used when modelling biologically-catalysed reactions, when the biomass is treated as a kinetic species, and the reactants and reactant-products are in equilibrium in the aqueous solution.  When one mole of reaction is catalysed, the biomass increases by kinetic_biological_efficiency moles"}>>> = 5
    energy_captured<<<{"description": "In biologically-catalysed kinetic reactions, this is the energy captured by the cell, per mol of reaction turnover.  Specifically, for each mole of kinetic reaction, the microbe will produce m moles of ATP via a reaction such as ADP + PO4--- -> ATP + H2O, with free-energy change G (usually around 45 kJ/mol).  Then, energy_captured = m * G.  For non-biologically-catalysed reactions, this should be zero.  The impact of energy_captured is that the reaction's equilibrium constant is K_database * exp(-energy_captured / R / T_in_Kelvin)"}>>> = 125E3
    theta<<<{"description": "Theta parameter, which appears in |1 - (Q/K)^theta|^eta"}>>> = 0.25
    eta<<<{"description": "Eta parameter, which appears in |1 - (Q/K)^theta|^eta"}>>> = 1
  []
[]

Most of the values are self-explanatory. Note:

• multiply_by_mass = true means the rate is multiplied by the mass (in grams) of the arsenate_reducer, as desired

• there is no need to use H2O in the promoting_species because is just the mass of the sulfate_reducer in grams

• kinetic_biological_efficiency = 5 because this is the number of moles of arsenate_reducer that is created for one mole Eq. (1) turnover: recall that its molar mass is g.mol

Results

As seen in Figure 1, the microbe mass initially grows rapidly, along with the total reaction rate, but after about 1.3 days, too many reaction products have accumulated and the thermodynamic drive reduces to zero.

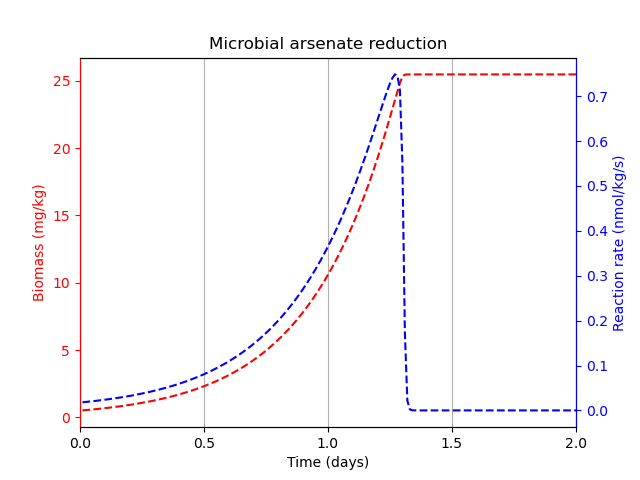
Figure 1: Results of the biologically-catalysed arsenate reduction