HTM-coupled RTES
Problem Statement
The circulation of hot fluid involved in RTES induces mechanical deformation due to pore pressure change and thermal expansion/shrinkage. In this example, we demonstrate the capability of FALCON for simulating hydro-thermo-mechanical (HTM) coupled problems. The Lower Tuscaloosa Sandstone formation with seasonal storage operation, similar to the hydro-thermal coupling example, is simulated in this example. The reader can refer Jin et al. (2022) for details of the problem.
FALCON Input File
Materials
The coupling of mechanical deformation is coded in FALCON via porosity change, see theory for details. A constitutive law is needed to related porosity with permeability for two-coupling. We find both the horizontal and vertical permeability of the Lower Tuscaloosa Sandstone layers can be fitted with porosity via the well-known Kozeny-Carmen relationship, using data from Doughty and Freifeld (2013). Figure 1 shows the fitted curve with Kozeny-Carmen exponent and .
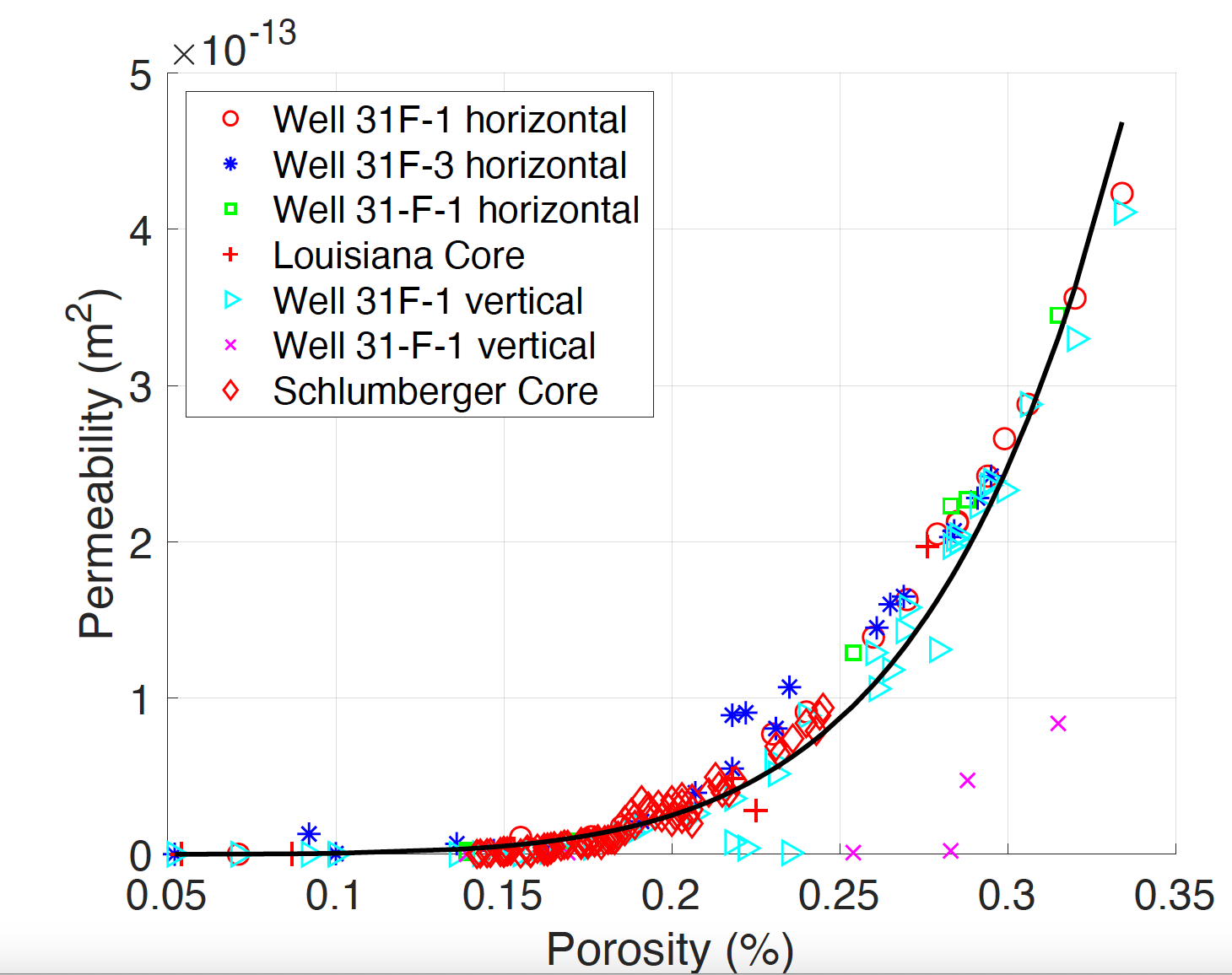
Figure 1: Fitted Kozeny-Carmen relationship between the measured porosity and measured permeability.
The other geomechanical related material parameters were extracted from Kim and Hosseini (2014), Doughty and Freifeld (2013) and listed in the following as:
Table 1: Geomechanical parameter values for HTM coupled problem with FALCON
| Parameter | Value |
|---|---|
| Rock shear modulus | 8.38 GPa |
| Poisson's ratio | 0.225 |
| In-situ vertical stress | 67.3 MPa |
| In-situ horizontal stress | 42.9 MPa |
| Thermal expansion coefficient |
The updated material section of the input file is then as
[Materials<<<{"href": "../syntax/Materials/index.html"}>>>]
[./elasticity_tensor]
type = ComputeIsotropicElasticityTensor<<<{"description": "Compute a constant isotropic elasticity tensor.", "href": "../source/materials/ComputeIsotropicElasticityTensor.html"}>>>
shear_modulus<<<{"description": "The shear modulus of the material."}>>> = 8.38E9
poissons_ratio<<<{"description": "Poisson's ratio for the material."}>>> = 0.225
[../]
[./strain]
type = ComputeSmallStrain<<<{"description": "Compute a small strain.", "href": "../source/materials/ComputeSmallStrain.html"}>>>
eigenstrain_names<<<{"description": "List of eigenstrains to be applied in this strain calculation"}>>> = 'thermal_contribution ini_stress'
[../]
[./ini_strain]
type = ComputeEigenstrainFromInitialStress<<<{"description": "Computes an eigenstrain from an initial stress", "href": "../source/materials/ComputeEigenstrainFromInitialStress.html"}>>>
initial_stress<<<{"description": "A list of functions describing the initial stress. There must be 9 of these, corresponding to the xx, yx, zx, xy, yy, zy, xz, yz, zz components respectively. To compute the eigenstrain correctly, your elasticity tensor should not be time-varying in the first timestep"}>>> = '-${sigmaH_ini_bc} 0 0 0 -${sigmaH_ini_bc} 0 0 0 -${sigmaV_ini_bc}'
eigenstrain_name<<<{"description": "Material property name for the eigenstrain tensor computed by this model. IMPORTANT: The name of this property must also be provided to the strain calculator."}>>> = ini_stress
[../]
[./thermal_contribution]
type = ComputeThermalExpansionEigenstrain<<<{"description": "Computes eigenstrain due to thermal expansion with a constant coefficient", "href": "../source/materials/ComputeThermalExpansionEigenstrain.html"}>>>
temperature<<<{"description": "Coupled temperature"}>>> = temperature
stress_free_temperature<<<{"description": "Reference temperature at which there is no thermal expansion for thermal eigenstrain calculation"}>>> = ${T_ini_bc} # using the intial temperature
thermal_expansion_coeff<<<{"description": "Thermal expansion coefficient"}>>> = 1.0e-5 # this is the linear thermal expansion coefficient
eigenstrain_name<<<{"description": "Material property name for the eigenstrain tensor computed by this model. IMPORTANT: The name of this property must also be provided to the strain calculator."}>>> = thermal_contribution
[../]
[./stress]
type = ComputeLinearElasticStress<<<{"description": "Compute stress using elasticity for small strains", "href": "../source/materials/ComputeLinearElasticStress.html"}>>>
[../]
[./density_aquifer]
type = GenericConstantMaterial<<<{"description": "Declares material properties based on names and values prescribed by input parameters.", "href": "../source/materials/GenericConstantMaterial.html"}>>>
prop_names<<<{"description": "The names of the properties this material will have"}>>> = density
prop_values<<<{"description": "The values associated with the named properties"}>>> = 2600.0
[../]
[./internal_energy_aquifer]
type = PorousFlowMatrixInternalEnergy<<<{"description": "This Material calculates the internal energy of solid rock grains, which is specific_heat_capacity * density * temperature. Kernels multiply this by (1 - porosity) to find the energy density of the porous rock in a rock-fluid system", "href": "../source/materials/PorousFlowMatrixInternalEnergy.html"}>>>
specific_heat_capacity<<<{"description": "Specific heat capacity of the rock grains (J/kg/K)."}>>> = 920.0
density<<<{"description": "Density of the rock grains"}>>> = 2600.0
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = 'inj_well ext_well caps layer_1 layer_2 layer_3 layer_4 layer_5 layer_6 layer_7 layer_8 layer_9 layer_10 layer_11 layer_12 layer_13 layer_14 layer_15 layer_16 layer_17 layer_18 layer_19 layer_20'
[../]
[./thermal_conductivity_aquifer]
type = PorousFlowThermalConductivityIdeal<<<{"description": "This Material calculates rock-fluid combined thermal conductivity by using a weighted sum. Thermal conductivity = dry_thermal_conductivity + S^exponent * (wet_thermal_conductivity - dry_thermal_conductivity), where S is the aqueous saturation", "href": "../source/materials/PorousFlowThermalConductivityIdeal.html"}>>>
dry_thermal_conductivity<<<{"description": "The thermal conductivity of the rock matrix when the aqueous saturation is zero"}>>> = '2.51 0 0 0 2.51 0 0 0 2.51'
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = 'inj_well ext_well caps layer_1 layer_2 layer_3 layer_4 layer_5 layer_6 layer_7 layer_8 layer_9 layer_10 layer_11 layer_12 layer_13 layer_14 layer_15 layer_16 layer_17 layer_18 layer_19 layer_20'
[../]
[./porosity_well]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../source/materials/PorousFlowPorosityConst.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = 'inj_well ext_well'
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.299
[../]
[./permeability_well]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../source/materials/PorousFlowPermeabilityConst.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = 'inj_well ext_well'
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '.2660E-12 0 0 0 .2660E-12 0 0 0 .2330E-09'
[../]
[./porosity_caps]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../source/materials/PorousFlowPorosityConst.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = caps
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.01
[../]
[./permeability_caps]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../source/materials/PorousFlowPermeabilityConst.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = caps
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1E-18 0 0 0 1E-18 0 0 0 1E-18'
[../]
[./porosity_layer_1]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_1
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.143
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc} # using the intial pore presure
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_1]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_1
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.3887'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 9.9856e-12
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_2]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_2
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.158
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_2]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_2
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.3902'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 2.4912e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_3]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_3
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.176
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_3]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_3
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.3920'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 4.5031e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_4]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_4
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.188
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_4]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_4
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.7292'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 5.3904e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_5]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_5
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.166
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_5]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_5
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.7091'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 3.0350e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_6]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_6
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.185
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_6]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_6
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.6723'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 5.4254e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_7]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_7
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.24
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_7]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_7
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.9737'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 6.6083e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_8]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_8
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.26
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_8]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_8
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.9281'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 6.4064e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_9]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_9
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.285
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_9]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_9
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.9434'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 5.7640e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_10]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_10
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.27
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_10]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_10
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.9693'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 6.0536e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_11]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_11
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.23
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_11]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_11
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.7779'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 7.0930e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_12]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_12
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = 0.306
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_12]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_12
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 1'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 5.1702e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_13]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_13
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = .285
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_13]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_13
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.9577'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 5.7912e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_14]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_14
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = .155
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_14]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_14
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.0203'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 8.6194e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_15]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_15
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = .299
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_15]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_15
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.8759'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 5.4697e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_16]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_16
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = .334
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_16]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_16
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.9716'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 4.5139e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_17]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_17
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = .32
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_17]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_17
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.9270'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 4.9059e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_18]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_18
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = .294
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_18]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_18
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.9752'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 5.4915e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_19]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_19
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = .279
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_19]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_19
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.6390'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 6.3038e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[./porosity_layer_20]
type = PorousFlowPorosity<<<{"description": "This Material calculates the porosity PorousFlow simulations", "href": "../source/materials/PorousFlowPorosity.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_20
porosity_zero<<<{"description": "The porosity at zero volumetric strain and reference temperature and reference effective porepressure and reference chemistry. This must be a real number or a constant monomial variable (not a linear lagrange or other type of variable)"}>>> = .071
fluid<<<{"description": "If true, porosity will be a function of effective porepressure"}>>> = true
biot_coefficient<<<{"description": "Biot coefficient"}>>> = 0.8
reference_porepressure<<<{"description": "Reference porepressure (only used if fluid=true)"}>>> = ${pp_ini_bc}
solid_bulk<<<{"description": "Bulk modulus of the drained porous solid skeleton (only used if fluid=true)"}>>> = 1.5E8
mechanical<<<{"description": "If true, porosity will be a function of total volumetric strain"}>>> = true
thermal_expansion_coeff<<<{"description": "Volumetric thermal expansion coefficient of the drained porous solid skeleton (only used if thermal=true)"}>>> = 1.0e-5 # Kim and Hosseini 2013
thermal<<<{"description": "If true, porosity will be a function of temperature"}>>> = true
reference_temperature<<<{"description": "Reference temperature (only used if thermal=true)"}>>> = ${T_ini_bc} # using the intial temperature
[../]
[./permeability_layer_20]
type = PorousFlowPermeabilityKozenyCarman<<<{"description": "This Material calculates the permeability tensor from a form of the Kozeny-Carman equation based on the spatially constant initial permeability and porosity or grain size.", "href": "../source/materials/PorousFlowPermeabilityKozenyCarman.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = layer_20
poroperm_function<<<{"description": "Function relating porosity and permeability. The options are: kozeny_carman_fd2 = f d^2 phi^n/(1-phi)^m (where phi is porosity, f is a scalar constant with typical values 0.01-0.001, and d is grain size). kozeny_carman_phi0 = k0 (1-phi0)^m/phi0^n * phi^n/(1-phi)^m (where phi is porosity, and k0 is the permeability at porosity phi0) kozeny_carman_A = A for directly supplying the permeability multiplying factor."}>>> = kozeny_carman_fd2
k_anisotropy<<<{"description": "A tensor to multiply the calculated scalar permeability, in order to obtain anisotropy if required. Defaults to isotropic permeability if not specified."}>>> = '1 0 0 0 1 0 0 0 0.0370'
f<<<{"description": "The multiplying factor, required for kozeny_carman_fd2"}>>> = 1.2915e-11
d<<<{"description": "The grain diameter, required for kozeny_carman_fd2"}>>> = 1
m<<<{"description": "(1-porosity) exponent"}>>> = 2
n<<<{"description": "Porosity exponent"}>>> = 5
[../]
[]Note for each layer of the simulated reservoir, we calculated the pemeability scale value of as the reference porosity varies layer by layer for the Kozeny Carman relationship. The two wells were treated as two high permeabeable columns with injection and extraction only at the top of the two wells, as explained in the hydro-thermal coupling case.
Geometry and boundary conditions
The geometry and boundary conditions for heat transfer and fluid flow is the same as the HT coupling case. For mechanical boundaries, we applied a fixed displacement in the vertical direction at the bottom surface (z=-24 m) and a fixed horizontal displacement for the two side surfaces (y=-10 m, x=-10 m). To ensure effective stress equilibrium, we applied normal stress boundary conditions of = 42.9 MPa for the two side surfaces (y=10 m, x=10 m) and = 67.3 MPa for the top surface (z=24 m). The input section for boundary condition is
[BCs<<<{"href": "../syntax/BCs/index.html"}>>>]
[./roller_y]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
value<<<{"description": "Value of the BC"}>>> = 0
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = south
[../]
[./total_stress_y]
type = NeumannBC<<<{"description": "Imposes the integrated boundary condition $\\frac{\\partial u}{\\partial n}=h$, where $h$ is a constant, controllable value.", "href": "../source/bcs/NeumannBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
value<<<{"description": "For a Laplacian problem, the value of the gradient dotted with the normals on the boundary."}>>> = -${sigmaH_ini_bc}
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = north
[../]
[./roller_x]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
value<<<{"description": "Value of the BC"}>>> = 0
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = west
[../]
[./total_stress_x]
type = NeumannBC<<<{"description": "Imposes the integrated boundary condition $\\frac{\\partial u}{\\partial n}=h$, where $h$ is a constant, controllable value.", "href": "../source/bcs/NeumannBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
value<<<{"description": "For a Laplacian problem, the value of the gradient dotted with the normals on the boundary."}>>> = -${sigmaH_ini_bc}
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = east
[../]
[./roller_z]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
value<<<{"description": "Value of the BC"}>>> = 0
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = bottom
[../]
[./overburden_total_stress]
type = NeumannBC<<<{"description": "Imposes the integrated boundary condition $\\frac{\\partial u}{\\partial n}=h$, where $h$ is a constant, controllable value.", "href": "../source/bcs/NeumannBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
value<<<{"description": "For a Laplacian problem, the value of the gradient dotted with the normals on the boundary."}>>> = -${sigmaV_ini_bc}
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = top
[../]
[]Instead of constant temperature injection at the injection well, a sinusoid temperature evolution with a peak temperature of 180 in summer and a valley temperature of 126 in winter was used to mimic the variation of hot water from surface solar energy. This was achieved through input file function as
[Functions<<<{"href": "../syntax/Functions/index.html"}>>>]
[./inj_function_summer_winter]
type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../source/functions/MooseParsedFunction.html"}>>>
value<<<{"description": "The user defined function."}>>> = '((t/24/3600/365.25-floor(t/24/3600/365.25))<=0.125) | ((t/24/3600/365.25-floor(t/24/3600/365.25))>0.375 & (t/24/3600/365.25-floor(t/24/3600/365.25)) <=0.625) | ((t/24/3600/365.25-floor(t/24/3600/365.25))>0.875)'
[../]
[./T_inj_function]
type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../source/functions/MooseParsedFunction.html"}>>>
value<<<{"description": "The user defined function."}>>> = '(453.15+399.15)/2+(453.15-399.15)/2*sin((-0.25+t/24/3600/365.25-floor(t/24/3600/365.25))*2*3.1415926535897932)'
[../]
[./rest_function]
type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../source/functions/MooseParsedFunction.html"}>>>
value<<<{"description": "The user defined function."}>>> = '((t/24/3600/365.25-floor(t/24/3600/365.25))>0.125 & (t/24/3600/365.25-floor(t/24/3600/365.25)) <= 0.375) | ((t/24/3600/365.25-floor(t/24/3600/365.25))>0.625 & (t/24/3600/365.25-floor(t/24/3600/365.25)) <=0.875) '
[../]
[./Fiss_Function]
type = PiecewiseLinear<<<{"description": "Linearly interpolates between pairs of x-y data", "href": "../source/functions/PiecewiseLinear.html"}>>>
x<<<{"description": "The abscissa values"}>>> = '0
3944700 11834100 19723500 27612900
35502300 43391700 51281100 59170500
67059900 74949300 82838700 90728100
98617500 106506900 114396300 122285700
130175100 138064500 145953900 153843300
161732700 169622100 177511500 185400900
193290300 201179700 209069100 216958500
224847900 232737300 240626700 248516100
256405500 264294900 272184300 280073700
287963100 295852500 303741900 311631300
315576000'
y<<<{"description": "The ordinate values"}>>> = '0
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
5'
[../]
[]Operation
For the THM simulations, two modes of operation were considered. In the flow-through operation, one well is always the injection well and the other well is always the production well, and fluid always flows through the formation in the same direction from the injection well to the production well. In the push-pull operation, one well acts as the injection/production well and the other well acts as the supply well. During summer, hot water is injected, and during winter, hot water is produced from the same well, thus the flow direction in the reservoir is reversed. For both the operational modes, the supply well always has the same magnitude of flow rate as the injection/production (hot/cold) well, to minimize pressure changes in the reservoir.
The two operation modes were realized by the combination of Functions, Controls and DiracKernals. Take push-pull operation case as an example, its input sections of Control and DiracKernals are
[Functions<<<{"href": "../syntax/Functions/index.html"}>>>]
[./inj_function_summer]
type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../source/functions/MooseParsedFunction.html"}>>>
value<<<{"description": "The user defined function."}>>> = ' ((t/24/3600/365.25-floor(t/24/3600/365.25))>0.375) & ((t/24/3600/365.25-floor(t/24/3600/365.25)) <=0.625) '
[../]
[./inj_function_winter]
type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../source/functions/MooseParsedFunction.html"}>>>
value<<<{"description": "The user defined function."}>>> = '((t/24/3600/365.25-floor(t/24/3600/365.25))<=0.125) | ((t/24/3600/365.25-floor(t/24/3600/365.25))>0.875)'
[../]
[./T_inj_function]
type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../source/functions/MooseParsedFunction.html"}>>>
value<<<{"description": "The user defined function."}>>> = '(453.15+399.15)/2+(453.15-399.15)/2*sin((-0.25+t/24/3600/365.25-floor(t/24/3600/365.25))*2*3.1415926535897932)'
[../]
[./rest_function]
type = ParsedFunction<<<{"description": "Function created by parsing a string", "href": "../source/functions/MooseParsedFunction.html"}>>>
value<<<{"description": "The user defined function."}>>> = '((t/24/3600/365.25-floor(t/24/3600/365.25))>0.125 & (t/24/3600/365.25-floor(t/24/3600/365.25)) <= 0.375) | ((t/24/3600/365.25-floor(t/24/3600/365.25))>0.625 & (t/24/3600/365.25-floor(t/24/3600/365.25)) <=0.875) '
[../]
[./Fiss_Function]
type = PiecewiseLinear<<<{"description": "Linearly interpolates between pairs of x-y data", "href": "../source/functions/PiecewiseLinear.html"}>>>
x<<<{"description": "The abscissa values"}>>> = '0
3944700 11834100 19723500 27612900
35502300 43391700 51281100 59170500
67059900 74949300 82838700 90728100
98617500 106506900 114396300 122285700
130175100 138064500 145953900 153843300
161732700 169622100 177511500 185400900
193290300 201179700 209069100 216958500
224847900 232737300 240626700 248516100
256405500 264294900 272184300 280073700
287963100 295852500 303741900 311631300
315576000'
y<<<{"description": "The ordinate values"}>>> = '0
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
5'
[../]
[]Results
Both the push-pull and flow-through operation cases were simulated for 10 years. Figure 2 and Figure 3 show the predicted pore pressure and temperature evolution at the two wells over 10 years of flow-through and push-pull operation, respectively.
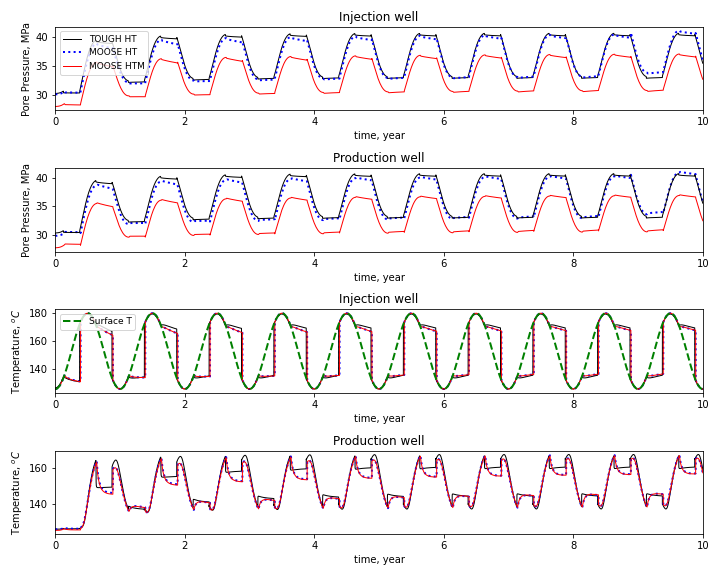
Figure 2: Simulated pore pressure and temperature evolution at the injection and production wells for the continous operation scenario.
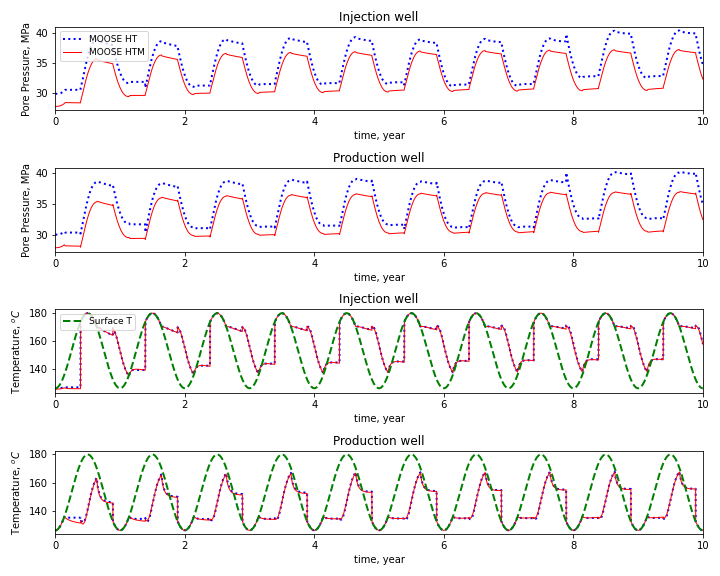
Figure 3: Simulated pore pressure and temperature evolution at the hot and cold wells for the push-pull operation scenario.
References
- Christine Doughty and Barry M Freifeld.
Modeling co2 injection at cranfield, mississippi: investigation of methane and temperature effects.
Greenhouse Gases: Science and Technology, 3(6):475–490, 2013.[BibTeX]
- W. Jin, T. Atkinson, G. Neupane, T. McLing, C. Doughty, Spycher, N., P. Dobson, and R. Smith.
Influence of mechanical deformation and mineral dissolution/precipitation on reservoir thermal energy storage.
In 56th US Rock Mechanics/Geomechanics Symposium. OnePetro, 2022.[BibTeX]
- Seunghee Kim and Seyyed Abolfazl Hosseini.
Above-zone pressure monitoring and geomechanical analyses for a field-scale co2 injection project in cranfield, ms.
Greenhouse Gases: Science and Technology, 4(1):81–98, 2014.[BibTeX]